Thermoresponsive Ionic Liquid/Water Mixtures: From Nanostructuring to Phase Separation
Abstract
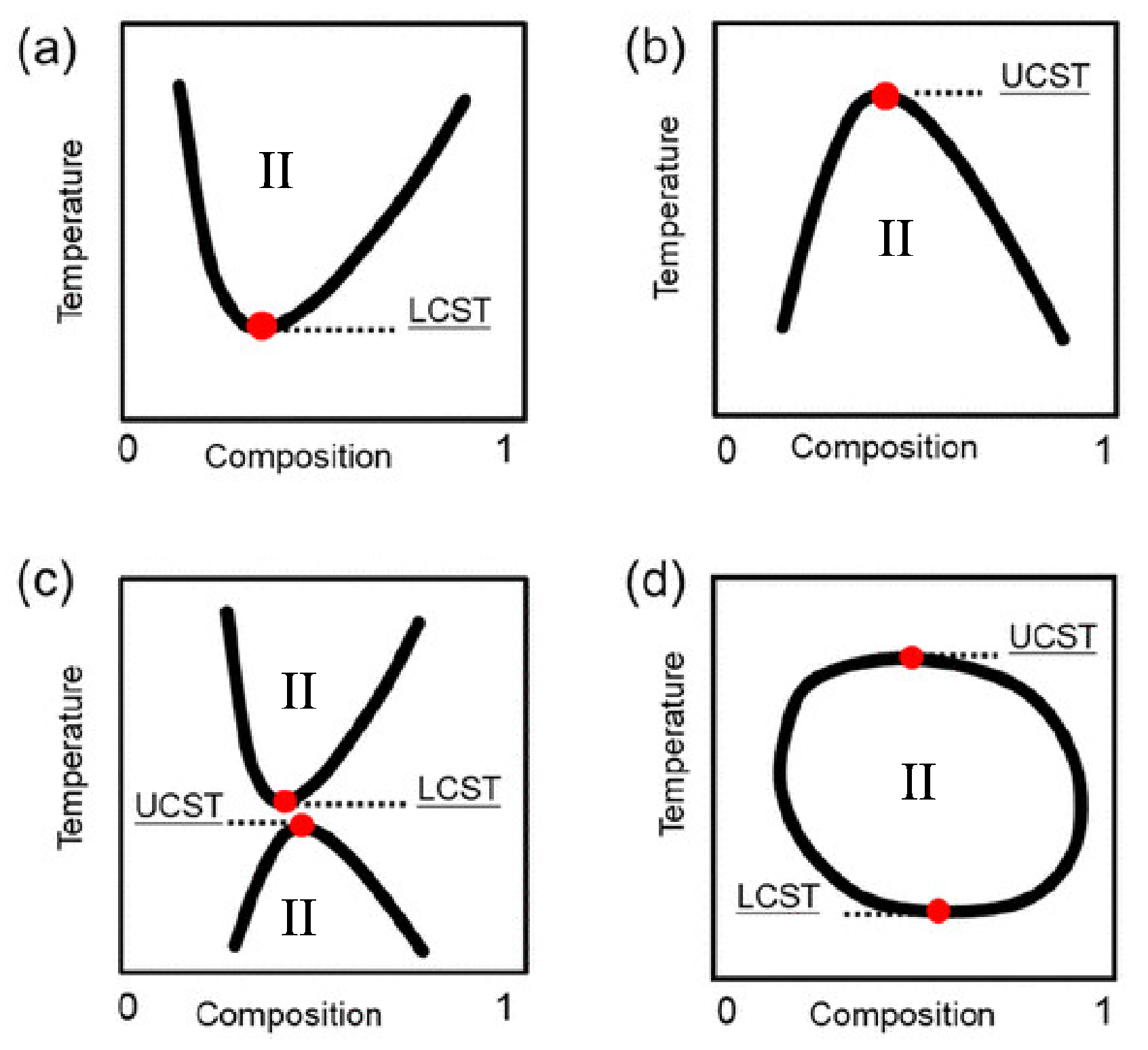
:1. Introduction
2. Theoretical, Computational, and Experimental Methods
3. Overview of Experimental and Computational Studies
3.1. Early Studies
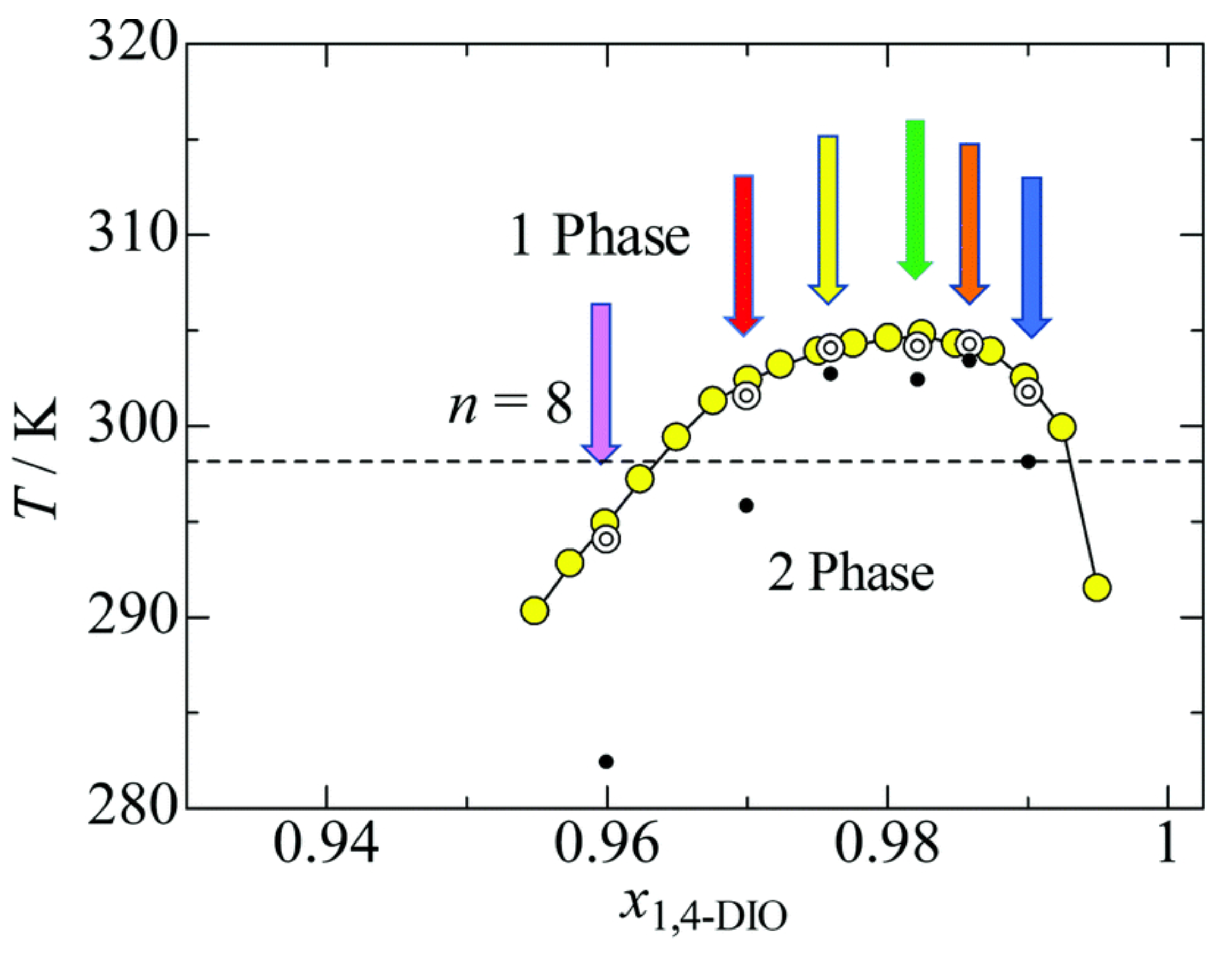
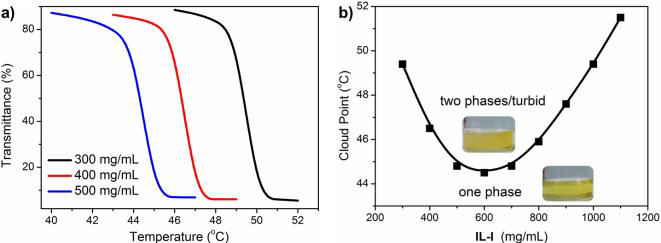
3.2. Focus on IL/Water Thermoresponsive Systems
3.3. Non-Water Solvents and Multicomponent Solutions
3.4. Polymerised ILs
3.5. Reversing the Role of Solute and Solvent
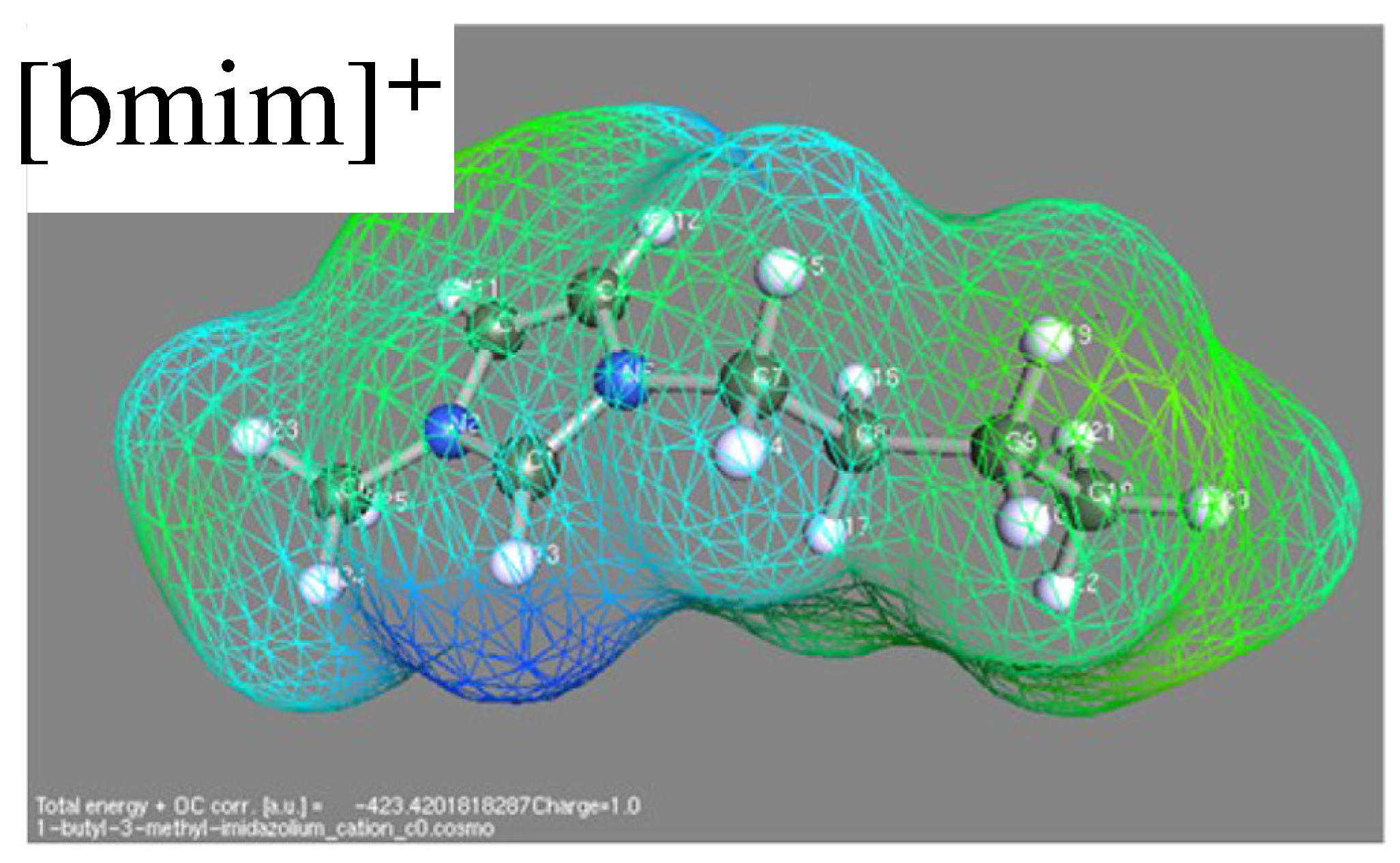
4. The Role of Computational Modeling
5. The Role of IL/Water Nanostructuring
6. Applications
6.1. Extraction and Separation, Catalysis
6.2. Water Desalination and Purification by Forward Osmosis, and Water Harvesting from the Atmosphere
6.3. Heat Storage in Thermoresponsive IL/Water Systems
7. Summary and Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stuart, M.; Huck, W.; Genzer, J.; Müller, M.; Ober, C.; Stamm, M.; Sukhorukov, G.B.; Szleifer, I.; Tsukruk, V.V.; Urban, M.; et al. Emerging applications of stimuli–responsive polymer materials. Nat. Mater. 2010, 9, 101–113. [Google Scholar] [CrossRef] [PubMed]
- Yuan, X.-Q.; Zhang, Y.-Q.; Li, Z.-Y.; Huo, F.; Dong, Y.-H.; He, H.-Y. Stimuli–responsive ionic liquids and the regulation of aggregation structure and phase behavior. Chin. J. Chem. 2021, 39, 729–744. [Google Scholar] [CrossRef]
- Kim, Y.-J.; Matsunaga, Y. Thermo-responsive polymers and their application as smart biomaterials. J. Mater. Chem. B 2017, 5, 4307–4321. [Google Scholar] [CrossRef] [PubMed]
- Hallett, J.P.; Welton, T. Room–temperature ionic liquids: Solvents for synthesis and catalysis. 2. Chem. Rev. 2010, 111, 3508–3576. [Google Scholar] [CrossRef]
- Maia, F.M.; Rodriguez, O.; Macedo, E.A. LLE for (water+ ionic liquid) binary systems using [Cxmim][BF4](x= 6, 8) ionic liquids. Fluid Phase Equilib. 2010, 296, 184–191. [Google Scholar] [CrossRef]
- Tsai, Y.-R.; Lin, S.-T. Prediction and reasoning for the occurrence of lower critical solution temperature in aqueous solution of ionic liquids. Ind. Eng. Chem. Res. 2019, 58, 10064–10072. [Google Scholar] [CrossRef]
- Shukla, S.K.; Pandey, S.; Pandey, S. Applications of ionic liquids in biphasic separation: Aqueous biphasic systems and liquid–liquid equilibria. J. Chromatogr. A 2018, 1559, 44–61. [Google Scholar] [CrossRef]
- Ott, J.B.; Boerio-Goates, J. Applications of thermodynamics to phase equilibria studies of mixtures. Chemical Thermodynamics: Advanced Applications. 2000, pp. 115–159. Available online: https://www.researchgate.net/publication/301189538_Applications_of_Thermodynamics_to_Phase_Equilibria_Studies_of_Mixtures (accessed on 16 January 2022).
- Anderson, E.M.; Greer, S.C. The liquid–liquid phase diagram of sulfur+biphenyl. J. Chem. Phys. 1988, 88, 2666–2671. [Google Scholar] [CrossRef]
- Morrison, G.; Knobler, C.M. Thermal expansion of isobutyric acid+water near the upper critical solution temperature. J. Chem. Phys. 1976, 65, 5507–5517. [Google Scholar] [CrossRef]
- Kohler, F.; Rice, O.K. Coexistence curve of the triethylamine–water system. J. Chem. Phys. 1957, 26, 1614–1618. [Google Scholar] [CrossRef]
- van Konynenburg, P.H.; Scott, R.L. Critical lines and phase equilibria in binary van der Waals mixtures. Philos. Trans. 1980, 298, 495–540. [Google Scholar]
- Schmitz, S.; Ritter, H. Unusual solubility properties of polymethacrylamides as a result of supramolecular interactions with cyclodextrin. Angew. Chem. Int. E 2005, 44, 5658. [Google Scholar] [CrossRef] [PubMed]
- Mukherji, D.; Marques, C.M.; Kremer, K. Smart responsive polymers: Fundamentals and design principles. Annu. Rev. Condens. Matter Phys. 2020, 11, 271–299. [Google Scholar] [CrossRef] [Green Version]
- Mukherji, D.; Marques, C.M.; Kremer, K. Polymer collapse in miscible good solvents is a generic phenomenon driven by preferential adsorption. Nat. Commun. 2014, 5, 4882. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoshimitsu, H.; Kanazawa, A.; Kanaoka, S.; Aoshima, S. Well–defined polymeric ionic liquids with an upper critical solution temperature in water. Macromology 2012, 45, 9427–9434. [Google Scholar] [CrossRef]
- Han, D.; Row, K.H. Recent applications of ionic liquids in separation technology. Molecules 2010, 15, 2405–2426. [Google Scholar] [CrossRef] [Green Version]
- Qiao, Y.; Ma, W.; Theyssen, N.; Chen, C.; Hou, Z. Temperature–responsive ionic liquids: Fundamental behaviors and catalytic applications. Chem. Rev. 2017, 117, 6881–6928. [Google Scholar] [CrossRef]
- Bianga, J.; Künnemann, K.U.; Gaide, T.; Vorholt, A.J.; Seidensticker, T.; Dreimann, J.M.; Vogt, D. Thermomorphyc multiphase systems: Switchable solvent mixtures for the recovery of homogeneous catalysts in batch and flow processes. Chem. Eur. J. 2019, 25, 11586–11608. [Google Scholar] [CrossRef]
- Anisimov, M.A. Crytical Phenomena in Liquids and Liquid Crystals; Gordon and Breach: Philadelphia, PA, USA, 1990. [Google Scholar]
- Anisimov, M.A.; Sengers, J.V. Critical region. In Equations of State for Fluids and Fluid Mixtures; Sengers, J.V., Kayser, R.F., Peters, C.J., White, H.J., Jr., Eds.; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Siggia, E.D.; Halperin, B.I.; Hohenberg, P.C. Renormalization–group treatment of the critical dynamics of the binary–fluid and gas–liquid transitions. Phys. Rev. B 1976, 13, 2110–2123. [Google Scholar] [CrossRef]
- Orkoulas, G.; Panagiotopoulos, A.Z. Free energy and phase equilibria for the restricted primitive model of ionic fluids from Monte Carlo simulations. J. Chem. Phys. 1994, 101, 1452–1459. [Google Scholar] [CrossRef]
- Weingärtner, H.; Kleemeier, M.; Wiegand, S.; Schröer, W. Coulombic and non–Coulombic contributions to the criticality of ionic fluids. An experimental approach. J. Stat. Phys. 1995, 78, 169–196. [Google Scholar] [CrossRef]
- Weingärtner, H. Thermodynamics of aqueous electrolyte solutions with liquid–liquid phase separation. Ber. Bunsenges. Phys. Chem. 1989, 93, 1058–1065. [Google Scholar] [CrossRef]
- Tokuda, H.; Tsuzuki, S.; Susan, M.A.B.H.; Hayamizu, K.; Watanabe, M. How ionic are room–temperature ionic liquids? An indicator of the physicochemical properties. J. Phys. Chem. B 2010, 109, 19593–19600. [Google Scholar] [CrossRef]
- e Silva, F.A.; Pereira, J.F.B.; Kurnia, K.A.; Ventura, S.P.M.; Silva, A.M.S.; Rogers, R.D.; Coutinho, J.A.P.; Freire, M.G. Temperature dependency of aqueous biphasic systems: An alternative approach for exploring the differences between Coulombic–dominated salts and ionic liquids. Chem. Commun. 2017, 53, 7298–7301. [Google Scholar] [CrossRef] [PubMed]
- McNally, J.S.; Wang, X.P.; Hoffmann, C.; Wilson, A.D. Self–assembly of molecular ions via like–charge ion interactions and thorugh–space defined organic domains. Chem. Commun. 2017, 53, 10934–10937. [Google Scholar] [CrossRef] [PubMed]
- Nockemann, P.; Binnemans, K.; Thijs, B.; Parac–Vogt, T.N.; Merz, K.; Anja–Verena Mudring, A.-V.; Menon, P.C.; Rajesh, R.N.; Cordoyiannis, G.; Thoen, J.; et al. Temperature–driven mixing–demixing behavior of binary mixtures of the ionic liquid choline bis(trifluoromethylsulfonyl)imide and water. J. Phys. Chem. B 2009, 113, 1429–1437. [Google Scholar] [CrossRef] [Green Version]
- Cerdeiriña, C.A.; Troncoso, J.; Ramos, C.P.; Romani, L.; Najdanovic–Visak, V.; Guedes, H.J.R.; Esperança, J.M.S.S.; Visak, Z.P.; da Ponte, M.N.; Rebelo, L.P.N. Criticality of the [C4mim][BF4] + water system. ACS Symp. Ser. 2005, 901, 175–186. [Google Scholar]
- Kleemeier, M.; Schröer, W.; Weingärtner, H. Critical behaviour of the ionic system n–propyl–tri–n–butylammonium iodide+water near its upper and lower consolute point. J. Mol. Liq. 1997, 73–74, 501–511. [Google Scholar] [CrossRef]
- Kawano, M.; Sadakane, K.; Iwase, H.; Matsugami, M.; Marekha, B.; Idrissi, A.; Takamura, T. Assessment of the UCST–type liquid–liquid phase separation mechanism of imidazolium–based ionic liquid, [C8mim][TFSI], and 1,4–dioxane by SANS, NMR, IR, and MD simulation. Phys. Chem. Chem. Phys. 2021, 23, 24449–24463. [Google Scholar] [CrossRef]
- Ma, K.-S. Modern Theory of Critical Phenomena; Taylor & Francis: London, UK, 2018. [Google Scholar]
- Kartzmark, E.M. System triethylamine–water: The equilibrium diagram and some physical properties. Can. J. Chem. 1967, 45, 1089–1091. [Google Scholar] [CrossRef]
- Hayes, R.; Warr, G.G.; Atkin, R. Structure and nanostructure in ionic liquids. Chem. Rev. 2015, 115, 6357–6426. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, H.J.; Atkin, R.; Warr, G.G. Nanostructured ionic liquids and their solutions: Recent advances and emerging challenges. Curr. Opin. Green Sustain. Chem. 2016, 12, 27–32. [Google Scholar] [CrossRef]
- Lei, Z.; Chen, B.; Koo, Y.-M.; MacFarlane, D.R. Introduction. Chem. Rev. 2017, 117, 6633–6635. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Greer, A.J.; Jacquemin, J.; Hardacre, C. Industrial applications of ionic liquids. Molecules 2020, 25, 5207. [Google Scholar] [CrossRef] [PubMed]
- Kaur, G.; Kumar, H.; Singla, M. Diverse applications of ionic liquids: A comprehensive review. J. Mol. Liq. 2022, 351, 118556. [Google Scholar] [CrossRef]
- Kurniawan, K.; Kim, S.; Lee, J.-C. Ionic liquids–assisted extraction of metals from electronic waste. In Ionic Liquid–Based Technologies for Environmental Sustainability; Jawaid, M., Ahmad, A., Reddy, A.V.B., Eds.; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Gonçalves, A.R.P.; Paredes, X.; Cristino, A.F.; Santos, F.J.V.; Queirós, C.S.G.P. Ionic liquids—-A review of their toxicity to living organisms. Int. J. Mol. Sci. 2021, 22, 5612. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Y.; Feng, X.; Chen, W.; Wang, X.; Huang, K.-W.; Gnanou, Y.; Lai, Z. Using UCST ionic liquid as a draw solute in forward osmosis to treat high–salinity water. Environ. Sci. Technol. 2016, 50, 1039–1045. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Shen, W.; Wei, J.; Chong, T.H.; Wang, R.; Krantz, W.B.; Fane, A.G.; Hu, X. Energy–efficient desalination by forward osmosis using responsive ionic liquid draw solutes. Environ. Sci. Water Res. Technol. 2015, 1, 341–347. [Google Scholar] [CrossRef] [Green Version]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation, 2nd ed.; Academic Press: San Diego, CA, USA, 2002. [Google Scholar]
- Maia, F.M.; Tsivintzelis, I.; Rodriguez, O.; Macedo, E.A.; Kontogeorgis, G.M. Equation of state modelling of systems with ionic liquids: Literature review and application with the Cubic Plus Association (CPA) model. Fluid Phase Equilib. 2012, 332, 128–143. [Google Scholar] [CrossRef]
- Sun, Y. Modeling Ionic Liquids with ePC–SAFT–Properties and Gas Solubilities; LuleÅ University of Technology: Luleå, Sweden, 2020; ISBN 978-91-7790-598-1. [Google Scholar]
- Yu, M.; Nishiumi, H. Theory of phase separation in mixtures with lower critical solution temperature. J. Phys. Chem. 1992, 96, 842–845. [Google Scholar] [CrossRef]
- Renon, H.; Prausnitz, J.M. Local compositions in thermodynamic excess functions for liquid mixtures. AIChE J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
- Xu, X.; Peng, C.; Liu, H.; Hu, Y. A lattice–fluid model for multi–component ionic–liquid systems. Fluid Phase Equilib. 2011, 302, 260–268. [Google Scholar] [CrossRef]
- Abrams, D.S.; Prausnitz, J.M. Statistical thermodynamics of liquid mixtures: A new expression for the excess Gibbs energy of partly or completely miscible systems. AIChE J. 1975, 21, 116–128. [Google Scholar] [CrossRef]
- Fredenslund, A.; Gmehling, J.; Rasmussen, P. Vapor–Liquid Equilibria Using UNIFAC: A Group Contribution Method; Elsevier Scientific: New York, NY, USA, 1979. [Google Scholar]
- Wilson, G.M. Vapor–liquid equilibrium. XI. A new expression for the excess free energy of mixing. J. Am. Chem. Soc. 1964, 86, 127–130. [Google Scholar] [CrossRef]
- Redlich, O.; Kwong, J.N.S. On the thermodynamics of solutions. V. An equation of state. Fugacities of gaseous solutions. Chem. Rev. 1949, 44, 233–244. [Google Scholar] [CrossRef]
- Soave, G. Equilibrium constants from a modified Redlich–Kwong equation of state. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Peng, D.Y.; Robinson, D.B. A new two–constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Patel, N.C.; Teja, A.S. A new cubic equation of state for fluids and fluid mixtures. Chem. Eng. Sci. 1982, 37, 463–473. [Google Scholar] [CrossRef]
- Gross, J.; Sadowski, G. Perturbed–chain SAFT: An equation of state based on a perturbation theory for chain molecules. Ind. Eng. Chem. Res. 2001, 40, 1244–1260. [Google Scholar] [CrossRef]
- Paduszyński, K.; Domańska, U. Thermodynamic modeling of ionic liquid systems: Development and detailed overview of novel methodology based on the PC–SAFT. J. Phys. Chem. B 2012, 116, 5002–5018. [Google Scholar] [CrossRef]
- Diedenhofen, M.; Klamt, A. COSMO–RS as a tool for property prediction of IL mixtures—-A review. Fluid Phase Equilib. 2010, 294, 31–38. [Google Scholar] [CrossRef] [Green Version]
- Paduszyński, K.; Królikowska, M. Extensive evaluation of performance of the COSMO–RS approach in capturing liquid—-liquid equilibria of binary mixtures of ionic liquids with molecular compounds. Ind. Eng. Chem. Res. 2020, 59, 11851–11863. [Google Scholar] [CrossRef]
- del Olmo, L.; Lage–Estebanez, I.; López, R.; de la Vega, J.M.G. Effect of dielectric constant on estimation of properties of ionic liquids: An analysis of 1–alkyl–3–methylimidazolium bis(trifluoromethylsulfonyl)–imide. RSC Adv. 2015, 5, 72709–72715. [Google Scholar] [CrossRef] [Green Version]
- Balchandani, S.; Ramesh Singh, R. COSMO–RS analysis of CO2 solubility in n–methyldiethanolamine, sulfolane, and 1–butyl–3–methyl–imidazolium acetate activated by 2–methylpiperazine for postcombustion carbon capture. ACS Omega 2021, 6, 747–761. [Google Scholar] [CrossRef] [PubMed]
- Weingärtner, H. The static dielectric permittivity of ionic liquids. J. Mol. Liq. 2014, 192, 185–190. [Google Scholar] [CrossRef]
- Löwen, H. Density functional theory of inhomogeneous classical fluids: Recent developments and new perspectives. J. Phys. Condens. Matter 2002, 14, 11897–11905. [Google Scholar] [CrossRef]
- Gross, J. A density functional theory for vapor–liquid interfaces using the PCP–SAFT equation of state. J. Chem. Phys. 2009, 131, 204705. [Google Scholar] [CrossRef] [Green Version]
- Yusuf, F.; Olayiwola, T.; Afagwu, C. Application of artificial intelligence—-based predictive methods in ionic liquid studies: A review. Fluid Phase Equil. 2021, 531, 112898. [Google Scholar] [CrossRef]
- Goscinny, R.; Uderzo, A. Le tour de Gaule; Hachette: Paris, France, 1999; ISBN 978-2012100053. [Google Scholar]
- Sepehri, B. A review on created QSPR models for predicting ionic liquids properties and their reliability from chemometric point of view. J. Mol. Liq. 2020, 297, 112013. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, M.C.; Zhao, Y.; Zhu, Z.; Xing, H.; Zhang, P.; Zhang, X.; Ding, Y. Machine learning assisted QSPR model for prediction of ionic liquid’s refractive index and viscosity: The effect of representations of ionic liquid and ensemble model development. J. Mol. Liq. 2021, 333, 115970. [Google Scholar] [CrossRef]
- Baskin, I.; Epshtein, A.; Ein-Eli, Y. Benchmarking machine learning methods for modeling physical properties of ionic liquids. J. Mol. Liq. 2022, 351, 118616. [Google Scholar] [CrossRef]
- Kohno, Y.; Ohno, H. Temperature–responsive ionic liquid/water interfaces: Relation between hydrophilicity of ions and dynamic phase change. Phys. Chem. Chem. Phys. 2012, 14, 5063–5070. [Google Scholar] [CrossRef] [PubMed]
- Carrick, B.R.; Seitzinger, C.L.; Lodge, T.P. Unusual lower critical solution temperature phase behavior of poly(benzyl methacrylate) in a pyrrolidinium–based ionic liquid. Molecules 2021, 26, 4850. [Google Scholar] [CrossRef] [PubMed]
- Feng, Z.; Ishikawa, K. Development of simultaneous measurement system of birefringence, optical rotational power, and transmission spectra for chiral liquid crystal phases. Jpn. J. Appl. Phys. 2016, 55, 050301. [Google Scholar] [CrossRef]
- Dong, S.; Heyda, J.; Yuan, J.; Schalley, C.A. Lower critical solution temperature (LCST) phase behaviour of an ionic liquid and its control by supramolecular host–guest interactions. Chem. Commun. 2016, 52, 7970–7973. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nitta, A.; Morita, T.; Nishikawa, K.; Koga, Y. Mixing scheme of an aqueous solution of tetrabutylphosphonium trifluoroacetate in the water–rich region. Phys. Chem. Chem. Phys. 2017, 19, 16888–16896. [Google Scholar] [CrossRef]
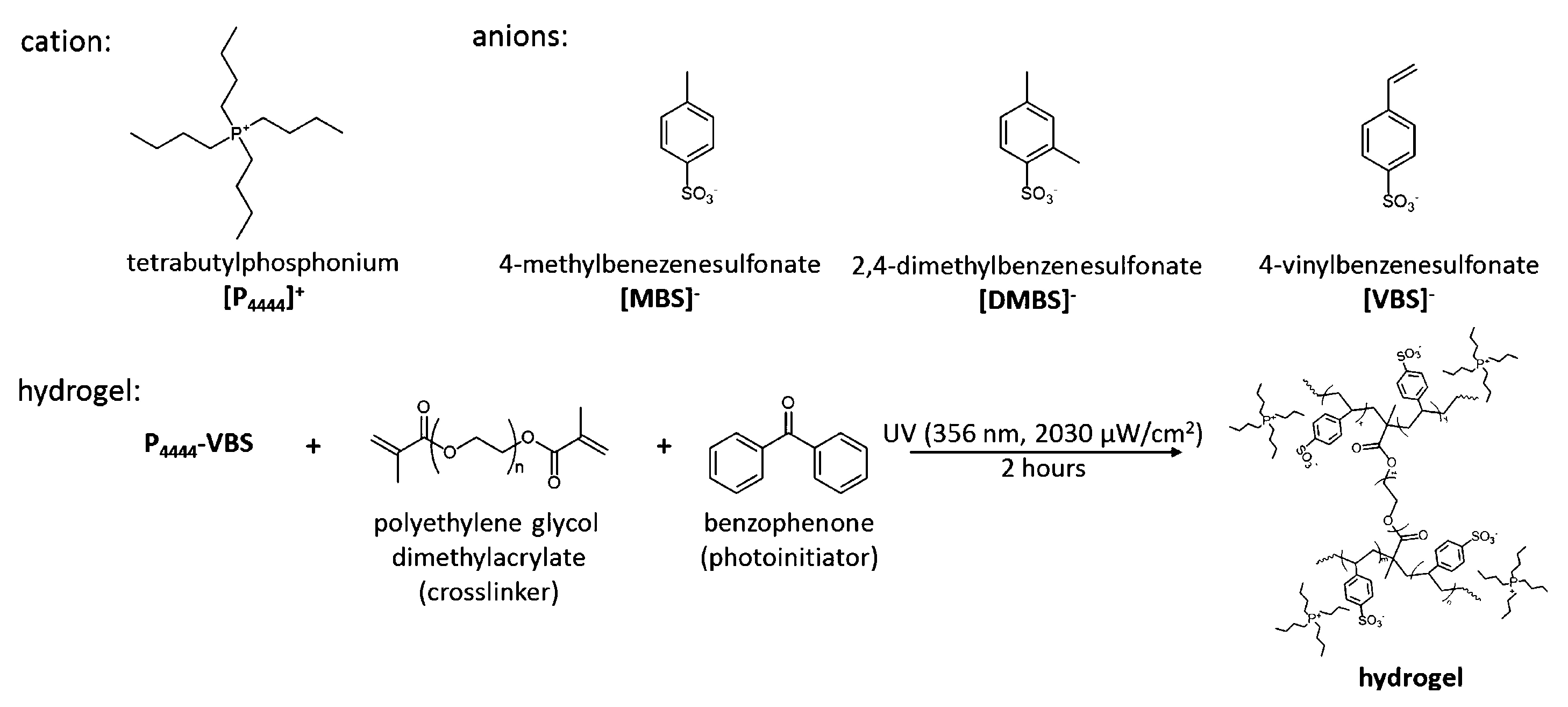
- Kang, H.; Suich, D.E.; Davies, J.F.; Wilson, A.D.; Urban, J.J.; Kostecki, R. Molecular insight into the lower critical solution temperature transition of aqueous alkyl phosphonium benzene sulfonates. Chem. Commun. 2019, 2, 51. [Google Scholar] [CrossRef] [Green Version]
- Heintz, A.; Lehmann, J.K.; Wertz, C.; Jacquemin, J. Thermodynamic properties of mixtures containing ionic liquids. 4. LLE of binary mixtures of [C2MIM][NTf2] with propan–1–ol, butan–1–ol, and pentan–1–ol and [C4MIM][NTf2] with cyclohexanol and 1,2–hexanediol including studies of the influence of small amounts of water. J. Chem. Eng. Data 2005, 50, 956–960. [Google Scholar]
- Nitta, A.; Morita, T.; Saita, S.; Kohno, Y.; Ohno, H.; Nishikawa, K. Density fluctuations in aqueous solution of ionic liquid with lower critical solution temperature: Mixture of tetrabutylphosphonium trifluoroacetate and water. Chem. Phys. Lett. 2015, 628, 108–112. [Google Scholar] [CrossRef]
- Bhatia, A.B.; Thornton, D.E. Structural aspects of the electrical resistivity of binary alloys. Phys. Rev. B 1970, 2, 3004–3012. [Google Scholar] [CrossRef]
- Hansen, J.P.; Mc Donald, I.R. Theory of Simple Liquids; Academic Press: London, UK, 1986. [Google Scholar]
- Kumari, P.; Pillai, V.V.S.; Gobbo, D.; Ballone, P.; Benedetto, A. The transition from salt–in–water to water–in–salt nanostructures in water solutions of organic ionic liquids relevant for biological applications. Phys. Chem. Chem. Phys. 2021, 23, 944–959. [Google Scholar] [CrossRef] [PubMed]
- Canongia Lopes, J.N.; Deschamps, J.; Pádua, A.A.H. Modeling ionic liquids using a systematic all–atom force field. J. Phys. Chem. B 2004, 108, 2038–2047. [Google Scholar] [CrossRef]
- Canongia Lopes, J.N.; Pádua, A.A.H. CL&P: A generic and systematic force field for ionic liquids modeling. Theor. Chem. Acc. 2012, 131, 1–11. [Google Scholar]
- Canongia Lopes, J.N.; Pádua, A.A.H. Molecular force field for ionic liquids III: Imidazolium, pyridinium, and phosphonium cations; chloride, bromide, and dicyanamide anions. J. Phys. Chem. B 2006, 110, 19586–19592. [Google Scholar] [CrossRef]
- de Souza, R.M.; Karttunen, M.; Ribeiro, M.C.C. Fine–tuning the polarizable CL&Pol force field for the deep eutectic solvent ethaline. J. Chem. Inf. Model. 2021, 61, 5938–5947. [Google Scholar]
- Goloviznina, K.; Canongia Lopes, J.N.; Costa Gomes, M.; Pádua, A.A.H. Transferable, Polarizable Force Field for Ionic Liquids. J. Chem. Theory Comput. 2019, 15, 5858–5871. [Google Scholar] [CrossRef]
- Goloviznina, K.; Gong, Z.; Pádua, A.A.H. The CL&Pol polarizable force field for the simulation of ionic liquids and eutectic solvents. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2021, e1572. [Google Scholar] [CrossRef]
- McDaniel, J.G. Polarization effects in binary [BMIM][BF4]/1,2–Dichloroethane, acetone, acetonitrile, and water electrolytes. J. Phys. Chem. B 2018, 122, 4345–4355. [Google Scholar] [CrossRef]
- Kirchner, B. Ionic liquids from theoretical investigations. Top. Curr. Chem. 2009, 290, 213–262. [Google Scholar]
- Du, S.; Yoo, S.; Li, J. Comparison of the melting temperatures of classical and quantum water potential models. Front. Phys. 2017, 5, 34. [Google Scholar] [CrossRef] [Green Version]
- Uhlig, F.; Zeman, J.; Smiatek, J.; Holm, C. First–principles parametrization of polarizable coarse–grained force fields for ionic liquids. J. Chem. Theory Comput. 2018, 14, 1471–1486. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Feng, S.; Voth, G.A. Transferable coarse–grained models for ionic liquids. J. Chem. Theory Comput. 2009, 5, 1091–1098. [Google Scholar] [CrossRef] [PubMed]
- Salanne, M. Simulations of room temperature ionic liquids: From polarizable to coarse–grained force fields. Phys. Chem. Chem. Phys. 2015, 17, 14270–14279. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Panagiotopoulos, A. Direct determination of phase coexistence properties of fluids by Monte–Carlo simulation in a new ensemble. Mol. Phys. 1987, 61, 813–826. [Google Scholar] [CrossRef]
- Marin–Rimoldi, E.; Shah, J.K.; Maginn, E.J. Monte Carlo simulations of water solubility in ionic liquids: A force field assessment. Fluid Phase Equilib. 2016, 407, 117–125. [Google Scholar] [CrossRef]
- Venkatesan, S.S.; Huda, M.M.; Rai, N. Molecular insights into ionic liquid/aqueous interface of phosphonium based phase–separable ionic liquids. AIP Adv. 2019, 9, 045115. [Google Scholar] [CrossRef] [Green Version]
- Schnell, S.K.; Vlugt, T.J.H.; Simon, J.M.; Bedeaux, D.; Kjelstrup, S. Thermodynamics of a small system in a μt reservoir. Chem. Phys. Lett. 2011, 504, 199–201. [Google Scholar] [CrossRef]
- Cortes–Huerto, R.; Kremer, K.; Potestio, R. Communication: Kirkwood–Buff integrals in the thermodynamic limit from small–sized molecular dynamics simulations. J. Chem. Phys. 2016, 145, 141103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dawass, N.; Krüger, P.; Schnell, S.K.; Simon, J.-M.; Vlugt, T.J.H. Kirkwood–Buff integrals from molecular simulations. Fluid Phse Equilib. 2019, 486, 21–36. [Google Scholar] [CrossRef]
- Schnell, S.K.; Englebienne, P.; Simon, J.-M.; Krüger, P.; Balaji, S.P.; Kjelstrup, S.; Bedeaux, D.; Bardow, A.; Vlugt, T.J.H. How to apply the Kirkwood–Buff theory to individual species in salt solutions. Chem. Phys. Lett. 2013, 582, 154–157. [Google Scholar] [CrossRef]
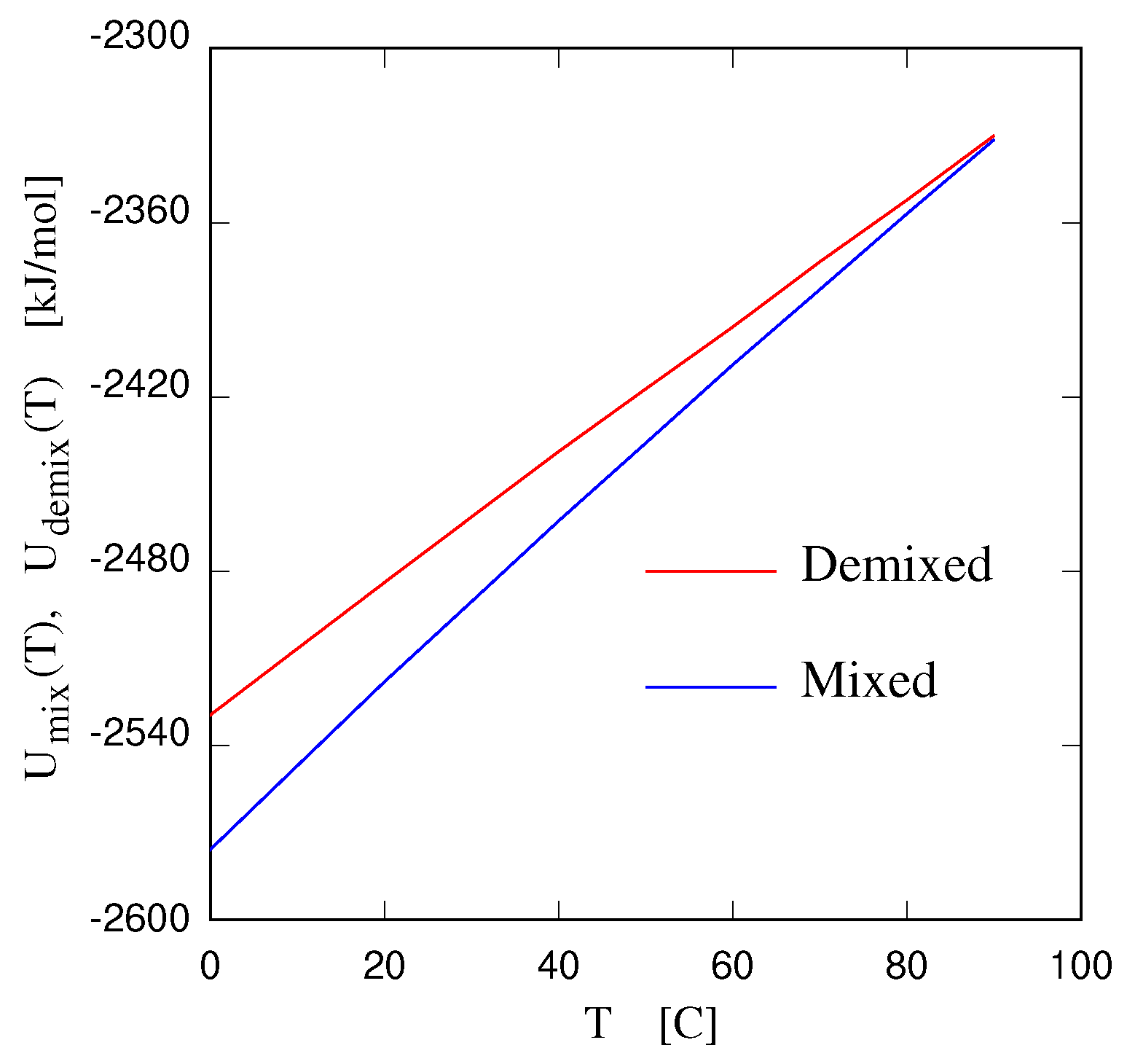
- Gobbo, D.; Ballone, P.; Garabato, B.D. Coarse–grained model of entropy–driven demixing. J. Phys. Chem. B 2020, 124, 9267–9274. [Google Scholar] [CrossRef]
- Walden, P.; Centnerszwer, M. Ober Verbindungen des Schwefeldioxyds mit Salzen. Z. Phys. Chem. (Leipzig) 1903, 42, 432. [Google Scholar] [CrossRef]
- Friedman, H.L. Electrolyte solutions that unmix to form two liquid phases. Solutions in benzene and diethyl ether. J. Phys. Chem. 1962, 66, 1595–1600. [Google Scholar] [CrossRef]
- Weingärtner, H.; Steinle, E. p, T, x surface of liquid–liquid immiscibility in aqueous solutions of tetraalkylammonium salts. J. Phys. Chem. 1992, 96, 2407–2409. [Google Scholar] [CrossRef]
- Dittmar, H.R.; Schröer, W.H. Lower critical solution temperature in the metastable region of an ionic solution in a non–polar solvent. J. Phys. Chem. B 2009, 113, 1249–1252. [Google Scholar] [CrossRef] [PubMed]
- Buckingham, S.A.; Garvey, C.J.; Warr, G.G. Effect of head–group size on micellization and phase behavior in quaternary ammonium surfactant systems. J. Phys. Chem. 1993, 97, 10236–10244. [Google Scholar] [CrossRef]
- Suarez, P.A.Z.; Einloft, S.; Dullius, J.E.L.; de Souza, R.F.; Dupont, J. Synthesis and physical-chemical properties of ionic liquids based on 1-n-butyl-3-methylimidazolium cation. J. Chim. Phys. 1998, 95, 1626–1639. [Google Scholar] [CrossRef]
- Dyson, P.J.; Ellis, D.J.; Welton, T. A temperature–controlled reversible ionic liquid–water two phase–single phase protocol for hydrogenation catalysis. Can. J. Chem. 2001, 79, 705–708. [Google Scholar] [CrossRef]
- Lachwa, J.; Szydlowski, J.; Najdanovic–Visak, V.; Rebelo, L.P.N.; Seddon, K.R.; da Ponte, M.N.; Esperança, J.M.S.S.; Guedes, H.J.R. Evidence for lower critical solution behavior in ionic liquid solutions. J. Am. Chem. Soc. 2005, 127, 6542–6543. [Google Scholar] [CrossRef]
- Lachwa, J.; Szydlowski, J.; Makowska, A.; Seddon, K.R.; Esperança, J.M.S.S.; Guedes, H.J.R.; Rebelo, L.P.N. Changing from an unusual high–temperature demixing to a UCST–type in mixtures of 1–alkyl–3–methylimidazolium bis{(trifluoromethyl)sulfonyl} amide and arenes. Green Chem. 2006, 8, 262–267. [Google Scholar] [CrossRef]
- Fukumoto, K.; Ohno, H. LCST–type phase changes of a mixture of water and ionic liquids derived from amino acids. Angew. Chem. Int. Ed. 2007, 46, 1852–1855. [Google Scholar] [CrossRef] [PubMed]
- Fukumoto, K.; Yoshizawa, M.; Ohno, H. Room temperature ionic liquids from 20 natural amino acids. J. Am. Chem. Soc. 2005, 127, 2398–2399. [Google Scholar] [CrossRef] [PubMed]
- Kohno, Y.; Saita, S.; Murata, K.; Nakamura, N.; Ohno, H. Extraction of proteins with temperature sensitive and reversible phase change of ionic liquid/water mixtures. Polym. Chem. 2011, 2, 862–867. [Google Scholar] [CrossRef]
- Fukaya, Y.; Sekikawa, K.; Murata, K.; Nakamura, N.; Ohno, H. Miscibility and phase behavior of water–dicarboxylic acid type ionic liquid mixed systems. Chem. Commun. 2007, 3089–3091. [Google Scholar] [CrossRef]
- Kohno, Y.; Arai, H.; Ohno, H. Dual stimuli–responsive phase transition of an ionic liquid/water mixture. Chem. Commun. 2011, 47, 4772–4774. [Google Scholar] [CrossRef]
- Rebelo, L.P.N.; Najdanovic–Visak, V.; Visak, Z.P.; Nunes da Ponte, M.; Szydlowski, J.; Cerdeirin, C.A.; Szydlowski, J.; Cerdeiriña, C.A.; Troncoso, J.; Romaní, L.; et al. A detailed thermodynamic analysis of [C4mim][BF4] + water as a case study to model ionic liquid aqueous solutions. Green Chem. 2004, 6, 369–381. [Google Scholar] [CrossRef]
- Xie, Z.-L.; Taubert, A. Thermomorphic behaviour of the ionic liquids [C4mim][FeCl4] and [C12mim][FeCl4]. Chem. Phys. Chem. 2011, 12, 364–368. [Google Scholar] [CrossRef]
- Chu, Y.-H.; Cheng, M.-F.; Chiang, Y.-H. Combinatorial discovery of small–molecule 1,2,3–triazolium ionic liquids exhibiting lower critical solution temperature phase transition. Sci. Rep. 2020, 10, 18247. [Google Scholar] [CrossRef]
- Pei, Y.; Cao, Y.; Huang, Y.; Song, X.; Wang, H.; Zhao, Y.; Wang, J. Tunable LCST–type phase behaviour of [FeCl4]−—based ionic liquids in water. Sci. China Chem. 2016, 59, 587–593. [Google Scholar] [CrossRef]
- Kohno, Y.; Arai, H.; Saita, S.; Ohno, H. Material design of ionic liquids to show temperature–sensitive LCST–type phase transition after mixing with water. Aust. J. Chem. 2011, 64, 1560–1567. [Google Scholar] [CrossRef]
- Ropel, L.; Belvèze, L.S.; Aki, S.N.V.K.; Stadtherr, M.A.; Brennecke, J.F. Octanol–water partition coefficients of imidazolium–based ionic liquids. Green Chem. 2005, 7, 83–90. [Google Scholar] [CrossRef]
- Saita, S.; Kohno, Y.; Nakamura, N.; Ohno, H. Ionic liquids showing phase separation with water prepared by mixing hydrophilic and polar amino acid ionic liquids. Chem. Commun. 2013, 49, 8988–8990. [Google Scholar] [CrossRef] [PubMed]
- Ando, T.; Kohno, Y.; Nakamura, N.; Ohno, H. Introduction of hydrophilic groups onto the ortho–position of benzoate anions induced phase separation of the corresponding ionic liquids with water. Chem. Commun. 2013, 49, 10248–10250. [Google Scholar] [CrossRef]
- Moura, L.; Brown, L.C.; Blesic, M.; Holbrey, J.D. LCST–phase behavior and complexation with water of an ionic liquid incorporating the 5–phenyltetrazolate anion. Phys. Chem. Phys. 2017, 8, 3384–3389. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morita, T.; Miki, K.; Nitta, A.; Ohgi, H.; Westh, P. Effects of constituent ions of a phosphonium–based ionic liquid on molecular organization of H2O as probed by 1–propanol: Tetrabutylphosphonium and trifluoroacetate ions. Phys. Chem. Chem. Phys. 2015, 17, 22170–22178. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zavitsas, A.A. Properties of water solutions of electrolytes and nonelectrolytes. J. Phys. Chem. B 2001, 105, 7805–7817. [Google Scholar] [CrossRef]
- Koga, Y. 1–Propanol probing methodology: Two–dimensional characterization of the effect of solute on H2O. Phys. Chem. Chem. Phys. 2013, 15, 14548–14565. [Google Scholar] [CrossRef]
- Batista, M.L.S.; Tomé, L.I.N.; Neves, C.M.S.S.; Rocha, E.M.; Gomes, J.R.B.; Coutinho, J.A.P. The origin of the LCST on the liquid–liquid equilibrium of thiophene with ionic liquids. J. Phys. Chem. B 2012, 116, 5985–5992. [Google Scholar] [CrossRef]
- Crosthwaite, J.M.; Aki, S.N.V.K.; Maginn, E.J.; Brennecke, J.F. Liquid phase behavior of imidazolium–based ionic liquids with alcohols. J. Phys. Chem. B 2004, 108, 5113–5119. [Google Scholar] [CrossRef]
- Turnaoglu, T.; Ritchie, S.G.; Shiflett, M.B. Liquid–liquid equilibria in binary mixtures of dihydroxy alcohols and imidazolium–based ionic liquids. J. Chem. Eng. Data 2019, 64, 3179–3186. [Google Scholar] [CrossRef]
- Makowska, A.; Ewa Sztank, E.; Szydłowski, J. Liquid phase behavior of hexafluorophosphate ionic liquids with polyhydric alcohols. Fluid Phase Equilibr. 2012, 314, 140–145. [Google Scholar] [CrossRef]
- Domańska, U.; Laskowska, M.; Pobudkowska, A. Phase equilibria study of the binary systems (1–butyl–3–methylimidazolium thiocyanate ionic liquid + organic solvent or water). J. Phys. Chem. B 2009, 113, 6397–6404. [Google Scholar] [CrossRef] [PubMed]
- Scurto, A.M.; Aki, S.N.V.K.; Brennecke, J.F. CO2 as a separation switch for ionic liquid/organic mixtures. J. Am. Chem. Soc. 2002, 124, 10276–10277. [Google Scholar] [CrossRef] [PubMed]
- Gutowski, K.E.; Broker, G.A.; Willauer, H.D.; Huddleston, J.G.; Swatloski, R.P.; Holbrey, J.D.; Rogers, R.D. Controlling the aqueous miscibility of ionic liquids: Aqueous biphasic systems of water–miscible ionic liquids and water–structuring salts for recycle, metathesis, and separations. J. Am. Chem. Soc. 2003, 125, 6632–6633. [Google Scholar] [CrossRef]
- Shahriari, S.; Neves, C.M.S.S.; Freire, M.G.; Coutinho, J.A.P. Role of the Hofmeister series in the formation of ionic–liquid–based aqueous biphasic systems. J. Phys. Chem. B 2012, 116, 7252–7258. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Guo, J.; Nie, F.; Ji, H.; Liu, S. LCST–type behaviour of aqueous biphasic systems composed of phosphonium–based ionic liquids and potassium phosphate. J. Chem. Eng. Data 2017, 62, 1335–1340. [Google Scholar] [CrossRef]
- Dupont, D.; Depuydt, D.; Binnemans, K. Overview of the effect of salts on biphasic ionic liquid/water solvent extraction systems: Anion exchange, mutual solubility, and thermomorphic properties. J. Phys. Chem. B 2015, 119, 6747–6757. [Google Scholar] [CrossRef] [PubMed]
- Passos, H.; Luís, A.; Coutinho, J.A.P.; Freire, M.G. Thermoreversible (ionic–liquid–based) aqueous biphasic systems. Sci. Rep. 2016, 6, 20276. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lu, J.; Yan, F.; Texter, J. Advanced applications of ionic liquids in polymer science. Prog. Polym. Sci. 2009, 34, 431–448. [Google Scholar] [CrossRef]
- Kohno, Y.; Deguchi, Y.; Ohno, H. Ionic liquid–derived cherged polymers to show highly thermoresponsive LCST–type transition with water at desired temperatures. Chem. Commun. 2012, 48, 11883–11885. [Google Scholar] [CrossRef]
- Li, W.; Wu, P. Unusual thermal phase transition behaviour of an ionic liquid and poly(ionic liquid) in water with significantly different LCST and dynamic mechanism. Polym. Chem. 2014, 5, 5578–5590. [Google Scholar] [CrossRef]
- Tsuda, R.; Kodama, K.; Ueki, T.; Kokubo, H.; Imabayashi, S.I.; Watanabe, M. LCST–type liquid–liquid phase separation behaviour of poly(ethylene oxide) derivatives in an ionic liquid. Chem. Commun. 2008, 4939–4941. [Google Scholar] [CrossRef] [Green Version]
- Lee, H.-N.; Lodge, T.P. Lower critical solution temperature (LCST) phase behavior of poly(ethylene oxide) in ionic liquids. J. Phys. Chem. Lett. 2010, 1, 1962–1966. [Google Scholar] [CrossRef]
- Lee, H.-N.; Newell, N.; Bai, Z.; Lodge, T.P. Unusual lower critical solution temperature phase behavior of poly(ethylene oxide) in ionic liquids. Macromolecules 2012, 45, 3627–3633. [Google Scholar] [CrossRef]
- Choi, E.; Yethiraj, A. Entropic mechanism for the lower critical solution temperature of poly(ethylene oxide) in room temperature ionic liquid. ACS Macro Lett. 2015, 4, 799–803. [Google Scholar] [CrossRef]
- Tsioptsias, C.; Tsivintzelis, I.; Panayiotou, C. Equation of state modeling of mixtures with ionic liquids. Phys. Chem. Chem. Phys. 2010, 12, 4843–4851. [Google Scholar] [CrossRef]
- Domańska, U.; Paduszyński, K.; Królikowski, M.; Wróblewska, A. Separation of 2-phenylethanol from water by liquid–liquid extraction with ionic liquids: New experimental data and modeling with modern thermodynamic tools. Ind. Eng. Chem. Res. 2016, 55, 5736–5747. [Google Scholar] [CrossRef]
- Simoni, L.D.; Lin, Y.; Brennecke, J.F.; Stadtherr, M.A. Modeling liquid–liquid equilibrium of ionic liquid systems with NRTL, electrolyte–NRTL, and UNIQUAC. Ind. Eng. Chem. Res. 2008, 47, 256–272. [Google Scholar] [CrossRef] [Green Version]
- Freire, M.G.; Ventura, S.P.M.; Santos, L.M.N.B.F.; Marrucho, I.M.; Coutinho, J.A.P. Evaluation of COSMO–RS for the prediction of LLE and VLE of water and ionic liquids binary systems. Fluid Phase Equilib. 2008, 268, 74–84. [Google Scholar] [CrossRef]
- Zhao, Y.; Tian, L.; Pei, Y.; Wang, H.; Wang, J. Effect of anionic structure on the LCST phase behavior of phosphonium ionic liquids in water. Ind. Eng. Chem. Res. 2018, 57, 12935–12941. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, H.; Pei, Y.; Liu, Z.; Wang, J. Understanding the mechanism of LCST phase separation of mixed ionic liquids in water by MD simulations. Phys. Chem. Chem. Phys. 2016, 18, 23238–23245. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-L.; Li, B.; Sarman, S.; Mocci, F.; Lu, Z.-Y.; Yuan, J.; Laaksonen, A.; Fayer, M. Microstructural and dynamical heterogeneities in ionic liquids. Chem. Rev. 2020, 120, 5798–5877. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Russina, O.; Triolo, A.; Gontrani, L.; Caminiti, R. Mesoscopic structural heterogeneities in room–temperature ionic liquids. J. Phys. Chem. Lett. 2012, 2, 27–33. [Google Scholar] [CrossRef]
- Greaves, T.L.; Kennedy, D.F.; Weerawardena, A.; Tse, N.M.K.; Kirby, N.; Drummond, C.J. Nanostructured protic ionic liquids retain nanoscale features in aqueous solution while precursor Brønsted acids and bases exhibit different behavior. J. Phys. Chem. B 2011, 115, 2055–2066. [Google Scholar] [CrossRef] [PubMed]
- Egorova, K.S.; Gordeev, E.G.; Ananikov, V.P. Biological activity of ionic liquids and their application in pharmaceutics and medicine. Chem. Rev. 2017, 117, 7132–7189. [Google Scholar] [CrossRef]
- Kashin, A.S.; Boiko, D.A.; Ananikov, V.P. Neural network analysis of electron microscopy video data reveals the temperature–driven microphase dynamics in the ions/water systems. Small 2021, 17, 2007726. [Google Scholar] [CrossRef]
- Wang, R.; Leng, W.; Gao, Y.; Yu, L. Microemulsion–like aggregation behaviour of an LCST–type ionic liquid in water. RSC Adv. 2014, 4, 14055–14062. [Google Scholar] [CrossRef]
- Zhao, Y.; Shi, L.; Qiu, J.; Pei, Y.; Wang, H.; Li, Z.; Fan, J.; Wang, J. Mechanism of emulsification and demulsification for temperature–sensitive ionic liquid microemulsion. J. Mol. Liq. 2020, 2020, 114352. [Google Scholar] [CrossRef]
- Sowmiah, S.; Srinivasadesikan, V.; Tseng, M.-C.; Chu, Y.-H. On the chemical stabilities of ionic liquids. Molecules 2009, 14, 3780–3813. [Google Scholar] [CrossRef] [Green Version]
- Beil, S.; Markiewicz, M.; Pereira, C.S.; Stepnowski, P.; Thöming, J.; Stolte, S. Toward the proactive design of sustainable chemicals: Ionic liquids as a prime example. Chem. Rev. 2021, 121, 13132–13173. [Google Scholar] [CrossRef]
- Freire, M.G.; Neves, C.M.S.S.; Marrucho, I.M.; Coutinho, J.A.P.; Fernandes, A.M. Hydrolysis of tetrafluoroborate and hexafluorophosphate counter ions in imidazolium–based ionic liquids. J. Phys. Chem. A 2010, 114, 3744–3749. [Google Scholar] [CrossRef] [PubMed]
- Steudte, S.; Neumann, J.; Bottin–Weber, U.; Diedenhofen, M.; Arning, J.; Stepnowski, P.; Stolte, S. Hydrolysis study of fluoroorganic and cyano–based ionic liquid anions—-Consequences for operational safety and environmental stability. Green Chem. 2012, 14, 2474–2483. [Google Scholar] [CrossRef]
- Jacquemin, J.; Goodrich, P.; Jiang, W.; Rooney, D.W.; Hardacre, C. Are alkyl sulfate–based protic and aprotic ionic liquids stable with water and alcohols? A thermodynamic approach. J. Phys. Chem. B 2013, 117, 1938–1949. [Google Scholar] [CrossRef] [PubMed]
- Ventura, S.P.M.; e Silva, F.A.; Quental, M.V.; Mondal, D.; Freire, M.G.; Coutinho, J.A.P. Ionic–liquid–mediated extraction and separation processes for bioactive compounds: Past, present, and future trends. Chem. Rev. 2017, 117, 6984–7052. [Google Scholar] [CrossRef]
- Arce, A.; Earle, M.J.; Katdare, S.P.; Rodríguez, H.; Seddon, K.R. Application of mutually immiscible ionic liquids to the separation of aromatic and aliphatic hydrocarbons by liquid extraction: A preliminary approach. Phys. Chem. Chem. Phys. 2008, 10, 2538–2542. [Google Scholar] [CrossRef]
- Hoogerstraete, T.V.; Onghena, B.; Binnemans, K. Homogeneous liquid–liquid extraction of metal ions with a functionalised ionic liquid. J. Phys. Chem. Lett. 2013, 4, 1659–1663. [Google Scholar] [CrossRef]
- Ambadipudi, S.; Biernat, J.; Riedel, D.; Mandelkow, E.; Zweckstetter, M. Liquid–liquid phase separation of the microtubule–binding repeats of the Alzheimer–related protein Tau. Nat. Commun. 2017, 8, 275. [Google Scholar] [CrossRef]
- Wang, L.; Chen, X.; Liu, J.; Tan, Z. A LCST–type ionic liquid used as the recyclable extractant for the extraction and separation of liquiritin and glycyrrhizin acid from licorice (Glycyrrhiza uralensis Fisch). J. Mol. Liq. 2021, 340, 117295. [Google Scholar] [CrossRef]
- Wang, T.; Wang, Q.; Li, P.; Yang, H. Temperature–responsive ionic liquids to set up a method for the simultaneous extraction and in situ preconcentration of hydrophilic and lipophilic compounds from medicinal plant matrices. Green Chem. 2019, 21, 4133–4142. [Google Scholar] [CrossRef]
- Ismail, M.; Al–Zuhair, S. Thermo–responsive switchable solvents for simultaneous microalgae cell disruption, oil extraction–reaction, and product separation for biodiesel production. Biocatal. Agric. Biotechnol. 2020, 26, 101667. [Google Scholar] [CrossRef]
- Jiang, W.; Zhu, W.; Li, H.; Wang, X.; Yin, S.; Chang, Y.; Li, H. Temperature–responsive ionic liquid extraction and separation of the aromatic sulfur compounds. Fuel 2015, 140, 590–596. [Google Scholar] [CrossRef]
- Depuydt, D.; Liu, L.; Glorieux, C.; Dehaen, W.; Binnemans, K. Homogeneous liquid–liquid extraction of metal ions with non–fluorinated bis(2–ethylhexyl)phosphate ionic liquids having a lower critical solution temperature in combination with water. Chem. Commun. 2015, 51, 14183–14186. [Google Scholar] [CrossRef] [PubMed]
- Okamura, H.; Hirayama, N. Recent progress in ionic liquid extraction for the separation of rare earth elements. Anal. Sci. 2021, 37, 119–130. [Google Scholar] [CrossRef] [PubMed]
- Onghena, B.; Jacobs, J.; Van Meervelt, L.; Binnemans, K. Homogeneous liquid–liquid extraction of neodymium(III) by cholyne hexafluoroacetonate in the ionic liquid choline bis(trifluoromethylsulfonyl)imide. Dalton Trans. 2014, 43, 11566–11578. [Google Scholar] [CrossRef] [Green Version]
- Urban, J.J. Emerging scientific and engineering opportunities within the water–energy nexus. Joule 2017, 1, 665–688. [Google Scholar] [CrossRef]
- Neff, R.A. Solvent Extractor. U.S. Patent 3130156, 21 April 1964. [Google Scholar]
- Cath, T.Y.; Childress, A.E.; Elimelech, M. Forward osmosis: Principles, applications and recent developments. J. Membr. Sci. 2006, 281, 70–87. [Google Scholar] [CrossRef]
- Haddad, A.Z.; Menon, A.K.; Kang, H.; Urban, J.J.; Prasher, R.S.; Kostecki, R. Solar Desalination using thermally responsive ionic liquids regenerated with a photonic heater. Environ. Sci. Technol. 2021, 55, 3260–3269. [Google Scholar] [CrossRef]
- Kamio, E.; Takenaka, A.; Takahashi, T.; Matsuyama, H. Fundamental investigation of osmolality, thermo–responsive phase diagram, and water–drawing ability of ionic–liquid–based draw solution for forward osmosis membrane process. J. Membr. Sci. 2019, 570–571, 93–102. [Google Scholar] [CrossRef]
- Kamio, E.; Kurisu, H.; Takahashi, T.; Matsuoka, A.; Yoshioka, T.; Nakagawa, K.; Sun, Y.; Matsuyama, H. Effect of temperature on the osmotic behavior of LCST type ionic liquid solutions as draw solutions in the forward osmosis process. Sep. Purif. Technol. 2021, 275, 119164. [Google Scholar] [CrossRef]
- Zeweldi, H.G.; Bendoy, A.P.; Park, M.J.; Shon, H.K.; Johnson, E.M.; Kim, H.-S.; Kim, H.; Chung, W.-J.; Nisola, G.M. Forward osmosis with direct contact membrane distillation using tetrabutylphosphonium p–toluenesulfonate as an effective and safe thermo–recyclable osmotic agent for seawater desalination. Chemosphere 2021, 263, 128070. [Google Scholar] [CrossRef] [PubMed]
- Zeweldi, H.G.; Bendoy, A.P.; Park, M.J.; Shon, H.K.; Kim, H.-S.; Johnson, E.M.; Kim, H.; Lee, S.-P.; Chung, W.-J.; Nisola, G.M. Tetrabutylammonium 2,4,6–trimethylbenzenesulfonate as an effective and regenerable thermo–responsive ionic liquid drawing agent in forward osmosis for seawater desalination. Desalination 2020, 495, 114635. [Google Scholar] [CrossRef]
- Yang, Q.; Lau, C.H.; Ge, Q. Novel ionic grafts that enhance arsenic removal via forward osmosis. ACS Appl. Mater. Interfaces 2019, 11, 17828–17835. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.-H.; Ma, C.; Bui, N.; Song, Z.; Wilson, A.D.; Kostecki, R.; Diederichsen, K.M.; McCloskey, B.D.; Urban, J.J. Enhanced forward osmosis desalination with a hybrid ionic liquid/hydrogel thermoresponsive draw agent system. ACS Omega 2019, 4, 4296–4303. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guo, J.; Tucker, Z.D.; Wang, Y.; Ashfeld, B.L.; Luo, T. Ionic liquid enables highly efficient low temperature desalination by directional solvent extraction. Nat. Commun. 2021, 12, 437. [Google Scholar] [CrossRef]
- Lord, J.; Thomas, A.; Treat, N.; Forkin, M.; Bain, R.; Dulac, P.; Behroozi, C.H.; Mamutov, T.; Fongheiser, J.; Kobilansky, N.; et al. Global potential for harvesting drinking water from air using solar energy. Nature 2021, 598, 611–617. [Google Scholar] [CrossRef]
- Zhou, X.; Lu, H.; Zhao, F.; Yu, G. Atmospheric water harvesting: A review of material and structural designs. ACS Mater. Lett. 2020, 2, 671–684. [Google Scholar] [CrossRef]
- Cao, Y.; Chen, Y.; Sun, X.; Zhang, Z.; Mu, T. Water sorption in ionic liquids: Kinetics, mechanisms and hydrophilicity. Phys. Chem. Chem. Phys. 2012, 14, 12252–12262. [Google Scholar] [CrossRef]
- Zhao, F.; Zhou, X.; Liu, Y.; Shi, Y.; Dai, Y.; Yu, G. Super moisture–absorbent gels for all–weather atmospheric water harvesting. Adv. Mater. 2019, 31, 1806446. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, K.; Sakikawa, N.; Miyata, T. Thermo–Responsive Gels That Absorb Moisture and Ooze Water. Nat. Commun. 2018, 9, 2315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Piper, S.L.; Kar, M.; MacFarlane, D.R.; Matuszek, K.; Pringle, J.M. Ionic liquids for renewable thermal energy storage—A perspective. Green Chem. 2022, 24, 102–117. [Google Scholar] [CrossRef]
- Billeci, F.; Gunaratne, H.Q.N.; D’Anna, F.; Morgan, G.G.; Seddon, K.R.; Plechkova, N.V. A magnetic self–contained thermochromic system with convenient temperature range. Green Chem. 2019, 21, 1412–1416. [Google Scholar] [CrossRef] [Green Version]
- MacFarlane, D.R.; Forsyth, M.; Howlett, P.C.; Kar, M.; Passerini, S.; Pringle, J.M.; Ohno, H.; Watanabe, M.; Yan, F.; Zheng, W.; et al. Ionic liquids and their solid–state analogues as materials for energy generation and storage. Nat. Rev. Mater. 2016, 1, 15005. [Google Scholar] [CrossRef]
- Mehrkesh, A.; Karunanithi, A.T. Optimal design of ionic liquids for thermal energy storage. Comput. Chem. Eng. 2016, 93, 402–412. [Google Scholar] [CrossRef] [Green Version]
- Čanji, M.; Bendová, M.; Bogdanov, M.G.; Wagner, Z.; Zdolšek, N.; Quirion, F.; Jandová, V.; Vrbka, P. Phase transitions in higher-melting imidazolium-based ionic liquids: Experiments and advanced data analysis. J. Mol. Liq. 2019, 292, 111222. [Google Scholar] [CrossRef]
- Bendova, M.; Canji, M.; Wagner, Z.; Zdolsek, N.; Quirion, F. Phase transitions in higher–melting ionic liquids: Thermal storage materials or liquid crystals? Chem. Eng. Trans. 2018, 69, 37–42. [Google Scholar]
- Tullo, A.H. The time is now for ionic liquids. C&EN 2020, 98, 24–27. [Google Scholar]


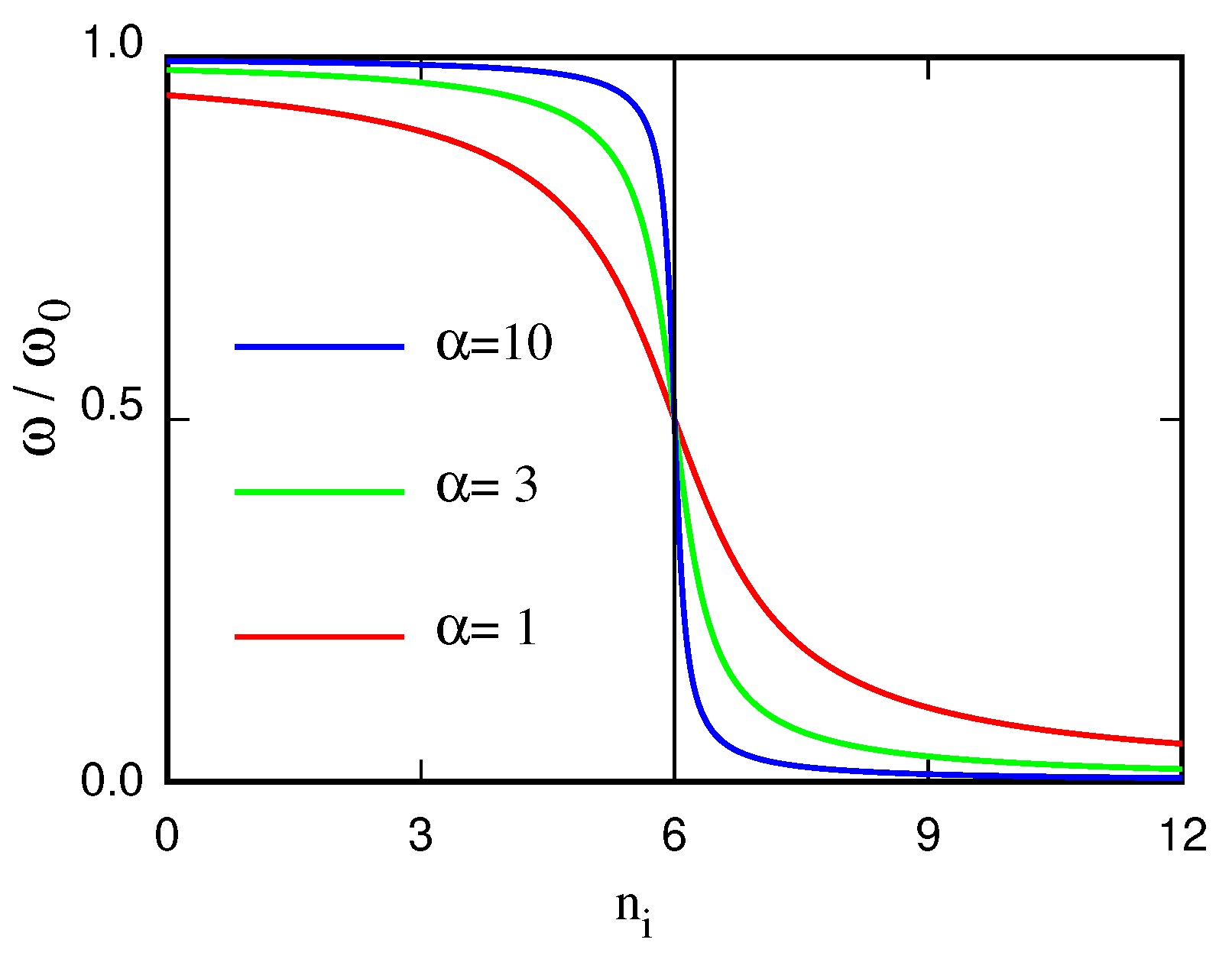

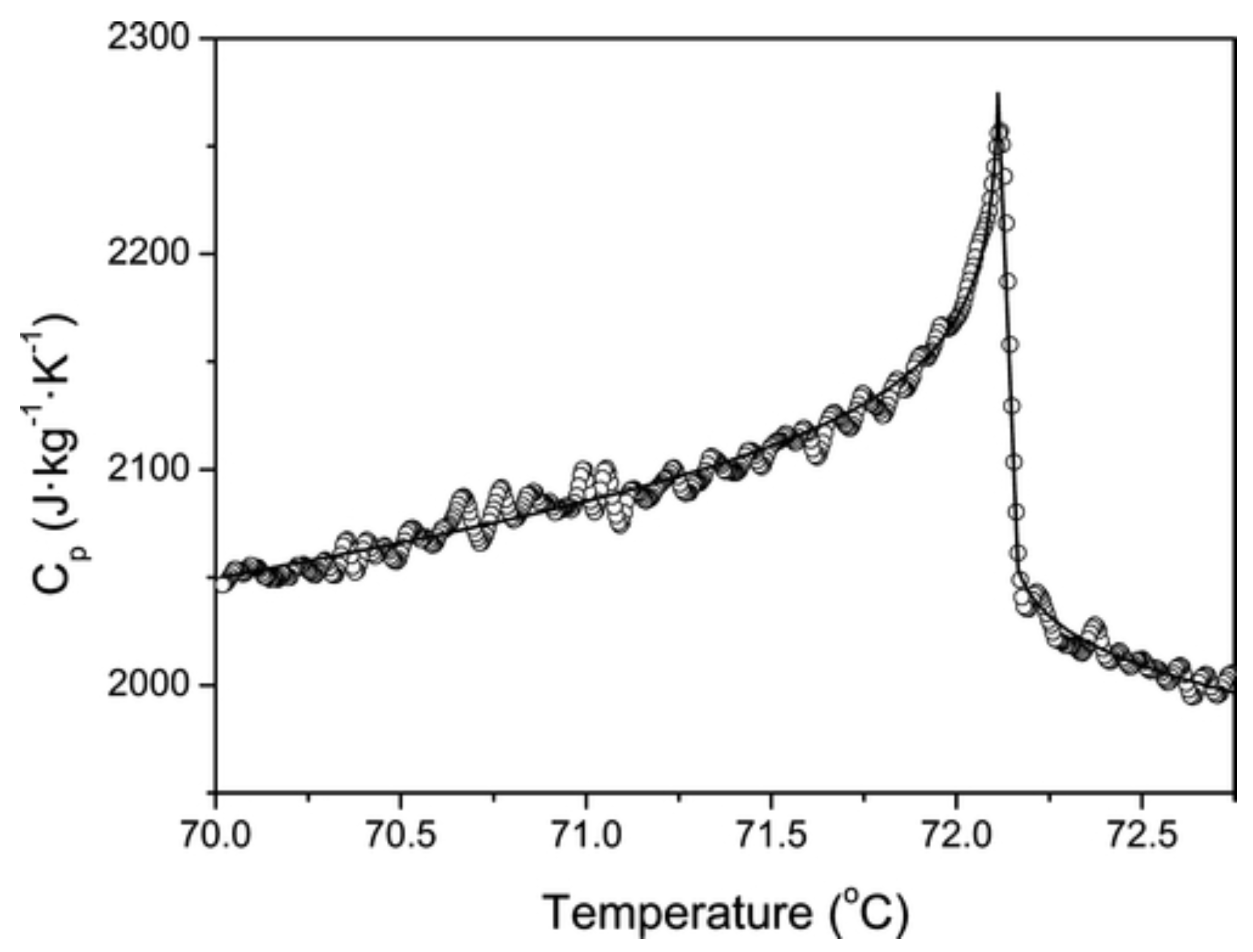
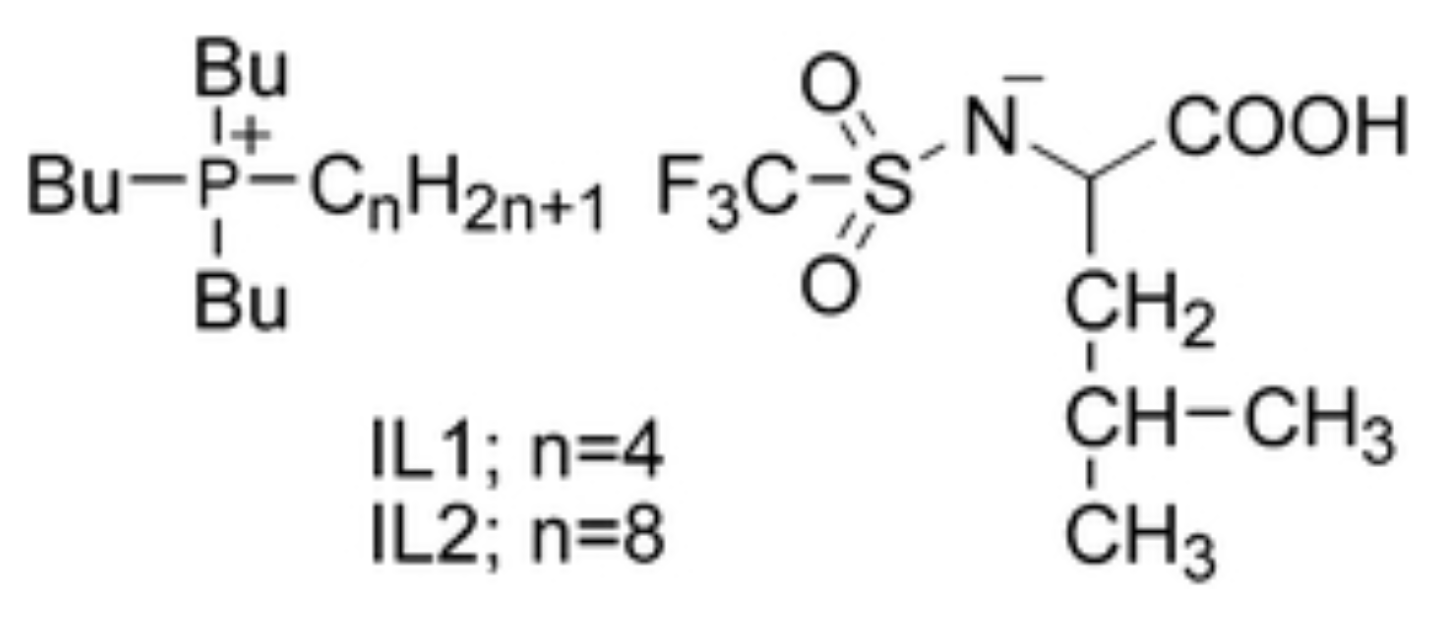
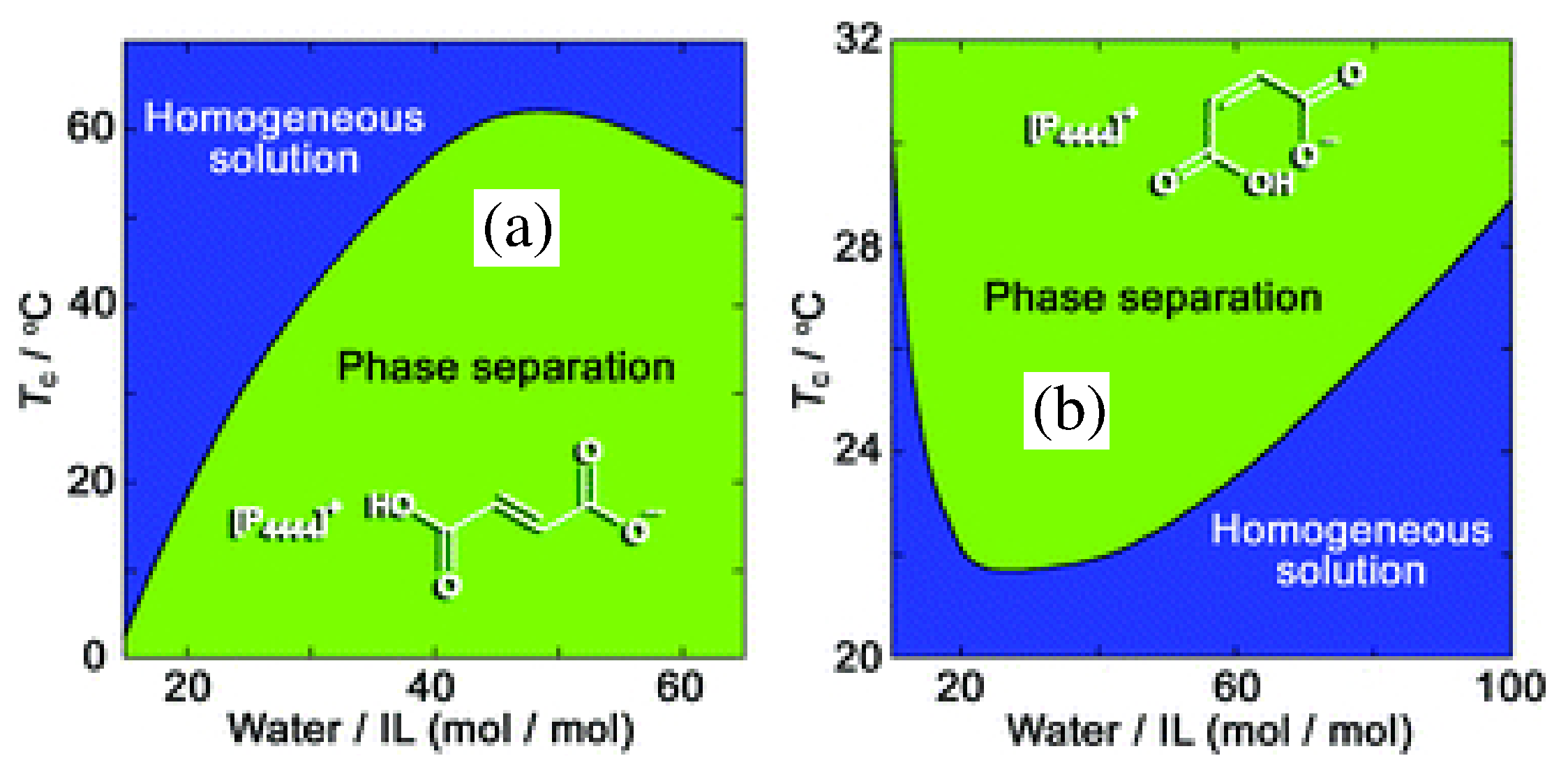
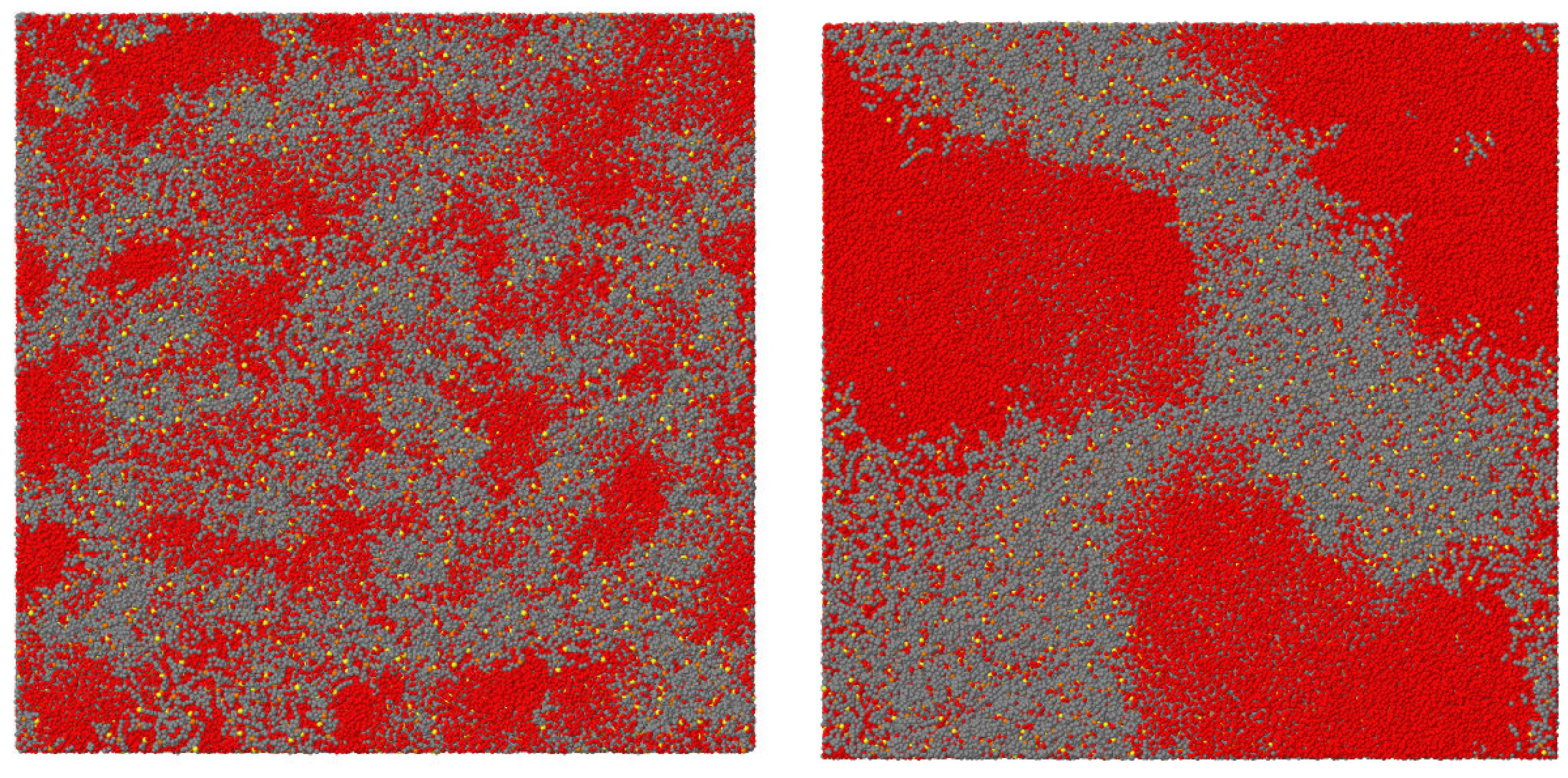
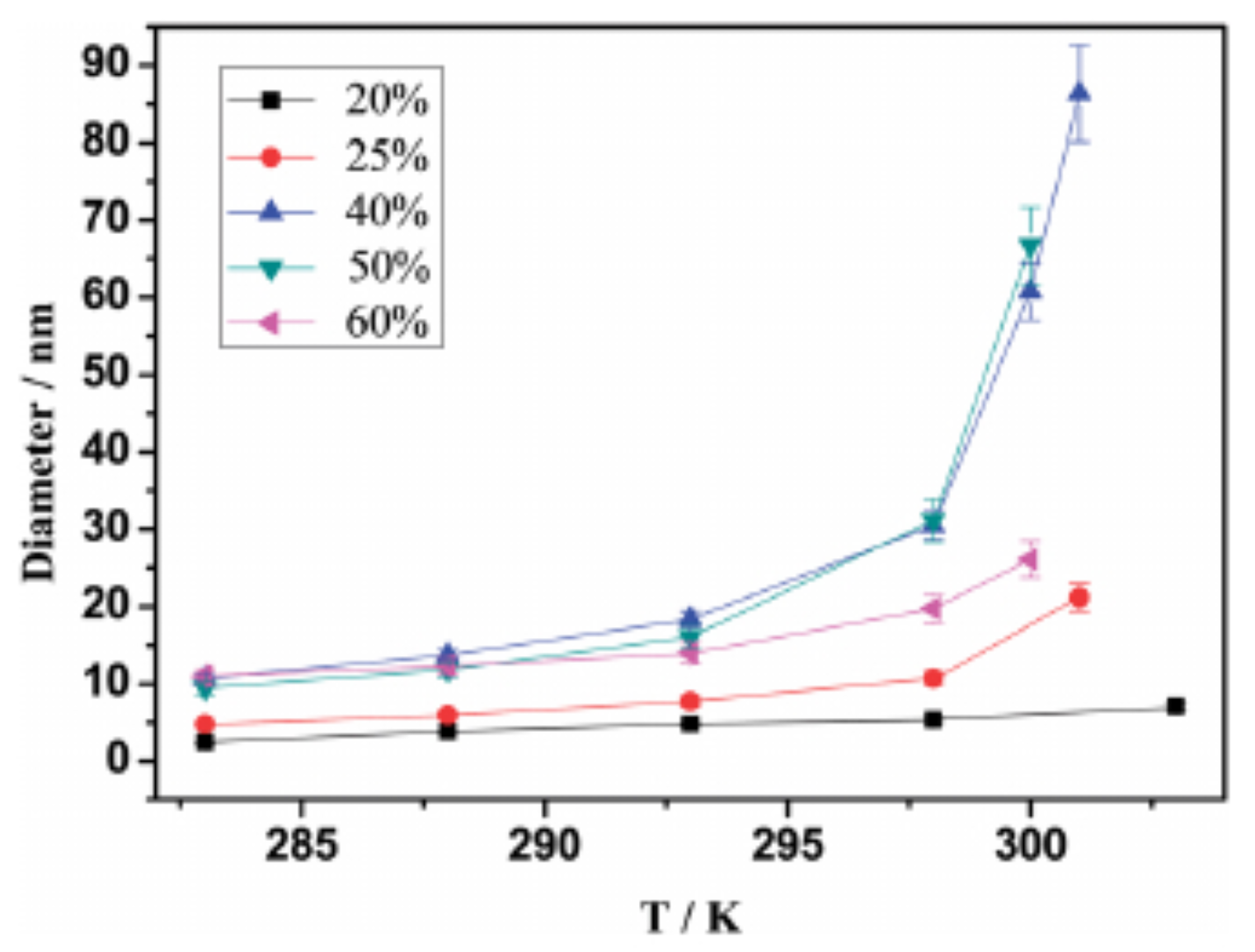
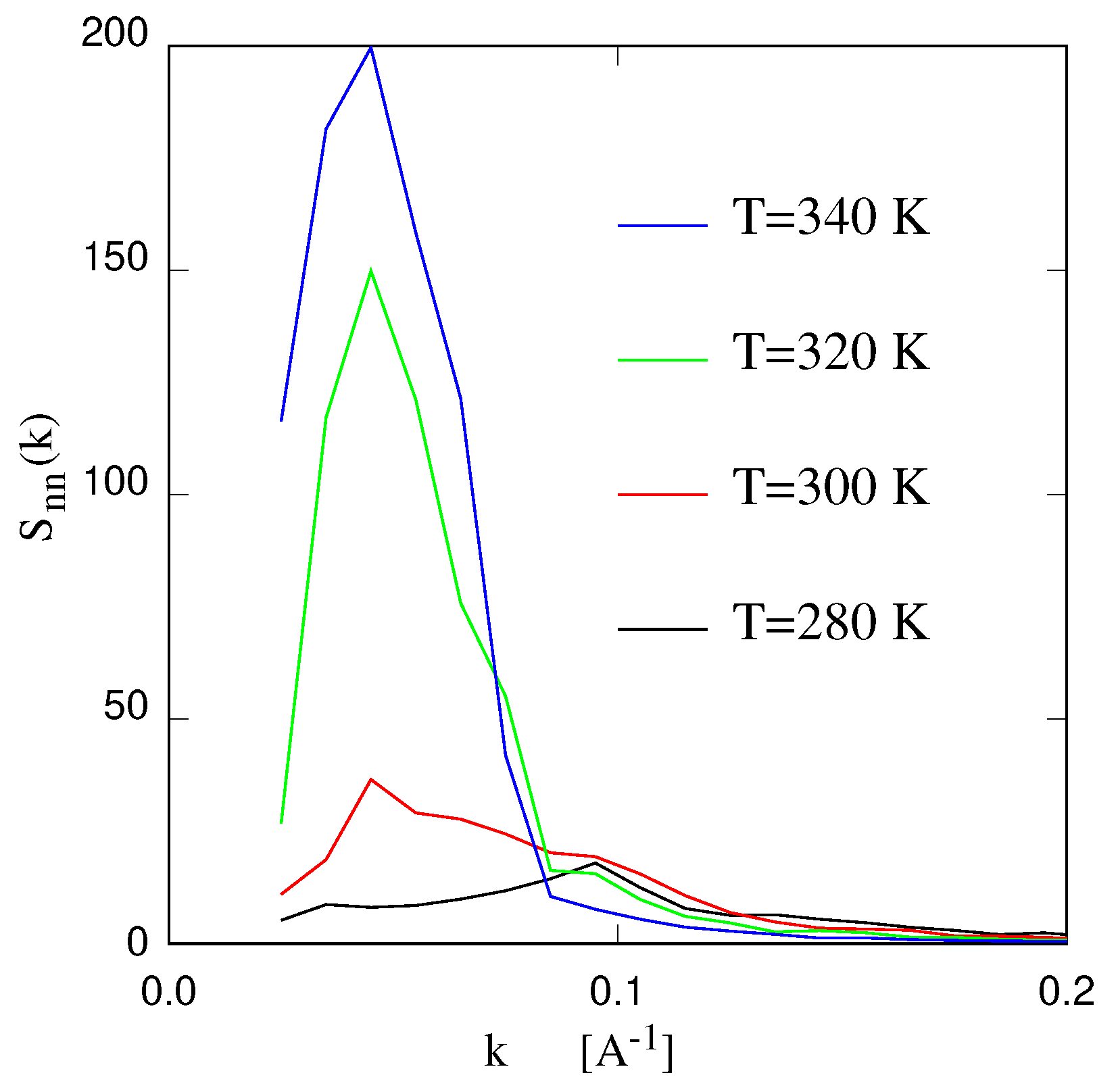
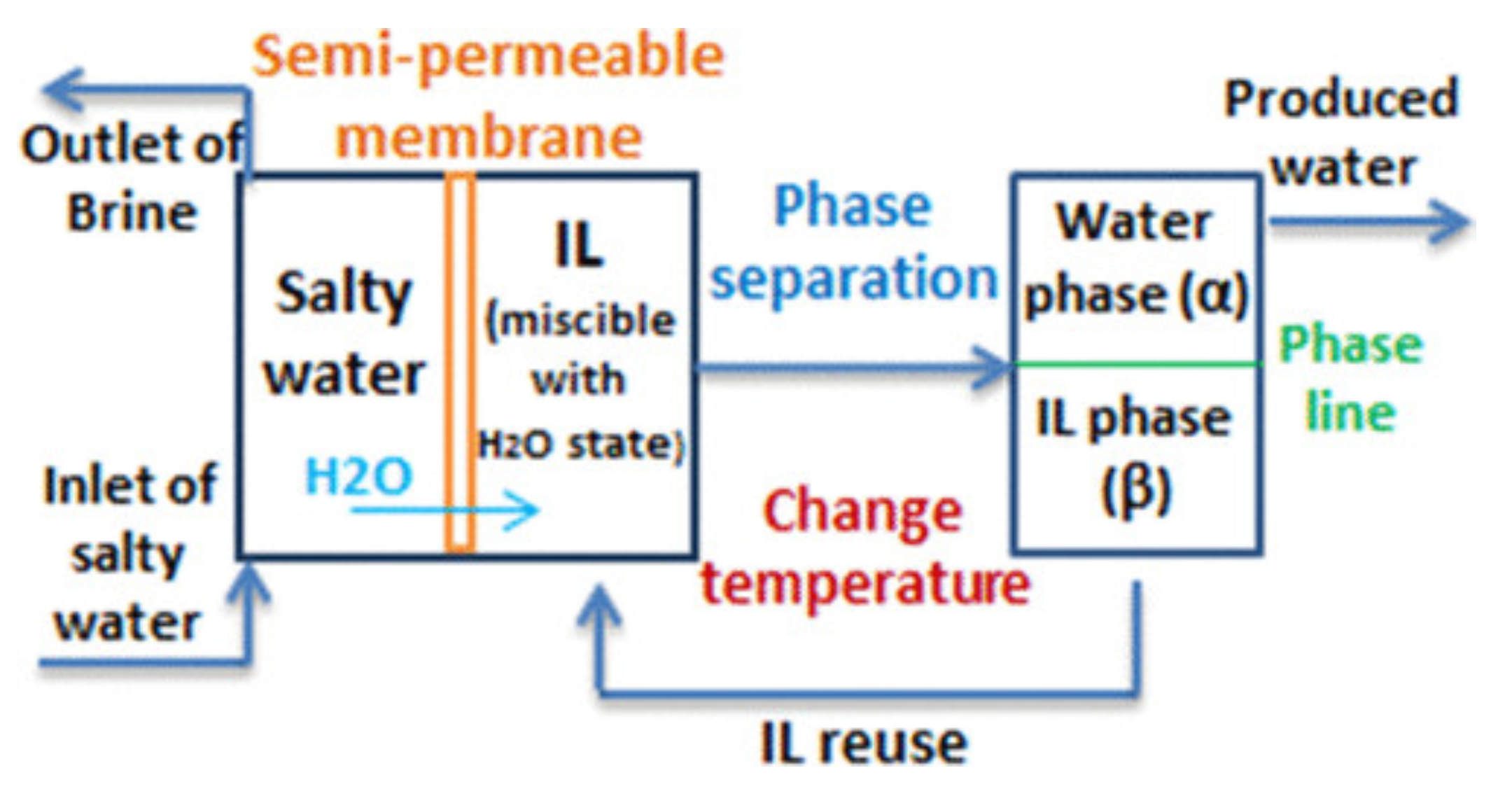
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Forero-Martinez, N.C.; Cortes-Huerto, R.; Benedetto, A.; Ballone, P. Thermoresponsive Ionic Liquid/Water Mixtures: From Nanostructuring to Phase Separation. Molecules 2022, 27, 1647. https://doi.org/10.3390/molecules27051647
Forero-Martinez NC, Cortes-Huerto R, Benedetto A, Ballone P. Thermoresponsive Ionic Liquid/Water Mixtures: From Nanostructuring to Phase Separation. Molecules. 2022; 27(5):1647. https://doi.org/10.3390/molecules27051647
Chicago/Turabian StyleForero-Martinez, Nancy C., Robinson Cortes-Huerto, Antonio Benedetto, and Pietro Ballone. 2022. "Thermoresponsive Ionic Liquid/Water Mixtures: From Nanostructuring to Phase Separation" Molecules 27, no. 5: 1647. https://doi.org/10.3390/molecules27051647
APA StyleForero-Martinez, N. C., Cortes-Huerto, R., Benedetto, A., & Ballone, P. (2022). Thermoresponsive Ionic Liquid/Water Mixtures: From Nanostructuring to Phase Separation. Molecules, 27(5), 1647. https://doi.org/10.3390/molecules27051647






