Molecular Forcefield Methods for Describing Energetic Molecular Crystals: A Review
Abstract
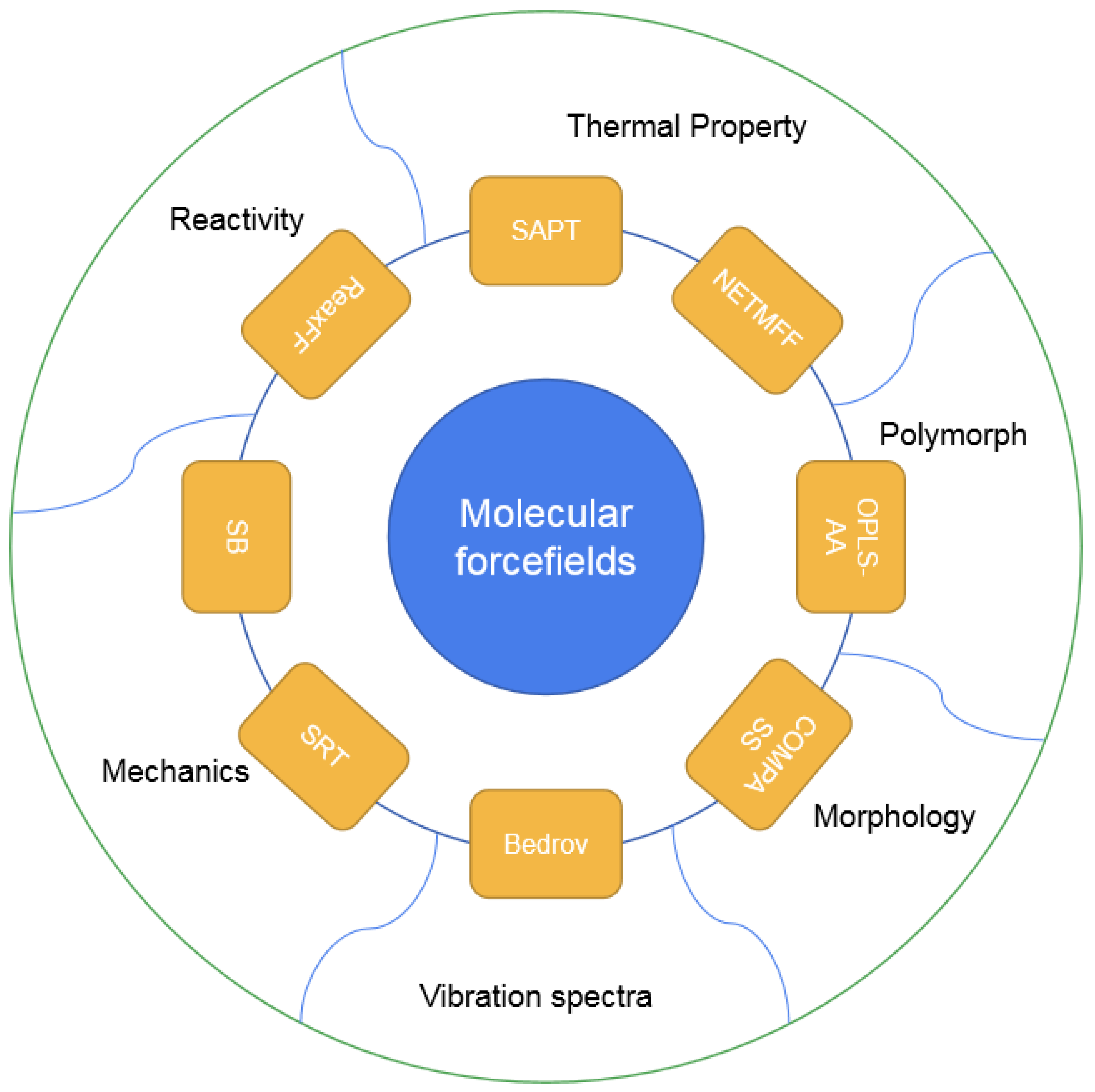
1. Introduction
2. Classic Forcefield Refitted for EMs and Their Applications
2.1. Development of Refitted FFs
| FFs | Valence Terms | van der Waals Interaction Term | Electrostatic Interaction Term | Applications |
|---|---|---|---|---|
| SRT [20] | \ | Buckingham 6-exp form | Coulomb function | RDX HMX CL-20 FOX-7 PETN (lattice parameter, density, mechanics) |
| SAPT [38] | \ | Buckingham 6-exp form | Simplified Coulomb function | FOX-7 (thermal properties, pressure responses, isothermo) |
| SRT-AMBER [32] | Harmonic bond stretching, harmonic angle bending, cosine torsion term | Buckingham 6-exp form | Coulomb function | RDX (lattice parameter, density, melting point, mechanics) TNAZ (lattice parameter, density, melting point) |
| SB [27] | Harmonic bond term, angle term, dihedral term, anharmonic torsion term | Buckingham form | Coulomb function | RDX HMX CL-20 (shock compression, shear bands, elastic constants and modulus) |
| Boyd’s [34] | Bond stretching described by Morse function, angle bending described by harmonic function | Buckingham LJ 6-12 form | Coulomb function | RDX (lattice parameter, density, thermodynamics, vibration spectra, thermal expansion, mechanics) |
| NETMFF [40] | Bond term, angle term, dihedral (torsion angle) term, out-of-plane bending angle term, cross-coupling terms of bond–bond, bond–angle couplings | Damped Buckingham form | Coulomb function | RDX (lattice parameter, density, thermal expansion) |
| GRBF [35] | Harmonic bond stretch term, bond-angle bend term, dihedral angle torsion term | Lennard–Jones 12-6 form | Coulomb function | TATB (lattice parameters, density, thermal expansion, isotherm) |
| Bedrov’s [36] | Harmonic functions of covalent bonds, three-center bends, and improper dihedrals | Buckingham 6-exp form | Coulomb function | TATB (lattice parameter, thermal expansion, mechanics, vibration spectra, thermal conductivity) |
| Neyertz’s [39] | Angle-bending deformations described by harmonic function, torsional motions around the dihedral angles τ, sp2 ring and NO2 structures kept planar described by harmonic function | Lenard-Jones 12-6 form | Coulomb function | TNT DNT (lattice parameter, density, tensile, bulk and shear modulus) |
| Dreiding [41] | Bond stretching interaction term, angle bending interaction term, dihedral angle interaction term, inversion interaction term | Lennard–Jones 12-6 form | Coulomb function | TATB (geometries, crystal packing, thermal expansion) |
| OPLS-AA [43] | Bond term, angle term, dihedral term | Lennard–Jones 12-6 form | Coulomb function | CL-20 (lattice parameter, density, polymorph prediction) |
2.2. Functional Forms of the Refitted FFs
2.3. Application of Prediction
2.3.1. Cell Parameters and Density
2.3.2. Polymorphism
2.3.3. Vibration Spectra
2.3.4. Thermal Property
2.3.5. Mechanical Property
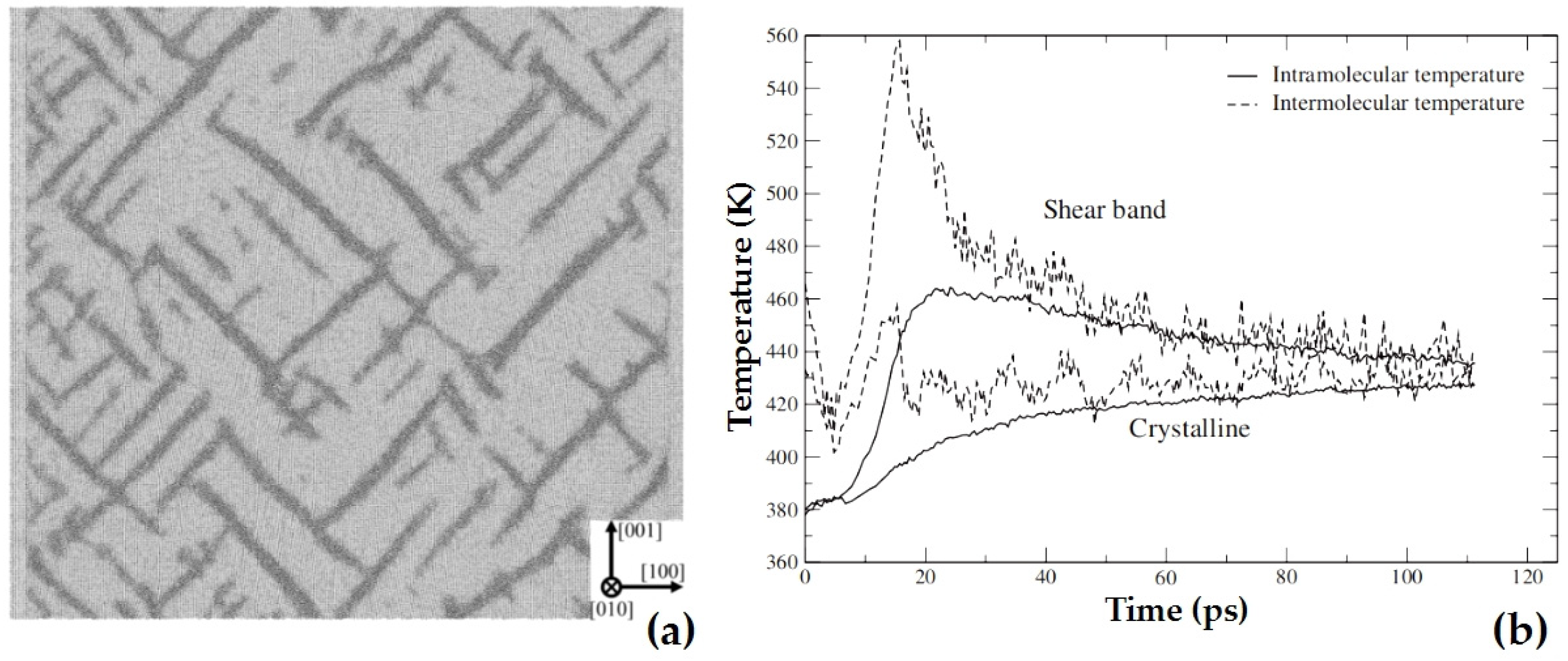
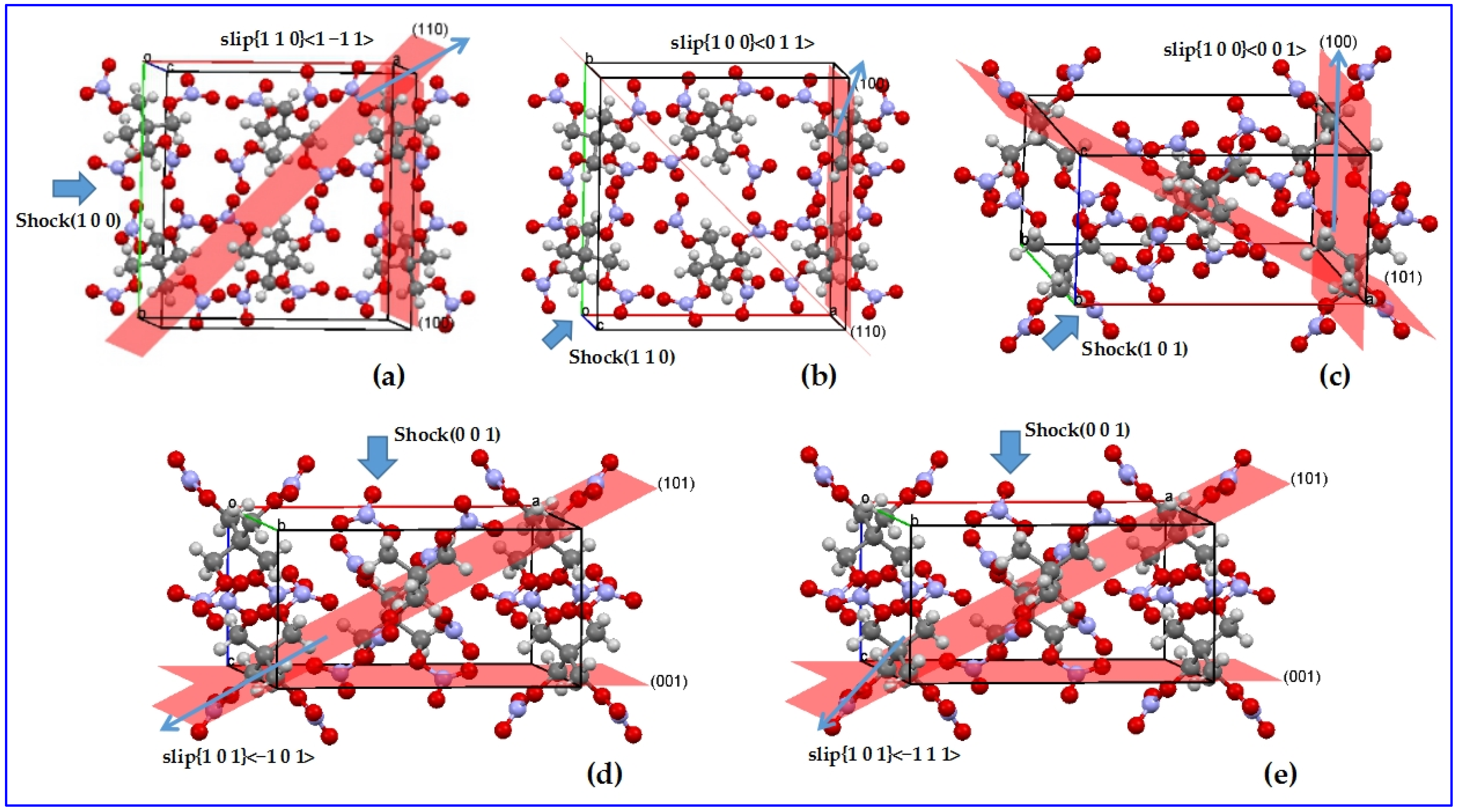
2.3.6. Shock Responses
3. Consistent Forcefields and Their Applications for EMs
3.1. Theory
3.2. Applications
3.2.1. Morphology
3.2.2. Polymorphism
3.2.3. Properties
4. Reactive Forcefields and the Applications for EMs
4.1. Theory
4.2. Applications
4.2.1. Structural Optimization
4.2.2. Vibration Spectra
4.2.3. Shock-Induced Chemistry
4.2.4. Thermal Decomposition
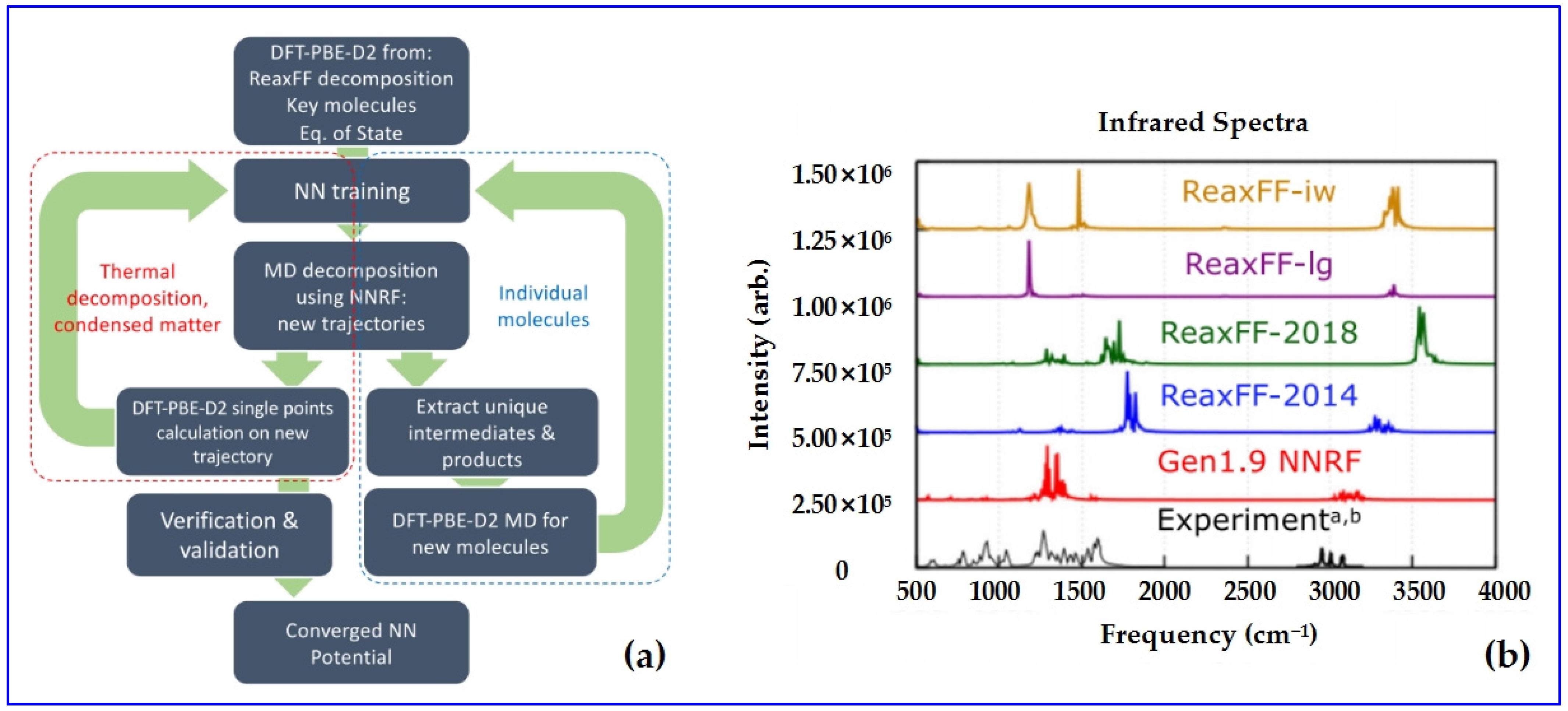
4.2.5. NN-Trained ReaxFF (NNRF)
5. Conclusions and Outlooks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BTF: | benzotrifuroxan |
| CL-20: | 2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexaazaisowurtzitane |
| DATNBI: | 4,4′,5,5′-tetranitro-1H,1′H-[2,2′-bi-imidazole]-1,1′-diamine |
| DNAN: | 2,4-dinitroanisole |
| DNP: | 3,4-dinitro-1H-pyrazole |
| DNT: | 2,4-dinitrotoluene |
| FOX-7: | 1,1-diamino-2,2-dinitroethene |
| HMX: | octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine |
| MATNB: | 1-methyl-amino-2,4,6-trinitrobenzene |
| MTNP: | 1-methyl-3,4,5-trinitro-1H-pyrazole |
| MTO: | 2,4,6-triamino-1,3,5-triazine-1,3,5-trioxide |
| MTO3N: | 2,4,6-trinitro-1,3,5-triazine-1,3,5-trioxide |
| NM: | nitromethane |
| PETN: | 2,2-bis[(nitrooxy)methyl]propane-1,3-diyldinitrate |
| RDX: | 1,3,5-trinitro-1,3,5-triazinane |
| TATB: | 1,3,5-triamino-2,4,6-trinitrobenzene |
| TATP: | triacetone triperoxide |
| TNA: | 2,4,6-trinitroaniline |
| TNAZ: | 1,3,3-trinitroazetidine |
| TNB: | 1,3,5-trinitrobenzene |
| TNT: | 1,3,5-trinitrotoluene |
References
- Akhavan, J. The Chemistry of Explosives; The Royal Society of Chemistry: Cambridge, UK, 2004. [Google Scholar]
- Zhang, X.X.; Yang, Z.J.; Nie, F.D.; Yan, Q.L. Recent advances on the crystallization engineering of energetic materials. Energetic Mater. Front. 2020, 1, 141–156. [Google Scholar] [CrossRef]
- Li, H.Z.; Zhou, X.Q.; Xu, R.; Hao, S.L.; Chen, D.; Zhou, X. Anomalous sensitivity related to crystal characteristics of 2,6-diamino-3,5- dinitropyrazing-1-oxide (LLM-105). Energetic Mater. Front. 2020, 1, 178–185. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications, 2nd ed.; Academic Press, Inc.: Cambridge, MA, USA, 1996. [Google Scholar]
- Gunsteren, W.; Berendsen, H. Computer-simulation of molecular-dynamics-methodology, applications, and perspectives in chemistry. Angew. Chem. Int. Ed. 2010, 29, 992–1023. [Google Scholar] [CrossRef]
- Zhang, C.Y. Characteristics and enlightenment from the intermolecular interactions in energetic crystals. Chin. J. Energetic Mater. 2020, 28, 889–901. [Google Scholar]
- Zhang, C.Y.; Xiong, Y.; Jiao, F.B.; Wang, M.M.; Li, H.Z. Redefining the term of “cocrystal” and broadening its intention. Cryst. Growth Des. 2019, 19, 1471–1478. [Google Scholar] [CrossRef]
- Liu, G.R.; Wei, S.H.; Zhang, C.Y. Review of the intermolecular interactions in energetic molecular cocrystals. Cryst. Growth Des. 2020, 20, 7065–7079. [Google Scholar] [CrossRef]
- Bu, R.P.; Xiong, Y.; Zhang, C.Y. Π-Π Stacking contributing to the low or reduced impact sensitivity of energetic materials. Cryst. Growth Des. 2020, 20, 2824–2841. [Google Scholar] [CrossRef]
- Cao, Y.L.; Yu, T.; Lai, W.P.; Liu, Y.Z.; Wang, B.Z. Analysis of intermolecular interactions in homologous molecular crystals of energetic materials. Energetic Mater. Front. 2020, 1, 95–102. [Google Scholar] [CrossRef]
- Li, G.; Zhang, C.Y. Review of the molecular and crystal correlations on sensitivities of energetic materials. J. Hazard. Mater. 2020, 398, 122910. [Google Scholar] [CrossRef] [PubMed]
- Xiong, X.X.; He, X.D.; Xiong, Y.; Xue, X.G.; Yang, H.J.; Zhang, C.Y. Correlation between the self-sustaining ignition ability and the impact sensitivity of energetic materials. Energetic Mater. Front. 2020, 1, 40–49. [Google Scholar] [CrossRef]
- Wang, L.L.; Xiong, Y.; Xie, W.Y.; Niu, L.L.; Zhang, C.Y. Review of crystal density prediction methods for energetic materials. Chin. J. Energetic Mater. 2020, 28, 1–12. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: Oxford, UK, 1987. [Google Scholar]
- Ray, J.R. Elastic constants and statistical ensembles in molecular dynamics. Comput. Phys. Rep. 1988, 8, 109–111. [Google Scholar] [CrossRef]
- Andersen, H.C. Molecular dynamics simulations at constant pressure and/or temperature. J. Chem. Phys. 1980, 72, 2384. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tobias, J.T.; Klein, M.L. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 1994, 101, 4177–4189. [Google Scholar] [CrossRef]
- Hahn, T. International Tables for Crystallography (Vol. A): Space-Group Symmetry; Springer: Dordrecht, The Netherlands, 1983. [Google Scholar]
- Sorescu, D.C.; Rice, B.M.; Thompson, D.L. Intermolecular potential for the hexahydro-1,3,5-trinitro-1,3,5-s-triazine crystal (RDX): A crystal packing, monte carlo and molecular dynamics study. J. Phys. Chem. B 1997, 101, 798–808. [Google Scholar] [CrossRef]
- Sorescu, D.C.; Rice, B.M.; Thompson, D.L. Molecular packing and NPT-molecular dynamics investigation of the transferability of the RDX intermolecular potential to 2,4,6,8,10,12-hexanitrohexaazaisowurtzitane. J. Phys. Chem. B 1998, 102, 948–952. [Google Scholar] [CrossRef]
- Sorescu, D.C.; Rice, B.M.; Thompson, D.L. Isothermal- isobaric molecular dynamics simulations of 1,3,5,7-tetranitro-1,3,5,7-tetraazacyclooctane (HMX) crystals. J. Phys. Chem. B 1998, 102, 6692–6695. [Google Scholar] [CrossRef]
- Sorescu, D.C.; Rice, B.M.; Thompson, D.L. A transferable intermolecular potential for nitramine crystals. J. Phys. Chem. A 1998, 102, 8386–8392. [Google Scholar] [CrossRef]
- Sorescu, D.C.; Rice, B.M.; Thompson, D.L. Molecular packing and molecular dynamics study of the transferability of a generalized nitramine intermolecular potential to non-nitramine crystals. J. Phys. Chem. A 1999, 103, 989–998. [Google Scholar] [CrossRef][Green Version]
- Sorescu, D.C.; Rice, B.M.; Thompson, D.L. Theoretical studies of the hydrostatic compression of RDX, HMX, HNIW, and PETN crystals. J. Phys. Chem. B 1999, 103, 6783–6790. [Google Scholar] [CrossRef]
- Sorescu, D.C.; Boatz, J.A.; Thompson, D.L. Classical and quantum-mechanical studies of crystalline FOX-7 (1,1-diamino-2,2-dinitroethylene). J. Phys. Chem. A 2001, 105, 5010–5021. [Google Scholar] [CrossRef]
- Smith, G.D.; Bharadwaj, R.K. Quantum chemistry based force field for simulations of HMX. J. Phys. Chem. B 1999, 103, 3570. [Google Scholar] [CrossRef]
- Cawkwell, M.J.; Sewell, T.D.; Zheng, L.; Thompson, D.L. Shock-induced shear bands in an energetic molecular crystal: Application of shock-front absorbing boundary conditions to molecular dynamics simulations. Phys. Rev. B 2008, 78, 014107. [Google Scholar] [CrossRef]
- Bedrov, D.; Hooper, J.B.; Smith, G.D.; Sewell, T.D. Shock-induced transformations in crystalline RDX: A uniaxial constant-stress Hugoniostat molecular dynamics simulation study. J. Chem. Phys. 2009, 131, 034712. [Google Scholar] [CrossRef] [PubMed]
- Cawkwell, M.J.; Ramos, K.J.; Hooks, D.E.; Sewell, T.D. Homogeneous dislocation nucleation in cyclotrimethylene trinitramine under shock loading. J. Appl. Phys. 2010, 107, 063512. [Google Scholar] [CrossRef]
- Bidault, X.; Chaudhuri, S. A flexible-molecule force field to model and study hexanitrohexaazaisowurtzitane (CL-20)-polymorphism under extreme conditions. RSC Adv. 2019, 9, 39649. [Google Scholar] [CrossRef]
- Agrawal, P.M.; Rice, B.M.; Zheng, L.Q.; Thompson, D.L. Molecular dynamics simulations of hexahydro-1,3,5-trinitro-1,3,5-s-triazine (RDX) using a combined Sorescu-Rice-Thompson AMBER force field. J. Phys. Chem. B 2006, 110, 26185–26188. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, P.M.; Rice, B.M.; Zheng, L.Q.; Velardez, G.F.; Thompson, D.L. Molecular dynamics simulations of the melting of 1,3,3-trinitroazetidine. J. Phys. Chem. B 2006, 110, 5721–5726. [Google Scholar] [CrossRef]
- Boyd, S.; Gravelle, M.; Politzer, P. Nonreactive molecular dynamics force field for crystalline hexahydro-1,3,5-trinitro-1,3,5-triazine. J. Chem. Phys. 2006, 124, 104508. [Google Scholar] [CrossRef] [PubMed]
- Gee, R.H.; Roszak, S.; Balasubramanian, K.; Fried, L.E. Ab initio based force field and molecular dynamics simulations of crystalline TATB. J. Chem. Phys. 2004, 120, 15. [Google Scholar] [CrossRef] [PubMed]
- Bedrov, D.; Borodin, O.; Smith, G.D.; Sewell, T.D.; Dattelbaum, D.M.; Stevens, L.L. A molecular dynamics simulation study of crystalline 1,3,5-triamino-2,4,6-trinitrobenzene as a function of pressure and temperature. J. Chem. Phys. 2009, 131, 224703. [Google Scholar] [CrossRef]
- Kroonblawd, M.P.; Sewell, T.D. Theoretical determination of anisotropic thermal conductivity for crystalline 1,3,5-triamino-2,4,6-trinitrobenzene (TATB). J. Chem. Phys. 2013, 139, 074503. [Google Scholar] [CrossRef]
- Taylor, D.E.; Rob, F.; Rice, B.M.; Podeszwa, R.; Szalewicz, K. A molecular dynamics study of 1,1-diamino-2,2-dinitroethylene (FOX-7) crystal using a symmetry adapted perturbation theory-based intermolecular force field. Phys. Chem. Chem. Phys. 2011, 13, 16629–16636. [Google Scholar] [CrossRef]
- Neyertz, S.; Mathieu, D.; Khanniche, S.; Brown, D. An empirically optimized classical force-field for molecular simulations of 2,4,6-trinitrotoluene (TNT) and 2,4-dinitrotoluene (DNT). J. Phys. Chem. A 2012, 116, 8374–8381. [Google Scholar] [CrossRef] [PubMed]
- Song, H.J.; Zhang, Y.G.; Li, H.; Zhou, T.T.; Huang, F.L. All-atom, non-empirical, and tailor-made force field for a-RDX from first principles. RSC Adv. 2014, 4, 40518–40533. [Google Scholar] [CrossRef]
- Mayo, S.L.; Olafson, B.D.; Goddard, W.A., III. DREIDING: A generic forcefield. J. Phys. Chem. 1990, 94, 8897–8909. [Google Scholar] [CrossRef]
- Qian, W.; Zhang, C.Y.; Xiong, Y.; Zong, H.H.; Zhang, W.B.; Shu, Y.J. Thermal expansion of explosive molecular crystal: Anisotropy and molecular stacking. Cent. Eur. J. Energetic Mater. 2014, 11, 569–580. [Google Scholar]
- Jorgensen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and testing of the OPLS all-atom force field on conformational energetics and properties of organic liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Wang, C.Y.; Ni, Y.X.; Zhang, C.Y.; Xue, X.G. Crystal structure prediction of 2,4,6,8,10,12-Hexanitro- 2,4,6,8,10,12-hexaazaisowurtzitane (CL-20) by a tailor-made OPLS-AA force field. Cryst. Growth Des. 2021, 21, 3037–3046. [Google Scholar] [CrossRef]
- Choi, S.; Prince, E. The crystal structure of cyclotrimethylenetrinitramine. Acta Crystallogr. 1972, B28, 2857–2862. [Google Scholar] [CrossRef]
- Dlott, D.D.; Fayer, M.D. Shocked molecular solids: Vibrational up pumping, defect hot spot formation, and the onset of chemistry. J. Chem. Phys. 1990, 92, 3798. [Google Scholar] [CrossRef]
- Qian, W.; Zhang, C.Y. Review of the phonon spectrum modelings for energetic crystals and their applications. Energetic Mater. Front. 2021, 2, 154–164. [Google Scholar] [CrossRef]
- Dobratz, M. Properties of Chemical Explosive and Explosive Simulants; Report No. UCRL 52997; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1981; pp. 19–131. [Google Scholar]
- Kolb, J.R.; Rizzo, H.F. Growth of 1,3,5-triamino-2,4,6-trinitrobenzene (TATB) I. Anisotropic thermal expansion. Propellants and Explos. 1979, 4, 10. [Google Scholar] [CrossRef]
- Allinger, N.L.; Yuh, Y.H.; Lii, J.H. Molecular mechanics: The MM3 force field for hydrocarbons. J. Am. Chem. Soc. 1989, 111, 8551–8566. [Google Scholar] [CrossRef]
- Weiner, S.J.; Kollman, P.A.; Case, D.A.; Singh, U.C.; Ghio, C.; Alagona, G.; Profeta, S.; Weiner, P.K. A new force field for molecular mechanical simulation of nucleic acids and proteins. J. Am. Chem. Soc. 1984, 106, 765–784. [Google Scholar] [CrossRef]
- Weiner, S.J.; Kollman, P.A.; Nguyen, D.T.; Case, D.A. An all atom force field for simulations of proteins and nucleic acids. J. Comp. Chem. 1986, 7, 230–252. [Google Scholar] [CrossRef] [PubMed]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.; Karplus, M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comp. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Dauber-Osguthorpe, P.; Roberts, V.A.; Osguthorpe, D.J.; Wolff, J.; Genest, M.; Hagler, A.T. Structure and energetics of ligand binding to proteins: E. coli dihydrofolate reductase-trimethoprim, a drug-receptor system. Proteins Struct Funct. Genet. 1988, 4, 31–47. [Google Scholar] [CrossRef] [PubMed]
- Rappé, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A., III; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable potentials for phase equilibria. 1. United-atom description of n-alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Maple, J.R.; Dinur, U.; Hagler, A.T. Derivation of force fields for molecular mechanics and dynamics from ab initio energy surfaces. Proc. Nat. Acad. Sci. USA 1988, 85, 5350–5354. [Google Scholar] [CrossRef] [PubMed]
- Hagler, A.T.; Ewig, C.S. On the use of quantum energy surfaces in the derivation of molecular force-fields. Comp. Phys. Comm. 1994, 84, 131–155. [Google Scholar] [CrossRef]
- Maple, J.R.; Thacher, T.S.; Dinur, U.; Hagler, A.T. Biosym forcefield research results in new techniques for the extraction of inter- and intramolecular forces. Chem. Des. Autom. News 1990, 5, 5–10. [Google Scholar]
- Maple, J.R.; Hwang, M.J.; Stockfisch, T.P.; Dinur, U.; Waldman, M.; Ewig, C.S.; Hagler, A.T. Derivation of Class II force fields. 1. Methodology and quantum forcefield for the alkyl functional group and alkane molecules. J. Comput. Chem. 1994, 15, 162–182. [Google Scholar] [CrossRef]
- Maple, J.R.; Hwang, M.J.; Stockfisch, T.P.; Hagler, A.T. Derivation of Class II forcefields. 3. Characterization of a quantum forcefield for the alkanes. Israel J. Chem. 1994, 34, 195–231. [Google Scholar] [CrossRef]
- Sun, H.; Mumby, S.J.; Maple, J.R.; Hagler, A.T. An ab initio CFF93 all-atom forcefield for polycarbonates. J. Am. Chem. Soc. 1994, 116, 2978–2987. [Google Scholar] [CrossRef]
- Sun, H. Ab initio calculations and forcefield development for computer simulation of polysilanes. Macromolecules 1995, 28, 701. [Google Scholar] [CrossRef]
- Hill, J.R.; Sauer, J. Molecular mechanics potential for silica and zeolite catalysts based on ab initio calculations. 1. Dense and microporous silica. J. Phys. Chem. 1994, 98, 1238–1244. [Google Scholar] [CrossRef]
- Sun, H. COMPASS: An ab initio forcefield optimized for condensed-phase applications—overview with details on alkane and benzene compounds. J. Phys. Chem B 1998, 102, 7338. [Google Scholar] [CrossRef]
- Sun, H.; Ren, P.; Fried, J.R. The COMPASS forcefield: Parameterization and validation for polyphosphazenes. Comput. Theor. Polym. Sci. 1998, 8, 229. [Google Scholar] [CrossRef]
- Rigby, D.; Sun, H.; Eichinger, B.E. Computer simulations of poly(ethylene oxides): Forcefield, PVT diagram and cyclization behavior. Polym. Int. 1998, 44, 311–330. [Google Scholar] [CrossRef]
- Peng, Z.; Ewig, C.S.; Hwang, M.J.; Waldman, M.; Hagler, A.T. Derivation of Class II force fields, 4. van der Waals parameters of alkali metal cations and halide anions. J. Phys. Chem. A 1997, 101, 7243. [Google Scholar] [CrossRef]
- Berkovitch-Yellin, Z. Toward an ab initio derivation of crystal morphology. J. Am. Chem. Soc. 1985, 107, 8239. [Google Scholar] [CrossRef]
- Hartman, P.; Bennema, P. The attachment energy as a habit controlling factor: I. theoretical considerations. J. Cryst. Growth 1980, 49, 145–156. [Google Scholar] [CrossRef]
- Docherty, R.; Clydesdale, G.; Roberts, K.J.; Bennema, P. Application of Bravais-Friedel-Donnay-Harker, attachment energy and Ising models to predicting and understanding the morphology of molecular crystals. J. Phys. D Appl. Phys. 1991, 24, 89–99. [Google Scholar] [CrossRef]
- Bravais, A. Etudes Crystallographiques; Academie des Sciences: Paris, France, 1913. [Google Scholar]
- Donnay, J.D.H.; Harker, D.A. New law of crystal morphology extending the Law of Bravais. Am. Mineral. 1937, 22, 446–467. [Google Scholar]
- Friedel, G. Studies on the Law of Bravais. Bull. Soc. Fr. Mineral. 1907, 30, 326–455. [Google Scholar]
- Gong, F.Y.; Yang, Z.J.; Qian, W.; Liu, Y.; Zhang, J.H.; Ding, L.; Lin, C.M.; Zeng, C.C.; Yan, Q.L. Kinetics for the inhibited polymorphic transition of HMX crystal after strong surface confinement. J. Phys. Chem. C 2019, 123, 11011–11019. [Google Scholar] [CrossRef]
- Zhang, M.H.; Qian, W.; Zhao, X.; Tan, Y.X.; Xu, Y.B.; Liu, Y.; Yang, Z.J. Constructing novel RDX with hierarchical structure via dye-assisted solvent induction and interfacial self-assembly. Cryst. Growth Des. 2020, 20, 4919–4927. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, M.H.; Qian, W.; Gong, F.Y.; Liu, J.H.; Zhang, Q.H.; Yang, Z.J. Interfacial engineering endowing energetic co-particles with high density and reduced sensitivity. Chem. Eng. J. 2020, 387, 124209. [Google Scholar] [CrossRef]
- Lin, C.M.; Liu, S.J.; Qian, W.; Gong, F.Y.; Zhao, X.; Pan, L.P.; Zhang, J.H.; Yang, Z.J.; Li, J.; Guo, S.Y. Controllable tuning of energetic crystals by bioinspired polydopamine. Energetic Mater. Front. 2020, 1, 59–66. [Google Scholar] [CrossRef]
- Duan, X.H.; Wei, C.X.; Liu, Y.G.; Pei, C.H. A molecular dynamics simulation of solvent effects on the crystal morphology of HMX. J. Hazard. Mater. 2010, 174, 175–180. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.Y.; Ji, C.L.; Li, H.Z.; Zhou, Y.; Xu, J.J.; Xu, R.J.; Li, J.; Luo, Y.J. Occupancy model for predicting the crystal morphologies influenced by solvents and temperature, and its application to nitroamine explosives. Cryst. Growth Des. 2013, 13, 282–290. [Google Scholar] [CrossRef]
- Song, L.; Chen, L.Z.; Wang, J.L.; Chen, F.; Lan, G.C. Prediction of crystal morphology of 3,4-dinitro-1H-pyrazole (DNP) in different solvent. J. Mol. Graphics. Model. 2017, 75, 62–70. [Google Scholar] [CrossRef]
- Zhu, S.F.; Zhang, S.H.; Gou, R.J.; Wu, C.L.; Han, G.; Jia, H.Y. Understanding the effect of solvent on the growth and crystal morphology of MTNP/CL-20 cocrystal explosive: Experimental and theoretical studies. Cryst. Res. Technol. 2018, 53, 1700299. [Google Scholar] [CrossRef]
- Xu, X.J.; Xiao, H.M.; Ju, X.H.; Gong, X.D.; Zhu, W.H. Computational studies on polynitrohexaazaadmantanes as potential high energy density materials (HEDMs). J. Phys. Chem. A 2006, 110, 5929–5933. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.J.; Xiao, H.M.; Gong, X.D.; Ju, X.H.; Chen, Z.X. Theoretical studies on the vibrational spectra, thermodynamic properties, detonation properties and pyrolysis mechanisms for polynitroadamantanes. J. Phys. Chem. A 2005, 109, 11268–11274. [Google Scholar] [CrossRef]
- Wei, X.F.; Xu, J.J.; Li, H.Z.; Long, X.P.; Zhang, C.Y. Comparative study of experiments and calculations on the polymorphisms of 2,4,6,8,10,12-hexanitro-2,4,6,8,10,12- hexaazaisowurtzitane (CL-20) precipitated by solvent/antisolvent method. J. Phys. Chem. C 2016, 120, 5042–5051. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Cao, Y.F.; Li, H.Z.; Zhou, Y.; Zhou, J.H.; Gao, T.; Zhang, H.B.; Yang, Z.W.; Jiang, G. Toward low-sensitive and high-energetic cocrystal I: Evaluation of the power and the safety of observed energetic cocrystals. Cryst. Eng. Comm. 2013, 15, 4003. [Google Scholar] [CrossRef]
- Qiu, L.; Xiao, H.M.; Zhu, W.H.; Xiao, J.J.; Zhu, W. Ab initio and molecular dynamics studies of crystalline TNAD (trans-1,4,5,8-tetranitro-1,4,5,8-tetraazadecalin). J. Phys. Chem. B 2006, 110, 10651–10661. [Google Scholar] [CrossRef]
- Qiu, L.; Zhu, W.H.; Xiao, J.J.; Zhu, W.; Xiao, H.M.; Huang, H.; Li, J.S. Molecular dynamics simulations of TNAD (trans-1,4,5,8-tetranitro-1,4,5,8-tetraazadecalin)- based PBXs. J. Phys. Chem. B 2007, 111, 1559–1566. [Google Scholar] [CrossRef]
- Qiu, L.; Zhu, W.H.; Xiao, J.J.; Xiao, H.M. Theoretical studies of solid bicyclo-HMX: Effects of hydrostatic pressure and temperature. J. Phys. Chem. B 2008, 112, 3882–3893. [Google Scholar] [CrossRef] [PubMed]
- Weiner, J.H. Statistical Mechanics of Elasticity; Dover Publication: New York, NY, USA, 1983. [Google Scholar]
- Swenson, R.J. Comments for viral systems for bounded systems. Am. J. Phys. 1983, 51, 940–942. [Google Scholar] [CrossRef]
- Zhu, W.; Xiao, J.J.; Zhu, W.H.; Xiao, H.M. Molecular dynamics simulations of RDX and RDX-based plastic-bonded explosives. J. Hazard. Mater. 2009, 164, 1082–1088. [Google Scholar] [CrossRef]
- Qiu, L.; Xiao, H.M. Molecular dynamics study of binding energies, mechanical properties and detonation performances of bicyclo-HMX-based PBXs. J. Hazard. Mater. 2009, 164, 329–336. [Google Scholar] [CrossRef]
- Xiao, J.J.; Wang, W.R.; Chen, J.; Ji, G.F.; Zhu, W.; Xiao, H.M. Study on structures, sensitivity and mechanical properties of HMX and HMX-based PBXs with molecular dynamics simulation. Comput. Theor. Chem. 2012, 999, 21–27. [Google Scholar] [CrossRef]
- Xu, X.J.; Xiao, H.M.; Xiao, J.J.; Zhu, W.; Huang, H.; Li, J.S. Molecular dynamics simulations for pure ε-CL-20 and ε-CL-20-based PBXs. J. Phys. Chem. B 2006, 110, 7203–7207. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.Q.; Qian, W.; Lu, H.C.; Yang, W.; Zhang, C.Y.; Fan, G.J.; Ma, Q. Polymorphism in a non-sensitive-high-energy material: Discovery of a new polymorph and crystal structure of 4,4′,5,5′-tetranitro- 1H,1′H-[2,2′-bi-imidazole]-1,1′-diamine. Cryst. Growth Des. 2020, 20, 8005. [Google Scholar] [CrossRef]
- Brenner, D.W.; Shendarova, O.A.; Harrison, J.A.; Stuart, S.J.; Ni, B.; Sinnott, S.B. A second-generation reactive emprical bond order (REBO) potential energy expression for hydrocarbons. J. Phys. Condens. Matter. 2002, 1, 783–802. [Google Scholar] [CrossRef]
- van Duin, A.C.T.; Dasgupta, S.; Lorant, F.; Goddard, W.A., III. ReaxFF: A reactive force field for hydrocarbons. J. Phys. Chem. A 2001, 10, 9396–9409. [Google Scholar] [CrossRef]
- van Duin, A.C.T.; Merinov, B.V.; Han, S.S.; Dorso, C.A.; Goddard, W.A., III. ReaxFF reactive force field for the Y-doped BaZrO3 proton conductor with applications to diffusion rates for multigranular systems. J. Phys. Chem. A 2008, 112, 11414–11422. [Google Scholar] [CrossRef] [PubMed]
- van Duin, A.C.T.; Bryantsev, V.S.; Diallo, M.S.; Goddard, W.A., III; Rahaman, O.; Doren, D.J.; Raymand, D.; Hermansson, K. Development and validation of a ReaxFF reactive force field for Cu cation/water interactions and copper metal/metal oxide/metal hydroxide condensed phases. J. Phys. Chem. A 2010, 114, 9507–9514. [Google Scholar] [CrossRef] [PubMed]
- Ye, C.C.; An, Q.; Goddard, W.A., III; Cheng, T.; Liu, W.G.; Zybin, S.V.; Ju, X.H. Initial decomposition reaction of di-tetrazine-tetroxide (DTTO) from quantum molecular dynamics: Implications for a promising energetic material. J. Mater. Chem. A 2015, 3, 1972–1978. [Google Scholar] [CrossRef]
- Ye, C.C.; An, Q.; Cheng, T.; Zybin, S.V.; Naserifar, S.; Ju, X.H.; Goddard, W.A., III. Reaction mechanism from quantum molecular dynamics for the initial thermal decomposition of 2,4,6-triamino-1,3,5-triazine- 1,3,5-trioxide (MTO) and 2,4,6-trinitro-1,3,5-triazine-1,3,5-trioxide (MTO3N), promising green energetic materials. J. Mater. Chem. A 2015, 3, 12044. [Google Scholar] [CrossRef]
- Zhu, W.H.; Huang, H.; Huang, H.J.; Xiao, H.M. Initial chemical events in shocked octahydro-1,3,5,7-tetranitro -1,3,5,7-tetrazocine: A new initiation decomposition mechanism. J. Chem. Phys. 2012, 136, 044516. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.T.; Cheng, T.; Zybin, S.V.; Goddard, W.A., III; Huang, F.L. Reaction mechanisms and sensitivity of silicon nitrocarbamate and related systems from quantum mechanics reaction dynamics. J. Mater. Chem. A 2018, 6, 5082. [Google Scholar] [CrossRef]
- Zhou, T.T.; Zybin, S.V.; Goddard, W.A., III; Cheng, T.; Naserifar, S.; Jaramillo-Boterob, A.; Huang, F.L. Predicted detonation properties at the Chapman-Jouguet state for proposed energetic materials (MTO and MTO3N) from combined ReaxFF and quantum mechanics reactive dynamics. Phys. Chem. Chem. Phys. 2018, 20, 3953. [Google Scholar] [CrossRef]
- Naserifar, S.; Zybin, S.V.; Ye, C.C.; Goddard, W.A., III. Prediction of structures and properties of 2,4,6-triamino- 1,3,5-triazine-1,3,5-trioxide (MTO) and 2,4,6-trinitro-1,3,5-triazine- 1,3,5-trioxide (MTO3N) green energetic materials from DFT and ReaxFF molecular modeling. J. Mater. Chem. A 2016, 4, 1264. [Google Scholar] [CrossRef]
- Guo, D.Z.; Zybin, S.V.; An, Q.; Goddard, W.A., III; Huang, F.L. Prediction of the Chapman-Jouguet chemical equilibrium state in a detonation wave from first principles based reactive molecular dynamics. Phys. Chem. Chem. Phys. 2016, 18, 2015. [Google Scholar] [CrossRef]
- Xue, X.G.; Wen, Y.S.; Zhang, C.Y. Early decay mechanism of shocked ε-CL-20: A molecular dynamics simulation study. J. Phys. Chem. C 2016, 120, 21169–21177. [Google Scholar] [CrossRef]
- He, Z.; Chen, J.; Ji, G.; Liu, L.; Zhu, W.; Wu, Q. Dynamic responses and initial decomposition under shock loading: A DFTB calculation combined with MSST method for β-HMX with molecular vacancy. J. Phys. Chem. B 2015, 119, 10673–10681. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.Y.; Jiao, Q.J.; Zhang, C.Y. Early events when heating 1,1-diamino-2,2-dinitroethylene: Self-consistent charge density-functional tight-binding molecular dynamics simulations. J. Phys. Chem. C 2018, 122, 15125–15132. [Google Scholar] [CrossRef]
- Wang, J.K.; Xiong, Y.; Li, H.Z.; Zhang, C.Y. Reversible hydrogen transfer as new sensitivity mechanism for energetic materials against external stimuli: A case of the insensitive 2,6-diamino-3,5-dinitropyrazine-1-oxide. J. Phys. Chem. C 2018, 122, 1109–1118. [Google Scholar] [CrossRef]
- Wu, X.W.; Liu, Z.C.; Zhu, W.H. Coupling effect of high temperature and pressure on the decomposition mechanism of crystalline HMX. Energetic Mater. Front. 2020, 1, 90–94. [Google Scholar] [CrossRef]
- Liu, G.R.; Xiong, Y.; Gou, R.J.; Zhang, C.Y. Difference in the thermal stability of polymorphic organic crystals: A comparative study of the early events of the thermal decay of 2,4,6,8,10,12-hexanitro- 2,4,6,8,10,12-hexaazaisowurtzitane (CL-20) polymorphs under the volume constraint condition. J. Phys. Chem. C 2019, 123, 16565–16576. [Google Scholar] [CrossRef]
- Manner, V.W.; Cawkwell, M.J.; Kober, E.M.; Myers, T.W.; Brown, G.W.; Tian, H.Z.; Snyder, C.J.; Perriot, R.; Preston, D.N. Examining the chemical and structural properties that influence the sensitivity of energetic nitrate esters. Chem. Sci. 2018, 9, 3649. [Google Scholar] [CrossRef]
- Liu, L.C.; Liu, Y.; Zybin, S.V.; Sun, H.; Goddard, W.A., III. ReaxFF-lg: Correction of the ReaxFF reactive force field for London dispersion, with applications to the equations of state for energetic materials. J. Phys. Chem. A 2011, 115, 11016–11022. [Google Scholar] [CrossRef]
- Katz, G.; Zybin, S.; Goddard, W.A., III; Zeiri, Y.; Kosloff, R. Direct MD simulations of Terahertz absorption and 2D spectroscopy applied to explosive crystals. J. Phys. Chem. Lett. 2014, 5, 772–776. [Google Scholar] [CrossRef] [PubMed]
- Strachan, A.; van Duin, A.C.T.; Chakraborty, D.; Dasgupta, S.; Goddard, W.A., III. Shock waves in high-energy materials: The initial chemical events in nitramine RDX. Phys. Rev. Lett. 2003, 91, 098301. [Google Scholar] [CrossRef]
- Zhang, L.Z.; Zybin, S.V.; van Duin, A.C.T.; Dasgupta, S.; Goddard, W.A., III; Kober, E.M. Carbon cluster formation during thermal decomposition of octahydro-1,3,5,7-tetranitro -1,3,5,7-tetrazocine and 1,3,5-Triamino-2,4,6- trinitrobenzene high explosives from ReaxFF reactive molecular dynamics simulations. J. Phys. Chem. A 2009, 113, 10619–10640. [Google Scholar] [CrossRef]
- Zhou, T.T.; Liu, L.C.; Goddard, W.A., III; Zybin, S.V.; Huang, F.L. ReaxFF reactive molecular dynamics on silicon pentaerythritol tetranitrate crystal validates the mechanism for the colossal sensitivity. Phys. Chem. Chem. Phys. 2014, 16, 23779. [Google Scholar] [CrossRef]
- Guo, D.Z.; An, Q.; Zybin, S.V.; Goddard, W.A., III; Huang, F.L.; Tang, B. The co-crystal of TNT/CL-20 leads to decreased sensitivity toward thermal decomposition from first principles based reactive molecular dynamics. J. Mater. Chem. A 2015, 3, 5409. [Google Scholar] [CrossRef]
- Zybin, S.V.; Goddard, W.A., III; Xu, P.; van Duin, A.C.T.; Thompson, A.P. Physical mechanism of anisotropic sensitivity in pentaerythritol tetranitrate from compressive-shear reaction dynamics simulations. Appl. Phys. Lett. 2010, 96, 081918. [Google Scholar] [CrossRef]
- An, Q.; Liu, Y.; Zybin, S.V.; Kim, H.J.; Goddard, W.A., III. Anisotropic shock sensitivity of cyclotrimethylene trinitramine (RDX) from compress-and-shear reactive dynamics. J. Phys. Chem. C 2012, 116, 10198–10206. [Google Scholar] [CrossRef]
- Zhou, T.T.; Zybin, S.V.; Liu, Y.; Huang, F.L.; Goddard, W.A., III. Anisotropic shock sensitivity for β-octahydro-1,3,5,7-tetranitro-1,3,5,7-tetrazocine energetic material under compressive-shear loading from ReaxFF-lg reactive dynamics simulations. J. Appl. Phys. 2012, 111, 124904. [Google Scholar] [CrossRef]
- Song, H.J.; Zhou, T.T.; Huang, F.L.; Hong, T. Microscopic physical and chemical responses of slip systems in the β-HMX single crystal under low pressure and long pulse loading. Acta Phys. Chim. Sin. 2014, 30, 2024–2034. [Google Scholar]
- Zhou, T.T.; Lou, J.F.; Song, H.J.; Huang, F.L. Anisotropic shock sensitivity in a single crystal δ-cyclotetramethylene tetranitramine: A reactive molecular dynamics study. Phys. Chem. Chem. Phys. 2015, 17, 7924. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.T.; Zhang, Y.G.; Lou, J.F.; Song, H.J.; Huang, F.L. A reactive molecular dynamics study on the anisotropic sensitivity in single crystal α-cyclotetramethylene tetranitramine. RSC Adv. 2015, 5, 8609. [Google Scholar] [CrossRef]
- Zhou, T.T.; Song, H.J.; Huang, F.L. The slip and anisotropy of TATB crystal under shock loading via molecular dynamics simulation. Acta Phys. Chim. Sin. 2017, 33, 949–959. [Google Scholar] [CrossRef]
- Wen, Y.S.; Xue, X.G.; Zhou, X.Q.; Guo, F.; Long, X.P.; Zhou, Y.; Li, H.Z.; Zhang, C.Y. Twin induced sensitivity enhancement of HMX versus shock: A molecular reactive force field simulation. J. Phys. Chem. C 2013, 117, 24368–24374. [Google Scholar] [CrossRef]
- Xue, X.G.; Wen, Y.S.; Long, X.P.; Li, J.S.; Zhang, C.Y. Influence of dislocations on the shock sensitivity of RDX: Molecular dynamics simulations by reactive force field. J. Phys. Chem. C 2015, 119, 13735–13742. [Google Scholar] [CrossRef]
- Deng, C.; Liu, J.; Xue, X.G.; Long, X.P.; Zhang, C.Y. Coupling effect of shock, heat, and defect on the decay of energetic materials: A case of reactive molecular dynamics simulations on 1,3,5-trinitro-1,3,5-triazinane. J. Phys. Chem. C 2018, 122, 27875–27884. [Google Scholar] [CrossRef]
- Zhong, K.; Xiong, Y.; Liu, J.; Zhang, C.Y. Enhanced shockwave-absorption ability of the molecular disorder rooting for the reactivity elevation of energetic materials. Energetic Mater. Front. 2020, 1, 103–116. [Google Scholar] [CrossRef]
- Deng, C.; Xue, X.G.; Chi, Y.; Li, H.Z.; Long, X.P.; Zhang, C.Y. Nature of the enhanced self-heating ability of imperfect energetic crystals relative to perfect ones. J. Phys. Chem. C 2017, 121, 12101–12109. [Google Scholar] [CrossRef]
- Wen, Y.S.; Zhang, C.Y.; Xue, X.G.; Long, X.P. Cluster evolution during the early stages of heating explosives and its relationship to sensitivity: A comparative study of TATB, β-HMX and PETN by molecular reactive force field simulations. Phys. Chem. Chem. Phys. 2015, 17, 12013. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Wen, Y.S.; Xue, X.G.; Liu, J.; Ma, Y.; He, X.D.; Long, X.P. Sequential molecular dynamics simulations: A strategy for complex chemical reactions and a case study on the graphitization of cooked 1,3,5-triamino-2,4,6-trinitrobenzene. J. Phys. Chem. C 2016, 120, 25237–25245. [Google Scholar] [CrossRef]
- Xue, X.G.; Ma, Y.; Zeng, Q.; Zhang, C.Y. Initial decay mechanism of the heated CL-20/HMX cocrystal: A case of the cocrystal mediating the thermal stability of the two pure components. J. Phys. Chem. C 2017, 121, 4899–4908. [Google Scholar] [CrossRef]
- Zhong, K.; Xiong, Y.; Zhang, C.Y. Reactive molecular dynamics insight into the influence of volume filling degree on the thermal explosion of energetic materials and its origin. Energetic Mater. Front. 2020, 1, 201–215. [Google Scholar] [CrossRef]
- Senftle, T.P.; Hong, S.; Islam, M.M.; Kylasa, S.B.; Zheng, Y.X.; Shin, Y.K.; Junkermeier, C.; Engel-Herbert, R.; Janik, M.J.; Aktulga, H.M.; et al. The ReaxFF reactive force-field: Development, applications and future directions. NPJ Comput. Mater. Sci. 2016, 2, 15011. [Google Scholar] [CrossRef]
- Bartók, A.P.; Payne, M.C.; Kondor, R.; Csányi, G. Gaussian approximation potentials: The accuracy of quantum mechanics, without the electrons. Phys. Rev. Lett. 2010, 104, 136403. [Google Scholar] [CrossRef]
- Thompson, A.P.; Swiler, L.P.; Trott, C.R.; Foiles, S.M.; Tucker, G.J. Spectral neighbor analysis method for automated generation of quantum-accurate interatomic potentials. J. Comput. Phys. 2015, 285, 316–330. [Google Scholar] [CrossRef]
- Butler, K.T.; Davies, D.W.; Cartwright, H.; Isayev, O.; Walsh, A. Machine learning for molecular and materials science. Nature 2018, 559, 547–555. [Google Scholar] [CrossRef]
- Musil, F.; De, S.; Yang, J.; Campbell, J.E.; Day, G.M.; Ceriotti, M. Machine learning for the structure-energy-property landscapes of molecular crystals. Chem. Sci. 2018, 9, 1289–1300. [Google Scholar] [CrossRef]
- Wang, P.J.; Fan, J.Y.; Su, Y.; Zhao, J.J. Energetic potential of hexogen constructed by machine learning. Acta Phys. Sin. 2020, 69, 238702. [Google Scholar] [CrossRef]
- Yoo, P.; Sakano, M.; Desai, S.; Islam, M.M.; Liao, P.L.; Strachan, A. Neural network reactive force field for C, H, N, and O systems. NPJ Comput. Mater. Sci. 2021, 7, 9. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qian, W.; Xue, X.; Liu, J.; Zhang, C. Molecular Forcefield Methods for Describing Energetic Molecular Crystals: A Review. Molecules 2022, 27, 1611. https://doi.org/10.3390/molecules27051611
Qian W, Xue X, Liu J, Zhang C. Molecular Forcefield Methods for Describing Energetic Molecular Crystals: A Review. Molecules. 2022; 27(5):1611. https://doi.org/10.3390/molecules27051611
Chicago/Turabian StyleQian, Wen, Xianggui Xue, Jian Liu, and Chaoyang Zhang. 2022. "Molecular Forcefield Methods for Describing Energetic Molecular Crystals: A Review" Molecules 27, no. 5: 1611. https://doi.org/10.3390/molecules27051611
APA StyleQian, W., Xue, X., Liu, J., & Zhang, C. (2022). Molecular Forcefield Methods for Describing Energetic Molecular Crystals: A Review. Molecules, 27(5), 1611. https://doi.org/10.3390/molecules27051611






