Hedgehog, Chamomile, and Multipetal Polymeric Structures on the Nanoparticle Surface: Computer Modelling
Abstract
1. Introduction
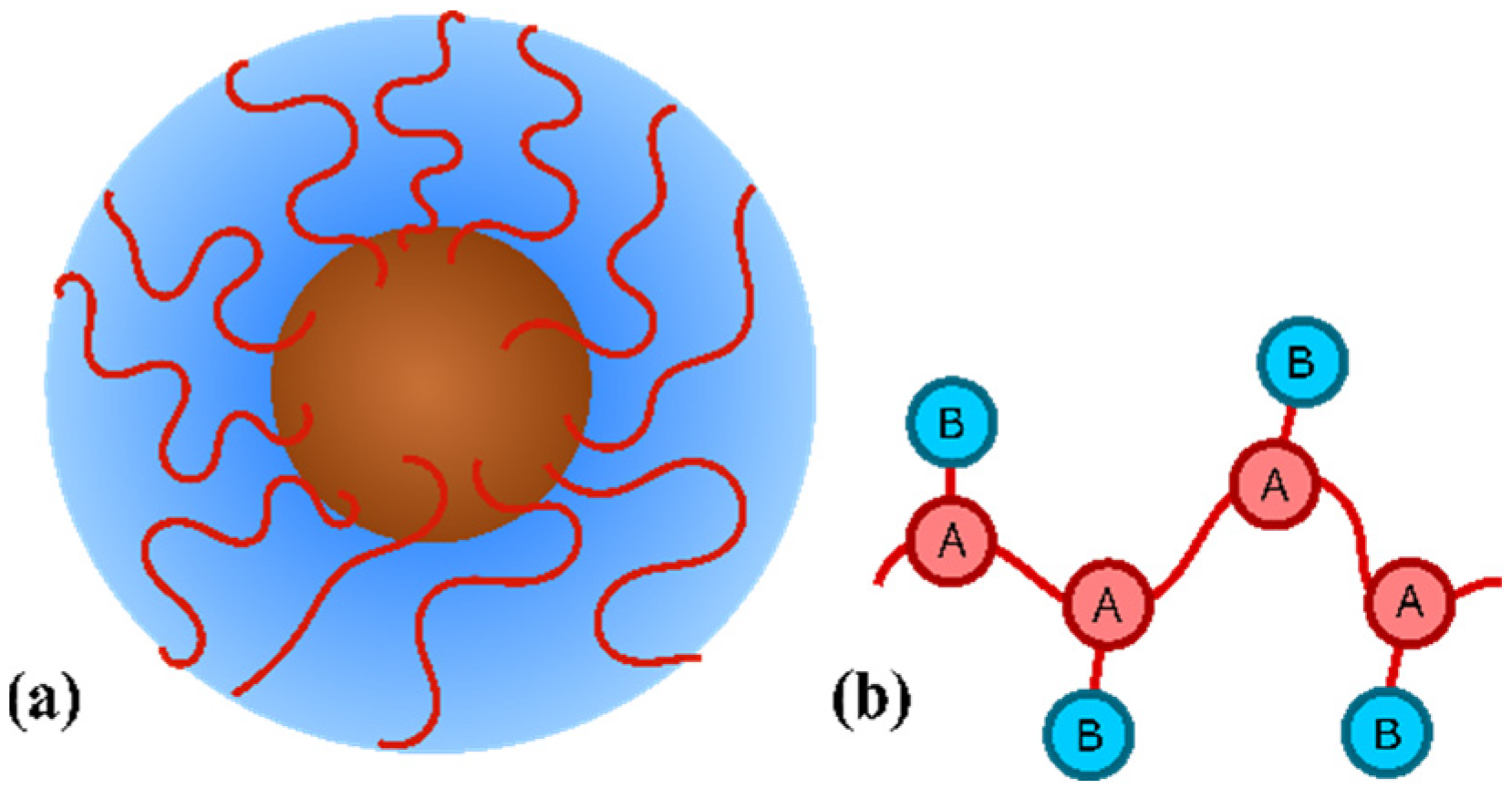
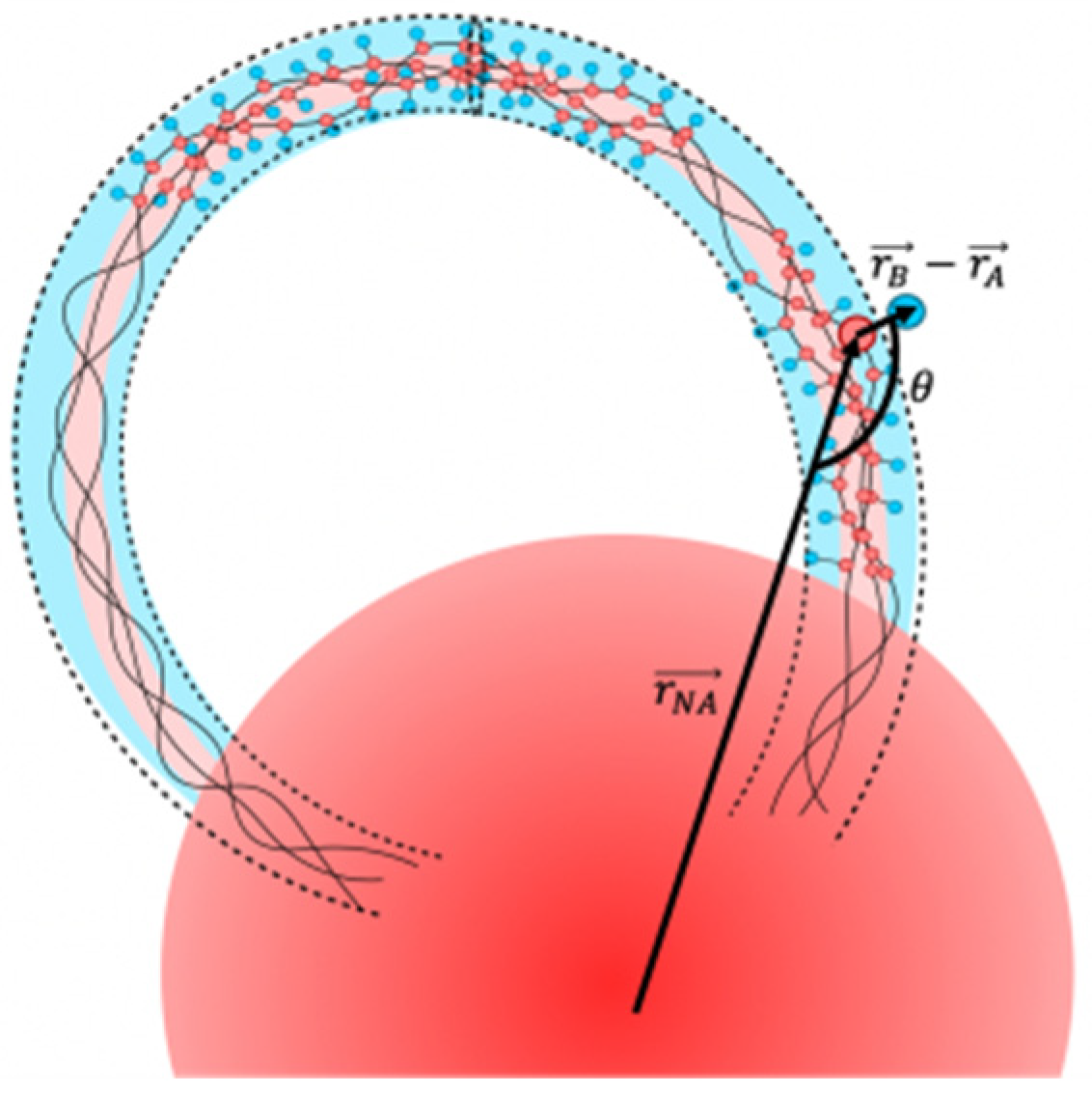
2. Model and Experimental Technique
3. Results of Computer Modeling
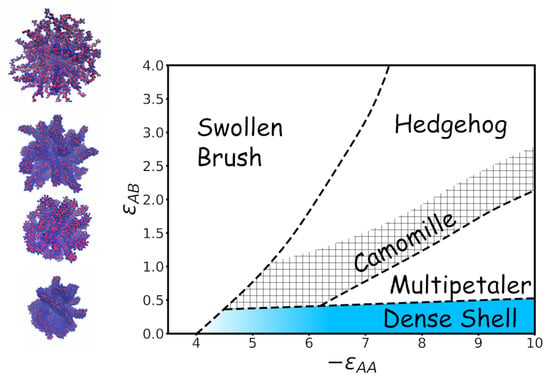
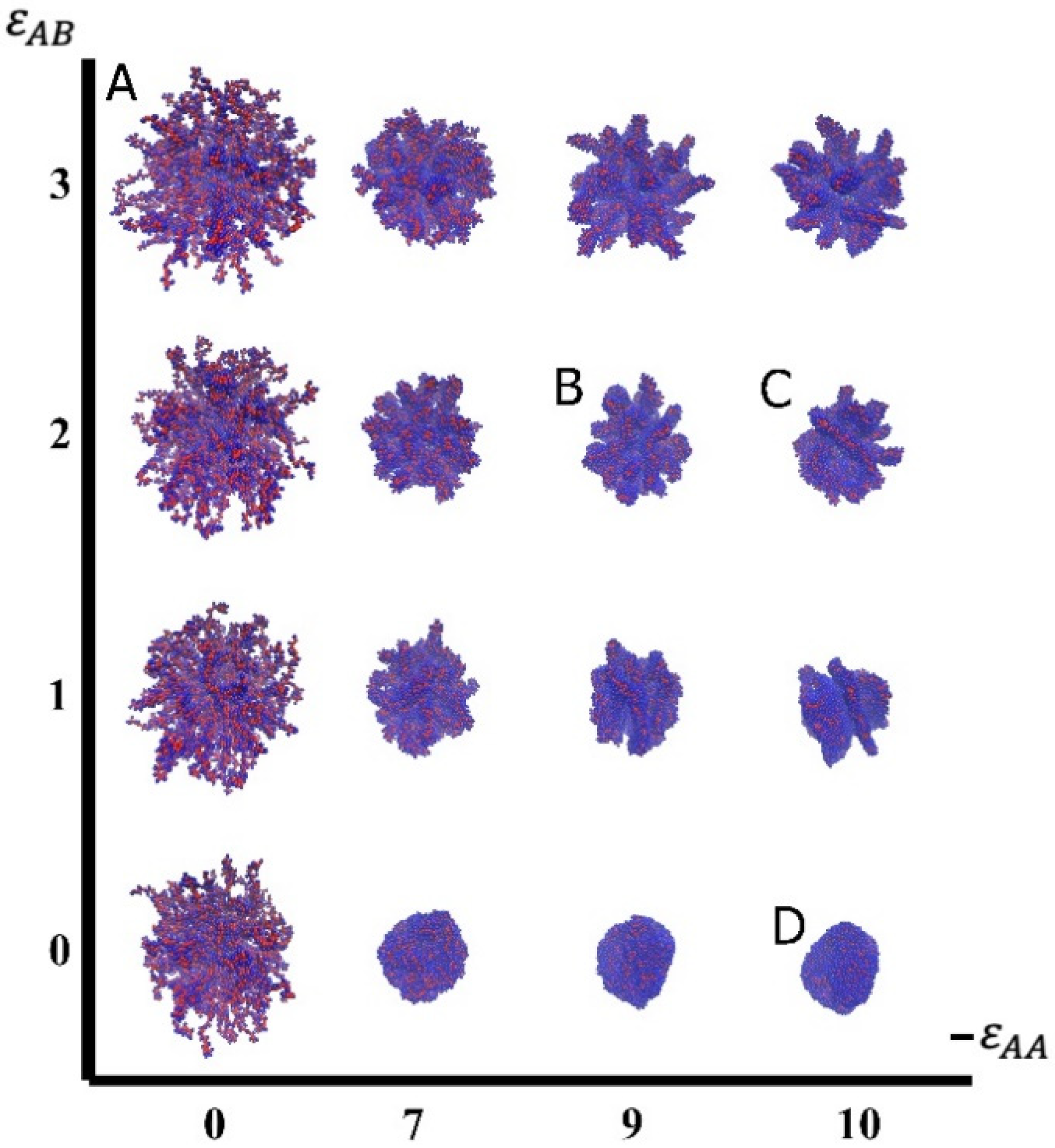
3.1. Visualization
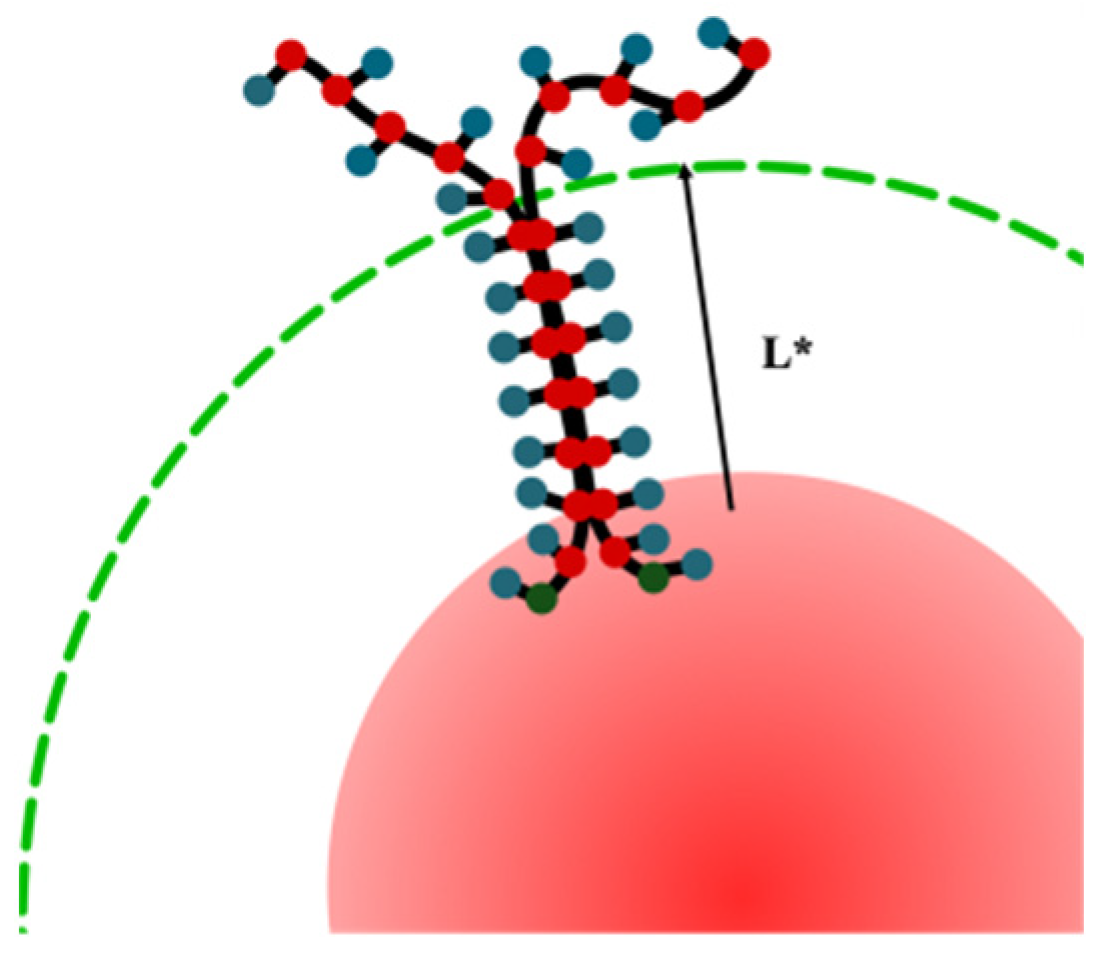
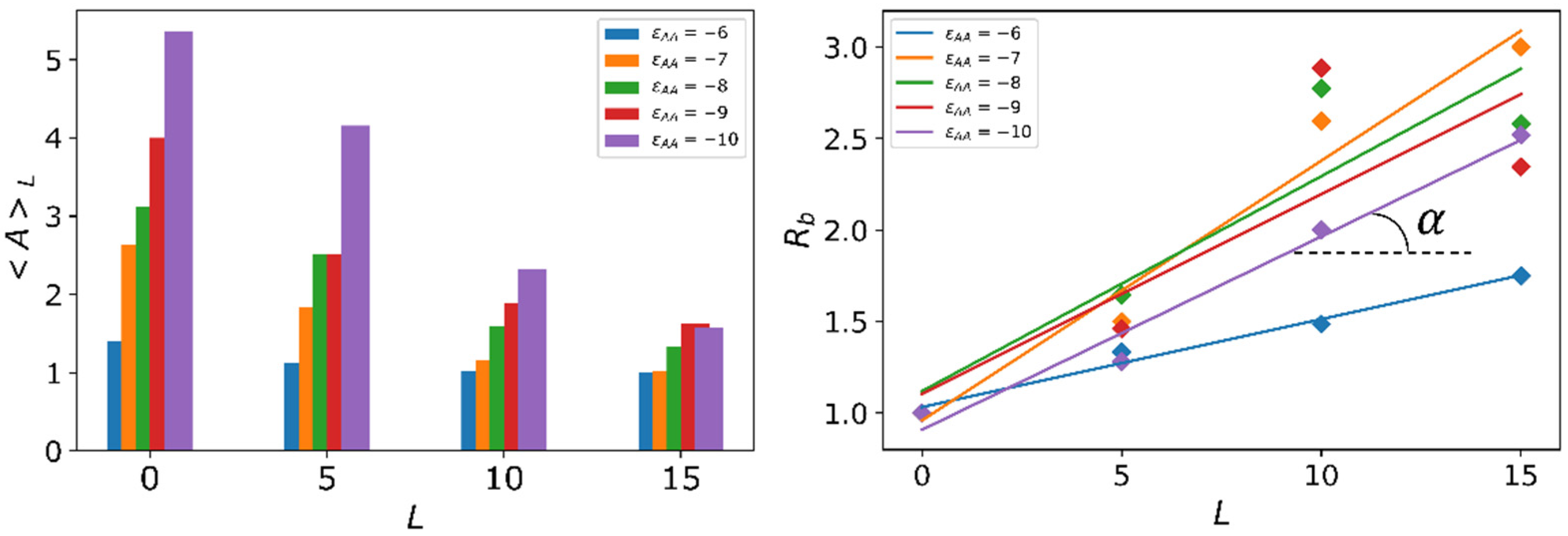
3.2. Quantitative Characteristics
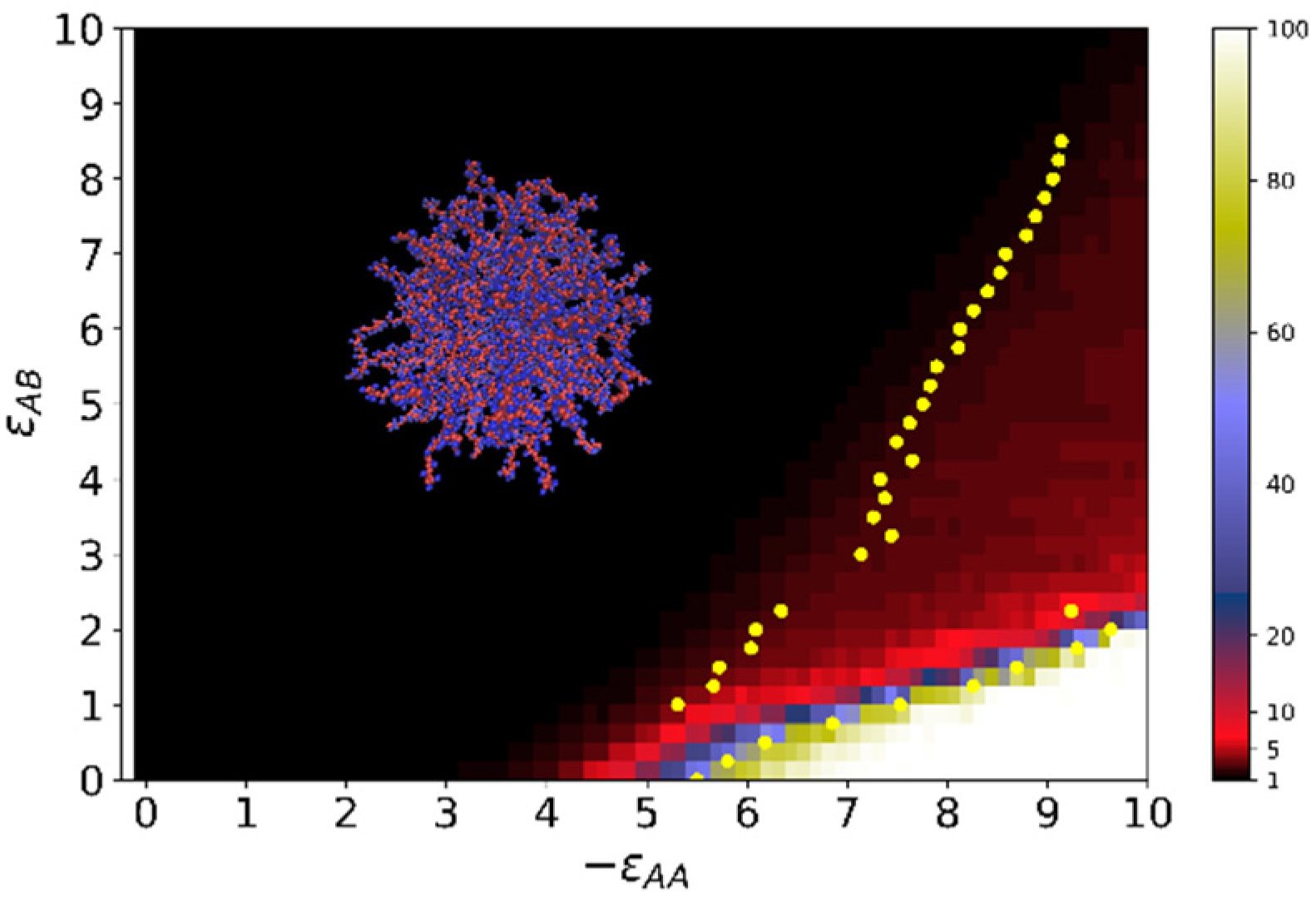
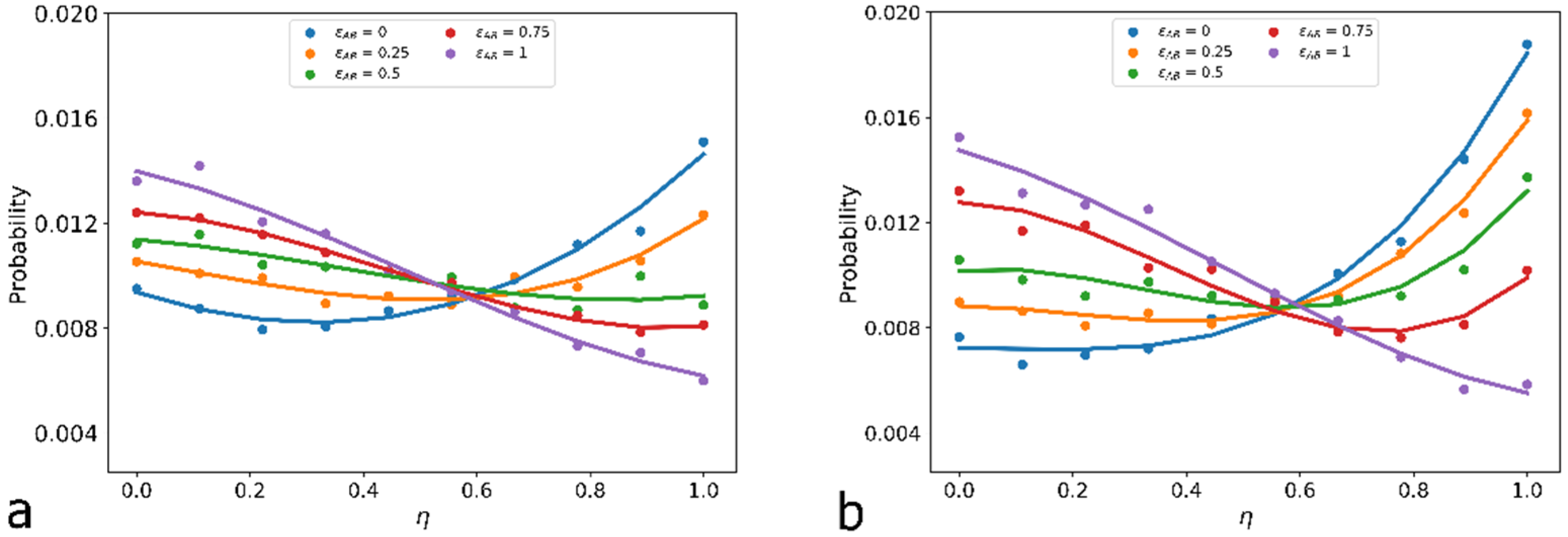
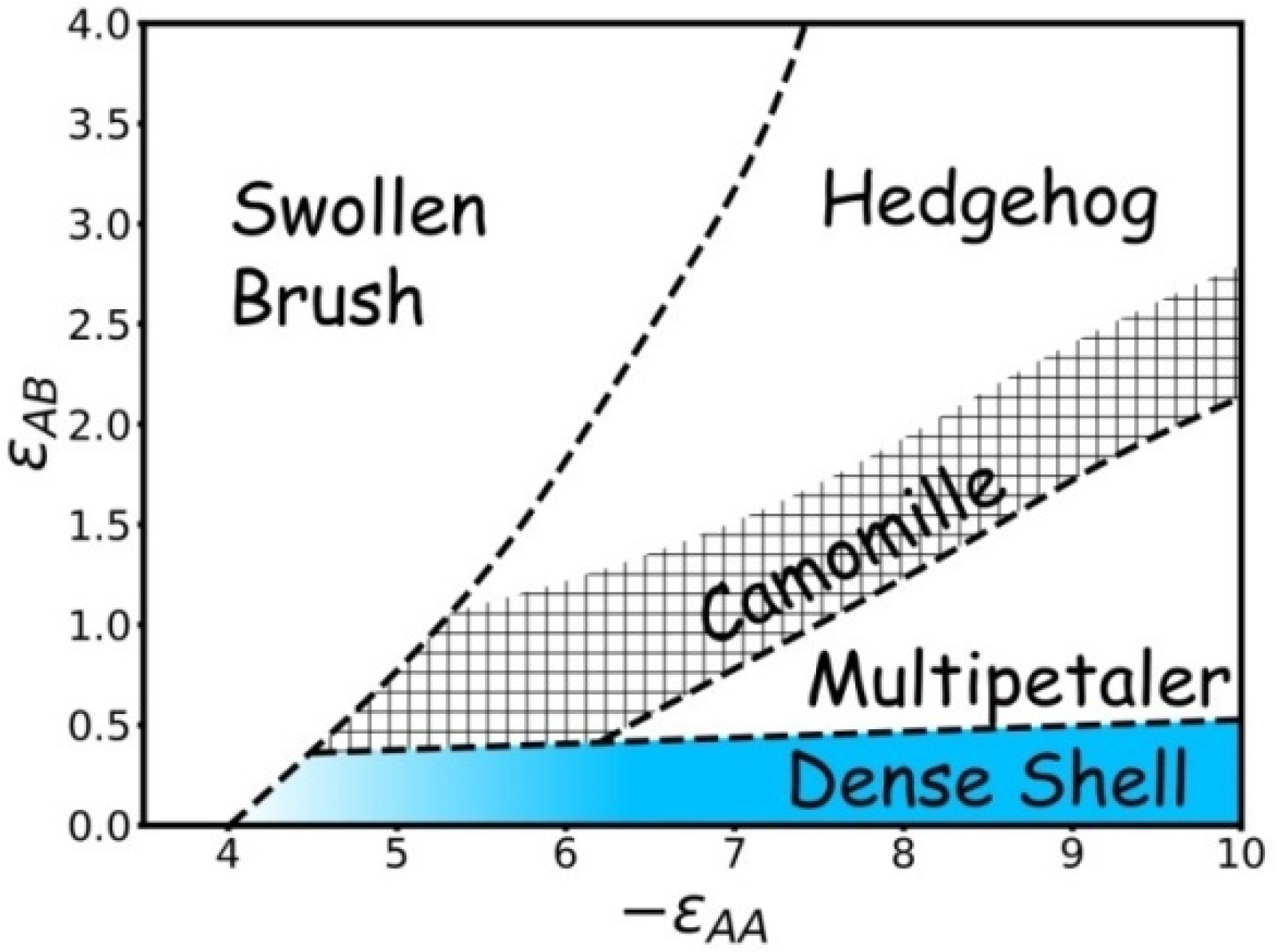
3.3. Results of Calculations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Soppimath, K.S.; Aminabhavi, T.M.; Kulkarni, A.R.; Rudzinski, W.E. Biodegradable Polymeric Nanoparticles as Drug Delivery Devices. J. Control. Release 2001, 70, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Patel, T.; Zhou, J.; Piepmeier, J.M.; Saltzman, W.M. Polymeric Nanoparticles for Drug Delivery to the Central Nervous System. Adv. Drug Deliv. Rev. 2012, 64, 701–705. [Google Scholar] [CrossRef] [PubMed]
- Masood, F. Polymeric Nanoparticles for Targeted Drug Delivery System for Cancer Therapy. Mater. Sci. Eng. C 2016, 60, 569–578. [Google Scholar] [CrossRef] [PubMed]
- Kamaly, N.; Yameen, B.; Wu, J.; Farokhzad, O.C. Degradable Controlled-Release Polymers and Polymeric Nanoparticles: Mechanisms of Controlling Drug Release. Chem. Rev. 2016, 116, 2602–2663. [Google Scholar] [CrossRef]
- Sun, Y.; Li, B.; Cao, Q.; Liu, T.; Li, J. Targeting Cancer Stem Cells with Polymer Nanoparticles for Gastrointestinal Cancer Treatment. Stem Cell Res. Ther. 2022, 13, 489. [Google Scholar] [CrossRef] [PubMed]
- Caraway, C.A.; Gaitsch, H.; Wicks, E.E.; Kalluri, A.; Kunadi, N.; Tyler, B.M. Polymeric Nanoparticles in Brain Cancer Therapy: A Review of Current Approaches. Polymers 2022, 14, 2963. [Google Scholar] [CrossRef]
- Bigaj-Józefowska, M.J.; Grześkowiak, B.F. Polymeric Nanoparticles Wrapped in Biological Membranes for Targeted Anticancer Treatment. Eur. Polym. J. 2022, 176, 111427. [Google Scholar] [CrossRef]
- La Barbera, L.; Mauri, E.; D’Amelio, M.; Gori, M. Functionalization Strategies of Polymeric Nanoparticles for Drug Delivery in Alzheimer’s Disease: Current Trends and Future Perspectives. Front. Neurosci. 2022, 16, 939855. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhang, G.C.; Ge, J.J.; Li, G.H.; Zhang, J.Q.; Ding, B.D. Preparation of Microgel Nanospheres and Their Application in EOR. Presented at the International Oil and Gas Conference and Exhibition in China, Beijing, China, 8 June 2010; p. SPE-130357-MS. [Google Scholar]
- ShamsiJazeyi, H.; Miller, C.A.; Wong, M.S.; Tour, J.M.; Verduzco, R. Polymer-Coated Nanoparticles for Enhanced Oil Recovery. J. Appl. Polym. Sci. 2014, 131, 40576. [Google Scholar] [CrossRef]
- Mao, H.; Qiu, Z.; Shen, Z.; Huang, W. Hydrophobic Associated Polymer Based Silica Nanoparticles Composite with Core–Shell Structure as a Filtrate Reducer for Drilling Fluid at Ultra-High Temperature. J. Pet. Sci. Eng. 2015, 129, 1–14. [Google Scholar] [CrossRef]
- Kakati, A.; Bera, A.; Al-Yaseri, A. A Review on Advanced Nanoparticle-Induced Polymer Flooding for Enhanced Oil Recovery. Chem. Eng. Sci. 2022, 262, 117994. [Google Scholar] [CrossRef]
- Balazs, A.C.; Emrick, T.; Russell, T.P. Nanoparticle Polymer Composites: Where Two Small Worlds Meet. Science 2006, 314, 1107–1110. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; He, Q.; Li, J. Smart Core/Shell Nanocomposites: Intelligent Polymers Modified Gold Nanoparticles. Adv. Colloid Interface Sci. 2009, 149, 28–38. [Google Scholar] [CrossRef] [PubMed]
- Hanemann, T.; Szabó, D.V. Polymer-Nanoparticle Composites: From Synthesis to Modern Applications. Materials 2010, 3, 3468–3517. [Google Scholar] [CrossRef]
- Kumar, S.K.; Jouault, N.; Benicewicz, B.; Neely, T. Nanocomposites with Polymer Grafted Nanoparticles. Macromolecules 2013, 46, 3199–3214. [Google Scholar] [CrossRef]
- Rong, M.Z.; Zhang, M.Q.; Zheng, Y.X.; Zeng, H.M.; Walter, R.; Friedrich, K. Structure–Property Relationships of Irradiation Grafted Nano-Inorganic Particle Filled Polypropylene Composites. Polymer 2001, 42, 167–183. [Google Scholar] [CrossRef]
- Rong, M.Z.; Zhang, M.Q.; Ruan, W.H. Surface Modification of Nanoscale Fillers for Improving Properties of Polymer Nanocomposites: A Review. Mater. Sci. Technol. 2006, 22, 787–796. [Google Scholar] [CrossRef]
- Zou, H.; Wu, S.; Shen, J. Polymer/Silica Nanocomposites: Preparation, Characterization, Properties, and Applications. Chem. Rev. 2008, 108, 3893–3957. [Google Scholar] [CrossRef]
- Huang, Y.; Zheng, Y.; Sarkar, A.; Xu, Y.; Stefik, M.; Benicewicz, B.C. Matrix-Free Polymer Nanocomposite Thermoplastic Elastomers. Macromolecules 2017, 50, 4742–4753. [Google Scholar] [CrossRef]
- Kaldéus, T.; Telaretti Leggieri, M.R.; Cobo Sanchez, C.; Malmström, E. All-Aqueous SI-ARGET ATRP from Cellulose Nanofibrils Using Hydrophilic and Hydrophobic Monomers. Biomacromolecules 2019, 20, 1937–1943. [Google Scholar] [CrossRef]
- Hou, G.; Xia, X.; Liu, J.; Wang, W.; Dong, M.; Zhang, L. Designing Superlattice Structure via Self-Assembly of One-Component Polymer-Grafted Nanoparticles. J. Phys. Chem. B 2019, 123, 2157–2168. [Google Scholar] [CrossRef] [PubMed]
- Bilchak, C.R.; Huang, Y.; Benicewicz, B.C.; Durning, C.J.; Kumar, S.K. High-Frequency Mechanical Behavior of Pure Polymer-Grafted Nanoparticle Constructs. ACS Macro Lett. 2019, 8, 294–298. [Google Scholar] [CrossRef] [PubMed]
- Shimomura, M.; Sawadaishi, T. Bottom-up Strategy of Materials Fabrication: A New Trend in Nanotechnology of Soft Materials. Curr. Opin. Colloid Interface Sci. 2001, 6, 11–16. [Google Scholar] [CrossRef]
- Seeman, N.C.; Belcher, A.M. Emulating Biology: Building Nanostructures from the Bottom Up. Proc. Natl. Acad. Sci. USA 2002, 99, 6451–6455. [Google Scholar] [CrossRef] [PubMed]
- Tu, R.S.; Tirrell, M. Bottom-up Design of Biomimetic Assemblies. Adv. Drug Deliv. Rev. 2004, 56, 1537–1563. [Google Scholar] [CrossRef] [PubMed]
- Glotzer, S.C.; Solomon, M.J. Anisotropy of Building Blocks and Their Assembly into Complex Structures. Nat. Mater 2007, 6, 557–562. [Google Scholar] [CrossRef]
- Palberg, T. Crystallization Kinetics of Colloidal Model Suspensions: Recent Achievements and New Perspectives. J. Phys. Condens. Matter 2014, 26, 333101. [Google Scholar] [CrossRef]
- Kawasaki, T.; Tanaka, H. Formation of a Crystal Nucleus from Liquid. Proc. Natl. Acad. Sci. USA 2010, 107, 14036–14041. [Google Scholar] [CrossRef]
- Walther, A.; Müller, A.H.E. Janus Particles: Synthesis, Self-Assembly, Physical Properties, and Applications. Chem. Rev. 2013, 113, 5194–5261. [Google Scholar] [CrossRef]
- Xu, W.; Li, Z.; Yin, Y. Colloidal Assembly Approaches to Micro/Nanostructures of Complex Morphologies. Small 2018, 14, 1801083. [Google Scholar] [CrossRef]
- Sacanna, S.; Pine, D.J.; Yi, G.-R. Engineering Shape: The Novel Geometries of Colloidal Self-Assembly. Soft Matter 2013, 9, 8096. [Google Scholar] [CrossRef]
- Damasceno, P.F.; Engel, M.; Glotzer, S.C. Predictive Self-Assembly of Polyhedra into Complex Structures. Science 2012, 337, 453–457. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Chen, L.; Shen, X.; Zhu, L.; He, J.; Chen, H. Unconventional Chain-Growth Mode in the Assembly of Colloidal Gold Nanoparticles. Angew. Chem. Int. Ed. 2012, 51, 8021–8025. [Google Scholar] [CrossRef]
- Li, Z.; Fan, Q.; Yin, Y. Colloidal Self-Assembly Approaches to Smart Nanostructured Materials. Chem. Rev. 2022, 122, 4976–5067. [Google Scholar] [CrossRef] [PubMed]
- Ohno, K.; Koh, K.; Tsujii, Y.; Fukuda, T. Fabrication of Ordered Arrays of Gold Nanoparticles Coated with High-Density Polymer Brushes. Angew. Chem. Int. Ed. 2003, 42, 2751–2754. [Google Scholar] [CrossRef]
- Ohno, K.; Morinaga, T.; Takeno, S.; Tsujii, Y.; Fukuda, T. Suspensions of Silica Particles Grafted with Concentrated Polymer Brush: A New Family of Colloidal Crystals. Macromolecules 2006, 39, 1245–1249. [Google Scholar] [CrossRef]
- Lai, P.; Binder, K. Structure and Dynamics of Polymer Brushes near the Θ Point: A Monte Carlo Simulation. J. Chem. Phys. 1992, 97, 586–595. [Google Scholar] [CrossRef]
- Weinhold, J.D.; Kumar, S.K. Monte Carlo Simulations of End-grafted Polymer Matrices under Poor Solvent Conditions. J. Chem. Phys. 1994, 101, 4312–4323. [Google Scholar] [CrossRef]
- Guo, L.; Nie, J.; Du, B.; Peng, Z.; Tesche, B.; Kleinermanns, K. Thermoresponsive Polymer-Stabilized Silver Nanoparticles. J. Colloid Interface Sci. 2008, 319, 175–181. [Google Scholar] [CrossRef]
- Lo Verso, F.; Yelash, L.; Egorov, S.A.; Binder, K. Effect of the Solvent Quality on the Structural Rearrangement of Spherical Brushes: Coarse-Grained Models. Soft Matter 2012, 8, 4185. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, T.; Zhu, L.; Zhao, B.; Tang, P.; Qiu, F. Hierarchical Superstructures Assembled by Binary Hairy Nanoparticles. ACS Macro Lett. 2016, 5, 718–723. [Google Scholar] [CrossRef] [PubMed]
- Guzman-Juarez, B.; Abdelaal, A.; Kim, K.; Toader, V.; Reven, L. Fabrication of Amphiphilic Nanoparticles via Mixed Homopolymer Brushes and NMR Characterization of Surface Phase Separation. Macromolecules 2018, 51, 9951–9960. [Google Scholar] [CrossRef]
- Chancellor, A.J.; Seymour, B.T.; Zhao, B. Characterizing Polymer-Grafted Nanoparticles: From Basic Defining Parameters to Behavior in Solvents and Self-Assembled Structures. Anal. Chem. 2019, 91, 6391–6402. [Google Scholar] [CrossRef] [PubMed]
- Synatschke, C.V.; Nomoto, T.; Cabral, H.; Förtsch, M.; Toh, K.; Matsumoto, Y.; Miyazaki, K.; Hanisch, A.; Schacher, F.H.; Kishimura, A.; et al. Multicompartment Micelles with Adjustable Poly(Ethylene Glycol) Shell for Efficient in Vivo Photodynamic Therapy. ACS Nano 2014, 8, 1161–1172. [Google Scholar] [CrossRef] [PubMed]
- Löbling, T.I.; Haataja, J.S.; Synatschke, C.V.; Schacher, F.H.; Müller, M.; Hanisch, A.; Gröschel, A.H.; Müller, A.H.E. Hidden Structural Features of Multicompartment Micelles Revealed by Cryogenic Transmission Electron Tomography. ACS Nano 2014, 8, 11330–11340. [Google Scholar] [CrossRef]
- Malho, J.-M.; Morits, M.; Löbling, T.I.; Nonappa; Majoinen, J.; Schacher, F.H.; Ikkala, O.; Gröschel, A.H. Rod-Like Nanoparticles with Striped and Helical Topography. ACS Macro Lett. 2016, 5, 1185–1190. [Google Scholar] [CrossRef] [PubMed]
- Ushakova, A.S.; Lazutin, A.A.; Vasilevskaya, V.V. Flowerlike Multipetal Structures of Nanoparticles Decorated by Amphiphilic Homopolymers. Macromolecules 2021, 54, 6285–6295. [Google Scholar] [CrossRef]
- Lazutin, A.A.; Vasilevskaya, V.V. Matrix Free Polymer Nanocomposites from Amphiphilic Hairy Nanoparticles: Solvent Selectivity and Mechanical Properties. Polymer 2022, 255, 125172. [Google Scholar] [CrossRef]
- Vasilevskaya, V.V.; Khalatur, P.G.; Khokhlov, A.R. Conformational Polymorphism of Amphiphilic Polymers in a Poor Solvent. Macromolecules 2003, 36, 10103–10111. [Google Scholar] [CrossRef]
- Savariar, E.N.; Aathimanikandan, S.V.; Thayumanavan, S. Supramolecular Assemblies from Amphiphilic Homopolymers: Testing the Scope. J. Am. Chem. Soc. 2006, 128, 16224–16230. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, K.; Müllen, K.; Yin, M. Self-Assemblies of Amphiphilic Homopolymers: Synthesis, Morphology Studies and Biomedical Applications. Chem. Commun. 2015, 51, 11541–11555. [Google Scholar] [CrossRef] [PubMed]
- Vasilevskaya, V.V.; Govorun, E.N. Hollow and Vesicle Particles from Macromolecules with Amphiphilic Monomer Units. Polym. Rev. 2019, 59, 625–650. [Google Scholar] [CrossRef]
- Maresov, E.A.; Semenov, A.N. Mesoglobule Morphologies of Amphiphilic Polymers. Macromolecules 2008, 41, 9439–9457. [Google Scholar] [CrossRef]
- Buglakov, A.I.; Larin, D.E.; Vasilevskaya, V.V. Self-Assembly in Solutions of Amphiphilic Homopolymers: Computer Modeling and Analytical Theory. Macromolecules 2020, 53, 4783–4795. [Google Scholar] [CrossRef]
- Ushakova, A.S.; Vasilevskaya, V.V. Hedgehog, Chamomile and Multipetal Polymeric Structures on the Nanoparticle Surface: Theoretical Insights. Polymers 2022, 14, 4358. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of Repulsive Forces in Determining the Equilibrium Structure of Simple Liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Verlet, L. Computer “Experiments” on Classical Fluids. I. Thermodynamical Properties of Lennard-Jones Molecules. Phys. Rev. 1967, 159, 98–103. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 2017; Volume 1, ISBN 978-0-19-880319-5. [Google Scholar]
- Smith, J. A Molecular Dynamics Simulation Study of Nanoparticle Interactions in a Model Polymer-Nanoparticle Composite. Compos. Sci. Technol. 2003, 63, 1599–1605. [Google Scholar] [CrossRef]
- Bishop, M.; Kalos, M.H.; Frisch, H.L. Molecular Dynamics of Polymeric Systems. J. Chem. Phys. 1979, 70, 1299–1304. [Google Scholar] [CrossRef]
- Grest, G.S.; Kremer, K. Molecular Dynamics Simulation for Polymers in the Presence of a Heat Bath. Phys. Rev. A 1986, 33, 3628–3631. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saraev, Z.R.; Lazutin, A.A.; Vasilevskaya, V.V. Hedgehog, Chamomile, and Multipetal Polymeric Structures on the Nanoparticle Surface: Computer Modelling. Molecules 2022, 27, 8535. https://doi.org/10.3390/molecules27238535
Saraev ZR, Lazutin AA, Vasilevskaya VV. Hedgehog, Chamomile, and Multipetal Polymeric Structures on the Nanoparticle Surface: Computer Modelling. Molecules. 2022; 27(23):8535. https://doi.org/10.3390/molecules27238535
Chicago/Turabian StyleSaraev, Zakhar R., Alexei A. Lazutin, and Valentina V. Vasilevskaya. 2022. "Hedgehog, Chamomile, and Multipetal Polymeric Structures on the Nanoparticle Surface: Computer Modelling" Molecules 27, no. 23: 8535. https://doi.org/10.3390/molecules27238535
APA StyleSaraev, Z. R., Lazutin, A. A., & Vasilevskaya, V. V. (2022). Hedgehog, Chamomile, and Multipetal Polymeric Structures on the Nanoparticle Surface: Computer Modelling. Molecules, 27(23), 8535. https://doi.org/10.3390/molecules27238535