Nearest-Neighbour and Non-Nearest-Neighbour Non-Covalent Interactions between Substituents in the Aromatic Systems: Experimental and Theoretical Investigation of Functionally Substituted Benzophenones
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Absolute Vapour Pressures and Thermodynamics of Vaporisation/Sublimation
| Compound | M a | T-Range | Ref. | ||
|---|---|---|---|---|---|
| CAS | K | kJ·mol−1 | kJ·mol−1 | ||
| 4-methoxy-benzophenone (liq) [611-94-9] | Jx | 93.5 ± 2.0 | Table 5 | ||
| Tb | 628.2 [21] | 90.2 ± 2.0 | Table 6 | ||
| 91.8 ± 1.4d | average | ||||
| benzophenone (liq) | 77.6 ± 0.5 | Table 7 | |||
| 2-hydroxy-benzophenone (cr) [117-99-7] | C | 401.6 | 123.1 ± 1.7 | 97.9 ± 1.9 | [15] |
| 2-hydroxy-benzophenone (liq) | PhT | 80.2 ± 2.0 | Table 7 | ||
| 3-hydroxy-benzophenone (cr) [13020-57-0] | K-QCM | 361.2–378.2 | 129.9 ± 0.7 | 131.7 ± 0.9 | [15] |
| 3-hydroxy-benzophenone (liq) | PhT | 110.8 ± 2.2 | Table 7 | ||
| 4-hydroxy-benzophenone(cr) [1137-42-4] | K-QCM | 377.2–394.2 | 128.6 ± 0.7 | 130.3 ± 1.0 | [15] |
| 4-hydroxy-benzophenone (liq) | PhT | 113.7 ± 2.5 | Table 7 | ||
| 2-methoxy-benzophenone (liq) [2553-04-0] | 87.4 ± 3.0 c | this work | |||
| 3-methoxy-benzophenone (liq) [6136-67-0] | Tb | 621.4 [21] | 88.7 ± 2.0 | Table 6 | |
| 2,4-di-hydroxy-benzophenone (cr) | IG | 323–363 | 93 ± 16 | (95 ± 16) | [22] |
| [131-56-6] | n/a | 312–353 | 134.0 ± 2.0 | 135.3 ± 2.1 | [23] |
| K | 366.6–406.8 | 129.5 ± 2.8 | 133.0 ± 2.9 | Table 2 | |
| 134.5 ± 1.7d | average | ||||
| 2,4-di-hydroxy-benzophenone (liq) | UVS | 418–485 | 86.8 ± 5.0 | (105.8 ± 5.0) | [24] |
| PhT | 112.3 ± 4.2 | Table 7 | |||
| 2-hydroxy-4-methoxy-benzophenone (cr) | n/a | 281–337 | 118.8 ± 5.0 | 119.3 ± 5.0 | [23] |
| [131-57-7] | K | 306.5–320.5 | 109.0 ± 5.0 | 109.6 ± 5.1 | [25] |
| PhT | 117.1 ± 1.3 | Table 7 | |||
| 116.8 ± 1.2d | average | ||||
| 2-hydroxy-4-methoxy-benzophenone (liq) | UVS | 337–413 | 74.2 ± 5.0 | (83.5 ± 5.0) | [24] |
| T | 341.2–368.2 | 91.6 ± 0.9 | 98.4 ± 1.0 | Table 1 | |
| 2,2′-dihydroxy-benzophenone (cr) [835-11-0] | PhT | 101.9 ± 1.3 | Table 7 | ||
| 2,2′-dihydroxy-benzophenone (liq) | T | 363.1–408.4 | 74.7 ± 0.8 | 84.9 ± 0.9 | Table 1 |
| 2,2′-dihydroxy-4-methoxy-benzophenone (cr) | n/a | 303-342 | 228 ± 5 | (229 ± 5.0) | [23] |
| [131-53-3] | PhT | 118.6 ± 1.6 | Table 7 | ||
| 2,2′-dihydroxy-4-methoxy-benzophenone (liq) | TGA | 343–573 | 81.8 ± 0.2 | 103.9 ± 4.4 | [26] |
| [131-53-3] | UVS | 342–481 | 74.1 ± 5.0 | (89.7 ± 5.0) | [24] |
| T | 365.1–430.9 | 87.1 ± 0.7 | 100.7 ± 0.9 | Table 1 | |
| 100.8 ± 0.9d | average | ||||
| 2,2′,4,4′-tetrahydroxy-benzophenone (cr) | n/a | 363–471 | 143.2 ± 5.0 | (148.7 ± 5.0) | [23] |
| [131-55-5] | K | 431.8–453.8 | 153.6 ± 2.6 | 159.8 ± 3.1 | Table 2 |
| 2,2′,4,4′-tetrahydroxy-benzophenone (liq) | TGA | 472–573 | 150.5 ± 0.2 | (186.2 ± 7.1) | [26] |
| PhT | 152.0 ± 6.8 | Table 7 | |||
| 2,2′-dihydroxy-4,4′-dimethoxybenzophenone (cr) | n/a | 325–408 | 146.8 ± 5.0 | (150.4 ± 5.0) | [23] |
| [131-54-4] | T | 368.5–399.3 | 134.8 ± 2.2 | 139.4 ± 2.4 | Table 1 |
| 2,2′-dihydroxy-4,4′- | TGA | 412–573 | 96.9 ± 0.2 | 126.7 ± 6.0 | [26] |
| dimethoxybenzophenone (liq) | K | 412.6–435.1 | 98.0 ± 2.8 | 117.2 ± 2.9 | Table 1 |
| PhT | 117.6 ± 4.2 | Table 7 | |||
| 118.6 ± 2.2d | average |
3.2. Consistency of Results on Vaporisation/Sublimation Enthalpies
3.2.1. Kovats Retention Indices for Validation of Experimental Vaporisation Enthalpies
| Jxa | Δ c | |||
|---|---|---|---|---|
| Compound | kJ·mol−1 | kJ·mol−1 | kJ·mol−1 | |
| methoxybenzene | 900 | 46.6 ± 0.2 [31] | 46.8 | −0.2 |
| acetophenone | 1048 | 55.4 ± 0.3 [32] | 54.5 | 0.9 |
| 2′-methoxy-acetophenone | 1269 | 64.6 ± 0.4 [27] | 65.9 | −1.3 |
| 3′-methoxy-acetophenone | 1279 | 65.8 ± 0.4 [27] | 66.4 | −0.6 |
| 4′-methoxy-acetophenone | 1327 | 70.4 ± 0.6 [27] | 68.9 | 1.5 |
| 4′-methoxy-benzophenone | 1804 [33] | - | 93.5 ± 2.0 |
3.2.2. Normal Boiling Temperatures for Validation of Experimental Vaporisation Enthalpies
| Tba | Δ c | |||
|---|---|---|---|---|
| Compound | kJ·mol−1 | kJ·mol−1 | kJ·mol−1 | |
| methoxybenzene | 426.8 | 46.6 ± 0.2 [31] | 46.2 | 0.4 |
| acetophenone | 475.8 | 55.4 ± 0.3 [32] | 56.9 | −1.5 |
| 2′-methoxy-acetophenone | (511.5) d | 64.6 ± 0.4 [27] | 64.6 | 0.0 |
| 3′-methoxy-acetophenone | 513.2 | 65.8 ± 0.4 [27] | 65.1 | 0.7 |
| 4′-methoxy-acetophenone | 531.2 | 70.4 ± 0.6 [27] | 69.0 | 1.4 |
| benzophenone | 578.6 | 78.0 ± 0.2 [36] | 79.4 | −1.4 |
| 2′-methyl-benzophenone | 582.7 | 81.2 ± 1.7 [37] | 80.3 | 0.9 |
| 3′-methyl-benzophenone | 586.2 | 80.7 ± 0.4 [36] | 81.0 | −0.3 |
| 4′-methyl-benzophenone | (583.6) d | 80.5 ± 0.5 [36] | 80.5 | 0.0 |
| 3′-methoxy-benzophenone | 621.5 [21] | 88.7 ± 2.0 | ||
| 4′-methoxy-benzophenone | 628.2 [21] | 90.2 ± 2.0 |
3.2.3. Consistency of Phase Transitions Enthalpies
| Compounds | Tfus, K | at Tfus | |||
|---|---|---|---|---|---|
| 298.15 K | |||||
| 1 | 2 | 3 | 4 | 5 | 6 |
| benzophenone [38] | 321.0 ± 0.1 | 18.6 ± 0.3 | 17.4 ± 0.5 | 95.0 ± 0.1 | 77.6 ± 0.5 |
| 2-hydroxy-benzophenone [15] | 312.3 ± 0.1 | 18.7 ± 0.1 | 17.7 ± 0.3 | 97.9 ± 1.9 | 80.2 ± 2.0 |
| 3-hydroxy-benzophenone [15] | 390.5 ± 0.3 | 27.4 ± 0.2 | 20.9 ± 2.0 | 131.7 ± 0.9 | 110.8 ± 2.2 |
| 4-hydroxy-benzophenone [15] | 407.7 ± 0.5 | 24.4 ± 0.1 | 16.6 ± 2.3 | 130.3 ± 1.0 | 113.7 ± 2.5 |
| 2,4-dihydroxy-benzophenone [this work] | 417.7 ± 0.2 | 30.8 ± 0.7 | 20.7 ± 3.1 | 133.0 ± 2.9 | 112.3 ± 4.2 |
| 2,2′-dihydroxy-benzophenone [16] | 334.5 ± 0.1 | 20.1 ± 0.1 | 17.0 ± 1.0 | 101.9 ± 1.3 e | 84.9 ± 0.9 f |
| 2-hydroxy-4-methoxy-benzophenone [25] | 336.7 ± 0.5 | 21.8 ± 0.1 | 18.7 ± 0.9 | 117.1 ± 1.3 e | 98.4 ± 1.0 f |
| 2,2′-dihydroxy-4-methoxy-benzophenone [26] | 343.0 ± 0.5 | 22.0 ± 0.5 | 17.9 ± 1.3 | 118.7 ± 1.6 e | 100.8 ± 0.9 f |
| 2,2′,4,4′-tetrahydroxy-benzophenone [26] | 472.0 ± 0.5 | 28.0 ± 0.5 | 7.8 ± 6.1 | 159.8 ± 3.1 | 152.0 ± 6.8 |
| 2,2′-dihydroxy-4,4′-dimethoxy-benzophenone [26] | 412.3 ± 0.5 | 33.2 ± 0.5 | 21.8 ± 3.4 | 139.4 ± 2.4 | 117.6 ± 4.2 |
3.3. Gas-Phase Standard Molar Enthalpies of Formation
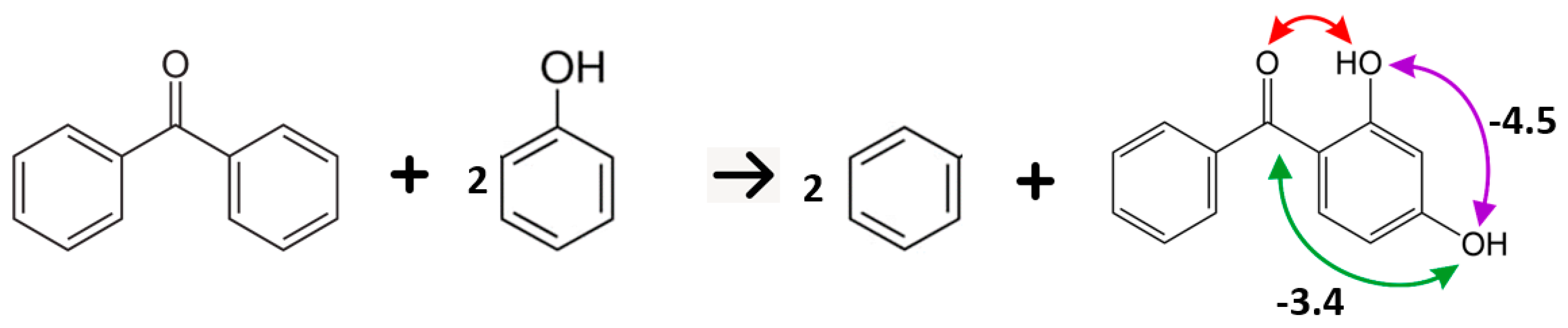
2 × hydroxybenzene + methoxybenzene + benzophenone
2 × hydroxybenzene + 2 × methoxybenzene + 2 × benzophenone
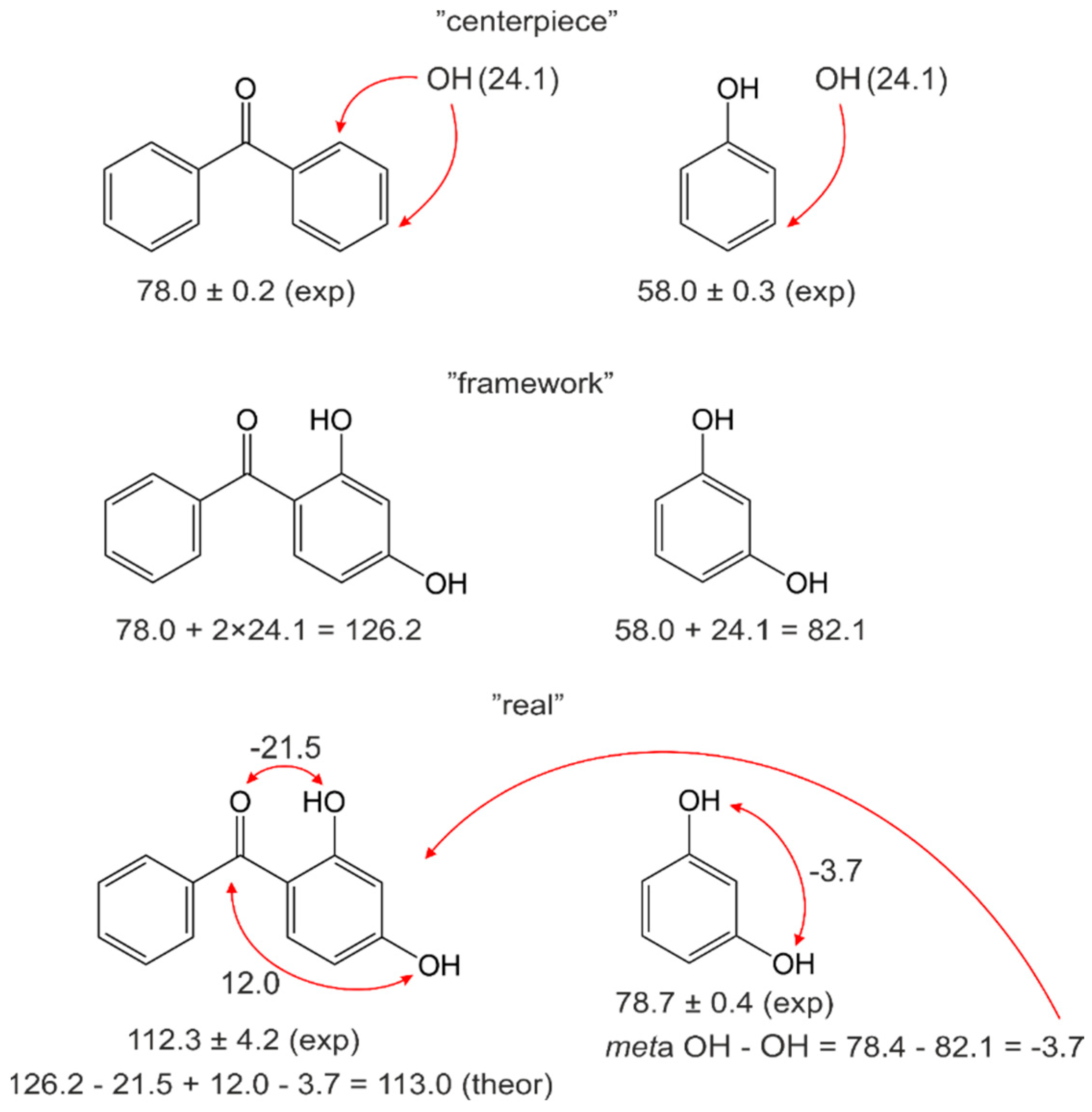
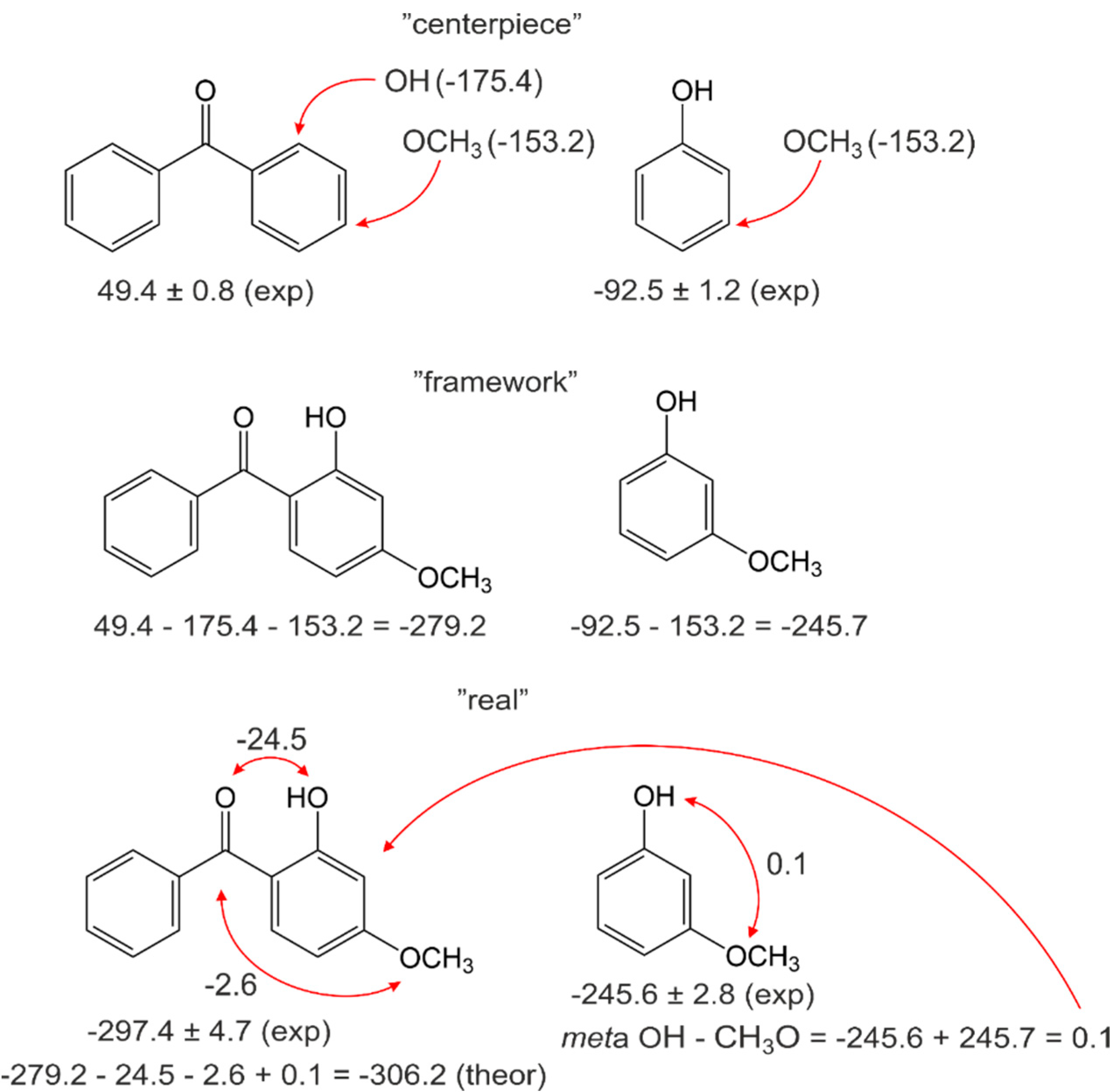
4. Development and Practical Application of the “Centrepiece” Group-Contribution Approach
4.1. Construction of a Theoretical Framework
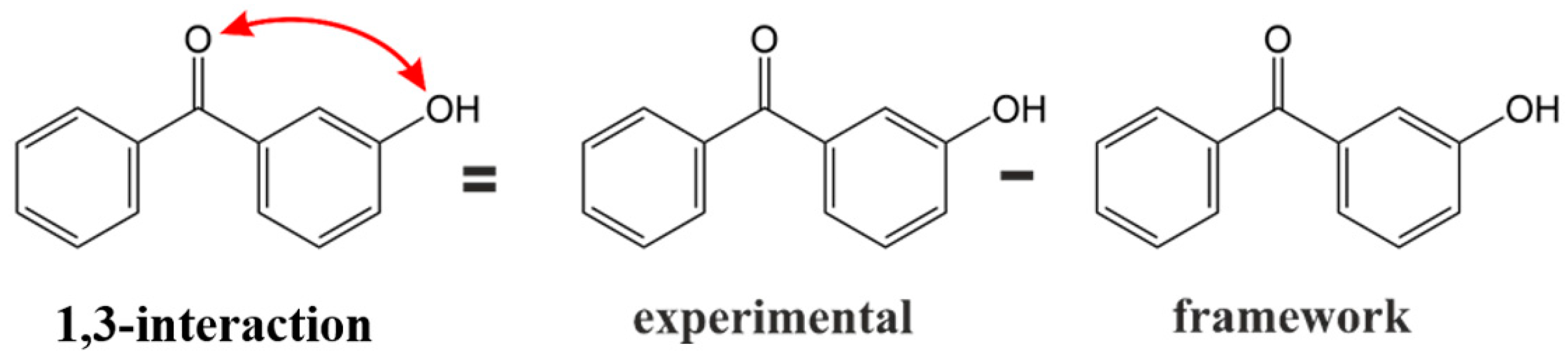
4.2. Pairwise Interactions of Substituents on the Benzene Ring
4.3. Practical Application of the Centerpiece Approach for Prediction of Enthalpies of Substituted Benzophenones
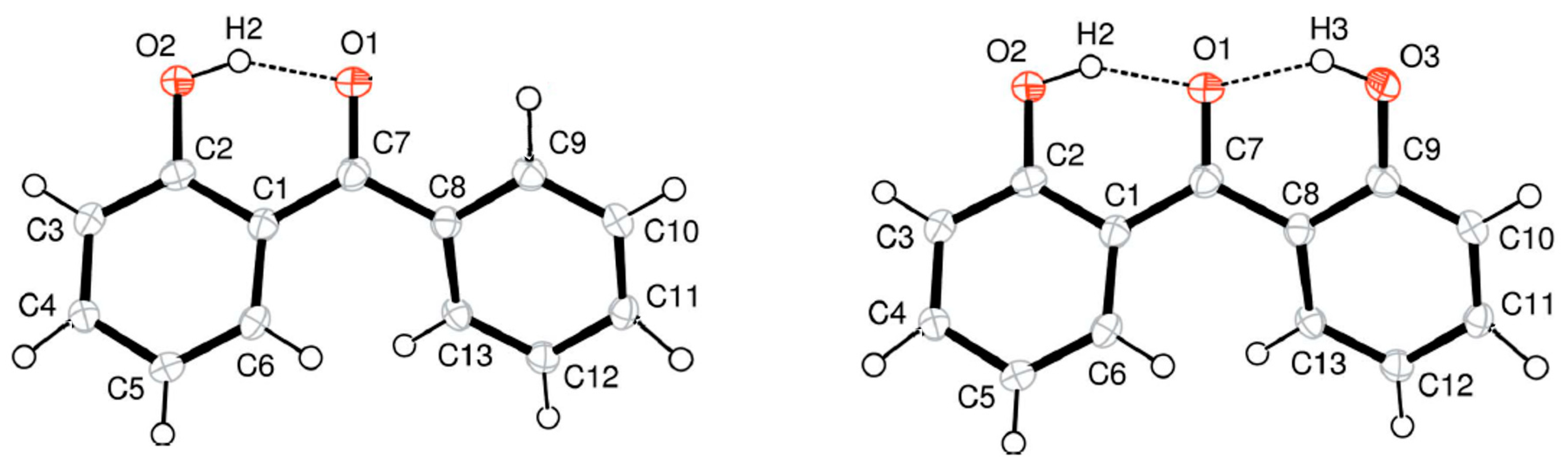
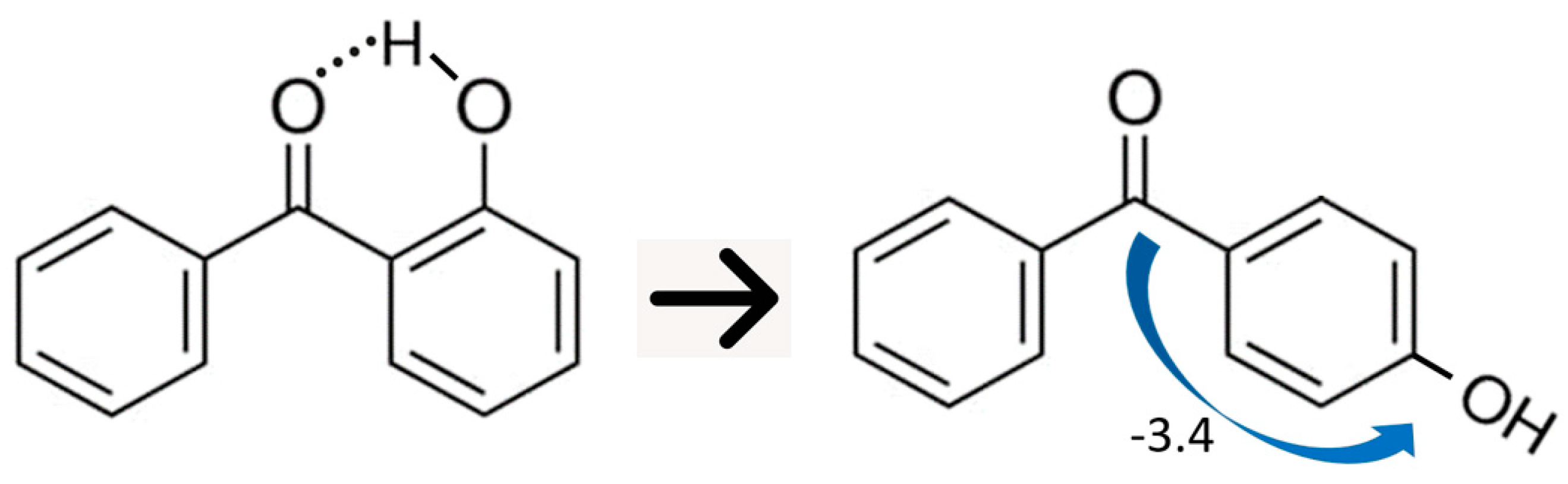
5. Strength of Intra-Molecular Hydrogen Bonding in Ortho-Substituted Benzophenones
5.1. Strength of Intra-Molecular Hydrogen Bonding from the “Ortho-Para” Method
5.2. Strength of Intra-Molecular Hydrogen Bonding from the Well-Balanced Reactions
5.3. Strength of Intra-Molecular Hydrogen Bonding from the “HB and Out” Method
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Perperopoulou, F.D.; Tsoungas, P.G.; Thireou, T.N.; Rinotas, V.E.; Douni, E.K.; Eliopoulos, E.E.; Labrou, N.E.; Clonis, Y.D. 2,2′-Dihydroxybenzophenones and Their Carbonyl N-Analogues as Inhibitor Scaffolds for MDR-Involved Human Glutathione Transferase Isoenzyme A1-1. Bioorg. Med. Chem. 2014, 22, 3957–3970. [Google Scholar] [CrossRef]
- Price, D.M. Vapor Pressure Determination by Thermogravimetry. Thermochim. Acta 2001, 367–368, 253–262. [Google Scholar] [CrossRef]
- Deanin, R.D. Aspects of degradation and stabilization of polymers, H. H. G. Jellinek, Ed., Elsevier, Oxford and New York, 1978, 690 pp. J. Polym. Sci. Polym. Lett. Ed. 1978, 16, 482–483. [Google Scholar] [CrossRef]
- Vink, P.; Van Veen, T.J. The Mechanism of u.v. Stabilization of Polypropylene Films by 2-Hydroxy-4-Octyloxybenzophenone. Eur. Polym. J. 1978, 14, 533–537. [Google Scholar] [CrossRef]
- Allen, N.S. Recent Advances in the Photo-Oxidation and Stabilization of Polymers. Chem. Soc. Rev. 1986, 15, 373. [Google Scholar] [CrossRef]
- Gilli, G.; Gilli, P. The Nature of the Hydrogen Bond; Oxford University Press: Oxford, UK, 2009; ISBN 9780199558964. [Google Scholar]
- Kulikov, D.; Verevkin, S.P.; Heintz, A. Determination of Vapor Pressures and Vaporization Enthalpies of the Aliphatic Branched C 5 and C 6 Alcohols. J. Chem. Eng. Data 2001, 46, 1593–1600. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Emel’yanenko, V.N. Transpiration Method: Vapor Pressures and Enthalpies of Vaporization of Some Low-Boiling Esters. Fluid Phase Equilib. 2008, 266, 64–75. [Google Scholar] [CrossRef]
- Verevkin, S.P. Chapter 1. Pure Component Phase Changes Liquid and Gas. In Experimental Thermodynamics: Measurement of the Thermodynamic Properties of Multiple Phases; Weir, R.D., de Loos, T.W., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; Volume 7. [Google Scholar]
- Emel’yanenko, V.N.; Zaitsau, D.H.; Shoifet, E.; Meurer, F.; Verevkin, S.P.; Schick, C.; Held, C. Benchmark Thermochemistry for Biologically Relevant Adenine and Cytosine. A Combined Experimental and Theoretical Study. J. Phys. Chem. A 2015, 119, 9680–9691. [Google Scholar] [CrossRef] [PubMed]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gaussian-4 Theory. J. Chem. Phys. 2007, 126, 084108. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Revision A.03; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Verevkin, S.P.; Sazonova, A.Y.; Emel’yanenko, V.N.; Zaitsau, D.H.; Varfolomeev, M.A.; Solomonov, B.N.; Zherikova, K.V. Thermochemistry of Halogen-Substituted Methylbenzenes. J. Chem. Eng. Data 2015, 60, 89–103. [Google Scholar] [CrossRef]
- Emel’yanenko, V.N.; Verevkin, S.P. Benchmark Thermodynamic Properties of 1,3-Propanediol: Comprehensive Experimental and Theoretical Study. J. Chem. Thermodyn. 2015, 85, 111–119. [Google Scholar] [CrossRef]
- Dàvalos, J.Z.; Guerrero, A.; Herrero, R.; Jimenez, P.; Chana, A.; Abboud, J.L.M.; Lima, C.F.R.A.C.; Santos, L.M.N.B.F.; Lago, A.F. Neutral, Ion Gas-Phase Energetics and Structural Properties of Hydroxybenzophenones. J. Org. Chem. 2010, 75, 2564–2571. [Google Scholar] [CrossRef] [PubMed]
- Tomitaka, S.; Mizukami, M.; Paladi, F.; Oguni, M. Thermal and Dielectric Studies of 2,2’-Dihydroxybenzophenone: PPPProgress of Crystal Nucleation and Growth below the Glass Transition Temperature. J. Therm. Anal. Calorim. 2005, 81, 637–643. [Google Scholar] [CrossRef]
- Chickos, J.S.; Hosseini, S.; Hesse, D.G.; Liebman, J.F. Heat Capacity Corrections to a Standard State: A Comparison of New and Some Literature Methods for Organic Liquids and Solids. Struct. Chem. 1993, 4, 271–278. [Google Scholar] [CrossRef]
- Acree, W.; Chickos, J.S. Phase Transition Enthalpy Measurements of Organic and Organometallic Compounds. Sublimation, Vaporization and Fusion Enthalpies from 1880 to 2015. Part 1. C1−C10. J. Phys. Chem. Ref. Data 2016, 45, 033101. [Google Scholar] [CrossRef]
- Chickos, J.S.; Acree, W.E. Enthalpies of Sublimation of Organic and Organometallic Compounds. 1910–2001. J. Phys. Chem. Ref. Data 2002, 31, 537–698. [Google Scholar] [CrossRef]
- Chickos, J.S.; Acree, W.E. Enthalpies of Vaporization of Organic and Organometallic Compounds, 1880–2002. J. Phys. Chem. Ref. Data 2003, 32, 519–878. [Google Scholar] [CrossRef]
- Guidechem Chemical Network. Available online: https://Www.Guidechem.Com (accessed on 31 October 2022).
- Gray, D.N.; Burton, G. Evaporation Rates and Vapor Pressures of Some Fluoro- and Trifluoromethyl-Substituted 2-Hydroxy-4-Methoxybenzophenones. J. Chem. Eng. Data 1966, 11, 59–60. [Google Scholar] [CrossRef]
- Stephenson, R.M.; Malanowski, S. Handbook of the Thermodynamics of Organic Compounds; Springer: Dordrecht, The Netherlands, 1987; ISBN 978-94-010-7923-5. [Google Scholar]
- Schmitt, R.G.; Hirt, R.C. Investigation of the Protective Ultraviolet Absorbers in a Space Environment. I. Rate of Evaporation and Vapor Pressure Studies. J. Polym. Sci. 1960, 45, 35–47. [Google Scholar] [CrossRef]
- Lago, A.F.; Jimenez, P.; Herrero, R.; Dávalos, J.Z.; Abboud, J.L.M. Thermochemistry and Gas-Phase Ion Energetics of 2-Hydroxy-4-Methoxy- Benzophenone (Oxybenzone). J. Phys. Chem. A 2008, 112, 3201–3208. [Google Scholar] [CrossRef] [PubMed]
- Price, D.M.; Hawkins, M. Vapour Pressures of Hydroxybenzophenone UV Absorbers. Thermochim. Acta 1999, 329, 73–76. [Google Scholar] [CrossRef]
- Samarov, A.A.; Riabchunova, A.V.; Verevkin, S.P. Interactions between Substituents in the Benzene Ring. Experimental and Theoretical Study of Methoxy Substituted Acetophenones. J. Chem. Thermodyn. 2022, 173, 106847. [Google Scholar] [CrossRef]
- Tret´yakov, K.V. Retention Data; NIST Mass Spectrometry Data Center: Gaithersburg, MD, USA, 2008. [Google Scholar]
- Verevkin, S.P. Vapour Pressures and Enthalpies of Vaporization of a Series of the Linear N-Alkyl-Benzenes. J. Chem. Thermodyn. 2006, 38, 1111–1123. [Google Scholar] [CrossRef]
- Kováts, E. Gas-chromatographische Charakterisierung Organischer Verbindungen. Teil 1: Retentionsindices Aliphatischer Halogenide, Alkohole, Aldehyde Und Ketone. Helv. Chim. Acta 1958, 41, 1915–1932. [Google Scholar] [CrossRef]
- Verevkin, S.P. Weaving a Web of Reliable Thermochemistry around Lignin Building Blocks: Phenol, Benzaldehyde, and Anisole. J. Therm. Anal. Calorim. 2021, 147, 6073–6085. [Google Scholar] [CrossRef]
- Steele, W.V.; Chirico, R.D.; Knipmeyer, S.E.; Nguyen, A. Vapor Pressure of Acetophenone, (±)-1,2-Butanediol, (±)-1,3-Butanediol, Diethylene Glycol Monopropyl Ether, 1,3-Dimethyladamantane, 2-Ethoxyethyl Acetate, Ethyl Octyl Sulfide, and Pentyl Acetate. J. Chem. Eng. Data 1996, 41, 1255–1268. [Google Scholar] [CrossRef]
- Ardrey, R.E.; Moffat, A.C. Gas-Liquid Chromatographic Retention Indices of 1318 Substannces of Toxicalogical Interest on SE-30 or OV-a Stationary Phase. J. Chromatogr. A 1981, 220, 195–252. [Google Scholar] [CrossRef] [PubMed]
- Vinogradov, B.A. Production, Composition, Properties and Application of Essential Oils. 2004. Available online: http://Viness.Narod.Ru (accessed on 31 October 2022).
- Benson, S.W. New Methods for Estimating the Heats of Formation, Heat Capacities, and Entropies of Liquids and Gases. J. Phys. Chem. A 1999, 103, 11481–11485. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Samarov, A.A. Thermochemistry in 21st Century—Quo Vadis? In Silico Assisted Diagnostics of Available Thermochemical Data. Struct. Chem. 2022; submitted. [Google Scholar]
- Ribeiro da Silva, M.A.V.; Amaral, L.M.P.F.; Guedes, F.C.R.; Gomes, J.R.B. Standard Molar Enthalpies of Formation of Methylbenzophenones. J. Phys. Org. Chem. 2006, 19, 689–696. [Google Scholar] [CrossRef]
- Štejfa, V.; Fulem, M.; Růžička, K.; Morávek, P. New Static Apparatus for Vapor Pressure Measurements: Reconciled Thermophysical Data for Benzophenone. J. Chem. Eng. Data 2016, 61, 3627–3639. [Google Scholar] [CrossRef]
- Emel’yanenko, V.N.; Zaitseva, K.V.; Agapito, F.; Martinho Simões, J.A.; Verevkin, S.P. Benchmark Thermodynamic Properties of Methylanisoles: Experimental and Theoretical Study. J. Chem. Thermodyn. 2015, 85, 155–162. [Google Scholar] [CrossRef]
- Zaitseva, K.V.; Emel´yanenko, V.N.; Agapito, F.; Pimerzin, A.A.; Varfolomeev, M.A.; Verevkin, S.P. Benchmark Thermochemistry of Methylbenzonitriles: Experimental and Theoretical Study. J. Chem. Thermodyn. 2015, 91, 186–193. [Google Scholar] [CrossRef]
- Contineanu, I.; Marchidan, D.I. Heats of Combustion and Formation of 2,4-Dihydroxybenzophenone. Rev. Chim. 1979, 30, 1096–1097. [Google Scholar]
- Pedley, J.B.; Naylor, R.D.; Kirby, S.P. Thermochemical Data of Organic Compounds; Chapman and Hall: New York, NY, USA, 1986; pp. 1–792. [Google Scholar]
- Pracht, P.; Bohle, F.; Grimme, S. Automated Exploration of the Low-Energy Chemical Space with Fast Quantum Chemical Methods. Phys. Chem. Chem. Phys. 2020, 22, 7169–7192. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Andreeva, I.V.; Verevkin, S.P. Thermochemistry of Substituted Benzenes: Acetophenones with Methyl, Ethyl, Cyano and Acetoxy Substituents. J. Therm. Anal. Calorim. 2022, 147, 11401–11415. [Google Scholar] [CrossRef]
- Roux, M.V.; Temprado, M.; Chickos, J.S.; Nagano, Y. Critically Evaluated Thermochemical Properties of Polycyclic Aromatic Hydrocarbons. J. Phys. Chem. Ref. Data 2008, 37, 1855–1996. [Google Scholar] [CrossRef]
- Allen, F.H. The Cambridge Structural Database: A Quarter of a Million Crystal Structures and Rising. Acta Crystallogr. Sect. B Struct. Sci. 2002, 58, 380–388. [Google Scholar] [CrossRef] [PubMed]
- Schlemper, E.O. 2,2’-Dihydroxybenzophenone. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1982, 38, 1619–1622. [Google Scholar] [CrossRef]
- Tzeli, D.; Tsoungas, P.G.; Petsalakis, I.D.; Kozielewicz, P. Intramolecular Single H Bonding vs. Bifurcation in Tuning the Conformation of 2,2′-Dihydroxybenzophenone and Its Derivatives: A DFT Insight. Struct. Chem. 2017, 28, 925–943. [Google Scholar] [CrossRef]
- Siewert, R.; Ludwig, R.; Verevkin, S.P. Non-Covalent Interactions in Molecular Systems: Thermodynamic Evaluation of the Hydrogen Bond Strength in Aminoalcohols. Phys. Chem. Chem. Phys. 2021, 23, 25226–25238. [Google Scholar] [CrossRef] [PubMed]
- Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Definition of the Hydrogen Bond (IUPAC Recommendations 2011). Pure Appl. Chem. 2011, 83, 1637–1641. [Google Scholar] [CrossRef]
- Hansen, P.E. NMR Studies of Compounds with Intramolecular Hydrogen Bonds. In Isotope Effects in Chemistry and Biology; Kohen, A., Limbach, H.-H., CRC, Eds.; Taylor and Francis: Milton Park, UK, 2006; pp. 253–280. [Google Scholar]
- Perrin, C.L. Are Short, Low-Barrier Hydrogen Bonds Unusually Strong? Acc. Chem. Res. 2010, 43, 1550–1557. [Google Scholar] [CrossRef] [PubMed]
- Estácio, S.G.; Cabral do Couto, P.; Costa Cabral, B.J.; Minas da Piedade, M.E.; Martinho Simões, J.A. Energetics of Intramolecular Hydrogen Bonding in Di-Substituted Benzenes by the Ortho−para Method. J. Phys. Chem. A 2004, 108, 10834–10843. [Google Scholar] [CrossRef]
- Varfolomeev, M.A.; Abaidullina, D.I.; Solomonov, B.N.; Verevkin, S.P.; Emel’yanenko, V.N. Pairwise Substitution Effects, Inter- and Intramolecular Hydrogen Bonds in Methoxyphenols and Dimethoxybenzenes. Thermochemistry, Calorimetry, and First-Principles Calculations. J. Phys. Chem. B 2010, 114, 16503–16516. [Google Scholar] [CrossRef]
- Čuma, M.; Scheiner, S.; Kar, T. Competition between Rotamerization and Proton Transfer in o -Hydroxybenzaldehyde. J. Am. Chem. Soc. 1998, 120, 10497–10503. [Google Scholar] [CrossRef]
- Hansen, P.E.; Kamounah, F.S.; Saeed, B.A.; MacLachlan, M.J.; Spanget-Larsen, J. Intramolecular Hydrogen Bonds in Normal and Sterically Compressed O-Hydroxy Aromatic Aldehydes. Isotope Effects on Chemical Shifts and Hydrogen Bond Strength. Molecules 2019, 24, 4533. [Google Scholar] [CrossRef] [PubMed]
- Wahlbeck, P.G.; Effusion, V.I.I. The Failure of Isotropy of a Gas in an Effusion Cell and the Transition Region. J. Chem. Phys. 1971, 55, 1709–1715. [Google Scholar] [CrossRef]
- Nesmeianov, A.N.; Carasso, I.J. Vapour Pressure of the Elements; Academic Press: New York, NY, USA, 1963. [Google Scholar]
- Zaitsau, D.; Kabo, G.J.; Kozyro, A.A.; Sevruk, V.M. The effect of the failure of isotropy of a gas in an effusion cell on the vapor pressure and enthalpy of sublimation for alkyl derivatives of carbamide. Thermochim. Acta 2003, 406, 17–28. [Google Scholar] [CrossRef]
- Bazyleva, A.B.; Blokhin, A.V.; Kabo, G.J.; Kabo, A.G.; Sevruk, V.M. Thermodynamic properties of 2-adamantanone in the condensed and ideal gaseous states. Thermochim. Acta 2006, 451, 65–72. [Google Scholar] [CrossRef]
- Colomina, M.; Latorre, C.; Perez-Ossorio, R. Heats of combustion of five alkyl phenyl ketones. Pure Appl. Chem. 1961, 2, 133–136. [Google Scholar] [CrossRef][Green Version]
- Verevkin, S.P.; Konnova, M.E.; Turovtsev, V.V.; Riabchunova, A.V.; Pimerzin, A.A. Weaving a Network of Reliable Thermochemistry around Lignin Building Blocks: Methoxy-Phenols and Methoxy-Benzaldehydes. Ind. Eng. Chem. Res. 2020, 59, 22626–22639. [Google Scholar] [CrossRef]
- Gobble, C.; Chickos, J.; Verevkin, S.P. Vapor Pressures and Vaporization Enthalpies of a Series of Dialkyl Phthalates by Correlation Gas Chromatography. J. Chem. Eng. Data 2014, 59, 1353–1365. [Google Scholar] [CrossRef]

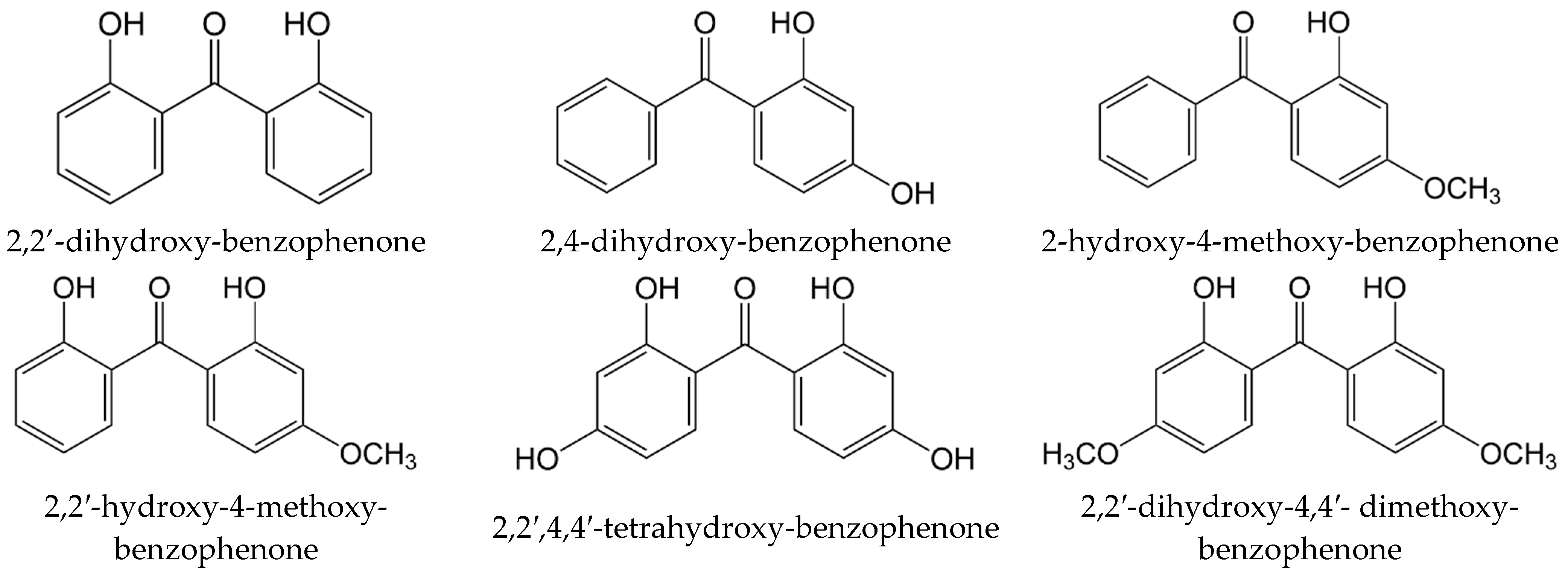
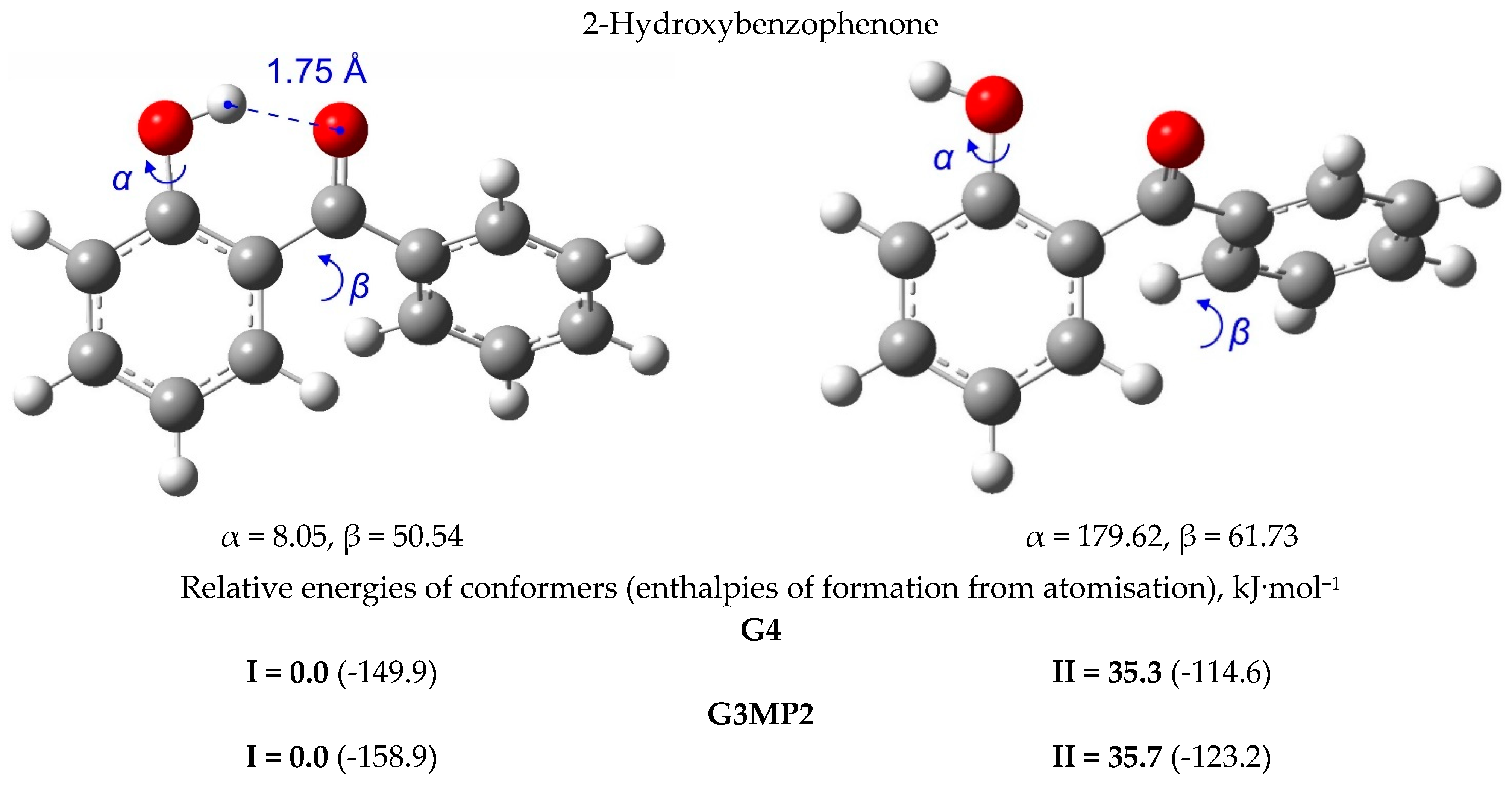
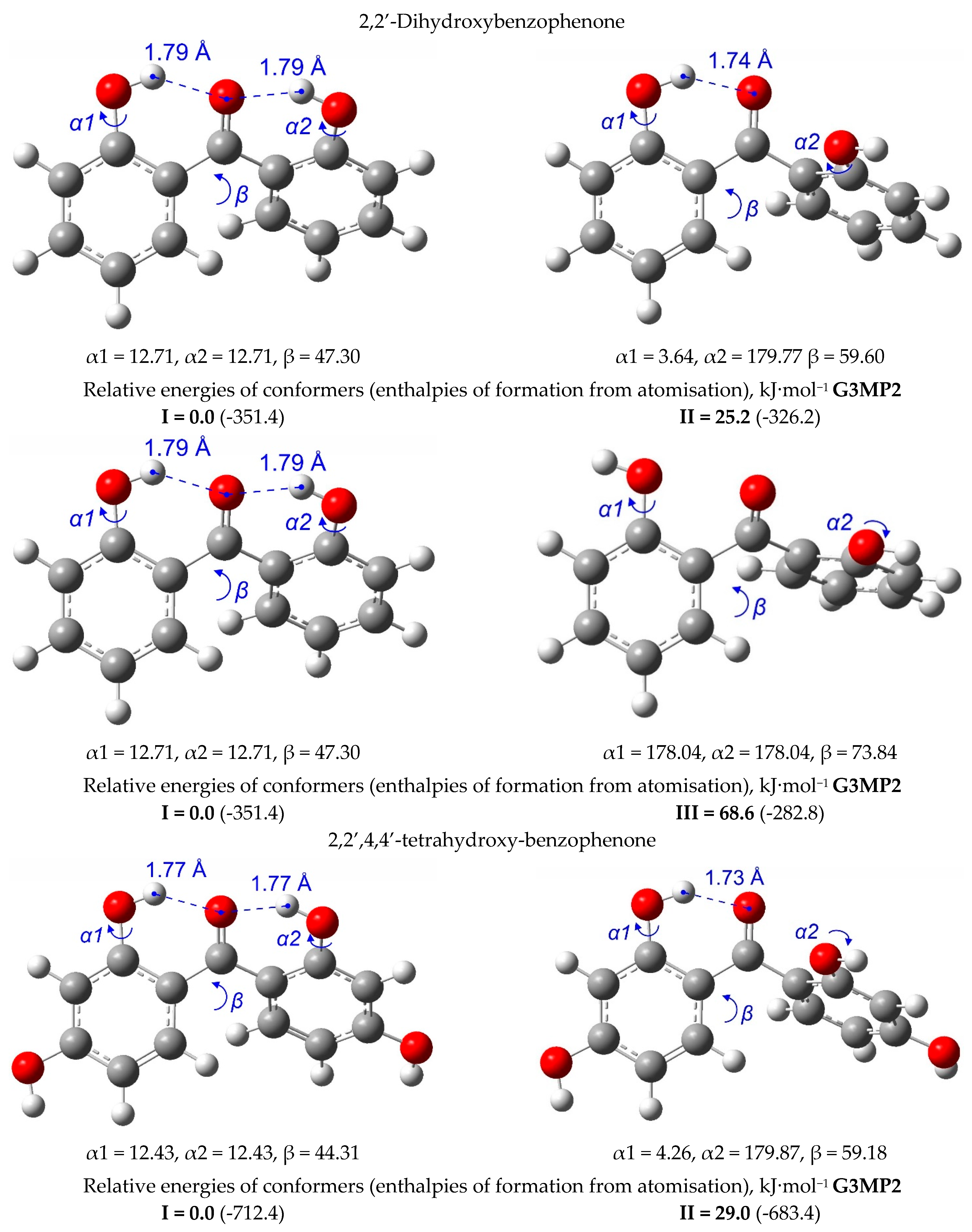
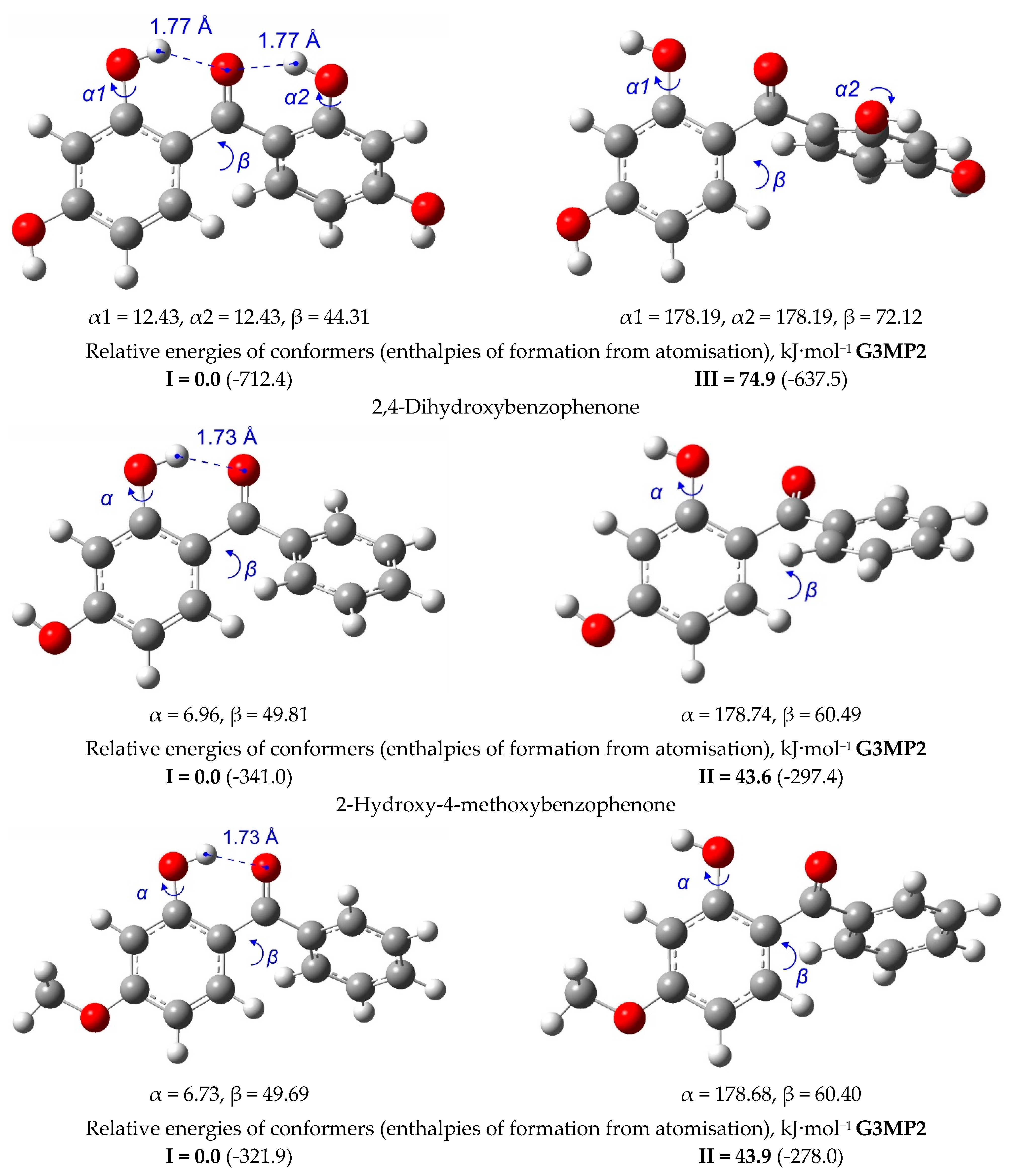
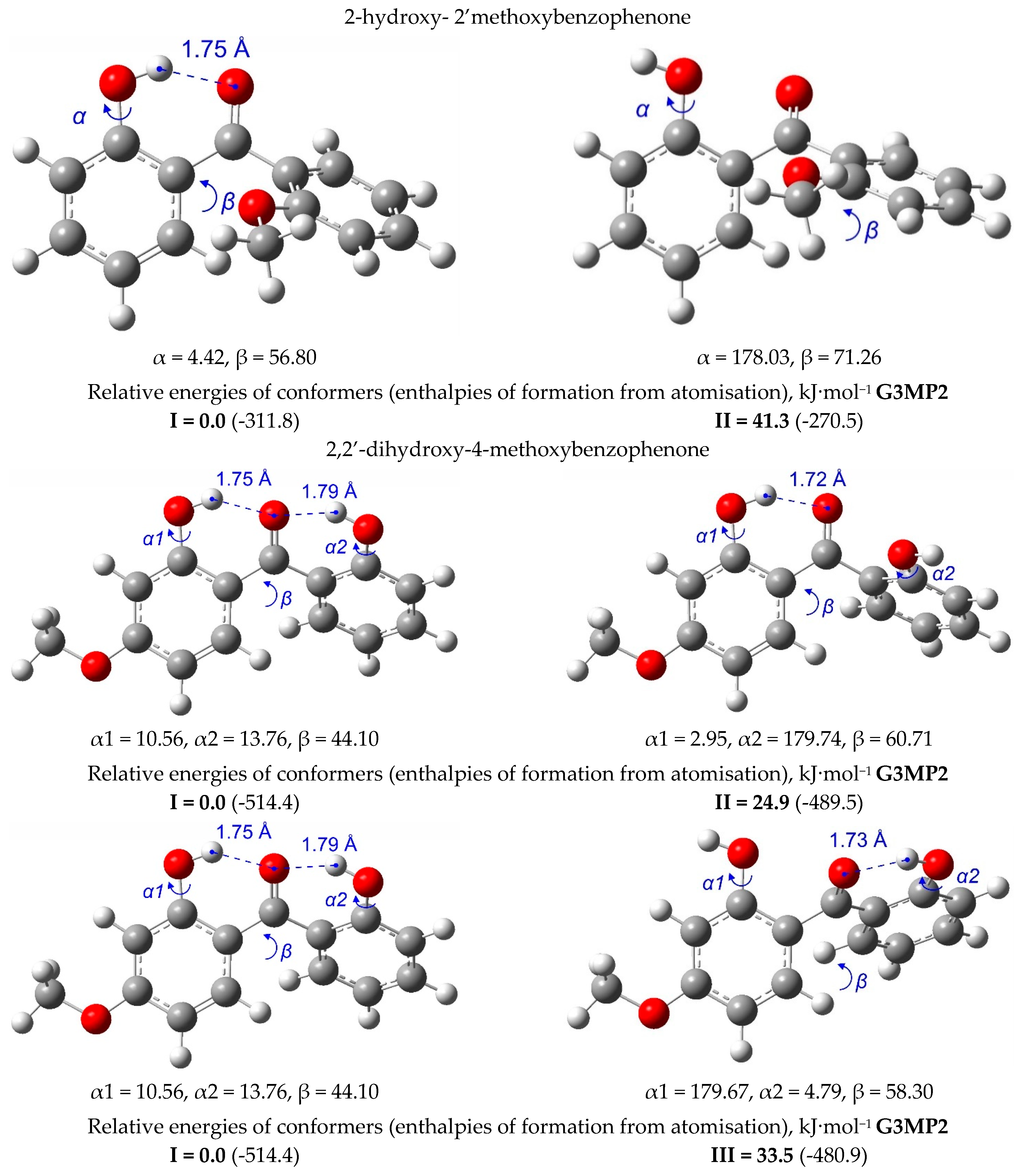
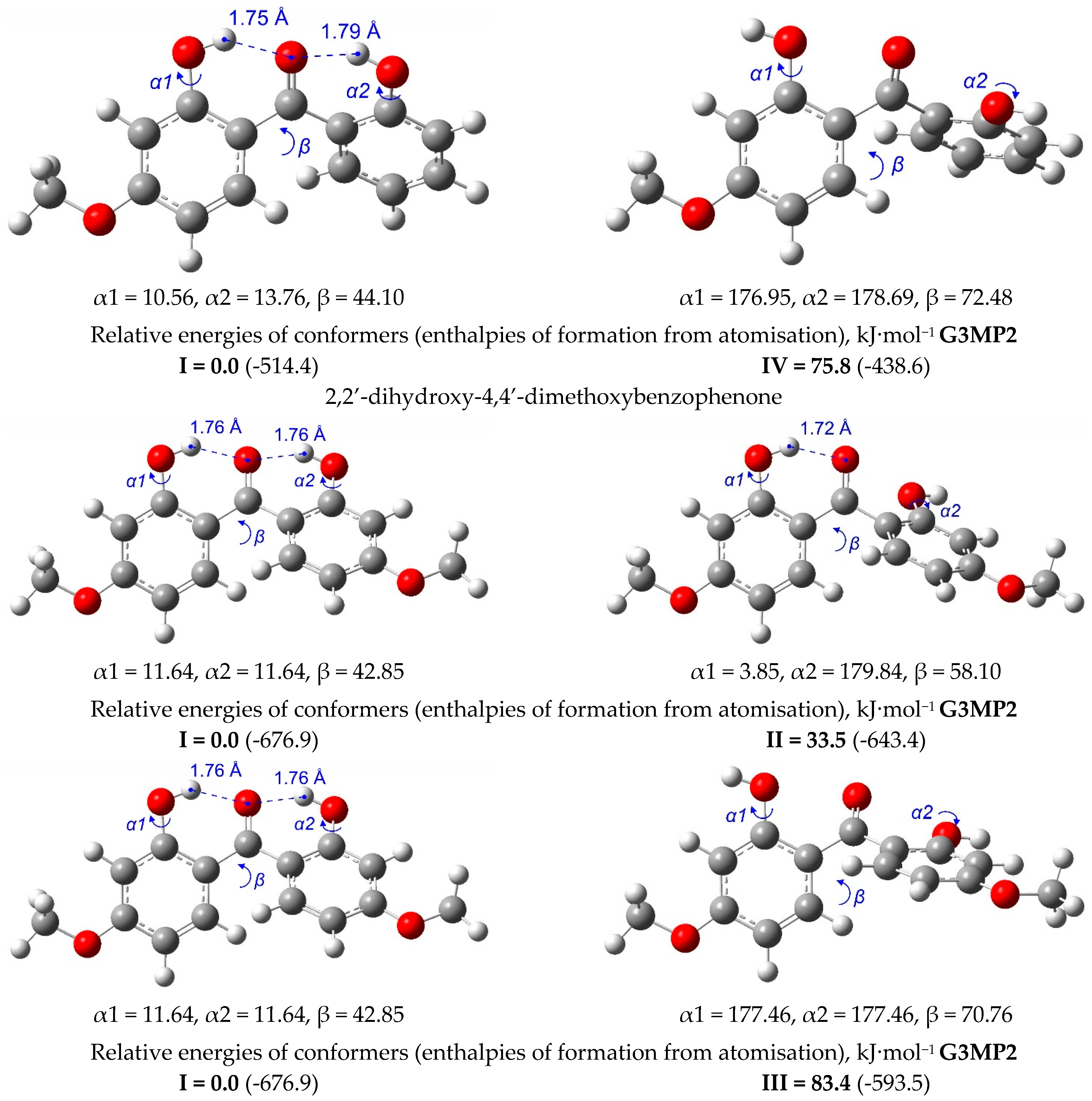



| T/ K a | m/ mg b | V(N2) c/dm3 | Ta/ K d | Flow/ dm3·h−1 | p/ Pa e | u(p)/ Pa f | kJ·mol−1 | J·K−1·mol−1 |
|---|---|---|---|---|---|---|---|---|
| 2,2′-di-hydroxy-benzophenone (298.15 K) = (84.9 ± 0.9) kJ·mol−1 ; pref = 1 Pa | ||||||||
| 363.1 | 0.69 | 1.274 | 295.7 | 2.94 | 6.18 | 0.18 | 76.9 | 131.3 |
| 368.2 | 1.55 | 2.065 | 295.9 | 1.18 | 8.62 | 0.24 | 76.3 | 129.4 |
| 363.2 | 1.31 | 2.439 | 295.2 | 1.18 | 6.14 | 0.18 | 76.9 | 131.1 |
| 368.6 | 1.29 | 1.666 | 295.9 | 1.02 | 8.89 | 0.25 | 76.2 | 129.3 |
| 373.5 | 1.62 | 1.475 | 295.9 | 1.18 | 12.59 | 0.34 | 75.6 | 127.8 |
| 373.6 | 0.53 | 0.479 | 295.7 | 1.07 | 12.72 | 0.34 | 75.6 | 127.8 |
| 375.8 | 1.31 | 1.014 | 295.9 | 1.01 | 14.85 | 0.40 | 75.3 | 127.2 |
| 378.7 | 1.71 | 1.088 | 295.9 | 2.04 | 18.05 | 0.48 | 75.0 | 126.3 |
| 378.8 | 1.52 | 0.998 | 295.9 | 1.02 | 17.51 | 0.46 | 75.0 | 126.0 |
| 383.8 | 1.53 | 0.715 | 295.9 | 1.02 | 24.56 | 0.64 | 74.4 | 124.7 |
| 383.8 | 1.55 | 0.710 | 295.2 | 1.01 | 24.99 | 0.65 | 74.4 | 124.8 |
| 383.8 | 1.29 | 0.610 | 295.2 | 1.18 | 24.30 | 0.63 | 74.4 | 124.5 |
| 387.9 | 1.25 | 0.457 | 295.2 | 1.14 | 31.23 | 0.81 | 73.8 | 123.3 |
| 388.1 | 1.09 | 0.408 | 295.9 | 0.98 | 30.58 | 0.79 | 73.8 | 123.0 |
| 388.7 | 1.80 | 0.633 | 295.2 | 1.00 | 32.53 | 0.84 | 73.8 | 123.0 |
| 393.0 | 1.02 | 0.286 | 295.2 | 1.14 | 40.81 | 1.05 | 73.2 | 121.4 |
| 393.1 | 1.33 | 0.372 | 295.2 | 1.01 | 41.09 | 1.05 | 73.2 | 121.4 |
| 398.1 | 1.36 | 0.291 | 295.7 | 1.03 | 53.59 | 1.36 | 72.6 | 119.7 |
| 398.3 | 1.15 | 0.237 | 295.9 | 1.02 | 55.80 | 1.42 | 72.6 | 119.9 |
| 403.2 | 1.72 | 0.274 | 295.7 | 1.03 | 71.82 | 1.82 | 72.0 | 118.3 |
| 408.4 | 2.11 | 0.257 | 295.2 | 1.03 | 93.81 | 2.37 | 71.3 | 116.7 |
| 2-hydroxy-4-methoxy-benzophenone (298.15 K) = (98.4 ± 1.0) kJ·mol−1 ; pref = 1 Pa | ||||||||
| 341.2 | 0.16 | 8.480 | 299.3 | 5.09 | 0.207 | 0.010 | 93.2 | 164.4 |
| 343.2 | 0.15 | 6.716 | 296.3 | 5.04 | 0.243 | 0.011 | 93.0 | 163.4 |
| 346.2 | 0.15 | 5.014 | 300.4 | 5.01 | 0.335 | 0.013 | 92.6 | 162.7 |
| 348.2 | 0.05 | 1.329 | 298.6 | 2.05 | 0.397 | 0.015 | 92.4 | 161.9 |
| 348.2 | 0.15 | 4.070 | 299.4 | 5.09 | 0.404 | 0.015 | 92.4 | 162.0 |
| 350.2 | 0.18 | 4.057 | 298.6 | 3.01 | 0.476 | 0.017 | 92.1 | 161.2 |
| 350.2 | 0.15 | 3.562 | 299.4 | 5.09 | 0.474 | 0.017 | 92.1 | 161.2 |
| 353.2 | 0.15 | 2.667 | 295.4 | 3.02 | 0.608 | 0.020 | 91.8 | 160.0 |
| 353.2 | 0.15 | 2.714 | 299.3 | 5.09 | 0.620 | 0.020 | 91.8 | 160.1 |
| 357.2 | 0.16 | 2.015 | 298.8 | 5.04 | 0.867 | 0.027 | 91.3 | 158.7 |
| 358.2 | 0.10 | 1.107 | 295.4 | 3.02 | 0.958 | 0.029 | 91.2 | 158.5 |
| 359.2 | 0.14 | 1.503 | 298.6 | 3.01 | 1.025 | 0.031 | 91.0 | 158.0 |
| 359.2 | 0.15 | 1.611 | 301.3 | 5.09 | 1.027 | 0.031 | 91.0 | 158.0 |
| 360.2 | 0.15 | 1.511 | 299.4 | 5.04 | 1.108 | 0.033 | 90.9 | 157.6 |
| 362.1 | 0.15 | 1.208 | 299.8 | 3.02 | 1.337 | 0.038 | 90.7 | 157.2 |
| 363.2 | 0.16 | 1.180 | 301.8 | 3.08 | 1.450 | 0.041 | 90.6 | 156.7 |
| 365.1 | 0.15 | 0.906 | 300.3 | 3.02 | 1.760 | 0.049 | 90.3 | 156.4 |
| 366.2 | 0.16 | 0.923 | 301.8 | 3.08 | 1.887 | 0.052 | 90.2 | 155.9 |
| 367.2 | 0.18 | 0.981 | 300.4 | 3.02 | 2.042 | 0.056 | 90.1 | 155.5 |
| 368.2 | 0.14 | 0.719 | 299.4 | 2.98 | 2.190 | 0.060 | 90.0 | 155.1 |
| 2,2′-di-hydroxy-4-methoxy-benzophenone (298.15 K) = (100.7 ± 0.9) kJ·mol−1 ; pref = 1 Pa | ||||||||
| 365.1 | 0.36 | 5.608 | 294.7 | 3.06 | 0.64 | 0.02 | 91.4 | 151.0 |
| 370.2 | 0.35 | 3.824 | 294.2 | 3.06 | 0.93 | 0.03 | 90.7 | 148.7 |
| 375.0 | 0.38 | 2.679 | 293.7 | 2.92 | 1.44 | 0.04 | 90.0 | 147.4 |
| 375.3 | 2.15 | 14.89 | 294.2 | 1.02 | 1.45 | 0.04 | 90.0 | 147.2 |
| 380.3 | 0.37 | 1.861 | 295.2 | 3.06 | 1.98 | 0.05 | 89.3 | 144.9 |
| 385.3 | 1.51 | 5.243 | 293.2 | 3.15 | 2.87 | 0.08 | 88.6 | 143.1 |
| 390.3 | 0.42 | 1.011 | 295.9 | 1.17 | 4.18 | 0.11 | 87.9 | 141.5 |
| 390.4 | 1.40 | 3.220 | 293.7 | 3.12 | 4.36 | 0.11 | 87.9 | 141.7 |
| 390.7 | 0.48 | 1.122 | 295.2 | 1.87 | 4.31 | 0.11 | 87.9 | 141.4 |
| 395.4 | 1.13 | 1.940 | 294.7 | 3.15 | 5.85 | 0.17 | 87.2 | 139.6 |
| 400.2 | 1.30 | 1.558 | 293.7 | 3.12 | 8.35 | 0.23 | 86.6 | 138.2 |
| 400.4 | 0.38 | 0.466 | 295.9 | 1.17 | 8.10 | 0.23 | 86.5 | 137.8 |
| 400.7 | 0.43 | 0.504 | 294.7 | 0.98 | 8.57 | 0.24 | 86.5 | 138.0 |
| 405.4 | 1.30 | 1.170 | 294.7 | 3.05 | 11.17 | 0.30 | 85.8 | 136.0 |
| 405.4 | 1.30 | 1.170 | 294.7 | 3.05 | 11.17 | 0.30 | 85.8 | 136.0 |
| 410.6 | 1.61 | 0.987 | 293.7 | 3.12 | 16.32 | 0.43 | 85.1 | 134.8 |
| 410.9 | 1.31 | 0.818 | 293.7 | 2.34 | 16.07 | 0.43 | 85.1 | 134.4 |
| 415.5 | 1.49 | 0.691 | 294.2 | 1.93 | 21.61 | 0.57 | 84.4 | 133.1 |
| 415.9 | 1.45 | 0.651 | 294.7 | 1.95 | 22.39 | 0.58 | 84.4 | 133.1 |
| 415.9 | 1.43 | 0.647 | 293.7 | 1.02 | 22.17 | 0.58 | 84.4 | 133.0 |
| 420.9 | 1.38 | 0.476 | 294.2 | 1.02 | 28.95 | 0.75 | 83.7 | 131.1 |
| 420.9 | 1.38 | 0.488 | 295.2 | 1.95 | 28.48 | 0.74 | 83.7 | 130.9 |
| 425.9 | 1.20 | 0.315 | 294.2 | 0.99 | 38.20 | 0.98 | 83.0 | 129.5 |
| 430.9 | 1.15 | 0.232 | 295.2 | 0.99 | 49.83 | 1.27 | 82.3 | 127.8 |
| 2,2′-di-hydroxy-4,4′-di-methoxy-benzophenone (298.15 K) = (117.2 ± 2.9) kJ·mol−1 ; pref = 1 Pa | ||||||||
| 412.6 | 0.58 | 1.914 | 296.2 | 3.06 | 2.74 | 0.07 | 99.7 | 154.3 |
| 415.0 | 1.11 | 3.062 | 294.2 | 3.06 | 3.24 | 0.09 | 99.3 | 153.4 |
| 420.0 | 1.98 | 3.776 | 295.2 | 3.06 | 4.69 | 0.12 | 98.6 | 151.8 |
| 424.0 | 1.74 | 2.552 | 295.2 | 3.06 | 6.10 | 0.18 | 97.9 | 150.3 |
| 435.1 | 1.68 | 1.250 | 293.7 | 3.06 | 11.96 | 0.32 | 96.3 | 146.2 |
| 2,2′-di-hydroxy-4,4′-di-methoxy-benzophenone (298.15 K) = (139.4 ± 2.4) kJ·mol−1 ; pref = 1 Pa | ||||||||
| 368.5 | 0.28 | 96.12 | 294.2 | 6.07 | 0.0258 | 0.0056 | 135.7 | 242.0 |
| 372.9 | 0.54 | 108.5 | 295.9 | 6.00 | 0.0443 | 0.0061 | 135.4 | 241.5 |
| 375.0 | 0.56 | 87.94 | 295.9 | 6.00 | 0.0575 | 0.0064 | 135.3 | 241.3 |
| 376.0 | 0.30 | 42.31 | 295.9 | 2.82 | 0.0628 | 0.0066 | 135.3 | 241.1 |
| 376.7 | 0.31 | 43.12 | 295.9 | 3.06 | 0.0650 | 0.0066 | 135.2 | 240.5 |
| 378.9 | 0.24 | 25.30 | 294.2 | 6.07 | 0.0849 | 0.0071 | 135.1 | 240.4 |
| 382.9 | 0.27 | 18.00 | 295.9 | 6.00 | 0.1361 | 0.0084 | 134.9 | 240.0 |
| 383.0 | 0.27 | 18.00 | 292.7 | 6.00 | 0.1312 | 0.0083 | 134.9 | 239.6 |
| 386.4 | 0.31 | 14.42 | 293.7 | 6.07 | 0.1916 | 0.0098 | 134.7 | 239.2 |
| 389.0 | 0.22 | 7.504 | 293.7 | 6.00 | 0.2663 | 0.0117 | 134.6 | 239.3 |
| 392.1 | 0.34 | 8.704 | 295.9 | 6.00 | 0.3509 | 0.0138 | 134.4 | 238.4 |
| 395.1 | 0.35 | 6.100 | 295.9 | 6.00 | 0.5143 | 0.0179 | 134.3 | 238.6 |
| 399.3 | 0.28 | 3.137 | 293.7 | 6.07 | 0.7853 | 0.0246 | 134.0 | 237.9 |
| T/ K a | m/ mg b | T/s | p/ Pa c | u(p)/ Pa d | kJ·mol−1 | J·K−1·mol−1 |
|---|---|---|---|---|---|---|
| 2,4-di-hydroxy-benzophenone (298.15 K) = (133.0 ± 2.9) kJ·mol−1 ; pref = 1 Pa | ||||||
| 403.4 | 35.5 | 4417 | 4.159 | 0.109 | 128.8 | 235.5 |
| 386.5 | 12.9 | 8951 | 0.794 | 0.025 | 129.5 | 237.4 |
| 396.6 | 11.4 | 2756 | 2.208 | 0.060 | 129.1 | 236.4 |
| 406.8 | 8.2 | 14,260 | 5.602 | 0.165 | 128.7 | 235.0 |
| 366.7 | 11.3 | 75,182 | 0.084 | 0.007 | 130.3 | 238.9 |
| 376.5 | 10.2 | 20,355 | 0.279 | 0.012 | 129.9 | 238.7 |
| 2,2′,4,4′-tetra-hydroxy-benzophenone (298.15 K) = (159.8 ± 3.1) kJ·mol−1 ; pref = 1 Pa | ||||||
| 431.8 | 8.31 | 17,366 | 0.251 | 0.011 | 154.1 | 249.6 |
| 436.6 | 11.87 | 14,993 | 0.414 | 0.015 | 153.9 | 249.4 |
| 441.9 | 20.99 | 16,139 | 0.676 | 0.022 | 153.6 | 248.7 |
| 448.2 | 13.67 | 18,965 | 1.236 | 0.036 | 153.4 | 248.2 |
| 448.9 | 14.96 | 5987 | 1.277 | 0.037 | 153.3 | 247.9 |
| 453.8 | 15.78 | 13,385 | 1.990 | 0.055 | 153.1 | 247.4 |
| 455.7 | 15.9 | 3250 | 2.433 | 0.066 | 153.0 | 247.5 |
| Compounds | ||||
|---|---|---|---|---|
| 2-hydroxy-benzophenone | 225.4 [15] | 34.6 | 366.4 | 105.8 |
| 3-hydroxy-benzophenone | 233.7 [15] | 35.8 | 366.4 | 105.8 |
| 4-hydroxy-benzophenone | 226.0 [15] | 34.7 | 366.4 | 105.8 |
| 2,4-dihydroxy-benzophenone | 254.9 | 39.0 | 434.8 | 123.6 |
| 2,2′-dihydroxy-benzophenone | 253.0 [16] | 38.7 | 434.8 | 123.6 |
| 2-hydroxy-4-methoxy-benzophenone | 286.6 | 43.8 | 422.8 | 120.5 |
| 2,2′-hydroxy-4-methoxy-benzophenone | 301.0 | 45.9 | 491.2 | 138.3 |
| 2,2′,4,4′-tetrahydroxy-benzophenone | 283.2 | 43.2 | 571.6 | 159.2 |
| 2,2′-dihydroxy-4,4′-dimethoxybenzophenone | 347.0 | 52.8 | 547.6 | 153.0 |
| Compound | WBR | AT | (theor) | |||
|---|---|---|---|---|---|---|
| benzophenone | 95.0 ± 0.4 | 49.3 f | 50.1 | 49.4 ± 0.8 g | ||
| 2-hydroxy-benzophenone (cr) [15] | −245.7 ± 3.8 | 97.9 ± 1.9 | −147.8 ± 4.3 | −150.5 | −149.9 | −150.2 ± 2.5 |
| 3-hydroxy-benzophenone (cr) [15] | −247.3 ± 4.0 | 131.7 ± 0.9 | −115.6 ± 3.9 | −125.1 | −124.5 | −124.8 ± 2.5 |
| 4-hydroxy-benzophenone(cr) [15] | −252.4 ± 3.3 | 130.3 ± 1.0 | −122.1 ± 3.8 | −129.4 | −128.8 | −129.1 ± 2.5 |
| 2-methoxy-benzophenone (liq) | 87.4 ± 3.0 | −100.3 | −101.2 | −100.8 ± 2.5 | ||
| 3-methoxy-benzophenone (liq) | 88.7 ± 2.0 | −106.4 | −107.3 | −106.9 ± 2.5 | ||
| 4-methoxy-benzophenone (liq) | 90.2 ± 2.0 | −107.6 | −108.5 | −108.1 ± 2.5 | ||
| 2,4-di-hydroxy-benzophenone (cr) | (−492.8 ± 1.9) [41] | 134.5 ± 1.7 | (−358.3 ± 2.5) | −333.6 | −333.1 | −333.4 ± 2.5 |
| 2-hydroxy-4-methoxy-benzophenone(cr) [25] | −414.2 ± 4.5 | 116.8 ± 1.2 | −297.4 ± 4.7 | −313.2 | −314.2 | −313.7 ± 2.5 |
| 2-hydroxy-2′-methoxy-benzophenone | −302.8 | −303.8 | −303.3 ± 2.5 | |||
| 2,2′-di-hydroxy-benzophenone (cr) | 101.9 ± 1.3 | −342.2 | −342.2 | −342.0 ± 2.5 | ||
| 2,2′-di-hydroxy-4-methoxy-benzophenone (cr) | 118.7 ± 1.6 | −505.2 | −506.4 | −505.8 ± 2.5 | ||
| 2,2′,4,4′-tetra-hydroxy-benzophenone (cr) | 159.8 ± 3.1 | −704.7 | −704.7 | −704.6 ± 2.5 | ||
| 2,2′-di-hydroxy-4,4′-dimethoxybenzophenone(cr) | 139.4 ± 2.4 | −667.0 | −669.8 | −668.4 ± 2.5 |
| Centrepiece | ||
|---|---|---|
| benzene [46] | 82.9 | 33.9 |
| benzophenone [36] | 49.4 | 78.0 |
| Contributionsa | ||
| ΔH(H → CH3O) | −153.2 | 12.7 |
| ΔH(H → OH) | −175.4 | 24.1 |
| Interactionsb | ||
| ortho C = O(C6H5) − OH | −24.5 c | −21.5 |
| meta C = O(C6H5) − OH | 0.9 c | 9.1 |
| para C = O(C6H5) − OH | −3.4 c | 12.0 |
| ortho C = O(C6H5) − CH3O | 3.5 c | −2.9 |
| meta C = O(C6H5) − CH3O | −2.6 c | −1.6 |
| para C = O(C6H5) − CH3O | −3.8 c | 1.5 |
| ortho OH − OH | 2.5 | −11.4 |
| meta OH − OH | −4.5 | −3.7 |
| para OH − OH | 2.9 | 2.3 |
| ortho OH − CH3O | −2.1 | −9.3 |
| meta OH − CH3O | 0.1 | 4.1 |
| para OH − CH3O | 8.7 | 3.0 |
| ortho CH3O − CH3O | 17.5 | 5.2 |
| meta CH3O − CH3O | −0.1 | 0.4 |
| para CH3O − CH3O | 7.3 | 2.3 |
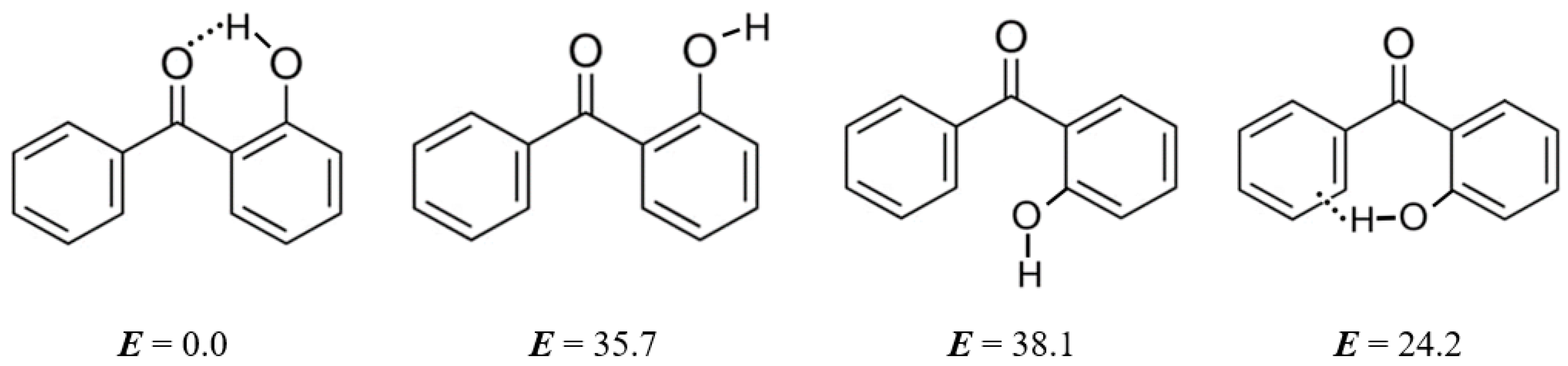
| Ortho-Substituted Benzophenones | ΔHWBR b | ΔHconf c | Δ d | |
|---|---|---|---|---|
| 2-hydroxy-benzophenone | −24.5 | −24.5 | −35.7 | 11.2 |
| 2,4-di-hydroxy-benzophenone | −32.2 | −24.3 | −43.6 | 19.3 |
| 2-hydroxy-4-methoxy-benzophenone | −34.0 | −30.3 | −43.9 | 13.6 |
| 2,2’-di-hydroxy-benzophenone | −40.8 | −40.8 (−20.4) e | −68.6 | 27.8 |
| 2,2’-di-hydroxy-4-methoxy-benzophenone | −50.7 | −47.0 (−23.5) e | −75.8 | 24.4 |
| 2,2’,4,4’-tetra-hydroxy-benzophenone | −52.5 | −36.7 (−18.4) e | −74.9 | 38.2 |
| 2,2’-di-hydroxy-4,4’-dimethoxybenzophenone | −59.2 | −51.8 (−25.9) e | −83.4 | 31.6 |
| 2-hydroxy-2’-methoxy-benzophenone | −23.6 | −27.1 | −41.3 | 14.2 |
| 2-methoxy-benzophenone | 3.5 | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samarov, A.A.; Kondratev, S.O.; Verevkin, S.P. Nearest-Neighbour and Non-Nearest-Neighbour Non-Covalent Interactions between Substituents in the Aromatic Systems: Experimental and Theoretical Investigation of Functionally Substituted Benzophenones. Molecules 2022, 27, 8477. https://doi.org/10.3390/molecules27238477
Samarov AA, Kondratev SO, Verevkin SP. Nearest-Neighbour and Non-Nearest-Neighbour Non-Covalent Interactions between Substituents in the Aromatic Systems: Experimental and Theoretical Investigation of Functionally Substituted Benzophenones. Molecules. 2022; 27(23):8477. https://doi.org/10.3390/molecules27238477
Chicago/Turabian StyleSamarov, Artemiy A., Stanislav O. Kondratev, and Sergey P. Verevkin. 2022. "Nearest-Neighbour and Non-Nearest-Neighbour Non-Covalent Interactions between Substituents in the Aromatic Systems: Experimental and Theoretical Investigation of Functionally Substituted Benzophenones" Molecules 27, no. 23: 8477. https://doi.org/10.3390/molecules27238477
APA StyleSamarov, A. A., Kondratev, S. O., & Verevkin, S. P. (2022). Nearest-Neighbour and Non-Nearest-Neighbour Non-Covalent Interactions between Substituents in the Aromatic Systems: Experimental and Theoretical Investigation of Functionally Substituted Benzophenones. Molecules, 27(23), 8477. https://doi.org/10.3390/molecules27238477









