Electron Correlation or Basis Set Quality: How to Obtain Converged and Accurate NMR Shieldings for the Third-Row Elements?
Abstract
1. Introduction
2. Results
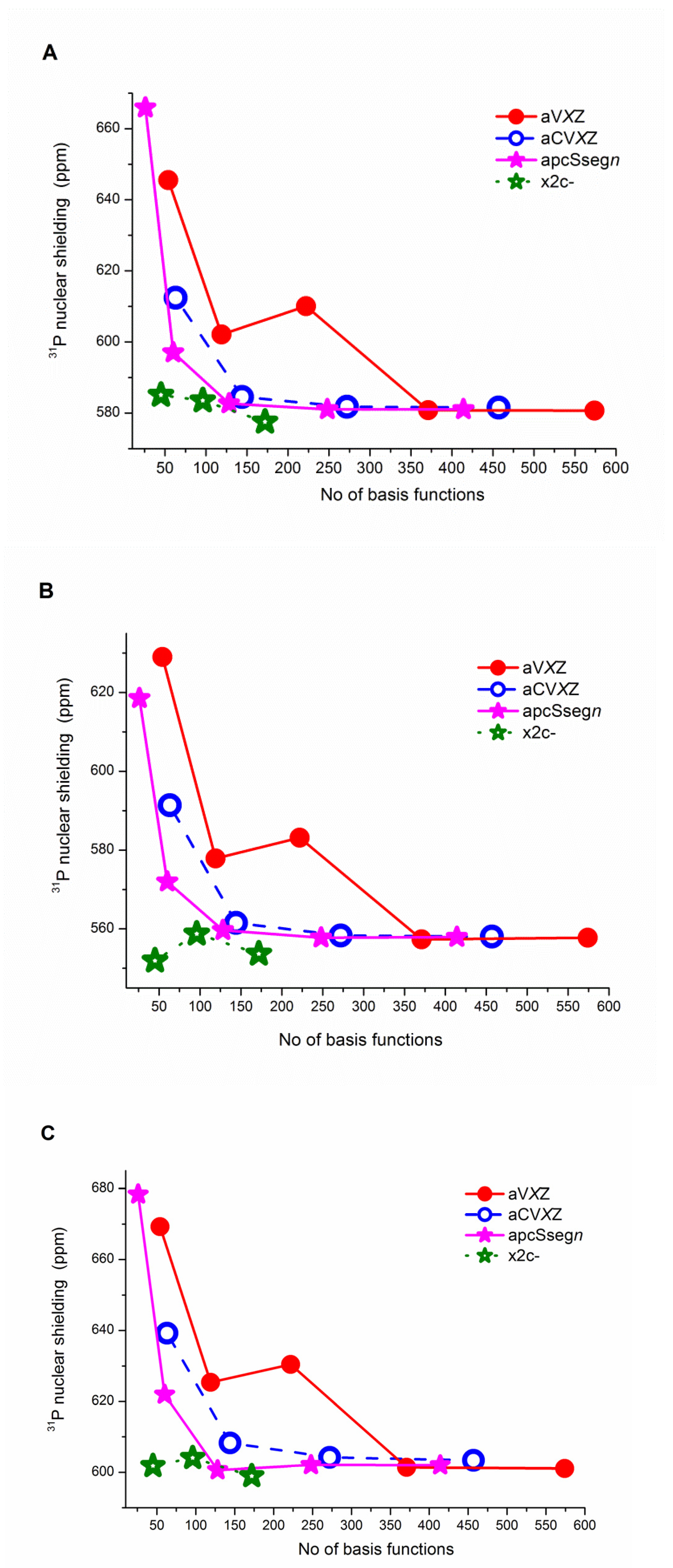
2.1. Sensitivity of Total Shieldings of the Third-Row Nuclei to the Basis Set Quality
2.1.1. Sensitivity of 31P NMR Parameters to the Basis Set Quality
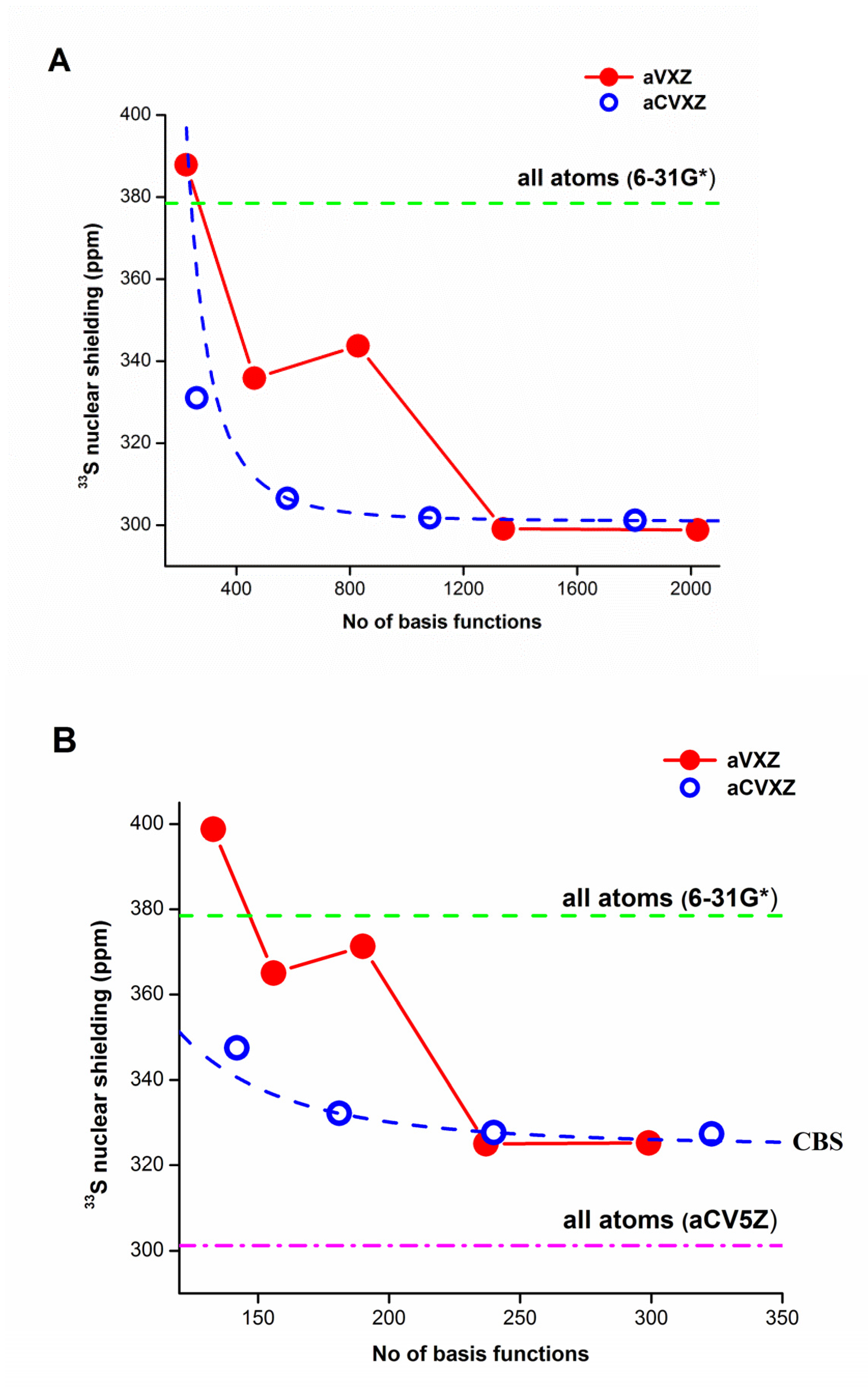
2.1.2. Other Third-Row Elements
2.1.3. Estimated CBS Nuclear Shielding Values of the Studied Systems
2.2. 33S shielding Components and Total Shielding of 2-Thiouracil (2-TU)
2.3. Corrections to Isotropic Nuclear Magnetic Shieldings of Third Row Elements
3. Discussion
4. Materials and Methods
4.1. Geometry
4.2. NMR Shieldings
4.3. Zero-Point Vibrational and Thermal Corrections
4.4. Relativistic Corrections
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Helgaker, T.; Jaszunski, M.; Ruud, K. Ab Initio Methods for the Calculation of NMR shielding and Indirect Spin-Spin Coupling Constants. Chem. Rev. 1999, 99, 293–352. [Google Scholar] [CrossRef] [PubMed]
- Gauss, J.; Stanton, J.F. Gauge-invariant calculation of nuclear magnetic shielding constants at the coupled-cluster singles and doubles level. J. Chem. Phys. 1995, 102, 251–253. [Google Scholar] [CrossRef]
- Gauss, J.; Stanton, J.F. Perturbative treatment of triple excitations in coupled-cluster calculations of nuclear magnetic shielding constants. J. Chem. Phys. 1996, 104, 2574–2583. [Google Scholar] [CrossRef]
- Kupka, T.; Stachów, M.; Nieradka, M.; Kaminský, J.; Pluta, T. Convergence of nuclear magnetic shieldings in the Kohn-Sham limit for several small molecules. J. Chem. Theor. Comput. 2010, 6, 1580–1589. [Google Scholar] [CrossRef]
- Gauss, J. Calculation of NMR chemical shifts at second-order many-body perturbation theory using gauge-including atomic orbitals. Chem. Phys. Lett. 1992, 191, 614–620. [Google Scholar] [CrossRef]
- Crittenden, D.L. A new double-reference correction scheme for accurate and efficient computation of NMR chemical shieldings. Phys. Chem. Chem. Phys. 2022, 24, 27055–27063. [Google Scholar] [CrossRef]
- Nazarski, R.B.; Wałejko, P.; Witkowski, S. Multi-conformer molecules in solutions: An NMR-based DFT/MP2 conformational study of two glucopyranosides of a vitamin E model compound. Org. Biomol. Chem. 2016, 11, 3142–3158. [Google Scholar] [CrossRef] [PubMed]
- Nazarski, R.B. Summary of DFT calculations coupled with current statistical and/or artificial neural network (ANN) methods to assist experimental NMR data in identifying diastereomeric structures. Tetrahedron Lett. 2021, 71, 152548. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Ditchfield, R. Self-consistent perturbation theory of diamagnetism I. A gauge-invariant LCAO method for N.M.R. chemical shifts. Mol. Phys. 1974, 27, 789–807. [Google Scholar] [CrossRef]
- Feller, D. Application of systematic sequences of wave functions to the water dimer. J. Chem. Phys. 1992, 96, 6104–6114. [Google Scholar] [CrossRef]
- Feller, D. The use of systematic sequences of wave functions for estimating the complete basis set, full configuration interaction limit in water. J. Chem. Phys. 1993, 98, 7059–7071. [Google Scholar] [CrossRef]
- Kupka, T.; Ruscic, B.; Botto, R.E. Hartree-Fock and Density Functional Complete Basis-Set (CBS) Predicted Nuclear Shielding Anisotropy and Shielding Tensor Components. Solid State Nucl. Magn. Reson. 2003, 2, 143–167. [Google Scholar] [CrossRef]
- Kupka, T.; Ruscic, B.; Botto, R.E. Toward Hartree-Fock- and Density Functional Complete Basis-Set Predicted NMR Parameters. J. Phys. Chem. A. 2002, 106, 10396–10407. [Google Scholar] [CrossRef]
- Kupka, T.; Leszczyńska, M.; Ejsmont, K.; Mnich, A.; Broda, M.; Thangavel, K.; Kaminský, J. Phosphorus mononitride: A difficult case for theory. Int. J. Quantum Chem. 2019, 119, e26032. [Google Scholar] [CrossRef]
- Jensen, F. The basis set convergence of spin-spin coupling constants calculated by density functional methods. J. Chem. Theor. Comput. 2006, 2, 1360–1369. [Google Scholar] [CrossRef] [PubMed]
- Jensen, F. Basis set convergence of nuclear magnetic shielding constants calculated by density functional methods. J. Chem. Theor. Comput 2008, 4, 719–727. [Google Scholar] [CrossRef] [PubMed]
- Jensen, F. Unifying General and Segmented Contracted Basis Sets. Segmented Polarization Consistent Basis Sets. J. Chem. Theory Comput. 2014, 10, 1074–1085. [Google Scholar] [CrossRef] [PubMed]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
- Van Mourik, T.; Dunning, T.H., Jr. Gaussian Basis Sets for Use in Correlated Molecular Calculations. VIII. Standard and Augmented Sextuple Zeta Correlation Consistent Basis Sets for Aluminum Through Argon. Int. J. Quantum Chem. 2000, 76, 205–221. [Google Scholar] [CrossRef]
- Peterson, K.A.; Woon, D.E.; Dunning, T.H., Jr. Benchmark calculations with correlated molecular wave functions. IV. The classical barrier height of the H + H2→H2 + H reaction. J. Chem. Phys. 1994, 100, 7410–7415. [Google Scholar] [CrossRef]
- Peterson, K.A.; Dunning, T.H. Accurate correlation consistent basis sets for molecular core–valence correlation effects: The second row atoms Al–Ar, and the first row atoms B–Ne revisited. J. Chem. Phys. 2002, 117, 10548–10560. [Google Scholar] [CrossRef]
- Prascher, B.P.; Woon, D.E.; Peterson, K.A.; Dunning, T.H.; Wilson, A.K. Gaussian basis sets for use in correlated molecular calculations. VII. Valence, core-valence, and scalar relativistic basis sets for Li, Be, Na, and Mg. Theor. Chem. Acc. 2011, 128, 69–82. [Google Scholar] [CrossRef]
- Jensen, F. Polarization consistent basis sets: Principles. J. Chem. Phys. 2001, 115, 9113–9125. [Google Scholar] [CrossRef]
- Jensen, F. Polarization consistent basis sets. II. Estimating the Kohn-Sham basis set limit. J. Chem. Phys. 2002, 116, 7372–7379. [Google Scholar] [CrossRef]
- Jensen, F. Polarization consistent basis sets. III. The importance of diffuse functions. J. Chem. Phys. 2002, 117, 9234–9240. [Google Scholar] [CrossRef]
- Jensen, F. Polarization consistent basis sets. IV. The basis set convergence of equilibrium geometries, harmonic vibrational frequencies, and intensities. J. Chem. Phys. 2003, 118, 2459–2463. [Google Scholar] [CrossRef]
- Jensen, F. The optimum contraction of basis sets for calculating spin-spin coupling constants. Theor. Chem. Acc. 2010, 126, 371–382. [Google Scholar] [CrossRef]
- Kupka, T.; Stachow, M.; Nieradka, M.; Kaminsky, J.; Pluta, T.; Sauer, S.P.A. From CCSD(T)/aug-cc-pVTZ-J to CCSD(T) complete basis set limit isotropic nuclear magnetic shieldings via affordable DFT/CBS calculations. Magn. Reson. Chem. 2011, 49, 231–236. [Google Scholar] [CrossRef]
- Jankowska, M.; Kupka, T.; Stobinski, L.; Faber, R.; Lacerda, E.G.; Sauer, S.P.A. Spin-Orbit ZORA and Four-Component Dirac-Coulomb Estimation of Relativistic Corrections to Isotropic Nuclear Shieldings and Chemical Shifts of Noble Gas Dimers. J. Comput. Chem. 2016, 37, 395–403. [Google Scholar] [CrossRef] [PubMed]
- Kupka, T.; Stachów, M.; Chełmecka, E.; Pasterny, K.; Stobińska, M.; Stobiński, L.; Kaminský, J. Efficient modeling of NMR parameters in carbon nanosystems. J. Chem. Theor. Comput. 2013, 9, 4275–4286. [Google Scholar] [CrossRef] [PubMed]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Franzke, Y.J.; Spiske, L.; Pollak, P.; Weigend, F. Segmented Contracted Error-Consistent Basis Sets of Quadruple-ζ Valence Quality for One- and Two-Component Relativistic All-Electron Calculations. J. Chem. Theory Comput. 2020, 16, 5658–5674. [Google Scholar] [CrossRef]
- Franzke, Y.J.; Weigend, F. NMR Shielding Tensors and Chemical Shifts in Scalar-Relativistic Local Exact Two-Component Theory. J. Chem. Theory Comput. 2019, 15, 1028–1043. [Google Scholar] [CrossRef]
- Franzke, Y.J.; Treß, R.; Pazdera, T.M.; Weigend, F. Error-consistent segmented contracted all-electron relativistic basis sets of double- and triple-zeta quality for NMR shielding constants. Phys. Chem. Chem. Phys. 2019, 21, 16658–16664. [Google Scholar] [CrossRef]
- de Jong, W.A.; Harrison, R.J.; Dixon, D.A. Parallel Douglas–Kroll energy and gradients in NWChem: Estimating scalar relativistic effects using Douglas–Kroll contracted basis sets. J. Chem. Phys. 2001, 114, 48–53. [Google Scholar] [CrossRef]
- Teale, A.M.; Lutnas, O.B.; Helgaker, T.; Tozer, D.J.; Gauss, J. Benchmarking density-functional theory calculations of NMR shielding constants and spin-rotation constants using accurate coupled-cluster calculations. J. Chem. Phys. 2013, 138, 024111. [Google Scholar] [CrossRef]
- Field-Theodore, T.E.; Olejniczak, M.; Jaszuński, M.; Wilson, D.J.D. NMR shielding constants in group 15 trifluorides. Phys. Chem. Chem. Phys. 2018, 20, 23025–23033. [Google Scholar] [CrossRef] [PubMed]
- Stoychev, G.L.; Auer, A.A.; Izsák, R.; Neese, F. Self-Consistent Field Calculation of Nuclear Magnetic Resonance Chemical Shielding Constants Using Gauge-Including Atomic Orbitals and Approximate Two-Electron Integrals. J. Chem. Theory Comput. 2018, 14, 619–637. [Google Scholar] [CrossRef]
- Martinez-Baez, E.; Feng, R.; Pearce, C.I.; Schenter, G.K.; Clark, A.E. Al27 NMR chemical shift of Al(OH)4− calculated from first principles: Assessment of error cancellation in chemically distinct reference and target systems. J. Chem. Phys. 2020, 152, 134303. [Google Scholar] [CrossRef] [PubMed]
- Lee, V.Y.; Uhlig, F. Organosilicon Compounds; Academic Press: Cambridge, MA, USA, 2017; p. 59. [Google Scholar]
- Bhinderwala, F.; Evans, P.; Jones, K.; Laws, B.R.; Smith, T.G.; Morton, M.; Powers, R. Phosphorus NMR and Its Application to Metabolomics. Anal. Chem. 2020, 92, 9536–9545. [Google Scholar] [CrossRef]
- Ruud, K.; Astrand, P.-O.; Taylor, P.R. An efficient approach for calculating vibrational wave functions and zero-point vibrational corrections to molecular properties of polyatomic molecules. J. Chem. Phys. 2000, 112, 2668–2683. [Google Scholar] [CrossRef]
- Ruud, K.; Astrand, P.-O.; Taylor, P.R. Zero-point vibrational effects on proton shieldings: Functional-group contributions from ab initio calculations. J. Am. Chem. Soc. 2001, 123, 4826–4833. [Google Scholar] [CrossRef] [PubMed]
- Vıícha, J.; Novotný, J.; Komorovsky, S.; Straka, M.; Kaupp, M.; Marek, R. Relativistic Heavy-Neighbor-Atom Effects on NMR Shifts: Concepts and Trends Across the Periodic Table. Chem. Rev. 2020, 120, 7065–7103. [Google Scholar] [CrossRef] [PubMed]
- Lantto, P.; Standara, S.; Riedel, S.; Vaara, J.; Straka, M. Exploring new 129Xe chemical shift ranges in HXeY compounds: Hydrogen more relativistic than xenon. Phys. Chem. Chem. Phys. 2012, 14, 10944–10952. [Google Scholar] [CrossRef]
- Krivdin, L.B. Recent advances in computational liquid-phase 77Se NMR. Russ. Chem. Rev. 2021, 90, 265–279. [Google Scholar] [CrossRef]
- Rusakov, Y.Y.; Krivdin, L.B.; Sauer, S.P.A.; Levanova, E.P.; Levkovskaya, G.G. Structural trends of 77Se-1H spin-spin coupling constants and conformational behavior of 2-substituted selenophenes. Magn. Reson. Chem. 2010, 48, 44–52. [Google Scholar] [CrossRef] [PubMed]
- Sarotti, A.M.; Pellegrinet, S.C. A Multi-standard Approach for GIAO 13C NMR Calculations. J. Org. Chem. 2009, 74, 7254–7260. [Google Scholar] [CrossRef]
- Lodewyk, M.W.; Siebert, M.R.; Tantillo, D.J. Computational Prediction of 1H and 13C Chemical Shifts: A Useful Tool for Natural Product, Mechanistic, and Synthetic Organic Chemistry. Chem. Rev. 2012, 112, 1839–1862. [Google Scholar] [CrossRef] [PubMed]
- Gamov, G.A.; Kuranova, N.N.; Pogonin, A.E.; Aleksandriiskii, V.V.; Sharnin, V.A. Hydrogen bonds determine the signal arrangement in 13C NMR spectra of nicotinate. J. Mol. Struct. 2018, 1154, 565–569. [Google Scholar] [CrossRef]
- Alkorta, I.; Elguero, J. Ab initio (GIAO) calculations of absolute nuclear shieldings for representative compounds containing 1(2)H, 6(7)Li, 11B, 13C, 14(15)N, 17O, 19F, 29Si, 31P, 33S and 35Cl nuclei. Struct. Chem. 1998, 9, 187–202. [Google Scholar]
- Prochnow, E.; Auer, A.A. Quantitative prediction of gas-phase 15N and 31P nuclear magnetic shielding constants. J. Chem. Phys. 2010, 132, 064109. [Google Scholar] [CrossRef]
- NIST. Available online: https://cccbdb.nist.gov/geom2x.asp (accessed on 1 January 2020).
- Antušek, A.; Jaszuński, M. Coupled cluster study of NMR shielding constants and spin-rotation constants in SiH4, PH3 and H2S molecules. Mol. Phys. 2006, 104, 1463–1474. [Google Scholar]
- Lu, T.; Hao, Q.; Wilke, J.J.; Yamaguchi, Y.; Fang, D.-C.; Schaefer, H.F. Silylidene (SiCH2) and its isomers: Anharmonic rovibrational analyses for silylidene, silaacetylene, and silavinylidene. J. Mol. Struct. 2012, 1009, 103–110. [Google Scholar] [CrossRef]
- Blicharska, B.; Kupka, T. Theoretical DFT and experimental NMR studies on uracil and 5-fluorouracil. J. Mol. Struct. 2002, 613, 153–166. [Google Scholar] [CrossRef]
- Kupka, T.; Pasterna, G.; Lodowski, P.; Szeja, W. GIAO-DFT Prediction of Accurate NMR Parameters in Selected Glucose Derivatives. Magn. Reson. Chem. 1999, 37, 421–429. [Google Scholar] [CrossRef]
- Vincent, J.; Mignot, G.; Chalmin, F.; Ladoire, S.; Bruchard, M.; Chevriaux, A.; Martin, F.; Apetoh, L.; Rébé, C.; Ghiringhelli, F. 5-Fluorouracil Selectively Kills Tumor-Associated Myeloid-Derived Suppressor Cells Resulting in Enhanced T Cell–Dependent Antitumor Immunity. Cancer Res. 2010, 70, 3052–3061. [Google Scholar] [CrossRef]
- Rzepiela, K.; Buczek, A.; Kupka, T.; Broda, M.A. Factors Governing the Chemical Stability and NMR Parameters of Uracil Tautomers and Its 5-Halogen Derivatives. Molecules 2020, 25, 3931. [Google Scholar] [CrossRef]
- Rzepiela, K.; Buczek, A.; Kupka, T.; Broda, M.A. On the aromaticity of uracil and its 5-halogeno derivatives as revealed by theoretically derived geometric and magnetic indexes. Struct. Chem. 2021, 32, 275–283. [Google Scholar] [CrossRef]
- Jarzembska, K.N.; Kubsik, M.; Kamiński, R.; Woźniak, K.; Dominiak, P.M. From a Single Molecule to Molecular Crystal Architectures: Structural and Energetic Studies of Selected Uracil Derivatives. Cryst. Growth Des. 2012, 12, 2508–2524. [Google Scholar]
- Francl, M.M.; Pietro, W.J.; Hehre, W.J.; Binkley, J.S.; Gordon, M.S.; DeFrees, D.J.; Pople, J.A. Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row elements. J. Chem. Phys. 1982, 77, 3654–3665. [Google Scholar] [CrossRef]
- Chesnut, D.B.; Moore, K.D. Locally dense basis sets for chemical shift calculations. J. Comput. Chem. 1989, 10, 648–659. [Google Scholar] [CrossRef]
- Reid, D.M.; Kobayashi, R.; Collins, M.A. Systematic study of locally dense basis sets for NMR shielding constants. J. Chem. Theor. Comp. 2014, 10, 146–152. [Google Scholar] [CrossRef]
- Provasi, P.F.; Aucar, G.A.; Sauer, S.P.A. The use of locally dense basis sets in the calculation of indirect nuclear spin–spin coupling constants: The vicinal coupling constants in H3C–CH2X (X = H, F, Cl, Br, I). J. Chem. Phys. 2000, 112, 6201–6208. [Google Scholar] [CrossRef]
- Semenov, V.A.; Krivdin, L.B. DFT computational schemes for 1H and 13C NMR chemical shifts of natural products, exemplified by strychnine. Magn. Reson. Chem. 2020, 58, 56–64. [Google Scholar] [CrossRef]
- Krivdin, L.B. Computational NMR of heavy nuclei involving 109Ag, 113Cd, 119Sn, 125Te, 195Pt, 199Hg, 205Tl, and 207Pb. Russ. Chem. Rev. 2021, 90, 1166–1212. [Google Scholar]
- Faber, R.; Kaminský, J.; Sauer, S.P.A. Rovibrational and Temperature Effects in Theoretical Studies of NMR Parameters. In New Developments in NMR. Gas Phase NMR.; Jackowski, K., Jaszuński, M., Eds.; The Royal Society of Chemistry: Piccadilly, UK, 2016; Volume 6, pp. 218–266. [Google Scholar]
- Jaszuński, M.; Repisky, M.; Demissie, T.B.; Komorovsky, S.; Malkin, E.; Ruud, K.; Garbacz, P.; Jackowski, K.; Makulski, W. Spin-rotation and NMR shielding constants in HCl. J. Chem. Phys. 2013, 139, 234302. [Google Scholar] [CrossRef]
- Yoshizawa, T.; Hada, M. Calculations of nuclear magnetic shielding constants based on the exact two-component relativistic method. J. Chem. Phys. 2017, 147, 154104. [Google Scholar] [CrossRef]
- Stoychev, G.L.; Auer, A.A.; Neese, F. Efficient and Accurate Prediction of Nuclear Magnetic Resonance Shielding Tensors with Double-Hybrid Density Functional Theory. J. Chem. Theory Comput. 2018, 14, 4756–4771. [Google Scholar] [CrossRef] [PubMed]
- Jameson, C.J.; Jameson, A.K. Absolute shielding scale for 29Si. Chem. Phys. Lett. 1988, 149, 300–305. [Google Scholar] [CrossRef]
- Jameson, C.J.; de Dios, A.C.; Jameson, A.K. The 31P shielding in phosphine. J. Chem. Phys. 1991, 95, 9042–9053. [Google Scholar] [CrossRef]
- Lantto, P.; Jackowski, K.; Makulski, W.; Olejniczak, M.; Jaszuński, M. NMR Shielding Constants in PH3, Absolute Shielding Scale, and the Nuclear Magnetic Moment of 31P. J. Phys. Chem. A 2011, 115, 10617–10623. [Google Scholar] [CrossRef]
- Kudo, K.; Fukui, H. Calculation of nuclear magnetic shieldings using an analytically differentiated relativistic shielding formula. J. Chem. Phys. 2005, 123, 114102. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01. Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Stanton, J.F.; Gauss, J.; Cheng, L.; Harding, M.E.; Matthews, D.A.; Szalay, P.G. CFOUR. Available online: http://www.cfour.de (accessed on 1 January 2020).
- Bouř, P. Program S4; Czech Academy of Sciences: Prague, Czech Republic, 2009. [Google Scholar]
- Feller, D. The Role of Databases in Support of Computational Chemistry Calculations. J. Comput. Chem. 1996, 17, 1571–1586. [Google Scholar] [CrossRef]
- Schuchardt, K.L.; Didier, B.T.; Elsethagen, T.; Sun, L.; Gurumoorthi, V.; Chase, J.; Li, J.; Windus, T.L. Basis Set Exchange: A Community Database for Computational Sciences. J. Chem. Inf. Model. 2007, 47, 1045–1052. [Google Scholar] [CrossRef]
- Pritchard, B.P.; Altarawy, D.; Didier, B.; Gibson, T.D.; Windus, T.L. New Basis Set Exchange: An Open, Up-to-Date Resource for the Molecular Sciences Community. J. Chem. Inf. Model. 2019, 59, 4814–4820. [Google Scholar] [CrossRef]
- EMSL, Basis Set Exchange. Available online: https://bse.pnl.gov/bse/portal (accessed on 1 January 2020).
- Helgaker, T.; Klopper, W.; Koch, H.; Noga, J. Basis-set convergence of correlated calculations on water. J. Chem. Phys. 1997, 106, 9639–9646. [Google Scholar] [CrossRef]
- Kupka, T.; Lim, C. Polarization-consistent versus correlation-consistent basis sets in predicting molecular and spectroscopic properties. J. Phys. Chem. A 2007, 111, 1927–1932. [Google Scholar] [CrossRef]
- Papoušek, D.; Aliev, M.R. Molecular Vibrational-Rotational Spectra: Theory and Applications of High Resolution Infrared, Microwave, and Raman Spectroscopy of Polyatomic Molecules; Elsevier Scientific Pub. Co.: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Kaminský, J.; Buděšínský, M.; Taubert, S.; Bouř, P.; Straka, M. Fullerene C70 characterization by 13C NMR and the importance of the solvent and dynamics in spectral simulations. Phys. Chem. Chem. Phys. 2013, 15, 9223–9230. [Google Scholar] [CrossRef]
- Danecek, P.; Bour, P. Comparison of the Numerical Stability of Methods for Anharmonic Calculations of Vibrational Molecular Energies. J. Comput. Chem. 2007, 28, 1617–1624. [Google Scholar] [CrossRef] [PubMed]
- Repisky, M.; Komorovsky, S.; Kadek, M.; Konecny, L.; Ekström, U.; Malkin, E.; Kaupp, M.; Ruud, K.; Malkina, O.L.; Malkin, V.G. ReSpect: Relativistic spectroscopy DFT program package. J. Chem. Phys. 2020, 152, 184101. [Google Scholar] [CrossRef] [PubMed]
- Komorovský, S.; Repiský, M.; Malkina, O.L.; Malkin, V.G.; Malkin Ondík, I.; Kaupp, M. A fully relativistic method for calculation of nuclear magnetic shielding tensors with a restricted magnetically balanced basis in the framework of the matrix Dirac-Kohn-Sham equation. J. Chem. Phys. 2008, 128, 104101. [Google Scholar] [CrossRef] [PubMed]
- Komorovsky, S.; Repisky, M.; Malkina, O.L.; Malkin, V.G. Fully relativistic calculations of NMR shielding tensors using restricted magnetically balanced basis and gauge including atomic orbitals. J. Chem. Phys. 2010, 132, 154101. [Google Scholar] [CrossRef]
| Basis Set/Full Name | Abbreviation |
|---|---|
| (aug)-cc-pVXZ | (a)XZ |
| (aug)-cc-pCVXZ | (a)CXZ |
| (aug)-cc-pwVXZ | (a)wXZ |
| (aug)-cc-pwCVXZ | (a)wCXZ |
| aug-pc-n | apcn |
| aug-pcSseg-n | apcSsegn |
| aug-pcJ-n | apcJn |
| Karlsruhe-type basis set | x2c-Def |
| x2c-SVPall-s | x2cSV |
| x2c-TZVPPall-s | x2cTZ |
| x2c-QZVPPall-s | x2cQZ |
| Complete basis set limit | CBS |
| Zero-point vibration correction | ZPVC |
| Temperature correction | TC |
| Relativistic correction | RC |
| Gauge-including atomic orbital | GIAO |
| Polarized continuum model of solvent | PCM |
| 31P | 15N | |||||||
|---|---|---|---|---|---|---|---|---|
| CBS Type | σxx | σzz | σiso | σaniso | σxx | σzz | σiso | σaniso |
| aVXZ | ||||||||
| (5-6) | −575.605 | 966.522 | −61.563 | 1542.127 | −829.620 | 341.858 | −439.128 | 1171.478 |
| aCVXZ | ||||||||
| (Q-5) | −572.407 | 966.332 | −59.494 | 1538.739 | −827.668 | 341.860 | −437.825 | 1169.527 |
| awCVXZ | ||||||||
| (Q-5) | −572.721 | 966.333 | −59.703 | 1539.052 | −828.236 | 341.860 | −438.204 | 1170.095 |
| Apcn | ||||||||
| (3-4) | −572.069 | 966.686 | −59.150 | 1538.755 | −829.711 | 341.862 | −439.186 | 1171.573 |
| apcSsegn | ||||||||
| (3-4) | −572.596 | 966.399 | −59.598 | 1538.995 | −828.249 | 341.870 | −438.210 | 1170.119 |
| apcJn | ||||||||
| (3-4) | −573.360 | 966.087 | −60.210 | 1539.447 | −828.154 | 341.853 | −438.151 | 1170.007 |
| Method | Literature | |||||||
| CCSD(T)/aVXZ c | 58.080 | 1362.090 | ||||||
| CCSD(T)/aCVXZ c | 59.090 | 1361.250 | ||||||
| B3LYP/6-311++G** d | −57.48 | −406.54 | ||||||
| CCSD(T)/15s12p4d3f2g e | 49.0 | |||||||
| Methods | HF-SCF | B3LYP | CCSD(T) | Δ (%) from CCSD(T) | |
|---|---|---|---|---|---|
| SCF | B3LYP | ||||
| NaH | |||||
| aVXZ(T-5) | 562.384 | 565.305 | 549.057 | 2.4 | 3.0 |
| aCVXZ(T-5) | 565.269 | 572.698 | 569.555 | −0.8 | 0.6 |
| apcSseg-n(2-4) | 565.478 | 572.789 | 572.180 | −1.2 | 0.1 |
| MgH2 | |||||
| aVXZ(T-5) | 475.048 | 397.813 | 441.802 | 7.5 | −10.0 |
| aCVXZ(T-5) | 462.948 | 426.089 | 447.156 | 3.5 | −4.7 |
| apcSseg-n(2-4) | 460.706 | 426.588 | 443.87 | 3.8 | −3.9 |
| AlH3 | |||||
| aVXZ(Q-6) | 340.417 | 260.370 | 301.061 | 13.1 | −13.5 |
| aCVXZ(T-5) | 346.671 | 267.211 | 307.762 | 12.6 | −13.2 |
| apcSseg-n(2-4) | 344.362 | 265.630 | 305.775 | 12.7 | −13.1 |
| SiH4 | |||||
| aVXZ(T-5) | 489.275 | 445.37 | 483.294 | 1.2 | −7.8 |
| aCVXZ(T-5) | 477.703 | 435.416 | 470.854 | 1.5 | −7.5 |
| apcSseg-n(2-4) | 473.790 | 434.990 | 468.972 | 1.0 | −7.2 |
| aVXZ(T-5) | 917.646 | 498.605 | 619.338 | 48.2 | −19.5 |
| aCVXZ(T-5) | 907.666 | 501.293 | 630.101 | 44.1 | −20.4 |
| apcSseg-n(2-4) | 915.536 | 501.697 | 628.762 | 45.6 | −20.2 |
| PH3 | |||||
| aVXZ(Q-6) | 576.501 | 553.876 | 596.957 | −3.4 | −7.2 |
| aCVXZ(T-5) | 581.367 | 557.847 | 603.326 | −3.6 | −7.5 |
| apcSseg-n(2-4) | 580.892 | 557.661 | 588.578 | −1.3 | −5.3 |
| H3PO | |||||
| aVXZ(5-6) | 398.514 | 349.201 | - | - | - |
| aCVXZ(T-5) | 397.276 | 346.109 | - | - | - |
| apcSseg-n(2-4) | 396.549 | 347.681 | - | - | - |
| PN a | |||||
| aVXZ(5-6) | −91.460 | −58.882 | 58.080 | −257.5 | −201.4 |
| aCVXZ(5-6) | −91.560 | −60.030 | 59.090 | −255.0 | −201.6 |
| apcSseg-n(3-4) | −90.720 | −58.833 | 58.780 | −254.3 | −200.1 |
| H2S | |||||
| aVXZ(Q-6) | 708.776 | 694.933 | 736.852 | −3.8 | −5.7 |
| aCVXZ(T-5) | 712.644 | 698.246 | 741.209 | −3.9 | −5.8 |
| apcSseg-n(2-4) | 715.929 | 698.071 | 742.245 | −3.5 | −6.0 |
| HCl | |||||
| aVXZ(Q-6) | 944.476 | 930.256 | 955.745 | −1.2 | −2.7 |
| aCVXZ(T-5) | 931.858 | 946.403 | 957.943 | −2.7 | −1.2 |
| apcSseg-n(2-4) | 946.06 | 931.705 | 957.3498 | −1.2 | −2.7 |
| Ar | |||||
| aVXZ(Q-6) | 1237.659 | 1238.172 | 1237.509 | 0.0 | 0.1 |
| aCVXZ(T-5) | 1237.660 | 1237.868 | 1237.924 | 0.0 | 0.0 |
| apcSseg-n(2-4) | 1237.534 | 1237.930 | 1237.516 | 0.0 | 0.0 |
| NaH | MgH2 | AlH3 | SiH4 | PH3 | H3PO | PN | H2S | HCl | Ar | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| This work | |||||||||||
| Isotropic σ | 569.56 | 447.16 | 307.76 | 470.85 | 628.76 | 603.33 | 389.34 * | 59.09 | 741.21 | 957.94 | 1237.92 |
| ZPVCmixed | 1.03 | 6.61 | −0.13 | 1.85 | 30.77 | −5.60 | 69.39 | −4.40 | −21.12 | −17.35 | - |
| ZPVCB3LYP | 0.29 | 10.66 | −1.06 | 20.28 | −0.69 | −10.81 | −4.72 | −6.21 | −22.36 | −18.29 | - |
| TC (273K) | −0.01 | 1.36 | 0.01 | −0.75 | −1.30 | −0.42 | −0.15 | −0.04 | −0.51 | −0.42 | - |
| RCKT2 | 8.08 | 9.96 | 11.52 | 14.87 | 20.99 | 20.80 | 18.31 | 11.45 | 27.26 | 33.21 | 33.72 |
| RCB3LYP | 7.74 | 9.97 | 11.97 | 14.92 | 25.84 | 18.86 | 22.35 | 12.37# | 24.80 | 32.16 | - |
| Final value | 577.59 | 467.79 | 278.12 | 506.05 | 653.91 | 611.38 | 406.97 | 65.25 | 743.65 | 971.81 | 1271.64 |
| Literature | |||||||||||
| Isotropic σ | 470.64 a | 605.83 a | 737.92 a | 961.92 f | 1237.50 e; 1237.76 g | ||||||
| ZPVC | −1.41 a | −9.50 c | −20.86 a | −17.09 f | |||||||
| TC (273K) | 0.01 a | −0.32 a | −0.89 a | −0.59 f | |||||||
| RC | 31.82 f | 37.52 e | |||||||||
| Final value | 469.24 | 596.01 | 716.17 | 976.06 | 1275.02; 1275.28; 1273.89 h | ||||||
| Exp. Total | 594.45 d | 717.24 a | - | ||||||||
| Exp. σ | 475.3 ± 10 b | −266.10 e | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rzepiela, K.; Kaminský, J.; Buczek, A.; Broda, M.A.; Kupka, T. Electron Correlation or Basis Set Quality: How to Obtain Converged and Accurate NMR Shieldings for the Third-Row Elements? Molecules 2022, 27, 8230. https://doi.org/10.3390/molecules27238230
Rzepiela K, Kaminský J, Buczek A, Broda MA, Kupka T. Electron Correlation or Basis Set Quality: How to Obtain Converged and Accurate NMR Shieldings for the Third-Row Elements? Molecules. 2022; 27(23):8230. https://doi.org/10.3390/molecules27238230
Chicago/Turabian StyleRzepiela, Kacper, Jakub Kaminský, Aneta Buczek, Małgorzata A. Broda, and Teobald Kupka. 2022. "Electron Correlation or Basis Set Quality: How to Obtain Converged and Accurate NMR Shieldings for the Third-Row Elements?" Molecules 27, no. 23: 8230. https://doi.org/10.3390/molecules27238230
APA StyleRzepiela, K., Kaminský, J., Buczek, A., Broda, M. A., & Kupka, T. (2022). Electron Correlation or Basis Set Quality: How to Obtain Converged and Accurate NMR Shieldings for the Third-Row Elements? Molecules, 27(23), 8230. https://doi.org/10.3390/molecules27238230








