Predictive Models of Gas/Particulate Partition Coefficients (KP) for Polycyclic Aromatic Hydrocarbons and Their Oxygen/Nitrogen Derivatives
Abstract
1. Introduction
2. Materials and Methods
2.1. Log KP Experimental Values
2.2. Descriptors
2.3. Model Construction and Verification
2.4. Define the Application Domain
3. Results and Discussion
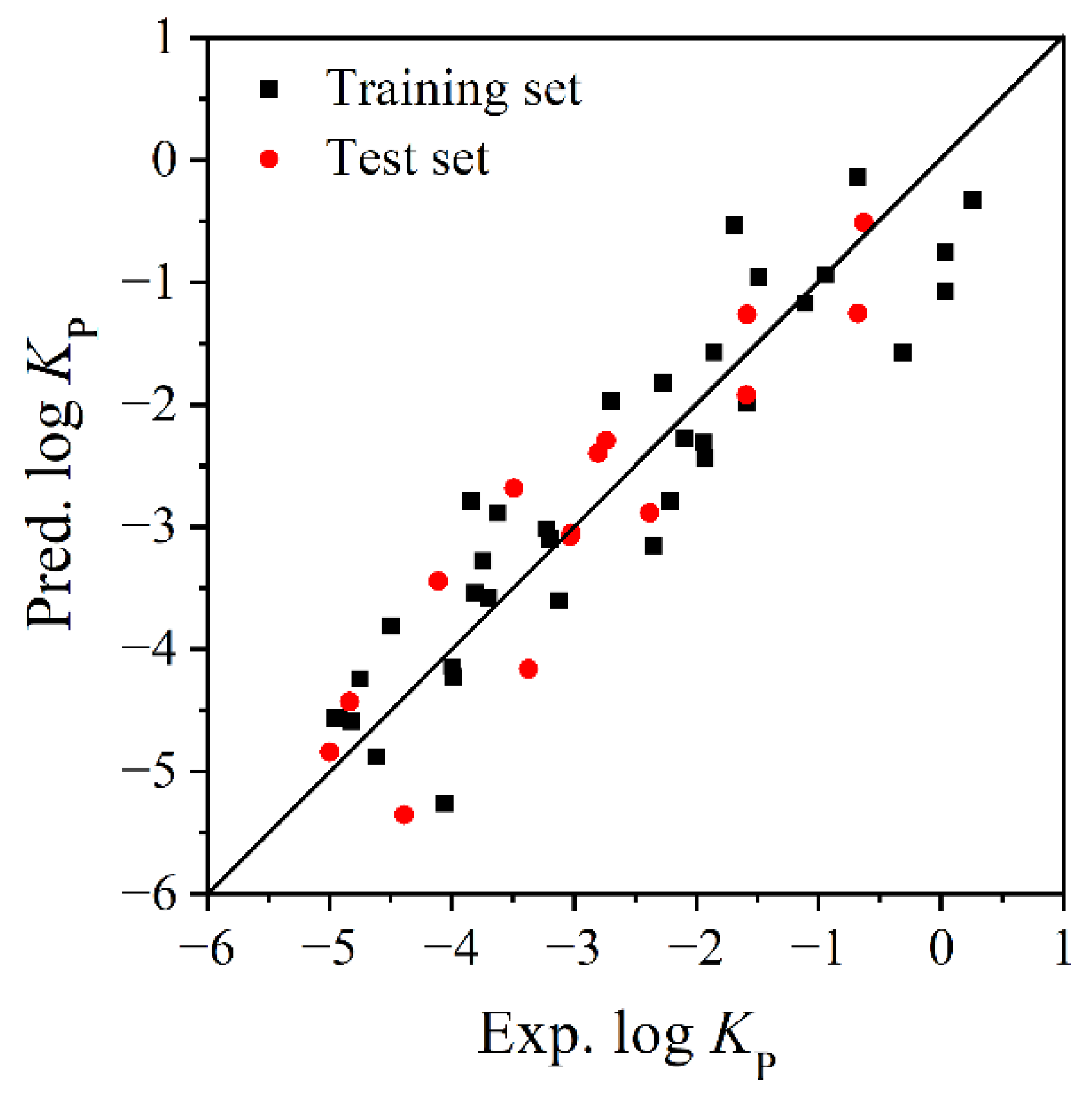
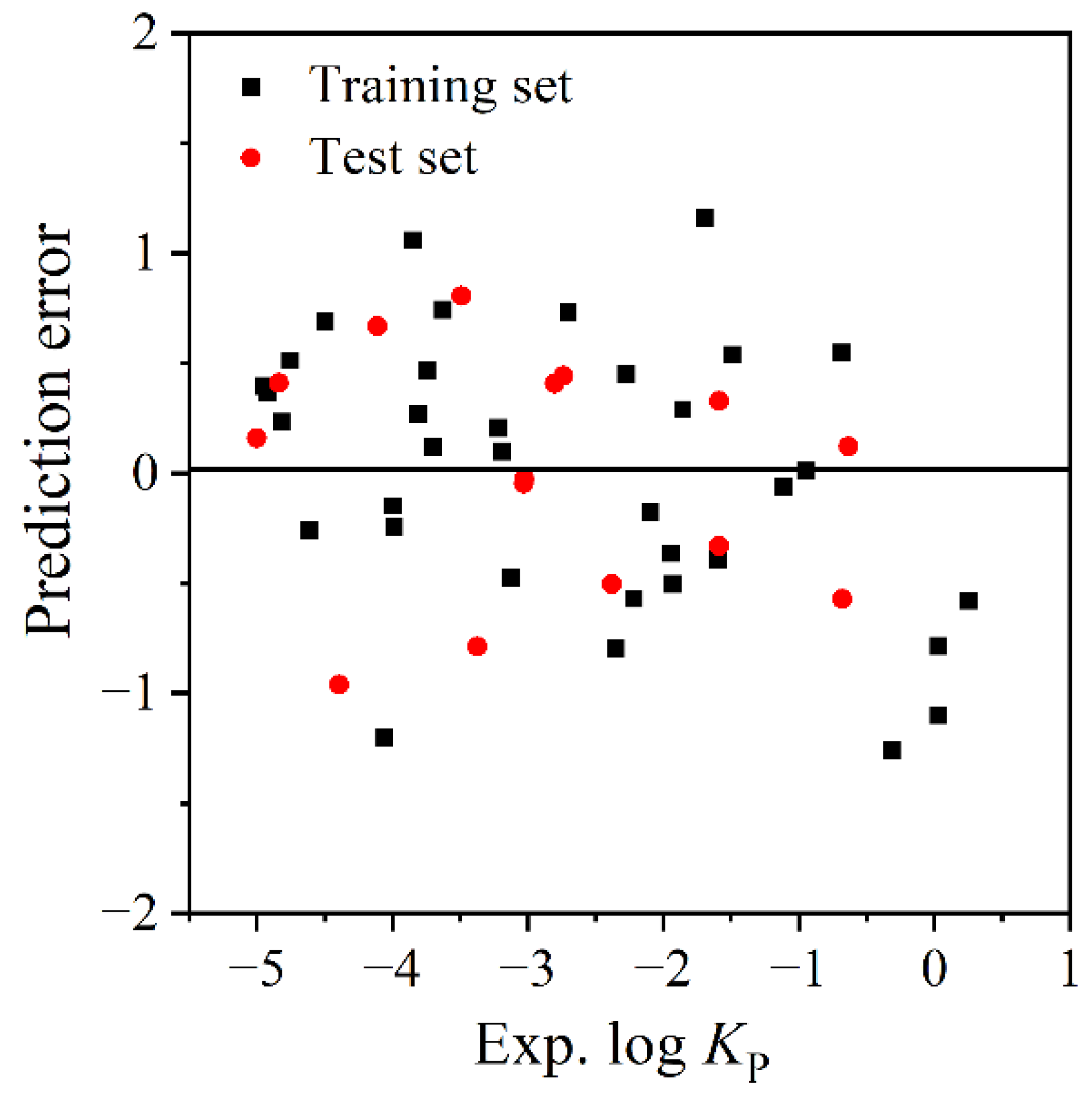
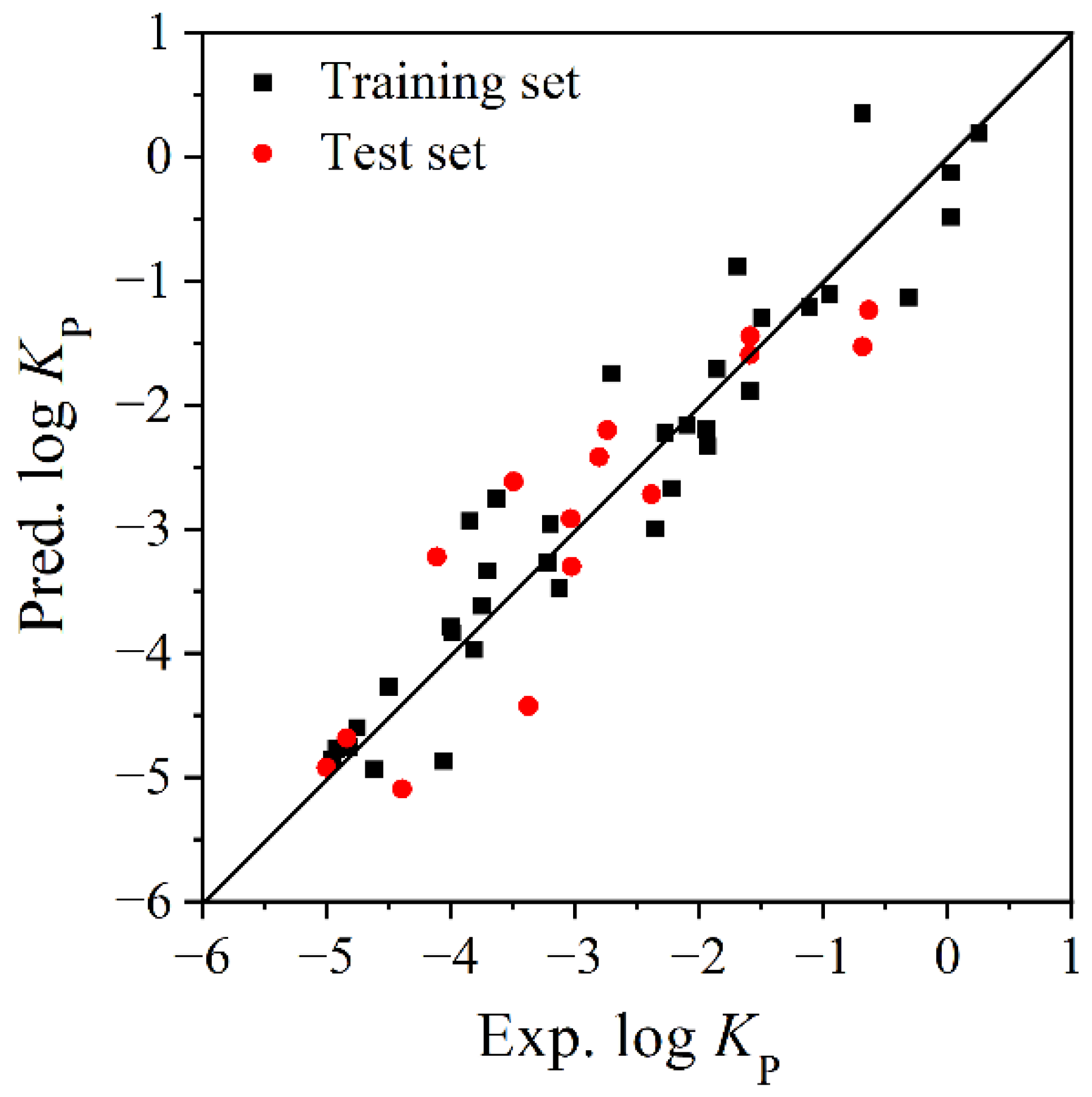
3.1. Model Establishment and Verification
- (1)
- log KOA model
- (2)
- MLR model
- (3)
- SVM model
- (4)
- Comparison of the different models
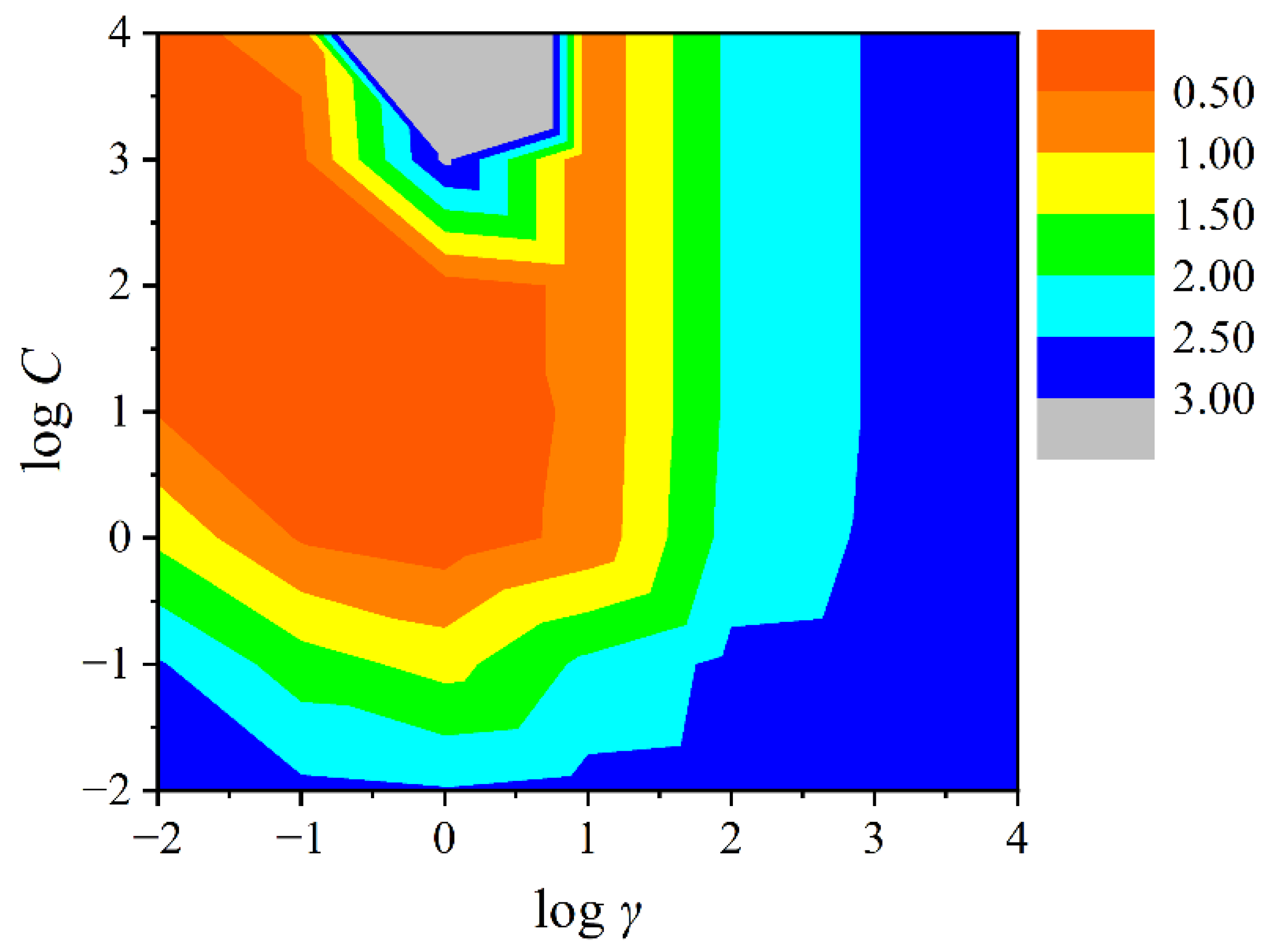
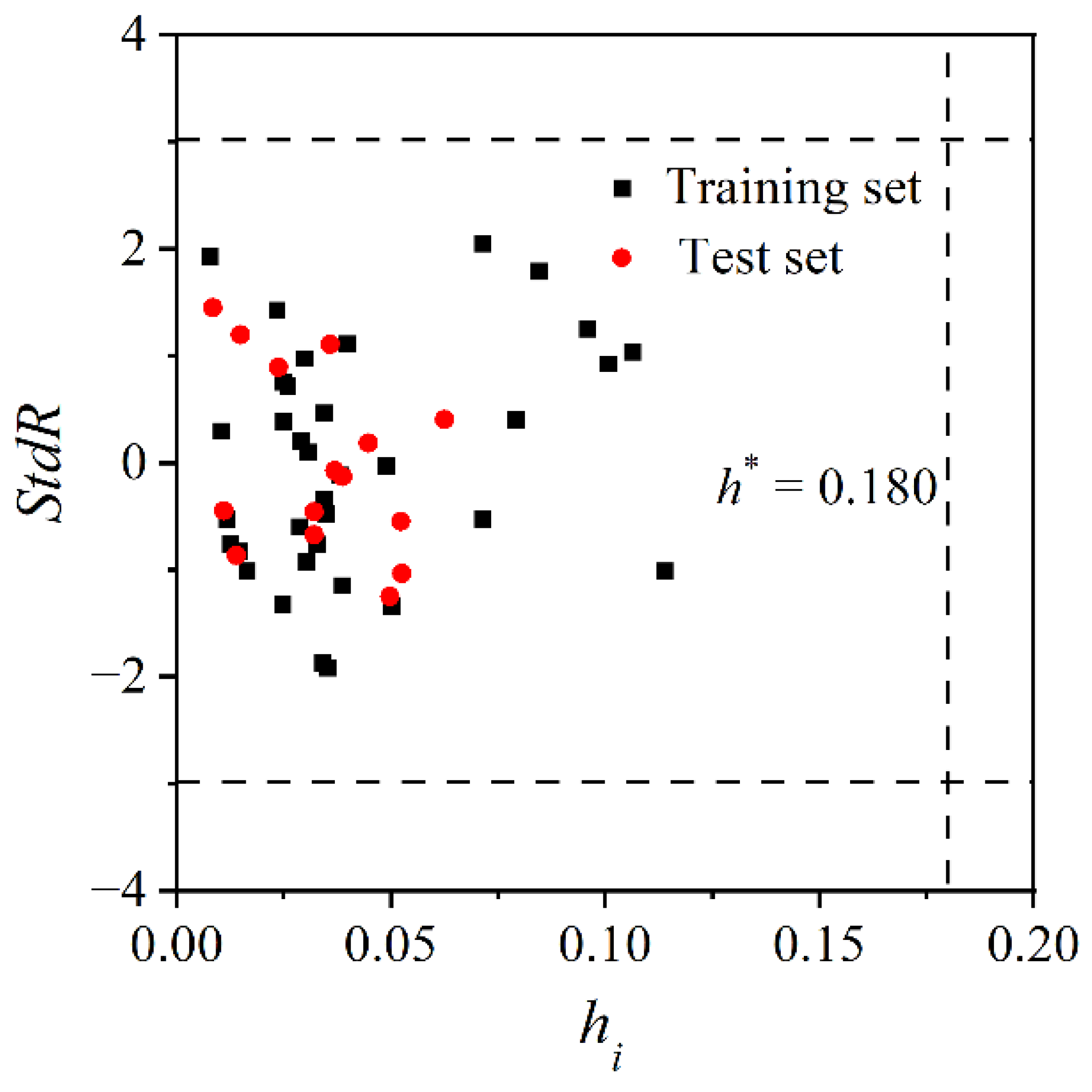
3.2. Characterization of the Model Application Domain
3.3. Mechanism Analysis
3.4. Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Kim, K.H.; Jahan, S.A.; Kabir, E.; Brown, R.J.C. A review of airborne polycyclic aromatic hydrocarbons (PAHs) and their human health effects. Environ. Int. 2013, 60, 71–80. [Google Scholar] [CrossRef] [PubMed]
- Yu, H. Environment carcinogenic polycyclic aromatic hydrocabons: Photochemistry and phototoxicity. J. Environ. Health Sci. Eng. Part. C 2002, 20, 149–183. [Google Scholar] [CrossRef] [PubMed]
- Rajpara, R.K.; Dudhagara, D.R.; Bhatt, J.K.; Gosai, H.B.; Dave, B.P.J.M.P.B. Polycyclic aromatic hydrocarbons (PAHs) at the Gulf of Kutch, Gujarat, India: Occurrence, source apportionment, and toxicity of PAHs as an emerging issue. Mar. Pollut. Bull. 2017, 119, 231–238. [Google Scholar] [CrossRef] [PubMed]
- Holme, J.A.; Brinchmann, B.C.; Refsnes, M.; Lg, M.; Øvrevik, J. Potential role of polycyclic aromatic hydrocarbons as mediators of cardiovascular effects from combustion particles. Environ. Health 2019, 18, 74. [Google Scholar] [CrossRef]
- Mallah, M.A.; Changxing, L.; Mallah, M.A.; Noreen, S.; Liu, Y.; Saeed, M.; Xi, H.; Ahmed, B.; Feng, F.; Mirjat, A.A.; et al. Polycyclic aromatic hydrocarbon and its effects on human health: An overeview. Chemosphere 2022, 296, 133948. [Google Scholar] [CrossRef]
- Han, F.; Guo, H.; Hu, J.; Zhang, J.; Ying, Q.; Zhang, H. Sources and health risks of ambient polycyclic aromatic hydrocarbons in China. Sci. Total Environ. 2020, 698, 134229. [Google Scholar] [CrossRef]
- Albinet, A.; Leoz-Garziandia, E.; Budzinski, H.; ViIlenave, E. Polycyclic aromatic hydrocarbons (PAHs), nitrated PAHs and oxygenated PAHs in ambient air of the Marseilles area (South of France): Concentrations and sources. Sci. Total Environ. 2007, 384, 280–292. [Google Scholar] [CrossRef]
- Bleeker, E.A.J.; Van Der Geest, H.G.; Klamer, H.J.C.; De Voogt, P.; Wind, E.; Kraak, M.H.S. Toxic and genotoxic effects of azaarenes: Isomers and metabolites. Polycycl. Aromat. Compd. 1999, 13, 191–203. [Google Scholar] [CrossRef]
- Ma, Y.; Cheng, Y.; Qiu, X.; Lin, Y.; Cao, J.; Hu, D.J.E.P. A quantitative assessment of source contributions to fine particulate matter (PM2.5)-bound polycyclic aromatic hydrocarbons (PAHs) and their nitrated and hydroxylated derivatives in Hong Kong. Environ. Pollut. 2016, 219, 742–749. [Google Scholar] [CrossRef]
- Lima, A.L.C.; Farrington, J.W.; Reddy, C.M. Combustion-Derived polycyclic aromatic hydrocarbons in the environment—A review. Environ. Forensics 2005, 6, 109–131. [Google Scholar] [CrossRef]
- Huang, R.J.; Zhang, Y.; Bozzetti, C.; Ho, K.F.; Cao, J.J.; Han, Y.; Daellenbach, K.R.; Slowik, J.G.; Platt, S.M.; Canonaco, F.; et al. High secondary aerosol contribution to particulate pollution during haze events in China. Nature 2014, 514, 218–222. [Google Scholar] [CrossRef] [PubMed]
- Keyte, I.J.; Albinet, A.; Harrison, R.M. On-road traffic emissions of polycyclic aromatic hydrocarbons and their oxy- and nitro- derivative compounds measured in road tunnel environments. Sci. Total Environ. 2016, 566–567, 1131–1142. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Chernyak, S.M.; Batterman, S.A. PAHs, nitro-PAHs, hopanes, and steranes in lake trout from Lake Michigan. Environ. Toxicol. Chem. 2014, 33, 1792–1801. [Google Scholar] [CrossRef] [PubMed]
- Krzyszczak, A.; Czech, B. Occurrence and toxicity of polycyclic aromatic hydrocarbons derivatives in environmental matrices. Sci. Total Environ. 2021, 788, 147738. [Google Scholar] [CrossRef]
- Sun, C.; Qu, L.; Wu, L.; Wu, X.; Sun, R.; Li, Y. Advances in analysis of nitrated polycyclic aromatic hydrocarbons in various matrices. TrAC Trends Anal. Chem. 2020, 127, 115878. [Google Scholar] [CrossRef]
- Li, W.; Wang, C.; Shen, H.; Su, S.; Shen, G.; Huang, Y.; Zhang, Y.; Chen, Y.; Chen, H.; Lin, N.; et al. Concentrations and origins of nitro-polycyclic aromatic hydrocarbons and oxy-polycyclic aromatic hydrocarbons in ambient air in urban and rural areas in northern China. Environ. Pollut. 2015, 197, 156–164. [Google Scholar] [CrossRef]
- Cai, C.; Li, J.; Wu, D.; Wang, X.; Tsang, D.C.W.; Li, X.; Sun, J.; Zhu, L.; Shen, H.; Tao, S.; et al. Spatial distribution, emission source and health risk of parent PAHs and derivatives in surface soils from the Yangtze River Delta, eastern China. Chemosphere 2017, 178, 301–308. [Google Scholar] [CrossRef]
- Qiao, M.; Qi, W.; Liu, H.; Qu, J. Oxygenated, nitrated, methyl and parent polycyclic aromatic hydrocarbons in rivers of Haihe River System, China: Occurrence, possible formation, and source and fate in a water-shortage area. Sci. Total Environ. 2014, 481, 178–185. [Google Scholar] [CrossRef]
- Minero, C.; Maurino, V.; Borghesi, D.; Pelizzetti, E.; Vione, D. An overview of possible processes able to account for the occurrence of nitro-PAHs in Antarctic particulate matter. Microchem. J. 2010, 96, 213–217. [Google Scholar] [CrossRef]
- Ma, T.; Kong, J.J.; Han, M.S. Review on the pollution status and toxicity effects of nitrated polycyclic aromatic hydrocarbons in the environment. Environ. Chem. 2020, 39, 2430–2440. [Google Scholar]
- Zhang, Y.J.; Yun, Y. Oxygenated polycyclic aromatic hydrocarbons in the environment:A review. Environ. Chem. 2021, 40, 150–163. [Google Scholar]
- Xu, X.B. Nitro polycyclic aromatic hydrocarbons—Recently discovered direct mutagens and potential carcinogens in the environment. Environ. Chem. 1984, 3, 1–16. [Google Scholar]
- Durant, J.L.; Busby, W.F.; Lafleur, A.L.; Penman, B.W.; Crespi, C.L. Human cell mutagenicity of oxygenated, nitrated and unsubstituted polycyclic aromatic hydrocarbons associated with urban aerosols. Mutat. Res. Genet. Toxicol. 1996, 371, 123–157. [Google Scholar] [CrossRef]
- Zhang, Q.; Gao, R.; Xu, F.; Zhou, Q.; Wang, W. Role of water molecule in the gas-phase formation process of nitrated polycyclic aromatic hydrocarbons in the atmosphere: A computational study. Environ. Sci. Technol. 2014, 48, 5051–5057. [Google Scholar] [CrossRef] [PubMed]
- Idowu, O.; Semple, K.T.; Ramadass, K.; O’Connor, W.; Hansbro, P.; Thavamani, P. Beyond the obvious: Environmental health implications of polar polycyclic aromatic hydrocarbons. Environ. Int. 2019, 123, 543–557. [Google Scholar] [CrossRef]
- Yaffe, D.; Cohen, Y.; Arey, J.; Grosovsky, A.J. Multimedia analysis of PAHs and Nitro-PAH daughter products in the Los Angeles basin. Risk Anal. 2008, 72, 1567–1572. [Google Scholar] [CrossRef]
- Wang, P.; Wang, S.L.; Fan, C.Q. Atmospheric distribution of particulate- and gas-phase phthalic esters (PAEs) in a Metropolitan City, Nanjing, East China. Chemosphere 1987, 21, 2275–2283. [Google Scholar] [CrossRef]
- Harner, T.; Bidleman, T.F. Octanol-air partition coefficient for describing particle/gas partitioning of aromatic compounds in urban air. Environ. Sci. Technol. 1998, 32, 1494–1502. [Google Scholar] [CrossRef]
- Finizio, A.; Mackay, D.; Bidleman, T.; Harner, T.J.A.E. Octanol-air partition coefficient as a predictor of partitioning of semi-volatile organic chemicals to aerosols. Atmos. Environ. 1997, 31, 2289–2296. [Google Scholar] [CrossRef]
- Cao, S.; Hu, J.; Wu, Q.; Wei, X.; Ma, G.; Yu, H. Prediction study on the distribution of polycyclic aromatic hydrocarbons and their halogenated derivatives in the atmospheric particulate phase. Ecotox. Environ. Safe 2022, 245, 114111. [Google Scholar] [CrossRef]
- Hong, H.; Lu, Y.; Zhu, X.; Wu, Q.; Jin, L.; Jin, Z.; Wei, X.; Ma, G.; Yu, H. Cytotoxicity of nitrogenous disinfection byproducts: A combined experimental and computational study. Sci. Total Environ. 2023, 856, 159273. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.; Li, M.; Wang, Y.; Jin, L.; Ma, G.; Yu, H. Developing predictive models for carrying ability of micro-plastics towards organic pollutants. Molecules 2019, 24, 1784. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Jin, L.; Yu, H.; Lv, L.; Chen, C.-E.; Ying, G.-G. Understanding and predicting the diffusivity of organic chemicals for diffusive gradients in thin-films using a QSPR model. Sci. Total Environ. 2020, 706, 135691. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Yu, H.; Wang, Y.; Li, J.; Ma, G.; Wei, X. QSPR models for predicting the adsorption capacity for microplastics of polyethylene, polypropylene and polystyrene. Sci. Rep. 2020, 10, 14597. [Google Scholar] [CrossRef]
- Wei, C.; Han, Y.; Bandowe, B.A.M.; Cao, J.; Huang, R.J.; Ni, H.; Tian, J. Occurrence, gas/particle partitioning and carcinogenic risk of polycyclic aromatic hydrocarbons and their oxygen and nitrogen containing derivatives in Xi’an, central China. Sci. Total Environ. 2015, 505, 814–822. [Google Scholar] [CrossRef]
- Goss, K.U.; Schwarzenbach, R.P. Linear free energy relationships used to evaluate Equilibrium partitioning of organic compounds. Environ. Sci. Technol. 2001, 35, 1–9. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Goss, K.U.; Ball, W.P. Polyparameter linear free energy relationships for estimating the equilibrium partition of organic compounds between water and the natural organic matter in soils and sediments. Environ. Sci. Technol. 2005, 39, 913–924. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 16, Revision, D.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Tian, L. GsGrid: Extracting Data from Gaussian Grid File and Grid File Calculation, Version 1.7. Available online: http://gsgrid.codeplex.com (accessed on 31 October 2022).
- Zang, Q.D.; Mansouri, K.; Williams, A.J. In silico prediction of physicochemical properties of environmental chemicals using molecular fingerprints and machine learning. J. Chem. Inf. Model 2016, 57, 36–49. [Google Scholar] [CrossRef]
- Pallant, J. SPSS Survival Manual: A step by step guide to data analysis using IBM SPSS. Aust. N. Z. J. Public Health 2013, 37, 597–598. [Google Scholar]
- Guidance Document on the Validation of (Quantitative) Structure-Activity Relationship [(Q)SAR] Models; OECD Environment Health and Safety Publications Series on Testing and Assessment, No. 69; OECD: Paris, France, 2007.
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA data mining software: An update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Roy, K.; Ambure, P.; Aher, R.B. How important is to detect systematic error in predictions and understand statistical applicability domain of QSAR models? Chemometr. Intell. Lab. 2017, 162, 44–54. [Google Scholar] [CrossRef]
- Roy, K.; Das, R.N.; Ambure, P.; Aher, R.B. Be aware of error measures. Further studies on validation of predictive QSAR models. Chemometr. Intell. Lab. Syst. 2016, 152, 18–33. [Google Scholar]
- Tropsha, A.; Gramatica, P.; Gombar, V.K. The importance of being earnest: Validation is the absolute essential for successful application and interpretation of QSPR models. QSAR Comb. Sci. 2003, 22, 69–77. [Google Scholar] [CrossRef]
- Huang, X.X.; Yang, H.W. Study on the relationship between octanol-air partition coefficient and molecular structure of PCBs. J. Beijing Union Univ. 2014, 28, 34–39. [Google Scholar]
- Yu, H.Y.; Chen, W.; Liang, C.C. Predicting the n-octanol/air partitioning coefficients of selected polybrominated diphenyl ethers and their metabolites. J. Zhejiang Norm. Univ. 2015, 38, 266–272. [Google Scholar]
- Zou, J.W.; Zhang, B.; Hu, G.X. QSPR studies on the physicochemical properties of polycyclic aromatic hydrocarbons—The application of theoretical descriptors derived from electrostatic potentials on molecular surface. Acta Chem. 2004, 62, 241–246. [Google Scholar]
- Zou, J.W.; Jiang, Y.J.; Hu, G.X. QSPR (activity) relationship of polychlorinated biphenyls. Acta Phys. Chem. 2005, 21, 267–272. [Google Scholar]
- Yuan, Q.; Ma, G.C.; Xu, T.; Serge, B.; Yu, H.Y.; Chen, J.R.; Lin, H.J. Developing QSPR model of gas/particle partition coefficients of neutral poly-/perfluoroalkyl substances. Atmos. Environ. 2016, 143, 270–277. [Google Scholar] [CrossRef]
- Sun, C.; Feng, L. A method for estimating the air/particulate matter partition coefficient of organic matter. Sci. Bull. 2005, 50, 961–963. [Google Scholar]

| Compound | Abbreviations | log KP | log KOA | α | VS.min (×10−2) | |||
|---|---|---|---|---|---|---|---|---|
| Exp. | Pred. (log KOA) | Pred. (MLR Model) | Pred. (SVM Model) | |||||
| 1,2,3,4-Tetrahydronaphthalene | TH-NAPH | −4.060 | −5.231 | −5.184 | −4.867 | 4.75 | 108.571 | −3.397 |
| Naphthalene | NAPH b | −4.392 | −5.038 | −5.239 | −5.093 | 5.05 | 112.345 | −2.698 |
| 2-Methylnaphthalene | 2-MNAPH b | −5.001 | −4.729 | −4.738 | −4.920 | 5.53 | 126.847 | −2.924 |
| 1-Methylnaphthalene | 1-MNAPH | −4.617 | −4.716 | −4.789 | −4.932 | 5.55 | 125.047 | −2.944 |
| Biphenyl | BIPH | −4.955 | −4.484 | −4.469 | −4.851 | 5.91 | 137.036 | −2.739 |
| 1,3-Dimethylnaphthalene | 1,3DMNAPH b | −4.837 | −4.407 | −4.330 | −4.680 | 6.03 | 139.231 | −3.030 |
| Acenaphthylene | ACEY | −4.921 | −4.253 | −4.476 | −4.766 | 6.27 | 134.493 | −3.034 |
| Acenaphthene | ACEN | −4.821 | −4.401 | −4.511 | −4.750 | 6.04 | 132.491 | −3.141 |
| Fluorene | FLUO | −4.756 | −4.047 | −4.163 | −4.599 | 6.59 | 145.606 | −2.912 |
| Phenanthrene | PHE | −4.500 | −3.642 | −3.724 | −4.268 | 7.22 | 162.006 | −2.643 |
| Anthracene | ANT | −3.811 | −3.725 | −3.459 | −3.967 | 7.09 | 170.616 | −2.639 |
| 2-Methylphenanthrene | 2-MPHE | −3.747 | −3.461 | −3.205 | −3.614 | 7.50 | 177.433 | −2.820 |
| 3,6-Dimethylphenanthrene | 3,6-DMPHE | −3.847 | −3.120 | −2.728 | −2.930 | 8.03 | 191.260 | −3.031 |
| Fluoranthene | FLUA | −3.223 | −2.754 | −2.946 | −3.266 | 8.60 | 186.008 | −2.796 |
| Pyrene | PYR b | −3.027 | −3.017 | −2.950 | −3.300 | 8.19 | 187.779 | −2.555 |
| Retene | RET | −2.703 | −2.689 | −1.919 | −1.743 | 8.70 | 217.138 | −3.080 |
| Benzo[a]anthracene | BaA b | −1.592 | −2.451 | −1.828 | −1.593 | 9.07 | 223.989 | −2.590 |
| Benzo[e]pyrene | BeP | −0.316 | −0.984 | −1.513 | −1.130 | 11.35 | 234.532 | −2.550 |
| Benzo[a]pyrene | BaP | 0.028 | −1.300 | −1.016 | −0.482 | 10.86 | 250.507 | −2.568 |
| Indeno [1,2,3-cd]pyrene | IcdP | 0.255 | −0.856 | −0.284 | 0.192 | 11.55 | 272.695 | −2.774 |
| Dibenzo[a,h]anthracene | DahA | −0.687 | −0.708 | −0.094 | 0.352 | 11.78 | 280.623 | −2.553 |
| Benzo[g,h,i]perylene | BghiP | 0.028 | −0.888 | −0.702 | −0.127 | 11.50 | 261.269 | −2.498 |
| 1-Indanone | 1-IND | −3.998 | −4.542 | −4.235 | −3.784 | 5.82 | 99.753 | −8.388 |
| 1,4-Naphthoquinone | 1,4-NQ | −3.990 | −2.625 | −4.261 | −3.834 | 8.80 | 113.590 | −6.535 |
| 1-Naphthaldehyde | 1-NALD b | −4.111 | −3.680 | −3.506 | −3.224 | 7.16 | 127.809 | −7.844 |
| 2-Biphenylcarboxaldehyde | 2-BPCA b | −3.491 | −3.236 | −2.760 | −2.615 | 7.85 | 149.944 | −8.101 |
| 9-Fluorenone | 9-FLU | −3.630 | −3.050 | −2.959 | −2.748 | 8.14 | 148.889 | −7.418 |
| 1,2-Acenaphthenequinone | 1,2-ACEQ | −3.196 | −2.625 | −3.180 | −2.953 | 8.80 | 138.303 | −7.854 |
| 9,10-Anthraquinone | 9,10-AQ b | −2.382 | −2.233 | −2.902 | −2.718 | 9.41 | 159.881 | −6.271 |
| 1,8-Naphtalic anhydride | 1,8-NA b | −3.033 | −3.243 | −3.140 | −2.912 | 7.84 | 141.118 | −7.659 |
| 4H-Cyclopenta[d,e,f]phenanthrenone | 4-CPHE b | −2.739 | −2.110 | −2.345 | −2.201 | 9.60 | 170.679 | −7.191 |
| 2-Meth-9,10-anthraquinone | 2-MAQ | −1.944 | −1.383 | −2.362 | −2.194 | 10.73 | 175.048 | −6.566 |
| Benzo[a]florenone | BAFLU b | −1.590 | −1.660 | −1.322 | −1.442 | 10.30 | 203.092 | −7.291 |
| 7H-Benzo[d,e]anthracene-7-one | BdeAQ b | −0.682 | −1.608 | −1.328 | −1.527 | 10.38 | 199.470 | −7.715 |
| Benzo[a]anthracene-7,12-dione | BaAQ | −1.112 | −0.373 | −1.231 | −1.211 | 12.30 | 214.077 | −6.284 |
| 5,12-Naphthacenequinone | 5,12-NQ | −0.949 | −0.296 | −1.006 | −1.105 | 12.42 | 219.462 | −6.523 |
| 6H-Benzo[c,d]pyren-6-one | BcdPQ b | −0.635 | −0.701 | −0.592 | −1.231 | 11.79 | 222.901 | −7.780 |
| 1-Nitronaphthalene | 1-NNAP | −3.703 | −3.571 | −3.635 | −3.333 | 7.33 | 129.792 | −7.060 |
| 2-Nitrobiphenyl | 2-NBP | −2.352 | −3.301 | −3.184 | −2.993 | 7.75 | 151.356 | −6.187 |
| 5-Nitroacenaphthene | 5-NACE | −2.219 | −3.017 | −2.867 | −2.671 | 8.19 | 151.022 | −7.526 |
| 2-Nitrofluorene | 2-NFLU | −1.932 | −3.178 | −2.501 | −2.329 | 7.94 | 167.360 | −6.969 |
| 9-Nitrophenanthrene | 9-NPHE | −2.098 | −2.342 | −2.324 | −2.158 | 9.24 | 177.214 | −6.454 |
| 9-Nitroanthracene | 9-NANT | −1.858 | −1.943 | −1.660 | −1.703 | 9.86 | 190.063 | −7.545 |
| 1-Nitropyrene | 1-NPYR | −1.496 | −1.255 | −1.048 | −1.295 | 10.93 | 211.741 | −7.317 |
| 2,7-Dinitrofluorene | 2,7-DNFLU | −1.595 | −1.647 | −2.037 | −1.888 | 10.32 | 187.649 | −6.309 |
| 6-Nitrochrysene | 6-NCHR | −1.696 | −0.933 | −0.604 | −0.879 | 11.43 | 232.917 | −6.475 |
| Quinoline | QUI | −3.127 | −4.298 | −3.731 | −3.475 | 6.20 | 107.069 | −9.535 |
| Benzo[h]quinoline | BhQ b | −2.804 | −2.767 | −2.483 | −2.417 | 8.58 | 156.877 | −8.358 |
| Acridine | ACR | −2.275 | −2.522 | −1.969 | −2.222 | 8.96 | 165.008 | −9.437 |
| Carbazole | CAR b | −3.372 | −2.471 | −4.071 | −4.423 | 9.04 | 145.738 | −3.265 |
| Parameter | Coefficient | t | p | VIF |
|---|---|---|---|---|
| α | 0.031 | 15.839 | <0.001 | 1.056 |
| Vs.min | −24.453 | −6.638 | <0.001 | 1.056 |
| N | R2 | Q2 | RMSE | BIAS | MAE | MPE | MNE | |
|---|---|---|---|---|---|---|---|---|
| MLR model | 50 | 0.847 | 0.847 | 0.584 | 0.000 | 0.491 | 1.119 | −1.197 |
| Training set | 35 | 0.842 | 0.842 | 0.618 | 0.000 | 0.509 | 1.162 | −1.259 |
| Validation set | 15 | 0.854 | 0.847 | 0.535 | 0.002 | 0.438 | 0.807 | −0.961 |
| Compound | Model | Characterization Results | References |
|---|---|---|---|
| PAHs | log KP = (0.018 ± 0.003) × α + (−0.080 ± 0.033) × T + (18.245 ± 9.979) | N = 28, R2 = 0.624, Q2 = 0.624, RMSE = 0.395 | [45] |
| Organic chemicals | log (103 KP1) = −17.426 + 0.406 × d + 0.058 × α − 0.580 × EHOMO + 10.236 × qH+ | N = 15, R2 = 0.971, Q2 = 0.971, RMSE = 0.185 | [46] |
| log (103 KP2) = −21.307 + 0.162 × d + 0.0424 × α − 1.531 × EHOMO − 0.582 × ELUMO | N = 17, R2 = 0.839, Q2 = 0.839, RMSE = 0.634 | ||
| PAHs, O-PAHs, N-PAHs | log KP = (0.031 ± 0.002) × α + (−24.453 ± 3.684) × Vs.min + (−9.358 ± 0.433) | N = 50, R2 = 0.847, Q2 = 0.847, RMSE = 0.584 | This research |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, Q.; Cao, S.; Chen, Z.; Wei, X.; Ma, G.; Yu, H. Predictive Models of Gas/Particulate Partition Coefficients (KP) for Polycyclic Aromatic Hydrocarbons and Their Oxygen/Nitrogen Derivatives. Molecules 2022, 27, 7608. https://doi.org/10.3390/molecules27217608
Wu Q, Cao S, Chen Z, Wei X, Ma G, Yu H. Predictive Models of Gas/Particulate Partition Coefficients (KP) for Polycyclic Aromatic Hydrocarbons and Their Oxygen/Nitrogen Derivatives. Molecules. 2022; 27(21):7608. https://doi.org/10.3390/molecules27217608
Chicago/Turabian StyleWu, Qiang, Siqi Cao, Zhenyi Chen, Xiaoxuan Wei, Guangcai Ma, and Haiying Yu. 2022. "Predictive Models of Gas/Particulate Partition Coefficients (KP) for Polycyclic Aromatic Hydrocarbons and Their Oxygen/Nitrogen Derivatives" Molecules 27, no. 21: 7608. https://doi.org/10.3390/molecules27217608
APA StyleWu, Q., Cao, S., Chen, Z., Wei, X., Ma, G., & Yu, H. (2022). Predictive Models of Gas/Particulate Partition Coefficients (KP) for Polycyclic Aromatic Hydrocarbons and Their Oxygen/Nitrogen Derivatives. Molecules, 27(21), 7608. https://doi.org/10.3390/molecules27217608






