A Theoretical Study of the C–X Bond Cleavage Mediated by Cob(II)Aloxime
Abstract
1. Introduction
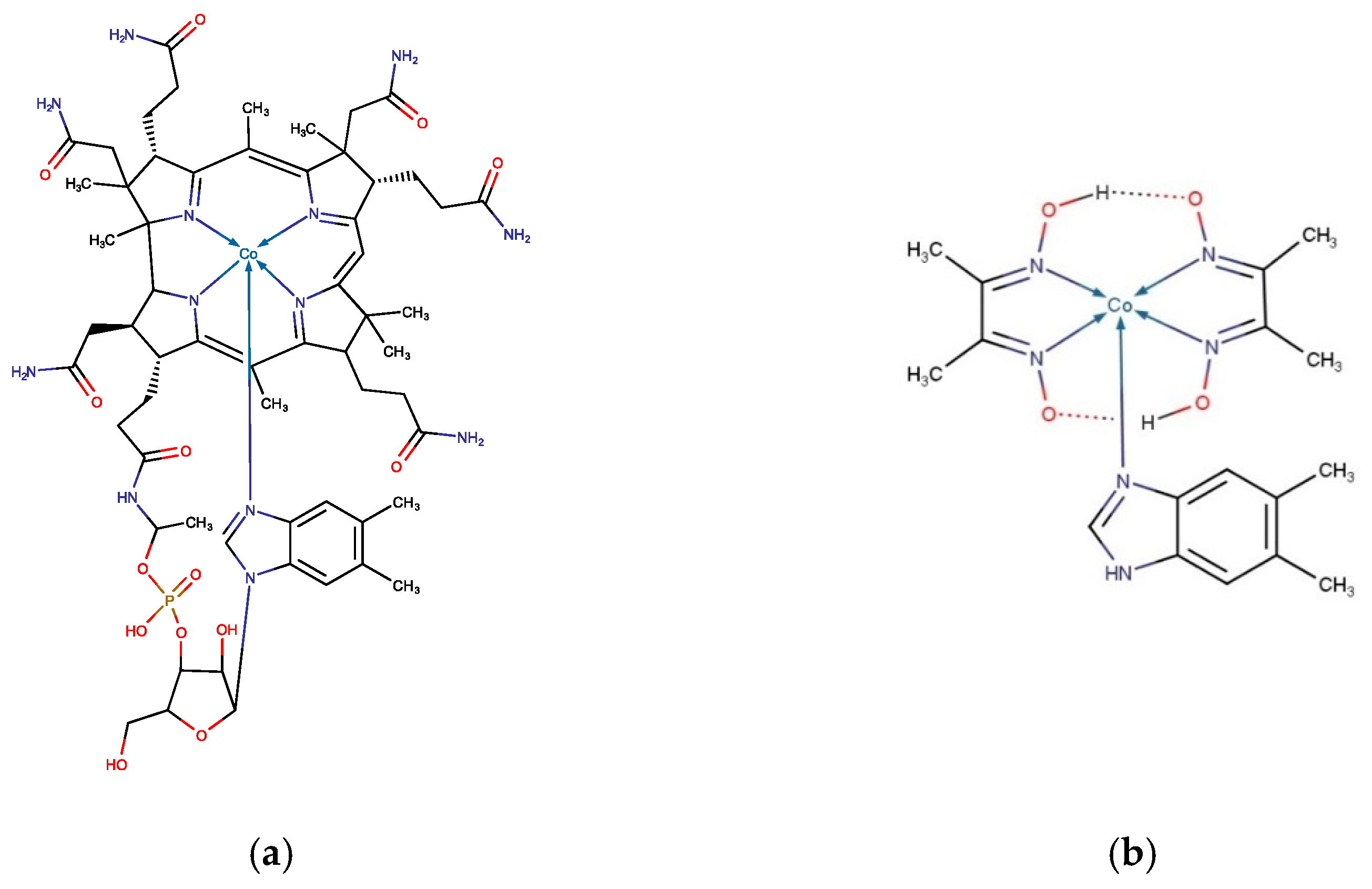
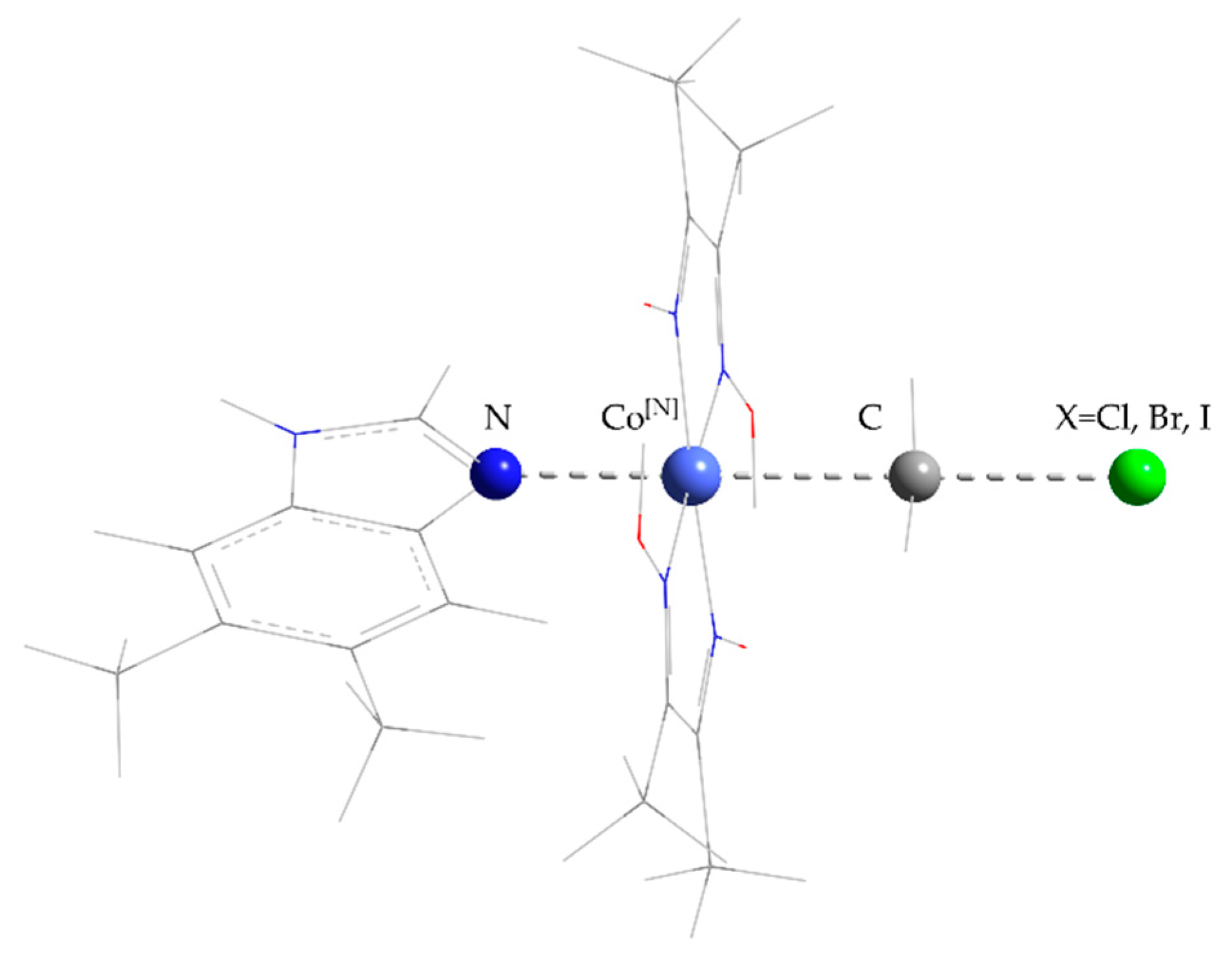
2. Models and Methods
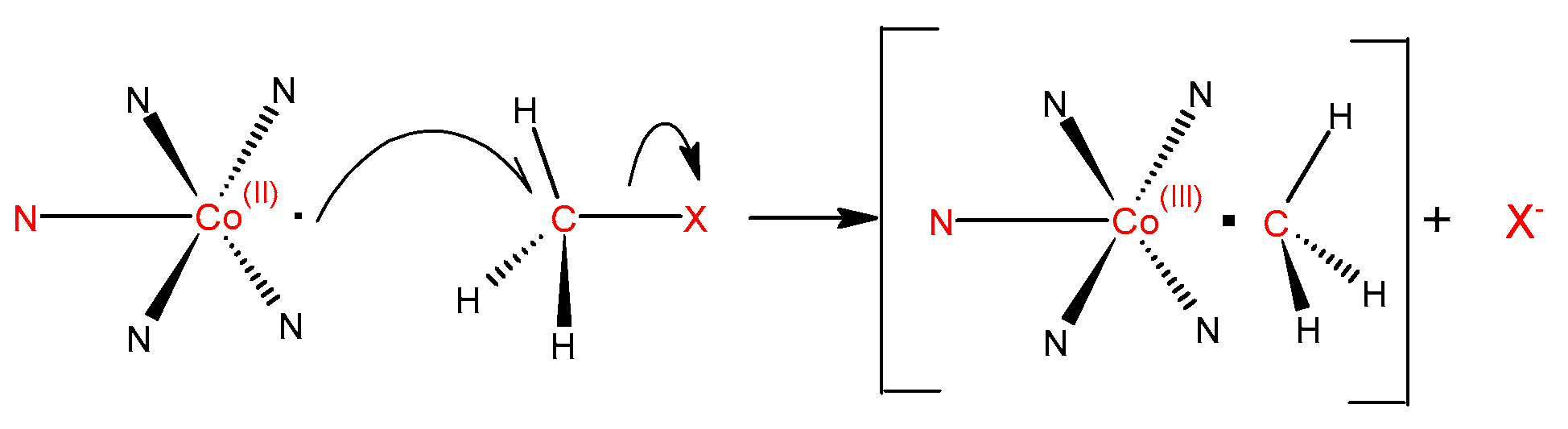
3. Results and Discussion
3.1. IRC and Reaction Force (RF)
3.2. Source Function and QTAIM Analysis
3.3. KLD Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Sample Availability
References
- Patai, S.E. Patai Chemistry of Carbon-Halogen Bond; The Chemistry of Functional Groups The Chemistry of the Carbon-Halogen Bond; John Wiley & Sons: Hoboken, NJ, USA, 2010; ISBN 9780470771426. [Google Scholar]
- Öberg, G. The Natural Chlorine Cycle—Fitting the Scattered Pieces. Appl. Microbiol. Biotechnol. 2002, 58, 565–581. [Google Scholar] [CrossRef]
- Svensson, T.; Kylin, H.; Montelius, M.; Sandén, P.; Bastviken, D. Chlorine Cycling and the Fate of Cl in Terrestrial Environments. Environ. Sci. Pollut. Res. Int. 2021, 28, 7691–7709. [Google Scholar] [CrossRef] [PubMed]
- Leys, D.; Adrian, L.; Smidt, H. Organohalide Respiration: Microbes Breathing Chlorinated Molecules. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2013, 368, 20120316. [Google Scholar] [CrossRef]
- Kodavanti, P.R.S.; Loganathan, B.G. Organohalogen Pollutants and Human Health. Int. Encycl. Public Health (Second Ed.) 2017, 359–366. [Google Scholar] [CrossRef]
- Stringer, R.; Johnston, P. Chlorine and the Environment: An Overview of the Chlorine Industry; Kluwer Academic Publishers: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Yao, L.; Zhao, J.L.; Liu, Y.S.; Zhang, Q.Q.; Jiang, Y.X.; Liu, S.; Liu, W.R.; Yang, Y.Y.; Ying, G.G. Personal Care Products in Wild Fish in Two Main Chinese Rivers: Bioaccumulation Potential and Human Health Risks. Sci. Total Environ. 2018, 621, 1093–1102. [Google Scholar] [CrossRef]
- ATSDR ATSDR. Available online: https://www.atsdr.cdc.gov/spl/ (accessed on 30 June 2022).
- Zhang, T.; Zhang, B.; Bai, X.; Yao, Y.; Wang, L.; Shu, Y.; Kannan, K.; Huang, X.; Sun, H. Health Status of Elderly People Living Near E-Waste Recycling Sites: Association of E-Waste Dismantling Activities with Legacy Perfluoroalkyl Substances (PFASs). Environ. Sci. Technol. Lett. 2019, 6, 133–140. [Google Scholar] [CrossRef]
- He, H.; Li, Y.; Shen, R.; Shim, H.; Zeng, Y.; Zhao, S.; Lu, Q.; Mai, B.; Wang, S. Environmental Occurrence and Remediation of Emerging Organohalides: A Review. Environ. Pollut. 2021, 290, 118060. [Google Scholar] [CrossRef]
- Gupta, V.K.; Fakhri, A.; Azad, M.; Agarwal, S. Synthesis of CdSe Quantum Dots Decorated SnO2 Nanotubes as Anode for Photo-Assisted Electrochemical Degradation of Hydrochlorothiazide: Kinetic Process. J. Colloid Interface Sci. 2017, 508, 575–582. [Google Scholar] [CrossRef]
- Couto Petro, A.G.; Thapa, B.; Karty, J.A.; Raghavachari, K.; Baker, L.A.; Peters, D.G. Direct Electrochemical Reduction of Acetochlor at Carbon and Silver Cathodes in Dimethylformamide. J. Electrochem. Soc. 2020, 167, 155517. [Google Scholar] [CrossRef]
- Farré, M.J.; Franch, M.I.; Malato, S.; Ayllón, J.A.; Peral, J.; Doménech, X. Degradation of Some Biorecalcitrant Pesticides by Homogeneous and Heterogeneous Photocatalytic Ozonation. Chemosphere 2005, 58, 1127–1133. [Google Scholar] [CrossRef]
- Jugder, B.-E.; Ertan, H.; Bohl, S.; Lee, M.; Marquis, C.P.; Manefield, M. Organohalide Respiring Bacteria and Reductive Dehalogenases: Key Tools in Organohalide Bioremediation. Front. Microbiol. 2016, 7, 249. [Google Scholar] [CrossRef]
- Yan, J.; Im, J.; Yang, Y.; Löffler, F.E. Guided Cobalamin Biosynthesis Supports Dehalococcoides Mccartyi Reductive Dechlorination Activity. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2013, 368, 20120320. [Google Scholar] [CrossRef] [PubMed]
- Guerrero-Barajas, C.; Field, J.A. Enhanced Anaerobic Biotransformation of Carbon Tetrachloride with Precursors of Vitamin B12 Biosynthesis. Biodegradation 2006, 17, 317–329. [Google Scholar] [CrossRef]
- Field, J.A. Vitamin B12 Precursors Enhance Bioremediation. Ind. Bioprocess. 2006, 28, 5–6. [Google Scholar]
- Assaf-Anid, N.; Nies, L.; Vogel, T.M. Reductive Dechlorination of a Polychlorinated Biphenyl Congener and Hexachlorobenzene by Vitamin B12. Appl. Environ. Microbiol. 1992, 58, 1057–1060. [Google Scholar] [CrossRef]
- Assaf-Anid, N.; Lin, K.-Y. Carbon Tetrachloride Reduction by Fe2+, S2−, and FeS with Vitamin B12 as Organic Amendment. J. Environ. Eng. 2002, 128, 94–99. [Google Scholar] [CrossRef]
- Assaf-Anid, N.; Hayes, K.F.; Vogel, T.M. Reduction Dechlorination of Carbon Tetrachloride by Cobalamin(II) in the Presence of Dithiothreitol: Mechanistic Study, Effect of Redox Potential and PH. Environ. Sci. Technol. 1994, 28, 246. [Google Scholar] [CrossRef]
- Chiu, P.-C.; Reinhard, M. Transformation of Carbon Tetrachloride by Reduced Vitamin B12 in Aqueous Cysteine Solution. Environ. Sci. Technol. 1996, 30, 1882. [Google Scholar] [CrossRef]
- Lewis, T.A.; Morra, M.J.; Brown, P.D. Comparative Product Analysis of Carbon Tetrachloride Dehalogenation Catalyzed by Cobalt Corrins in the Presence of Thiol or Titanium(III) Reducing Agents. Environ. Sci. Technol. 1996, 30, 292. [Google Scholar] [CrossRef]
- Guo, M.; Chen, Y. Coenzyme Cobalamin: Biosynthesis, Overproduction and Its Application in Dehalogenation—A Review. Rev. Environ. Sci. Biotechnol. 2018, 17, 259–284. [Google Scholar] [CrossRef]
- Koenig, J.; Lee, M.; Manefield, M. Aliphatic Organochlorine Degradation in Subsurface Environments. Rev. Environ. Sci. Biotechnol. 2015, 14, 49–71. [Google Scholar] [CrossRef]
- Liptak, M.D.; Brunold, T.C. Spectroscopic and Computational Studies of Co1+ Cobalamin: Spectral and Electronic Properties of the “Superreduced” B12 Cofactor. J. Am. Chem. Soc. 2006, 128, 9144–9156. [Google Scholar] [CrossRef] [PubMed]
- Jensen, K.P. Electronic Structure of Cob(I)Alamin: The Story of an Unusual Nucleophile. J. Phys. Chem. B 2005, 109, 10505–10512. [Google Scholar] [CrossRef]
- Charland, J.P.; Zangrando, E.; Bresciani-Pahor, N.; Randaccio, L.; Marzilli, L.G. Binding of the Lopsided 1,5,6-Trimethylbenzimidazole Ligand to Inorganic and Organometallic Cobaloxime B12 Models. Inorg. Chem. 1993, 32, 4256–4267. [Google Scholar] [CrossRef]
- Krone, U.E.; Thauer, R.K.; Hogenkamp, H.P.C.; Steinbach, K. Reductive Formation of Carbon Monoxide from CCl4 and FREONs 11, 12 and 13 Catalyzed by Corrinoids. Biochemistry 1991, 30, 2713. [Google Scholar] [CrossRef]
- Cortés-Arriagada, D.; Toro-Labbe, A.; Mora, J.R.; Rincón, L.; Mereau, R.; Torres, F.J. Theoretical Analysis of C–F Bond Cleavage Mediated by Cob[I]Alamin-Based Structures. J. Mol. Model. 2017, 23, 264. [Google Scholar] [CrossRef]
- Kliegman, S.; McNeill, K. Reconciling Disparate Models of the Involvement of Vinyl Radicals in Cobalamin-Mediated Dechlorination Reactions. Environ. Sci. Technol. 2009, 43, 8961. [Google Scholar] [CrossRef]
- Glod, G.; Brodmann, U.; Angst, W.; Holliger, C.; Schwarzenbach, R.P. Cobalamin-Mediated Reduction of Cis- and Trans-Dichloroethene, and Vinylchloride in Homogeneous Aqueous Solution: Reaction Kinetics and Mechanistic Considerations. Environ. Sci. Technol. 1997, 31, 3154. [Google Scholar] [CrossRef]
- Kliegman, S.; McNeill, K. Dechlorination of Chloroethylenes by Cob(i)Alamin and Cobalamin Model Complexes. Dalton Trans. 2008, 4191–4201. [Google Scholar] [CrossRef]
- Arguello, J.E.; Costentin, C.; Griveau, S.; Saveant, J.-M. Role of Protonation and of Axial Ligands in the Reductive Dechlorination of Alkyl Chlorides by Vitamin B-12 Complexes. Reductive Cleavage of Chloroacetonitrile by Co(I) Cobalamins and Cobinamides. J. Am. Chem. Soc. 2005, 127, 5049. [Google Scholar] [CrossRef]
- Heckel, B.; McNeill, K.; Elsner, M. Chlorinated Ethene Reactivity with Vitamin B12 Is Governed by Cobalamin Chloroethylcarbanions as Crossroads of Competing Pathways. ACS Catal. 2018, 8, 3054. [Google Scholar] [CrossRef]
- Terán, J.E.; Zambrano, C.H.; Mora, J.R.; Rincón, L.; Torres, F.J. Theoretical Investigation of the Mechanism for the Reductive Dehalogenation of Methyl Halides Mediated by the CoI-Based Compounds Cobalamin and Cobaloxime. J. Mol. Model. 2018, 24, 316. [Google Scholar] [CrossRef]
- Hill, H.A.O.; Pratt, J.M.; O’Riordan, M.P.; Williams, F.R.; Williams, R.J.P. The Chemistry of Vitamin B12. Part XV. Catalysis of Alkyl Halide Reduction by Vitamin B12a: Studies Using Controlled Potential Reduction. J. Chem. Soc. A Inorg. Phys. Theor. 1971, 1859–1862. [Google Scholar] [CrossRef]
- Schrauzer, G.N.; Deutsch, E. Reactions of Cobalt(I) Supernucleophiles. The Alkylation of Vitamin B12s, Cobaloximes(I), and Related Compounds. J. Am. Chem. Soc. 1969, 91, 3341–3350. [Google Scholar] [CrossRef]
- Schrauzer, G.N. Organocobalt Chemistry of Vitamin B12 Model Compounds (Cobaloximes). Acc. Chem. Res. 1968, 1, 97–103. [Google Scholar] [CrossRef]
- Schrauzer, G.N.; Ribeiro, A.; Lee, L.P.; Ho, R.K.Y. Novel Degradation Reactions of Halomethyl Derivatives of Bis(Diacetyldioximato)Cobalt. Angew. Chem. Int. Ed. Engl. 1971, 10, 807–808. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
- Gonzalez, C.; Schlegel, H.B. Reaction Path Following in Mass-Weighted Internal Coordinates. J. Phys. Chem. 1990, 94, 5523–5527. [Google Scholar] [CrossRef]
- Hratchian, H.P.; Schlegel, H.B. Using Hessian Updating to Increase the Efficiency of a Hessian Based Predictor-Corrector Reaction Path Following Method. J. Chem. Theory Comput. 2005, 1, 61–69. [Google Scholar] [CrossRef]
- Hratchian, H.P.; Schlegel, H.B. Accurate Reaction Paths Using a Hessian Based Predictor–Corrector Integrator. J. Chem. Phys. 2004, 120, 9918–9924. [Google Scholar] [CrossRef] [PubMed]
- Toro-Labbé, A. Characterization of Chemical Reactions from the Profiles of Energy, Chemical Potential, and Hardness. J. Phys. Chem. A 1999, 103, 4398–4403. [Google Scholar] [CrossRef]
- Herrera, B.; Toro-Labbé, A. The Role of the Reaction Force to Characterize Local Specific Interactions That Activate the Intramolecular Proton Transfers in DNA Bases. J. Chem. Phys. 2004, 121, 7096. [Google Scholar] [CrossRef]
- Politzer, P.; Toro-Labbé, A.; Gutiérrez-Oliva, S.; Murray, J.S. Perspectives on the Reaction Force. Adv. Quantum Chem. 2012, 64, 189–209. [Google Scholar] [CrossRef]
- Politzer, P.; Toro-Labbé, A.; Gutiérrez-Oliva, S.; Herrera, B.; Jaque, P.; Concha, M.C.; Murray, J.S. The Reaction Force: Three Key Points along an Intrinsic Reaction Coordinate. J. Chem. Sci. 2005, 117, 467–472. [Google Scholar] [CrossRef]
- Bader, R.W. Atoms in Molecules: A Quantum Theory; International Series of Monographs on Chemistry; Oxford Science: Oxford, UK, 1990; Volume 22. [Google Scholar]
- Bader, R.F.W.; Gatti, C. A Green’s Function for the Density. Chem. Phys. Lett. 1998, 287, 233–238. [Google Scholar] [CrossRef]
- Rohman, S.S.; Kashyap, C.; Ullah, S.S.; Mazumder, L.J.; Sahu, P.P.; Kalita, A.; Reza, S.; Hazarika, P.P.; Borah, B.; Guha, A.K. Revisiting Ultra-Weak Metal-Metal Bonding. Chem. Phys. Lett. 2019, 730, 411–415. [Google Scholar] [CrossRef]
- Gatti, C. The Source Function Descriptor as a Tool to Extract Chemical Information from Theoretical and Experimental Electron Densities. In Electron Density and Chemical Bonding II: Theoretical Charge Density Studies; Stalke, D., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 193–285. ISBN 978-3-642-30808-6. [Google Scholar]
- Lu, T.; Chen, F. Multiwfn: A Multifunctional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Rincón, L.; Torres, F.J.; Almeida, R. Is the Pauli Exclusion Principle the Origin of Electron Localisation? Mol. Phys. 2018, 116, 578–587. [Google Scholar] [CrossRef]
- Rincón, L.; Almeida, R.; Contreras, P.L.; Javier Torres, F. The Information Content of the Conditional Pair Probability. Chem. Phys. Lett. 2015, 635, 116–119. [Google Scholar] [CrossRef]
- Urbina, A.S.; Torres, F.J.; Rincon, L. The Electron Localization as the Information Content of the Conditional Pair Density. J. Chem. Phys. 2016, 144, 244104. [Google Scholar] [CrossRef]
- Torres, F.J.; Rincón, L.; Zambrano, C.; Mora, J.R.; Méndez, M. A Review on the Information Content of the Pair Density as a Tool for the Description of the Electronic Properties in Molecular Systems. Int. J. Quantum Chem. 2019, 119, e25763. [Google Scholar] [CrossRef]
- Hwu, W.W.; Kirk, D.; Hajj, I.E. Programming Massively Parallel Processors. A Hands-on Approach, 4th ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Rincon, L.; Torres, F.J.; Mora, J.R.; Zambrano, C.H.; Rodriguez, V. A Valence Bond Perspective of the Reaction Force Formalism. Theor. Chem. Acc. 2019, 139, 13. [Google Scholar] [CrossRef]
- Dreos, R.; Geremia, S.; Randaccio, L.; Siega, P. Properties, Structure and Reactivity of Cobaloximes. In PATAI’s Chemistry of Functional Groups; John Wiley & Sons, Ltd.: Chichester, UK, 2010. [Google Scholar]
- Cuevas, G. Hydrogen Bond Type Contributions to the Anomeric Effect in S−C−P(O) and S−C−P(S) Segments. J. Am. Chem. Soc. 2000, 122, 692–698. [Google Scholar] [CrossRef]
- Pauling, L. The Nature of the Chemical Bond II. The One-Electron Bond and the Three-Electron Bond. J. Am. Chem. Soc. 1931, 53, 3225–3237. [Google Scholar] [CrossRef]
- Clark, T. Odd-Electron Sigma Bonds. J. Am. Chem. Soc. 1988, 110, 1672–1678. [Google Scholar] [CrossRef]
- Hübner, A.; Diehl, A.M.; Diefenbach, M.; Endeward, B.; Bolte, M.; Lerner, H.-W.; Holthausen, M.C.; Wagner, M. Confirmed by X-Ray Crystallography: The B⋅B One-Electron σ Bond. Angew. Chem. Int. Ed. 2014, 53, 4832–4835. [Google Scholar] [CrossRef]
- De Sousa, D.W.O.; Nascimento, M.A.C. Are One-Electron Bonds Any Different from Standard Two-Electron Covalent Bonds? Acc. Chem. Res. 2017, 50, 2264–2272. [Google Scholar] [CrossRef]
- De Sousa, D.W.O.; Nascimento, M.A.C. One-Electron Bonds Are Not “Half-Bonds”. Phys. Chem. Chem. Phys. 2019, 21, 13319–13336. [Google Scholar] [CrossRef]
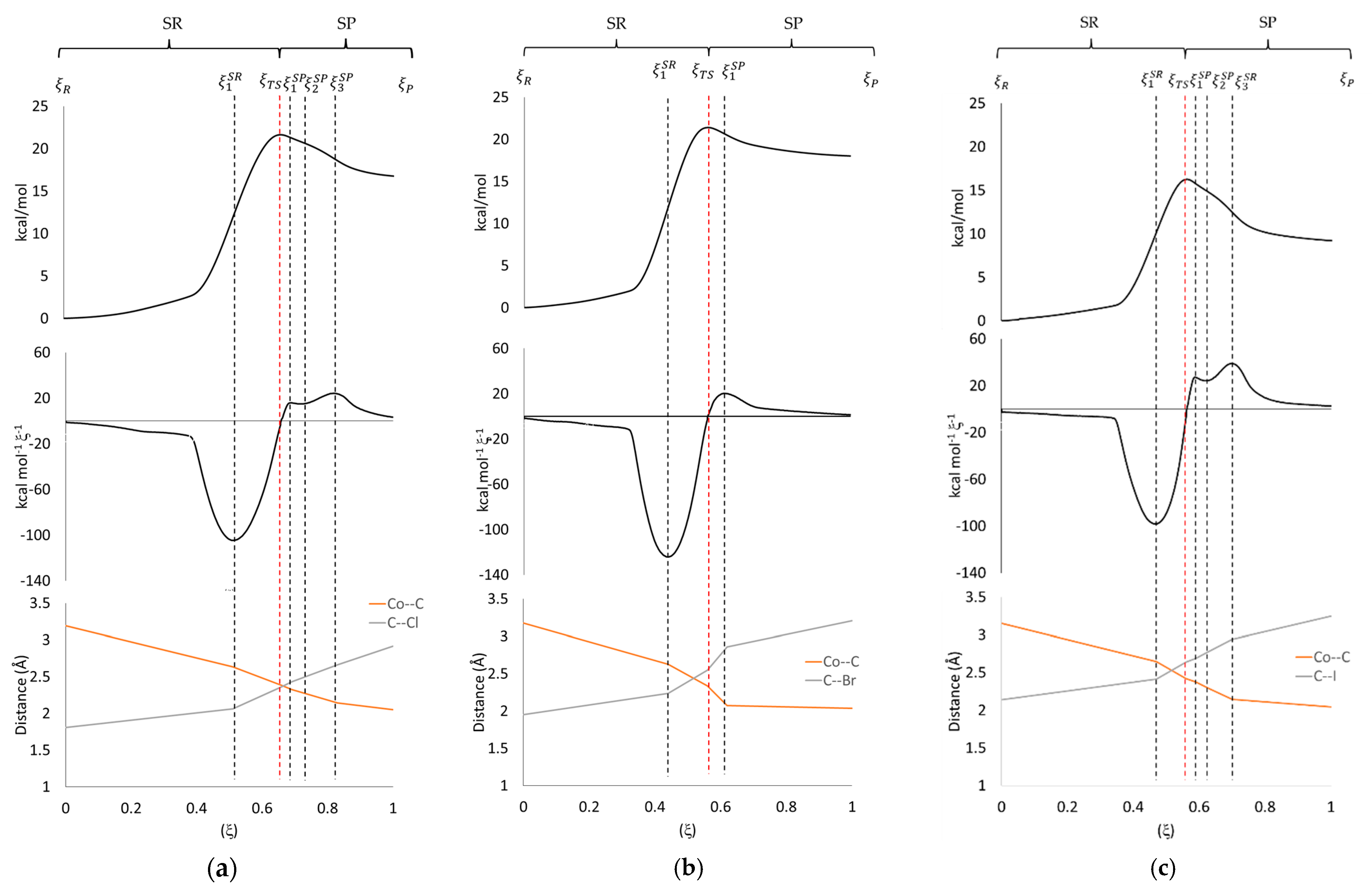
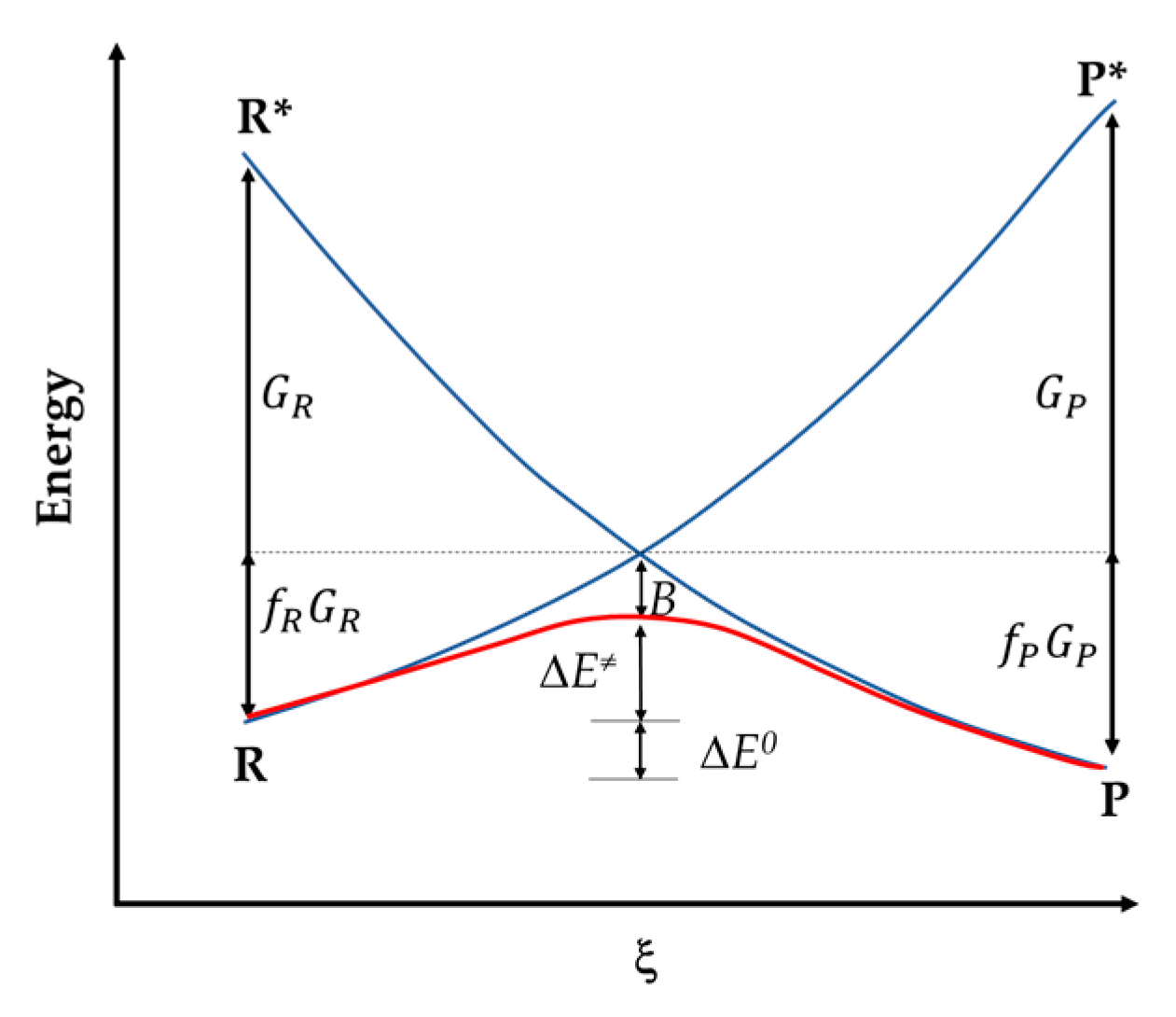
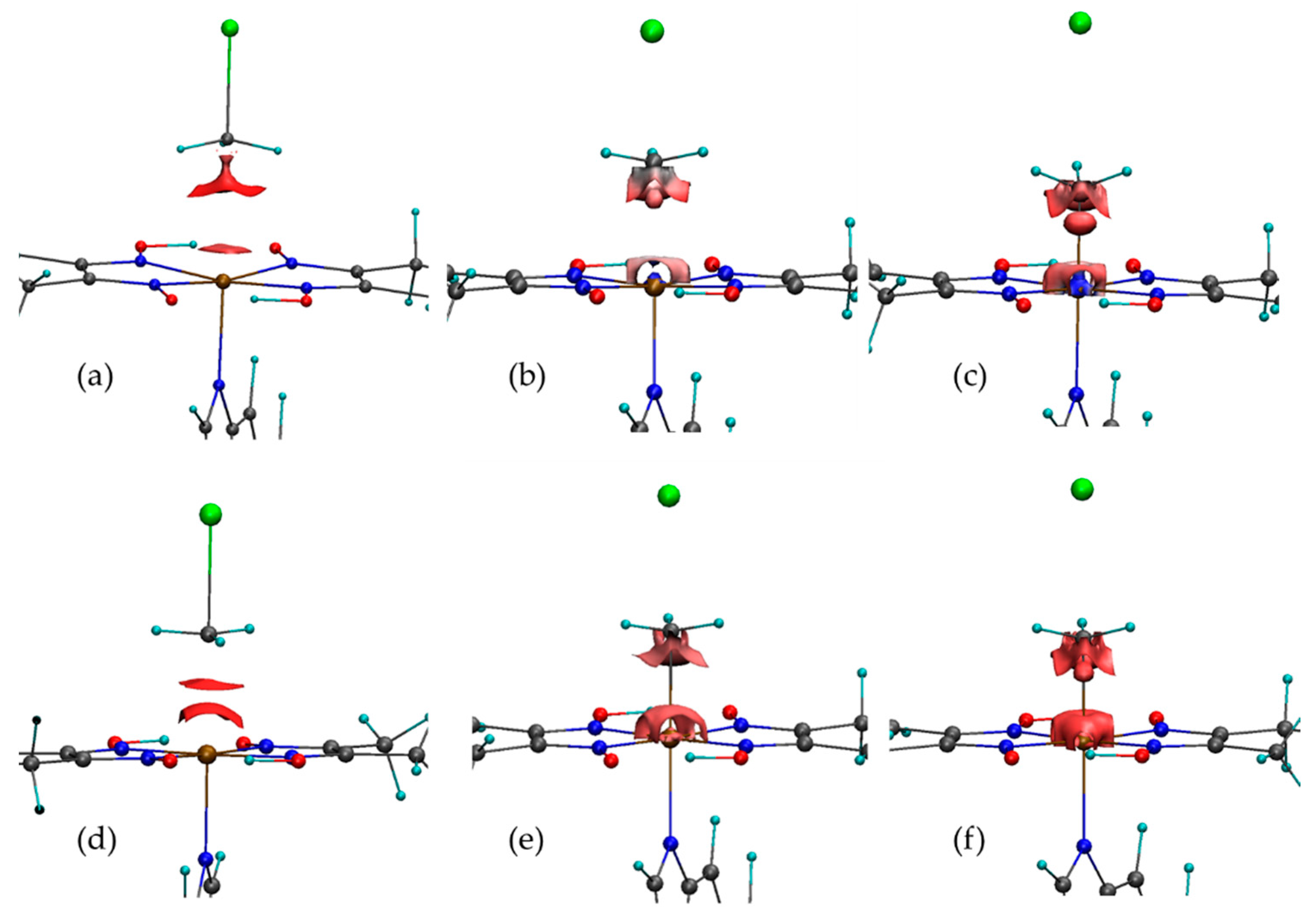
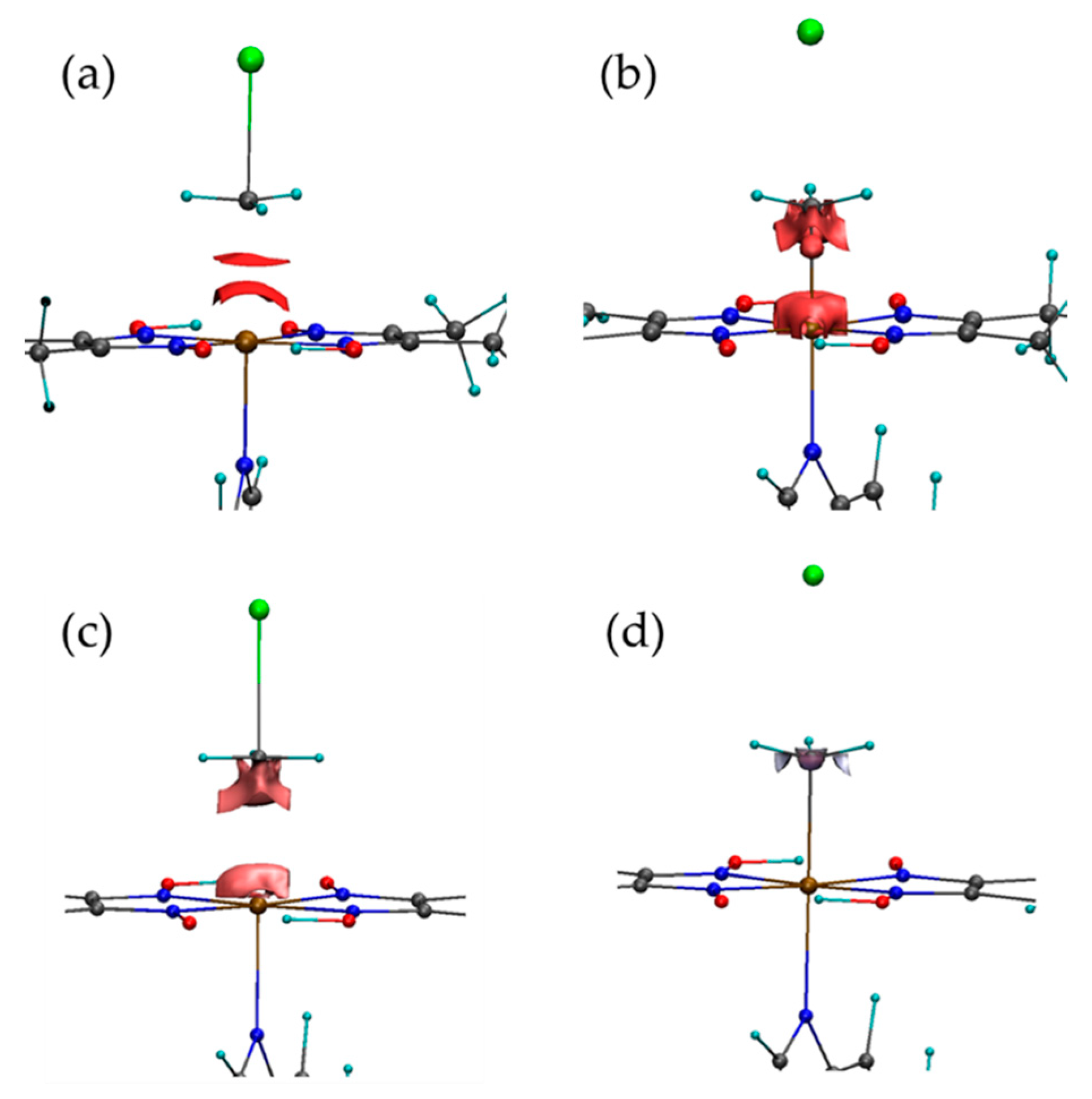
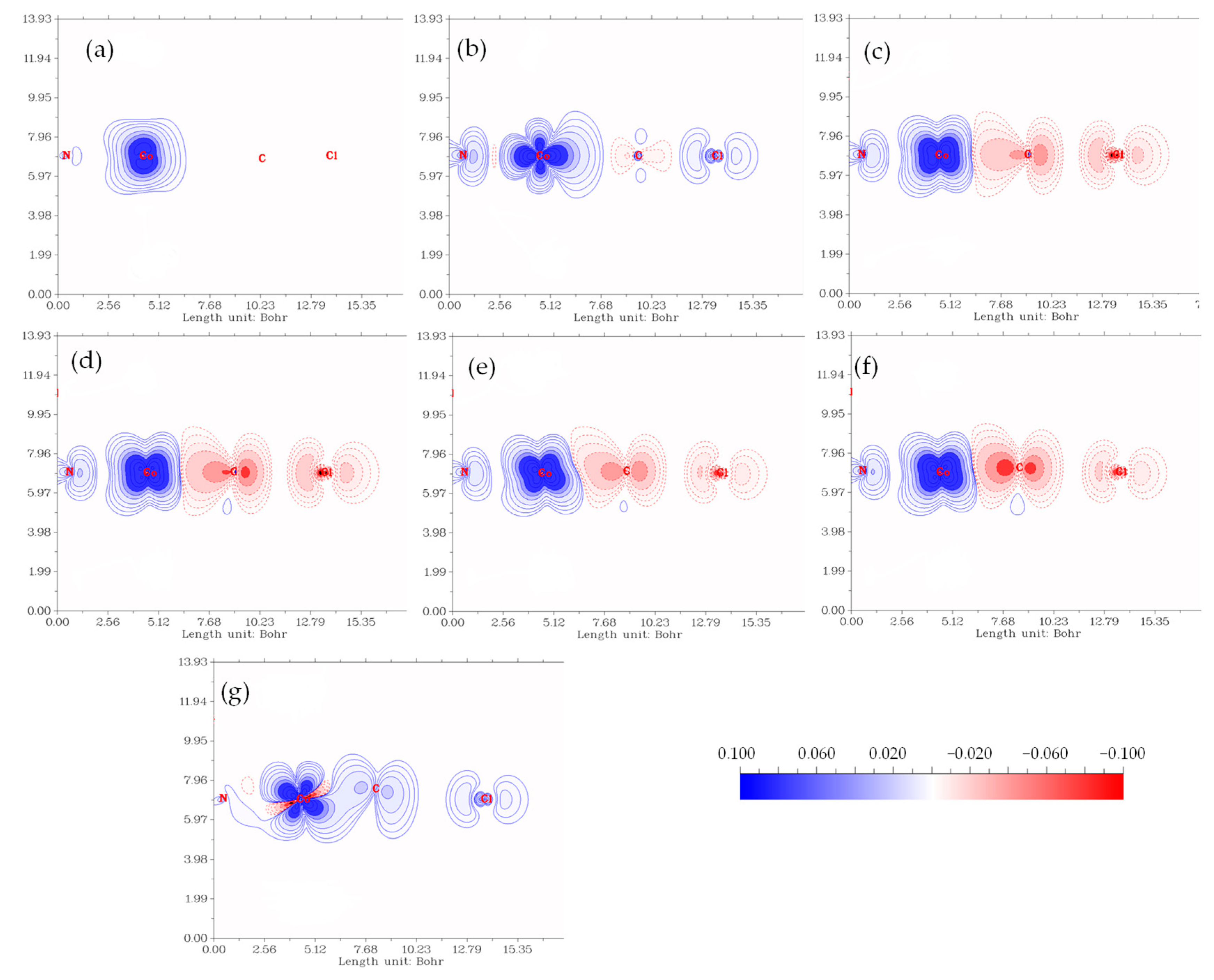
| Methyl Halide | ΔE≠ | ΔE0 | ||||||
|---|---|---|---|---|---|---|---|---|
| CH3Cl | 11.1 (3.5) | 10.2 (2.3) | −0.3 (−19.0) | −0.4 (−29.4) | −1.8 | −2.1 | 21.3 (5.7) | 16.5 (−42.7) |
| CH3Br | 11.6 (3.3) | 9.5 (1.7) | −0.6 (−16.8) | −2.7 (−27.2) | --- | --- | 21.1 (5.0) | 17.8 (−39.1) |
| CH3I * | 9.4 (2.3) | 6.7 (0.6) | −0.4 (−21.6) | −0.7 (−31.6) | −2.4 | −3.3 | 16.0 (2.8) | 9.1 (−50.4) |
| Interaction (A–B) | IRC | ρ(rBCP) 1 | S%(rbcp,ΩA,ΩB) | ||
|---|---|---|---|---|---|
| CoICbx | CoIICbx | CoICbx | CoIICbx | ||
| N–Co | 1.00 × 10−1 | 7.94 × 10−2 | 60.03 | 25.97 | |
| 9.53 × 10−2 | 7.28 × 10−2 | 57.72 | 46.45 | ||
| 9.22 × 10−2 | 7.69 × 10−2 | 56.27 | 47.96 | ||
| 8.42 × 10−2 | 7.77 × 10−2 | 51.73 | 47.57 | ||
| 7.25 × 10−2 | 7.63 × 10−2 | 42.61 | 46.38 | ||
| Co–C | 1.07 × 10−2 | 8.41 × 10−3 | −169.05 | −213.8 | |
| 1.94 × 10−2 | 1.85 × 10−2 | −84.41 | −98.81 | ||
| 2.71 × 10−2 | 4.84 × 10−2 | −40.43 | −27.27 | ||
| 5.94 × 10−2 | 5.44 × 10−2 | 28.60 | 21.34 | ||
| 1.25 × 10−1 | 9.44 × 10−2 | 61.16 | 50.09 | ||
| C–Cl | 1.64 × 10−1 | 1.69 × 10−1 | 82.69 | 83.65 | |
| 1.24 × 10−1 | 1.03 × 10−1 | 77.89 | 75.14 | ||
| 8.78 × 10−2 | 4.92 × 10−2 | 69.48 | 48.61 | ||
| 3.66 × 10−2 | 4.27 × 10−2 | 15.73 | 40.25 | ||
| 9.99 × 10−3 | 1.66 × 10−2 | −48.95 | −13.02 | ||
| CoICbx | CoIICbx | |||||
|---|---|---|---|---|---|---|
| IRC Point | Ω | q (Ω) (e) | q (Ω) (e) | qα (Ω) (e) | qβ (Ω) (e) | Nspin 2 |
| Nu 1 | −0.946 | +0.014 | +113.007 | +114.008 | 1.00 | |
| CH3 | +0.245 | +0.260 | +4.631 | +4.654 | 0.02 | |
| Cl | −0.304 | −0.275 | +8.362 | +8.337 | −0.02 | |
| Nu 1 | −0.868 | +0.028 | +113.034 | +113.993 | 0.96 | |
| CH3 | +0.276 | +0.329 | +4.684 | +4.675 | −0.01 | |
| Cl | −0.409 | −0.357 | +8.282 | +8.332 | 0.05 | |
| Nu 1 | −0.711 | +0.395 | +113.065 | +114.342 | 1.28 | |
| CH3 | +0.269 | +0.294 | +4.740 | +4.553 | −0.19 | |
| Cl | −0.558 | −0.689 | +8.195 | +8.105 | −0.09 | |
| Nu 1 | −0.215 | +0.498 | +113.067 | +114.440 | 1.37 | |
| CH3 | +0.197 | +0.253 | +4.760 | +4.486 | −0.27 | |
| Cl | −0.979 | −0.750 | +8.173 | +8.075 | −0.10 | |
| Nu 1 | --- | +0.495 | +113.119 | +114.383 | 1.26 | |
| CH3 | --- | +0.274 | +4.742 | +4.527 | −0.21 | |
| Cl | --- | −0.769 | +8.141 | +8.090 | −0.05 | |
| Nu 1 | --- | +0.687 | +113.152 | +114.556 | 1.40 | |
| CH3 | --- | +0.177 | +4.756 | +4.407 | −0.35 | |
| Cl | --- | −0.865 | +8.092 | +8.037 | −0.05 | |
| Nu 1 | +0.170 | +0.712 | +113.471 | +114.247 | 0.78 | |
| CH3 | −0.194 | +0.181 | +4.500 | +4.678 | 0.18 | |
| Cl | −0.976 | −0.893 | +8.029 | +8.074 | 0.04 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seijas, L.E.; Zambrano, C.H.; Rodríguez, V.; Alí-Torres, J.; Rincón, L.; Torres, F.J. A Theoretical Study of the C–X Bond Cleavage Mediated by Cob(II)Aloxime. Molecules 2022, 27, 7283. https://doi.org/10.3390/molecules27217283
Seijas LE, Zambrano CH, Rodríguez V, Alí-Torres J, Rincón L, Torres FJ. A Theoretical Study of the C–X Bond Cleavage Mediated by Cob(II)Aloxime. Molecules. 2022; 27(21):7283. https://doi.org/10.3390/molecules27217283
Chicago/Turabian StyleSeijas, Luis E., Cesar H. Zambrano, Vladimir Rodríguez, Jorge Alí-Torres, Luis Rincón, and F. Javier Torres. 2022. "A Theoretical Study of the C–X Bond Cleavage Mediated by Cob(II)Aloxime" Molecules 27, no. 21: 7283. https://doi.org/10.3390/molecules27217283
APA StyleSeijas, L. E., Zambrano, C. H., Rodríguez, V., Alí-Torres, J., Rincón, L., & Torres, F. J. (2022). A Theoretical Study of the C–X Bond Cleavage Mediated by Cob(II)Aloxime. Molecules, 27(21), 7283. https://doi.org/10.3390/molecules27217283







