Merits and Demerits of ODE Modeling of Physicochemical Systems for Numerical Simulations
Abstract
:1. Introduction
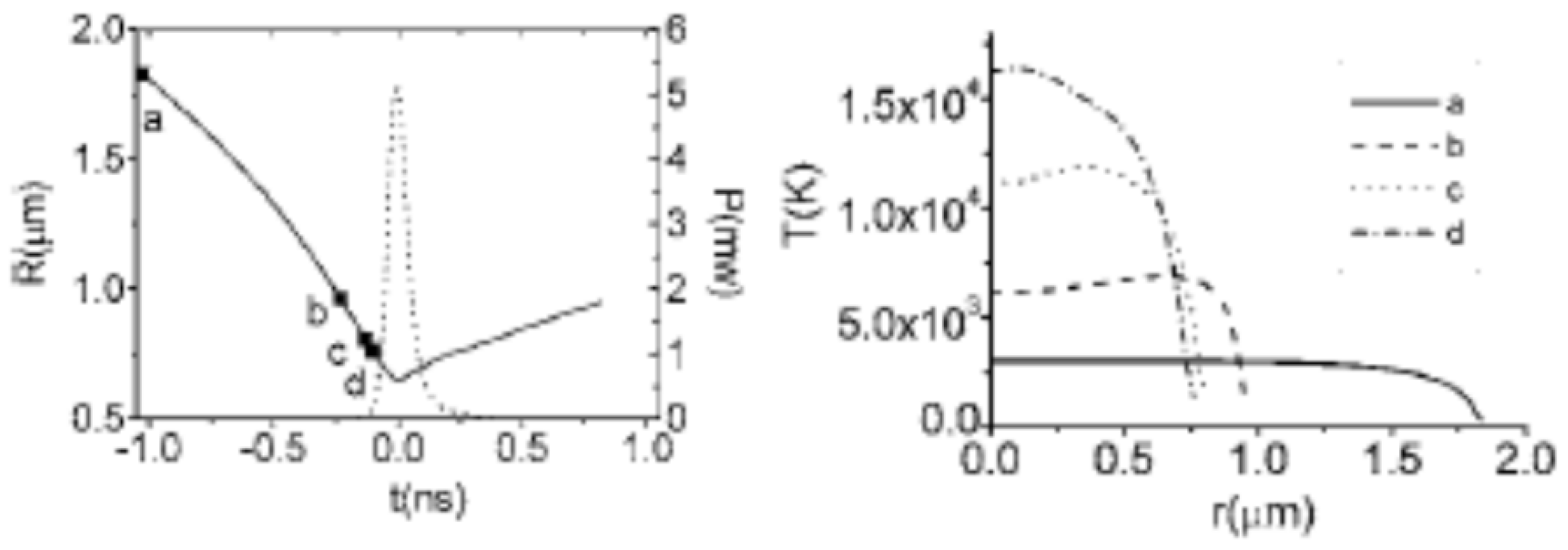
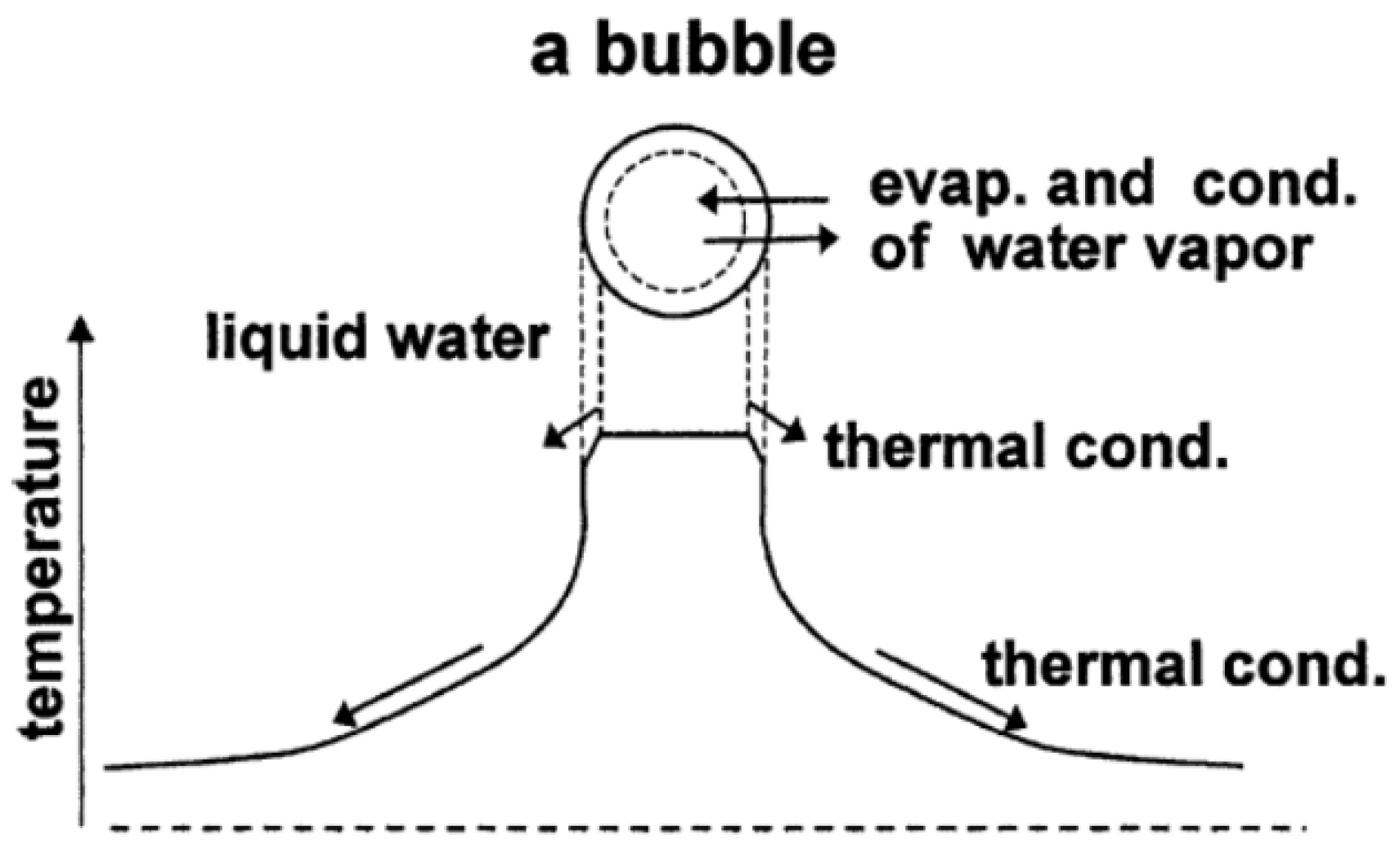
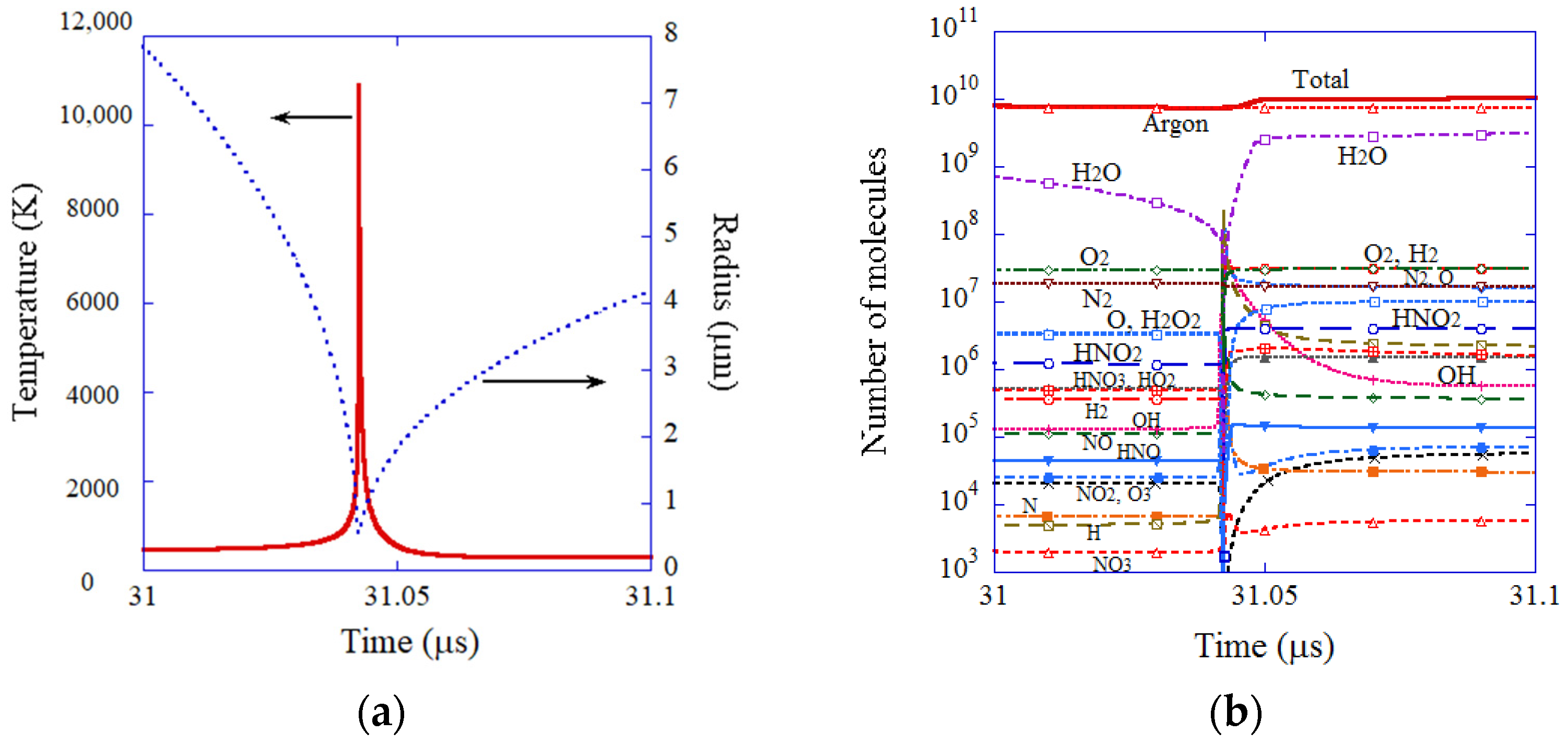
2. Chemical Reactions inside a Cavitation Bubble
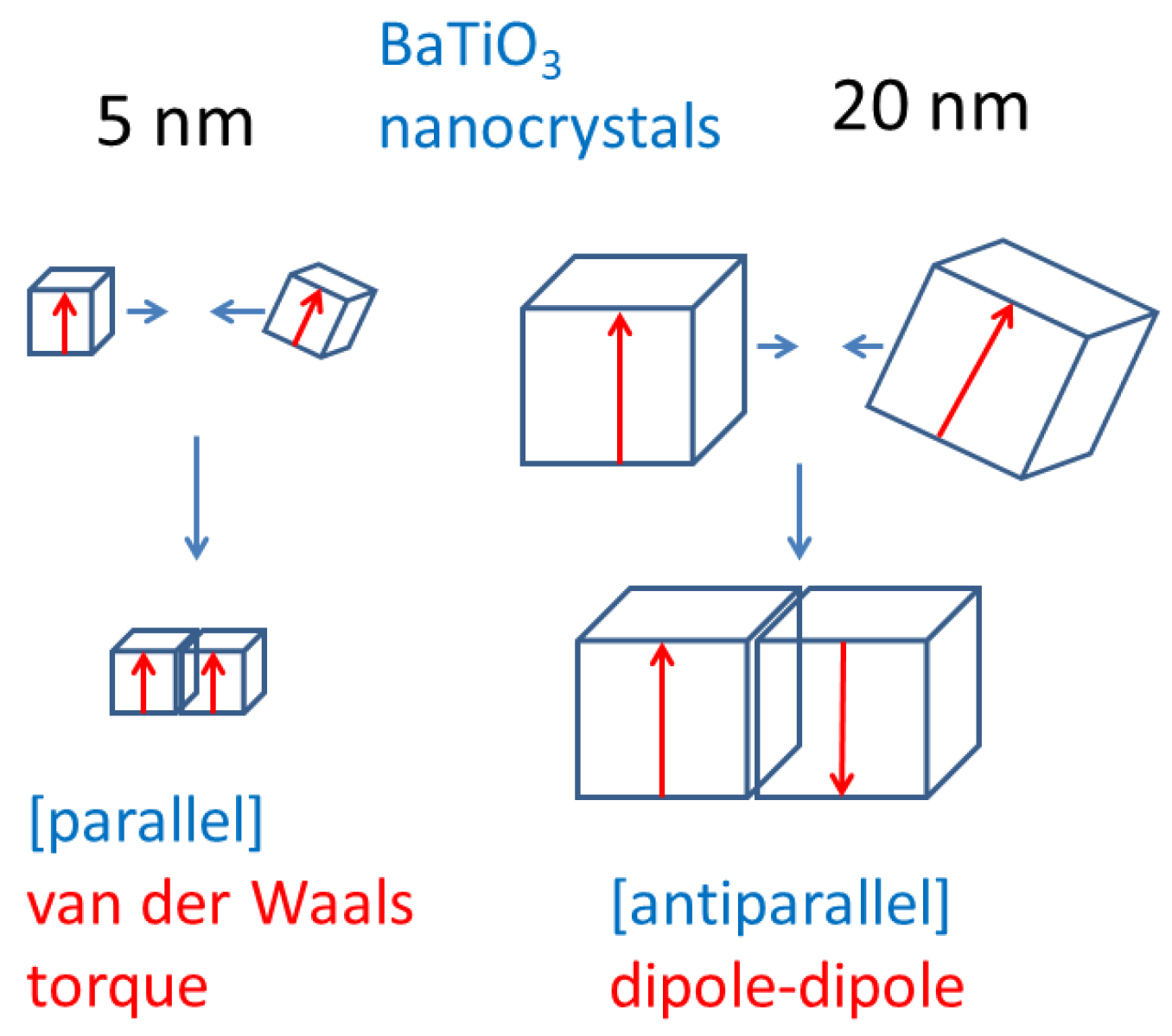
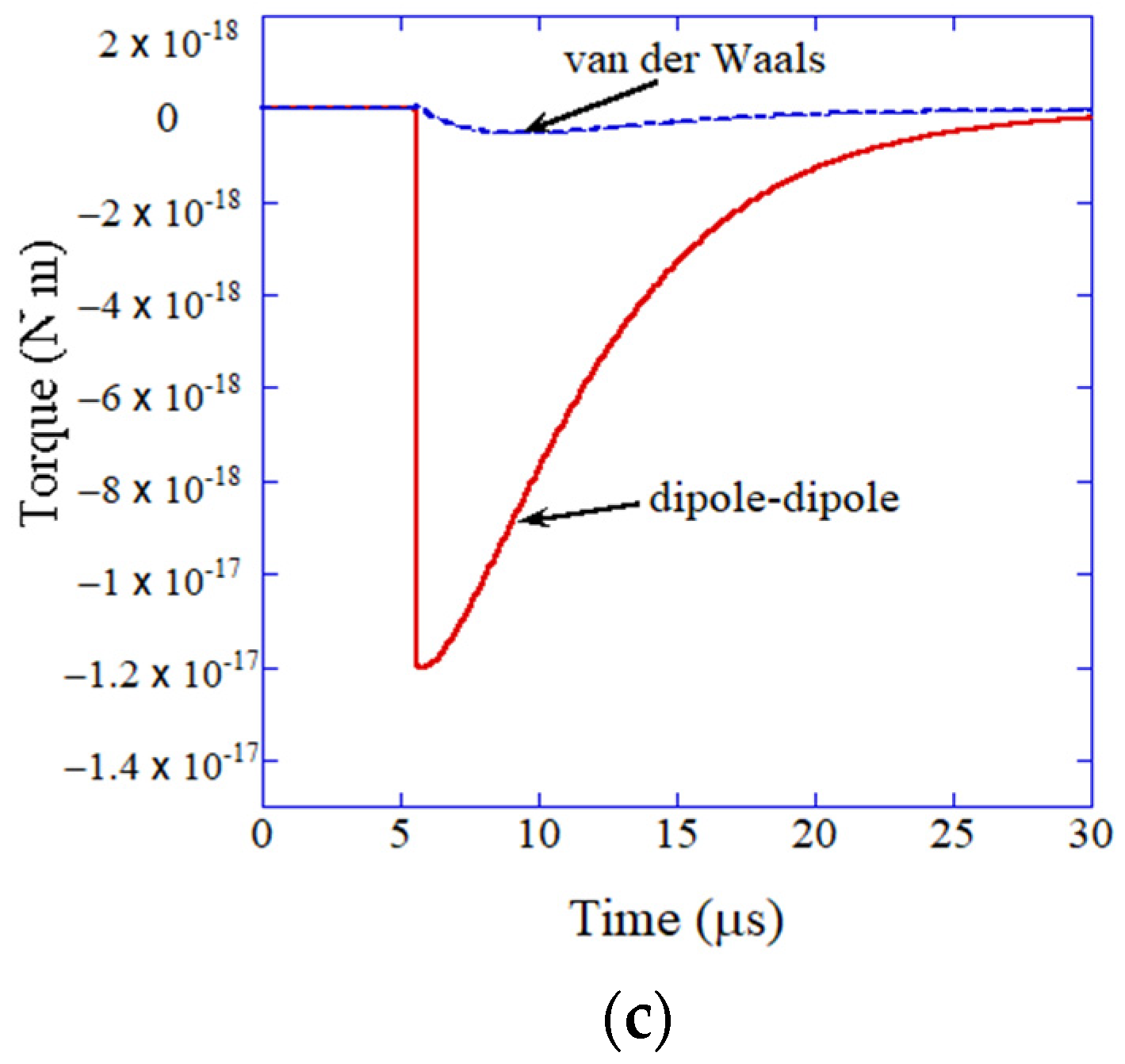
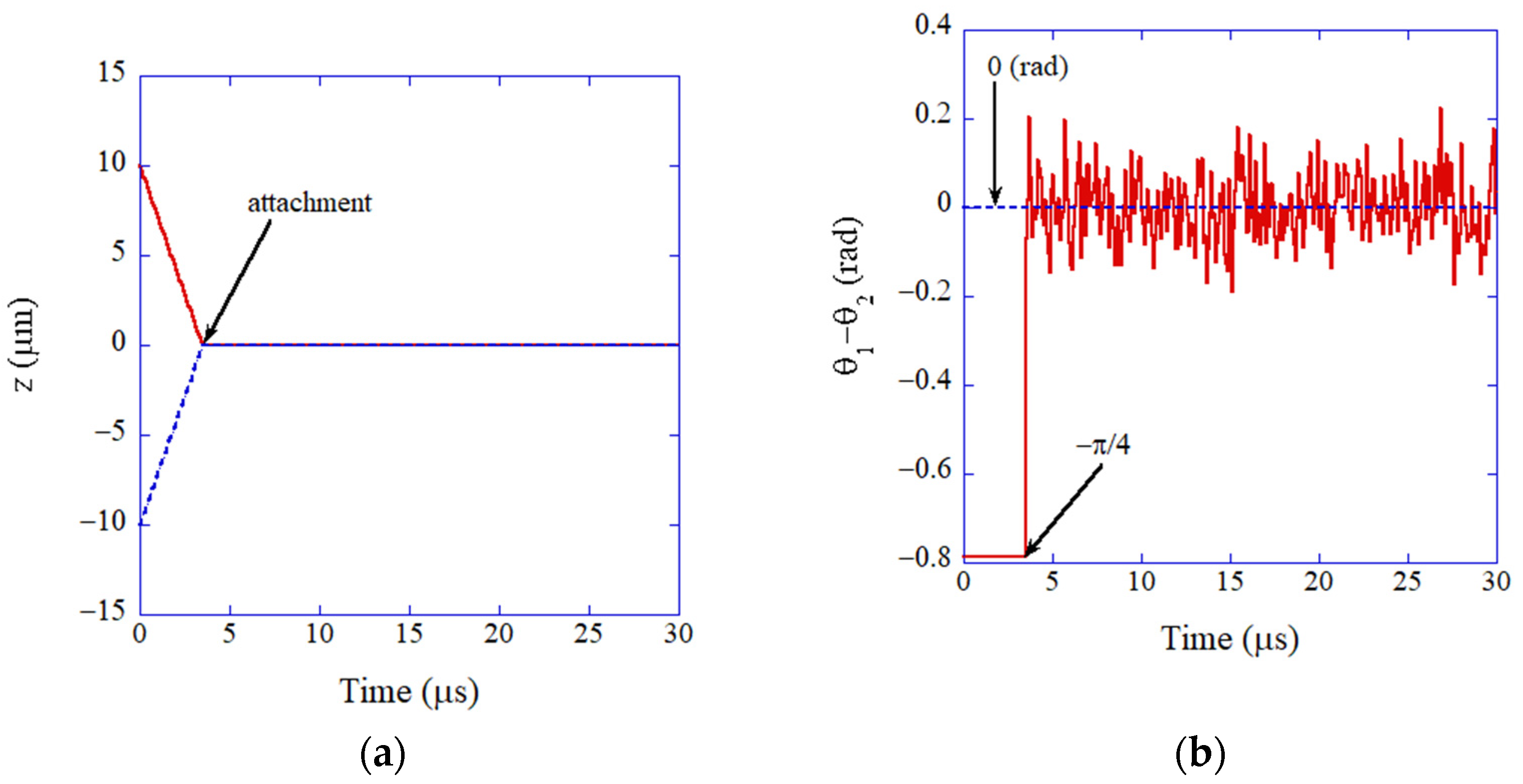
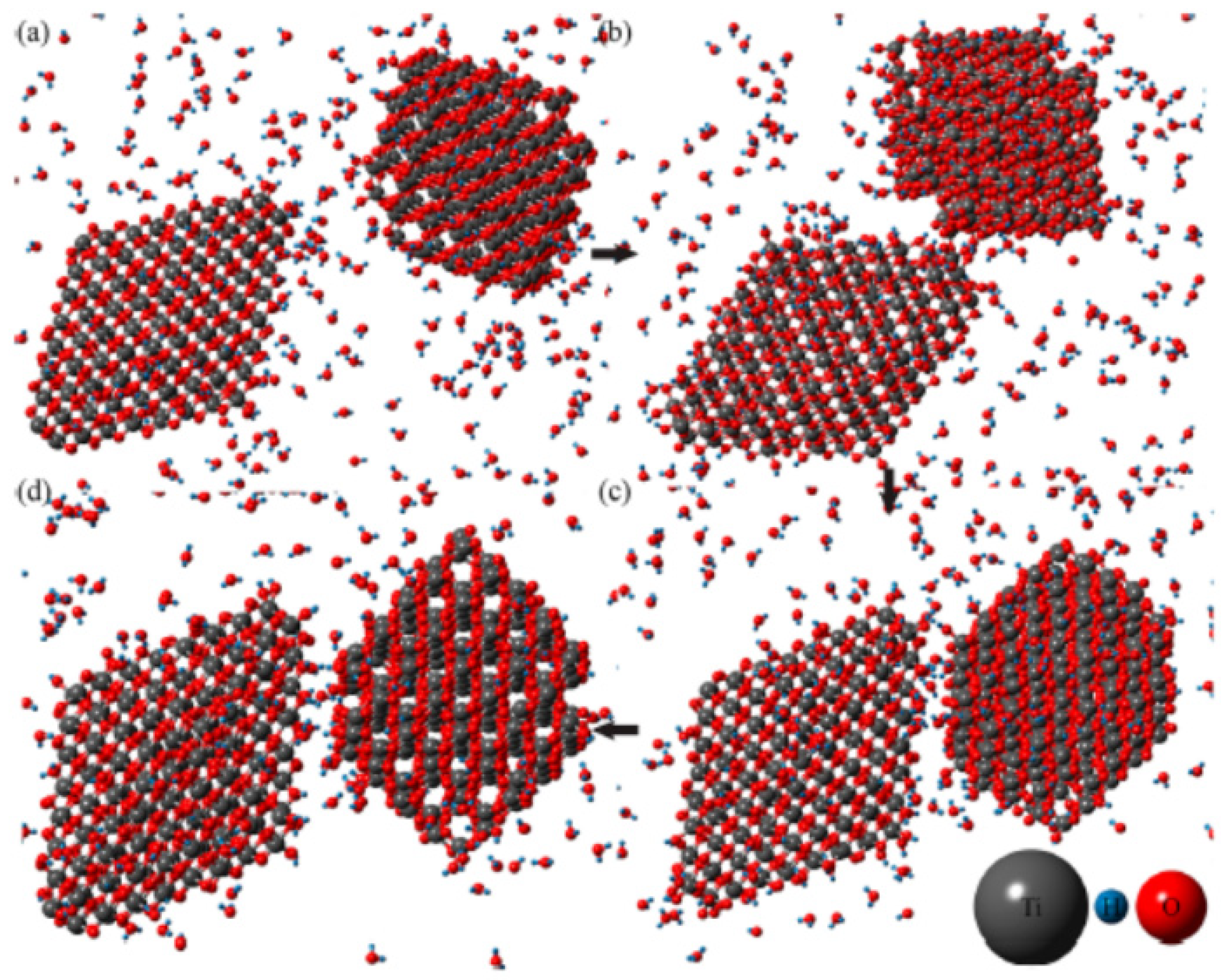
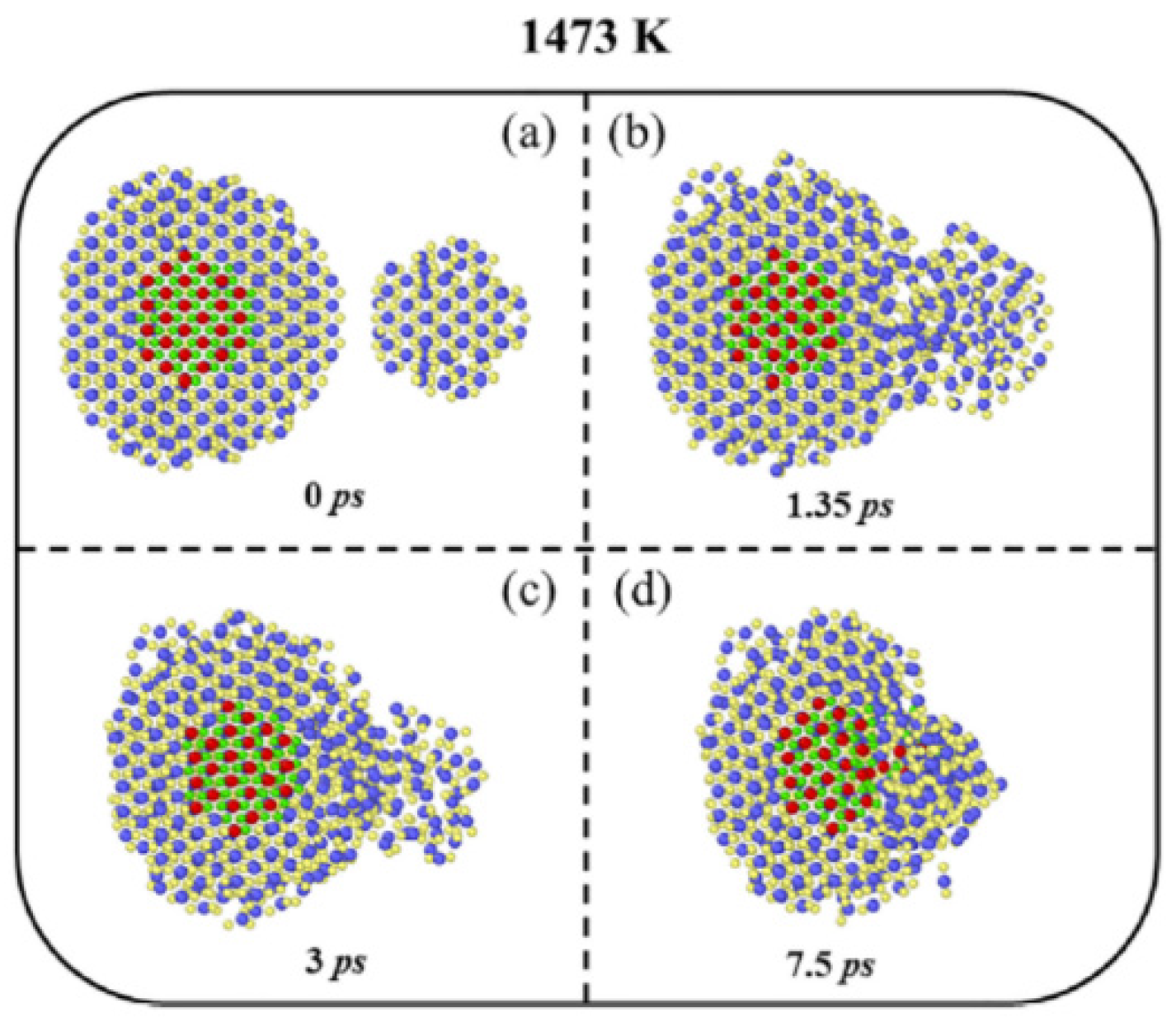
3. Oriented Attachment of Nanocrystals
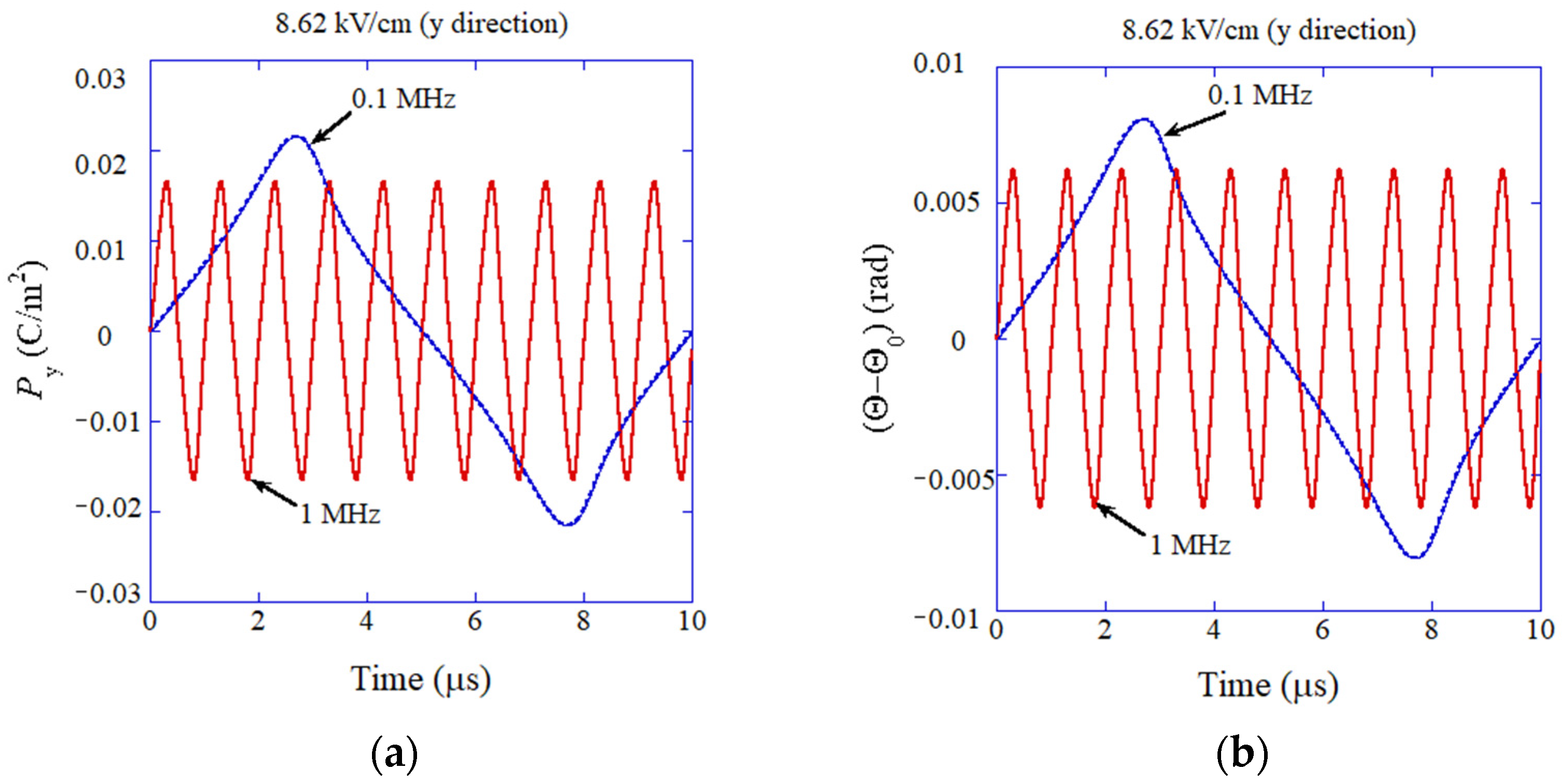
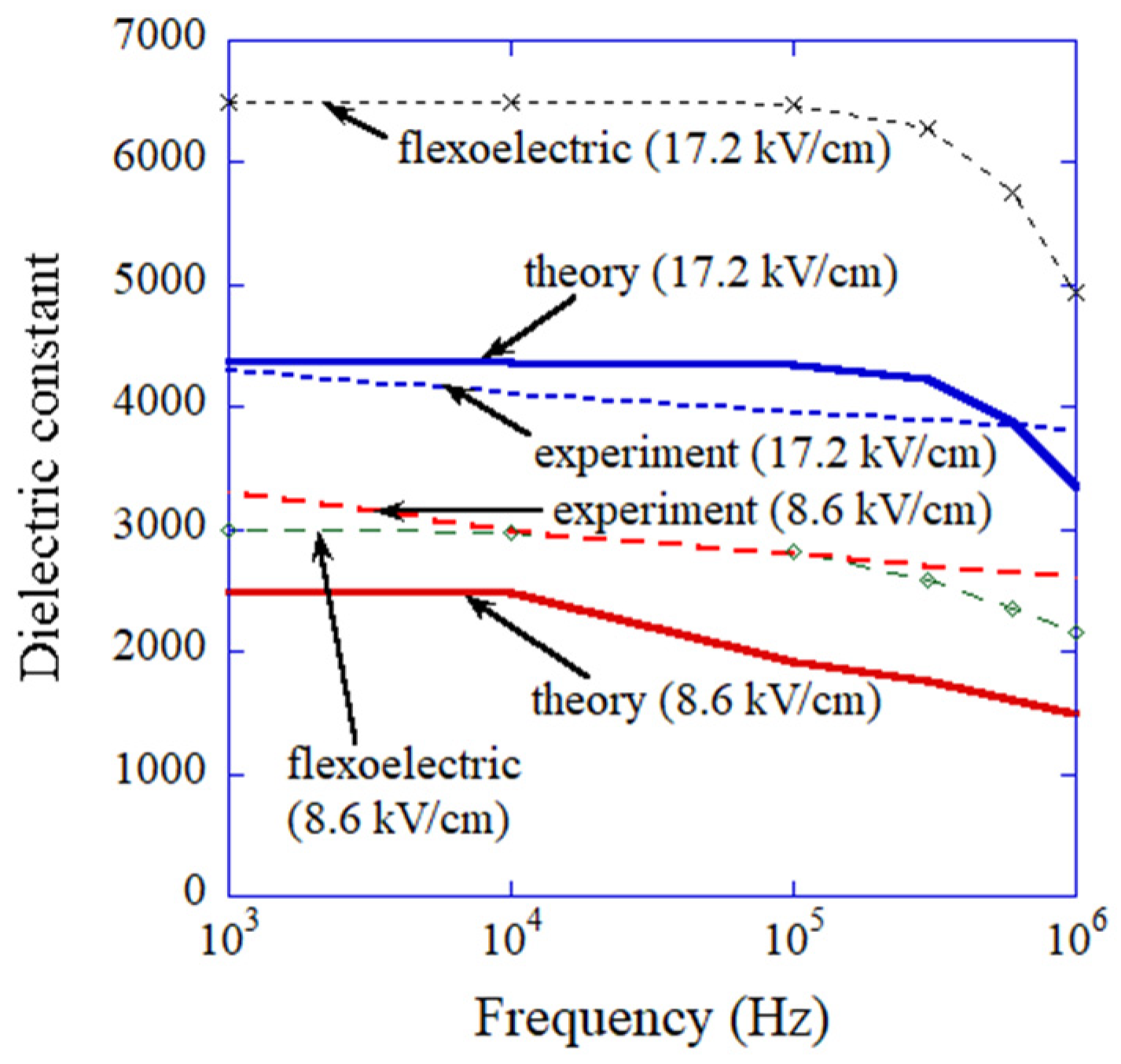
4. Dynamic Response of Flexoelectric Polarization
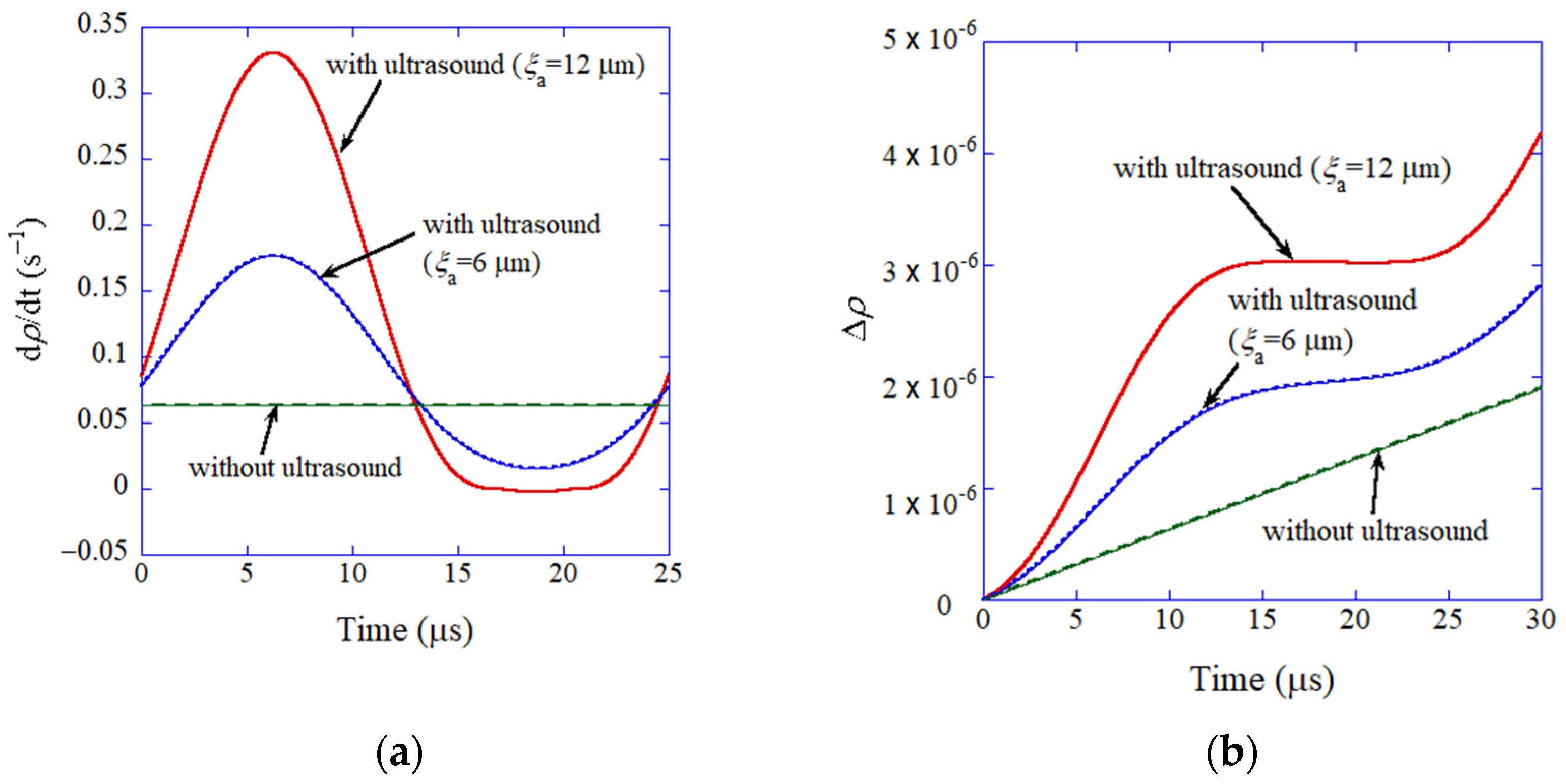
5. Ultrasound-Assisted Sintering
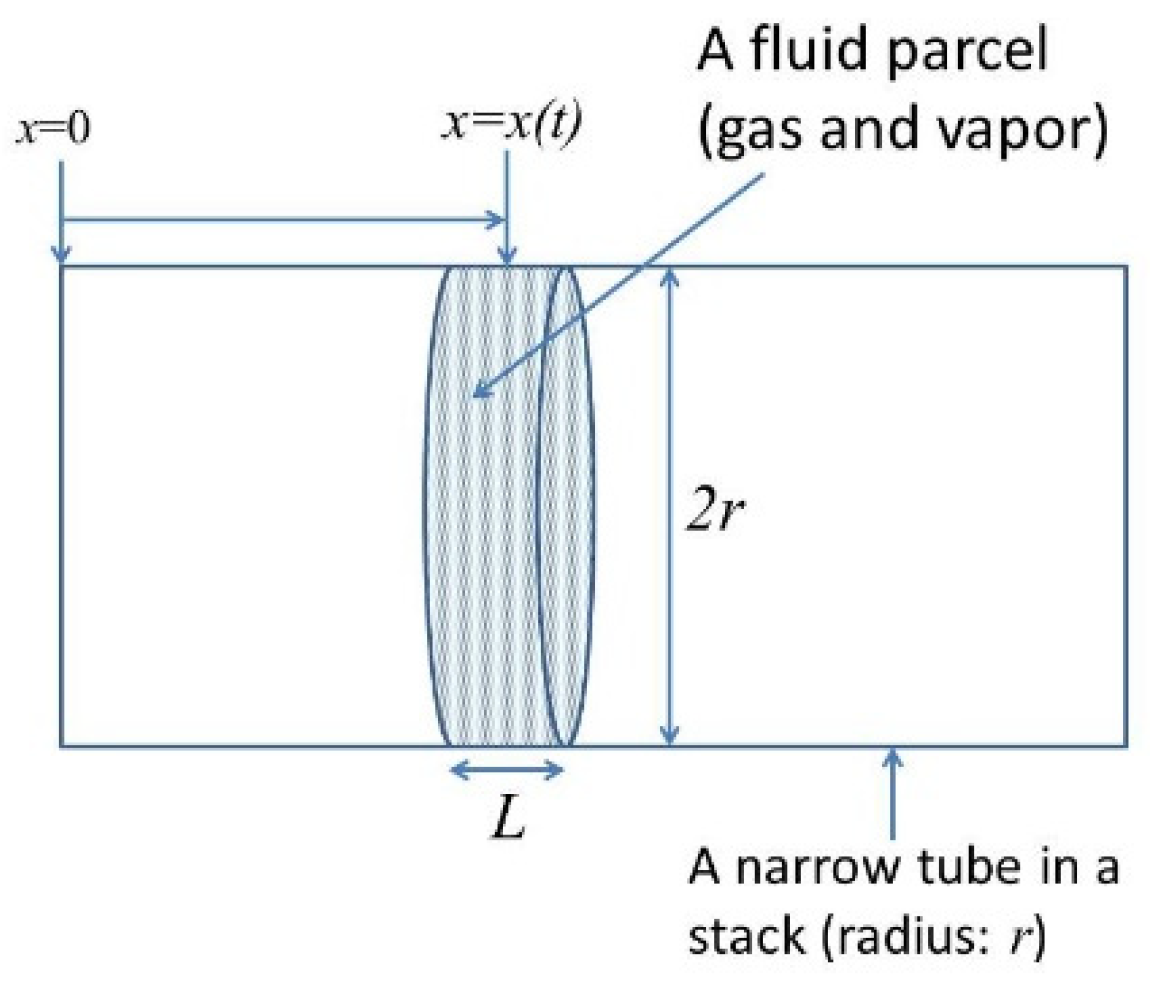
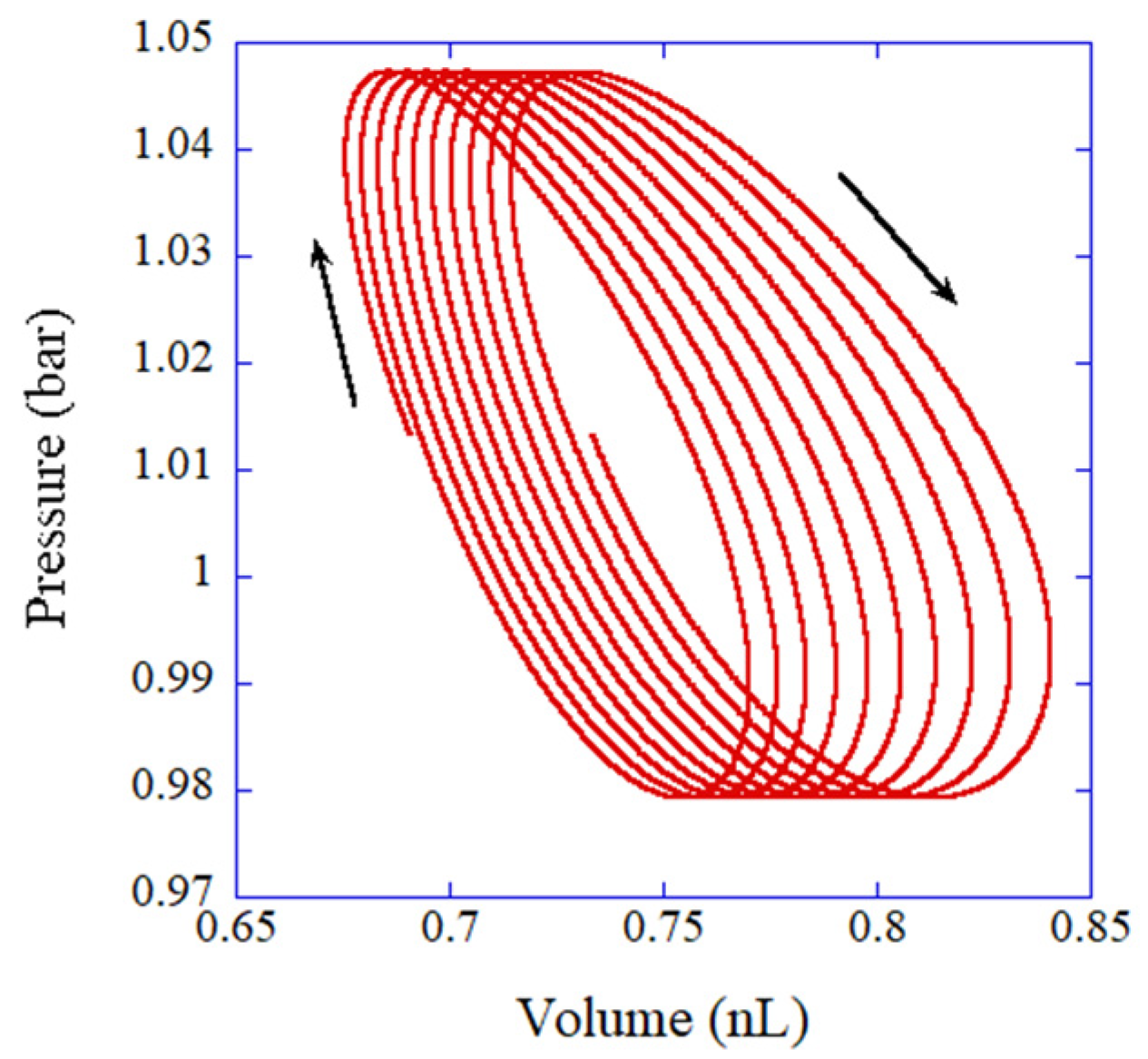
6. Dynamics of a Gas Parcel in a Thermoacoustic Engine
7. Mathematical Models
7.1. A Cavitation Bubble (ODE Model) [95]
7.2. A Cavitation Bubble (PDE Model) [109,169]
7.3. Flexoelectric Polarization (ODE Model) [87]
7.4. Flexoelectric Polarization (PDE Model) [136]
8. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Winsberg, E.B. Science in the Age of Computer Simulation; University Chicago Press: Chicago, IL, USA, 2010. [Google Scholar]
- Fletcher, C.A.J. Computational Techniques for Fluid Dynamics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 6th ed.; Elsevier: Oxford, UK, 2005. [Google Scholar]
- Toparlar, Y.; Blocken, B.; Maiheu, B.; van Heijst, G.J.F. A review on the CFD analysis of urban microclimate. Renew. Sustain. Energy Rev. 2017, 80, 1613–1640. [Google Scholar] [CrossRef]
- Kuang, S.; Zhou, M.; Yu, A. CFD-DEM modelling and simulation of pneumatic conveying: A review. Powder Technol. 2020, 365, 186–207. [Google Scholar] [CrossRef]
- Wang, J. Continuum theory for dense gas-solid flow: A state-of-the-art review. Chem. Eng. Sci. 2020, 215, 115428. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estelle, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Siavashi, M.; Taylor, R.A.; Niazmand, H.; et al. Recent advances in modeling and simulation of nanofluid flows—Part I: Fundamentals and theory. Phys. Rep. 2019, 790, 1–48. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estelle, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Taylor, R.A.; Abu-Nada, E.; Rashidi, S.; et al. Recent advances in modeling and simulation of nanofluid flows—Part II: Applications. Phys. Rep. 2019, 791, 1–59. [Google Scholar] [CrossRef]
- Johnstone, C.P.; Gudel, M.; Lammer, H.; Kislyakova, K.G. Upper atmospheres of terrestrial planets: Carbon dioxide cooling and the earth’s thermospheric evolution. Astron. Astrophys. 2018, 617, A107. [Google Scholar] [CrossRef]
- Yasui, K.; Kozuka, T.; Tuziuti, T.; Towata, A.; Iida, Y.; King, J.; Macey, P. FEM calculation of an acoustic field in a sonochemical reactor. Ultrason. Sonochem. 2007, 14, 605–614. [Google Scholar] [CrossRef]
- Zulkifli, N.; Hashim, N.; Harith, H.H.; Shukery, M.F.M. Finite element modelling for fruit stress analysis—A review. Trends Food Sci. Technol. 2020, 97, 29–37. [Google Scholar] [CrossRef]
- Marinkovic, D.; Zehn, M. Survey of finite element method–based real-time simulations. Appl. Sci. 2019, 9, 2775. [Google Scholar] [CrossRef]
- Graca, A.; Vincze, G. A short review on the finite element method for asymmetric rolling processes. Metals 2021, 11, 762. [Google Scholar] [CrossRef]
- Silva, R.P.; Rolim, M.M.; Gomes, I.F.; Pedrosa, E.M.R.; Tavares, U.E.; Santos, A.N. Numerical modeling of soil compaction in a sugarcane crop using the finite element method. Soil Tillage Res. 2018, 181, 1–10. [Google Scholar] [CrossRef]
- Wang, B.; Cai, Y.; Li, Z.; Ding, C.; Yang, T.; Cui, X. Stochastic stable node-based smoothed finite element method for uncertainty and reliability analysis of thermo-mechanical problems. Eng. Anal. Bound. Elem. 2020, 114, 23–44. [Google Scholar] [CrossRef]
- Ming, W.; Zhang, S.; Zhang, G.; Du, J.; Ma, J.; He, W.; Cao, C.; Liu, K. Progress in modeling of electrical discharge machining process. Intern. J. Heat Mass Transf. 2022, 187, 122563. [Google Scholar] [CrossRef]
- Marques, E.S.V.; Silva, F.J.G.; Pereira, A.B. Comparison of finite element methods in fusion welding processes a review. Metals 2020, 10, 75. [Google Scholar] [CrossRef]
- Shen, B.; Grilli, F.; Coombs, T. Review of the AC loss computation for HTS using H formulation. Supercond. Sci. Technol. 2020, 33, 033002. [Google Scholar] [CrossRef]
- Marrink, S.J.; Corradi, V.; Souza, P.C.T.; Ingolfsson, H.I.; Tieleman, D.P.; Sansom, M.S.P. Computational modeling of realistic cell membranes. Chem. Rev. 2019, 119, 6184–6226. [Google Scholar] [CrossRef]
- Hollingsworth, S.A.; Dror, R.O. Molecular dynamics simulation for all. Neuron 2018, 99, 1129–1143. [Google Scholar] [CrossRef]
- Bedrov, D.; Piquemal, J.-P.; Borodin, O.; MacKerell, A.D., Jr.; Roux, B.; Schroder, C. Molecular dynamics simulations of ionic liquids and electrolytes using polarizable force fields. Chem. Rev. 2019, 119, 7940–7995. [Google Scholar] [CrossRef]
- Nelson, T.R.; White, A.J.; Bjorgaard, J.A.; Sifain, A.E.; Zhang, Y.; Nebgen, B.; Fernandez-Alberti, S.; Mozyrsky, D.; Roitberg, A.E.; Tretiak, S. Non-adiabatic excited-state molecular dunamics: Theory and applications for modeling photophysics in extended molecular materials. Chem. Rev. 2020, 120, 2215–2287. [Google Scholar] [CrossRef]
- Xing, H.; Hu, P.; Li, S.; Zuo, Y.; Han, J.; Hua, X.; Wang, K.; Yang, F.; Feng, P.; Chang, T. Adsorption and diffusion of oxygen on metal surfaces studied by first-principle study: A review. J. Mater. Sci. Technol. 2021, 62, 180–194. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
- Chen, B.W.J.; Xu, L.; Mavrikakis, M. Computational methods in heterogeneous catalysis. Chem. Rev. 2021, 121, 1007–1048. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, Y.; Grabowski, B.; Kormann, F. Ab initio phase stabilities and mechanical properties of multicomponent alloys: A comprehensive review for high entropy alloys and compositionally complex alloys. Mater. Charact. 2019, 147, 464–511. [Google Scholar] [CrossRef]
- Zhu, B.; Cheng, B.; Zhang, L.; Yu, J. Review on DFT calculation of s-triazine-based carbon nitride. Carbon Energy 2019, 1, 32–56. [Google Scholar] [CrossRef]
- Villa, A.; Barbieri, L.; Gondola, M.; Leon-Garzon, A.R.; Malgesini, R. A PDE-based partial discharge simulator. J. Comp. Phys. 2017, 345, 687–705. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, L.; Shen, Z.; LI, Z.; Menshov, I. A reduced model for compressible viscous heat-conducting multicomponent flows. Comp. Fluids 2022, 236, 105311. [Google Scholar] [CrossRef]
- Ni, X.; Weng, C.; Hu, H.; Bai, Q. Numerical analysis of heat flow in wall of detonation tube during pulse detonation cycle. Appl. Therm. Eng. 2021, 187, 116528. [Google Scholar] [CrossRef]
- Jourdon, A.; May, D.A. An efficient partial-differential-equation-based method to compute pressure boundary conditions in regional geodynamic models. Solid Earth 2022, 13, 1107–1125. [Google Scholar] [CrossRef]
- Sgura, I.; Lawless, A.S.; Bozzini, B. Parameter estimation for a morphochemical reaction-diffusion model of electrochemical pattern formation. Inv. Prob. Sci. Eng. 2019, 27, 618–647. [Google Scholar] [CrossRef]
- Li, R.-Q.; Song, Y.-R.; Jiang, G.-P. Prediction of epidemics dynamics on networks with partial differential equations: A case study for COVID-19 China. Chin. Phys. B 2021, 30, 120202. [Google Scholar] [CrossRef]
- Rosa, R.; Ferreira, F.V.; Saravia, A.P.K.; Rocco, S.A.; Sforca, M.L.; Gouveia, R.F.; Lona, L.M.F. A combined computational and experimental study on the polymerization of ε-caprolactone. Ind. Eng. Chem. Res. 2018, 57, 13387–13395. [Google Scholar] [CrossRef]
- Giessmann, R.T.; Krausch, N.; Kaspar, F.; Bournazou, M.N.C.; Wagner, A.; Neubauer, P.; Gimpel, M. Dynamic modelling of phosphorolytic cleavage catalyzed by pyrimidine-nucleoside phosphorylase. Processes 2019, 7, 380. [Google Scholar] [CrossRef]
- Coman, P.T.; Rayman, S.; White, R.E. A lumped model of venting during thermal runaway in a cylindrical Lithium Cobalt Oxide lithium-ion cell. J. Power Sources 2016, 307, 56–62. [Google Scholar] [CrossRef]
- Roueff, E.; Bourlot, J.L. Sustained oscillations in intersteller chemistry models. Astron. Astrophys. 2020, 643, A121. [Google Scholar] [CrossRef]
- Rajasingh, H.; Oyehaug, L.; Vague, D.I.; Omholt, S.W. Carotenoid dynamics in Atlantic salmon. BMC Biol. 2006, 4, 10. [Google Scholar] [CrossRef]
- Gao, S.; Xiang, C.; Qin, K.; Sun, C. Mathematical modeling reveals the role of hypoxia in the promotion of human mesenchymal stem cell long-term expansion. Stem Cells Int. 2018, 2018, 9283432. [Google Scholar] [CrossRef]
- Muto, D.; Daimon, Y.; Negishi, H.; Shimizu, T. Wall modeling of turbulent methane/oxygen reacting flows for predicting heat transfer. Int. J. Heat Fluid Flow 2021, 87, 108755. [Google Scholar] [CrossRef]
- Huang, Y.; Seinfeld, J.H. A neural network-assisted Euler integrator for stiff kinetics in atmospheric chemistry. Environ. Sci. Technol. 2022, 56, 4676–4685. [Google Scholar] [CrossRef]
- Ferrell, J.E.; Tsai, T.Y.-C.; Yang, Q. Modeling the cell cycle: Why do certain circuits oscillate? Cell 2011, 144, 874–885. [Google Scholar] [CrossRef]
- Cassani, A.; Monteverde, A.; Piumetti, M. Belousov-Zhabotinsky type reactions: The non-linear behavior of chemical systems. J. Math. Chem. 2021, 59, 792–826. [Google Scholar] [CrossRef]
- Guzev, E.; Bunimovich-Mendrazitsky, S.; Firer, M.A. Differential response to cytotoxic drugs explains the dynamics of leukemic cell death: Insights from experiments and mathematical modeling. Symmetry 2022, 14, 1269. [Google Scholar] [CrossRef]
- Weber, L.; Raymond, W.; Munsky, B. Identification of gene regulation models from single-cell data. Phys. Biol. 2018, 15, 055001. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Cleary, T.; Wang, D.; Li, G.; Rahn, C.; Wang, D.; Rajamani, R.; Fathy, H.K. Online state estimation for a physics-based Lithium-Sulfur battery model. J. Power Sources 2021, 489, 229495. [Google Scholar] [CrossRef]
- Ghareghashi, A.; Shahraki, F.; Razzaghi, K.; Ghader, S.; Torangi, M.A. Enhancement of gasoline selectivity in combined reactor system consisting of steam reforming of methane and Fischer-Tropsch synthesis. Korean J. Chem. Eng. 2017, 34, 87–99. [Google Scholar] [CrossRef]
- Baba, I.A.; Yusuf, A.; Nisar, K.S.; Abdel-Aty, A.-H.; Nofal, T.A. Mathematical model to assess the imposition of lockdown during COVID-19 pandemic. Results Phys. 2021, 20, 103716. [Google Scholar] [CrossRef]
- Stadter, P.; Schalte, Y.; Schmiester, L.; Hasenauer, J.; Stapor, P.L. Benchmarking of numerical integration methods for ODE models of biological systems. Sci. Rep. 2021, 11, 2696. [Google Scholar] [CrossRef]
- Ashraf, C.; Pfaendtner, J. Assessing the performance of various stochastic optimization methods on chemical kinetic modeling of combustion. Ind. Eng. Chem. Res. 2020, 59, 19212–19225. [Google Scholar] [CrossRef]
- Murshed, A.K.M.M.; Huang, B.; Nandakumar, K. Control relevant modeling of planer solid oxide fuel cell system. J. Power Sources 2007, 163, 830–845. [Google Scholar] [CrossRef]
- Cumsille, P.; Godoy, M.; Gerdtzen, Z.P.; Conca, C. Parameter estimation and mathematical modeling for the quantitative description of therapy failure due to drug resistance in gastrointestinal stromal tumor metastasis to the liver. PLoS ONE 2019, 14, e0217332. [Google Scholar] [CrossRef]
- Mani, K.; Zournas, A.; Dismukes, G.C. Bridging the gap between Kok-type and kinetic models of photosynthetic electron transport within Photosystem II. Photosyn. Res. 2022, 151, 83–102. [Google Scholar] [CrossRef]
- Morimoto, K.; Nakanishi, S.; Mukouyama, Y. An ordinary differential equation model for simulating secondary battery reactions. Electrochem. Commun. 2021, 126, 107011. [Google Scholar] [CrossRef]
- Weaver, J.J.A.; Shoemaker, J.E. Mathematical modeling of RNA virus sensing pathways reveals paracrine signaling as the primary factor regulating excessive cytokine production. Processes 2020, 8, 719. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; Guo, Q.; Ramadass, P.; White, R.E. Review of models for predicting the cycling performance of lithium ion batteries. J. Power Sources 2006, 156, 620–628. [Google Scholar] [CrossRef]
- Marasco, A.; Ferrara, L.; Romano, A. Modeling eutrophic lakes: From mass balance laws to ordinary differential equations. Int. J. Geom. Meth. Mod. Phys. 2017, 14, 1750151. [Google Scholar] [CrossRef]
- Matveev, S.A.; Stadnichuk, V.I.; Tyrtyshnikov, E.E.; Smirnov, A.P.; Ampilogova, N.V.; Brilliantov, N.V. Anderson acceleration method of finding steady-state particle size distribution for a wide class of aggregation-fragmentation models. Comp. Phys. Commun. 2018, 224, 154–163. [Google Scholar] [CrossRef]
- Hass, H.; Loos, C.; Raimundez-Alvarez, E.; Timmer, J.; Hasenauer, J.; Kreutz, C. Benchmark problems for dynamic modeling of intercellular processes. Bioinformatics 2019, 35, 3073–3082. [Google Scholar] [CrossRef]
- Remigio, A.S. In silico simulation of the effect of hypoxia on MCF-7 cell cycle kinetics under fractionated radiotherapy. J. Biol. Phys. 2021, 47, 301–321. [Google Scholar] [CrossRef]
- Menon, M.; Ponta, F.L. Dynamic aeroelastic behavior of wind turbine rotors in rapid pitch-control actions. Renew. Energy 2017, 107, 327–339. [Google Scholar] [CrossRef]
- Mukouyama, Y.; Nakanishi, S. An ordinary differential equation model of simulating local-pH change at electrochemical interfaces. Front. Energy Res. 2020, 8, 582284. [Google Scholar] [CrossRef]
- Singh, A.; Marcoline, F.V.; Veshaguri, S.; Kao, A.W.; Bruchez, M.; Mindell, J.A.; Stamou, D.; Grabe, M. Protons in small spaces: Discrete simulations of vesicle acidification. PLoS Comput. Biol. 2019, 15, e1007539. [Google Scholar] [CrossRef] [Green Version]
- Bae, H.; Go, Y.-H.; Kwon, T.; Sung, B.J.; Cha, H.-J. A theoretical model for the cell cycle and drug induced cell cycle arrest of FUCCI systems with cell-to-cell variation during mitosis. Pharm. Res. 2019, 36, 57. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Jia, M.; Chang, Y.; Li, Y. An improved approach towards more robust deep learning models for chemical kinetics. Combust. Flame 2022, 238, 111934. [Google Scholar] [CrossRef]
- Gutoeska, K.; Kogut, D.; Kardynska, M.; Formanowicz, P.; Smieja, J.; Puszynski, K. Petri nets and ODEs as complementary methods for comprehensive analysis on an example of the ATM-p53-NF−κB signaling pathways. Sci. Rep. 2022, 12, 1135. [Google Scholar] [CrossRef] [PubMed]
- Pacella, M.S.; Mardanlou, V.; Agarwal, S.; Patel, A.; Jelezniakov, E.; Mohammed, A.M.; Franco, E.; Shulman, R. Characterizing the length-dependence of DNA nanotube end-to-end joining rates. Mol. Syst. Des. Eng. 2020, 5, 544–559. [Google Scholar] [CrossRef]
- Talkington, A.; Dantoin, C.; Durrett, R. Ordinary differential equation models for adoptive immunotherapy. Bull. Math. Biol. 2018, 80, 1059–1083. [Google Scholar] [CrossRef]
- Spector, A.A.; Yuan, D.; Somers, S.; Grayson, W.L. Biomechanics of stem cells. J. Phys. Conf. Ser. 2018, 991, 012074. [Google Scholar] [CrossRef]
- Sharpe, S.; Dobrovolny, H.M. Predicting the effectiveness of chemotherapy using stochastic ODE models of tumor growth. Commun. Nonlinear Sci. Numer. Simulat. 2021, 101, 105883. [Google Scholar] [CrossRef]
- Yasui, K. Alternative model of single-bubble sonoluminescence. Phys. Rev. E 1997, 56, 6750–6760. [Google Scholar] [CrossRef]
- Yasui, K. Variation of liquid temperature at bubble wall near the sonoluminescence threshold. J. Phys. Soc. Jpn. 1996, 65, 2830–2840. [Google Scholar] [CrossRef]
- Yasui, K. Effect of liquid temperature on sonoluminescence. Phys. Rev. E 2001, 64, 016310. [Google Scholar] [CrossRef]
- Yasui, K.; Tuziuti, T.; Sivakumar, M.; Iida, Y. Theoretical study of single-bubble sonochemistry. J. Chem. Phys. 2005, 122, 224706. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K.; Tuziuti, T.; Iida, Y. Optimum bubble temperature for the sonochemical production of oxidants. Ultrasonics 2004, 42, 579–584. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K.; Iida, Y.; Tuziuti, T.; Kozuka, T.; Towata, A. Strongly interacting bubbles under an ultrasonic horn. Phys. Rev. E 2008, 77, 016609. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K.; Tuziuti, T.; Lee, J.; Kozuka, T.; Towata, A.; Iida, Y. Numerical simulations of acoustic cavitation noise with the temporal fluctuation in the number of bubbles. Ultrason. Sonochem. 2010, 17, 460–472. [Google Scholar] [CrossRef]
- Yasui, K.; Lee, J.; Tuziuti, T.; Towata, A.; Kozuka, T.; Iida, Y. Influence of the bubble-bubble interaction on destruction of encapsulated microbubbles under ultrasound. J. Acoust. Soc. Am. 2009, 126, 973–982. [Google Scholar] [CrossRef]
- Yasui, K.; Tuziuti, T.; Kanematsu, W. Extreme conditions in a dissolving air nanobubble. Phys. Rev. E 2016, 94, 013106. [Google Scholar] [CrossRef]
- Toegel, R.; Gompf, B.; Pecha, R.; Lohse, D. Does water vapor prevent upscaling sonoluminescence? Phys. Rev. Lett. 2000, 85, 3165–3168. [Google Scholar] [CrossRef]
- Toegel, R.; Lohse, D. Phase diagrams for sonoluminescing bubbles: A comparison between experiment and theory. J. Chem. Phys. 2003, 118, 1863–1875. [Google Scholar] [CrossRef]
- Storey, B.D.; Szeri, A.J. A reduced model of cavitation physics for use in sonochemistry. Proc. R. Soc. Lond. A 2001, 457, 1685–1700. [Google Scholar] [CrossRef]
- Merouani, S.; Hamdaoui, O.; Rezgui, Y.; Guemini, M. Sensitivity of free radicals production in acoustically driven bubble to the ultrasonic frequency and nature of dissolved gases. Ultrason. Sonochem. 2015, 22, 41–50. [Google Scholar] [CrossRef]
- Yasui, K.; Kato, K. Dipole-dipole interaction model for oriented attachment of BaTiO3 nanocrystals: A route to mesocrystal formation. J. Phys. Chem. C 2012, 116, 319–324. [Google Scholar] [CrossRef]
- Yasui, K.; Kato, K. Oriented attachment of cubic or spherical BaTiO3 nanocrystals by van der Waals torque. J. Phys. Chem. C 2015, 119, 24597–24605. [Google Scholar] [CrossRef]
- Yasui, K.; Itasaka, H.; Mimura, K.; Kato, K. Dynamic dielectric-response model of flexoelectric polarization from kHz to MHz range in an ordered assembly of BaTiO3 nanocubes. J. Phys. Condens. Matter 2020, 32, 495301. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K.; Itasaka, H.; Mimura, K.; Kato, K. Coexistence of flexo- and ferro-electric effects in an ordered assembly of BaTiO3 nanocubes. Nanomaterials 2022, 12, 188. [Google Scholar] [CrossRef]
- Yasui, K.; Hamamoto, K. Importance of dislocations in ultrasound-assisted sintering of silver nanoparticles. J. Appl. Phys. 2021, 130, 194901. [Google Scholar] [CrossRef]
- Yasui, K.; Hamamoto, K. Comparison between cold sintering and dry pressing of CaCO3 at room temperature by numerical simulations. AIP Adv. 2022, 12, 045304. [Google Scholar] [CrossRef]
- Yasui, K.; Izu, N. Effect of evaporation and condensation on a thermoacoustic engine: A Lagrangian simulation approach. J. Acoust. Soc. Am. 2017, 141, 4398–4407, Erratum in J. Acoust. Soc. Am. 2020, 147, 267–272. [Google Scholar] [CrossRef]
- Yasui, K. Relationship of Lagrangian microscopic energy efficiency of a gas parcel in a thermoacoustic engine to macroscopic one. AIP Adv. 2021, 11, 045106. [Google Scholar] [CrossRef]
- Yasui, K.; Tuziuti, T.; Kato, K. Numerical simulations of sonochemical production of BaTiO3 nanoparticles. Ultrason. Sonochem. 2011, 18, 1211–1217. [Google Scholar] [CrossRef]
- Yasui, K.; Kato, K. Numerical simulations of sonochemical production and oriented aggregation of BaTiO3 nanocrystals. Ultrason. Sonochem. 2017, 35, 673–680. [Google Scholar] [CrossRef]
- Schiesser, W.E. Differential Equation Analysis in Biomedical Science and Engineering; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Yasui, K. Acoustic Cavitation and Bubble Dynamics; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Li, Y.; Wik, T.; Xie, C.; Huang, Y.; Xiong, B.; Tang, J.; Zou, C. Control-oriented modeling of all-solid-state batteries using physics-based equivalent circuits. IEEE Trans. Transp. Electrif. 2022, 8, 2080–2092. [Google Scholar] [CrossRef]
- Cen, Z.; Kubiak, P. Lithium-ion battery SOC/SOH adaptive estimation via simplified single particle model. Int. J. Energy Res. 2020, 44, 12444–12459. [Google Scholar] [CrossRef]
- Zhong, J.; Liang, S.; Zeng, C.; Yuan, Y.; Xiong, Q. Approximate finite-dimensional ODE temperature model for microwave heating. Nonlinear Anal. Model. Control 2016, 21, 498–514. [Google Scholar] [CrossRef]
- Ranade, R.; Hill, C.; Pathak, J. DiscretizationNet: A machine-learning based solver for Navier-Stokes equations using finite volume discretization. Comput. Methods Appl. Mech. Engrg. 2021, 378, 113722. [Google Scholar] [CrossRef]
- Nakamura, Y.; Shiratori, S.; Takagi, R.; Sutoh, M.; Sugihara, I.; Nagano, H.; Shimano, K. Physics-informed neural network applied to surface-tension-driven liquid film flows. Int. J. Numer. Meth. Fluids 2022, 94, 1359–1378. [Google Scholar] [CrossRef]
- Barber, B.P.; Putterman, S.J. Observation of synchronous picosecond sonoluminescence. Nature 1991, 352, 318–320. [Google Scholar] [CrossRef]
- Gaitan, D.F.; Crum, L.A. Observation of sonoluminescence from a single, stable cavitation bubble in a water glycerin mixture. In Frontiers of Nonlinear Acoustics, Proceedings of the 12th ISNA, Austic, TX, USA, 27–31 August 1990; Hamilton, M.F., Blackstock, D.T., Eds.; Elsevier: London, UK, 1990; pp. 459–463. [Google Scholar]
- Yosioka, K.; Omura, A. The light emission from a single bubble driven by ultrasound and the spectra of acoustic oscillation. Proc. Annu. Meet. Acoust. Soc. Jpn. 1962, 1962, 125–126. (In Japanese) [Google Scholar]
- Young, F.R. Sonoluminescence; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Wu, C.C.; Roberts, P.H. Shock-wave propagation in a sonoluminescing gas bubble. Phys. Rev. Lett. 1993, 70, 3424–3427. [Google Scholar] [CrossRef]
- Kondic, L.; Gersten, J.I.; Yuan, C. Theoretical studies of sonoluminescence radiation: Radiative transfer and parametric dependence. Phys. Rev. E 1995, 52, 4976–4990. [Google Scholar] [CrossRef]
- Moss, W.C.; Clarke, D.B.; White, J.W.; Young, D.A. Hydrodynamic simulations of bubble collapse and picosecond sonoluminescence. Phys. Fluids 1994, 6, 2979–2985. [Google Scholar] [CrossRef]
- Gompf, B.; Gunther, R.; Nick, G.; Pecha, R.; Eisenmenger, W. Resolving sonoluminescence pulse width with time-correlated single photon counting. Phys. Rev. Lett. 1997, 79, 1405–1408. [Google Scholar] [CrossRef]
- An, Y. Mechanism of single-bubble sonoluminescence. Phys. Rev. E 2006, 74, 026304. [Google Scholar] [CrossRef]
- Vuong, V.Q.; Szeri, A.J.; Young, D.A. Shock formation within sonoluminescence bubbles. Phys. Fluids 1999, 11, 10–17. [Google Scholar] [CrossRef]
- Didenko, Y.T.; Suslick, K.S. The energy efficiency of formation of photons, radicals and ions during single-bubble cavitation. Nature 2002, 418, 394–397. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K. Multibubble sonoluminescence from a theoretical perspective. Molecules 2021, 26, 4624. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K. Numerical simulations for sonochemistry. Ultrason. Sonochem. 2021, 78, 105728. [Google Scholar] [CrossRef] [PubMed]
- Brenner, M.P.; Hilgenfeldt, S.; Lohse, D. Single-bubble sonoluminescence. Rev. Mod. Phys. 2002, 74, 425–484. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, W.; Wang, Y.; Li, L.; Yao, F.; Miao, L.; Zhao, W.; Kong, X.; Feng, Q.; Hu, D. Formation mechanisms and electrical properties of perovskite mesocrystals. Ceram. Intern. 2021, 47, 1479–1512. [Google Scholar] [CrossRef]
- Sturm, E.V.; Colfen, H. Mesocrystals: Past, presence, future. Crystals 2017, 7, 207. [Google Scholar] [CrossRef]
- Sun, S.; Yu, X.; Yang, Q.; Yang, Z.; Liang, S. Mesocrystals for photocatalysis: A comprehensive review on synthesis engineering and functional modifications. Nanoscale Adv. 2019, 1, 34–63. [Google Scholar] [CrossRef]
- Zhang, B.; Cao, S.; Du, M.; Ye, X.; Wang, Y.; Ye, J. Titanium dioxide (TiO2) mesocrystals: Synthesis, growth mechanisms and photocatalytic properties. Catalysts 2019, 9, 91. [Google Scholar] [CrossRef] [Green Version]
- Balankura, T.; Yan, T.; Jahanmahin, O.; Narukatpichai, J.; Ng, A.; Fichthorn, K.A. Oriented attachment mechanism of triangular Ag nanoplates: A molecular dynamics study. Nanoscale Adv. 2020, 2, 2265–2270. [Google Scholar] [CrossRef]
- Sushko, M.L. Understanding the driving forces for crystal growth by oriented attachment through theory and simulations. J. Mater. Res. 2019, 34, 2914–2927. [Google Scholar] [CrossRef]
- Boles, M.A.; Engel, M.; Talapin, D.V. Self-assembly of colloidal nanocrystals: From intricate structures to functional materials. Chem. Rev. 2016, 116, 11220–11289. [Google Scholar] [CrossRef]
- Mimura, K.; Kato, K. Enhanced dielectric properties of BaTiO3 nanocube assembled film in metal-insulator-metal capacitor structure. Appl. Phys. Express 2014, 7, 061501. [Google Scholar] [CrossRef]
- Ma, Q.; Kato, K. Crystallographic fusion behavior and interface evolution of mono-layer BaTiO3 nanocube arrangement. CrstEngComm 2016, 18, 1543–1549. [Google Scholar] [CrossRef]
- Esquivel-Sirvent, R.; Schatz, G.C. Van der Waals torque coupling between slabs composed of planar arrays of nanoparticles. J. Phys. Chem. C 2013, 117, 5492–5496. [Google Scholar] [CrossRef]
- Somers, D.A.T.; Garrett, J.L.; Palm, K.J.; Munday, J.N. Measurement of the Casimir torque. Nature 2018, 564, 386–389. [Google Scholar] [CrossRef]
- Xu, Z.; Li, T. Detecting Casimir torque with an optically levitated nanorod. Phys. Rev. A 2017, 96, 033843. [Google Scholar] [CrossRef]
- Yasui, K.; Kato, K. Influence of adsorbate-induced charge screening, depolarization factor, mobile carrier concentration, and defect-induced microstrain on the size effect of a BaTiO3 nanoparticle. J. Phys. Chem. C 2013, 117, 19632–19644. [Google Scholar] [CrossRef]
- Raju, M.; van Duin, A.C.T.; Fichthorn, K.A. Mechanisms of oriented attachment of TiO2 nanocrystals in vacuum and humid environments: Reactive molecular dynamics. Nano Lett. 2014, 14, 1836–1842. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Huang, W.; Zhang, S. Flexoelectric nano-generator: Materials, structures and devices. Nano Energy 2013, 2, 1079–1092. [Google Scholar] [CrossRef]
- Yudin, P.V.; Tagantsev, A.K. Fundamentals of flexoelectricity in solids. Nanotechnology 2013, 24, 432001. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Gu, Y.; Zhang, S.; Chen, L.-Q. Flexoelectricity in solids: Progress, challenges, and perspectives. Prog. Mater. Sci. 2019, 106, 100570. [Google Scholar] [CrossRef]
- Ma, W.; Cross, L.E. Flexoelectricity of barium titanate. Appl. Phys. Lett. 2006, 88, 232902. [Google Scholar] [CrossRef]
- Zhuang, X.; Nguyen, B.H.; Nanthakumar, S.S.; Tran, T.Q.; Alajlan, N.; Rabczuk, T. Computational modeling of flexoelectricity—A review. Energies 2020, 13, 1326. [Google Scholar] [CrossRef]
- Morozovska, A.N.; Eliseev, E.A.; Scherbakov, C.M.; Vysochanskii, Y.M. Influence of elastic strain gradient on the upper limit of flexocoupling strength, spatially modulated phases, and soft phonon dispersion in ferroics. Phys. Rev. B 2016, 94, 174112. [Google Scholar] [CrossRef]
- Morozovska, A.N.; Vysochanskii, Y.M.; Varenyk, O.V.; Silibin, M.V.; Kalinin, S.V.; Eliseev, E.A. Flexocoupling impact on the generalized susceptibility and soft phonon modes in the ordered phase of ferroics. Phys. Rev. B 2015, 92, 094308. [Google Scholar] [CrossRef]
- Ahluwalia, R.; Tagantsev, A.K.; Yudin, P.; Setter, N.; Ng, N.; Srolovitz, D.J. Influence of flexoelectric coupling on domain patterns in ferroelectrics. Phys. Rev. B 2014, 89, 174105. [Google Scholar] [CrossRef]
- Sahin, E.; Dost, S. A strain-gradients theory of elastic dielectrics with spatial dispersion. Int. J. Eng. Sci. 1988, 26, 1231–1245. [Google Scholar] [CrossRef]
- Abdollahi, A.; Peco, C.; Millan, D.; Arroyo, M.; Arias, I. Computational evaluation of the flexoelectric effect in dielectric solids. J. Appl. Phys. 2014, 116, 093502. [Google Scholar] [CrossRef] [Green Version]
- Tagantsev, A.K. Piezoelectricity and flexoelectricity in crystalline dielectrics. Phys. Rev. B 1986, 34, 5883–5889. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K.; Mimura, K.; Izu, N.; Kato, K. Numerical calculations of temperature dependence of dielectric constant for an ordered assembly of BaTiO3 nanocubes with small tilt angles. Jpn. J. Appl. Phys. 2018, 57, 031501. [Google Scholar] [CrossRef]
- Tsurumi, T.; Li, J.; Hoshina, T.; Kakemoto, H.; Nakada, M.; Akedo, J. Ultrawide range dielectric spectroscopy of BaTiO3-based perovskite dielectrics. Appl. Phys. Lett. 2007, 91, 182905. [Google Scholar] [CrossRef]
- Teranishi, T.; Hoshina, T.; Tsurumi, T. Wide range dielectric spectroscopy on perovskite dielectrics. Mater. Sci. Eng. B 2009, 161, 55–60. [Google Scholar] [CrossRef]
- Guo, J.; Guo, H.; Baker, A.L.; Lanagan, M.T.; Kupp, E.R.; Messing, G.L.; Randall, C.A. Cold sintering: A paradigm shift for processing and integration of ceramics. Angew. Chem. Int. Ed. 2016, 55, 11457–11461. [Google Scholar] [CrossRef]
- Galotta, A.; Sglavo, V.M. The cold sintering process: A review on processing features, densification mechanisms and perspectives. J. Eur. Ceram. Soc. 2021, 41, 1–17. [Google Scholar] [CrossRef]
- Bouville, F.; Studart, A.R. Geologically-inspired strong bulk ceramics made with water at room temperature. Nat. Commun. 2017, 8, 14655. [Google Scholar] [CrossRef]
- Vakifahmetoglu, C.; Karacasulu, L. Cold sintering of ceramics and glasses: A review. Curr. Opin. Solid State Mat. Sci. 2020, 24, 100807. [Google Scholar] [CrossRef]
- Li, H.; Zhong, J.; Shen, J.; Liu, J.; Li, B.; Tang, X.; Pan, J.; Xu, Z.; Lu, J.; Li, Y.Y. Water-assisted sintering of silica: Densification mechanisms and their possible implications in biomineralization. J. Am. Ceram. Soc. 2022, 105, 2945–2954. [Google Scholar] [CrossRef]
- Yamaguchi, Y. The development of low-temperature sintering techniques for functional ceramic devices using chemical reactions. J. Ceram. Soc. Jpn. 2020, 128, 747–755. [Google Scholar] [CrossRef]
- Wang, F.; Nie, N.; He, H.; Tang, Z.; Chen, Z.; Zhu, W. Ultrasonic-assisted sintering of silver nanoparticles for flexible electronics. J. Phys. Chem. C 2017, 121, 28515–28519. [Google Scholar] [CrossRef]
- Liu, Z.; Ge, Y.; Zhao, D.; Lou, Y.; Liu, Y.; Wu, Y.; Yu, P.; Yu, C. Ultrasonic assisted sintering using heat converted from mechanical energy. Metals 2020, 10, 971. [Google Scholar] [CrossRef]
- Chen, P.; Liao, W.B.; Liu, L.H.; Luo, F.; Wu, X.Y.; Li, P.J.; Yang, C.; Yan, M.; Liu, Y.; Zhang, L.C.; et al. Ultrafast consolidation of bulk nanocrystalline titanium alloy through ultrasonic vibration. Sci. Rep. 2018, 8, 801. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Cui, H.; Qin, Q.H. Influence of ultrasonic vibration on the plasticity of metals during compression process. J. Mater. Process. Technol. 2018, 251, 146–159. [Google Scholar] [CrossRef]
- Wang, X.; Wang, C.; Liu, Y.; Liu, C.; Wang, Z.; Guo, B.; Shan, D. An energy based modeling for the acoustic softening effect on the Hall-Petch behavior of pure titanium in ultrasonic vibration assisted micro-tension. Int. J. Plast. 2021, 136, 102879. [Google Scholar] [CrossRef]
- Langenecker, B. Ultrasonic treatment of specimens in the electron microscope. Rev. Sci. Instrum. 1966, 37, 103–106. [Google Scholar] [CrossRef]
- Westmacott, K.H.; Langenecker, B. Dislocation structure in ultrasonically irradiated aluminum. Phys. Rev. Lett. 1965, 14, 221–222. [Google Scholar] [CrossRef]
- Kraft, T.; Riedel, H. Numerical simulation of solid state sintering; model and application. J. Eur. Ceram. Soc. 2004, 24, 345–361. [Google Scholar] [CrossRef]
- Buzolin, R.H.; Lasnik, M.; Krumphals, A.; Poletti, M.C. A dislocation-based model for the microstructure evolution and the flow stress of a Ti5553 alloy. Int. J. Plast. 2021, 136, 102862. [Google Scholar] [CrossRef]
- Lindgren, L.-E.; Domkin, K.; Hansson, S. Dislocations, vacancies and solute diffusion in physical based plasticity model for AISI 316L. Mech. Mater. 2008, 40, 907–919. [Google Scholar] [CrossRef]
- Yang, H.; Sun, B.; Zhu, Y.; Yin, D.; Yao, J. Critical role of surficial activity in the sintering process of TiO2 nanoparticels by molecular dynamics simulation. Powder Technol. 2022, 398, 117071. [Google Scholar] [CrossRef]
- Swift, G.W. Thermoacoustics: A Unifying Perspective for Some Engines and Refrigerators, 2nd ed.; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Yasui, K.; Kozuka, T.; Yasuoka, M.; Kato, K. Revisiting the difference between traveling-wave and standing-wave thermoacoustic engines—A simple analytical model for the standing-wave one. J. Korean Phys. Soc. 2015, 67, 1755–1766. [Google Scholar] [CrossRef]
- Yang, Y.; Chi, J.; Wu, Z.; Yang, R.; Xu, J.; Zhang, L.; Hu, J.; Luo, E. A heat-driven combined cooling and heating system based on thermoacoustic technology. Appl. Phys. Lett. 2022, 120, 223902. [Google Scholar] [CrossRef]
- Yang, R.; Wang, Y.; Luo, J.; Tan, J.; Jin, T. Performance comparison of looped thermoacoustic electric generators with various thermoacoustic stages. Int. J. Energy Res. 2020, 44, 1103–1112. [Google Scholar] [CrossRef]
- Tsuda, K.; Ueda, Y. Abrupt reduction of the critical temperature difference of a thermoacoustic engine by adding water. AIP Adv. 2015, 5, 097173. [Google Scholar] [CrossRef]
- Meir, A.; Offner, A.; Ramon, G.Z. Low-temperature energy conversion using a phase-change acoustic heat engine. Appl. Energy 2018, 231, 372–379. [Google Scholar] [CrossRef]
- Kawashima, Y.; Sakamoto, S.; Onishi, R.; Hiramatsu, K.; Watanabe, Y. Energy conversion in the thermoacoustic system using a stack wetted with water. Jpn. J. Appl. Phys. 2021, 60, SDDD05. [Google Scholar] [CrossRef]
- Raspet, R.; Hickey, C.J.; Sabatier, J.M. The effect of evaporation-condensation on sound propagation in cylindrical tubes using the low reduced frequency approximation. J. Acoust. Soc. Am. 1999, 105, 65–73. [Google Scholar] [CrossRef]
- Raspet, R.; Slaton, W.V.; Hickey, C.J.; Hiller, R.A. Theory of inert gas-condensing vapor thermoacoustics: Propagation equation. J. Acoust. Soc. Am. 2002, 112, 1414–1422. [Google Scholar] [CrossRef]
- An, Y.; Ying, C.F. Model of single bubble sonoluminescence. Phys. Rev. E 2005, 71, 036308. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasui, K. Merits and Demerits of ODE Modeling of Physicochemical Systems for Numerical Simulations. Molecules 2022, 27, 5860. https://doi.org/10.3390/molecules27185860
Yasui K. Merits and Demerits of ODE Modeling of Physicochemical Systems for Numerical Simulations. Molecules. 2022; 27(18):5860. https://doi.org/10.3390/molecules27185860
Chicago/Turabian StyleYasui, Kyuichi. 2022. "Merits and Demerits of ODE Modeling of Physicochemical Systems for Numerical Simulations" Molecules 27, no. 18: 5860. https://doi.org/10.3390/molecules27185860
APA StyleYasui, K. (2022). Merits and Demerits of ODE Modeling of Physicochemical Systems for Numerical Simulations. Molecules, 27(18), 5860. https://doi.org/10.3390/molecules27185860





