2.1. Implementation
The MM parameters were applied as implemented in Gaussian [
13] software, i.e., for each atom type (i.e., “HP”), the atomic radius (
in Å) (i.e., “1.1000”) and the well depth (
in kcal/mol) (i.e., 0.0157) are included in the following format:
These atomic parameters are essential for the calculation of the non-bonded terms: Lennard–Jones and Coulomb potentials. In the case of the Coulomb potential, the atomic charge for each atom is also required. These parameters are directly obtained from the force field, depending on the atom type. However, they can also be derived charges (e.g., RESP) for non-standard molecules.
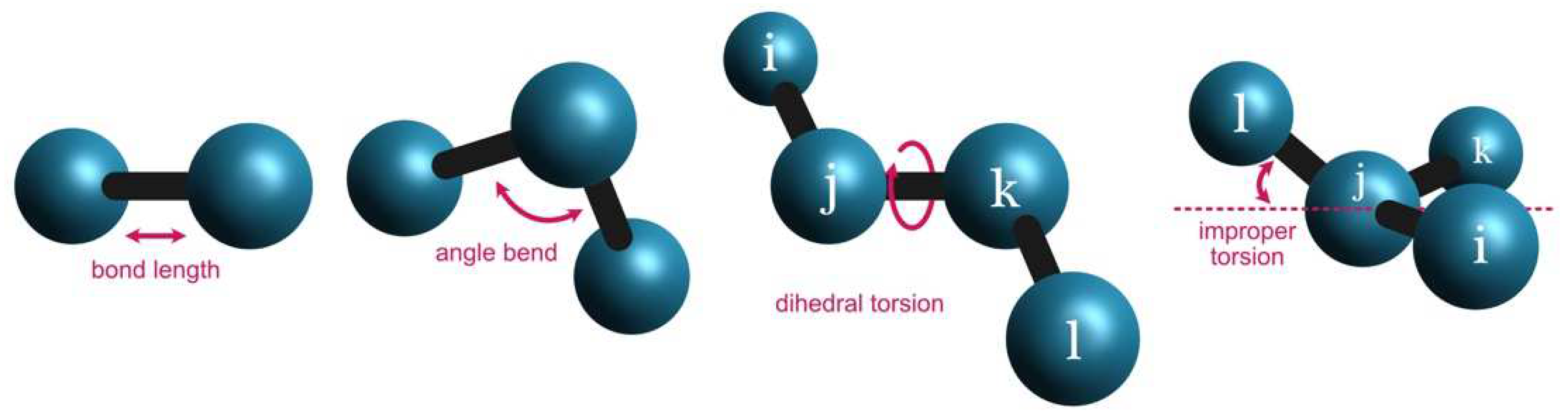
For each pair of atom types (i.e., “CT” and “HC”) that appears in the system covalently bonded to each other (
Figure 1), the bond force constant (
in kcal/mol/Å
2) (i.e., “340.00”) and equilibrium bond length (
in Å) (i.e., “1.0900”) are included:
This approach is similar to the angular bend between sets of three atoms (
Figure 1). The trio of atom types (i.e., “C”, “N”, and “H”) is associated with the respective angular force constant (
in kcal/mol/rad
2) (i.e., “50.00”) and equilibrium angle value (
in °) (i.e., “120.0001”):
In the case of dihedral angles (
Figure 1), each set of four sequentially bonded atoms (i.e., “NJ”, “CJ”, “ND”, and “CK”) is included in the parameters section as:
The following four values “0”, “180”, “0”, and “0” correspond to the phase offsets ( in °). For each phase offset, a magnitude factor ( in kcal/mol) is also available (i.e., “0.000”, “4.750”, “0.000”, and “0.000”). The last value corresponds to the number of paths () (i.e., “1.0”).
Finally, the improper torsions (
Figure 1) are calculated based on the following MM parameters:
The improper torsion is calculated as the displacement of one atom in relation to a plane defined by three other atoms. Therefore, four atoms are needed to define an improper torsion (i.e., “CJ”, “NJ”, “CD”, and “NH”). The energy contribution of an improper torsion is calculated considering a magnitude factor ( in kcal/mol) (i.e., “1.1”), a phase offset ( in °) (i.e., “180.0”), and a period () (i.e., “2.0”). In the AMBER force field, the central atom for improper torsions is the third atom in the list.
Energy Split was developed to use these parameters, which are available in every Gaussian input file for AMBER calculations, for the respective energy equation:
Based on the connectivity data, it is possible to identify which atoms are bonded to each other. Connectivity includes a list of atom indexes that instructs the MM program with respect to how atoms are covalently bonded between to one another. This information is essential to calculate the bonded terms: bonds, angles, dihedrals, and improper torsions. It is also crucial to apply the appropriate scaling factors to the Lennard–Jones () and Coulomb () potentials.
For each bond, Energy Split calculates the arithmetic distance (
) between the respective
pair of atoms:
Then, this distance (), the equilibrium bond length (), and the bond force constant () are used to calculate the energy contribution of each bond in the system.
The angles are calculated following a similar approach, the first step of which is to calculate the angle between three atoms (
). Firstly, the vectors
and
are determined; then, the angle between these vectors is calculated following the dot product expression:
The calculated angle () enters the energy expression with the equilibrium value () and respective equilibrium value ().
Dihedral angles are considered any time four atoms () are covalently bonded in a sequence. The dihedral angle is, by definition, the angle established between the and planes and calculated by determining the and vectors for the plane and the and vectors for the plane. The cross product is used to compute the norm vectors for each plane. Finally, the angle between the two norm vectors is calculated using the same approach. Starting with the obtained value, the energy contribution for the dihedral angle is calculated as presented in the respective term in Equation (1).
Improper torsion is calculated by considering all atoms that are exactly bonded to three atoms. Improper torsion occurs when three atoms () are sequentially connected to each other and atom is connected to atom . The concept of improper torsion was developed to provide an energy penalty when atom exits the plane. The penalization is proportional to the displacement, according to the respective term. Similar to the dihedral angle calculation, two planes are defined: the and planes. Then, the norm vectors are calculated, and the angle between them is calculated as described above.
Finally, the non-bond interactions are calculated considering all atom pairs of the system, as no cutoff was applied. However, this part of the calculation is highly time-demanding and is parallelized through the Thread module of Tcl (
https://www.tcl.tk/man/tcl8.6/ThreadCmd/thread.htm version 2.8.7, accessed on 15 January 2022). The calculation of non-bond interactions is split into the number of available threads of the running machine.
The Coulomb term for each pair of atoms is simply calculated as the product of the atomic charges of those atoms ( and ) divided by the distance between them multiplied by two constants. In an MM calculation, the atomic charges are known and kept fixed for calculation; therefore, only the distance between the atoms needs to be calculated according to Equation (2). Because is the vacuum permittivity, the term is constant and equal to 332.063712827427 kcal·mol−1.Å. The Coulomb contribution is also affected by a scaling factor (), which depends on how the atoms are connected to each other. In the case of atoms spaced by one or two covalent bonds, the scaling factor is zero because the interaction between those atoms is already accounted for by the bond and angle terms (previously described). With respect to atoms spaced by three covalent bonds, the scaling factor is , following the implementation in Gaussian 09. All other case scenarios are entirely accounted for, so the scaling factor is 1. These values are purely empirical and were set to reproduce accurate calculations and/or experimental data.
The scaling factors are also employed for the calculation of Lennard–Jones potential. In this case, atoms spaced by as many as two covalent bonds are nulled, whereas atoms spaced by three covalent bonds are scaled by 0.5. The scaling for the remaining pair of atoms (
) is 1. Similarly to the Coulomb expression, the Lennard–Jones potential depends on the distance between the two atoms involved (
). Therefore, the distance calculated for the Coulomb term is used to determine the van der Waals contribution. However, the expression for the Lennard–Jones potential requires two additional parameters for each pair of type of atoms:
and
. These two terms are calculated according to the following equations:
In Equations (4) and (5), two variables are required for each pair of atoms. Those variables are calculated based on the atomic radius (
and
) and well depth (
and
) for each atom type. These data are also included in the MM parameters, as mentioned at the beginning of this section. The
and
terms are calculated according to the combination rule in Equations (6) and (7) (Lorentz-Berthelot rule [
16,
17]).
The MM energy function of AMBER was described in detail, including all the mathematic expressions required for the implementation. The MM paraments stored by Gaussian software are not consistent in terms of units. Therefore, the actual code implementation in Energy Split involves conversion of units.
The implementation of the MM energy function in Energy Split was tested and compared with the results obtained with Gaussian 09 for the same systems. A set of systems was used to compare the computed energies of each individual term: bond, angles, dihedral angles, improper torsions, and van der Waals and Coulomb interactions. Following validation, Energy Split was prepared to split the systems into as many fragments as requested by the user.
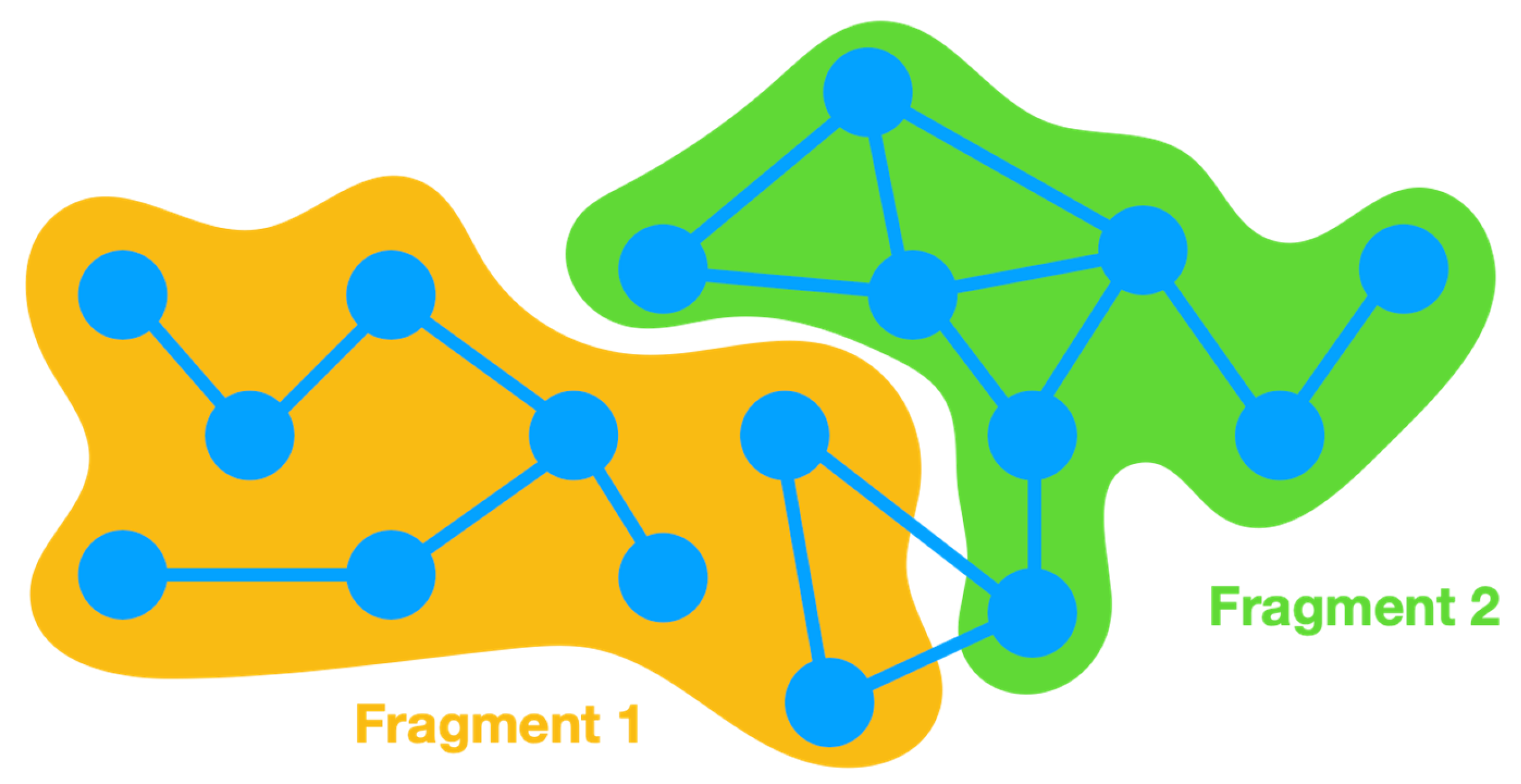
In order to clarify the implementation of energy partitioning in Energy Split, an
-atom system is split into two fragments (
Figure 2).
Energy partitioning accounts for the various energy terms of each fragment as separate sums. Therefore, in the case of a two-fragment system, two energy sums are included: and . The energy of fragment 1 () accounts for the energy of all terms (Equation 1) involving only atoms belonging to fragment 1. The same is applied for fragment 2 and all other possible fragments of the system. A third term is also required to account for the energy of the interactions between atoms that belong to more than one fragment. A covalent bond can span the boundary of two adjacent fragments and is therefore not considered in any of the cases. For such situations, the energy is accounted for in the third term, i.e., the interaction energy between fragments 1 and 2: . The same is applicable for all other terms wherein the involved atoms belong to different fragments, whether angles, dihedral angles, improper torsions, or van der Waals and Coulomb interactions.
In more complex systems with multiple fragments, the number of interaction terms depends on the interactions between all the atoms involved. Consequently, it is common to find , , , … The dual fragment interaction term can accommodate all interactions between terms that only involve two atoms (bond term and van der Waals and Coulomb interactions). However, angles can span three fragments, and dihedral angles and improper torsions can involve atoms from four fragments. In such cases, triple (e.g., ) and quadruple (e.g., ) interaction terms are considered.
The total energy of the system is expressed by the sum of all these contributions:
Energy Split calculates the MM energy of a molecular system in the same manner as standard MM software but offers a straightforward way to split the system into separate fragments. As a result, the energy is calculated in terms of fragments and the interactions between them.
2.3. Calculation Output
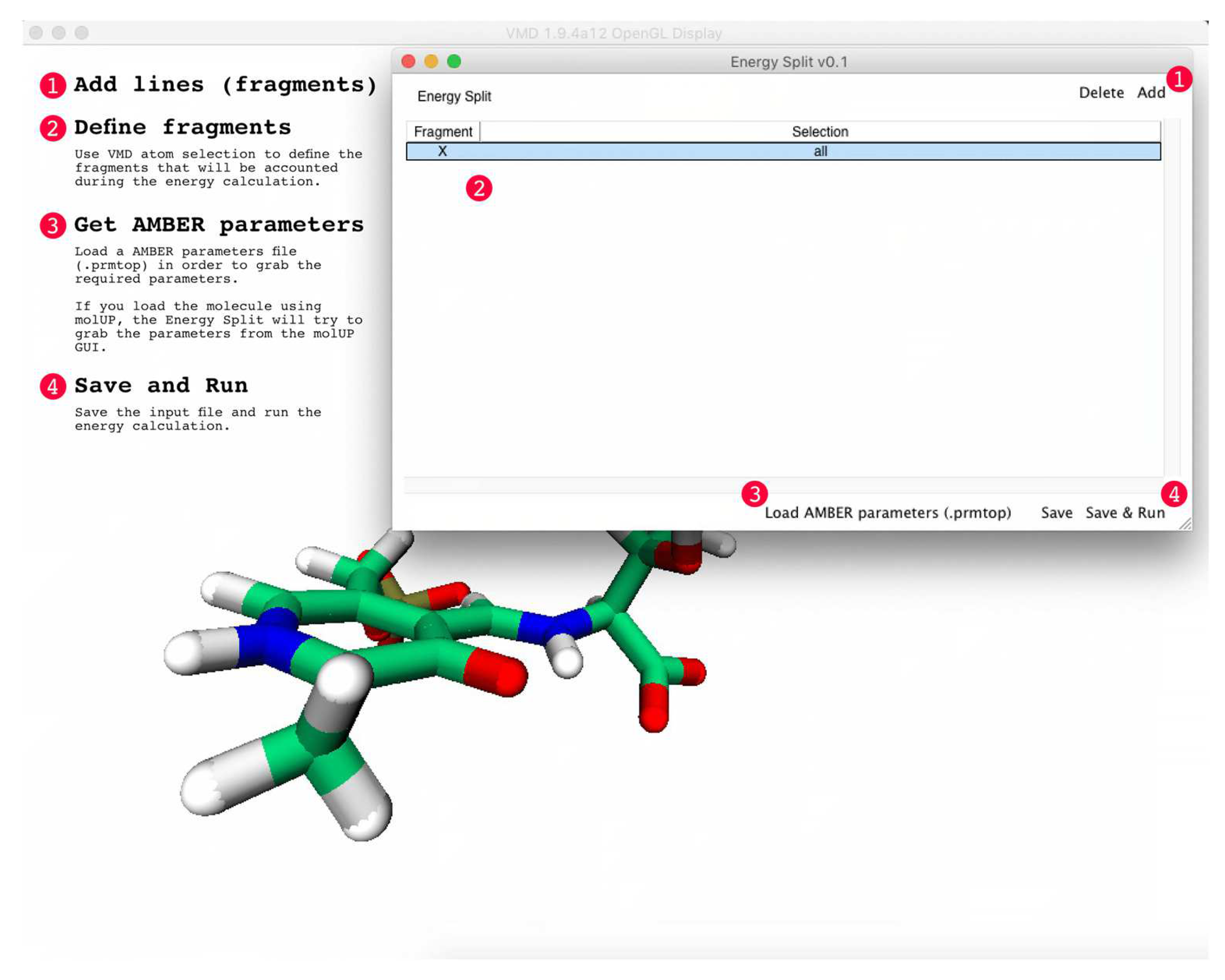
An Energy Split calculation can be started directly from the Energy Split extension for VMD by clicking on “Save & Run”. Otherwise, users can save the Energy Split input file and start the calculation in the terminal by running the following command:
tclsh energySplitPath/energySplitCalculation.tcl <inputfile>.tcl
Energy Split automatically detects the number of available CPU cores to parallelize the most time-demanding tasks. Once the calculation is finished, the output of the calculation has the following structure:
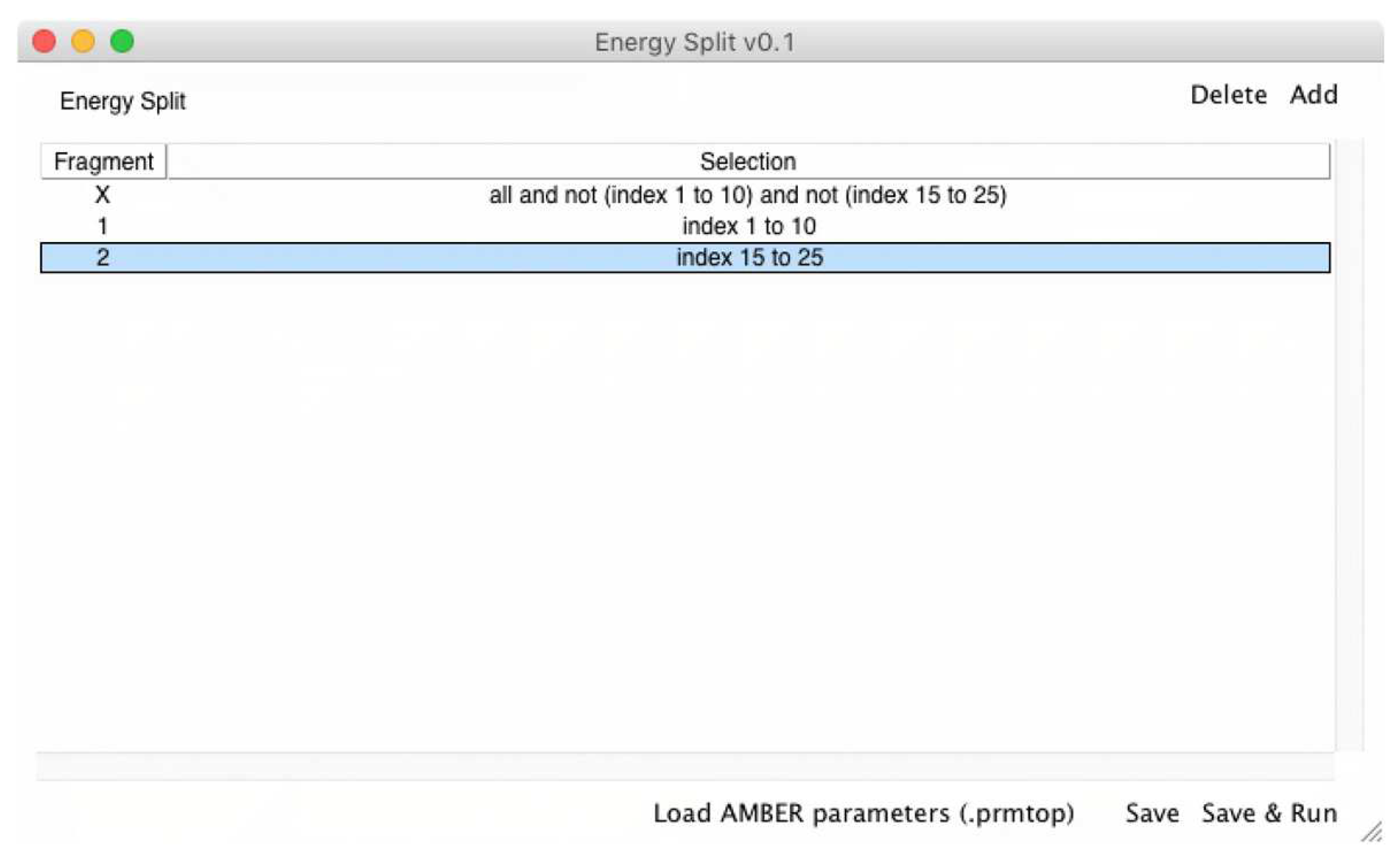
The output provides information about how many CPU cores were detected and used during the calculation. Then, a “Fragments” section lists all the fragments considered in the calculation, with each fragment is followed by a list of atoms included in that particular fragment (atom indexes). In the above example, two fragments were defined by the user (Fragments 0 and 1). Therefore, the calculation was accomplished considering three fragments: fragments 0, 1, and X.
Then, four sections are presented corresponding to the energy calculation for all bond terms: bonds (Bonds), angles (Angles), dihedral angles (Torsions), and improper torsions (Out-of-Plane). The improper torsions are presented with warnings about missing parameters as a consequence of how improper torsions are evaluated in Energy Split. Because Energy Split considers all atoms bonded to exactly three other atoms as potentially improper torsions, some of those calculations are not accomplished due to a lack of MM parameters. The warning is displayed only to advise users of such a situation, suggesting that such atoms should be carefully checked.
After these four sections, the energy for van der Walls (VDW) and Coulomb (Coulomb) interactions are displayed. Finally, the total energy of the system (Total Energy) is presented.
For all sections, the energy is presented following the energy partitioning described by Equation (1). The energy of each fragment is presented as “Fragment N”, where N can be “0”, “1”, or “X”. In addition, the interaction energy, which corresponds to energy terms that involve atoms from different fragments, are represented as “Fragment N + Fragment M”, where N and M can be “0”, “1”, or “X”, and N ≠ M.