2.4.1. Support Vector Machine
Support vector machine (SVM) is based upon the principle of structural risk minimization, with salient properties of ease in generalization and fewer required training samples [
18]. An SVM displayed substantial benefits when compared to other classification approaches. It is challenging to construct a linear classifier to separate the classes of data. In SVM, the transfer function is introduced to map the input vectors a high-dimensional space (generally a Hilbert space), which can effectively reduce the optimization complexity and improve the generalization capability. It then constructs a linear classification decision to classify the input spectral data with a maximum margin hyperplane. An SVM has also been found to be more effective and faster than other machine learning methods.
The computational parameters of the SVM model can be obtained by solving the following convex optimization problem with a ε-insensitivity loss function:
In general, the model in Equation (1) can be addressed by constructing a primal optimization problem based on a Lagrange function, which is given as below:
Among,.
The dual function of linear indivisible problems is as below:
Then, the decision function for the SVM model can be described as below:
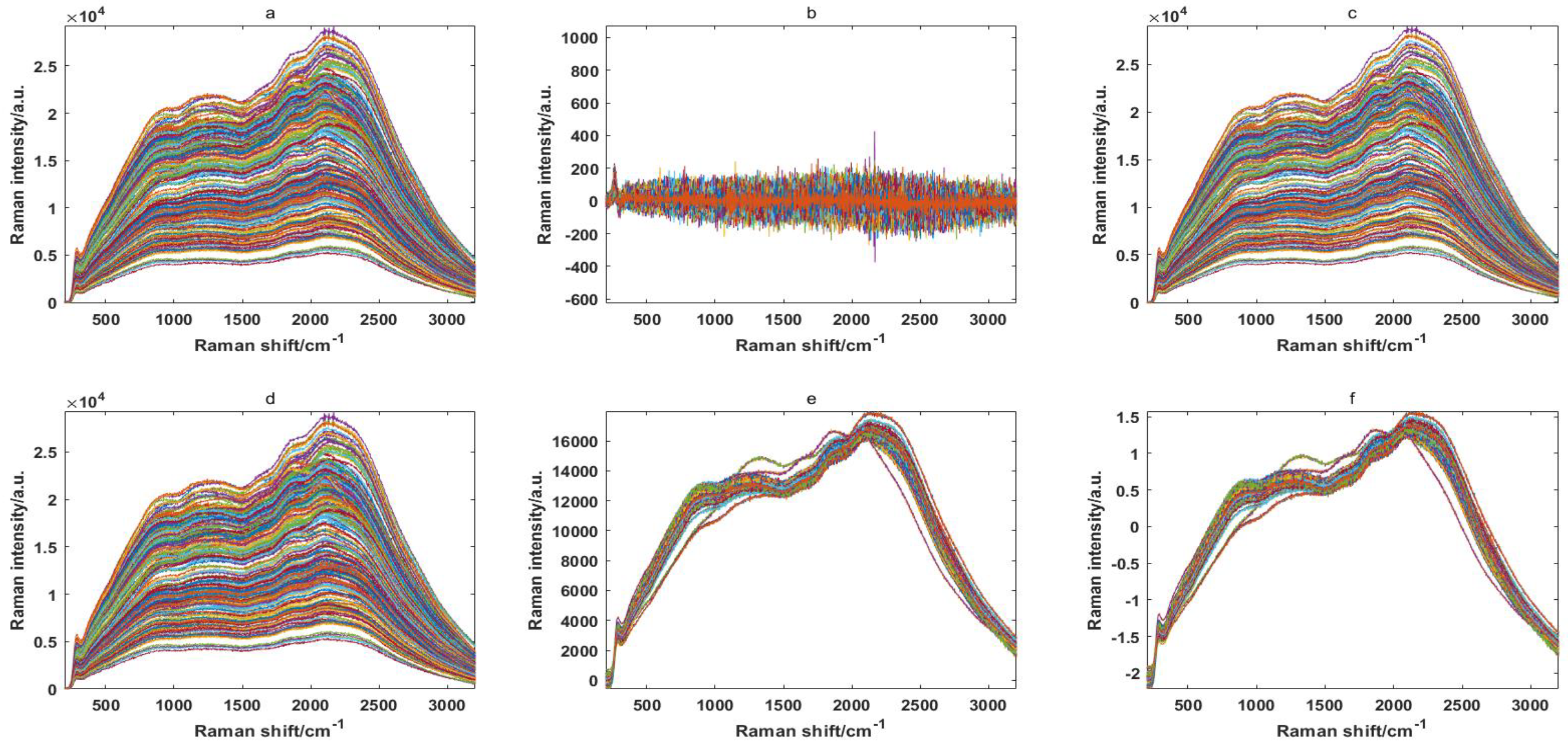
Three pattern-recognition methods (support vector machine (SVM), BP neural network (BP) and probabilistic neural network (PNN)) were applied to the building of rice-classification models. The results of resistant-rice-classification models built by different modeling methods are shown in
Table 1.
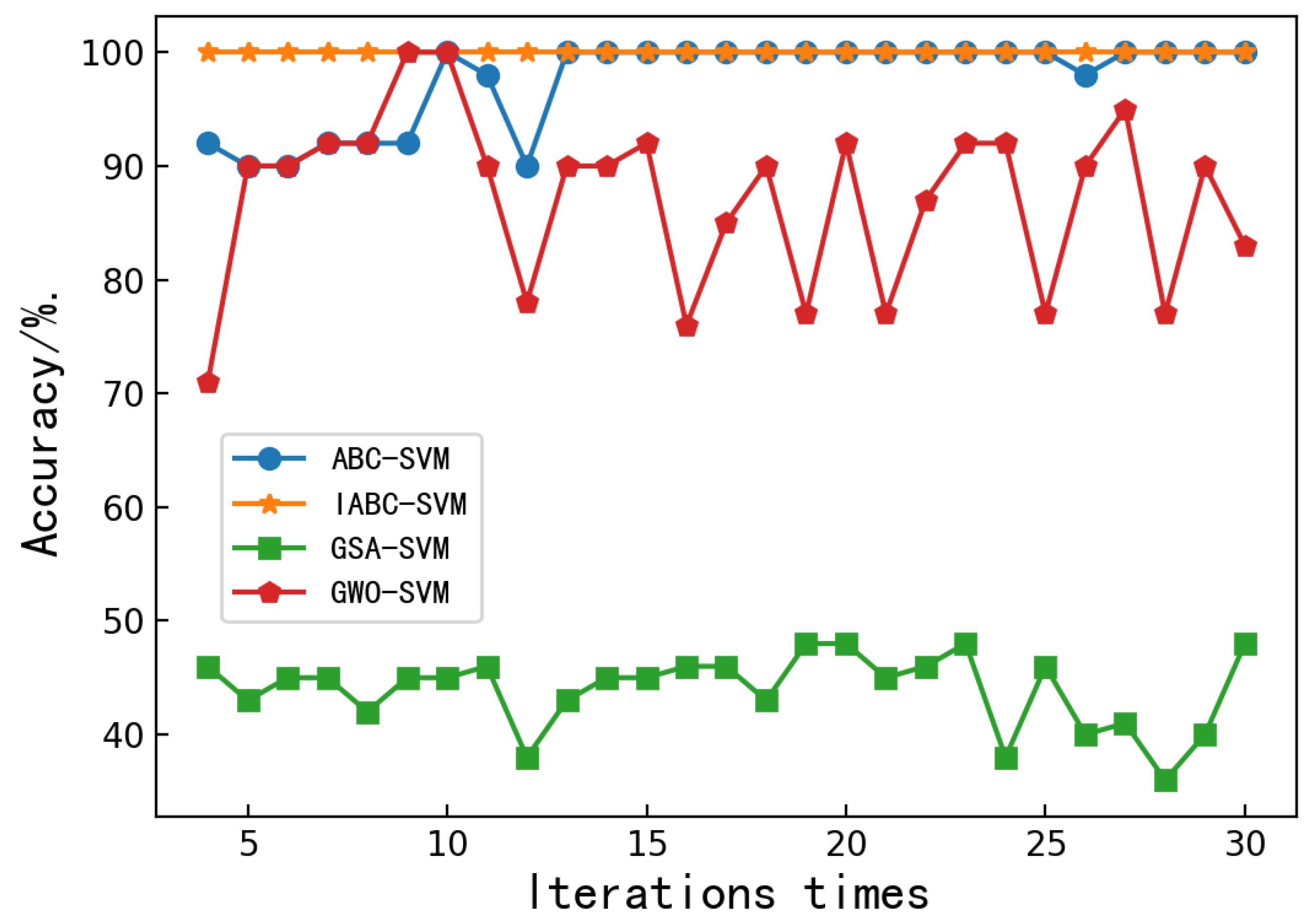
As can be seen, the optimum raw BP model (with classification accuracy of 97% and a running time of 487 s) was obtained using the raw spectra. The Raw-SVM model runs very fast, with an accuracy of 45%. If the raw BP model is optimized, the running time will be lengthier. With the research and development of swarm intelligence algorithms, many intelligent algorithms have been applied to the parameter optimization of SVM. In order to improve the classification results, the Raw-SVM model should be chosen for optimization and the optimal (c,g) parameters combination should be sought.
2.4.2. Optimize Support Vector Machine
In recent years, the swarm intelligence algorithm has been widely used to optimize SVM parameters [
19]. The artificial bee colony algorithm (ABC) is a new swarm intelligence algorithm that was proposed in 2005 by Karaboga [
20]. In order to find an optimal solution through iterations, ABC calculates the evaluation value of a food source by formula. The ABC algorithm can converge on the global optimum faster, thus improving the accuracy of SVM in classification and accelerating the convergence speed of (c,g) parameter optimization. However, the traditional artificial bee colony algorithm easily falls into local extreme points in the later stage. Many scholars take advantages of the ABC algorithm to optimize SVM parameters. Luo et al. [
21] introduced a chaotic sequence to re-initialize hireling bees. Zhou et al. [
22] used stepwise optimization to transform the selection strategy. Kuang et al. [
23] generated a chaotic sequence based on the local optimal solution and selected the optimal solution from the sequence as the new honey source location; Liu Xia et al. [
24] used chaotic mapping to initialize the population. Liu et al. [
25] optimized the ABC algorithm using a random dynamic local search operator. These optimizing ABC algorithms improved the search performance to a certain extent and at the same time fully verified the chaotic optimization algorithm’s advantages of being insensitive to initial values and demonstrating strong ergodicity.
In this paper, the ergodicity of the chaotic search algorithm (CS) is utilized. In the iterative process of the artificial bee colony algorithm, when the number of searches is greater than the set maximum number and a better nectar source has not been obtained, it will fall into the problem of local optimal solutions. The chaotic search algorithm [
26] is introduced to generate chaotic sequences to form an improved artificial bee colony algorithm (IABC) based on the chaotic update strategy. The IABC algorithm has a chaotic update strategy scout bee, which traverses the chaotic sequence and compares the corresponding fitness values with those of the stagnant solution to find a better solution to replace the stagnant solution, so that the algorithm jumps out of the local optimum. The experimental results show that the artificial bee colony algorithm based on the chaotic-update strategy has accelerated the convergence speed, enhanced the later local jump-out ability and improved the SVM classification performance.
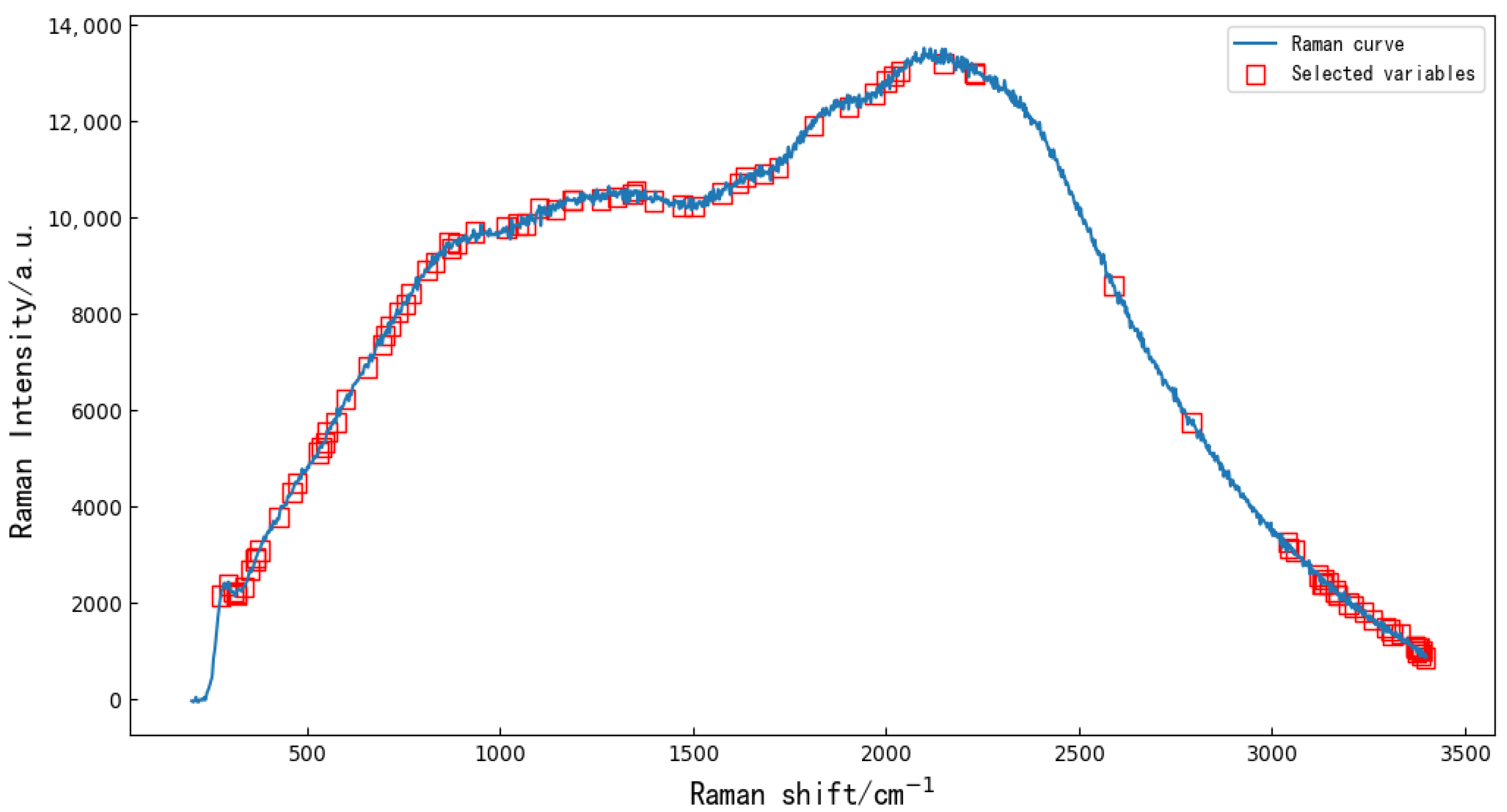
First, the bee colony is initialized. According to the results of many experiments, the value ranges of the nuclear parameter and the penalty factor C are determined to be (0, 0.01) and (1, 100), respectively. Using two-dimensional uniform design method, the value range of C is evenly divided into 25 squares. The range of the initial food source is represented by each square. Once the bee leaves the local optimal solution, it can find the square without the optimal solution among all the squares and generate the optimal solution among the remaining squares.
Second, the food sources are updated. The penalty factor C and the kernel function parameter
of SVM are both optimized. The Euclidean distance between food source
and food source
can be expressed as:
In the traditional ABC algorithm, the formula for generating a new food source is:
The formula for the selection of food sources by scout bees are as follows:
where
and
are selected randomly.
, which denotes a random value;
is the fitness value corresponding to the food source. When the value of
is small, the search range of the scout bees is small, which causes the algorithm to not converge or to converge in advance; On the contrary, the optimal solution may be ignored, thus affecting the convergence of the algorithm. Therefore, this article attempts to improve the convergence of the ABC algorithm.
Third, the weight value is defined as
, in the range of (0, 1), where the value of
is the distance between the current solution and the optimal solution, and the value of
is obtained by substituting the vertex (1, 0) and the vertex (100, 0.1) into Equation (1). The range of the food-source-update solution can be adjusted automatically by
. If
is smaller, it means that the search range of the update solution is smaller. Otherwise, it is larger. This update strategy can effectively reduce the number of iterations. Plugging
into Equation (6) gives the new formula for improved food sources, as follows.
In view of the lack of mathematical theory to guide the parameter search of support vector machines, the low efficiency of traditional artificial bee colony algorithm (ABC) search and the tendency to generate local optimal solutions, an artificial bee colony support vector machine model (IABC-SVM) based on a chaotic-update strategy is proposed. The model improves the convergence speed and classification accuracy of the ABC algorithm through two-dimensional uniform population initialization and food source update based on Euclidean distance.


.jpg)
.jpg)



