A Theoretical Model for Release Dynamics of an Antifungal Agent Covalently Bonded to the Chitosan
Abstract
1. Introduction
2. Experiment
2.1. Materials
2.2. Synthesis of Imino-Chitosan Derivatives
2.3. Methods
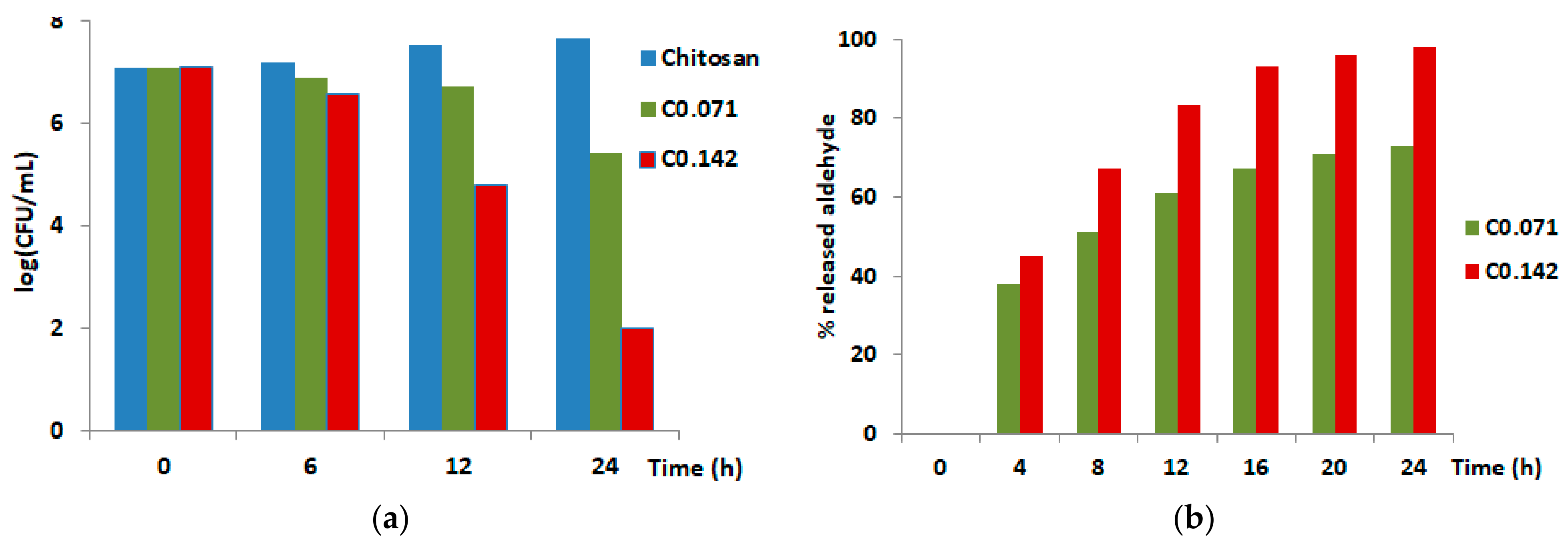
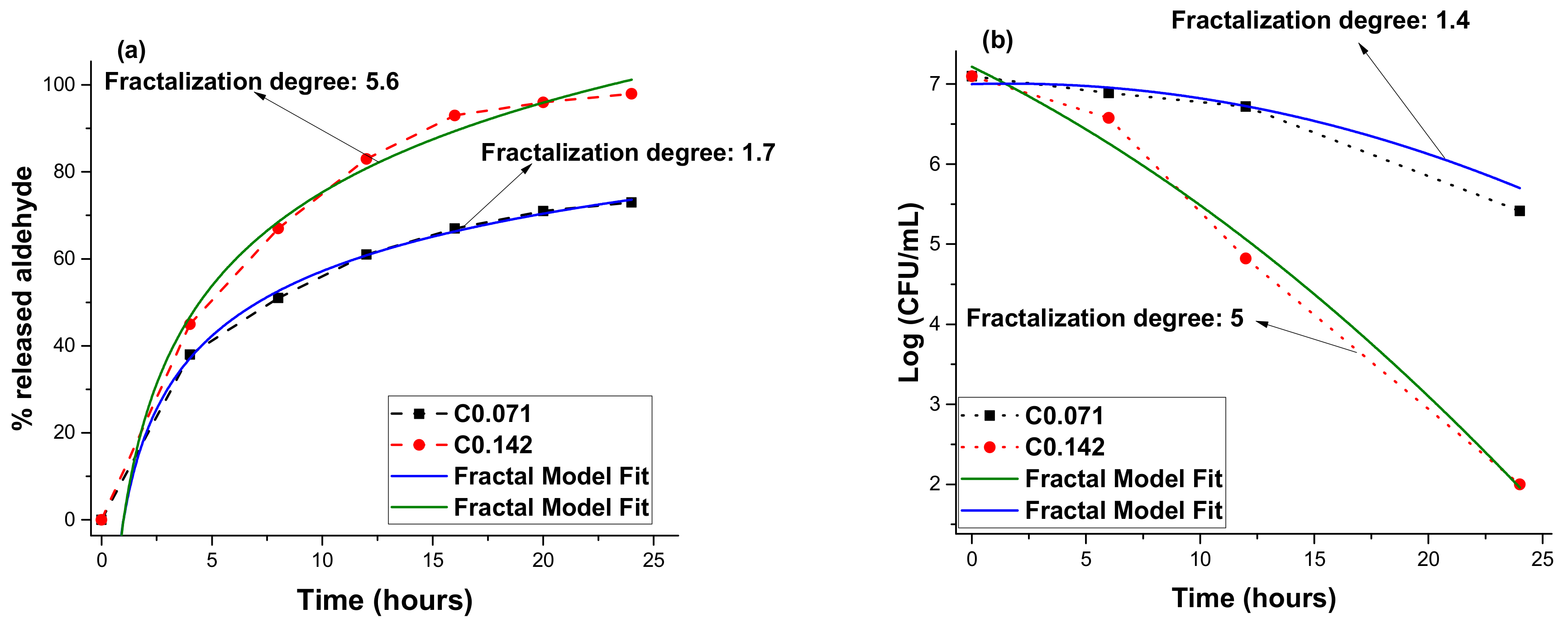
3. Empirical Data
4. Theoretical Considerations
- (i)
- Aldehyde compound release dynamics in the scale space, dynamics which will be assimilated with the fungicidal activity;
- (ii)
- Aldehyde compound release dynamics in the usual space, dynamics which will be assimilated with the antifungal aldehyde release;
- (iii)
- Aldehyde compound release dynamics, associated with the transition from the scale space to the usual space, as a global release mechanism.
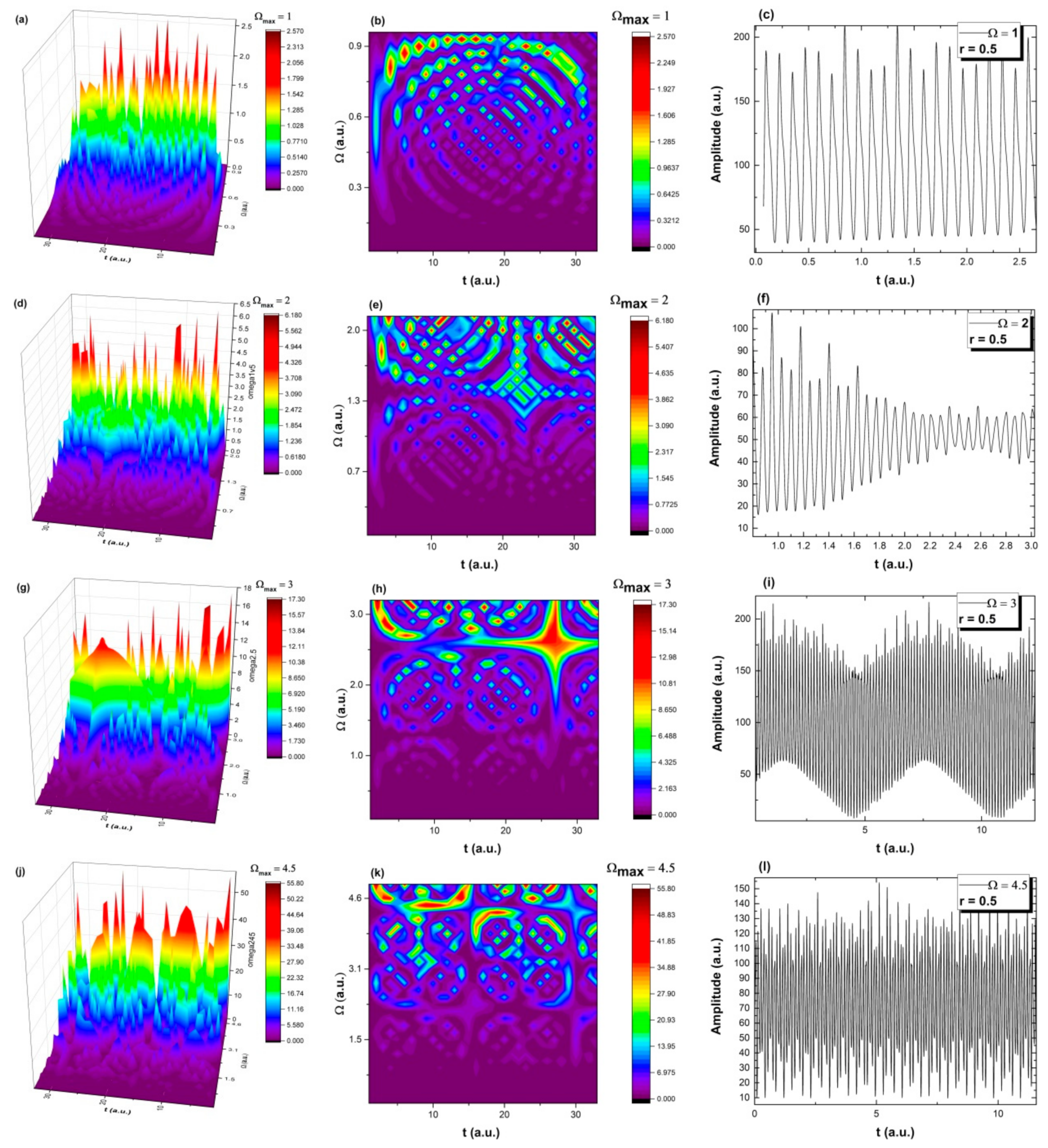
4.1. Aldehyde Compound Delivery Dynamics in Scale Space
4.2. Aldehyde Compound Delivery Dynamics in the Usual Space
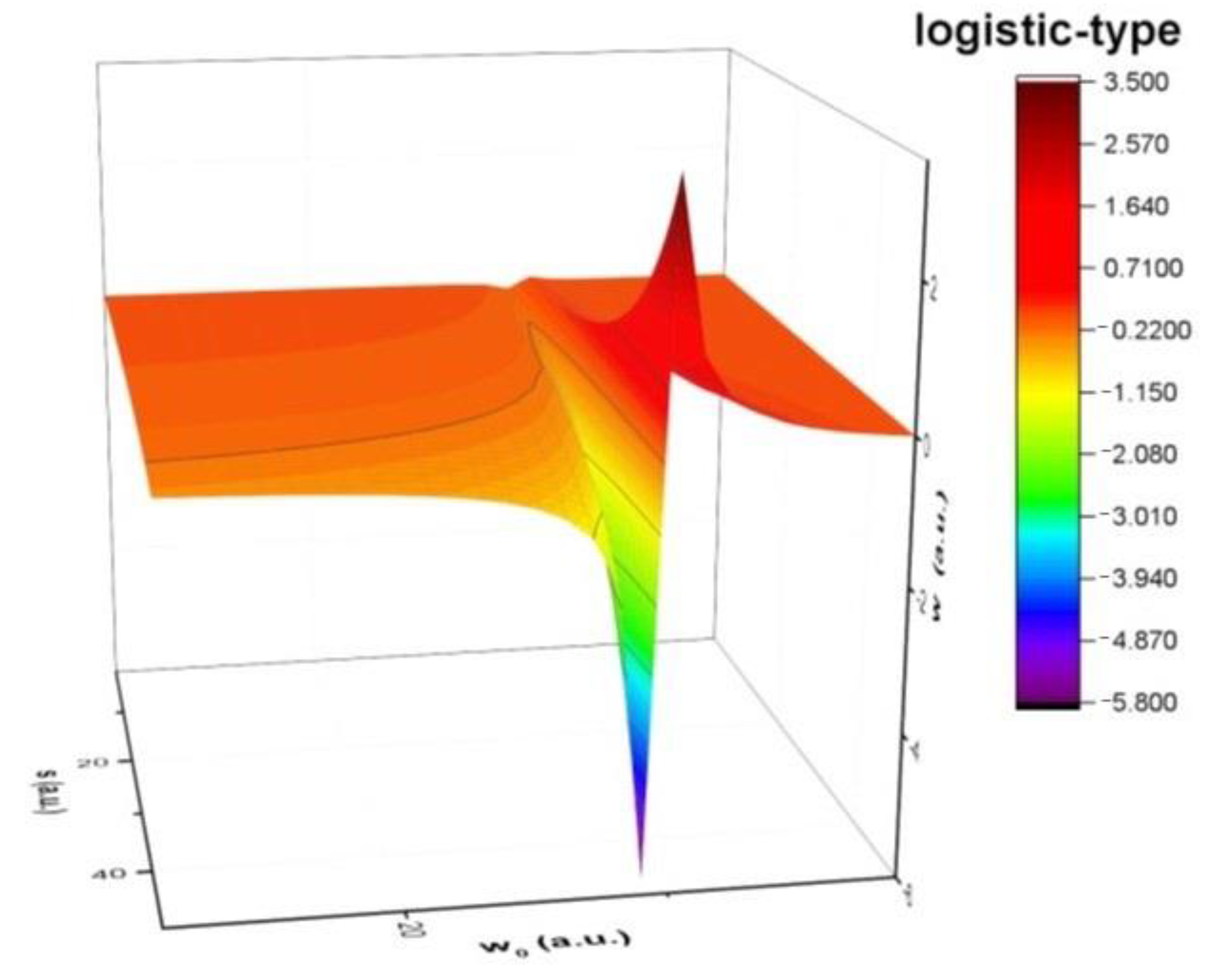
4.3. Aldehyde Compound Release Transitions from the Space Scale to the Usual One
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Crini, G. Historical review on chitin and chitosan biopolymers. Environ. Chem. Lett. 2019, 17, 1623–1643. [Google Scholar] [CrossRef]
- Pokhrel, S.; Yadav, P.N. Functionalization of chitosan polymer and their applications, Journal of Macromolecular Science Part A. Pure Appl. Chem. 2019, 56, 450–475. [Google Scholar]
- Marin, L.; Ailincai, D.; Mares, M.; Paslaru, E.; Cristea, M.; Nica, V.; Simionescu, B.C. Imino-chitosan biopolymeric films. Obtaining self-assembling, surface and antimicrobial properties. Carbohyd. Polym. 2015, 117, 762–770. [Google Scholar] [CrossRef] [PubMed]
- Jommanee, N.; Chanthad, C.; Manokruang, K. Preparation of injectable hydrogels from temperature and pH responsive grafted chitosan with tuned gelation temperature suitable for tumor acidic environment. Carbohyd. Polym. 2018, 198, 486–494. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Rashidpour, A.; Almajano, M.P.; Metón, I. Chitosan-Based Drug Delivery System: Applications in Fish Biotechnology. Polymers 2020, 12, 1177. [Google Scholar] [CrossRef] [PubMed]
- Iftime, M.M.; Ailiesei, G.L.; Ungureanu, E.; Marin, L. Designing chitosan based eco-friendly multifunctional soil conditioner systems with urea controlled release and water retention. Carbohyd. Polym. 2019, 223, 115040. [Google Scholar] [CrossRef] [PubMed]
- Chaiwong, N.; Leelapornpisid, P.; Jantanasakulwong, K.; Rachtanapun, P.; Seesuriyachan, P.; Sakdatorn, V.; Leksawasdi, N.; Phimolsiripol, Y. Antioxidant and Moisturizing Properties of Carboxymethyl Chitosan with Different Molecular Weights. Polymers 2020, 12, 1445. [Google Scholar] [CrossRef]
- Marin, L.; Dragoi, B.; Olaru, N.; Perju, E.; Coroaba, A.; Doroftei, F.; Scavia, G.; Destri, S.; Zappia, S.; Porzio, W. Nanoporous furfuryl-imine-chitosan fibers as a new pathway towards eco-materials for CO2 adsorption. Eur. Polym. J. 2019, 120, 109214. [Google Scholar] [CrossRef]
- Wan Ngah, W.S.; Teong, L.C.; Hanafiah, M.A.K.M. Adsorption of dyes and heavy metal ions by chitosan composites: A review. Carbohyd. Polym. 2011, 83, 1446–1456. [Google Scholar] [CrossRef]
- Bejan, A.; Doroftei, F.; Cheng, X.; Marin, L. Phenothiazine-chitosan based eco-adsorbents: A special design for mercury removal and fast naked eye detection. Int. J. Biol. Macromol. 2020, 162, 1839–1848. [Google Scholar] [CrossRef]
- Lehn, J.M. Perspectives in Chemistry—Aspects of Adaptive Chemistry and Materials. Angew. Chem. 2015, 54, 3276–3289. [Google Scholar] [CrossRef]
- Belowicha, M.E.; Stoddart, J.F. Dynamic imine chemistry. Chem. Soc. Rev. 2012, 41, 2003–2024. [Google Scholar] [CrossRef]
- Zhang, Y.; Pham, C.Y.; Yu, R.; Petit, E.; Li, S.; Barboiu, M. Dynamic Hydrogels Based on Double Imine Connections and Application for Delivery of Fluorouracil. Front. Chem. 2020, 8, 739. [Google Scholar] [CrossRef] [PubMed]
- Ailincai, D.; Marin, L.; Morariu, S.; Mares, M.; Bostanaru, A.C.; Pinteala, M.; Simionescu, B.C.; Barboiu, M. Dual crosslinked iminoboronate-chitosan hydrogels with strong antifungal activity against Candida planktonic yeasts and biofilms. Carbohyd. Polym. 2016, 152, 306–316. [Google Scholar] [CrossRef]
- Bar-Yam, Y. Dynamics of Complex Systems. The Advanced Book Program; Addison-Wesley: Reading, MA, USA, 1997. [Google Scholar]
- Mitchell, M. Complexity: A Guided Tour; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Badii, R. Complexity: Hierarchical Structures and Scaling in Physics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Flake, G.W. The Computational Beauty of Nature; MIT Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Singhvi, G.; Singh, M. Review: In-Vitro drug release characterization models. Int. J. Pharm. Stud. Res. 2011, 2, 77–84. [Google Scholar]
- Băceanu, D.; Diethelm, K.; Scalas, E.; Trujillo, H. Fractional Calculus, Models and Numerical Methods; World Scientific: Singapore, 2016. [Google Scholar]
- Ortigueria, M.D. Fractional Calculus for Scientists and Engineers; Springer: New York, NY, USA, 2011. [Google Scholar]
- Craciun, A.-M.; Barhalescu, M.L.; Agop, M.; Ochiuz, L. Theoretical Modeling of Long-Time Drug Release from Nitrosalicyl-Imine-Chitosan Hydrogels through Multifractal Logistic Type Laws. Comp. Math. Method. Med. 2019, 2019, 4091464. [Google Scholar] [CrossRef] [PubMed]
- Nottale, L. Scale Relativity and Fractal Space-Time: A New Approach to Unifying Relativity and Quantum Mechanics; Imperial College Press: London, UK, 2011. [Google Scholar]
- Merches, I.; Agop, M. Differentiability and Fractality in Dynamics of Physical Systems; World Scientific: Hackensack, NJ, USA, 2016. [Google Scholar]
- Agop, M.; Paun, V.P. On the New Perspectives of the Fractal Theory. Fundaments and Applications; Romanian Academy Publishing House: Bucharest, Romania, 2017. [Google Scholar]
- Ailincai, D.; Agop, M.; Marinas, I.C.; Zala, A.; Irimiciuc, S.A.; Dobreci, L.; Petrescu, T.-C.; Volovat, C. Theoretical model for the diclofenac release from PEGylated chitosan hydrogels. Drug Deliv. 2021, 28, 261–271. [Google Scholar] [CrossRef]
- Iftime, M.M.; Dobreci, D.L.; Irimiciuc, S.A.; Agop, M.; Petrescu, T.; Doroftei, B. A theoretical mathematical model for assessing diclofenac release from chitosan-based formulations. Drug Deliv. 2020, 27, 1125–1133. [Google Scholar] [CrossRef] [PubMed]
- Jackson, E.A. Perspective of Nonlinear Dynamics, Volume 2; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Cristescu, C.P. Nonlinear Dynamics and Chaos. Theoretical Fundaments and Applications; Academy Publishing House: Bucharest, Romanian, 2008. [Google Scholar]
- Marin, L.; Zabulica, A.; Sava, M. Symmetric Liquid Crystal Dimers Containing a Luminescent Mesogen: Synthesis, Mesomorphic Behavior and Optical Properties. Soft. Mater. 2013, 11, 32–39. [Google Scholar] [CrossRef]
- Liu, X.; Guo, N.; Guo, Z.; Hu, Z.; Chen, Z.; Hu, J.; Yang, L. Synthesis and liquid crystal properties of new cyclic carbonate monomers functionalised with cholesteryl moiety. Liq. Cryst. 2018, 45, 834–1843. [Google Scholar] [CrossRef]
- Craciun, A.M.; Mititelu Tartau, L.; Pinteala, M.; Marin, L. Nitrosalicyl-imine-chitosan hydrogels based drug delivery systems for long-term sustained release in local therapy. J. Colloid Interface Sci. 2019, 536, 196–207. [Google Scholar] [CrossRef] [PubMed]
- Sobel, J.D. Recurrent vulvovaginal candidiasis. Am. J. Obst. Gynecol. 2016, 214, 115–121. [Google Scholar] [CrossRef] [PubMed]
- Mansour, H.M.; Sohn, M.J.; Al-Ghananeem, A.; DeLuca, P.P. Materials for Pharmaceutical Dosage Forms: Molecular Pharmaceutics and Controlled Release Drug Delivery Aspects. Int. J. Mol. Sci. 2010, 11, 3298–3322. [Google Scholar] [CrossRef] [PubMed]
- Aitchison, J.R. An Informal Introduction to Gauge Field Theories; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Mazilu, N.; Agop, M. Skyrmions: A Great Finishing Touch to Classical Newtonian Philosophy; Nova Science Publisher: New York, NY, USA, 2014. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman and Co.: San Fracisco, CA, USA, 1982. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marin, L.; Popa, M.; Anisiei, A.; Irimiciuc, S.-A.; Agop, M.; Petrescu, T.-C.; Vasincu, D.; Himiniuc, L. A Theoretical Model for Release Dynamics of an Antifungal Agent Covalently Bonded to the Chitosan. Molecules 2021, 26, 2089. https://doi.org/10.3390/molecules26072089
Marin L, Popa M, Anisiei A, Irimiciuc S-A, Agop M, Petrescu T-C, Vasincu D, Himiniuc L. A Theoretical Model for Release Dynamics of an Antifungal Agent Covalently Bonded to the Chitosan. Molecules. 2021; 26(7):2089. https://doi.org/10.3390/molecules26072089
Chicago/Turabian StyleMarin, Luminita, Marcel Popa, Alexandru Anisiei, Stefan-Andrei Irimiciuc, Maricel Agop, Tudor-Cristian Petrescu, Decebal Vasincu, and Loredana Himiniuc. 2021. "A Theoretical Model for Release Dynamics of an Antifungal Agent Covalently Bonded to the Chitosan" Molecules 26, no. 7: 2089. https://doi.org/10.3390/molecules26072089
APA StyleMarin, L., Popa, M., Anisiei, A., Irimiciuc, S.-A., Agop, M., Petrescu, T.-C., Vasincu, D., & Himiniuc, L. (2021). A Theoretical Model for Release Dynamics of an Antifungal Agent Covalently Bonded to the Chitosan. Molecules, 26(7), 2089. https://doi.org/10.3390/molecules26072089









