Spectral and Texture Properties of Hydrophobic Aerogel Powders Obtained from Room Temperature Drying
Abstract
1. Introduction
2. Results and Discussion
2.1. Physical Properties
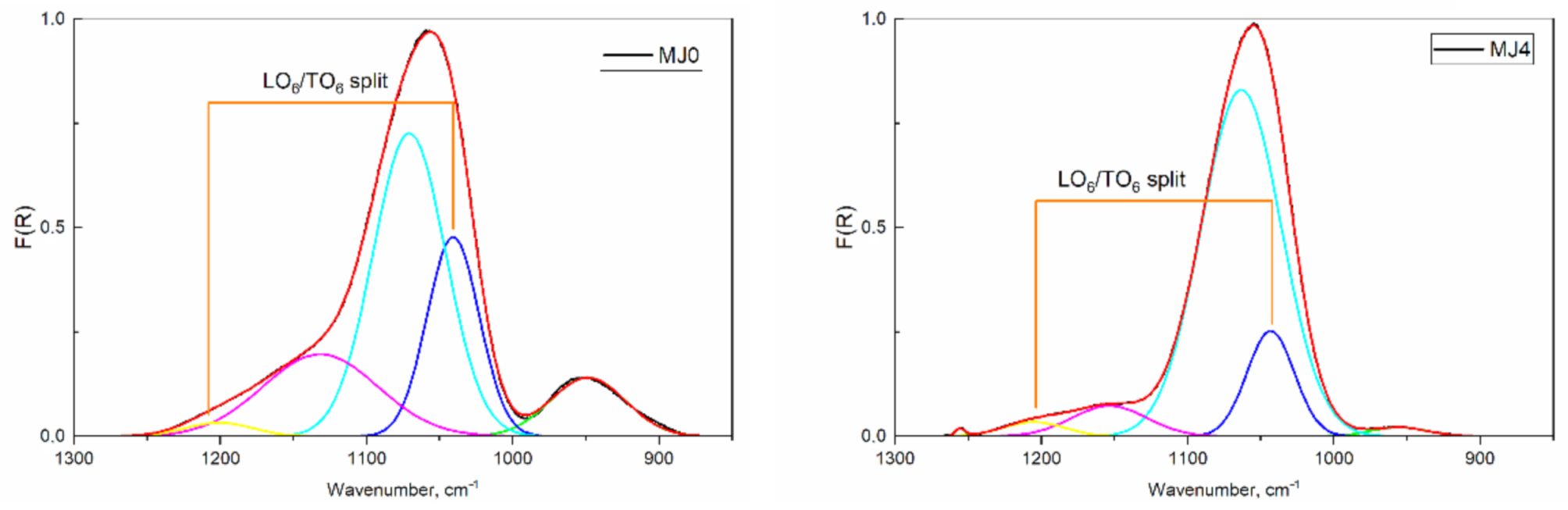
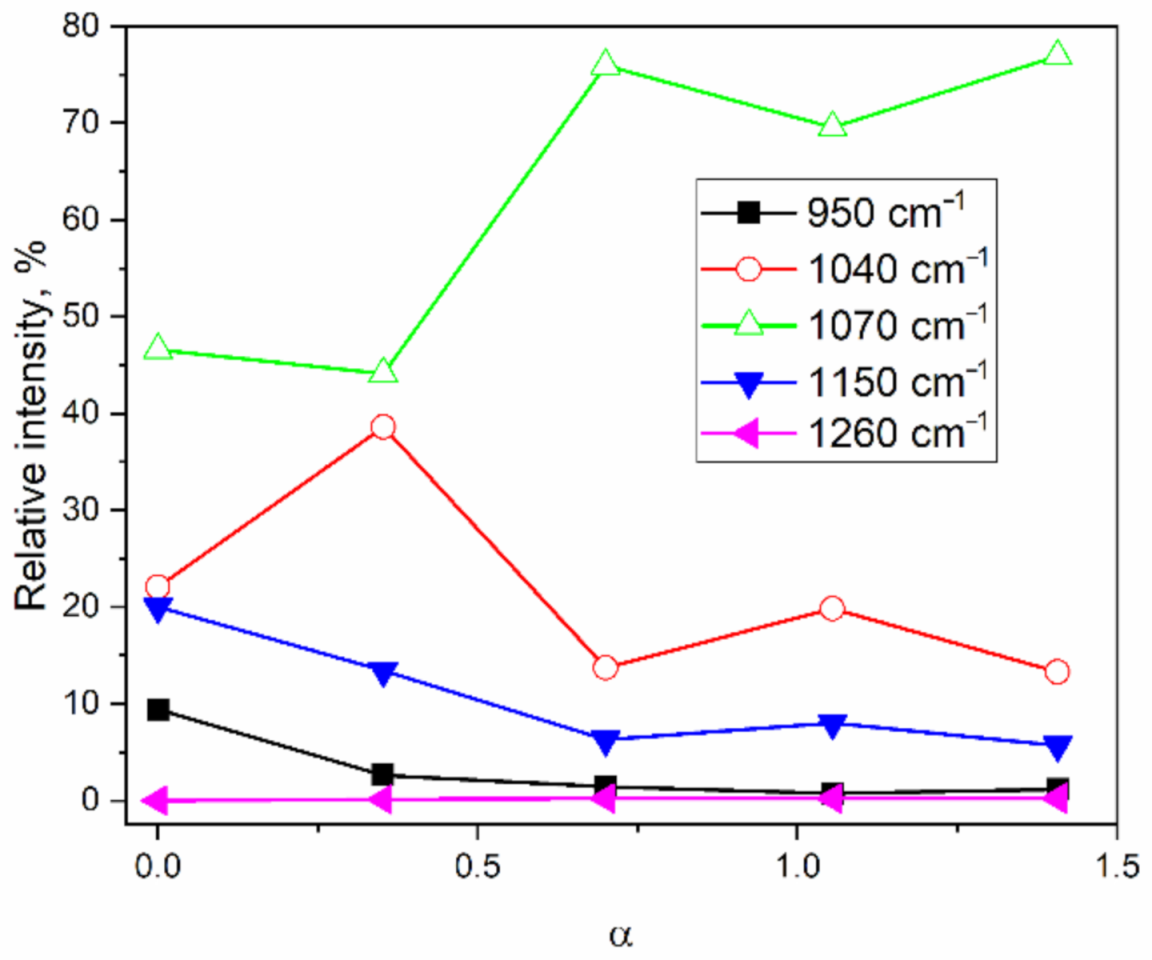
2.2. ATR-IR Spectroscopy

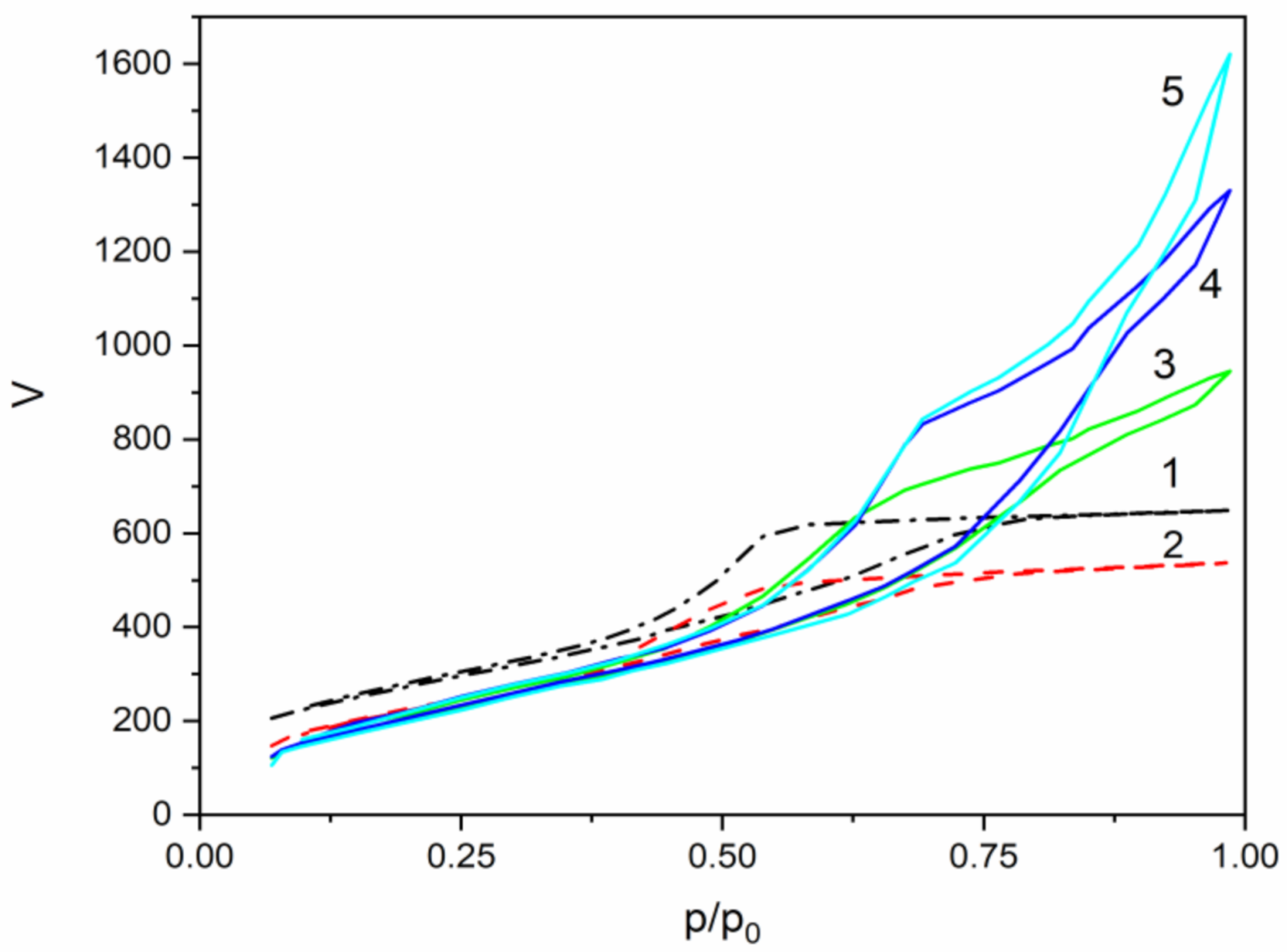
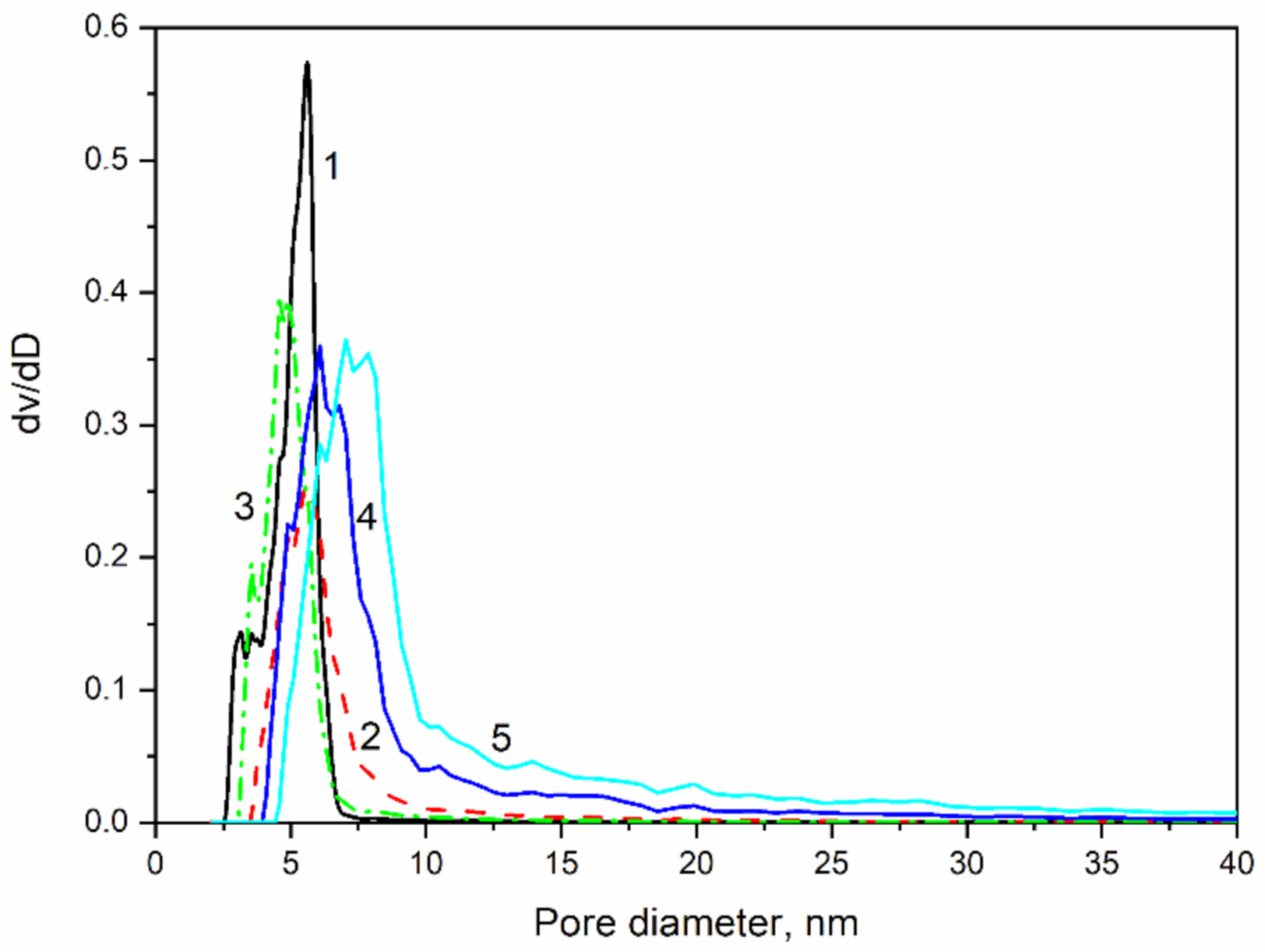
2.3. Texture Properties
3. Materials and Methods
3.1. Materials and Reagents
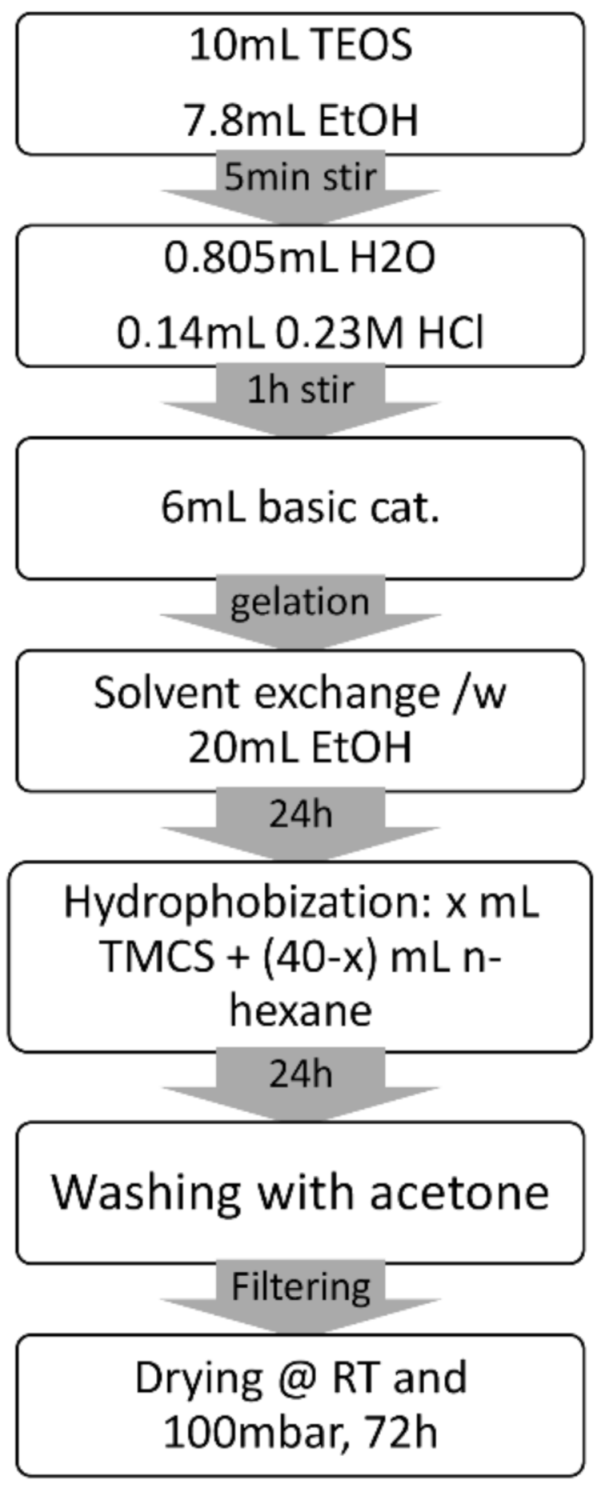
3.2. Aerogel Synthesis
3.3. ATR-IR Spectroscopy
3.4. Texture Characteristics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guglielmi, M. Sol-gel science. Mater. Chem. Phys. 1990, 26, 211–212. [Google Scholar] [CrossRef]
- Gomez-Romero, P.; Sanchez, C. Functional Hybrid Materials; Wiley-VCH: Weinheim, Germany, 2003; ISBN 9781787284395. [Google Scholar]
- Aegerter, M.A.; Leventis, N.; Koebel, M.M. Aerogels Handbook; Springer: New York, NY, USA, 2011. [Google Scholar]
- Petkova, N.; Gutzov, S.; Lesev, N.; Kaloyanova, S.; Stoyanov, S.; Deligeorgiev, T. Preparation and optical properties of silica gels doped with a new Eu (III) complex. Opt. Mater. 2011, 33, 1715–1720. [Google Scholar] [CrossRef]
- Sala, M.R.; Peng, C.; Skalli, O.; Sabri, F. Tunable neuronal scaffold biomaterials through plasmonic photopatterning of aerogels. MRS Commun. 2019, 9, 1249–1255. [Google Scholar] [CrossRef]
- Allisona, S.W.; Bakerb, E.S.; Lynchb, K.J.; Sabri, F. In vivo X-Ray excited optical luminescence from phosphor-doped aerogel and Sylgard 184 composites. Radiat. Phys. Chem. 2017, 135, 88–93. [Google Scholar] [CrossRef]
- Gutzov, S.; Danchova, N.; Kirilova, R.; Petrov, V.; Yordanova, S. Preparation and luminescence of silica aerogel composites containing an europium (III) phenanthroline nitrate complex. J. Lumin. 2017, 193, 108–112. [Google Scholar] [CrossRef]
- Kim, J.-S.; Lee, S.K.; Doh, H.; Kim, M.Y.; Kim, D.K. Real-Time Tracking of Highly Luminescent Mesoporous Silica Particles Modified with Europium β-Diketone Chelates in Living Cells. Nanomaterials 2021, 11, 343. [Google Scholar] [CrossRef]
- Pan, Y.; Cheng, X.; Zhou, T.; Gong, L.; Zhang, H. Spray freeze-dried monolithic silica aerogel based on water-glass with thermal superinsulating properties. Mater. Lett. 2018, 229, 265–268. [Google Scholar] [CrossRef]
- Farrell, E.S.; Schilt, Y.; Moshkovitz, M.Y.; Levi-Kalisman, Y.; Raviv, U.; Magdassi, S. 3D Printing of Ordered Mesoporous Silica Complex Structures. Nano Lett. 2020, 20, 6598–6605. [Google Scholar] [CrossRef]
- Saputra, R.E.; Astuti, Y.; Darmawan, A. Hydrophobicity of silica thin films: The deconvolution and interpretation by Fourier-transform infrared spectroscopy. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2018, 199, 12–20. [Google Scholar] [CrossRef]
- Ek, S.; Root, A.; Peussa, M.; Niinistö, L. Determination of the hydroxyl group content in silica by thermogravimetry and a comparison with 1H MAS NMR results. Thermochim. Acta 2001, 379, 201–212. [Google Scholar] [CrossRef]
- Maris, H. Phonon Scattering in Condensed Matter V. In Thermal Properties of Silica Gels; Springer: Berlin, Germany, 1986. [Google Scholar]
- Yang, X.; Zhu, L.; Chen, Y.; Bao, B.; Xu, J.; Zhou, W. Controlled hydrophilic/hydrophobic property of silica films by manipulating the hydrolysis and condensation of tetraethoxysilane. Appl. Surf. Sci. 2016, 376, 1–9. [Google Scholar] [CrossRef]
- Gutzov, S.; Danchova, N.; Karakashev, S.I.; Khristov, M.; Ivanova, J.; Ulbikas, J. Preparation and thermal properties of chemically prepared nanoporous silica aerogels. J. Sol-Gel Sci. Technol. 2014, 70, 511–516. [Google Scholar] [CrossRef]
- Innocenzi, P. Infrared spectroscopy of sol–gel derived silica-based films: A spectra-microstructure overview. J. Non. Cryst. Solids 2003, 316, 309–319. [Google Scholar] [CrossRef]
- Sen, P.N.; Thorpe, M.F. Phonons in AX2 glasses: From molecular to band-like modes. Phys. Rev. B 1977, 15, 4030–4038. [Google Scholar] [CrossRef]
- Galeener, F.L. Band limits and the vibrational spectra of tetrahedral glasses. Phys. Rev. B 1979, 19, 4292–4297. [Google Scholar] [CrossRef]
- Galeener, F.L.; Lucovsky, G. Longitudinal optical vibrations in glasses: GeO2 and SiO2. Phys. Rev. Lett. 1976, 37, 1474–1478. [Google Scholar] [CrossRef]
- Danchova, N.; Paskalev, D.; Gutzov, S. Aerogels—New materials with promising applications. Bulg. Chem. Commun. 2018, 50, 172–177. [Google Scholar]
- Fidalgo, A.; Ciriminna, R.; Ilharco, L.M.; Pagliaro, M. Role of the alkyl-alkoxide precursor on the structure and catalytic properties of hybrid sol-gel catalysts. Chem. Mater. 2005, 17, 6686–6694. [Google Scholar] [CrossRef]
- Capeletti, L.B.; Baibich, I.M.; Butler, I.S.; Santos, J.H.Z. dos Infrared and Raman spectroscopic characterization of some organic substituted hybrid silicas. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2014, 133, 619–625. [Google Scholar] [CrossRef]
- Thorpe, M.F.; Leeuw, S.W. de Coulomb effects in disordered solids. Phys. Rev. B 1986, 33, 8490–8505. [Google Scholar] [CrossRef]
- Jansson, P. Deconvolution: With Applications in Spectroscopy, 1st ed.; Academic Press: Cambridge, MA, USA, 1984. [Google Scholar]
- Rao, A.P.; Rao, A.V.; Pajonk, G. Hydrophobic and physical properties of the ambient pressure dried silica aerogels with sodium silicate precursor using various surface modification agents. Appl. Surf. Sci. 2007, 253, 6032–6040. [Google Scholar] [CrossRef]
- Yokogawa, H.; Yokoyama, M. Hydrophobic silica aerogels. J. Non. Cryst. Solids 1995, 186, 23–29. [Google Scholar] [CrossRef]
- Gregg, S.J.; Sing, K.S.W. Adsorbtion, Surface Area and Porosity; Academic Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Alothman, Z.A. A Review: Fundamental Aspects of Silicate Mesoporous Materials. Materials 2012, 5, 2874–2902. [Google Scholar] [CrossRef]
- Sing, K.S.W.; Everett, D.H.; Haul, R.A.W.; Moscoul, L.; Pierotti, R.A.; Rouquerol, J.; Seimieniewska, T. Reporting Physisorption Data for gas/Solid systems with Special Reference to the Determination of Surface Area and Porosity. Pure Appl. Chem. 1985, 57, 603–619. [Google Scholar] [CrossRef]
- Sing, K.S.W.; Williams, R.T. Physisorption Hysteresis Loops and the Characterization of Nanoporous Materials. Adsorpt. Sci. Technol. 2004, 22, 773–782. [Google Scholar] [CrossRef]
- Avnir, D.; Pfeifer, P. Fractal Dimension in Chemistry. An Intensive Characteristic of Surface Irregularity. Nouv. J. Chem 1983, 7, 71–72. [Google Scholar]
- Avnir, D.; Farin, D.; Pfeifer, P. Surface Geometric Irregularity of Particulate Materials: The Fractal Approach. J. Coll. Interface Sci. 1985, 103, 112–123. [Google Scholar] [CrossRef]
- Avnir, D.; Farin, D.; Pfeifer, P. Molecular fractal surfaces. Nature 1984, 308, 261–263. [Google Scholar] [CrossRef]
- Pfeifer, P.; Obert, M.; Cole, M.W. Fractal bet and FHH theories of adsorption: A comparative study. Proc. R. Soc. London. A. Math. Phys. Sci. 1989, 423, 169–188. [Google Scholar] [CrossRef]
- Ismail, I.; Pfeifer, P. Fractal analysis and surface roughness of nonporous carbon fibers and carbon blacks. Langmuir 1994, 10, 1532–1538. [Google Scholar] [CrossRef]
- Pfeifer, P.; Cole, M. Fractals in surface science: Scattering and thermodynamics of adsorbed films. II. New J. Chem. 1990, 14, 221–232. [Google Scholar]
- Mersmann, A.B.; Scholl, S.E. Fundamentals of Adsorption; Elsevier: New York, NY, USA, 1991. [Google Scholar]
- Pfeifer, P.; Wu, Y.J.; Cole, M.W.; Krim, J. Multilayer adsorption on a fractally rough surface. Phys. Rev. Lett. 1989, 62, 1997–2000. [Google Scholar] [CrossRef]
- Neimark, A.V. Determination of the surface fractal dimensionality from the results of an adsorption experiment. Russ.J.Phys. Chem. 1990, 64, 1397–1403. [Google Scholar]
- Neimark, A.V.; Ravikovitch, P.I. Capillary condensation in MMS and pore structure characterization. Micropor. Mesopor. Mater 2001, 44/45, 697–707. [Google Scholar] [CrossRef]
- Sahouli, B.; Blacher, S.; Brouers, F. Applicability of the fractal FHH equation. Langmuir 1997, 13, 4391–4394. [Google Scholar] [CrossRef]
- Venkatrman, A.; Fan, L.T.; Walawender, W.P. Fractal Analysis of a Sol–Gel-Derived Silica by Adsorption Revisited. J. Colloid Interface Sci. 1996, 183, 289–290. [Google Scholar] [CrossRef]
- Pfeifer, P.; Kenntner, J.; Cole, M.W. Fundamentals of Adsorption; LeVan, M.D., Ed.; Springer: Boston, MA, USA, 1993. [Google Scholar]
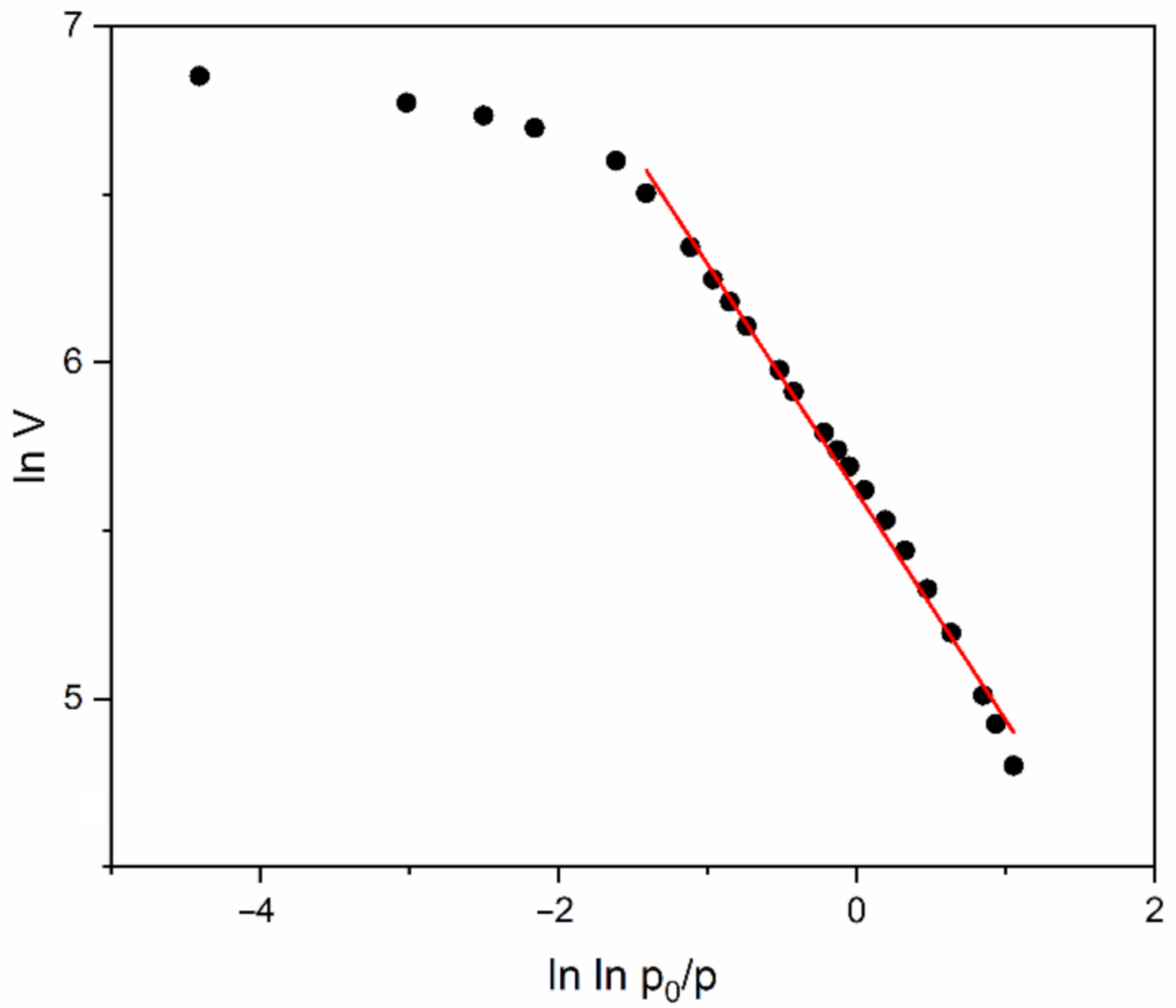
| Sample | α | ρ g/cm3 |
|---|---|---|
| MJ0 | 0 | 0.45 |
| MJ2 | 0.352 | 0.33 |
| MJ4 | 0.700 | 0.23 |
| MJ6 | 1.055 | 0.18 |
| MY8 | 1.407 | 0.20 |
| Sample; TO/LO Splitting | Peak Index | AreaIntg, - | FWHM cm−1 | Max Height - | Center cm−1 | AreaIntg, % |
|---|---|---|---|---|---|---|
| MJ0 160.3 cm−1 | 1 | 9.10 | 60.82 | 0.14 | 948.81 | 9.40 |
| 2 | 21.36 | 42.05 | 0.48 | 1040.84 | 22.06 | |
| 3 | 45.10 | 58.38 | 0.73 | 1070.83 | 46.58 | |
| 4 | 19.37 | 92.53 | 0.20 | 1131.65 | 20.01 | |
| 5 | 1.90 | 54.55 | 0.03 | 1201.10 | 1.96 | |
| 6 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| MJ2 163.8 cm−1 | 1 | 2.10 | 55.53 | 0.04 | 956.01 | 2.61 |
| 2 | 31.03 | 44.99 | 0.65 | 1045.12 | 38.58 | |
| 3 | 35.47 | 52.48 | 0.63 | 1075.94 | 44.10 | |
| 4 | 10.79 | 94.36 | 0.11 | 1143.47 | 13.42 | |
| 5 | 0.95 | 42.67 | 0.02 | 1208.96 | 1.18 | |
| 6 | 0.09 | 6.84 | 0.01 | 1256.28 | 0.11 | |
| MJ4 161.8 cm−1 | 1 | 1.06 | 45.96 | 0.02 | 955.75 | 1.42 |
| 2 | 10.25 | 38.17 | 0.25 | 1043.31 | 13.71 | |
| 3 | 56.78 | 64.25 | 0.83 | 1063.39 | 75.93 | |
| 4 | 4.72 | 60.74 | 0.07 | 1153.59 | 6.31 | |
| 5 | 1.81 | 49.63 | 0.03 | 1205.14 | 2.42 | |
| 6 | 0.16 | 7.89 | 0.02 | 1255.53 | 0.21 | |
| MJ6 165.7 cm−1 | 1 | 0.53 | 46.40 | 0.01 | 957.00 | 0.72 |
| 2 | 14.51 | 38.01 | 0.36 | 1045.07 | 19.82 | |
| 3 | 50.91 | 59.74 | 0.80 | 1068.75 | 69.53 | |
| 4 | 5.86 | 72.22 | 0.08 | 1155.84 | 8.00 | |
| 5 | 1.27 | 44.57 | 0.03 | 1210.80 | 1.73 | |
| 6 | 0.15 | 7.57 | 0.02 | 1255.78 | 0.20 | |
| MJ8 159.1 cm−1 | 1 | 0.85 | 48.67 | 0.02 | 958.34 | 1.13 |
| 2 | 9.93 | 37.15 | 0.25 | 1044.92 | 13.30 | |
| 3 | 57.41 | 64.44 | 0.84 | 1065.19 | 76.92 | |
| 4 | 4.24 | 55.74 | 0.07 | 1154.85 | 5.68 | |
| 5 | 2.04 | 50.21 | 0.04 | 1204.04 | 2.73 | |
| 6 | 0.18 | 7.89 | 0.02 | 1255.29 | 0.24 |
| Sample | SBET m2/g | Vt cm3/g | Dav Nm | Ds | α |
|---|---|---|---|---|---|
| MJ0 | 1008 | 1.01 | 4.0 | 2.75 | 0 |
| MJ2 | 888 | 0.83 | 4.6 | 2.80 | 0.352 |
| MJ4 | 860 | 1.47 | 6.0 | 2.60 | 0.7 |
| MJ6 | 872 | 2.06 | 7.0 | 2.55 | 1.055 |
| MY8 | 862 | 2.51 | 7.0 | 2.50 | 1.407 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shandurkov, D.; Ignatov, P.; Spassova, I.; Gutzov, S. Spectral and Texture Properties of Hydrophobic Aerogel Powders Obtained from Room Temperature Drying. Molecules 2021, 26, 1796. https://doi.org/10.3390/molecules26061796
Shandurkov D, Ignatov P, Spassova I, Gutzov S. Spectral and Texture Properties of Hydrophobic Aerogel Powders Obtained from Room Temperature Drying. Molecules. 2021; 26(6):1796. https://doi.org/10.3390/molecules26061796
Chicago/Turabian StyleShandurkov, Dimitar, Petar Ignatov, Ivanka Spassova, and Stoyan Gutzov. 2021. "Spectral and Texture Properties of Hydrophobic Aerogel Powders Obtained from Room Temperature Drying" Molecules 26, no. 6: 1796. https://doi.org/10.3390/molecules26061796
APA StyleShandurkov, D., Ignatov, P., Spassova, I., & Gutzov, S. (2021). Spectral and Texture Properties of Hydrophobic Aerogel Powders Obtained from Room Temperature Drying. Molecules, 26(6), 1796. https://doi.org/10.3390/molecules26061796








