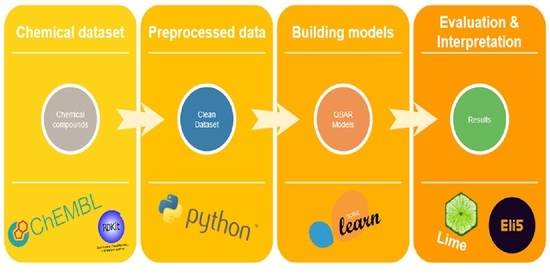
QSAR Models for Active Substances against Pseudomonas aeruginosa Using Disk-Diffusion Test Data
Abstract
1. Introduction
2. Results
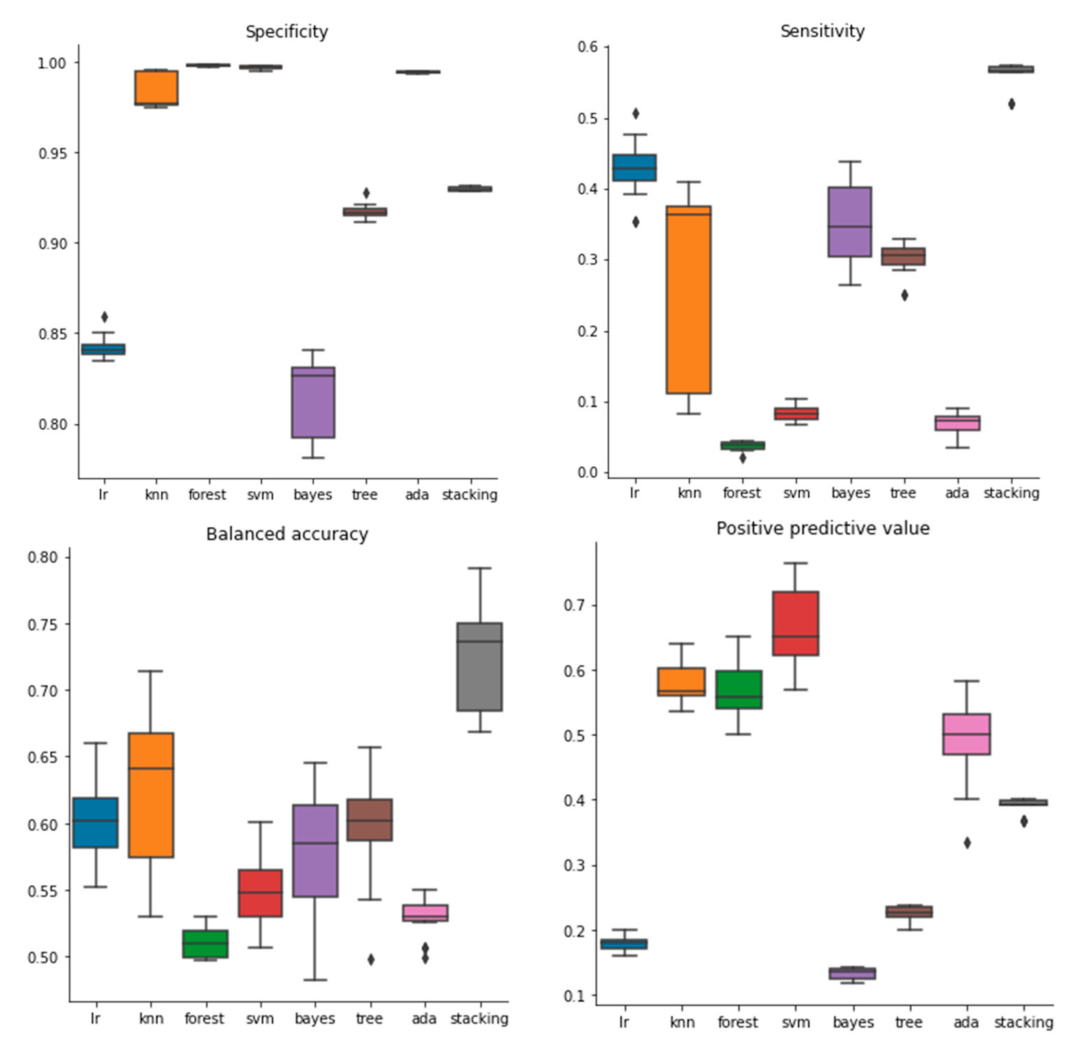
2.1. Performance of Models Built with Molecular Descriptors
2.2. Performance of Models Built with Molecular Fingerprints
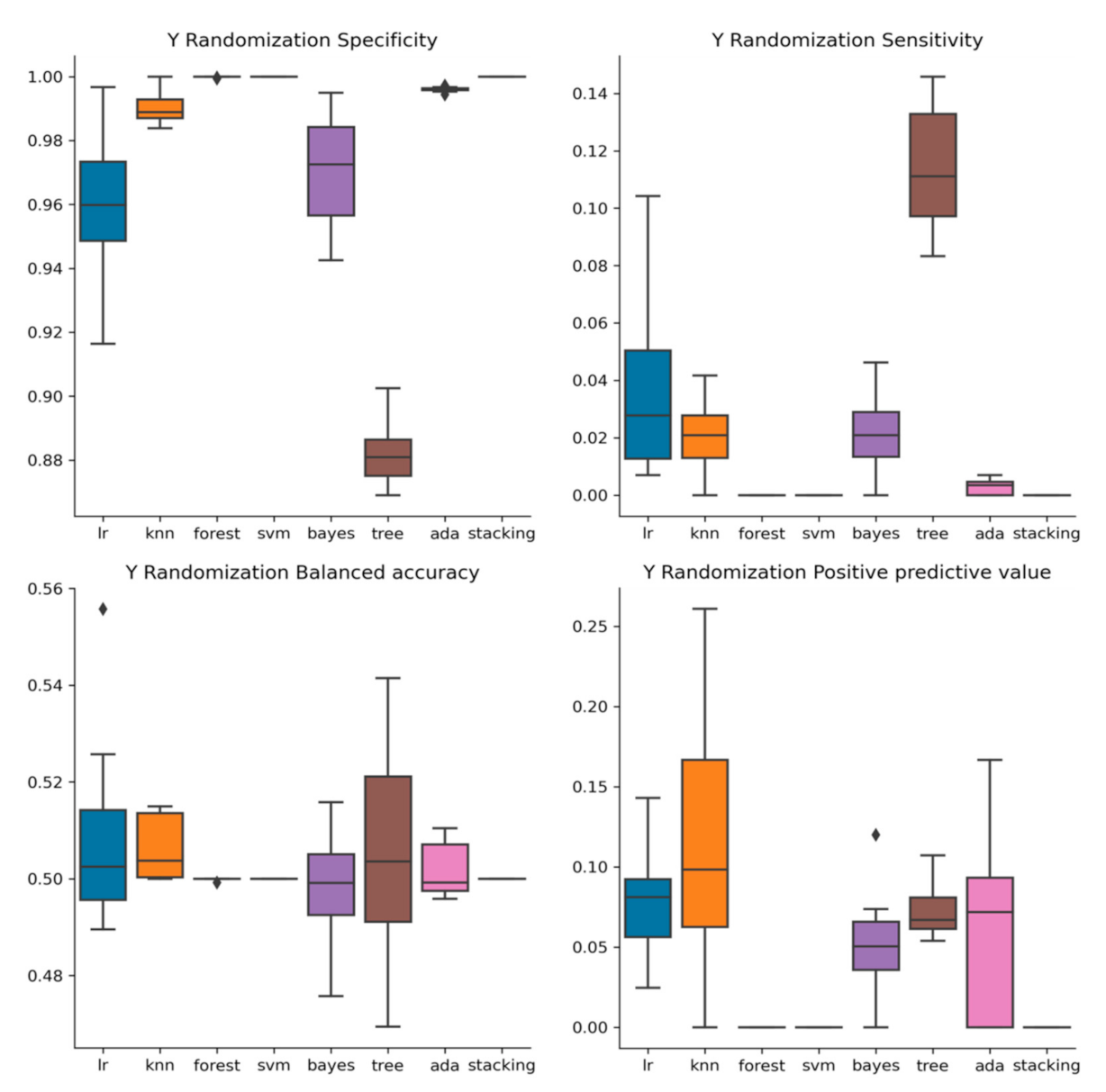
2.3. Y-Randomization
2.4. External Validation
2.5. Outliers and Applicability Domain
2.6. Descriptors
3. Discussion
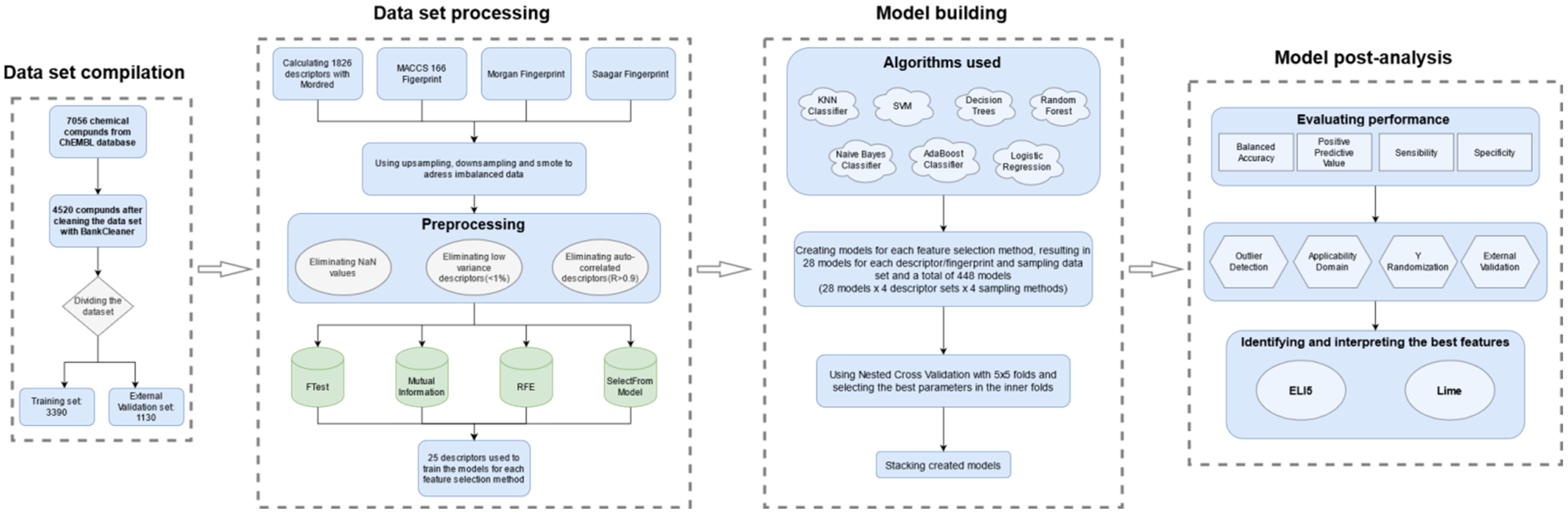
4. Materials and Methods
4.1. The Dataset
4.2. Descriptors and Feature Selection
4.3. Classification Algorithms
4.4. Performance Evaluation
4.5. Outlier Detection and Applicability Domain
4.6. External Validation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sharma, G.; Rao, S.; Bansal, A.; Dang, S.; Gupta, S.; Gabrani, R. Pseudomonas aeruginosa biofilm: Potential therapeutic targets. Biologicals 2014, 42, 1–7. [Google Scholar] [CrossRef]
- Azam, M.W.; Khan, A.U. Updates on the pathogenicity status of Pseudomonas aeruginosa. Drug Discov. Today 2019, 24, 350–359. [Google Scholar] [CrossRef]
- Moradali, M.F.; Ghods, S.; Rehm, B.H.A. Pseudomonas aeruginosa Lifestyle: A Paradigm for Adaptation, Survival, and Persistence. Front. Cell. Infect. Microbiol. 2017, 7, 39. [Google Scholar] [CrossRef]
- Botelho, J.; Grosso, F.; Peixe, L. Antibiotic resistance in Pseudomonas aeruginosa—Mechanisms, epidemiology and evolution. Drug Resist. Updates 2019, 44, 100640. [Google Scholar] [CrossRef]
- Oliver, A.; Mulet, X.; López-Causapé, C.; Juan, C. The increasing threat of Pseudomonas aeruginosa high-risk clones. Drug Resist. Updates 2015, 21–22, 41–59. [Google Scholar] [CrossRef] [PubMed]
- Paulsson, M.; Granrot, A.; Ahl, J.; Tham, J.; Resman, F.; Riesbeck, K.; Månsson, F. Antimicrobial combination treatment including ciprofloxacin decreased the mortality rate of Pseudomonas aeruginosa bacteraemia: A retrospective cohort study. Eur. J. Clin. Microbiol. Infect. Dis. 2017, 36, 1187–1196. [Google Scholar] [CrossRef]
- Tacconelli, E.; Carrara, E.; Savoldi, A.; Harbarth, S.; Mendelson, M.; Monnet, D.L.; Pulcini, C.; Kahlmeter, G.; Kluytmans, J.; Carmeli, Y.; et al. Discovery, research, and development of new antibiotics: The WHO priority list of antibiotic-resistant bacteria and tuberculosis. Lancet Infect. Dis. 2018, 18, 318–327. [Google Scholar] [CrossRef]
- Spellberg, B. The future of antibiotics. Crit. Care 2014, 18, 228. [Google Scholar] [CrossRef]
- Pang, Z.; Raudonis, R.; Glick, B.R.; Lin, T.-J.; Cheng, Z. Antibiotic resistance in Pseudomonas aeruginosa: Mechanisms and alternative therapeutic strategies. Biotechnol. Adv. 2019, 37, 177–192. [Google Scholar] [CrossRef]
- Bettiol, E.; Harbarth, S. Development of new antibiotics: Taking off finally? Swiss Med. Wkly. 2015, 145. [Google Scholar] [CrossRef] [PubMed]
- Gajdács, M. The Concept of an Ideal Antibiotic: Implications for Drug Design. Molecules 2019, 24, 892. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Wu, M.-B.; Lin, J.-P.; Yang, L.-R. Quantitative structure–activity relationship: Promising advances in drug discovery platforms. Expert Opin. Drug Discov. 2015, 10, 1283–1300. [Google Scholar] [CrossRef] [PubMed]
- Macalino, S.J.Y.; Billones, J.B.; Organo, V.G.; Carrillo, M.C.O. In Silico Strategies in Tuberculosis Drug Discovery. Molecules 2020, 25, 665. [Google Scholar] [CrossRef]
- Andrade, C.H.; Pasqualoto, K.F.M.; Ferreira, E.I.; Hopfinger, A.J. 4D-QSAR: Perspectives in Drug Design. Molecules 2010, 15, 3281–3294. [Google Scholar] [CrossRef] [PubMed]
- Aleksandrov, A.; Myllykallio, H. Advances and challenges in drug design against tuberculosis: Application of in silico approaches. Expert Opin. Drug Discov. 2018, 14, 35–46. [Google Scholar] [CrossRef] [PubMed]
- Halder, A.K.; Moura, A.S.; Cordeiro, M.N.D.S. QSAR modelling: A therapeutic patent review 2010-present. Expert Opin. Ther. Patents 2018, 28, 467–476. [Google Scholar] [CrossRef]
- Dobchev, D.A.; Karelson, M. Have artificial neural networks met expectations in drug discovery as implemented in QSAR framework? Expert Opin. Drug Discov. 2016, 11, 627–639. [Google Scholar] [CrossRef]
- Speck-Planche, A.; Kleandrova, V.V.; Cordeiro, M. Chemoinformatics for rational discovery of safe antibacterial drugs: Simultaneous predictions of biological activity against streptococci and toxicological profiles in laboratory animals. Bioorg. Med. Chem. 2013, 21, 2727–2732. [Google Scholar] [CrossRef]
- Nicolaou, C.A.; Brown, N. Multi-objective optimization methods in drug design. Drug Discov. Today Technol. 2013, 10, e427–e435. [Google Scholar] [CrossRef]
- Sánchez-Rodríguez, A.; Pérez-Castillo, Y.; Schürer, S.C.; Nicolotti, O.; Mangiatordi, G.F.; Borges, F.; Cordeiro, M.N.D.; Tejera, E.; Medina-Franco, J.L.; Cruz-Monteagudo, M. From flamingo dance to (desirable) drug discovery: A nature-inspired approach. Drug Discov. Today 2017, 22, 1489–1502. [Google Scholar] [CrossRef]
- Muresan, S.; Petrov, P.; Southan, C.; Kjellberg, M.J.; Kogej, T.; Tyrchan, C.; Varkonyi, P.; Xie, P.H. Making every SAR point count: The development of Chemistry Connect for the large-scale integration of structure and bioactivity data. Drug Discov. Today 2011, 16, 1019–1030. [Google Scholar] [CrossRef] [PubMed]
- Williams, A.J.; Ekins, S.; Tkachenko, V. Towards a gold standard: Regarding quality in public domain chemistry databases and approaches to improving the situation. Drug Discov. Today 2012, 17, 685–701. [Google Scholar] [CrossRef]
- Kalliokoski, T.; Kramer, C.; Vulpetti, A.; Gedeck, P. Comparability of Mixed IC50 Data—A Statistical Analysis. PLoS ONE 2013, 8, e61007. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, J.H.; Turnidge, J.D. Susceptibility test methods: Dilution and disk diffusion methods. In Manual of Clinical Microbiology; Jorgensen, J.H., Pfaller, M.A., Carroll, K.C., Landry, M.L., Funke, G., Richter, S.S., Warnock, D.V., Eds.; ASM Press: Washington, DC, USA, 2015; Volume 1, pp. 1253–1273. [Google Scholar]
- Sahigara, F.; Ballabio, D.; Todeschini, R.; Consonni, V. Defining a novel k-nearest neighbours approach to assess the applicability domain of a QSAR model for reliable predictions. J. Cheminform. 2013, 5, 27. [Google Scholar] [CrossRef] [PubMed]
- Datar, P.A. 2D-QSAR Study of Indolylpyrimidines Derivative as Antibacterial against Pseudomonas Aeruginosa and Staphylococcus Aureus: A Comparative Approach. J. Comput. Med. 2014, 2014. [Google Scholar] [CrossRef]
- Aleksic, I.; Jeremic, J.; Milivojevic, D.; Ilic-Tomic, T.; Šegan, S.; Zlatović, M.; Opsenica, D.M.; Senerovic, L. N-Benzyl Derivatives of Long-Chained 4-Amino-7-chloro-quionolines as Inhibitors of Pyocyanin Production in Pseudomonas aeruginosa. ACS Chem. Biol. 2019, 14, 2800–2809. [Google Scholar] [CrossRef] [PubMed]
- Kadam, R.U.; Roy, N. Cluster analysis and two-dimensional quantitative structure–activity relationship (2D-QSAR) of Pseudomonas aeruginosa deacetylase LpxC inhibitors. Bioorg. Med. Chem. Lett. 2006, 16, 5136–5143. [Google Scholar] [CrossRef] [PubMed]
- Zuo, K.; Liang, L.; Du, W.; Sun, X.; Liu, W.; Gou, X.; Wan, H.; Hu, J. 3D-QSAR, Molecular Docking and Molecular Dynamics Simulation of Pseudomonas aeruginosa LpxC Inhibitors. Int. J. Mol. Sci. 2017, 18, 761. [Google Scholar] [CrossRef]
- Speck-Planche, A.; Cordeiro, M.N.D.S. Computer-Aided Discovery in Antimicrobial Research: In Silico Model for Virtual Screening of Potent and Safe Anti-Pseudomonas Agents. Comb. Chem. High Throughput Screen. 2015, 18, 305–314. [Google Scholar] [CrossRef]
- Humphries, R.M.; Kircher, S.; Ferrell, A.; Krause, K.M.; Malherbe, R.; Hsiung, A.; Burnham, C.-A.D. The Continued Value of Disk Diffusion for Assessing Antimicrobial Susceptibility in Clinical Laboratories: Report from the Clinical and Laboratory Standards Institute Methods Development and Standardization Working Group. J. Clin. Microbiol. 2018, 56. [Google Scholar] [CrossRef]
- Yao, H.; Liu, J.; Jiang, X.; Chen, F.; Lu, X.; Zhang, J. Analysis of the Clinical Effect of Combined Drug Susceptibility to Guide Medication for Carbapenem-Resistant Klebsiella pneumoniae Patients Based on the Kirby–Bauer Disk Diffusion Method. Infect. Drug Resist. 2021, 14, 79–87. [Google Scholar] [CrossRef]
- Henwood, C.J.; Livermore, D.M.; James, D.; Warner, M. The Pseudomonas Study Group. Antimicrobial susceptibility of Pseudomonas aeruginosa: Results of a UK survey and evaluation of the British Society for Antimicrobial Chemotherapy disc susceptibility test. J. Antimicrob. Chemother. 2001, 47, 789–799. [Google Scholar] [CrossRef]
- Clinical and Laboratory Standards Institute. Performance Standards for Antimicrobial Susceptibility Testing, 30th ed.; CLSI Supplement M100; Clinical and Laboratory Standards Institute: Wayne, PA, USA, 2020; ISBN 978-1-68440-066-9. [Google Scholar]
- The European Committee on Antimicrobial Susceptibility Testing: Breakpoint Tables for Interpretation of MICs and Zone Diameters, Version 11.0 2021. Available online: https://eucast.org/clinical_breakpoints/ (accessed on 10 January 2021).
- Van, T.T.; Minejima, E.; Chiu, C.A.; Butler-Wu, S.M. Don’t Get Wound Up: Revised Fluoroquinolone Breakpoints for Enterobacteriaceae and Pseudomonas aeruginosa. J. Clin. Microbiol. 2019, 57. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Taylor, T.H.; Pettus, K.; Trees, D. Assessment of Etest as an Alternative to Agar Dilution for Antimicrobial Susceptibility Testing of Neisseria gonorrhoeae. J. Clin. Microbiol. 2014, 52, 1435–1440. [Google Scholar] [CrossRef] [PubMed]
- Cao, G.; Arooj, M.; Thangapandian, S.; Park, C.; Arulalapperumal, V.; Kim, Y.; Kwon, Y.; Kim, H.; Suh, J.; Lee, K. A lazy learning-based QSAR classification study for screening potential histone deacetylase 8 (HDAC8) inhibitors. SAR QSAR Environ. Res. 2015, 26, 397–420. [Google Scholar] [CrossRef]
- Zhao, L.; Xiang, Y.; Song, J.; Zhang, Z. A novel two-step QSAR modeling work flow to predict selectivity and activity of HDAC inhibitors. Bioorg. Med. Chem. Lett. 2013, 23, 929–933. [Google Scholar] [CrossRef] [PubMed]
- Luo, M.; Wang, X.S.; Tropsha, A. Comparative Analysis of QSAR-based vs. Chemical Similarity Based Predictors of GPCRs Binding Affinity. Mol. Inform. 2015, 35, 36–41. [Google Scholar] [CrossRef] [PubMed]
- Korotcov, A.; Tkachenko, V.; Russo, D.P.; Ekins, S. Comparison of Deep Learning With Multiple Machine Learning Methods and Metrics Using Diverse Drug Discovery Data Sets. Mol. Pharm. 2017, 14, 4462–4475. [Google Scholar] [CrossRef] [PubMed]
- Simeon, S.; Jongkon, N. Construction of Quantitative Structure Activity Relationship (QSAR) Models to Predict Potency of Structurally Diversed Janus Kinase 2 Inhibitors. Molecules 2019, 24, 4393. [Google Scholar] [CrossRef] [PubMed]
- Heikamp, K.; Bajorath, J. Support vector machines for drug discovery. Expert Opin. Drug Discov. 2013, 9, 93–104. [Google Scholar] [CrossRef]
- Darnag, R.; Minaoui, B.; Fakir, M. QSAR models for prediction study of HIV protease inhibitors using support vector machines, neural networks and multiple linear regression. Arab. J. Chem. 2017, 10, S600–S608. [Google Scholar] [CrossRef]
- Goya-Jorge, E.; Giner, R.M.; Veitía, M.S.-I.; Gozalbes, R.; Barigye, S.J. Predictive modeling of aryl hydrocarbon receptor (AhR) agonism. Chemosphere 2020, 256, 127068. [Google Scholar] [CrossRef] [PubMed]
- Guan, D.; Fan, K.; Spence, I.; Matthews, S. Combining machine learning models of in vitro and in vivo bioassays improves rat carcinogenicity prediction. Regul. Toxicol. Pharmacol. 2018, 94, 8–15. [Google Scholar] [CrossRef] [PubMed]
- Marrero-Ponce, Y.; Marrero, R.M.; Torrens, F.; Martinez, Y.; Bernal, M.G.; Zaldivar, V.R.; Castro, E.A.; Abalo, R.G. Non-stochastic and stochastic linear indices of the molecular pseudograph’s atom-adjacency matrix: A novel approach for computational in silico screening and “rational” selection of new lead antibacterial agents. J. Mol. Model. 2005, 12, 255–271. [Google Scholar] [CrossRef] [PubMed]
- Fassihi, A.; Abedi, D.; Saghaie, L.; Sabet, R.; Fazeli, H.; Bostaki, G.; Deilami, O.; Sadinpour, H. Synthesis, antimicrobial evaluation and QSAR study of some 3-hydroxypyridine-4-one and 3-hydroxypyran-4-one derivatives. Eur. J. Med. Chem. 2009, 44, 2145–2157. [Google Scholar] [CrossRef]
- Shanmugam, G.; Syed, M.; Natarajan, J. 2D-and 3D-QSAR Study of Acyl Homoserine Lactone Derivatives as Potent Inhibitors of Quorum Sensor, SdiA in Salmonella typhimurium. Int. J. Bioautomat. 2016, 20, 441. [Google Scholar]
- Lagorce, D.; Sperandio, O.; Baell, J.B.; Miteva, M.A.; Villoutreix, B.O. FAF-Drugs3: A web server for compound property calculation and chemical library design. Nucleic Acids Res. 2015, 43, W200–W207. [Google Scholar] [CrossRef]
- Lagorce, D.; Oliveira, N.; Miteva, M.A.; Villoutreix, B.O. Pan-assay interference compounds (PAINS) that may not be too painful for chemical biology projects. Drug Discov. Today 2017, 22, 1131–1133. [Google Scholar] [CrossRef]
- Tropsha, A. Best Practices for QSAR Model Development, Validation, and Exploitation. Mol. Inform. 2010, 29, 476–488. [Google Scholar] [CrossRef]
- Cao, D.-S.; Xiao, N.; Xu, Q.-S.; Chen, A.F. Rcpi: R/Bioconductor package to generate various descriptors of proteins, compounds and their interactions. Bioinformatics 2014, 31, 279–281. [Google Scholar] [CrossRef]
- Moerbeke, M.V. IntClust: Integration of Multiple Data Sets with Clustering Techniques, version 0.1.0; 2018. Available online: https://CRAN.R-project.org/package=IntClust (accessed on 11 January 2021).
- Hahsler, M.; Hornik, K.; Buchta, C. Getting Things in Order: An Introduction to theRPackageseriation. J. Stat. Softw. 2008, 25, 1–34. [Google Scholar] [CrossRef]
- Moriwaki, H.; Tian, Y.-S.; Kawashita, N.; Takagi, T. Mordred: A molecular descriptor calculator. J. Cheminform. 2018, 10, 1–14. [Google Scholar] [CrossRef]
- RDKit: Open-Source Cheminformatics Software. Available online: https://www.rdkit.org. (accessed on 3 March 2021).
- Sedykh, A.Y.; Shah, R.R.; Kleinstreuer, N.C.; Auerbach, S.S.; Gombar, V.K. Saagar–A New, Extensible Set of Molecular Substructures for QSAR/QSPR and Read-Across Predictions. Chem. Res. Toxicol. 2020, 34, 634–640. [Google Scholar] [CrossRef] [PubMed]
- Guha, R. Chemical Informatics Functionality inR. J. Stat. Softw. 2007, 18, 1–16. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Song, Q.; Jiang, H.; Liu, J. Feature selection based on FDA and F-score for multi-class classification. Expert Syst. Appl. 2017, 81, 22–27. [Google Scholar] [CrossRef]
- Akay, M.F. Support vector machines combined with feature selection for breast cancer diagnosis. Expert Syst. Appl. 2009, 36, 3240–3247. [Google Scholar] [CrossRef]
- Vergara, J.R.; Estévez, P.A. A review of feature selection methods based on mutual information. Neural Comput. Appl. 2013, 24, 175–186. [Google Scholar] [CrossRef]
- Ross, B.C. Mutual Information between Discrete and Continuous Data Sets. PLoS ONE 2014, 9, e87357. [Google Scholar] [CrossRef]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene Selection for Cancer Classification using Support Vector Machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Kramer, O. K-Nearest Neighbors. In Dimensionality Reduction with Unsupervised Nearest Neighbors; Intelligent Systems Reference Library; Springer: Berlin/Heidelberg, Germany, 2013; Volume 51, pp. 13–23. ISBN 978-3-642-38651-0. [Google Scholar]
- Zhang, Z. Introduction to machine learning: K-nearest neighbors. Ann. Transl. Med. 2016, 4, 218. [Google Scholar] [CrossRef] [PubMed]
- Batista, G.; Silva, D.F. How K-Nearest Neighbor Parameters Affect Its Performance. In Proceedings of the Argentine Symposium on Artificial Intelligence, Mar Del Plata, Argentina, 24–25 August 2009; pp. 1–12. [Google Scholar]
- Lavanya, D. Ensemble Decision Tree Classifier for Breast Cancer Data. Int. J. Inf. Technol. Converg. Serv. 2012, 2, 17–24. [Google Scholar] [CrossRef]
- Priyanka, N.; Kumar, D. Decision tree classifier: A detailed survey. Int. J. Inf. Decis. Sci. 2020, 12, 246. [Google Scholar] [CrossRef]
- Feretzakis, G.; Kalles, D.; Verykios, V.S. On Using Linear Diophantine Equations for in-Parallel Hiding of Decision Tree Rules. Entropy 2019, 21, 66. [Google Scholar] [CrossRef]
- Climent, M.T.; Pardo, J.; Muñoz-Almaraz, F.J.; Guerrero, M.D.; Moreno, L. Decision Tree for Early Detection of Cognitive Impairment by Community Pharmacists. Front. Pharmacol. 2018, 9, 1232. [Google Scholar] [CrossRef]
- Qian, Y.; Zhou, W.; Yan, J.; Li, W.; Han, L. Comparing Machine Learning Classifiers for Object-Based Land Cover Classification Using Very High Resolution Imagery. Remote Sens. 2014, 7, 153–168. [Google Scholar] [CrossRef]
- Oshiro, T.M.; Perez, P.S.; Baranauskas, J.A. How Many Trees in a Random Forest? In Machine Learning and Data Mining in Pattern Recognition; Perner, P., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; pp. 154–168. [Google Scholar] [CrossRef]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random Forests. In Ensemble Machine Learning; Zhang, C., Ma, Y.Q., Eds.; Springer: New York, NY, USA, 2012; pp. 157–175. [Google Scholar] [CrossRef]
- Ali, J.; Khan, R.; Ahmad, N.; Maqsood, I. Random Forests and Decision Trees. Int. J. Comput. Sci. Issues 2012, 9, 272. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. Random Forests. In Ensemble Machine Learning; Zhang, C., Ma, Y., Eds.; Springer: Boston, MA, USA, 2008; pp. 587–604. [Google Scholar] [CrossRef]
- Pisner, D.A.; Schnyer, D.M. Support Vector Machine. In Machine Learning; Elsevier: Amsterdam, The Netherlands, 2020; pp. 101–121. [Google Scholar] [CrossRef]
- Ali, L.; Wajahat, I.; Golilarz, N.A.; Keshtkar, F.; Bukhari, S.A.C. LDA–GA–SVM: Improved hepatocellular carcinoma prediction through dimensionality reduction and genetically optimized support vector machine. Neural Comput. Appl. 2020, 1–10. [Google Scholar] [CrossRef]
- He, Y.-L.; Zhao, Y.; Hu, X.; Yan, X.-N.; Zhu, Q.-X.; Xu, Y. Fault diagnosis using novel AdaBoost based discriminant locality preserving projection with resamples. Eng. Appl. Artif. Intell. 2020, 91, 103631. [Google Scholar] [CrossRef]
- Rahman, S.; Irfan, M.; Raza, M.; Ghori, K.M.; Yaqoob, S.; Awais, M. Performance Analysis of Boosting Classifiers in Recognizing Activities of Daily Living. Int. J. Environ. Res. Public Health 2020, 17, 1082. [Google Scholar] [CrossRef] [PubMed]
- Ontivero-Ortega, M.; Lage-Castellanos, A.; Valente, G.; Goebel, R.; Valdes-Sosa, M. Fast Gaussian Naïve Bayes for searchlight classification analysis. NeuroImage 2017, 163, 471–479. [Google Scholar] [CrossRef] [PubMed]
- Raizada, R.D.S.; Lee, Y.-S. Smoothness without Smoothing: Why Gaussian Naive Bayes Is Not Naive for Multi-Subject Searchlight Studies. PLoS ONE 2013, 8, e69566. [Google Scholar] [CrossRef]
- Musa, A.B. Comparative study on classification performance between support vector machine and logistic regression. Int. J. Mach. Learn. Cybern. 2012, 4, 13–24. [Google Scholar] [CrossRef]
- Raevsky, O.A.; Grigorev, V.Y.; Yarkov, A.V.; Polianczyk, D.E.; Tarasov, V.V.; Bovina, E.V.; Bryzhakina, E.N.; Dearden, J.C.; Avila-Rodriguez, M.; Aliev, G. Classification (Agonist/Antagonist) and Regression “Structure-Activity” Models of Drug Interaction with 5-HT6. Cent. Nerv. Syst. Agents Med. Chem. 2018, 18, 213–221. [Google Scholar] [CrossRef] [PubMed]
- Radovanović, S.; Delibašić, B.; Jovanović, M.; Vukićević, M.; Suknović, M. Framework for Integration of Do-main Knowledge into Logistic Regression. In Proceedings of the 8th International Conference on Web Intelligence, Mining and Semantics, ACM, Novi Sad, Serbia, 25–27 June 2018; pp. 1–8. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, P.; Gao, Z.; Wang, R.; Khalighi, K. Ensemble of machine learning algorithms using the stacked generalization approach to estimate the warfarin dose. PLoS ONE 2018, 13, e0205872. [Google Scholar] [CrossRef] [PubMed]
- Lemaître, G.; Nogueira, F.; Aridas, C.K. Imbalanced-Learn: A Python Toolbox to Tackle the Curse of Imbal-anced Datasets in Machine Learning. J. Mach. Learn. Res. 2017, 18, 1–5. [Google Scholar]
- Wang, F.; Kaushal, R.; Khullar, D. Should Health Care Demand Interpretable Artificial Intelligence or Accept “Black Box” Medicine? Ann. Intern. Med. 2019, 172, 59. [Google Scholar] [CrossRef] [PubMed]
- ELI5. Available online: https://eli5.readthedocs.io/en/latest/ (accessed on 4 March 2021).
- Lime. Available online: https://github.com/marcotcr/lime (accessed on 4 March 2021).
- Cawley, G.C.; Talbot, N.L. On Over-Fitting in Model Selection and Subsequent Selection Bias in Performance Evaluation. J. Mach. Learn. Res. 2010, 11, 2079–2107. [Google Scholar]
- Vabalas, A.; Gowen, E.; Poliakoff, E.; Casson, A.J. Machine learning algorithm validation with a limited sample size. PLoS ONE 2019, 14, e0224365. [Google Scholar] [CrossRef]
- Yang, H.; Du, Z.; Lv, W.-J.; Zhang, X.-Y.; Zhai, H.-L. In silico toxicity evaluation of dioxins using structure–activity relationship (SAR) and two-dimensional quantitative structure–activity relationship (2D-QSAR). Arch. Toxicol. 2019, 93, 3207–3218. [Google Scholar] [CrossRef] [PubMed]
- Ben-Gal, I. Outlier Detection. In Data Mining and Knowledge Discovery Handbook; Maimon, O., Rokach, L., Eds.; Springer: New York, NY, USA, 2005; pp. 131–146. [Google Scholar]
- Domingues, R.; Filippone, M.; Michiardi, P.; Zouaoui, J. A Comparative Evaluation of Outlier Detection Algorithms: Experiments and Analyses. Pattern Recognit. 2018, 74, 406–421. [Google Scholar] [CrossRef]
- Gajewicz, A. How to judge whether QSAR/read-across predictions can be trusted: A novel approach for establishing a model’s applicability domain. Environ. Sci. Nano 2017, 5, 408–421. [Google Scholar] [CrossRef]
- Grenet, I.; Merlo, K.; Comet, J.P.; Tertiaux, R.; Rouquié, D.; Dayan, F. Stacked Generalization with Applicability Domain Outperforms Simple QSAR on in Vitro Toxicological Data. J. Chem. Inf. Model. 2019, 59, 1486–1496. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bugeac, C.A.; Ancuceanu, R.; Dinu, M. QSAR Models for Active Substances against Pseudomonas aeruginosa Using Disk-Diffusion Test Data. Molecules 2021, 26, 1734. https://doi.org/10.3390/molecules26061734
Bugeac CA, Ancuceanu R, Dinu M. QSAR Models for Active Substances against Pseudomonas aeruginosa Using Disk-Diffusion Test Data. Molecules. 2021; 26(6):1734. https://doi.org/10.3390/molecules26061734
Chicago/Turabian StyleBugeac, Cosmin Alexandru, Robert Ancuceanu, and Mihaela Dinu. 2021. "QSAR Models for Active Substances against Pseudomonas aeruginosa Using Disk-Diffusion Test Data" Molecules 26, no. 6: 1734. https://doi.org/10.3390/molecules26061734
APA StyleBugeac, C. A., Ancuceanu, R., & Dinu, M. (2021). QSAR Models for Active Substances against Pseudomonas aeruginosa Using Disk-Diffusion Test Data. Molecules, 26(6), 1734. https://doi.org/10.3390/molecules26061734