1. Introduction
The development and application of methods of artificial evolution such as SELEX and in vitro selection has led to the discovery of myriad RNA and DNA molecules with interesting and useful properties [
1,
2,
3,
4,
5]. For instance, aptamers have been identified that bind diverse classes of ligands, often with affinities in the nanomolar to picomolar range [
6]. Ribozymes and deoxyribozymes that enhance reaction rates by factors of more than 10
6-fold (and sometimes much more) have also been described [
7]. Because nucleic acids (especially DNA molecules) are relatively inexpensive to synthesize and easy to work with, for some applications they represent promising alternatives to proteins. Examples include the use of aptamers as artificial antibodies [
8], allosterically regulated ribozymes and deoxyribozymes as sensors [
9,
10], fluorescent aptamers as genetic reporters [
11,
12,
13], and RNA-cleaving ribozymes and deoxyribozymes that recognize substrates by base pairing as artificial nucleases [
14].
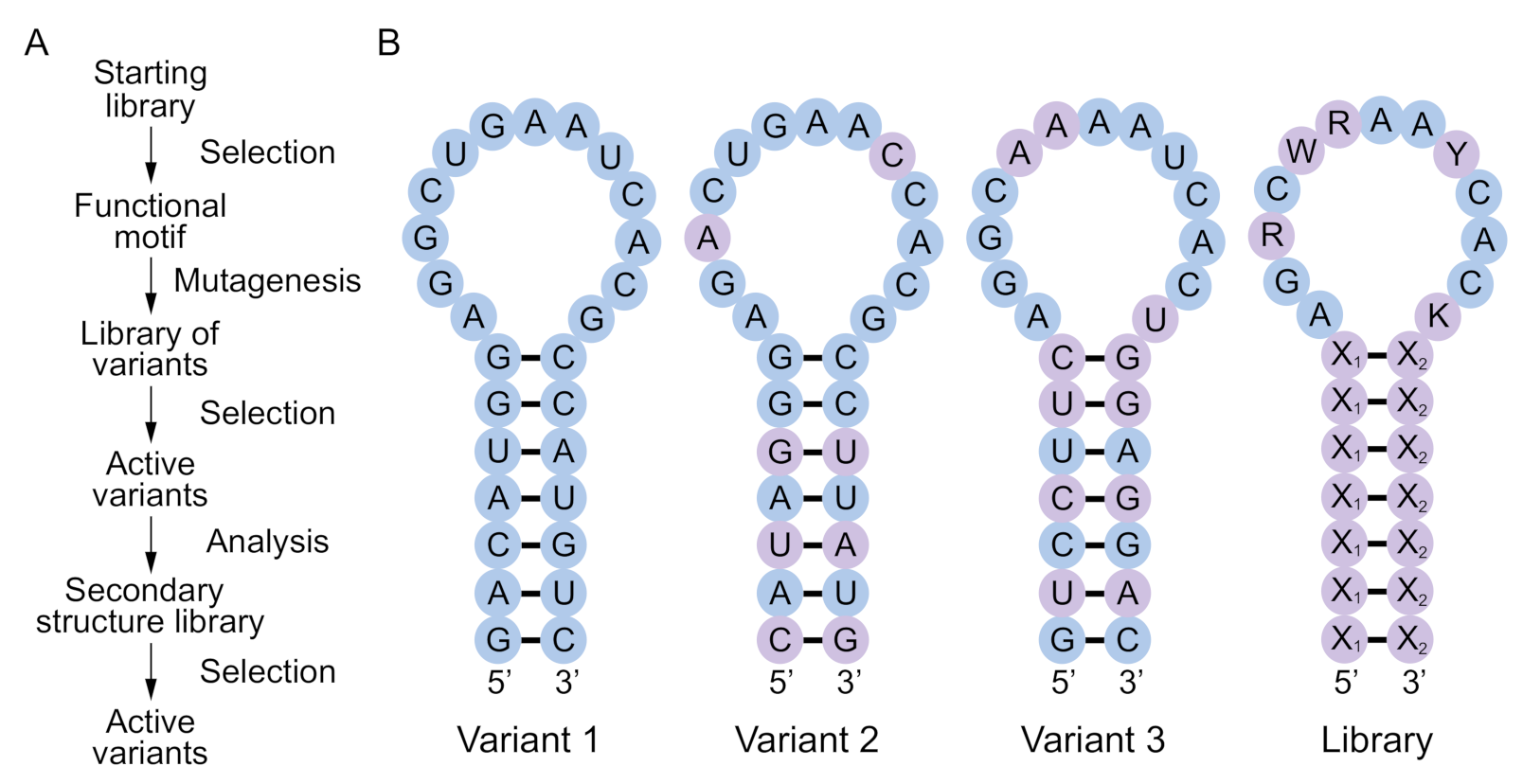
Functional RNA and DNA motifs are typically identified by synthesizing libraries containing ~10
15 random sequences and purifying rare variants with a desired biochemical function by iterative cycles of selection and amplification (
Figure 1A). Most selection experiments use libraries containing at least 40 randomized positions. The number of possible RNA or DNA sequences of this length is many orders of magnitude larger than 10
15. For example, the number of possible variants of a 40-nucleotide sequence is 4
40 = 1.2 × 10
24. This means that functional sequences identified in an initial selection experiment are unlikely to include the most active variants of the motif. More efficient variants can typically be identified by generating a second library by randomly mutating a single example of the motif (usually at a rate of 15% to 25% per position) and performing another selection experiment (
Figure 1A) [
15,
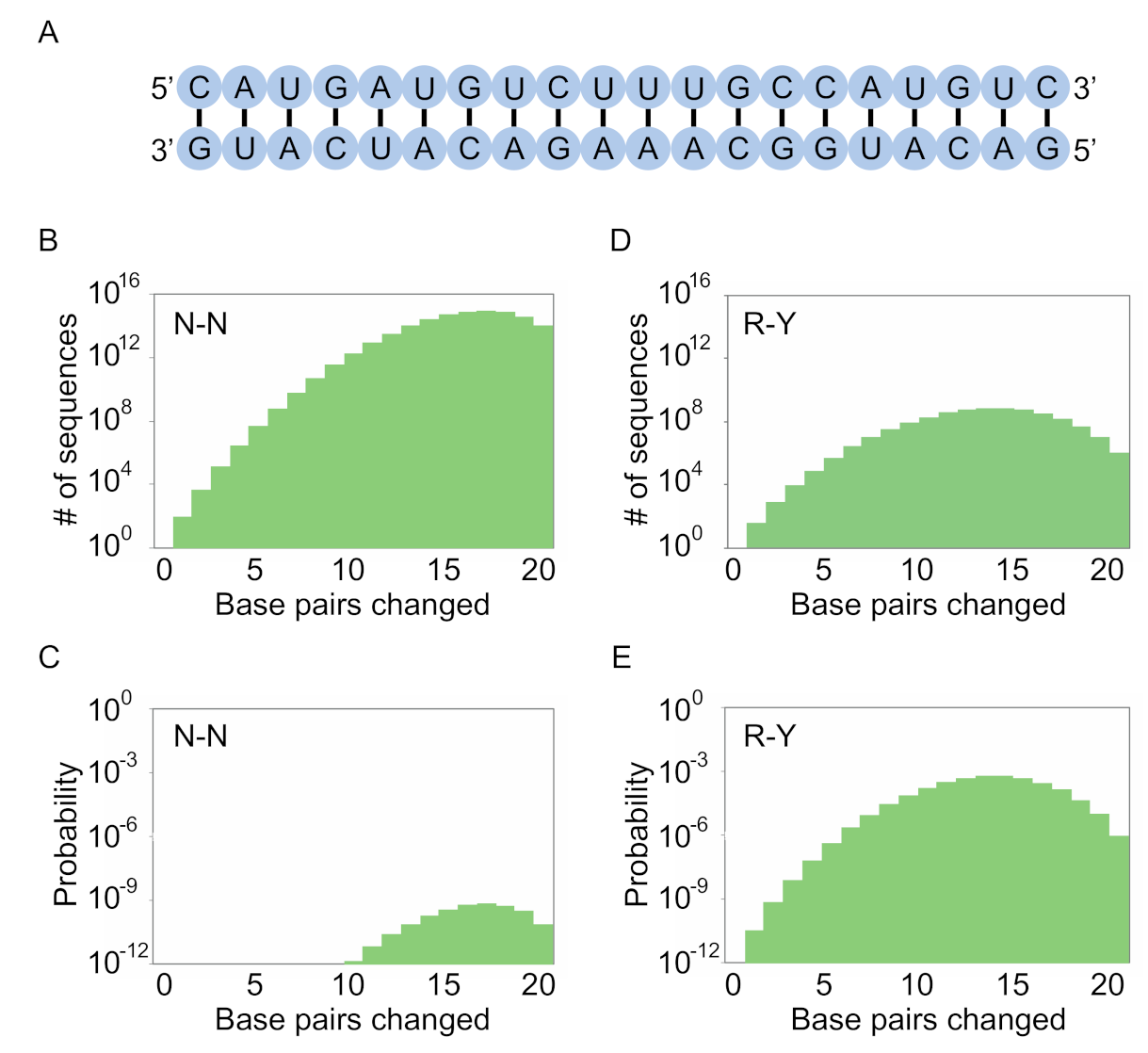
16]. However, such variants are still unlikely to represent global optima, because only a small fraction of the possible sequences with the secondary structure of the motif will have been present in either the initial random sequence library or the library used in the reselection. One way to appreciate this point is to consider the probability of obtaining variants of a secondary structure in a randomly mutagenized library in which all base pairs differ from those present in the starting sequence (see also [
16,
17]). For instance, in a library generated by randomly mutating a single variant of a motif made up of canonical base pairs (A-U, U-A, C-G, or G-C) at a standard rate of 20% per position, the probability of obtaining a canonical pair that differs from that present in the starting sequence is 0.013. For a secondary structure with 15 canonical pairs, the probability of obtaining a variant in which each of these pairs has changed to another canonical pair is therefore 0.013
15 = 7.5 × 10
−29. When the original base pairs can also change to G.U or U.G wobble pairs, this probability is 0.071
15 = 6.0 × 10
−18, which is considerably higher but still extremely low. These probabilities indicate that the 3
15 = 1.4 × 10
7 possible variants of the secondary structure in which each of the 15 base pairs present in the original variant has changed to a different canonical pair, or the 5
15 = 3.1 × 10
10 possible variants in which the original pair has changed to either a canonical or wobble pair, will be poorly represented, even in large randomly mutagenized libraries.
Motivated by this limitation, here we describe a simple method to synthesize libraries enriched for sequences with the potential to form a secondary structure of interest, such as that of an aptamer, ribozyme, or deoxyribozyme (
Figure 1B). Our approach does not use folding algorithms, so it can in principle be applied to any motif for which the sequence requirements are known. A library synthesized in such a way will contain a larger number of unique sequences with the potential to form a desired secondary structure than one generated by random mutagenesis, which should increase the probability of finding variants with improved or altered functions. In addition, analysis of the active variants of a motif in such a library by comparative sequence analysis can yield valuable information about interactions in the secondary and tertiary structure of the motif [
16,
18,
19,
20]. A secondary structure library as described in
Figure 1 cannot be generated in a single synthesis using current methods of solid-phase synthesis. By using biased nucleotide ratios, however, it is possible to modulate the probability that two positions in the library will have the potential to form an interaction such as a base pair [
21]. To further explore this idea, here we describe the possible ways a base pair can be encoded using degenerate positions, and show that different coding schemes involve a tradeoff between maximizing the probability of forming a base pair and maximizing the number of different types of base pairs that can occur in the library. We then determine the optimal coding scheme (which maximizes the number of unique sequences in a library with the potential to form a given secondary structure) for a range of model stems in which the number of base pairs is systematically varied. We also describe a split-and-pool strategy that can be used in combination with degenerate bases to synthesize secondary structure libraries. This can increase the fraction of library members with the potential to form a desired stem or secondary structure, but requires multiple oligonucleotides to be synthesized for each library. Finally, we propose designs for secondary structure libraries based on three functional motifs of increasing complexity from the literature: a 29-nucleotide streptavidin aptamer made of DNA [
22], a 40-nucleotide ATP aptamer made of RNA [
23,
24,
25], and a 50-nucleotide kinase ribozyme that thiophosphorylates itself using GTPγS as a substrate [
19,
20]. Our calculations indicate that these libraries contain up to 676-fold more unique sequences with the potential to form the desired secondary structure than libraries generated by random mutagenesis. We anticipate that secondary structure libraries of the type described here will facilitate the optimization and structural characterization of functional nucleic acids by significantly increasing the number of variants of a motif that can be sampled in a single artificial evolution experiment. In some cases, such libraries could also provide access to sequences that represent global maxima with respect to a given secondary structure and biochemical function (note that this is not necessarily the global maximum with respect to all possible sequences of a given length).
3. Discussion
DNA and RNA motifs with a range of functions have been identified in artificial evolution experiments [
1,
2,
3,
4,
5]. In most cases these motifs are initially isolated from random sequence libraries containing ~10
15 different sequences. Once the sequence of a functional motif is known, the sequence space around it is explored using a second library generated by randomly mutating a single variant of the motif at a rate of 15% to 25% per position. This library is usually generated by solid-phase synthesis, although mutagenic PCR can also be used when lower rates of mutagenesis (on the order of 1% per position) are desired [
26]. The synthetic protocol can also be modified in various ways to incorporate deletions [
27,
28]. Selections using such libraries often yield variants with improved biochemical properties, and also provide valuable information about the sequence requirements and secondary structure of the motif [
15,
16,
19,
20]. However, such experiments are unlikely to identify the most active variant of the motif. This is due to incomplete sampling: sequence space is vast, and only a tiny fraction of the possible variants of a given secondary structure are likely to be present in the neighborhood of a single sequence. Here we describe a method to more effectively explore the sequence space of a secondary structure of interest. Our method uses biased nucleotide frequencies to increase the probability that paired positions in the secondary structure of the motif will also have the potential to form pairs in sequences in the library. It also uses information about the sequence requirements of the motif to determine which mutations can occur in unpaired regions [
20]. By increasing the number of different variants of the secondary structure of a functional motif in the library, the likelihood of finding variants with improved properties should also increase.
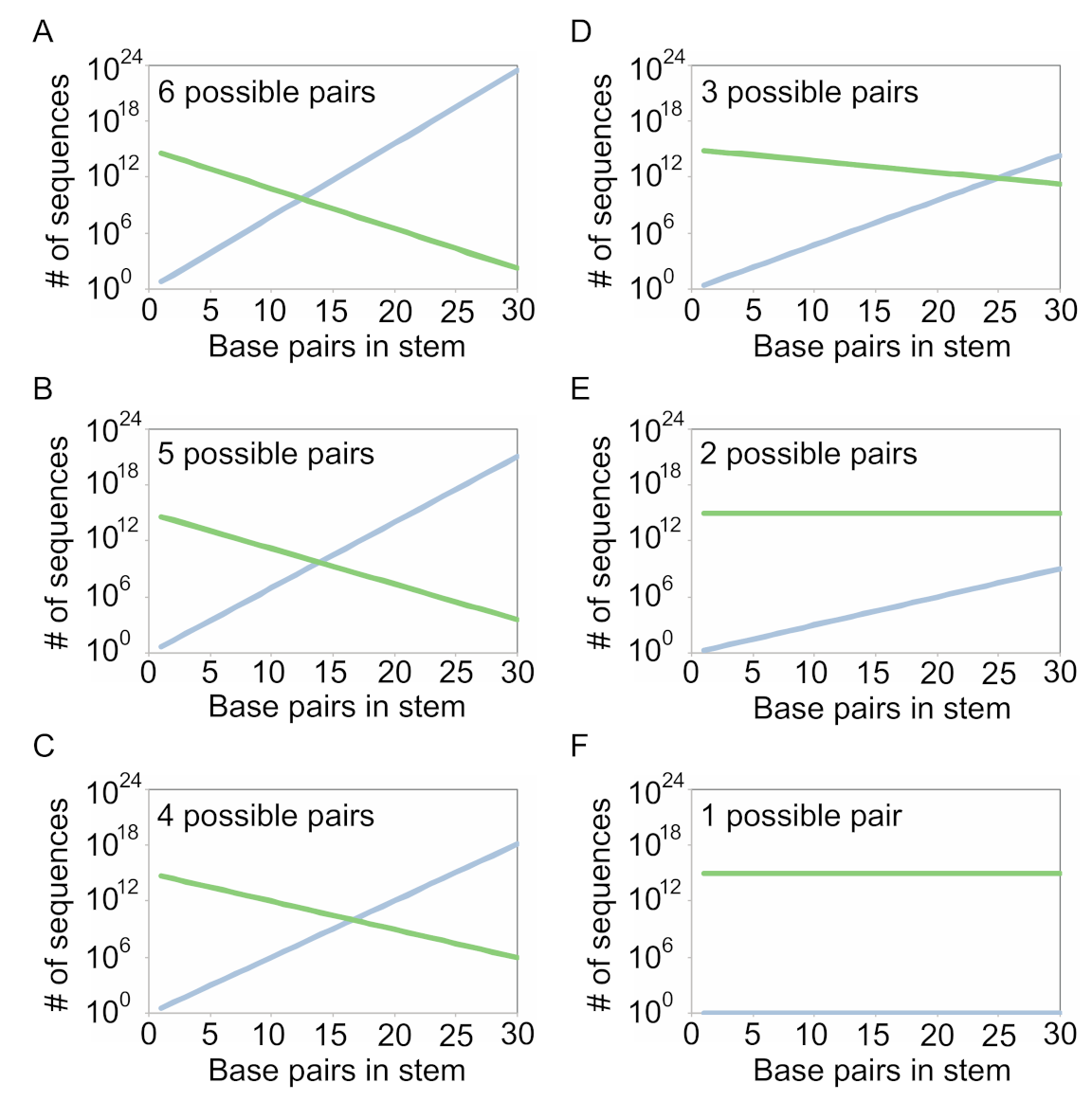
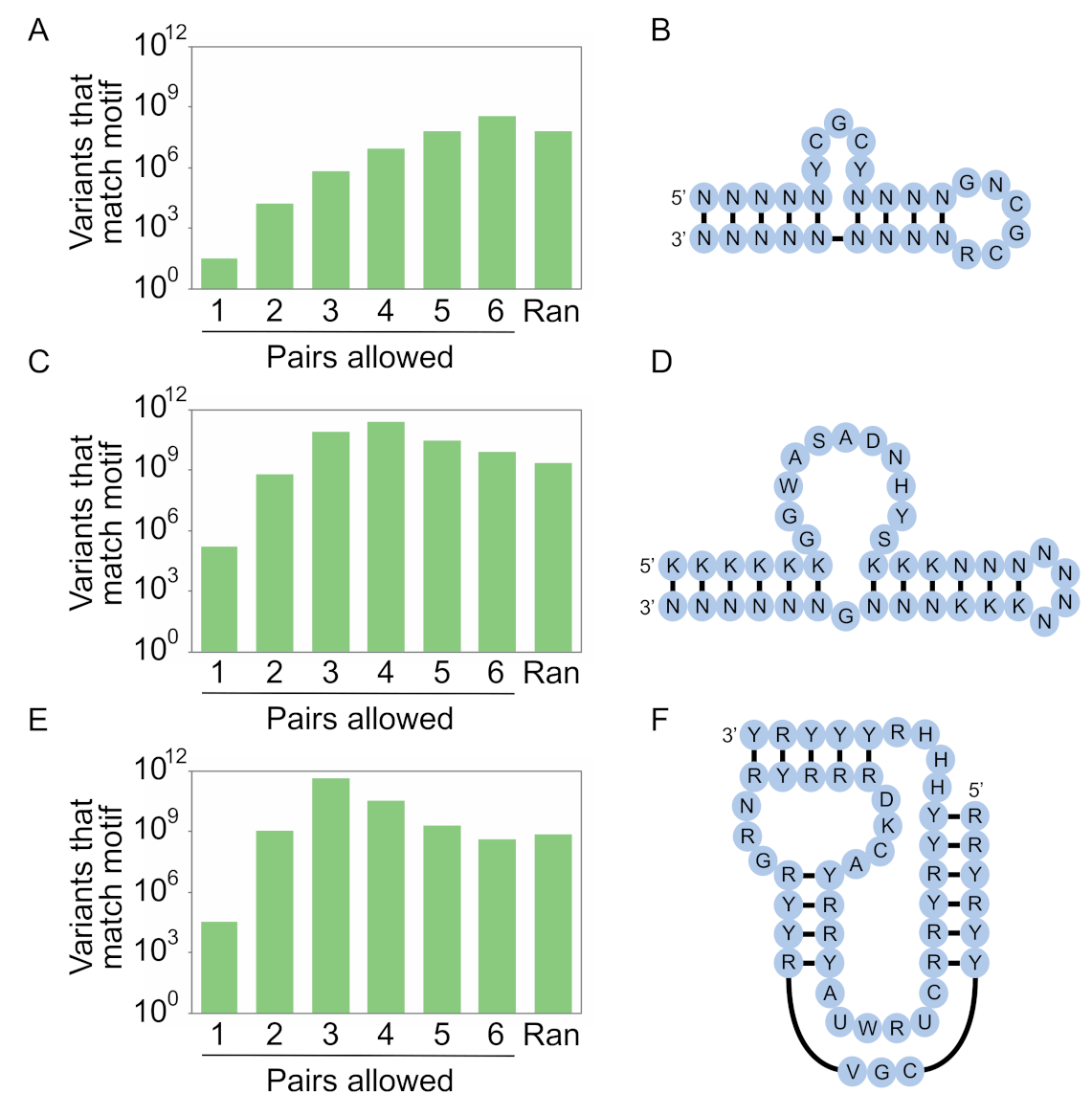
The benefit of our approach depends on the complexity of the motif. For a motif of 24 nucleotides or less, such an approach is not necessary: all possible sequences (including all possible variants of the motif) can be sampled by simply generating a random sequence library of the length of the motif containing at least 10
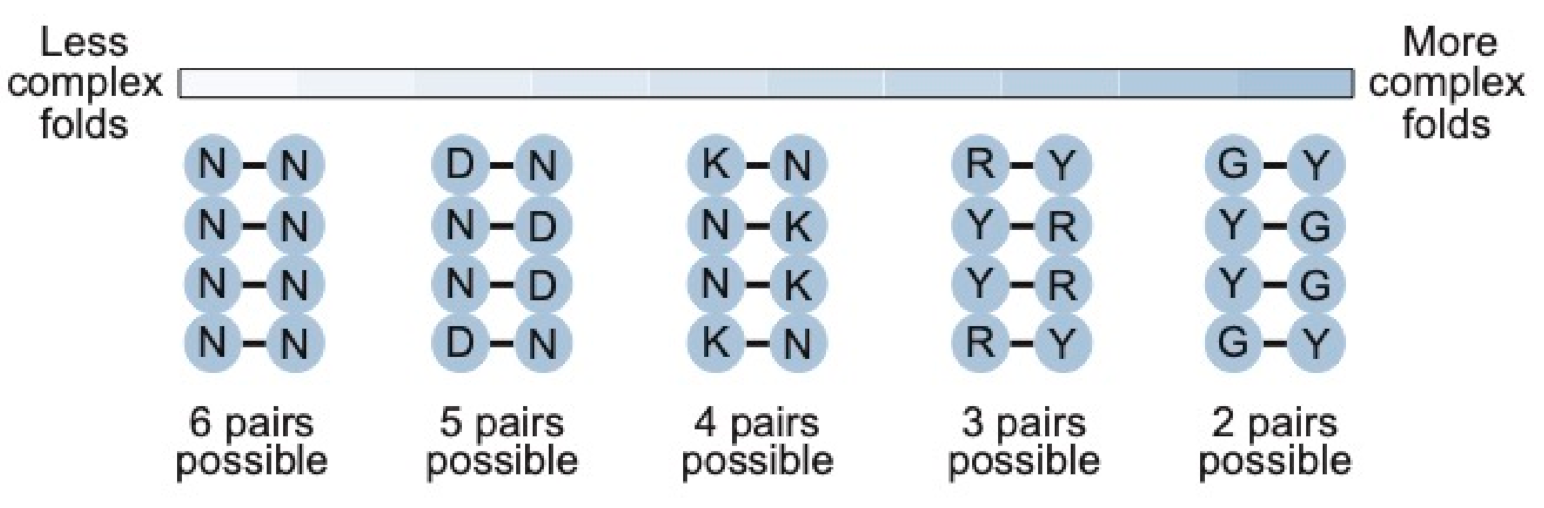
15 sequences. As the complexity of the motif increases, however, our calculations show that secondary structure libraries will contain significantly more unique sequences with the potential to form the secondary structure than either random sequence libraries or randomly mutagenized libraries based on a single example of a motif. They also indicate that the optimal coding strategy for pairs (in this study defined as canonical A-U, U-A, C-G, and G-C base pairs as well as G.U and U.G wobble pairs) depends on the complexity of the motif (
Figure 8). For less complex motifs such as the streptavidin aptamer, N-N (six possible pairs and a 0.375 probability of forming a base pair) is the optimal strategy. As the complexity of the motif increases, coverage can be maximized by encoding pairs with combinations of nucleotides that maximize the probability of obtaining a viable pair, although this comes at a cost of reducing the number of pairs that can occur. For instance, base pairs in a 40-nucleotide ATP aptamer can be optimally encoded using K-N (four possible pairs and a probability of 0.5 of forming a pair), while those in a 50-nucleotide kinase ribozyme are best encoded by R-Y (three possible pairs and a probability of 0.75 of forming a base pair). For more complex motifs, such as the 119-nucleotide b1-207 variant of the Class I ligase ribozyme (made up of 33 base pairs, 16 invariant unpaired positions, 10 unpaired positions at which two nucleotides are possible, 13 unpaired positions at which three nucleotides are possible, 8 positions at which four nucleotides are possible, and a six-nucleotide substrate binding site that was left constant for these calculations) [
16,
29,
30], the optimal coding strategy is one in which the probability of obtaining a pair in one and two pairs is possible. This could be achieved by encoding C-G (and U.G) pairs by Y-G, G-C (and G.U) pairs by G-Y, A-U pairs by R-U, and U-A pairs by U-R (note that this coding scheme also ensures that the starting sequence will be present in the library). Every variant in a library made in this way would have the potential to form each of the 33 pairs in the secondary structure of the ribozyme, and ~10
15 different variants of the secondary structure would be represented. In comparison, 62,707-fold fewer unique sequences consistent with the constraints of the secondary structure would be present in a library generated by randomly mutagenizing this ribozyme at an optimal rate of 6% per position. A library synthesized using restricted mutagenesis would also contain 62,707-fold fewer sequences (the same coverage is reachable by normal random mutagenesis), while a library generated using smart mutagenesis would contain 22,129-fold fewer sequences.
Although our approach can be used to achieve complete coverage of the sequence space of simple secondary structures, for complex motifs this is not possible. An important question in such cases is the choice of base pairs which can occur at specific positions in the library. This can have implications for motif optimization because, in the context of certain types of tertiary interactions such as base triples [
31,
32,
33], the identity of the base pair in a helix is constrained. For example, encoding the base pair in a C-G:G triple in a purine-motif triple helix with Y-R would be compatible with triple formation while encoding it with R-Y would not. For this reason, we recommend that secondary structure libraries be designed in such a way that the sequence of the initial isolate of the motif is represented in the library. We also note that information about high-order constraints can be incorporated into the design of a secondary structure library when it is available. However, the sequence requirements of tertiary interactions are in general not well understood, and for this reason cannot always be easily encoded in a library.
An important difference between secondary structure libraries and those generated by random mutagenesis is the distribution of sequences relative to the sequence used to generate the library. Random mutagenesis strongly favors variants similar to the starting sequence, so (for example) the original base pair is much more likely to occur than a mutated version. This is not the case, however, for secondary structure libraries. For example, if a coding scheme is used in which three different base pairs can occur, each of them will appear at a given position with a probability of one third, and the probability that a sequence will contain any combination of mutated base pairs (including combinations in which all base pairs are mutated) is the same as the probability that it will contain only the original base pairs. For this reason, secondary structure libraries should be particularly useful with respect to the discovery of variants with the same biochemical function and secondary structure but distinct sequences. Such variants can provide important structural information for molecular modeling. In addition, we envision that such variants could be used in combination with standard crystallographic screens to increase the likelihood of finding sequences that form well-ordered crystals.
The advantages of exploring secondary structure space are becoming more appreciated, and several methods to do this more efficiently have recently been described (reviewed in [
34,
35]). One uses information such as that shown in
Figure 1 to identify all possible sequences consistent with the sequence requirements of a motif. These are synthesized individually and used to construct a DNA microarray [
36]. An advantage of this approach is that, once the microarray has been manufactured, sequences can be rapidly tested for activity. However, it requires synthesis of thousands of oligonucleotides and is limited to libraries of ~10
6 sequences. In comparison, our approach can be used to generate libraries of ~10
15 sequences in a single synthesis. Another approach uses an algorithm to determine a mixing matrix (the nucleotide composition of degenerate positions) that can be used to synthesize a library which maximizes the fraction of sequences predicted to form a target structure [
37,
38,
39]. Because this approach uses an RNA folding algorithm to evaluate library quality, it cannot be applied to motifs which contain structural elements that cannot be effectively predicted, such as pseudoknots, triplexes, and G-quadruplexes. In comparison, the approach described here can be applied to any structure for which the sequence requirements have been determined.
In conclusion, we have described a simple method that can be used to generate libraries enriched for sequences with the potential to form a desired secondary structure. Because such libraries can significantly increase the number of variants of a motif that can be sampled in a single artificial evolution experiment, we anticipate that they will useful for the optimization and structural characterization of functional nucleic acid motifs such as aptamers, ribozymes, and deoxyribozymes.
4. Materials and Methods
4.1. Secondary Structure Library Design
We will first consider the simple case in which the secondary structure contains a stem, but no other types of position. Each library design has a defined probability
that a particular base pair will have the potential to form. It also specifies the number of base pairs
in the stem. If we want to calculate the number of unique sequences in the library with the potential to form all base pairs in this stem, we have to consider two limits. The first one is the number of unique sequences possible for a given library design. Not all sequences with a given number of base pairs can be generated using each library architecture. For example, if we use a 1-1 architecture, only 1 of the 6 possible pairs considered in this study (A-U, U-A, C-G, G-C, G.U, or U.G) can occur. For a given stem length
this is the number
. The second is the number of sequences in the library consistent with the model (note that these sequences are not necessarily unique). This can be calculated as
, where
is the size of the library (in this study 10
15) and
is the probability that the sequence will have the potential to form all of the pairs in the stem. Therefore, the maximum possible number of unique sequences in the library with the potential to form all base pairs in the stem is:
The actual number of unique sequences with the potential to form all pairs in the stem can be slightly lower, but this difference will be significant only if the average copy number (i.e., the ratio between sequences consistent with the model in the library and the number of distinct sequences which can be generated by the library design) is close to 1. However, this is a rare case, and moreover it cannot decrease the number of unique sequences by orders of magnitude.
Let us next consider a case in which the secondary structure model used for library design contains, in addition to base pairs, unpaired positions as well. Those positions can either be invariant or have a possibility to contain multiple nucleotides. In this case, we need to consider one additional parameter: the number of possible versions of the unpaired regions. This is straightforward to calculate. For example, consider a sequence with 10 unpaired positions, of which 3 are invariant, 2 have 2 possibilities, 1 has 3 possibilities, and 4 has 4 possibilities. The number of possible versions of unpaired positions
for this sequence is
. Given the library design, the sequence requirements for each of these positions are maintained in the entire library, so that the probability that all of the base pairs and all of the unpaired positions are maintained is
. The number of distinct sequences which can be generated in a given library design is now
, because each possible combination of unpaired positions can be combined with each possible combination of base pairs. Therefore, the maximum possible number of unique sequences in the library is:
4.2. Random Mutagenesis
This section firstly contains brief descriptions of three different ways to implement random mutagenesis and the calculations used for each of them. We then provide detailed descriptions of the calculations for each implementation in which formulas are included.
We used three different types of random mutagenesis in this study. The first is the simplest, and most commonly used approach: the entire sequence of the motif is mutagenized at a constant rate. The second approach takes into account the fact that we know from the secondary structure model that some positions are invariant. These positions are kept constant and only variable positions are mutagenized. The third approach is slightly more complicated and uses additional information from the secondary structure model. The model usually contains positions which are variable but at which certain nucleotides cannot occur. If we allow each of the four nucleotides to occur at such positions during mutagenesis, a significant fraction of library members will be generated which are not consistent with the secondary structure model. To avoid this, we can restrict the nucleotides that occur at certain positions during library synthesis. For example, a position which is A in a starting sequence but at which U can also occur would (for a mutagenesis rate of 20%) stay unmutated during library synthesis with a probability of 80% and be mutated to U with a probability of 20%. Similarly, for a position at which 3 nucleotides can occur, we simply change the nucleotide ratios during the synthesis to 80%, 10%, and 10% (in this case the probability of obtaining a mutation is still 20%). This way, we significantly increase the number of sequences consistent with the secondary structure model in the library.
Calculations for a given rate of mutagenesis consist of two steps. The first is to determine which types of sequences consistent with the secondary structure model will be present in the mutagenized library. By sequence type, we mean a combination of types of mutations. For example, one sequence type consists of variants containing one base pair with two mutations (such as C-G to G-C) and two mutated positions at which three nucleotides can occur. For the first two methods of mutagenesis, this is done by calculating the maximum number of mutations a sequence in the library can contain. In the third case, it must be done for each combination of mutations separately. This is because a sequence containing (for example) 3 mutations at positions with 2 allowed nucleotides has a different probability of being generated in the synthesis than a sequence with 3 mutations at positions with 4 allowed nucleotides. Therefore, we have to calculate the average number of copies of a sequence of a given sequence type in the library and compare it to the presence limit for each sequence type.
The second part of the calculation is to determine, for each sequence type, the number of distinct sequences in the library consistent with the secondary structure model. To do this we calculate the number of distinct sequences for each sequence type determined to be present (by the calculations described in the previous paragraph) in the pool and then sum up the numbers for all those sequence types. All calculations were performed for rates of mutagenesis between 1% and 75% with 1% steps. The optimal rate was defined as that which yielded the highest number of distinct sequences consistent with the secondary structure model in a library of defined size (in this study 1015). For the first two methods of mutagenesis, the rate with the highest number of allowed mutations is chosen without limiting the number of possible mutations to a whole number. For example, if we are comparing two rates and one allows a maximum of 5.0 mutations and the other allows a maximum of 5.5 mutations, the same types of sequences will be present in libraries generated at both rates. In the second case, however, the average copy number of sequences containing 5 mutations will be higher, so this rate is considered to be better. For the third method of mutagenesis, we compare results for rates which generate the highest number of distinct sequences consistent with the model by comparing the average copy number of sequences from the least abundant sequence type present in the library, and choose as the optimal rate that at which this minimum is the largest. For example, if we are comparing two rates for which the least abundant sequence type contains sequences with average copy numbers of 2.2 and 2.8, then the second rate is better.
4.3. Normal Random Mutagenesis in Which the Entire Sequence Is Mutagenized
We want to determine the maximum number of mutations a sequence with
nucleotides can contain to still be present in a library generated by random mutagenesis with a mutagenesis rate of
. We will start by calculating the average copy number of a given sequence in the library. The probability
that a library member is a given sequence with exactly
out of
unmutated nucleotides is:
where the first term is the probability that
nucleotides are unmutated and the second term is the probability that the rest of the
nucleotides are mutated in one specific way, where
is number of types of nucleotides (4 if not stated otherwise). The average number of copies of this sequence in a library with
sequences is
and we define that a sequence is considered to be present in the library if the average number of copies of this sequence is larger than the presence limit
(in this study
).
Next, we need to derive a formula for the smallest
which fulfills the condition:
with the limitation that the rate of mutagenesis is not bigger than 75% and not smaller than 1%, because we want to focus only on experimentally relevant cases. Therefore, we are looking for an
which solves the equation:
We first substitute from Equation (3):
the next step is rearranging terms:
Now we can use the logarithm to determine
:
and finally, we use rules for logarithms to simplify the formula:
and the maximal number of mutations is
.
4.4. Restricted Random Mutagenesis
This case differs from the previous one in only one detail. Instead of using the length of the full sequence , we use the number of positions at which two or more types of nucleotides are allowed according to the secondary structure model. All calculations are then the same, and we can use Formula (9) to calculate . This approach allows us to reach sequences at a slightly higher mutational distance from the original sequence than those accessed using the first approach. It can therefore increase the number of distinct sequences consistent with the secondary structure model in the mutagenized library.
4.5. Smart Random Mutagenesis
From the secondary structure model of the motif, we know the number of unpaired positions
N2,
N3, and
N4 at which 2, 3, or 4 nucleotides are allowed. Positions which form base pairs are also classified as positions at which 4 nucleotides are allowed. The total number of nucleotides which are randomly mutagenized is
. If we look again at formula (3) we see that it cannot be used directly in this case, because
is different for positions at which different numbers of nucleotides are allowed. For this reason, we have to write separate terms for sequence groups with constant
:
where
is the number of mutated positions at which two nucleotides are allowed,
is the number of mutated positions at which three nucleotides are allowed, and
is the number of mutated positions at which four nucleotides are allowed. It can be simplified by rearranging terms:
Again, we consider a sequence to be present in the library if it fulfills condition (4).
Now, there is no general way to calculate the maximum possible number of mutations. Instead, we must check, for each sequence type defined by and , if condition (4) is fulfilled. If all positions in the model have same , we can do the same calculation as for normal random mutagenesis and determine the maximum number of mutations. This is the case for model structures made up of stems but not unpaired regions. The results are therefore the same for smart random mutagenesis and restricted random mutagenesis.
4.6. Calculating the Number of Unique Sequences in a Library
We have shown how to determine whether a given sequence type is present in the library, and now show how to determine the number of distinct sequences which belong to a given sequence type. A sequence type is described by 5 numbers: the number of mutated positions at which 2 nucleotides can occur out of , the number of mutated positions at which 3 nucleotides can occur out of , the number of mutated positions at which 4 nucleotides can occur out of (positions forming base pairs are in this case not counted in this group), the number of base pairs with a single mutation out of , and the number of base pairs with a double mutation out of . We only consider cases in which each of the six possible pairs (A-U, U-A, C-G, G-C, G.U, or U.G) can occur at paired positions.
We wish to first determine the number of different ways in which the mutated positions can occur for different values of
and
. If we want to choose
positions out of
positions, this can happen in
different ways. Therefore, if we are choosing all 5 types of mutations at once, the number of ways in which they can occur is the product of 5 such terms:
where the number of mutated positions of a given type has to be less than or equal to the number of such positions in the secondary structure model. Note that base pairs containing two mutations (such as C-G to G-C) are chosen from all base pairs minus base pairs containing a single mutation (such as C-G to U.G), not from all base pairs.
Next, we need to determine the number of ways in which these mutations can occur such that they are consistent with the secondary structure model. For mutations at positions at which 2 nucleotides are allowed, this is simple. They can only change to another mutation consistent with the sequence requirements of the motif in one way, so the number of ways to realize of such mutations at defined positions is 1. Positions with 3 allowed nucleotides have 2 possible active mutations, so the number of ways to realize of such mutations at defined positions is . Positions with 4 allowed nucleotides have 3 possible active mutations, so the number of ways to realize of such mutations at defined positions is .
In the case of base pairs, we start with sequences containing only canonical pairs and consider mutations to be consistent with the sequence requirements of the motif if they generate a canonical base pair or a G.U or U.G wobble pair. A canonical base pair has 6 possible single mutant variants, only 1 of which is active (the one to a G.U or U.G wobble pair), so the number of ways to realize of such mutations at defined positions is 1. The number of possible double mutants is 9, of which 4 are consistent with pairing (one to a wobble pair and three to canonical base pairs), so the number of ways to realize of such mutations at defined positions is .
The total number of distinct sequences consistent with the secondary structure model for the given numbers of mutations is the product of Formula (12) and the number of ways to realize each type of mutation at the given positions: