Thermodynamics of Mg–Al Order-Disorder Reaction in MgAl2O4-Spinel: Constrained by Prolonged Annealing Experiments at 773–1123 K
Abstract
1. Introduction
2. Experimental and Analytical Methods
2.1. Natural MgAl2O4-Spinel Crystal
2.2. Annealing Experiments from 773 to 1123 K
2.3. Analyzing Methods
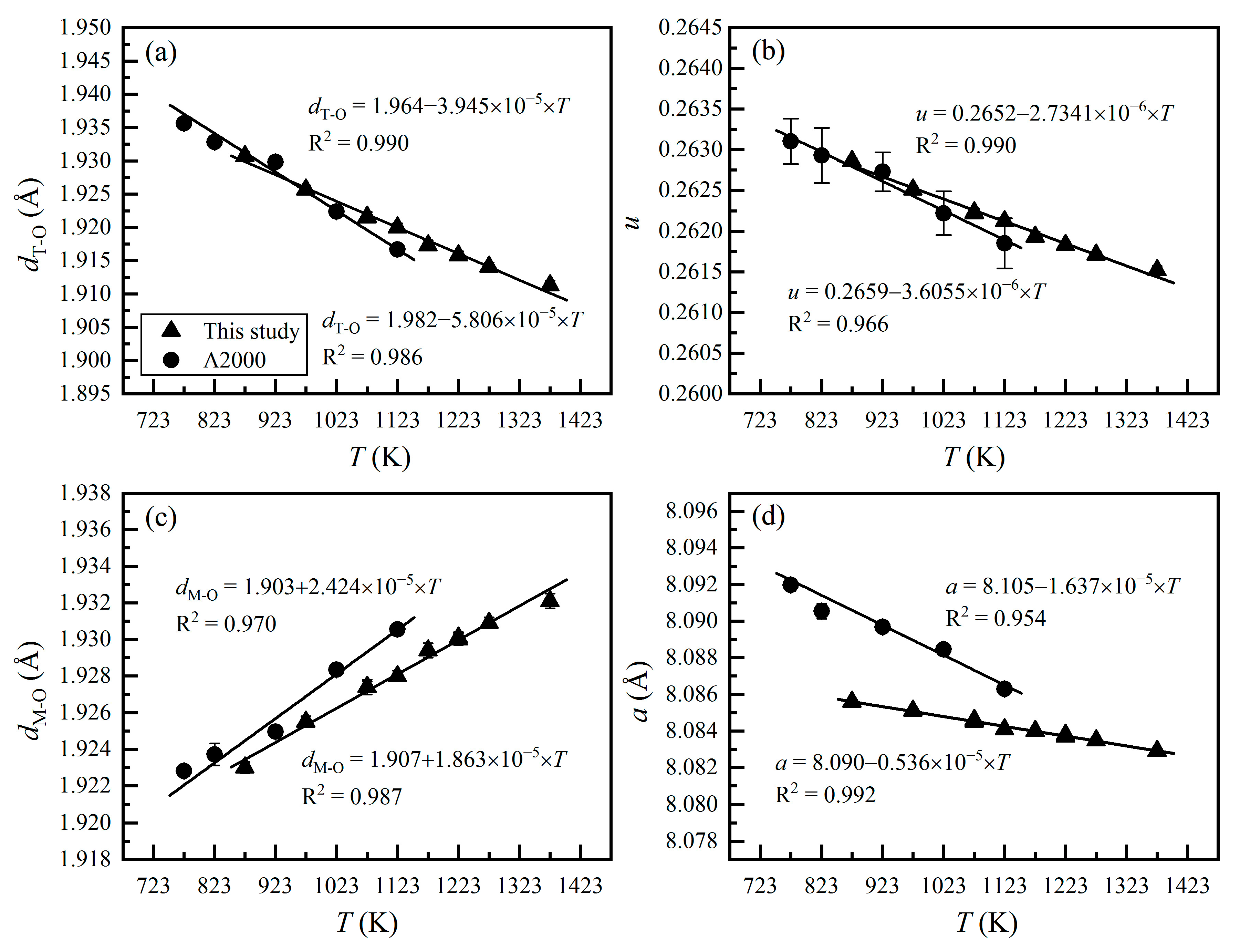
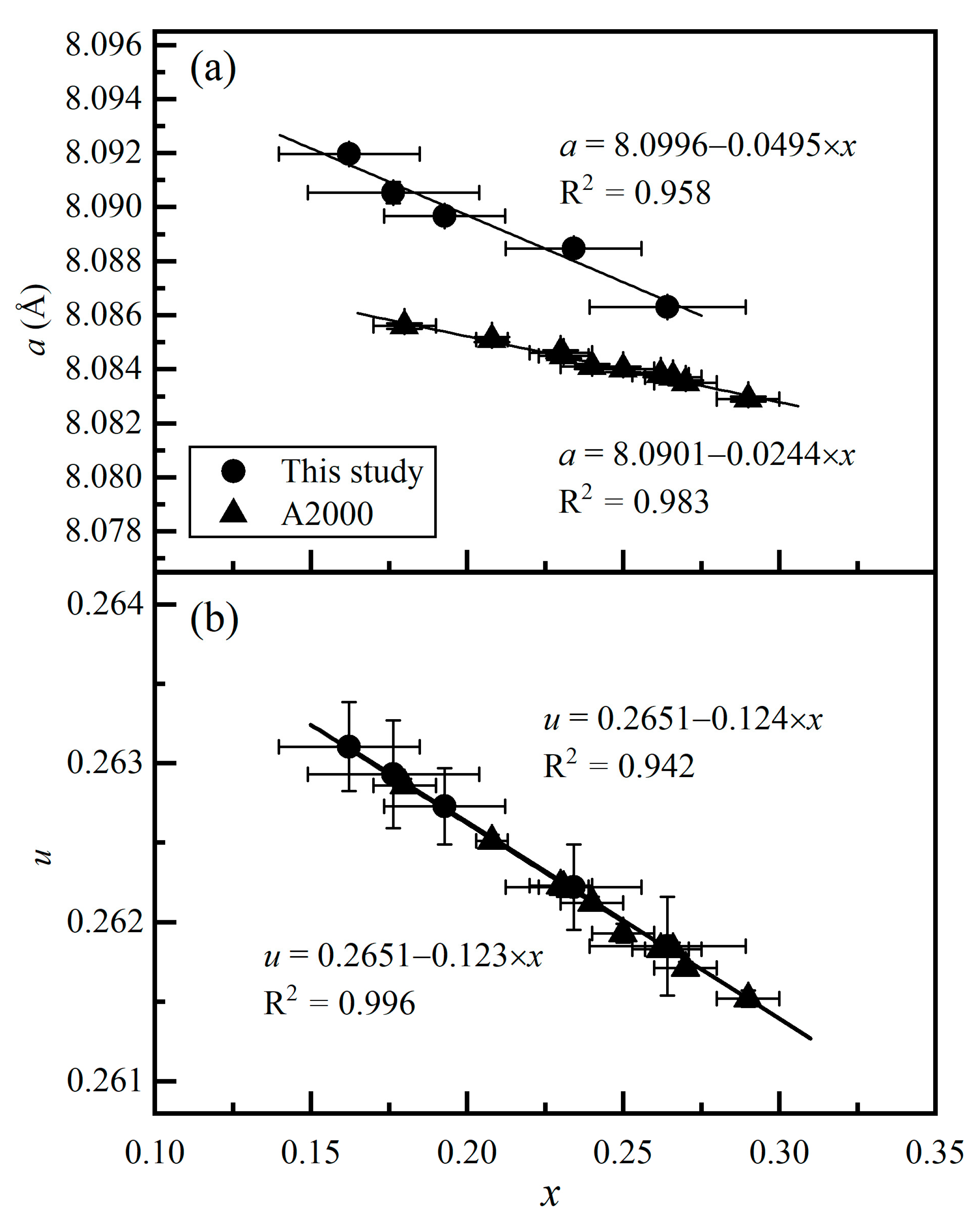
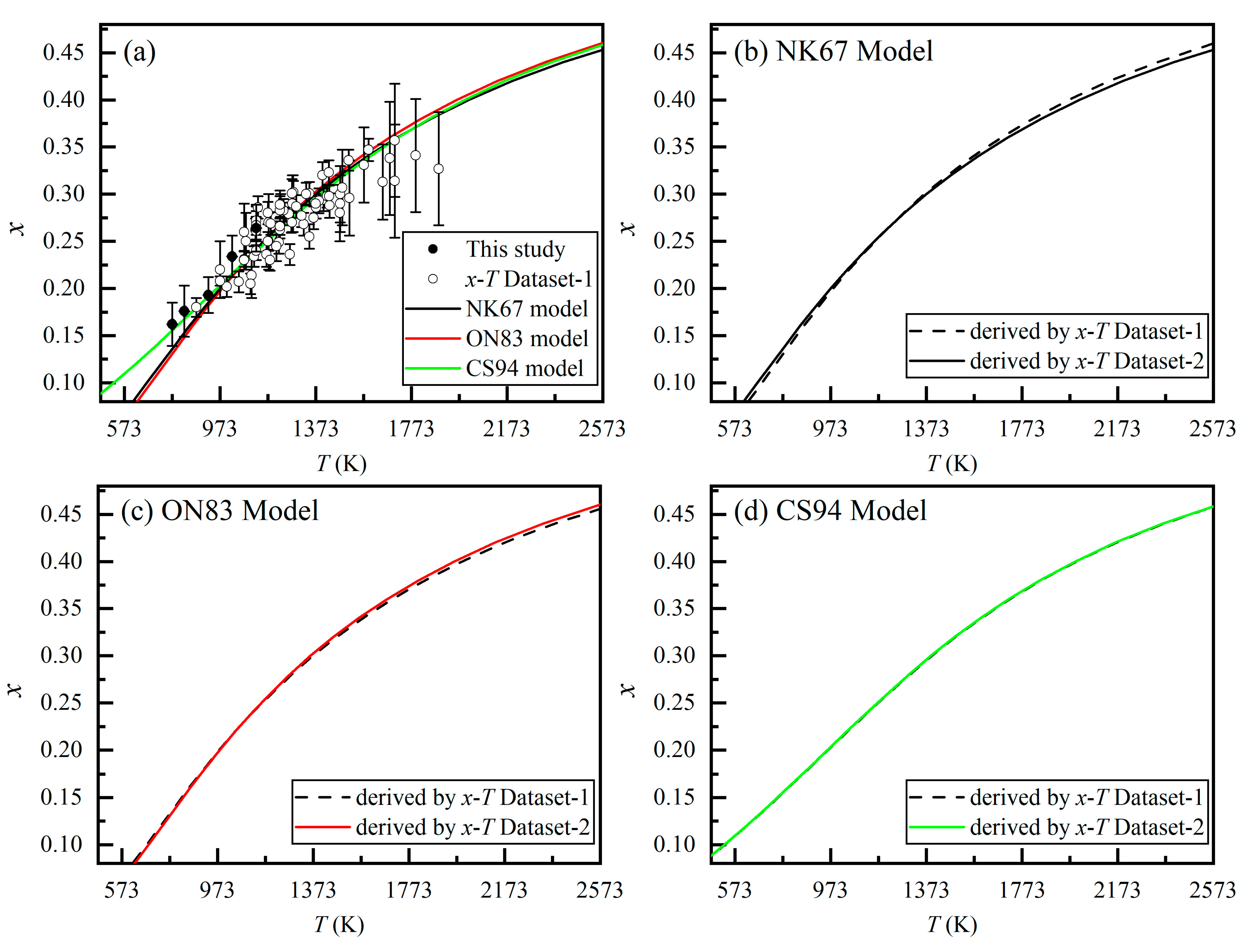
3. Results and Discussions
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Baudín, C.; Martínez, R.; Pena, P. High-temperature mechanical behavior of stoichiometric magnesium spinel. J. Am. Ceram. Soc. 1995, 78, 1857–1862. [Google Scholar] [CrossRef]
- Ganesh, I.; Bhattacharjee, S.; Saha, B.P.; Johnson, R.; Rajeshwari, K.; Sengupta, R.; Ramana Rao, M.V.; Mahajan, Y.R. An efficient MgAl2O4 spinel additive for improved slag erosion and penetration resistance of high-Al2O3 and MgO-C refractories. Ceram. Int. 2002, 28, 245–253. [Google Scholar] [CrossRef]
- Ganesh, I. A review on magnesium aluminate (MgAl2O4) spinel: Synthesis, processing and applications. Int. Mater. Rev. 2013, 58, 63–112. [Google Scholar] [CrossRef]
- Shimizu, Y.; Arai, H.; Seiyama, T. Theoretical studies on the impedance-humidity characteristics of ceramic humidity sensors. Sens. Actuators 1985, 7, 11–22. [Google Scholar] [CrossRef]
- Maschio, R.D.; Fabbri, B.; Fiori, C. Industrial applications of refractories containing magnesium aluminate spinel. Ind. Ceram. 1988, 8, 121–126. [Google Scholar]
- Mori, J.; Watanabe, N.; Yoshimura, M.; Oguchi, Y.; Kawakami, T.; Matsuo, A. Material design of monolithic refractories for steel ladle. Am. Ceram. Soc. Bull. 1990, 69, 1172–1176. [Google Scholar]
- Li, J.-G.; Ikegami, T.; Lee, J.-H.; Mori, T. Fabrication of translucent magnesium aluminum spinel ceramics. J. Am. Ceram. Soc. 2000, 83, 2866–2868. [Google Scholar] [CrossRef]
- Kehres, J.; Jakobsen, J.G.; Andreasen, J.W.; Wagner, J.B.; Liu, H.; Molenbroek, A.; Sehested, J.; Chorkendorff, I.; Vegge, T. Dynamical properties of a Ru/MgAl2O4 catalyst during reduction and dry methane reforming. J. Phys. Chem. C 2012, 116, 21407–21415. [Google Scholar] [CrossRef]
- Kim, B.-H.; Yang, E.-H.; Moon, D.J.; Kim, S.W. Ni/MgO-MgAl2O4 catalysts with bimodal pore structure for steam-CO2-reforming of methane. J. Nanosci. Nanotechnol. 2015, 15, 5959–5962. [Google Scholar] [CrossRef]
- Klemme, S. The influence of Cr on the garnet-spinel transition in the Earth’s mantle: Experiments in the system MgO-Cr2O3-SiO2 and thermodynamic modelling. Lithos 2004, 77, 639–646. [Google Scholar] [CrossRef]
- Duan, Y.; Li, X.; Sun, N.; Ni, H.; Tkachev, S.N.; Mao, Z. Single-crystal elasticity of MgAl2O4-spinel up to 10.9 GPa and 1000 K: Implication for the velocity structure of the top upper mantle. Earth Planet. Sci. Lett. 2018, 481, 41–47. [Google Scholar] [CrossRef]
- Sickafus, K.E.; Wills, J.M.; Grimes, N.W. Structure of Spinel. J. Am. Ceram. Soc. 1999, 82, 3279–3292. [Google Scholar] [CrossRef]
- Barnes, S.J.; Roeder, P.L. The range of spinel compositions in terrestrial mafic and ultramafic rocks. J. Petrol. 2001, 42, 2279–2302. [Google Scholar] [CrossRef]
- Liu, X.; O’Neill, H.S.C. The effect of Cr2O3 on the partial melting of spinel lherzolite in the system CaO-MgO-Al2O3-SiO2-Cr2O3 at 1.1 GPa. J. Petrol. 2004, 45, 2261–2286. [Google Scholar] [CrossRef]
- Bosi, F.; Biagioni, C.; Pasero, M. Nomenclature and classification of the spinel supergroup. Eur. J. Mineral. 2019, 31, 183–192. [Google Scholar] [CrossRef]
- Ringwood, A.E.; Major, A. The system Mg2SiO4-Fe2SiO4 at high pressures and temperatures. Phys. Earth Planet. Inter. 1970, 3, 89–108. [Google Scholar] [CrossRef]
- Sasaki, S.; Prewitt, C.T.; Sato, Y.; Ito, E. Single-crystal X ray study of γ Mg2SiO4. J. Geophys. Res. 1982, 87, 7829–7832. [Google Scholar] [CrossRef]
- Frost, D.J. The upper mantle and transition zone. Elements 2008, 4, 171–176. [Google Scholar] [CrossRef]
- Liu, X.; Xiong, Z.; Chang, L.; He, Q.; Wang, F.; Shieh, S.R.; Wu, C.; Li, B.; Zhang, L. Anhydrous ringwoodites in the mantle transition zone: Their bulk modulus, solid solution behavior, compositional variation, and sound velocity feature. Solid Earth Sci. 2016, 1, 28–47. [Google Scholar] [CrossRef]
- Carbonin, S.; Russo, U.; Della Giusta, A. Cation distribution in some natural spinels from X-ray diffraction and Mössbauer spectroscopy. Mineral. Mag. 1996, 60, 355–368. [Google Scholar] [CrossRef]
- Lucchesi, S.; Della Giusta, A. Crystal chemistry of a highly disordered Mg-Al natural spinel. Miner. Petrol. 1997, 59, 91–99. [Google Scholar] [CrossRef]
- Maekawa, H.; Kato, S.; Kawamura, K.; Yokokawa, T. Cation mixing in natural MgAl2O4 spinel: A high-temperature 27Al NMR study. Am. Mineral. 1997, 82, 1125–1132. [Google Scholar] [CrossRef]
- Carbonin, S.; Martignago, F.; Menegazzo, G.; Dal Negro, A. X-ray single-crystal study of spinels: In situ heating. Phys. Chem. Miner. 2002, 29, 503–514. [Google Scholar] [CrossRef]
- Nestola, F.; Boffa Ballaran, T.; Balic-Zunic, T.; Princivalle, F.; Secco, L.; Dal Negro, A. Comparative compressibility and structural behavior of spinel MgAl2O4 at high temperatures: The independency on the degree of cation order. Am. Mineral. 2007, 92, 1838–1843. [Google Scholar] [CrossRef]
- Liu, L.; Liu, X.; Bao, X.; He, Q.; Yan, W.; Ma, Y.; He, M.; Tao, R.; Zou, R. Si-disordering in MgAl2O4-spinel under high P-T conditions, with implications for Si-Mg disorder in Mg2SiO4-ringwoodite. Minerals 2018, 8, 210. [Google Scholar] [CrossRef]
- Hazen, R.M.; Yang, H. Effects of cation substitution and order-disorder on P-V-T equations of state of cubic spinels. Am. Mineral. 1999, 84, 1956–1960. [Google Scholar] [CrossRef]
- Andreozzi, G.B.; Princivalle, F.; Skogby, H.; Della Giusta, A. Cation ordering and structural variations with temperature in MgAl2O4 spinel: An X-ray single-crystal study. Am. Mineral. 2000, 85, 1164–1171. [Google Scholar] [CrossRef]
- Jackson, I.N.S.; Liebermann, R.C.; Ringwood, A.E. Disproportionation of spinels to mixed oxides: Significance of cation configuration and implications for the mantle. Earth Planet. Sci. Lett. 1974, 24, 203–208. [Google Scholar] [CrossRef]
- Liebermann, R.C.; Jackson, I.; Ringwood, A.E. Elasticity and phase equilibria of spinel disproportionation reactions. Geophys. J. R. astr. Soc. 1977, 50, 553–586. [Google Scholar] [CrossRef]
- Hazen, R.M.; Navrotsky, A. Effects of pressure on order-disorder reactions. Am. Mineral. 1996, 81, 1021–1035. [Google Scholar] [CrossRef]
- Liu, L.; Ma, Y.; Yan, W.; Liu, X. Trace element partitioning between MgAl2O4-spinel and carbonatitic silicate melt from 3 to 6 GPa, with emphasis on the role of cation order-disorder. Solid Earth Sci. 2019, 4, 43–65. [Google Scholar] [CrossRef]
- Navrotsky, A.; Kleppa, O.J. The thermodynamics of cation distributions in simple spinels. J. Inorg. Nucl. Chem. 1967, 29, 2701–2714. [Google Scholar] [CrossRef]
- O’Neill, H.S.C.; Navrotsky, A. Simple spinels: Crystallographic parameters, cation radii, lattice energies, and cation distribution. Am. Mineral. 1983, 68, 181–194. [Google Scholar]
- O’Neill, H.S.C.; Navrotsky, A. Cation distributions and thermodynamic properties of binary spinel solid solutions. Am. Mineral. 1984, 69, 733–753. [Google Scholar]
- Carpenter, M.A.; Powell, R.; Salje, E.K.H. Thermodynamics of nonconvergent cation ordering in minerals: I. An alternative approach. Am. Mineral. 1994, 79, 1053–1067. [Google Scholar]
- Carpenter, M.A.; Salje, E.K.H. Thermodynamics of nonconvergent cation ordering in minerals: II. Spinels and the orthopyroxene solid solution. Am. Mineral. 1994, 79, 1068–1083. [Google Scholar]
- Harrison, R.J.; Putnis, A. The coupling between magnetic and cation ordering: A macroscopic approach. Eur. J. Mineral. 1997, 9, 1115–1130. [Google Scholar] [CrossRef]
- Wood, B.J.; Kirkpatrick, R.J.; Montez, B. Order-disorder phenomena in MgAl2O4 spinel. Am. Mineral. 1986, 71, 999–1006. [Google Scholar]
- Millard, R.L.; Peterson, R.C.; Hunter, B.K. Temperature dependence of cation disorder in MgAl2O4 spinel using 27Al and 17O magic-angle spinning NMR. Am. Mineral. 1992, 77, 44–52. [Google Scholar]
- Redfern, S.A.T.; Harrison, R.J.; O’Neill, H.S.C.; Wood, D.R.R. Thermodynamics and kinetics of cation ordering in MgAl2O4 spinel up to 1600 °C from in situ neutron diffraction. Am. Mineral. 1999, 84, 299–310. [Google Scholar] [CrossRef]
- Kashii, N.; Maekawa, H.; Hinatsu, Y. Dynamics of the cation mixing of MgAl2O4 and ZnAl2O4 spinel. J. Am. Ceram. Soc. 1999, 82, 1844–1848. [Google Scholar] [CrossRef]
- Andreozzi, G.B.; Princivalle, F. Kinetics of cation ordering in synthetic MgAl2O4 spinel. Am. Mineral. 2002, 87, 838–844. [Google Scholar] [CrossRef]
- Ma, Y.; Liu, X. Kinetics and thermodynamics of Mg-Al disorder in MgAl2O4-spinel: A review. Molecules 2019, 24, 1704. [Google Scholar] [CrossRef] [PubMed]
- Lavina, B.; Salviulo, G.; Della Giusta, A. Cation distribution and structure modelling of spinel solid solutions. Phys. Chem. Miner. 2002, 29, 10–18. [Google Scholar] [CrossRef]
- Martignago, F.; Dal Negro, A.; Carbonin, S. How Cr3+ and Fe3+ affect Mg-Al order-disorder transformation at high temperature in natural spinels. Phys. Chem. Miner. 2003, 30, 401–408. [Google Scholar] [CrossRef]
- Bosi, F.; Andreozzi, G.B. Chromium influence on Mg-Al intracrystalline exchange in spinels and geothermometric implications. Am. Mineral. 2017, 102, 333–340. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in Halides and Chalcogenides. Acta Cryst. 1976, A32, 751–767. [Google Scholar] [CrossRef]
- Hill, R.J.; Craig, J.R.; Gibbs, G.V. Systematics of the spinel structure type. Phy. Chem. Miner. 1979, 4, 317–393. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Statistical Physics, Part 1, 3rd ed.; Pergamon: Oxford, UK, 1980; 544p. [Google Scholar]
- Della Giusta, A.; Carbonin, S.; Ottonello, G. Temperature-dependent disorder in a natural Mg-Al-Fe2+-Fe3+-spinel. Mineral. Mag. 1996, 60, 603–616. [Google Scholar] [CrossRef]
- Princivalle, F.; Della Giusta, A.; De Min, A.; Piccirillo, E.M. Crystal chemistry and significance of cation ordering in Mg-Al rich spinels from high-grade hornfels (Predazzo-Monzoni, NE Italy). Mineral. Mag. 1999, 63, 257–262. [Google Scholar] [CrossRef]
- Chopelas, A.; Hofmeister, A.M. Vibrational spectroscopy of aluminate spinels at 1 atm and of MgAl2O4 to over 200 kbar. Phys. Chem. Miner. 1991, 18, 279–293. [Google Scholar] [CrossRef]
- Cynn, H.; Sharma, S.K.; Cooney, T.F.; Nicol, M. High-temperature Raman investigation of order-disorder behavior in the MgAl2O4 spinel. Phys. Rev. B 1992, 45, 500–502. [Google Scholar] [CrossRef] [PubMed]
- Cynn, H.; Anderson, O.L.; Nicol, M. Effects of cation disordering in a natural MgAl2O4 spinel observed by rectangular parallelepiped ultrasonic resonance and Raman measurements. Pure Appl. Geophys. 1993, 141, 415–444. [Google Scholar] [CrossRef]
- Slotznick, S.P.; Shim, S.-H. In situ Raman spectroscopy measurements of MgAl2O4 spinel up to 1400 °C. Am. Mineral. 2008, 93, 470–476. [Google Scholar] [CrossRef]
- Haque, A.; Narayan, J. Electron field emission from Q-carbon. Diam. Relat. Mater. 2018, 86, 71–78. [Google Scholar] [CrossRef]
- Haque, A.; Narayan, J. Conversion of h-BN into c-BN for tuning optoelectronic properties. Mater. Adv. 2020, 1, 830. [Google Scholar] [CrossRef]

| Run # | HT3-1 | HT3-2 | HT3-3 | HT3-4 | HT3-5 |
|---|---|---|---|---|---|
| T (K) | 1123 | 1023 | 923 | 823 | 773 |
| x-int1 | ~0.145 | ~0.24 | ~0.24 | ~0.24 | ~0.18 |
| x-cal2 | ~0.24 | ~0.22 | ~0.20 | ~0.18 | ~0.17 |
| t-cal3 | ~11.9 h | ~1.88 h | ~1.32 d | ~37.1 d | ~147 d |
| t-exp4 | 24 h | 7 d | 30 d | 120 d | 360 d |
| a(Å) | 8.0863(1) 5 | 8.0885(1) | 8.0897(2) | 8.0905(4) | 8.0920(3) |
| u | 0.2619(3) | 0.2622(3) | 0.2627(2) | 0.2629(3) | 0.2631(3) |
| dT-O(Å) | 1.91666(1) | 1.92239(2) | 1.92982(3) | 1.93284(6) | 1.93562(5) |
| dM-O(Å) | 1.93054(3) | 1.92835(4) | 1.92496(5) | 1.92372(6) | 1.92281(8) |
| x | 0.258(25) | 0.227(22) | 0.190(19) | 0.173(27) | 0.162(23) |
| Ueq(T) (Å2) | 0.0008(2) | 0.0006(1) | 0.0004(1) | 0.0002(1) | 0.0001(1) |
| Ueq(M) (Å2) | 0.0008(2) | 0.0006(1) | 0.0004(1) | 0.0002(1) | 0.0001(1) |
| Ueq(O) (Å2) | 0.0008(2) | 0.0007(1) | 0.0008(1) | 0.0007(1) | 0.0005(1) |
| Refl. | 47 | 47 | 59 | 58 | 60 |
| Rint(%) | 9.10 | 4.79 | 4.29 | 4.67 | 4.12 |
| R1(%) | 2.07 | 2.06 | 3.36 | 4.04 | 3.89 |
| wR2 (%) | 9.03 | 8.96 | 8.46 | 9.76 | 8.73 |
| GooF | 1.004 | 1.046 | 1.006 | 1.066 | 1.013 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Bao, X.; Liu, X. Thermodynamics of Mg–Al Order-Disorder Reaction in MgAl2O4-Spinel: Constrained by Prolonged Annealing Experiments at 773–1123 K. Molecules 2021, 26, 872. https://doi.org/10.3390/molecules26040872
Ma Y, Bao X, Liu X. Thermodynamics of Mg–Al Order-Disorder Reaction in MgAl2O4-Spinel: Constrained by Prolonged Annealing Experiments at 773–1123 K. Molecules. 2021; 26(4):872. https://doi.org/10.3390/molecules26040872
Chicago/Turabian StyleMa, Yunlu, Xinjian Bao, and Xi Liu. 2021. "Thermodynamics of Mg–Al Order-Disorder Reaction in MgAl2O4-Spinel: Constrained by Prolonged Annealing Experiments at 773–1123 K" Molecules 26, no. 4: 872. https://doi.org/10.3390/molecules26040872
APA StyleMa, Y., Bao, X., & Liu, X. (2021). Thermodynamics of Mg–Al Order-Disorder Reaction in MgAl2O4-Spinel: Constrained by Prolonged Annealing Experiments at 773–1123 K. Molecules, 26(4), 872. https://doi.org/10.3390/molecules26040872






