Theoretical Estimate of the Glass Transition Line of Yukawa One-Component Plasmas
Abstract
1. Introduction
2. Theoretical Background
2.1. Mode Coupling Theory of the Glass Transition
2.2. Isomorph Theory
2.3. Integral Equation Theory of Liquids
3. Computational Approach
3.1. Combining MCT with Advanced IET Approaches
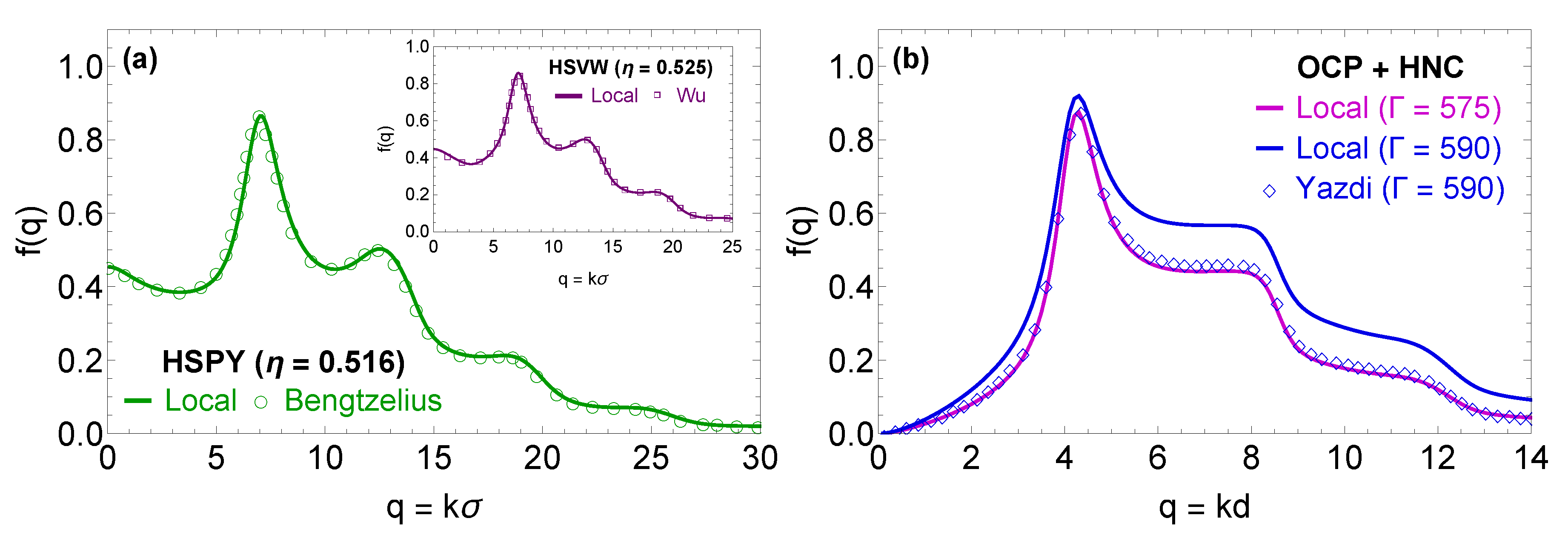
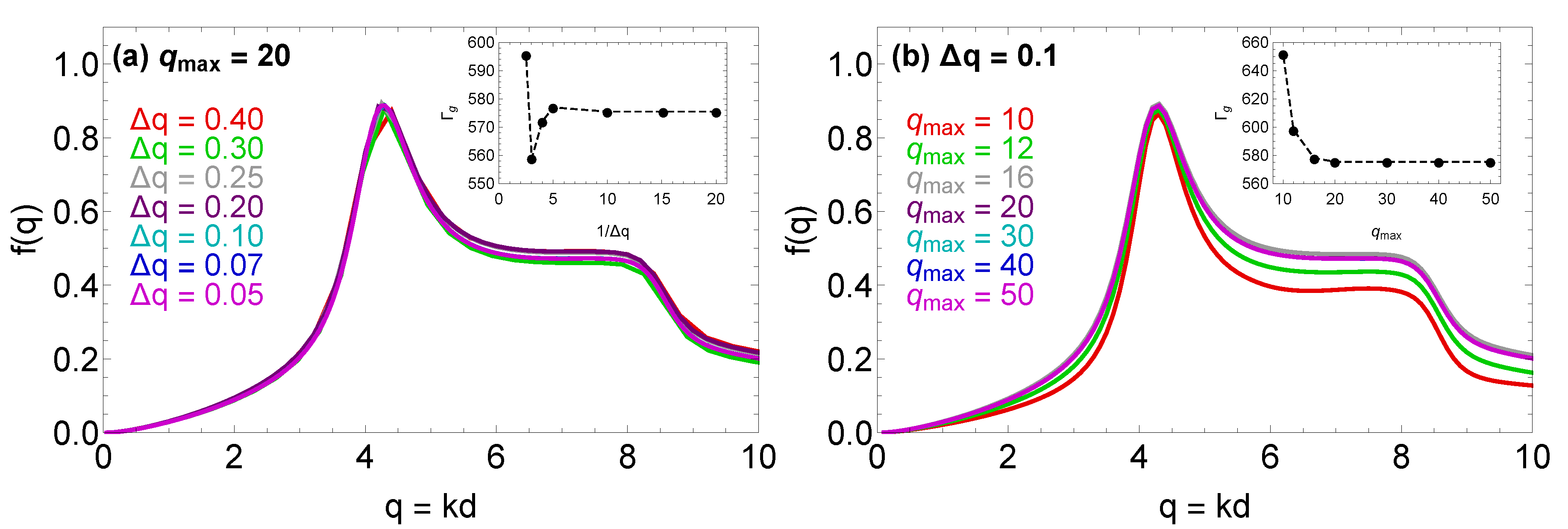
3.2. Numerical Implementation
3.3. Benchmarking and Convergence Study
4. Numerical Results
4.1. The MCT Glass Transition Line
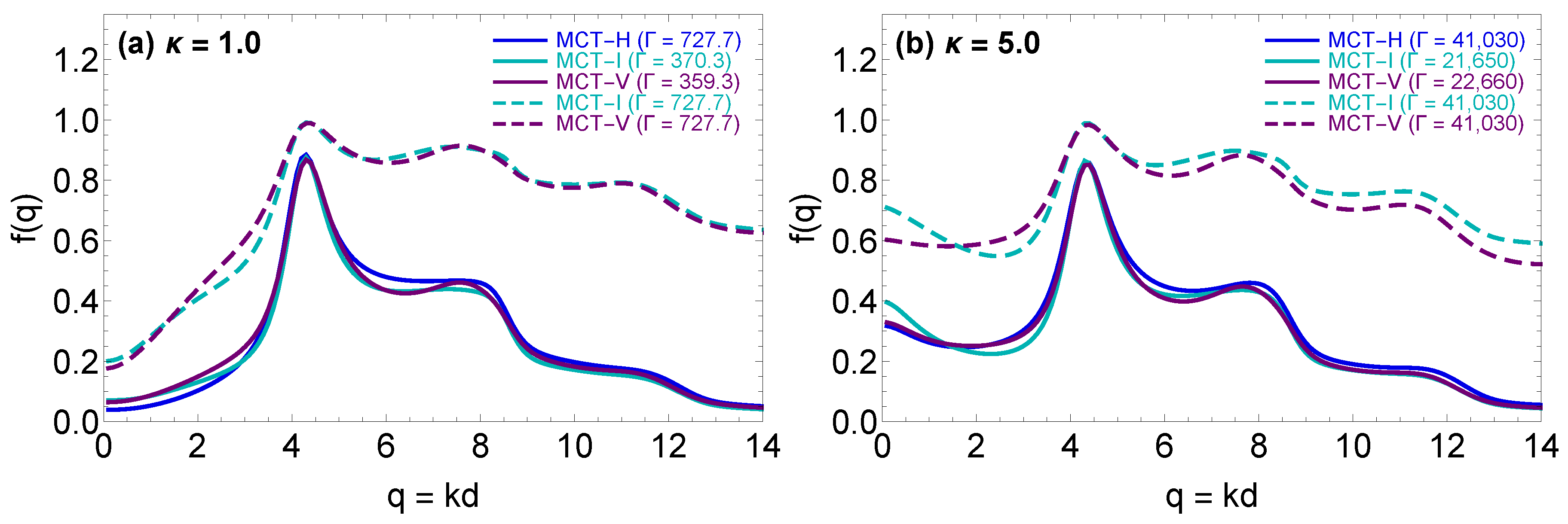
4.2. The MCT form Factors
4.3. The MCT Vitrification Indicators
5. Discussion and Future Work
5.1. Summary of the Results
5.2. Extension to Bi-Yukawa Systems
5.3. Quasi-Universality Aspects
5.4. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GMCT | Generalized Mode Coupling Theory |
| HNC | Hypernetted Chain |
| HS | Hard Sphere |
| HSPY | Hard Sphere Percus–Yevick |
| HSVW | Hard Sphere Verlet-Weis |
| IEMHNC | Isomorph-based Empirically Modified HNC |
| IET | Integral Equation Theory |
| IPL | Inverse Power Law |
| MCT | Mode Coupling Theory |
| MCT-H | MCT solved with structural input from the HNC approximation |
| MCT-I | MCT solved with structural input from the IEMHNC approximation |
| MCT-V | MCT solved with structural input from the VMHNC approximation |
| MD | Moleculary Dynamics |
| OCP | One-Component Plasma |
| PY | Percus–Yevick |
| YOCP | Yukawa One-Component Plasma |
| VMHNC | Variationally Modified HNC |
References
- Turnbull, D. Under what conditions can a glass be formed? Contemp. Phys. 1969, 10, 473–488. [Google Scholar] [CrossRef]
- Debenedetti, P.G.; Stillinger, F.H. Supercooled liquids and the glass transition. Nature 2001, 410, 259–267. [Google Scholar] [CrossRef] [PubMed]
- Dyre, J.C. Colloquium: The glass transition and elastic models of glass-forming liquids. Rev. Mod. Phys. 2006, 78, 953. [Google Scholar] [CrossRef]
- Cavagna, A. Supercooled liquids for pedestrians. Phys. Rep. 2009, 476, 51–124. [Google Scholar] [CrossRef]
- Biroli, G.; Garrahan, J.P. Perspective: The glass transition. J. Chem. Phys. 2013, 138, 12A301. [Google Scholar] [CrossRef]
- Pusey, P.N.; Van Megen, W. Phase behaviour of concentrated suspensions of nearly hard colloidal spheres. Nature 1986, 320, 340–342. [Google Scholar] [CrossRef]
- Van Megen, W.; Underwood, S.; Pusey, P. Nonergodicity parameters of colloidal glasses. Phys. Rev. Lett. 1991, 67, 1586. [Google Scholar] [CrossRef]
- Mattsson, J.; Wyss, H.M.; Fernandez-Nieves, A.; Miyazaki, K.; Hu, Z.; Reichman, D.R.; Weitz, D.A. Soft colloids make strong glasses. Nature 2009, 462, 83–86. [Google Scholar] [CrossRef]
- Keys, A.S.; Abate, A.R.; Glotzer, S.C.; Durian, D.J. Measurement of growing dynamical length scales and prediction of the jamming transition in a granular material. Nat. Phys. 2007, 3, 260–264. [Google Scholar] [CrossRef]
- Xia, C.; Li, J.; Cao, Y.; Kou, B.; Xiao, X.; Fezzaa, K.; Xiao, T.; Wang, Y. The structural origin of the hard-sphere glass transition in granular packing. Nat. Commun. 2015, 6, 1–9. [Google Scholar] [CrossRef]
- Hansen, H.W.; Sanz, A.; Adrjanowicz, K.; Frick, B.; Niss, K. Evidence of a one-dimensional thermodynamic phase diagram for simple glass-formers. Nat. Commun. 2018, 9, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Flenner, E.; Szamel, G. Relaxation in a glassy binary mixture: Comparison of the mode-coupling theory to a Brownian dynamics simulation. Phys. Rev. E 2005, 72, 031508. [Google Scholar] [CrossRef]
- Ashwin, S.S.; Sastry, S. Low-temperature behaviour of the Kob–Andersen binary mixture. J. Phys. Condens. Matter 2003, 15, S1253. [Google Scholar]
- Pedersen, U.R.; Schrøder, T.B.; Dyre, J.C. Phase diagram of Kob–Andersen-type binary Lennard-Jones mixtures. Phys. Rev. Lett. 2018, 120, 165501. [Google Scholar] [CrossRef] [PubMed]
- Foffi, G.; Götze, W.; Sciortino, F.; Tartaglia, P.; Voigtmann, T. Mixing effects for the structural relaxation in binary hard-sphere liquids. Phys. Rev. Lett. 2003, 91, 085701. [Google Scholar] [CrossRef] [PubMed]
- Voigtmann, T.; Puertas, A.M.; Fuchs, M. Tagged-particle dynamics in a hard-sphere system: Mode-coupling theory analysis. Phys. Rev. E 2004, 70, 061506. [Google Scholar] [CrossRef] [PubMed]
- Bengtzelius, U.; Gotze, W.; Sjolander, A. Dynamics of supercooled liquids and the glass transition. J. Phys. C Solid State Phys. 1984, 17, 5915. [Google Scholar] [CrossRef]
- Götze, W. The essentials of the mode-coupling theory for glassy dynamics. Condens. Matter Phys. 1998, 1, 873. [Google Scholar] [CrossRef]
- Kirkpatrick, T.R.; Thirumalai, D.; Wolynes, P.G. Scaling concepts for the dynamics of viscous liquids near an ideal glassy state. Phys. Rev. A 1989, 40, 1045. [Google Scholar] [CrossRef]
- Chandler, D.; Garrahan, J.P. Dynamics on the way to forming glass: Bubbles in space-time. Annu. Rev. Phys. Chem 2010, 61, 191–217. [Google Scholar] [CrossRef]
- Janssen, L. Mode-coupling theory of the glass transition: A primer. Front. Phys. 2018, 6, 97. [Google Scholar] [CrossRef]
- Berthier, L.; Biroli, G. Theoretical perspective on the glass transition and amorphous materials. Rev. Mod. Phys. 2011, 83, 587. [Google Scholar] [CrossRef]
- Fortov, V.; Ivlev, A.; Khrapak, S.; Khrapak, A.; Morfill, G. Complex (dusty) plasmas: Current status, open issues, perspectives. Phys. Rep. 2005, 421, 1–103. [Google Scholar] [CrossRef]
- Hamaguchi, S.; Farouki, R.; Dubin, D. Triple point of Yukawa systems. Phys. Rev. E 1997, 56, 4671. [Google Scholar] [CrossRef]
- Morfill, G.E.; Ivlev, A.V. Complex plasmas: An interdisciplinary research field. Rev. Mod. Phys. 2009, 81, 1353. [Google Scholar] [CrossRef]
- Su, Y.S.; Io, C.W.; Lin, I. Transient slowing down relaxation dynamics of the supercooled dusty plasma liquid after quenching. Phys. Rev. E 2012, 86, 016405. [Google Scholar] [CrossRef]
- Du, C.R.; Nosenko, V.; Thomas, H.M.; Lin, Y.F.; Morfill, G.E.; Ivlev, A.V. Slow dynamics in a quasi-two-dimensional binary complex plasma. Phys. Rev. Lett. 2019, 123, 185002. [Google Scholar] [CrossRef]
- Pustylnik, M.; Fink, M.; Nosenko, V.; Antonova, T.; Hagl, T.; Thomas, H.; Zobnin, A.; Lipaev, A.; Usachev, A.; Molotkov, V.; et al. Plasmakristall-4: New complex (dusty) plasma laboratory on board the International Space Station. Rev. Sci. Instrum. 2016, 87, 093505. [Google Scholar] [CrossRef]
- Yazdi, A.; Ivlev, A.; Khrapak, S.; Thomas, H.; Morfill, G.E.; Löwen, H.; Wysocki, A.; Sperl, M. Glass-transition properties of Yukawa potentials: From charged point particles to hard spheres. Phys. Rev. E 2014, 89, 063105. [Google Scholar] [CrossRef]
- Reichman, D.R.; Charbonneau, P. Mode-coupling theory. J. Stat. Mech. Theory Exp. 2005, 2005, P05013. [Google Scholar] [CrossRef]
- Zwanzig, R. Memory effects in irreversible thermodynamics. Phys. Rev. 1961, 124, 983. [Google Scholar] [CrossRef]
- Mori, H. Transport, collective motion, and Brownian motion. Prog. Theor. Phys. 1965, 33, 423–455. [Google Scholar] [CrossRef]
- Franosch, T.; Fuchs, M.; Götze, W.; Mayr, M.R.; Singh, A. Asymptotic laws and preasymptotic correction formulas for the relaxation near glass-transition singularities. Phys. Rev. E 1997, 55, 7153. [Google Scholar] [CrossRef]
- Hansen, J.P.; McDonald, I.R. Theory of Simple Liquids; Academic: New York, NY, USA, 2006. [Google Scholar]
- Kawasaki, K. Correlation-function approach to the transport coefficients near the critical point. I. Phys. Rev. 1966, 150, 291. [Google Scholar] [CrossRef]
- Mayer, P.; Miyazaki, K.; Reichman, D.R. Cooperativity beyond caging: Generalized mode-coupling theory. Phys. Rev. Lett. 2006, 97, 095702. [Google Scholar] [CrossRef]
- Gnan, N.; Schrøder, T.B.; Pedersen, U.R.; Bailey, N.P.; Dyre, J.C. Pressure-energy correlations in liquids. IV.“Isomorphs” in liquid phase diagrams. J. Chem. Phys. 2009, 131, 234504. [Google Scholar] [CrossRef]
- Dyre, J.C. Simple liquids’ quasiuniversality and the hard-sphere paradigm. J. Phys. Condens. Matter 2016, 28, 323001. [Google Scholar] [CrossRef] [PubMed]
- Schrøder, T.B.; Dyre, J.C. Simplicity of condensed matter at its core: Generic definition of a Roskilde-simple system. J. Chem. Phys. 2014, 141, 204502. [Google Scholar] [CrossRef] [PubMed]
- Veldhorst, A.A.; Schrøder, T.B.; Dyre, J.C. Invariants in the Yukawa system’s thermodynamic phase diagram. Phys. Plasmas 2015, 22, 073705. [Google Scholar] [CrossRef]
- Vaulina, O.; Khrapak, S.; Morfill, G. Universal scaling in complex (dusty) plasmas. Phys. Rev. E 2002, 66, 016404. [Google Scholar] [CrossRef]
- Hamaguchi, S.; Farouki, R.; Dubin, D. Phase diagram of Yukawa systems near the one-component-plasma limit revisited. J. Chem. Phys. 1996, 105, 7641. [Google Scholar] [CrossRef]
- Pedersen, U.R.; Costigliola, L.; Bailey, N.P.; Schrøder, T.B.; Dyre, J.C. Thermodynamics of freezing and melting. Nat. Commun. 2016, 7, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Rast, S.; Fries, P.H.; Krienke, H. A new biased Monte-Carlo method for computing coefficients of the bridge functions of liquids. Mol. Phys. 1999, 96, 1543. [Google Scholar] [CrossRef]
- Kwak, S.K.; Kofke, D.A. Evaluation of bridge-function diagrams via Mayer-sampling Monte Carlo simulation. J. Chem. Phys. 2005, 122, 104508. [Google Scholar] [CrossRef] [PubMed]
- Attard, P.; Patey, G. Hypernetted-chain closure with bridge diagrams. Asymmetric hard sphere mixtures. J. Chem. Phys. 1990, 92, 4970–4982. [Google Scholar] [CrossRef]
- Perkyns, J.S.; Dyer, K.M.; Pettitt, B.M. Computationally useful bridge diagram series. II. Diagrams in h-bonds. J. Chem. Phys. 2002, 116, 9404–9412. [Google Scholar] [CrossRef]
- Labík, S.; Gabrielová, H.; Kolafa, J.R.Í.; Malijevskỳ, A. Calculation of elementary diagrams using a Metropolis-like simulation method. Mol. Phys. 2003, 101, 1139–1146. [Google Scholar] [CrossRef]
- Bomont, J.M. Recent advances in the field of integral equation theories: Bridge functions and applications to classical fluids. Adv. Chem. Phys. 2008, 139, 1. [Google Scholar]
- Morita, T.; Hiroike, K. A new approach to the theory of classical fluids. I. Prog. Theor. Phys. 1960, 23, 1003. [Google Scholar] [CrossRef]
- Ng, K.C. Hypernetted chain solutions for the classical one-component plasma up to Γ = 7000. J. Chem. Phys. 1974, 61, 2680. [Google Scholar] [CrossRef]
- Tolias, P.; Lucco Castello, F. Isomorph-based empirically modified hypernetted-chain approach for strongly coupled Yukawa one-component plasmas. Phys. Plasmas 2019, 26, 043703. [Google Scholar] [CrossRef]
- Lucco Castello, F.; Tolias, P.; Dyre, J.C. Testing the isomorph invariance of the bridge functions of Yukawa one-component plasmas. J. Chem. Phys. 2021, 154, 034501. [Google Scholar]
- Lucco Castello, F.; Tolias, P.; Hansen, J.S.; Dyre, J.C. Isomorph invariance and thermodynamics of repulsive dense bi-Yukawa one-component plasmas. Phys. Plasmas 2019, 26, 053705. [Google Scholar] [CrossRef]
- Rosenfeld, Y.; Ashcroft, N.W. Theory of simple classical fluids: Universality in the short-range structure. Phys. Rev. A 1979, 20, 1208. [Google Scholar] [CrossRef]
- Rosenfeld, Y. Comments on the variational modified-hypernetted-chain theory for simple fluids. J. Stat. Phys. 1986, 42, 437. [Google Scholar] [CrossRef]
- Faussurier, G. Description of strongly coupled Yukawa fluids using the variational modified hypernetted chain approach. Phys. Rev. E 2004, 69, 066402. [Google Scholar] [CrossRef]
- Lucco Castello, F.; Tolias, P. On the advanced integral equation theory description of dense Yukawa one-component plasma liquids. Contrib. Plasma Phys. 2021, 61, e202000105. [Google Scholar]
- Nauroth, M.; Kob, W. Quantitative test of the mode-coupling theory of the ideal glass transition for a binary Lennard-Jones system. Phys. Rev. E 1997, 55, 657. [Google Scholar] [CrossRef]
- Winkler, A.; Latz, A.; Schilling, R.; Theis, C. Molecular mode-coupling theory applied to a liquid of diatomic molecules. Phys. Rev. E 2000, 62, 8004. [Google Scholar] [CrossRef]
- Sciortino, F.; Kob, W. Debye-waller factor of liquid silica: Theory and simulation. Phys. Rev. Lett. 2001, 86, 648. [Google Scholar] [CrossRef]
- Yazdi, A.; Heinen, M.; Ivlev, A.; Löwen, H.; Sperl, M. Glass transition of charged particles in two-dimensional confinement. Phys. Rev. E 2015, 91, 052301. [Google Scholar] [CrossRef]
- Wu, J.; Cao, J. High-order mode-coupling theory for the colloidal glass transition. Phys. Rev. Lett. 2005, 95, 078301. [Google Scholar] [CrossRef] [PubMed]
- Sperl, M. Nearly logarithmic decay in the colloidal hard-sphere system. Phys. Rev. E 2005, 71, 060401. [Google Scholar] [CrossRef] [PubMed]
- Elizondo-Aguilera, L.F.; Voigtmann, T. Glass-transition asymptotics in two theories of glassy dynamics: Self-consistent generalized Langevin equation and mode-coupling theory. Phys. Rev. E 2019, 100, 042601. [Google Scholar] [CrossRef] [PubMed]
- Barrat, J.L.; Latz, A. Mode coupling theory for the glass transition in a simple binary mixture. J. Phys. Condens. Matter 1990, 2, 4289. [Google Scholar] [CrossRef]
- Chen, H.; Lai, S. Application of the modified hypernetted-chain integral equation to supercooled and expanded liquid structures. Phys. Rev. E 1994, 49, R982. [Google Scholar] [CrossRef] [PubMed]
- Bayer, M.; Brader, J.M.; Ebert, F.; Fuchs, M.; Lange, E.; Maret, G.; Schilling, R.; Sperl, M.; Wittmer, J. Dynamic glass transition in two dimensions. Phys. Rev. E 2007, 76, 011508. [Google Scholar] [CrossRef] [PubMed]
- Barrat, J.L.; Klein, M.L. Molecular dynamics simulations of supercooled liquids near the glass transition. Annu. Rev. Phys. Chem. 1991, 42, 23–53. [Google Scholar] [CrossRef]
- Dzugutov, M. Glass formation in a simple monatomic liquid with icosahedral inherent local order. Phys. Rev. A 1992, 46, R2984. [Google Scholar] [CrossRef]
- Kob, W. Computer simulations of supercooled liquids and glasses. J. Phys. Condens. Matter 1999, 11, R85. [Google Scholar] [CrossRef]
- Angelani, L.; Ruocco, G.; Sampoli, M.; Sciortino, F. General features of the energy landscape in Lennard-Jones-like model liquids. J. Chem. Phys. 2003, 119, 2120. [Google Scholar] [CrossRef]
- Toxvaerd, S.; Pedersen, U.R.; Schrøder, T.B.; Dyre, J.C. Stability of supercooled binary liquid mixtures. J. Chem. Phys. 2009, 130, 224501. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, R.; Kob, W. Replica-exchange molecular dynamics simulation for supercooled liquids. Phys. Rev. E 2000, 61, 5473. [Google Scholar] [CrossRef] [PubMed]
- Callaham, J.; Machta, J. Population annealing simulations of a binary hard-sphere mixture. Phys. Rev. E 2017, 95, 063315. [Google Scholar] [CrossRef] [PubMed]
- Ninarello, A.; Berthier, L.; Coslovich, D. Models and Algorithms for the Next Generation of Glass Transition Studies. Phys. Rev. X 2017, 7, 021039. [Google Scholar] [CrossRef]
- Bell, I.H.; Dyre, J.C.; Ingebrigtsen, T.S. Excess-entropy scaling in supercooled binary mixtures. Nat. Commun. 2020, 11, 1–12. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comp. Phys 1995, 117, 1. [Google Scholar] [CrossRef]
- Iyetomi, H.; Ogata, S.; Ichimaru, S. Bridge functions and improvement on the hypernetted-chain approximation for classical one-component plasmas. Phys. Rev. A 1992, 46, 1051. [Google Scholar] [CrossRef]
- Llano-Restrepo, M.; Chapman, W.G. Bridge function and cavity correlation function for the soft sphere fluid from simulation: Implications on closure relations. J. Chem. Phys. 1994, 100, 5139–5148. [Google Scholar] [CrossRef]
- Kolafa, J.; Labík, S.; Malijevskỳ, A. The bridge function of hard spheres by direct inversion of computer simulation data. Mol. Phys. 2002, 100, 2629. [Google Scholar] [CrossRef]
- Tomazic, D.; Hoffgaard, F.; Kast, S.M. Bridge function of the repulsive Weeks–Chandler–Andersen (WCA) fluid. Chem. Phys. Lett. 2014, 591, 237–242. [Google Scholar] [CrossRef]
- Gough, B. NU Scientific Library Reference Manual, 3rd ed.; Network Theory Ltd.: London, UK, 2009; ISBN 0954612078. Available online: http://www.gnu.org/software/gsl/ (accessed on 27 January 2021).
- Wertheim, M.S. Exact solution of the Percus–Yevick integral equation for hard spheres. Phys. Rev. Lett. 1963, 10, 321. [Google Scholar] [CrossRef]
- Thiele, E. Equation of state for hard spheres. J. Chem. Phys. 1963, 39, 474–479. [Google Scholar] [CrossRef]
- Verlet, L.; Weis, J.J. Equilibrium theory of simple liquids. Phys. Rev. A 1972, 5, 939. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Rosenfeld, Y.; Tarazona, P. Density functional theory and the asymptotic high density expansion of the free energy of classical solids and fluids. Mol. Phys. 1998, 95, 141–150. [Google Scholar] [CrossRef]
- Rosenfeld, Y. Excess-entropy and freezing-temperature scalings for transport coefficients: Self-diffusion in Yukawa systems. Phys. Rev. E 2000, 62, 7524. [Google Scholar] [CrossRef]
- Dyre, J.C. Hidden scale invariance in condensed matter. J. Phys. Chem. B 2014, 118, 10007–10024. [Google Scholar] [CrossRef]
- Baus, M.; Hansen, J.P. Statistical mechanics of simple Coulomb systems. Phys. Rep. 1980, 59, 1–94. [Google Scholar] [CrossRef]
- Widom, B. Some topics in the theory of fluids. J. Chem. Phys. 1963, 39, 2808–2812. [Google Scholar] [CrossRef]
- Hansen, J.P.; Verlet, L. Phase transitions of the Lennard-Jones system. Phys. Rev. 1969, 184, 151. [Google Scholar] [CrossRef]
- Raveché, H.J.; Mountain, R.D.; Streett, W.B. Freezing and melting properties of the Lennard-Jones system. J. Chem. Phys. 1974, 61, 1970–1984. [Google Scholar] [CrossRef]
- Ratynskaia, S.; Rypdal, K.; Knapek, C.; Khrapak, S.; Milovanov, A.; Ivlev, A.; Rasmussen, J.J.; Morfill, G. Superdiffusion and viscoelastic vortex flows in a two-dimensional complex plasma. Phys. Rev. Lett. 2006, 96, 105010. [Google Scholar] [CrossRef] [PubMed]
- Pfleiderer, T.; Waldner, I.; Bertagnolli, H.; Tödheide, K.; Kirchner, B.; Huber, H.; Fischer, H.E. The structure of fluid argon from high-pressure neutron diffraction and ab initio molecular dynamics simulations. J. Chem. Phys. 1999, 111, 2641–2646. [Google Scholar] [CrossRef]
- Khrapak, S.A.; Ivlev, A.V.; Morfill, G.E. Shielding of a test charge: Role of plasma production and loss balance. Phys. Plasmas 2010, 17, 042107. [Google Scholar] [CrossRef]
- Tolias, P.; Ratynskaia, S.; de Angelis, U. Soft mean spherical approximation for dusty plasma liquids: One-component Yukawa systems with plasma shielding. Phys. Rev. E 2014, 90, 053101. [Google Scholar] [CrossRef]
- Szamel, G. Colloidal glass transition: Beyond mode-coupling theory. Phys. Rev. Lett. 2003, 90, 228301. [Google Scholar] [CrossRef]

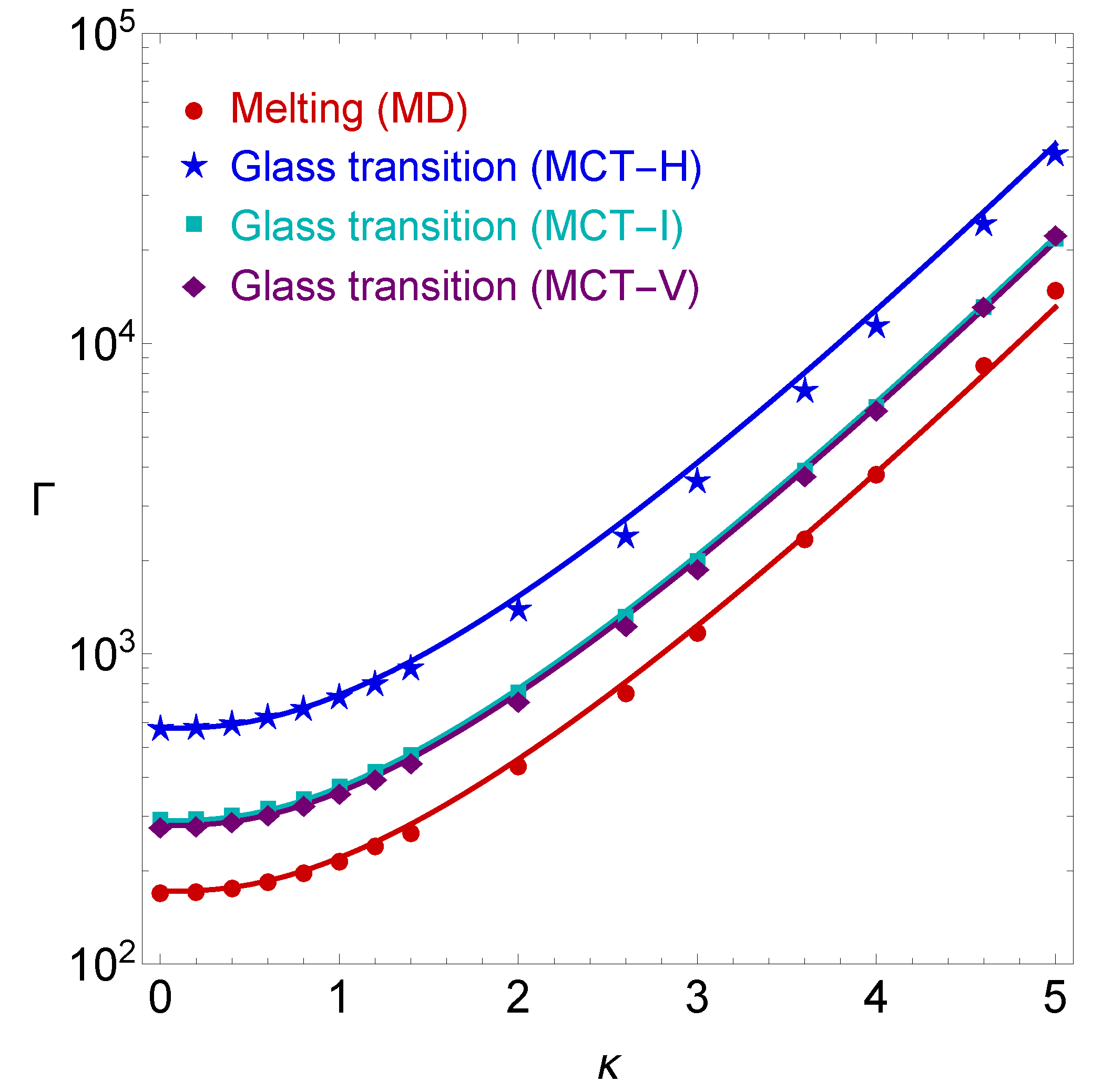
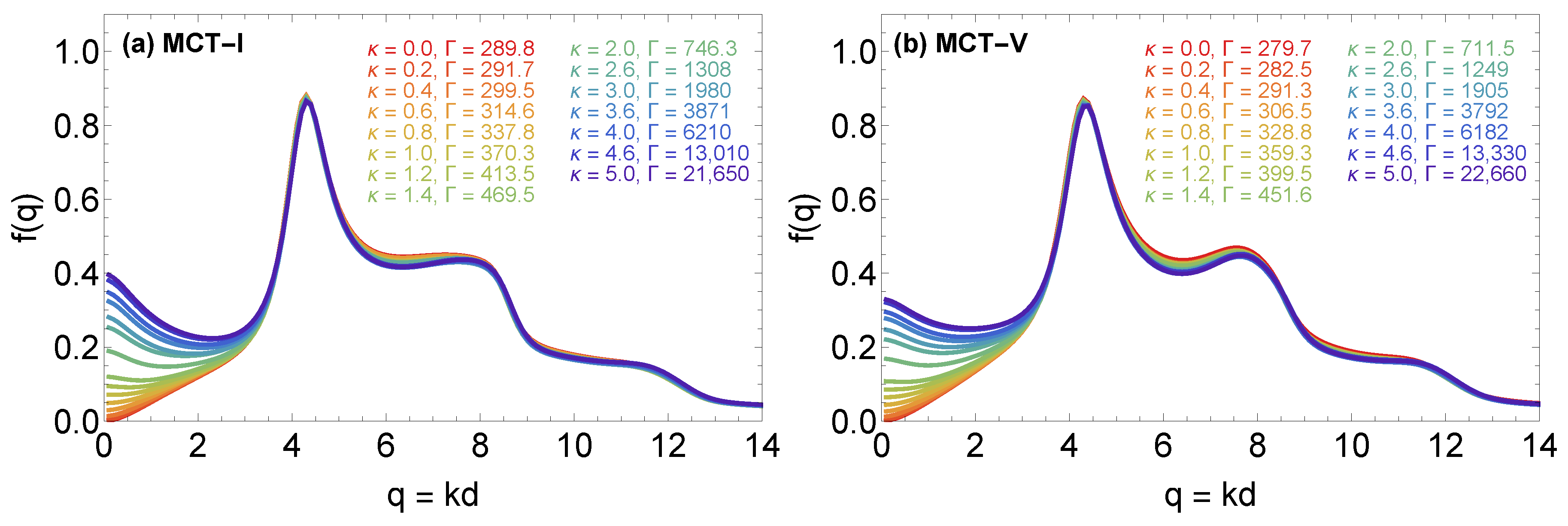
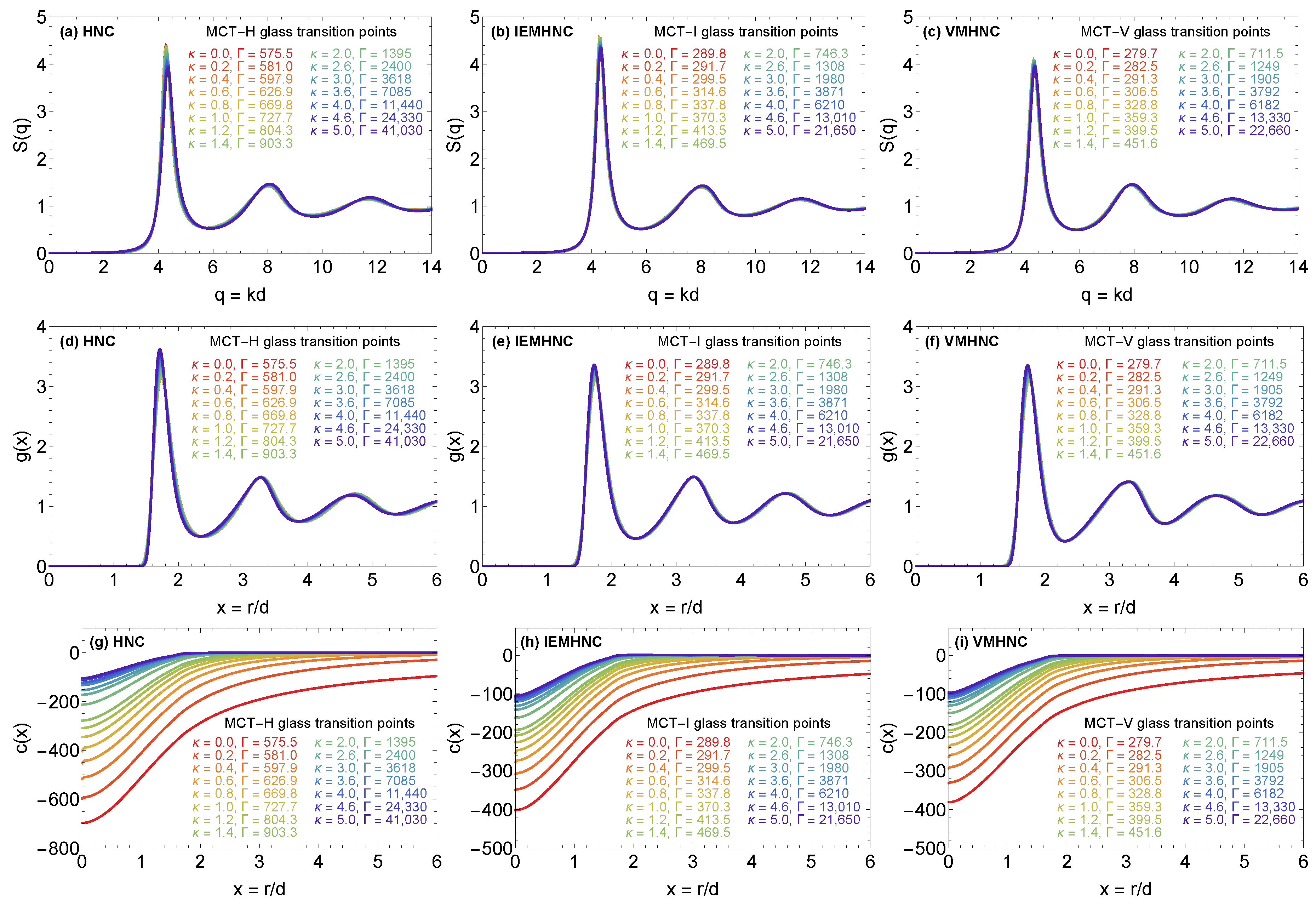
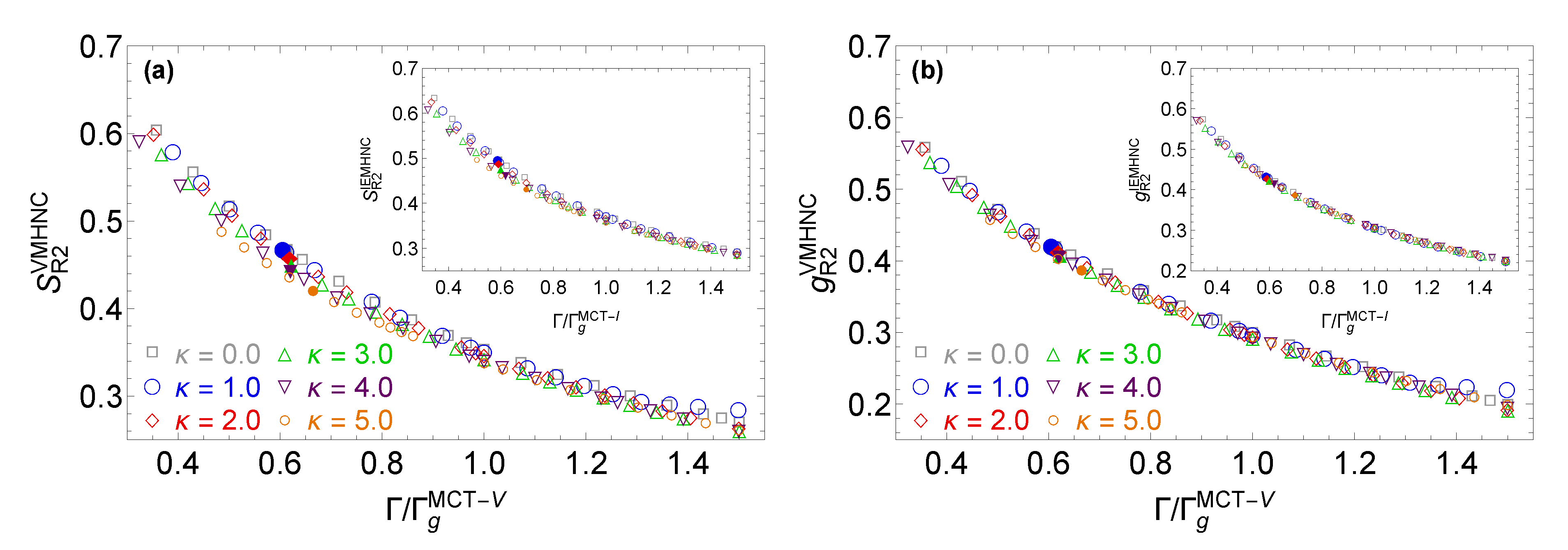
| 0.0 | 575.5 | 289.8 | 279.7 |
| 0.2 | 581.0 | 291.7 | 282.5 |
| 0.4 | 597.9 | 299.5 | 291.3 |
| 0.6 | 626.9 | 314.6 | 306.4 |
| 0.8 | 669.8 | 337.8 | 328.8 |
| 1.0 | 731.1 | 370.3 | 359.3 |
| 1.2 | 804.3 | 413.5 | 399.5 |
| 1.4 | 903.3 | 469.5 | 451.6 |
| 2.0 | 1395 | 746.3 | 711.5 |
| 2.6 | 2400 | 1308 | 1249 |
| 3.0 | 3618 | 1980 | 1905 |
| 3.6 | 7085 | 3871 | 3792 |
| 4.0 | 11,440 | 6210 | 6182 |
| 4.6 | 24,430 | 13,010 | 13,330 |
| 5.0 | 41,030 | 21,650 | 22,660 |
| 0.0 | 289.8 | −5.204 | −5.547 | 279.7 | −5.124 | −5.469 |
| 0.2 | 291.7 | −5.188 | −5.552 | 282.5 | −5.115 | −5.481 |
| 0.4 | 299.5 | −5.161 | −5.557 | 291.3 | −5.098 | −5.496 |
| 0.6 | 314.6 | −5.134 | −5.558 | 306.4 | −5.074 | −5.499 |
| 0.8 | 337.8 | −5.111 | −5.551 | 328.8 | −5.05 | −5.491 |
| 1.0 | 370.3 | −5.093 | −5.540 | 359.3 | −5.025 | −5.474 |
| 1.2 | 413.5 | −5.062 | −5.526 | 399.5 | −4.984 | −5.451 |
| 1.4 | 469.5 | −5.082 | −5.512 | 451.6 | −4.992 | −5.427 |
| 2.0 | 746.3 | −5.002 | −5.469 | 711.5 | −4.893 | −5.366 |
| 2.6 | 1308 | −4.932 | −5.444 | 1249 | −4.827 | −5.344 |
| 3.0 | 1980 | −4.884 | −5.436 | 1905 | −4.798 | −5.353 |
| 3.6 | 3871 | −4.782 | −5.441 | 3792 | −4.737 | −5.396 |
| 4.0 | 6210 | −4.602 | −5.453 | 6182 | −4.593 | −5.443 |
| 4.6 | 13,010 | −4.614 | −5.481 | 13,330 | −4.662 | −5.534 |
| 5.0 | 21,650 | −4.626 | −5.503 | 22,660 | −4.715 | −5.605 |
| AVE | −4.695 | −5.505 | −4.912 | −5.455 | ||
| (%) | 3.628 | 0.739 | 3.151 | 0.994 | ||
| (%) | 10.84 | 1.253 | 6.494 | 2.748 |
| 0.0 | 289.8 | 0.37 | 0.31 | 279.7 | 0.35 | 0.30 |
| 0.2 | 291.7 | 0.37 | 0.31 | 282.5 | 0.35 | 0.30 |
| 0.4 | 299.5 | 0.37 | 0.31 | 291.3 | 0.35 | 0.30 |
| 0.6 | 314.6 | 0.37 | 0.31 | 306.4 | 0.35 | 0.30 |
| 0.8 | 337.8 | 0.37 | 0.31 | 328.8 | 0.35 | 0.30 |
| 1.0 | 370.3 | 0.37 | 0.31 | 359.3 | 0.35 | 0.30 |
| 1.2 | 413.5 | 0.37 | 0.31 | 399.5 | 0.35 | 0.30 |
| 1.4 | 469.5 | 0.37 | 0.31 | 451.6 | 0.35 | 0.30 |
| 2.0 | 746.3 | 0.37 | 0.31 | 711.5 | 0.35 | 0.30 |
| 2.6 | 1308 | 0.37 | 0.31 | 1249 | 0.35 | 0.29 |
| 3.0 | 1980 | 0.37 | 0.31 | 1905 | 0.34 | 0.29 |
| 3.6 | 3871 | 0.36 | 0.31 | 3792 | 0.34 | 0.29 |
| 4.0 | 6210 | 0.36 | 0.31 | 6182 | 0.34 | 0.29 |
| 4.6 | 13,010 | 0.36 | 0.31 | 13,330 | 0.34 | 0.30 |
| 5.0 | 21,650 | 0.36 | 0.31 | 22,660 | 0.34 | 0.30 |
| AVE | 0.37 | 0.31 | 0.35 | 0.30 | ||
| (%) | 1.22 | 0.20 | 1.24 | 0.57 | ||
| (%) | 2.32 | 0.60 | 2.34 | 0.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lucco Castello, F.; Tolias, P. Theoretical Estimate of the Glass Transition Line of Yukawa One-Component Plasmas. Molecules 2021, 26, 669. https://doi.org/10.3390/molecules26030669
Lucco Castello F, Tolias P. Theoretical Estimate of the Glass Transition Line of Yukawa One-Component Plasmas. Molecules. 2021; 26(3):669. https://doi.org/10.3390/molecules26030669
Chicago/Turabian StyleLucco Castello, Federico, and Panagiotis Tolias. 2021. "Theoretical Estimate of the Glass Transition Line of Yukawa One-Component Plasmas" Molecules 26, no. 3: 669. https://doi.org/10.3390/molecules26030669
APA StyleLucco Castello, F., & Tolias, P. (2021). Theoretical Estimate of the Glass Transition Line of Yukawa One-Component Plasmas. Molecules, 26(3), 669. https://doi.org/10.3390/molecules26030669







