Electronegativity under Confinement
Abstract
:1. Introduction
1.1. Electronegativity
1.2. Confinement
2. Computational Details
3. Results
3.1. Electronegativity Formulas under Confinement
3.2. Testing of the Perturbation Theory Equations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miao, M.S.; Hoffmann, R. High Pressure Electrides: A Predictive Chemical and Physical Theory. Accounts Chem. Res. 2014, 47, 1311–1317. [Google Scholar] [CrossRef]
- Pauling, L. The Nature of the Chemical Bond, 3rd ed.; Cornell University Press: Ithaca, NY, USA, 1960. [Google Scholar]
- Tantardini, C.; Oganov, A.R. Thermochemical electronegativities of the elements. Nat. Commun. 2021, 12, 2087. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S. Electronegativity—A Perspective. J. Mol. Model. 2018, 24, 214. [Google Scholar] [CrossRef]
- Allen, L.C. Chemistry and Electronegativity. Int. J. Quantum Chem. 1994, 49, 253–277. [Google Scholar] [CrossRef]
- Mulliken, R.S. Chemical Bonding. Ann. Rev. Phys. Chem. 1978, 29, 1–31. [Google Scholar] [CrossRef]
- Parr, R.G.; Donnelly, R.A.; Levy, M.; Palke, W.E. Electronegativity: The Density Functional Viewpoint. J. Chem. Phys. 1978, 68, 3801–3807. [Google Scholar] [CrossRef]
- Guerra, D.; Vargas, R.; Fuentealba, P.; Garza, J. Modeling Pressure Effects on the Electronic Properties of Ca, Sr, and Ba by the Confined Atoms Model. In Advances in Quantum Chemistry 58; Academic Press: Cambridge, MA, USA, 2009; pp. 1–12. [Google Scholar]
- Martínez-Sánchez, M.A.; Rodriguez-Bautista, M.; Vargas, R.; Garza, J. Solution of the Kohn–Sham Equations for Many-Electron Atoms Confined by Penetrable Walls. Theor. Chem. Acc. 2016, 135, 207. [Google Scholar] [CrossRef]
- Martínez-Sánchez, M.A.; Aquino, N.; Vargas, R.; Garza, J. Exact Solution for the Hydrogen Atom Confined by a Dielectric Continuum and the Correct Basis Set to Study Many-electron Atoms Under Similar Confinements. Chem. Phys. Lett. 2017, 690, 14–19. [Google Scholar] [CrossRef]
- Rodriguez-Bautista, M.; Díaz-García, C.; Navarrete-López, A.M.; Vargas, R.; Garza, J. Roothaan’s Approach to Solve the Hartree-Fock Equations for Atoms Confined by Soft Walls: Basis Set with Correct Asymptotic Behavior. J. Chem. Phys. 2015, 143, 034103. [Google Scholar] [CrossRef]
- Rodriguez-Bautista, M.; Vargas, R.; Aquino, N.; Garza, J. Electron-density Delocalization in Many-electron Atoms Confined by Penetrable Walls: A Hartree–Fock study. Int. J. Quantum Chem. 2018, 118, e25571. [Google Scholar] [CrossRef]
- Holka, F.; Neogrády, P.; Kellö, V.; Urban, M.; Diercksen, G.H.F. Polarizabilities of Confined Two-Electron Systems: The 2-Electron Quantum Dot, The Hydrogen Anion, the Helium Atom and the Lithium Cation. Mol. Phys. 2005, 103, 2747–2761. [Google Scholar] [CrossRef]
- Sako, T.; Diercksen, G.H.F. Confined Quantum Systems: Spectral Properties of Two-Electron Quantum Dots. J. Phys.-Condens. Mat. 2003, 15, 5487–5509. [Google Scholar] [CrossRef]
- Sako, T.; Yamamoto, S.; Diercksen, G.H.F. Confined Quantum Systems: Dipole Transition Moment of Two- and Three-Electron Quantum Dots, and of Helium and Lithium Atoms in a Harmonic Oscillator Potential. J. Phys. B-At. Mol. Opt. 2004, 37, 1673–1688. [Google Scholar] [CrossRef]
- Sako, T.; Diercksen, G.H.F. Spectra and Correlated Wave Functions of Two Electrons Confined in a Quasi-One-Dimensional Nanostructure. Phys. Rev. B 2007, 75, 115413. [Google Scholar] [CrossRef] [Green Version]
- Sako, T.; Diercksen, G.H.F. Understanding the Spectra of a Few Electrons Confined in a Quasi-One-Dimensional Nanostructure. J. Phys.-Condens. Mat. 2008, 20, 155202. [Google Scholar] [CrossRef] [Green Version]
- Robles-Navarro, A.; Fuentealba, P.; Muñoz, F.; Cárdenas, C. Electronic Structure of First and Second Row Atoms under Harmonic Confinement. Int. J. Quantum Chem. 2020, 120, e26132. [Google Scholar] [CrossRef]
- Robles-Navarro, A.; Rodriguez-Bautista, M.; Fuentealba, P.; Cárdenas, C. The Change in the Nature of Bonding in the Li2 Dimer Under Confinement. Int. J. Quantum Chem. 2021, 121, e26644. [Google Scholar] [CrossRef]
- Cammi, R.J. A New Extension of the Polarizable Continuum Model: Toward a Quantum Chemical Description of Chemical Reactions at Extreme High Pressure. J. Comput. Chem. 2015, 36, 2246–2259. [Google Scholar] [CrossRef] [PubMed]
- Cammi, R.; Chen, B.; Rahm, M. Analytical Calculation of Pressure for Confined Atomic and Molecular Systems Using the eXtreme-Pressure Polarizable Continuum Model. J. Comput. Chem. 2018, 39, 2243–2250. [Google Scholar] [CrossRef] [Green Version]
- Connerade, J.P. Confining and Compressing the Atom. Eur. Phys. J. D 2020, 74, 211. [Google Scholar] [CrossRef]
- Connerade, J.P.; Dolmatov, V.K.; Lakshmi, P.A. The Filling of Shells in Compressed Atoms. J. Phys. B-At. Mol. Opt. 2000, 33, 251–264. [Google Scholar] [CrossRef]
- Dolmatov, V.K.; Connerade, J.P.; Lakshmi, P.A.; Manson, S.T. Spectral Properties of Confined Atoms. Surf. Rev. Lett. 2002, 9, 39–43. [Google Scholar] [CrossRef]
- Novoa, T.; Contreras-García, J.; Fuentealba, P.; Cárdenas, C. The Pauli Principle and the Confinement of Electron Pairs in a Double Well: Aspects of Electronic Bonding Under Pressure. J. Chem. Phys. 2019, 150, 204304. [Google Scholar] [CrossRef]
- Kobayashi, T.; Sekine, T.; Takemura, K.; Dykhne, T. Emission Spectroscopy of Eu-Doped CaF2 under Static and Dynamic High Pressures. Jpn. J. Appl. Phys. 2007, 46, 6696–6701. [Google Scholar] [CrossRef]
- Kume, T.; Ohura, H.; Takeichi, T.; Ohmura, A.; Machida, A.; Watanuki, T.; Aoki, K.; Sasaki, S.; Shimizu, H.; Takemura, K. High-Pressure Study of ScH3: Raman, Infrared, and Visible Absorption Spectroscopy. Phys. Rev. B 2011, 84, 064132. [Google Scholar] [CrossRef]
- Ohmura, A.; Machida, A.; Watanuki, T.; Aoki, K.; Nakano, S.; Takemura, K. Pressure-Induced Structural Change from Hexagonal to fcc Metal Lattice in Scandium Trihydride. J. Alloys Compd. 2007, 446, 598–602. [Google Scholar] [CrossRef]
- Grochala, W.; Hoffmann, R.; Feng, J.; Ashcroft, N.W. The Chemical Imagination at Work in Very Tight Places. Angew. Chem. Int. Edit. 2007, 46, 3620–3642. [Google Scholar] [CrossRef]
- Cioslowski, J. One-Electron Reduced Density Matrices of Strongly Correlated Harmonium Atoms. J. Chem. Phys. 2015, 142, 114104. [Google Scholar] [CrossRef]
- Cioslowski, J. Rovibrational States of Wigner Molecules in Spherically Symmetric Confining Potentials. J. Chem. Phys. 2016, 145, 054116. [Google Scholar] [CrossRef] [PubMed]
- Cioslowski, J.; Strasburger, K. Harmonium Atoms at Weak Confinements: The Formation of the Wigner Molecules. J. Chem. Phys. 2017, 146, 044308. [Google Scholar] [CrossRef]
- Chakraborty, D.; Das, R.; Chattaraj, P.K. Does Confinement Always Lead to Thermodynamically and/or Kinetically Favorable Reactions? A Case Study using Diels–Alder Reactions within ExBox+4 and CB[7]. ChemPhysChem 2017, 18, 2162–2170. [Google Scholar] [CrossRef]
- Chakraborty, D.; Chattaraj, P.K. Confinement Induced Thermodynamic and Kinetic Facilitation of Some Diels–Alder Reactions Inside a CB[7] Cavitand. J. Comput. Chem. 2018, 39, 151–160. [Google Scholar] [CrossRef]
- Rahm, M.; Cammi, R.; Ashcroft, N.W.; Hoffmann, R. Squeezing All Elements in the Periodic Table: Electron Configuration and Electronegativity of the Atoms under Compression. J. Am. Chem. Soc. 2019, 141, 10253–10271. [Google Scholar] [CrossRef]
- Cárdenas, C.; Heidar-Zadeh, F.; Ayers, P.W. Benchmark Values of Chemical Potential and Chemical Hardness for Atoms and Atomic Ions (Including Unstable Anions) from the Energies of Isoelectronic Series. Phys. Chem. Chem. Phys. 2016, 18, 25721–25734. [Google Scholar] [CrossRef] [PubMed]
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian09 Revision D.01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Cárdenas, C.; Ayers, P.W.; Cedillo, A. Reactivity Indicators for Degenerate States in the Density-Functional Theoretic Chemical Reactivity Theory. J. Chem. Phys. 2011, 134, 174103. [Google Scholar] [CrossRef]
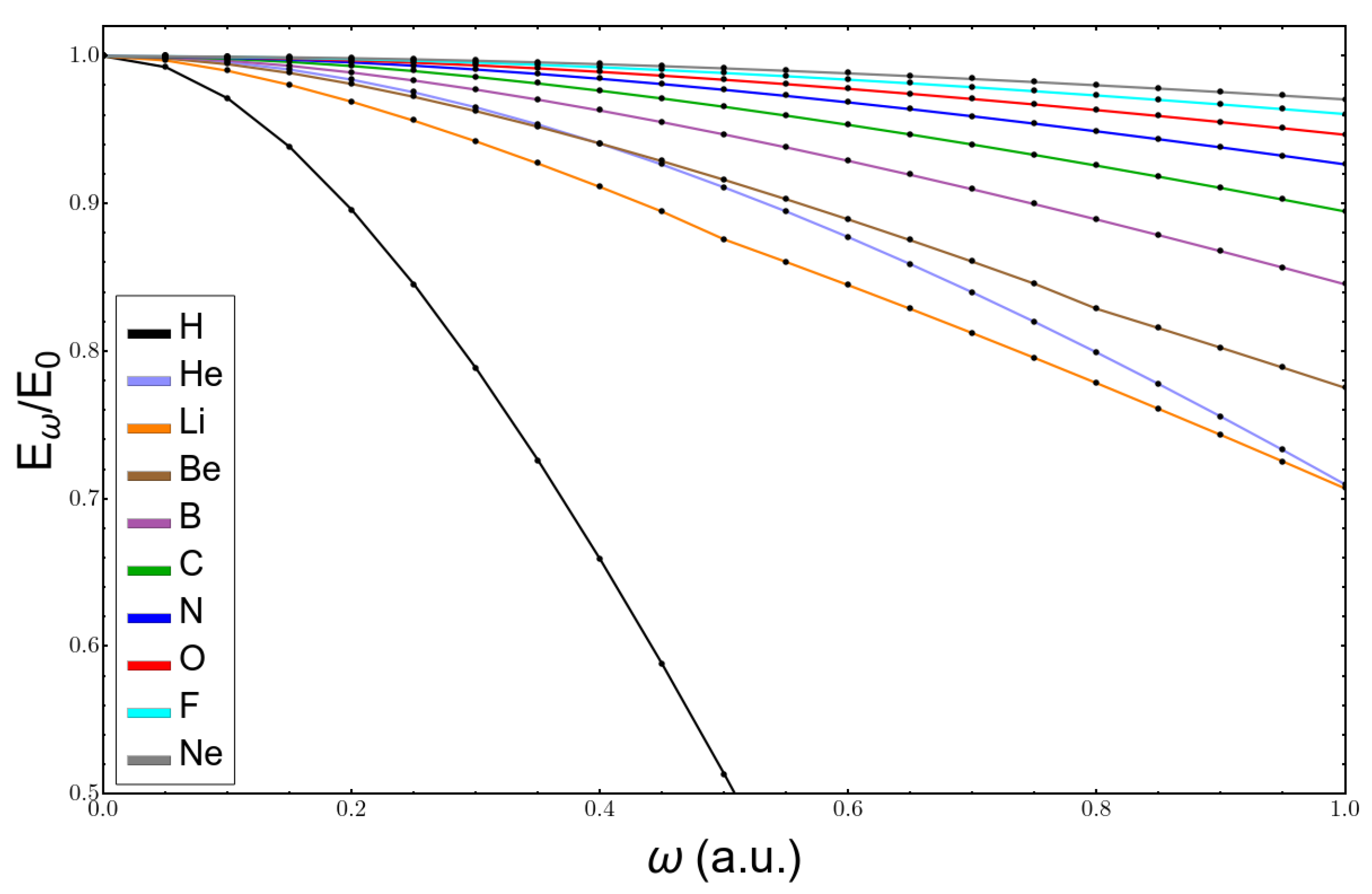
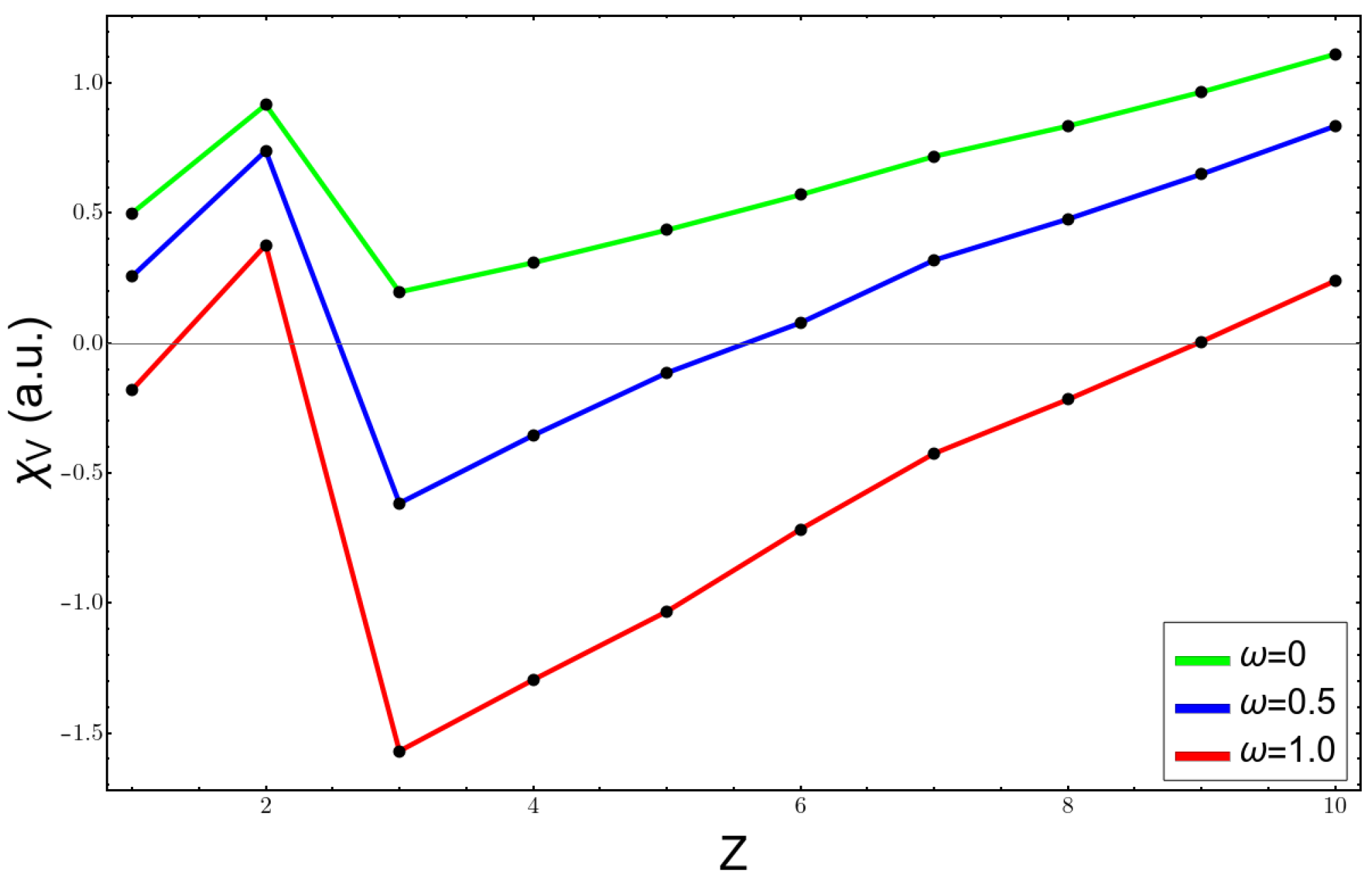







| ω | Li | Be | ||
|---|---|---|---|---|
| 0.49813 | 0.93145 | |||
| 0.61623 | 1.07021 | |||
| 0.86880 | 1.40422 | |||
| 0.89158 | 1.58778 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Robles-Navarro, A.; Cárdenas, C.; Fuentealba, P. Electronegativity under Confinement. Molecules 2021, 26, 6924. https://doi.org/10.3390/molecules26226924
Robles-Navarro A, Cárdenas C, Fuentealba P. Electronegativity under Confinement. Molecules. 2021; 26(22):6924. https://doi.org/10.3390/molecules26226924
Chicago/Turabian StyleRobles-Navarro, Andrés, Carlos Cárdenas, and Patricio Fuentealba. 2021. "Electronegativity under Confinement" Molecules 26, no. 22: 6924. https://doi.org/10.3390/molecules26226924
APA StyleRobles-Navarro, A., Cárdenas, C., & Fuentealba, P. (2021). Electronegativity under Confinement. Molecules, 26(22), 6924. https://doi.org/10.3390/molecules26226924






