Modern Theoretical Approaches to Modeling the Excited-State Intramolecular Proton Transfer: An Overview
Abstract
:1. Introduction
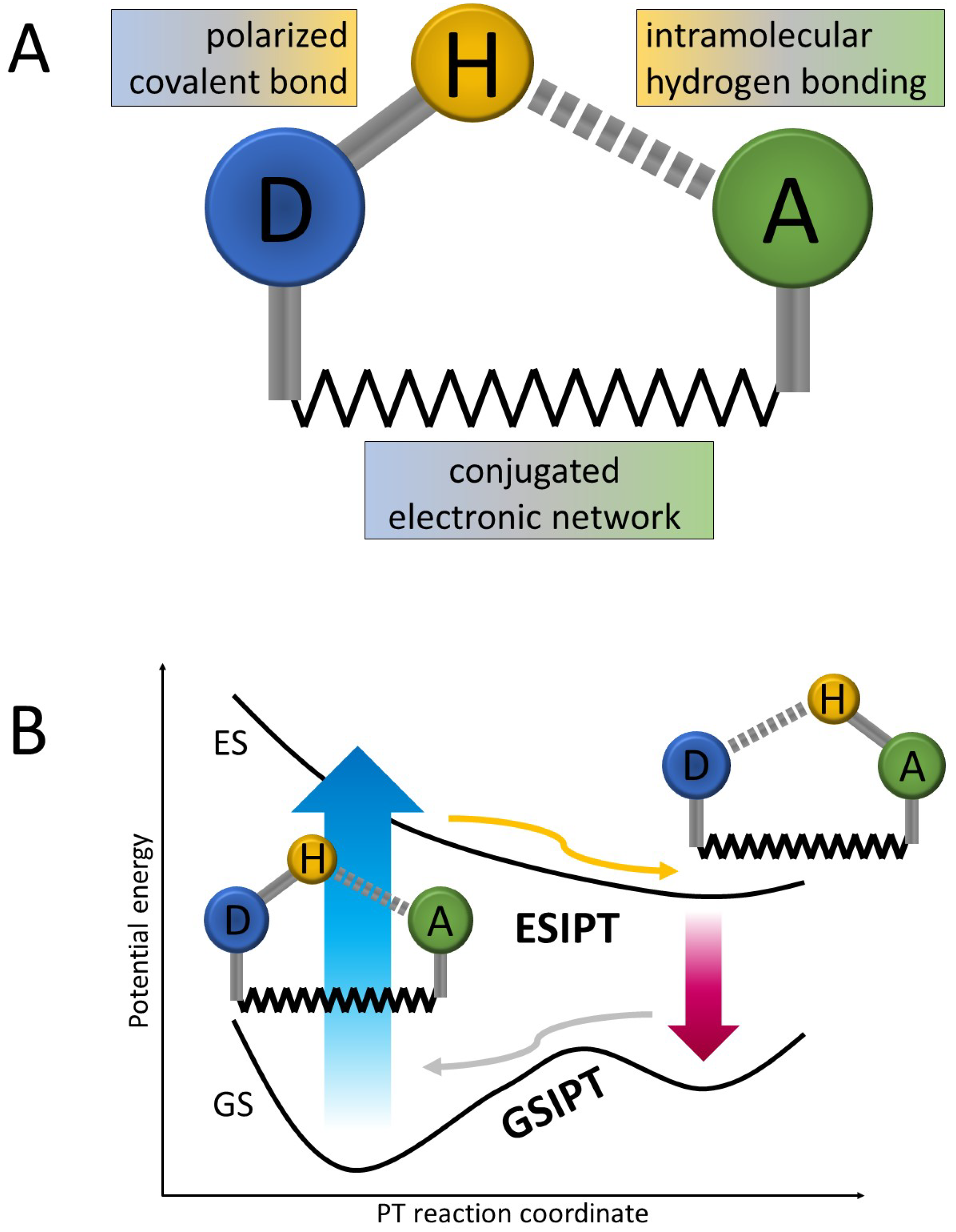
2. Static Investigation Approach
2.1. Objective of the Static Calculations
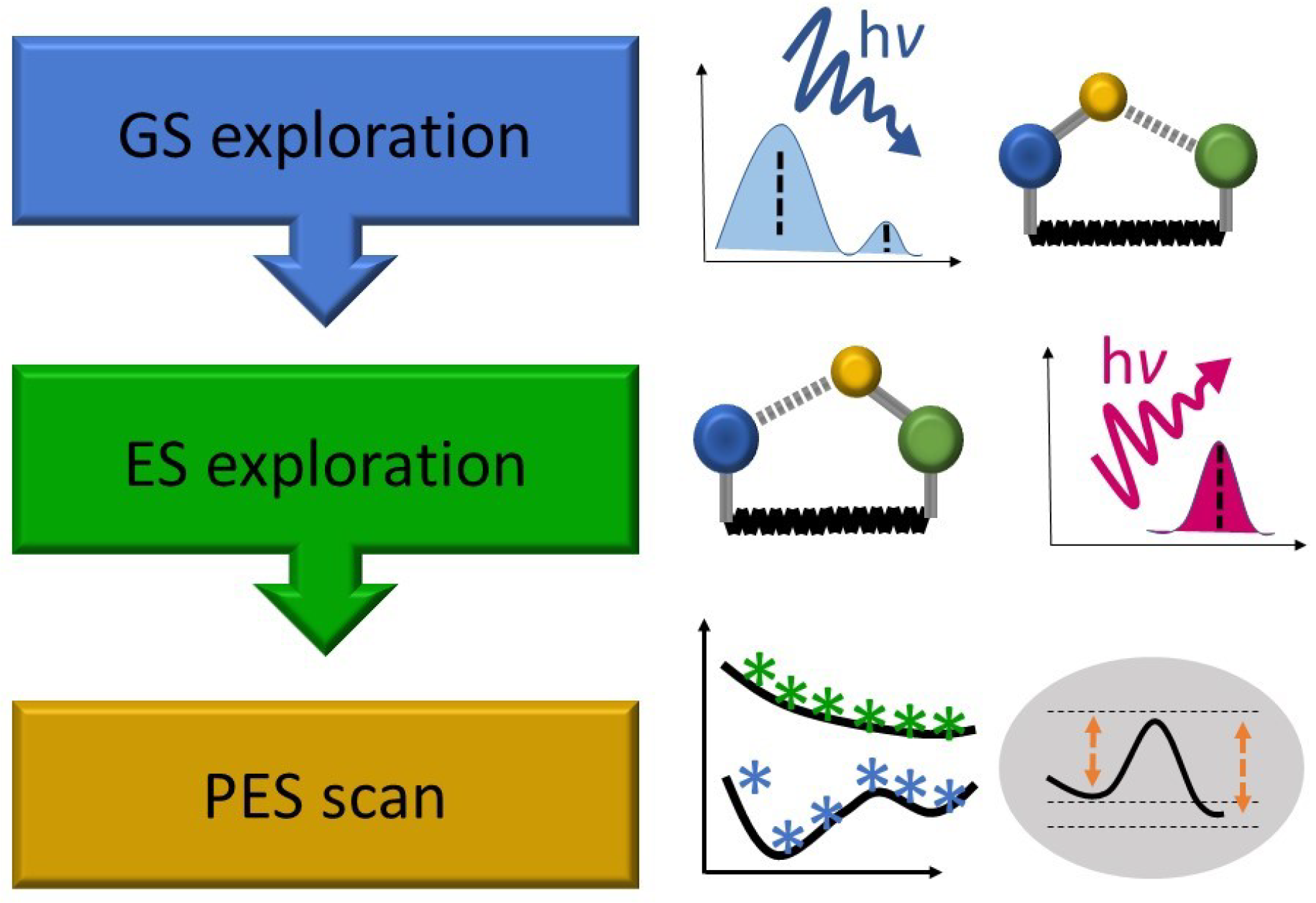
2.2. Typical Investigation Workflow
2.3. Applied Tools and Methods
2.3.1. Ab Initio Wave Function Approaches
2.3.2. Density Functional Theory Methods
2.3.3. Basis-Set Choice
2.3.4. Solvent Effects
2.4. Summary of the Static ESIPT Investigation Methods
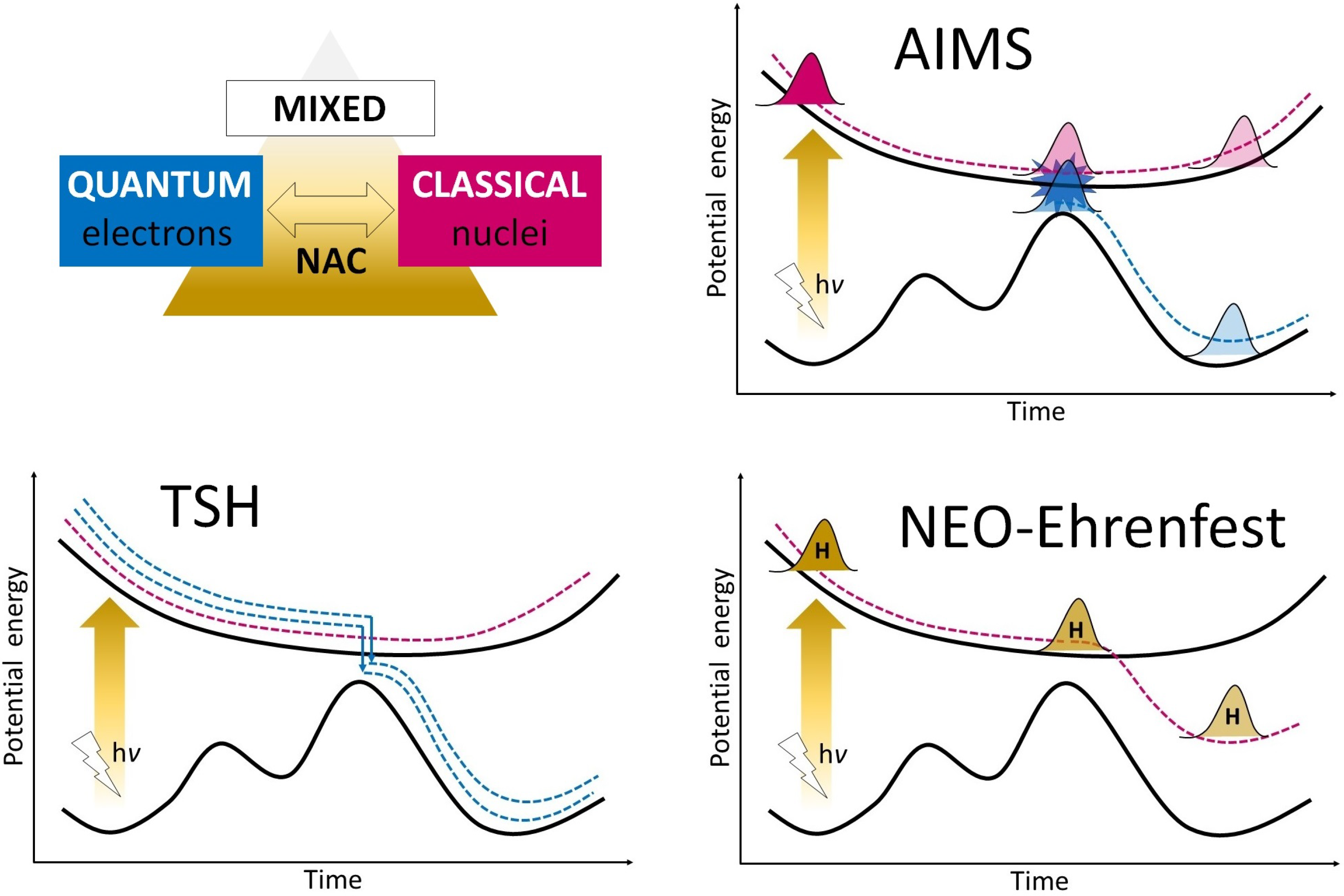
3. Nonadiabatic Molecular Dynamic Approaches
3.1. Mixed Quantum–Classical Dynamic Calculations in ESIPT Studies
3.1.1. Trajectory Surface Hopping Approach
3.1.2. Ab Initio Multiple Spawning Approach
3.1.3. Nuclear–Electronic Orbital Ehrenfest Approach
3.1.4. Summary of the NA-MQC Dynamic ESIPT Simulations
3.2. Quantum Dynamics Methods for ESIPT Simulations
Multiconfiguration Time-Dependent Hartree Method
4. Summary and Future Outlook
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gong, Y.; Wang, Z.; Zhang, S.; Luo, Z.; Gao, F.; Li, H. New ESIPT-inspired photostabilizers of two-photon absorption coumarin–benzotriazole dyads: From experiments to molecular modeling. Ind. Eng. Chem. 2016, 55, 5223–5230. [Google Scholar] [CrossRef]
- Maity, S.; Chatterjee, A.; Chakraborty, N.; Ganguly, J. A dynamic sugar based bio-inspired, self-healing hydrogel exhibiting ESIPT. New J. Chem. 2018, 42, 5946–5954. [Google Scholar] [CrossRef]
- Berenbeim, J.A.; Boldissar, S.; Owens, S.; Haggmark, M.R.; Gate, G.; Siouri, F.M.; Cohen, T.; Rode, M.F.; Schmidt Patterson, C.; De Vries, M.S. Excited state intramolecular proton transfer in hydroxyanthraquinones: Toward predicting fading of organic red colorants in art. Sci. Adv. 2019, 5, eaaw5227. [Google Scholar] [CrossRef] [Green Version]
- Sedgwick, A.C.; Wu, L.; Han, H.H.; Bull, S.D.; He, X.P.; James, T.D.; Sessler, J.L.; Tang, B.Z.; Tian, H.; Yoon, J. Excited-state intramolecular proton-transfer (ESIPT) based fluorescence sensors and imaging agents. Chem. Soc. Rev. 2018, 47, 8842–8880. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Long, R.; Tang, C.; Xu, J.; Li, T.; Tong, C.; Guo, Y.; Shi, S.; Wang, D. Novel natural myricetin with AIE and ESIPT characteristics for selective detection and imaging of superoxide anions in vitro and in vivo. Chem. Comm. 2019, 55, 10912–10915. [Google Scholar] [CrossRef]
- Li, Y.; Dahal, D.; Abeywickrama, C.S.; Pang, Y. Progress in tuning emission of the excited-state intramolecular proton transfer (ESIPT)-based fluorescent probes. ACS Omega 2021, 6, 6547–6553. [Google Scholar] [CrossRef]
- Hsieh, C.C.; Chou, P.T.; Shih, C.W.; Chuang, W.T.; Chung, M.W.; Lee, J.; Joo, T. Comprehensive studies on an overall proton transfer cycle of the ortho-green fluorescent protein chromophore. JACS 2011, 133, 2932–2943. [Google Scholar] [CrossRef] [PubMed]
- Vegh, R.B.; Bloch, D.A.; Bommarius, A.S.; Verkhovsky, M.; Pletnev, S.; Iwaï, H.; Bochenkova, A.V.; Solntsev, K.M. Hidden photoinduced reactivity of the blue fluorescent protein mKalama1. Phys. Chem. Chem. Phys. 2015, 17, 12472–12485. [Google Scholar] [CrossRef]
- Chatterjee, T.; Lacombat, F.; Yadav, D.; Mandal, M.; Plaza, P.; Espagne, A.; Mandal, P.K. Ultrafast dynamics of a green fluorescent protein chromophore analogue: Competition between excited-state proton transfer and torsional relaxation. J. Phys. Chem. B 2016, 5, 9716–9722. [Google Scholar] [CrossRef]
- Tang, K.C.; Chang, M.J.; Lin, T.Y.; Pan, H.A.; Fang, T.C.; Chen, K.Y.; Hung, W.Y.; Hsu, Y.H.; Chou, P.T. Fine tuning the energetics of excited-state intramolecular proton transfer (ESIPT): White light generation in a single ESIPT system. JACS 2011, 133, 17738–17745. [Google Scholar] [CrossRef]
- Wu, K.; Zhang, T.; Wang, Z.; Wang, L.; Zhan, L.; Gong, S.; Zhong, C.; Lu, Z.H.; Zhang, S.; Yang, C. De novo design of excited-state intramolecular proton transfer emitters via a thermally activated delayed fluorescence channel. JACS 2018, 140, 8877–8886. [Google Scholar] [CrossRef]
- Duarte, L.G.T.A.; Germino, J.C.; Berbigier, J.F.; Barboza, C.A.; Faleiros, M.M.; de Alencar Simoni, D.; Galante, M.T.; de Holanda, M.S.; Rodembusch, F.S.; Atvars, T.D.Z. White-light generation from all-solution-processed OLEDs using a benzothiazole–salophen derivative reactive to the ESIPT process. Phys. Chem. Chem. Phys. 2019, 21, 1172–1182. [Google Scholar] [CrossRef]
- Czernel, G.; Budziak, I.; Oniszczuk, A.; Karcz, D.; Pustuła, K.; Górecki, A.; Matwijczuk, A.; Gładyszewska, B.; Gagoś, M.; Niewiadomy, A.; et al. ESIPT-related origin of dual fluorescence in the selected model 1,3,4-thiadiazole derivatives. Molecules 2020, 25, 4168. [Google Scholar] [CrossRef]
- Trannoy, V.; Léaustic, A.; Gadan, S.; Guillot, R.; Allain, C.; Clavier, G.; Mazerat, S.; Geffroy, B.; Yu, P. A highly efficient solution and solid state ESIPT fluorophore and its OLED application. New J. Chem. 2021, 45, 3014–3021. [Google Scholar] [CrossRef]
- Rode, M.F.; Sobolewski, A.L. Effect of chemical substituents on the energetical landscape of a molecular photoswitch: An ab initio study. J. Phys. Chem. A 2010, 114, 11879–11889. [Google Scholar] [CrossRef]
- Jankowska, J.; Rode, M.F.; Sadlej, J.; Sobolewski, A.L. Photophysics of Schiff bases: Theoretical study of salicylidene methylamine. ChemPhysChem 2012, 13, 4287–4294. [Google Scholar] [CrossRef] [PubMed]
- Böhnke, H.; Bahrenburg, J.; Ma, X.; Röttger, K.; Näther, C.; Rode, M.F.; Sobolewski, A.L.; Temps, F. Ultrafast dynamics of the ESIPT photoswitch N -(3-pyridinyl)-2-pyridinecarboxamide. Phys. Chem. Chem. Phys. 2018, 20, 2646–2655. [Google Scholar] [CrossRef] [PubMed]
- Georgiev, A.; Todorov, P.; Dimov, D. Excited state proton transfer and E/Z photoswitching performance of 2-hydroxy-1-naphthalene and 1-naphthalene 5,5’-dimethyl- and 5,5’-diphenylhydantoin Schiff bases. J. Photochem. Photobiol. A 2020, 386, 112143. [Google Scholar] [CrossRef]
- Huang, A.; Hu, J.; Han, M.; Wang, K.; Xia, J.L.; Song, J.; Fu, X.; Chang, K.; Deng, X.; Liu, S.; et al. Tunable photocontrolled motions of anil-poly(ethylene terephthalate) systems through excited-state intramolecular proton transfer and trans–cis isomerization. Adv. Mater. 2021, 33, 2005249. [Google Scholar] [CrossRef]
- Hsieh, C.C.; Jiang, C.M.; Chou, P.T. Recent experimental advances on excited-state intramolecular proton coupled electron transfer reaction. Acc. Chem. Res. 2010, 43, 1364–1374. [Google Scholar] [CrossRef]
- Joshi, H.C.; Antonov, L. Excited-state intramolecular proton transfer: A short introductory review. Molecules 2021, 26, 1475. [Google Scholar] [CrossRef]
- Sobolewski, A.L.; Domcke, W. Photophysics of intramolecularly hydrogen-bonded aromatic systems: Ab initio exploration of the excited-state deactivation mechanisms of salicylic acid. Phys. Chem. Chem. Phys. 2006, 8, 3410. [Google Scholar] [CrossRef]
- Hammes-Schiffer, S. Theory of proton-coupled electron transfer in energy conversion processes. Acc. Chem. Res. 2009, 42, 1881–1889. [Google Scholar] [CrossRef] [Green Version]
- Weinberg, D.R.; Gagliardi, C.J.; Hull, J.F.; Murphy, C.F.; Kent, C.A.; Westlake, B.C.; Paul, A.; Ess, D.H.; McCafferty, D.G.; Meyer, T.J. Proton-coupled electron transfer. Chem. Rev. 2012, 112, 4016–4093. [Google Scholar] [CrossRef] [PubMed]
- Domcke, W.; Sobolewski, A.L.; Schlenker, C.W. Photooxidation of water with heptazine-based molecular photocatalysts: Insights from spectroscopy and computational chemistry. J. Chem. Phys. 2020, 153, 100902. [Google Scholar] [CrossRef]
- Tyburski, R.; Liu, T.; Glover, S.D.; Hammarström, L. Proton-coupled electron transfer guidelines, fair and square. JACS 2021, 143, 560–576. [Google Scholar] [CrossRef]
- Serdiuk, I.E.; Roshal, A.D. Exploring double proton transfer: A review on photochemical features of compounds with two proton-transfer sites. Dyes Pigm. 2017, 138, 223–244. [Google Scholar] [CrossRef]
- Chen, L.; Fu, P.Y.; Wang, H.P.; Pan, M. Excited-state intramolecular proton transfer (ESIPT) for optical sensing in solid state. Adv. Opt. Mater. 2021, 52, 2001952. [Google Scholar] [CrossRef]
- Demeter, A. Hydrogen bond basicity in the excited state: Concept and applications. In Hydrogen Bonding and Transfer in the Excited State; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Tomin, V.I. Proton transfer reactions in the excited electronic state. In Hydrogen Bonding and Transfer in the Excited State; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010. [Google Scholar] [CrossRef]
- Stasyuk, A.J.; Solá, M. Excited state intramolecular proton transfer (ESIPT) process: A brief overview of computational aspects, conformational changes, polymorphism, and solvent effects. In Theoretical and Quantum Chemistry at the Dawn of the 21st Century; Taylor & Francis Group: London, UK, 2018; Available online: https://www.taylorfrancis.com/books/edit/10.1201/9781351170963/theoretical-quantum-chemistry-dawn-21st-century-tanmoy-chakraborty-ramon-carbo-dorca (accessed on 3 July 2021). [CrossRef]
- Tang, Z.; Wang, Y.; Zhao, N. Theoretical investigation of excited-state intramolecular proton transfer mechanism of flavonoid derivatives. In Hydrogen-Bonding Research in Photochemistry, Photobiology, and Optoelectronic Materials; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2019; Chapter 8; pp. 179–213. Available online: https://www.worldscientific.com/doi/pdf/10.1142/9781786346087_0008 (accessed on 5 July 2021). [CrossRef]
- Zhang, M.; Zhou, Q.; Du, C.; Ding, Y.; Song, P. Detailed theoretical investigation on ESIPT process of pigment yellow 101. RSC Adv. 2016, 6, 59389–59394. [Google Scholar] [CrossRef]
- Barboza, C.A.; Gawrys, P.; Banasiewicz, M.; Suwinska, K.; Sobolewski, A.L. Photophysical transformations induced by chemical substitution to salicylaldimines. Phys. Chem. Chem. Phys. 2020, 22, 6698–6705. [Google Scholar] [CrossRef]
- Barboza, C.A.; Gawrys, P.; Banasiewicz, M.; Kozankiewicz, B.; Sobolewski, A.L. Substituent effects on the photophysical properties of tris(salicylideneanilines). Phys. Chem. Chem. Phys. 2021, 23, 1156–1164. [Google Scholar] [CrossRef]
- Liang, X.; Fang, H. Theoretical insights into the directionality of ESIPT behavior of BTHMB molecule with two proton acceptors in solution. Chem. Phys. Lett. 2021, 775, 138670. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Zhang, Q.; Zhao, J. Theoretical exploration about the ESIPT mechanism and hydrogen bonding interaction for 2-(3,5-dichloro-2-hydroxy-phenyl)-benzoxazole-6-carboxylicacid. J. Phys. Org. Chem. 2020, 33, e4020. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Hu, J.W.; Huang, T.H.; Chen, K.Y.; Chou, P.T. Excited-state intramolecular proton transfer in the kinetic-control regime. Phys. Chem. Chem. Phys. 2020, 22, 22271–22278. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Liu, Q.; Yang, D. Theoretical insights into excited-state hydrogen bonding effects and intramolecular proton transfer (ESIPT) mechanism for BTS system. Sci. Rep. 2020, 10, 5119. [Google Scholar] [CrossRef] [Green Version]
- Vérité, P.M.; Guido, C.A.; Jacquemin, D. First-principles investigation of the double ESIPT process in a thiophene-based dye. Phys. Chem. Chem. Phys. 2019, 21, 2307–2317. [Google Scholar] [CrossRef]
- Tsai, H.H.G.; Sun, H.L.S.; Tan, C.J. TD-DFT Study of the Excited-State Potential Energy Surfaces of 2-(2′-Hydroxyphenyl) benzimidazole and its Amino Derivatives. J. Phys. Chem. A 2010, 114, 4065–4079. [Google Scholar] [CrossRef]
- Houari, Y.; Chibani, S.; Jacquemin, D.; Laurent, A.D. TD-DFT assessment of the excited state intramolecular proton transfer in hydroxyphenylbenzimidazole (HBI) dyes. J. Phys. Chem. B 2015, 119, 2180–2192. [Google Scholar] [CrossRef]
- Ramu, Y.L.; Jagadeesha, K.; Shivalingaswamy, T.; Ramegowda, M. Microsolvation, hydrogen bond dynamics and excited state hydrogen atom transfer mechanism of 2′,4′-dihydroxychalcone. Chem. Phys. Lett. 2020, 739, 137030. [Google Scholar] [CrossRef]
- Zhao, G.J.; Han, K.L. Hydrogen bonding in the electronic excited state. Acc. Chem. Res. 2012, 45, 404–413. [Google Scholar] [CrossRef]
- De Carvalho, F.; Coutinho Neto, M.; Bartoloni, F.; Homem-de Mello, P. Density Functional Theory Applied to Excited State Intramolecular Proton Transfer in Imidazole-, Oxazole-, and Thiazole-Based Systems. Molecules 2018, 23, 1231. [Google Scholar] [CrossRef] [Green Version]
- Chrayteh, A.; Ewels, C.; Jacquemin, D. Dual fluorescence in strap ESIPT systems: A theoretical study. Phys. Chem. Chem. Phys. 2020, 22, 854–863. [Google Scholar] [CrossRef]
- Wu, D.; Guo, W.W.; Liu, X.Y.; Cui, G. Excited-state intramolecular proton transfer in a blue fluorescence chromophore induces dual emission. ChemPhysChem 2016, 17, 2340–2347. [Google Scholar] [CrossRef]
- Vivas, M.G.; Germino, J.C.; Barboza, C.A.; Simoni, D.D.A.; Vazquez, P.A.; De Boni, L.; Atvars, T.D.; Mendonça, C.R. Revealing the dynamic of excited state proton transfer of a π-conjugated salicylidene compound: An experimental and theoretical study. J. Phys. Chem. C 2017, 121, 1283–1290. [Google Scholar] [CrossRef]
- Chaiwongwattana, S.; Škalamera, D.; Došlić, N.; Bohne, C.; Basarić, N. Substitution pattern on anthrol carbaldehydes: Excited state intramolecular proton transfer (ESIPT) with a lack of phototautomer fluorescence. Phys. Chem. Chem. Phys. 2017, 19, 28439–28449. [Google Scholar] [CrossRef]
- Demchenko, A.P.; Tomin, V.I.; Chou, P.T. Breaking the Kasha Rule for More Efficient Photochemistry. Chem. Rev. 2017, 117, 13353–13381. [Google Scholar] [CrossRef] [PubMed]
- Coe, J.D.; Martínez, T.J. Ab initio molecular dynamics of excited-state intramolecular proton transfer around a three-state conical intersection in malonaldehyde. J. Phys. Chem. A 2006, 110, 618–630. [Google Scholar] [CrossRef] [PubMed]
- Sobolewski, A.L.; Domcke, W. Ab initio potential-energy functions for excited state intramolecular proton transfer: A comparative study of o-hydroxybenzaldehyde, salicylic acid and 7-hydroxy-1-indanone. Phys. Chem. Chem. Phys. 1999, 1, 3065–3072. [Google Scholar] [CrossRef]
- Cembran, A.; Gao, J. Excited state intramolecular proton transfer in 1-(trifluoroacetylamino) naphthaquinone: A CASPT2//CASSCF computational study. Mol. Phys. 2006, 104, 943–955. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L.; Guo, X.; Zhang, J. A CASSCF/CASPT2 insight into excited-state intramolecular proton transfer of four imidazole derivatives. J. Comput. Chem. 2015, 36, 2374–2380. [Google Scholar] [CrossRef]
- Hättig, C.; Weigend, F. CC2 Excitation Energy Calculations on Large Molecules Using the Resolution of the Identity Approximation. J. Chem. Phys. 2000, 113, 5154–5161. [Google Scholar] [CrossRef]
- Hättig, C. Geometry optimizations with the coupled-cluster model CC2 using the resolution-of-the-identity approximation. J. Chem. Phys. 2003, 118, 7751–7761. [Google Scholar] [CrossRef]
- Schirmer, J.; Trofimov, A.B. Intermediate state representation approach to physical properties of electronically excited molecules. J. Chem. Phys. 2004, 120, 11449–11464. [Google Scholar] [CrossRef]
- Dreuw, A.; Wormit, M. The algebraic diagrammatic construction scheme for the polarization propagator for the calculation of excited states. WIRES Comput. Mol. Sci. 2015, 5, 82–95. [Google Scholar] [CrossRef]
- Louant, O.; Champagne, B.; Liégeois, V. Investigation of the Electronic Excited-State Equilibrium Geometries of Three Molecules Undergoing ESIPT: A RI-CC2 and TDDFT Study. J. Phys. Chem. A 2018, 122, 972–984. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jacquemin, D.; Duchemin, I.; Blase, X. 0–0 Energies Using Hybrid Schemes: Benchmarks of TD-DFT, CIS(D), ADC(2), CC2, and BSE/ GW formalisms for 80 Real-Life Compounds. J. Chem. Theory Comput. 2015, 11, 5340–5359. [Google Scholar] [CrossRef] [Green Version]
- Hättig, C. Structure optimizations for excited states with correlated second-order methods: CC2 and ADC(2). Adv. Quantum Chem. 2005, 50, 37–60. [Google Scholar] [CrossRef]
- Plasser, F.; Crespo-Otero, R.; Pederzoli, M.; Pittner, J.; Lischka, H.; Barbatti, M. Surface hopping dynamics with correlated single-reference methods: 9H-adenine as a case study. J. Chem. Theory Comput. 2014, 10, 1395–1405. [Google Scholar] [CrossRef]
- Tuna, D.; Lefrancois, D.; Wolański, Ł.; Gozem, S.; Schapiro, I.; Andruniów, T.; Dreuw, A.; Olivucci, M. Assessment of approximate coupled-cluster and algebraic-diagrammatic-construction methods for ground- and excited-state reaction paths and the conical-intersection seam of a retinal-chromophore model. J. Chem. Theory Comput. 2015, 11, 5758–5781. [Google Scholar] [CrossRef]
- Tajti, A.; Stanton, J.F.; Matthews, D.A.; Szalay, P.G. Accuracy of coupled cluster excited state potential energy surfaces. J. Chem. Theory Comput. 2018, 14, 5859–5869. [Google Scholar] [CrossRef]
- Tajti, A.; Tulipán, L.; Szalay, P.G. Accuracy of spin-component ccaled ADC(2) excitation energies and potential energy surfaces. J. Chem. Theory Comput. 2020, 16, 468–474. [Google Scholar] [CrossRef] [Green Version]
- Hellweg, A.; Grün, S.A.; Hättig, C. Benchmarking the performance of spin-component scaled CC2 in ground and electronically excited states. Phys. Chem. Chem. Phys. 2008, 10, 4119. [Google Scholar] [CrossRef]
- Grimme, S. Improved second-order Møller-Plesset perturbation theory by separate scaling of parallel- and antiparallel-spin pair correlation energies. J. Chem. Phys. 2003, 118, 9095–9102. [Google Scholar] [CrossRef]
- Jung, Y.; Lochan, R.C.; Dutoi, A.D.; Head-Gordon, M. Scaled opposite-spin second order Moller-Plesset correlation energy: An economical electronic structure method. J. Chem. Phys. 2004, 121, 9793–9802. [Google Scholar] [CrossRef] [Green Version]
- Kielesiński, Ł.; Morawski, O.W.; Barboza, C.A.; Gryko, D.T. Polarized helical coumarins: [1, 5] sigmatropic rearrangement and excited-state intramolecular proton transfer. J. Org. Chem. 2021, 86, 6148–6159. [Google Scholar] [CrossRef]
- Li, T.C.; Tong, P.Q. Time-dependent density-functional theory for multicomponent systems. Phys. Rev. A 1986, 34, 529–532. [Google Scholar] [CrossRef]
- Hirata, S.; Head-Gordon, M. Time-dependent density functional theory within the Tamm–Dancoff approximation. Chem. Phys. Lett. 1999, 314, 291–299. [Google Scholar] [CrossRef]
- Sun, C.; Li, H.; Yin, H.; Li, Y.; Shi, Y. Effects of the cyano substitution at different positions on the ESIPT properties of alizarin: A DFT/TD-DFT investigation. J. Mol. Liq. 2018, 269, 650–656. [Google Scholar] [CrossRef]
- Muriel, W.A.; Morales-Cueto, R.; Rodríguez-Córdoba, W. Unravelling the solvent polarity effect on the excited state intramolecular proton transfer mechanism of the 1- and 2-salicylideneanthrylamine. A TD-DFT case study. Phys. Chem. Chem. Phys. 2019, 21, 915–928. [Google Scholar] [CrossRef]
- Ehrmaier, J.; Rabe, E.J.; Pristash, S.R.; Corp, K.L.; Schlenker, C.W.; Sobolewski, A.L.; Domcke, W. Singlet–triplet inversion in heptazine and in polymeric carbon nitrides. J. Phys. Chem. A 2019, 123, 8099–8108. [Google Scholar] [CrossRef]
- De Silva, P. Inverted singlet-triplet gaps and their relevance to thermally activated delayed fluorescence. J. Phys. Chem. Lett. 2019, 10, 5674–5679. [Google Scholar] [CrossRef]
- Savarese, M.; Raucci, U.; Fukuda, R.; Adamo, C.; Ehara, M.; Rega, N.; Ciofini, I. Comparing the performance of TD-DFT and SAC-CI methods in the description of excited states potential energy surfaces: An excited state proton transfer reaction as case study. J. Comput. Chem. 2017, 38, 1084–1092. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef] [Green Version]
- Chai, J.D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615. [Google Scholar] [CrossRef] [Green Version]
- Tasheh, N.S.; Nkungli, N.K.; Ghogomu, J.N. A DFT and TD-DFT study of ESIPT-mediated NLO switching and UV absorption by 2-(2′-hydroxy-5′-methylphenyl)benzotriazole. Theor. Chem. Acc. 2019, 138, 100. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange–correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Domcke, W.; Yarkony, D.R.; Köppel, H. Conical Intersections; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2004. [Google Scholar] [CrossRef]
- Jankowska, J.; Barbatti, M.; Sadlej, J.; Sobolewski, A.L. Tailoring the Schiff base photoswitching-a non-adiabatic molecular dynamics study of substituent effect on excited state proton transfer. Phys. Chem. Chem. Phys. 2017, 19, 5318–5325. [Google Scholar] [CrossRef] [Green Version]
- Grimme, S. Density functional theory with London dispersion corrections. WIREs Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
- Caldeweyher, E.; Ehlert, S.; Hansen, A.; Neugebauer, H.; Spicher, S.; Bannwarth, C.; Grimme, S. A generally applicable atomic-charge dependent London dispersion correction. J. Chem. Phys. 2019, 150, 154122. [Google Scholar] [CrossRef]
- Naka, K.; Sato, H.; Higashi, M. Theoretical study of the mechanism of the solvent dependency of ESIPT in HBT. Phys. Chem. Chem. Phys. 2021. [Google Scholar] [CrossRef] [PubMed]
- Laner, J.N.; Silva Junior, H.D.C.; Rodembusch, F.S.; Moreira, E.C. New insights on the ESIPT process based on solid-state data and state-of-the-art computational methods. Phys. Chem. Chem. Phys. 2021, 23, 1146–1155. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Siddique, F.; Aquino, A.J.A.; Lischka, H. Molecular dynamics simulation of the excited-state proton transfer mechanism in 3-hydroxyflavone using explicit hydration models. J. Phys. Chem. A 2021, 125, 5765–5778. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Krishnan, R.B.J.S.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Laurent, A.D.; Blondel, A.; Jacquemin, D. Choosing an atomic basis set for TD-DFT, SOPPA, ADC(2), CIS(D), CC2 and EOM-CCSD calculations of low-lying excited states of organic dyes. Theor. Chem. Acc. 2015, 134, 76. [Google Scholar] [CrossRef]
- Sinnecker, S.; Rajendran, A.; Klamt, A.; Diedenhofen, M.; Neese, F. Calculation of solvent shifts on electronic g-tensors with the conductor-like screening model (COSMO) and its self-consistent generalization to real solvents (direct COSMO-RS). J. Phys. Chem. A 2006, 110, 2235–2245. [Google Scholar] [CrossRef]
- Yang, Y.; Zhao, J.; Li, Y. Theoretical study of the ESIPT process for a new natural product quercetin. Sci. Rep. 2016, 6, 32152. [Google Scholar] [CrossRef] [Green Version]
- Scalmani, G.; Frisch, M.J.; Mennucci, B.; Tomasi, J.; Cammi, R.; Barone, V. Geometries and properties of excited states in the gas phase and in solution: Theory and application of a time-dependent density functional theory polarizable continuum model. J. Chem. Phys. 2006, 124, 094107. [Google Scholar] [CrossRef] [PubMed]
- Corni, S.; Cammi, R.; Mennucci, B.; Tomasi, J. Electronic excitation energies of molecules in solution within continuum solvation models: Investigating the discrepancy between state-specific and linear-response methods. J. Chem. Phys. 2005, 123, 134512. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Cammi, R.; Tomasi, J. Remarks on the use of the apparent surface charges (ASC) methods in solvation problems: Iterative versus matrix-inversion procedures and the renormalization of the apparent charges. J. Comput. Chem. 1995, 16, 1449–1458. [Google Scholar] [CrossRef]
- Cancès, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
- Mennucci, B.; Cancès, E.; Tomasi, J. Evaluation of solvent effects in isotropic and anisotropic dielectrics and in ionic solutions with a unified integral equation method: Theoretical bases, computational implementation, and numerical applications. J. Phys. Chem. B 1997, 101, 10506–10517. [Google Scholar] [CrossRef]
- Yuan, H.; Guo, X.; Zhang, J. Ab initio insights into the mechanism of excited-state intramolecular proton transfer triggered by the second excited singlet state of a fluorescent dye: An anti-Kasha behavior. Mater. Chem. Front. 2019, 3, 1225–1230. [Google Scholar] [CrossRef]
- Caricato, M.; Mennucci, B.; Tomasi, J.; Ingrosso, F.; Cammi, R.; Corni, S.; Scalmani, G. Formation and relaxation of excited states in solution: A new time dependent polarizable continuum model based on time dependent density functional theory. J. Chem. Phys. 2006, 124, 124520. [Google Scholar] [CrossRef] [PubMed]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G.; Guido, C.A.; Mennucci, B.; Scalmani, G.; Frisch, M.J. Practical computation of electronic excitation in solution: Vertical excitation model. Chem. Sci. 2011, 2, 2143. [Google Scholar] [CrossRef]
- Guido, C.A.; Scalmani, G.; Mennucci, B.; Jacquemin, D. Excited state gradients for a state-specific continuum solvation approach: The vertical excitation model within a Lagrangian TDDFT formulation. J. Chem. Phys. 2017, 146, 204106. [Google Scholar] [CrossRef]
- Peng, Y.; Ye, Y.; Xiu, X.; Sun, S. Mechanism of Excited-State Intramolecular Proton Transfer for 1,2-Dihydroxyanthraquinone: Effect of Water on the ESIPT. J. Phys. Chem. A 2017, 121, 5625–5634. [Google Scholar] [CrossRef]
- Crespo-Otero, R.; Barbatti, M. Recent advances and perspectives on nonadiabatic mixed quantum-classical dynamics. Chem. Rev. 2018, 118, 7026–7068. [Google Scholar] [CrossRef] [Green Version]
- Tully, J.C. Molecular dynamics with electronic transitions. J. Chem. Phys. 1990, 93, 1061. [Google Scholar] [CrossRef]
- Tully, J.C. Mixed quantum–classical dynamics. Faraday Discuss. 1998, 110, 407–419. [Google Scholar] [CrossRef]
- Barbatti, M. Nonadiabatic dynamics with trajectory surface hopping method. WIRES Comput. Mol. Sci. 2011, 1, 620–633. [Google Scholar] [CrossRef]
- Yarkony, D.R. Nonadiabatic quantum chemistry—Past, present, and future. Chem. Rev. 2012, 112, 481–498. [Google Scholar] [CrossRef] [PubMed]
- Ben-Nun, M.; Quenneville, J.; Martínez, T.J. Ab initio multiple spawning: Photochemistry from first principles quantum molecular dynamics. J. Phys. Chem. A 2000, 104, 5161–5175. [Google Scholar] [CrossRef]
- Curchod, B.F.E.; Martínez, T.J. Ab initio nonadiabatic quantum molecular dynamics. Chem. Rev. 2018, 118, 3305–3336. [Google Scholar] [CrossRef]
- Zhao, L.; Wildman, A.; Tao, Z.; Schneider, P.; Hammes-Schiffer, S.; Li, X. Nuclear–electronic orbital Ehrenfest dynamics. J. Chem. Phys. 2020, 153, 224111. [Google Scholar] [CrossRef] [PubMed]
- Belyaev, A.K.; Lasser, C.; Trigila, G. Landau–Zener type surface hopping algorithms. J. Chem. Phys. 2014, 140, 224108. [Google Scholar] [CrossRef] [Green Version]
- Suchan, J.; Janoš, J.; Slavíček, P. Pragmatic approach to photodynamics: Mixed Landau-Zener surface hopping with intersystem crossing. J. Chem. Theory Comput. 2020, 16, 5809–5820. [Google Scholar] [CrossRef]
- Pratihar, S.; Ma, X.; Homayoon, Z.; Barnes, G.L.; Hase, W.L. Direct chemical dynamics simulations. JACS 2017, 139, 3570–3590. [Google Scholar] [CrossRef]
- Barbatti, M.; Granucci, G.; Persico, M.; Ruckenbauer, M.; Vazdar, M.; Eckert-Maksić, M.; Lischka, H. The on-the-fly surface-hopping program system Newton-X: Application to ab initio simulation of the nonadiabatic photodynamics of benchmark systems. J. Photochem. Photobiol. A 2007, 190, 228–240. [Google Scholar] [CrossRef]
- Barbatti, M.; Ruckenbauer, M.; Plasser, F.; Pittner, J.; Granucci, G.; Persico, M.; Lischka, H. Newton-X: A surface-hopping program for nonadiabatic molecular dynamics. WIRES Comput. Mol. Sci. 2014, 4, 26–33. [Google Scholar] [CrossRef]
- Richter, M.; Marquetand, P.; González-Vázquez, J.; Sola, I.; González, L. SHARC: Ab initio molecular dynamics with surface hopping in the adiabatic representation including arbitrary couplings. J. Chem. Theory Comput. 2011, 7, 1253–1258. [Google Scholar] [CrossRef] [PubMed]
- Du, L.; Lan, Z. An on-the-fly surface-hopping program JADE for nonadiabatic molecular dynamics of polyatomic systems: Implementation and applications. J. Chem. Theory Comput. 2015, 11, 1360–1374. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Understanding the surface hopping view of electronic transitions and decoherence. Annu. Rev. Phys. Chem. 2016, 67, 387–417. [CrossRef] [PubMed]
- Tuna, D.; Spörkel, L.; Barbatti, M.; Thiel, W. Nonadiabatic dynamics simulations of photoexcited urocanic acid. Chem. Phys. 2018, 515, 521–534. [Google Scholar] [CrossRef]
- Xia, S.H.; Che, M.; Liu, Y.; Zhang, Y.; Cui, G. Photochemical mechanism of 1,5-benzodiazepin-2-one: Electronic structure calculations and nonadiabatic surface-hopping dynamics simulations. Phys. Chem. Chem. Phys. 2019, 21, 10086–10094. [Google Scholar] [CrossRef] [PubMed]
- Ben-Nun, M.; Martínez, T.J. Ab initio quantum molecular dynamics. In Advances in Chemical Physics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2002; pp. 439–512. [Google Scholar] [CrossRef]
- Leticia, G.; Roland, L. Quantum Chemistry and Dynamics of Excited States: Methods and Applications; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar]
- Fedorov, D.A.; Pruitt, S.R.; Keipert, K.; Gordon, M.S.; Varganov, S.A. Ab initio multiple spawning method for intersystem crossing dynamics: Spin-forbidden transitions between 3B1 and 1A1 States of GeH2. J. Phys. Chem. A 2016, 120, 2911–2919. [Google Scholar] [CrossRef]
- Barca, G.M.J.; Bertoni, C.; Carrington, L.; Datta, D.; De Silva, N.; Deustua, J.E.; Fedorov, D.G.; Gour, J.R.; Gunina, A.O.; Guidez, E.; et al. Recent developments in the general atomic and molecular electronic structure system. J. Chem. Phys. 2020, 152, 154102. [Google Scholar] [CrossRef] [Green Version]
- Levine, B.G.; Coe, J.D.; Virshup, A.M.; Martínez, T.J. Implementation of ab initio multiple spawning in the Molpro quantum chemistry package. Chem. Phys. 2008, 347, 3–16. [Google Scholar] [CrossRef]
- Werner, H.J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M. Molpro: A general-purpose quantum chemistry program package. WIRES Comput. Mol. Sci. 2012, 2, 242–253. [Google Scholar] [CrossRef]
- Granucci, G.; Persico, M.; Toniolo, A. Direct semiclassical simulation of photochemical processes with semiempirical wave functions. J. Chem. Phys. 2001, 114, 10608–10615. [Google Scholar] [CrossRef]
- Stewart, J. MOPAC: A semiempirical molecular orbital program. J. Comput. Aided 1990, 4, 1–103. [Google Scholar] [CrossRef] [PubMed]
- Pijeau, S.; Foster, D.; Hohenstein, E.G. Effect of nonplanarity on excited-state proton transfer and internal conversion in salicylideneaniline. J. Phys. Chem. A 2018, 122, 5555–5562. [Google Scholar] [CrossRef] [PubMed]
- Pijeau, S.; Foster, D.; Hohenstein, E.G. Excited-state dynamics of 2-(2′-hydroxyphenyl)benzothiazole: Ultrafast proton transfer and internal conversion. J. Phys. Chem. A 2017, 121, 4595–4605. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Wildman, A.; Pavošević, F.; Tully, J.C.; Hammes-Schiffer, S.; Li, X. Excited state intramolecular proton transfer with nuclear-electronic orbital Ehrenfest dynamics. J. Phys. Chem. Lett. 2021, 12, 3497–3502. [Google Scholar] [CrossRef]
- Webb, S.P.; Iordanov, T.; Hammes-Schiffer, S. Multiconfigurational nuclear-electronic orbital approach: Incorporation of nuclear quantum effects in electronic structure calculations. J. Chem. Phys. 2002, 117, 4106–4118. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Tully, J.C.; Schlegel, H.B.; Frisch, M.J. Ab initio Ehrenfest dynamics. J. Chem. Phys. 2005, 123, 084106. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Prezhdo, O.V. A simple solution to the trivial crossing problem in surface hopping. J. Phys. Chem. Lett. 2014, 5, 713–719. [Google Scholar] [CrossRef]
- Sun, Z.; Li, S.; Xie, S.; An, Z. Solution for the trivial crossing problem in surface hopping simulations by the classification on excited states. J. Phys. Chem. C 2018, 122, 8058–8064. [Google Scholar] [CrossRef]
- Qiu, J.; Bai, X.; Wang, L. Crossing classified and corrected fewest switches surface hopping. J. Phys. Chem. Lett. 2018, 9, 4319–4325. [Google Scholar] [CrossRef] [PubMed]
- Beck, M.; Jäckle, A.; Worth, G.A.; Meter, H.D. The multiconfiguration time-dependent Hartree (MCTDH) method: A highly efficient algorithm for propagating wavepackets. Phys. Rep. 2000, 324, 1–105. [Google Scholar] [CrossRef]
- Cederbaum, L.S.; Köppel, H.; Domcke, W. Multimode vibronic coupling effects in molecules. Int. J. Quantum Chem. 1981, 15, 251–267. [Google Scholar] [CrossRef]
- Cederbaum, L.S. The multistate vibronic coupling problem. J. Chem. Phys. 1983, 78, 5714–5728. [Google Scholar] [CrossRef]
- Worth, G.A.; Meyer, H.D.; Köppel, H.; Cederbaum, L.S.; Burghardt, I. Using the MCTDH wavepacket propagation method to describe multimode non-adiabatic dynamics. Int. Rev. Phys. Chem. 2008, 27, 569–606. [Google Scholar] [CrossRef]
- Vendrell, O.; Meyer, H.D. Multilayer multiconfiguration time-dependent Hartree method: Implementation and applications to a Henon–Heiles Hamiltonian and to pyrazine. J. Chem. Phys. 2011, 134, 044135. [Google Scholar] [CrossRef] [Green Version]
- Worth, G.A.; Beck, M.H.; Jäckle, A.; Meyer, H.D. The Heidelberg MCTDH Package; University of Heidelberg: Heidelberg, Germany, 2000. [Google Scholar]
- Worth, G.A.; Giri, K.; Richings, G.W.; Burghardt, I.; Beck, M.H.; Jäckle, A.; Meyer, H.D. The QUANTICS Package; University of Birmingham: Birmingham, UK, 2015. [Google Scholar]
- Perveaux, A.; Lorphelin, M.; Lasorne, B.; Lauvergnat, D. Fast and slow excited-state intramolecular proton transfer in 3-hydroxychromone: A two-state story? Phys. Chem. Chem. Phys. 2017, 19, 6579–6593. [Google Scholar] [CrossRef]
- Anand, N.; Isukapalli, S.V.K.; Vennapusa, S.R. Excited-state intramolecular proton transfer driven by conical intersection in hydroxychromones. J. Comput. Chem. 2020, 41, 1068–1080. [Google Scholar] [CrossRef]
- Anand, N.; Welke, K.; Irle, S.; Vennapusa, S.R. Nonadiabatic excited-state intramolecular proton transfer in 3-hydroxyflavone: S 2 state involvement via multi-mode effect. J. Chem. Phys. 2019, 151, 214304. [Google Scholar] [CrossRef]
- Anand, N.; Nag, P.; Kanaparthi, R.K.; Vennapusa, S.R. O-H vibrational motions promote sub-50 fs nonadiabatic dynamics in 3-hydroxypyran-4-one: Interplay between internal conversion and ESIPT. Phys. Chem. Chem. Phys. 2020, 22, 8745–8756. [Google Scholar] [CrossRef]
- Cao, Y.; Eng, J.; Penfold, T.J. Excited state intramolecular proton transfer dynamics for triplet harvesting in organic molecules. J. Phys. Chem. A 2019, 123, 2640–2649. [Google Scholar] [CrossRef] [PubMed]
- Richings, G.W.; Robertson, C.; Habershon, S. Can we use on-the-fly quantum simulations to connect molecular structure and sunscreen action? Faraday Discuss. 2019, 216, 476–493. [Google Scholar] [CrossRef] [PubMed]
- Westermayr, J.; Marquetand, P. Machine learning and excited-state molecular dynamics. MLST 2020, 1, 043001. [Google Scholar] [CrossRef]
- Westermayr, J.; Gastegger, M.; Marquetand, P. Combining SchNet and SHARC: The SchNarc machine learning approach for excited-state dynamics. J. Phys. Chem. Lett. 2020, 11, 3828–3834. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jankowska, J.; Sobolewski, A.L. Modern Theoretical Approaches to Modeling the Excited-State Intramolecular Proton Transfer: An Overview. Molecules 2021, 26, 5140. https://doi.org/10.3390/molecules26175140
Jankowska J, Sobolewski AL. Modern Theoretical Approaches to Modeling the Excited-State Intramolecular Proton Transfer: An Overview. Molecules. 2021; 26(17):5140. https://doi.org/10.3390/molecules26175140
Chicago/Turabian StyleJankowska, Joanna, and Andrzej L. Sobolewski. 2021. "Modern Theoretical Approaches to Modeling the Excited-State Intramolecular Proton Transfer: An Overview" Molecules 26, no. 17: 5140. https://doi.org/10.3390/molecules26175140
APA StyleJankowska, J., & Sobolewski, A. L. (2021). Modern Theoretical Approaches to Modeling the Excited-State Intramolecular Proton Transfer: An Overview. Molecules, 26(17), 5140. https://doi.org/10.3390/molecules26175140