Multibubble Sonoluminescence from a Theoretical Perspective
Abstract
1. Introduction
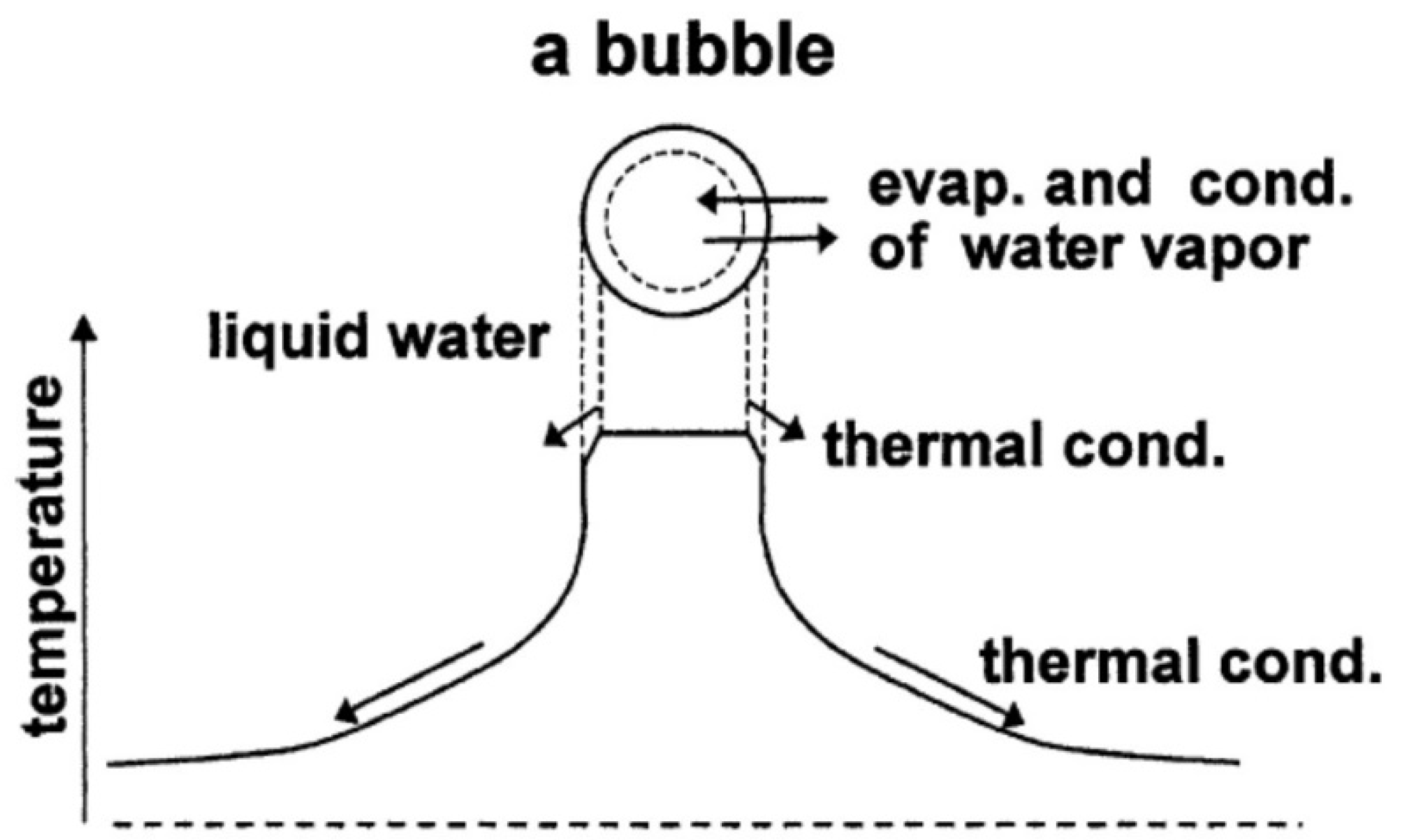
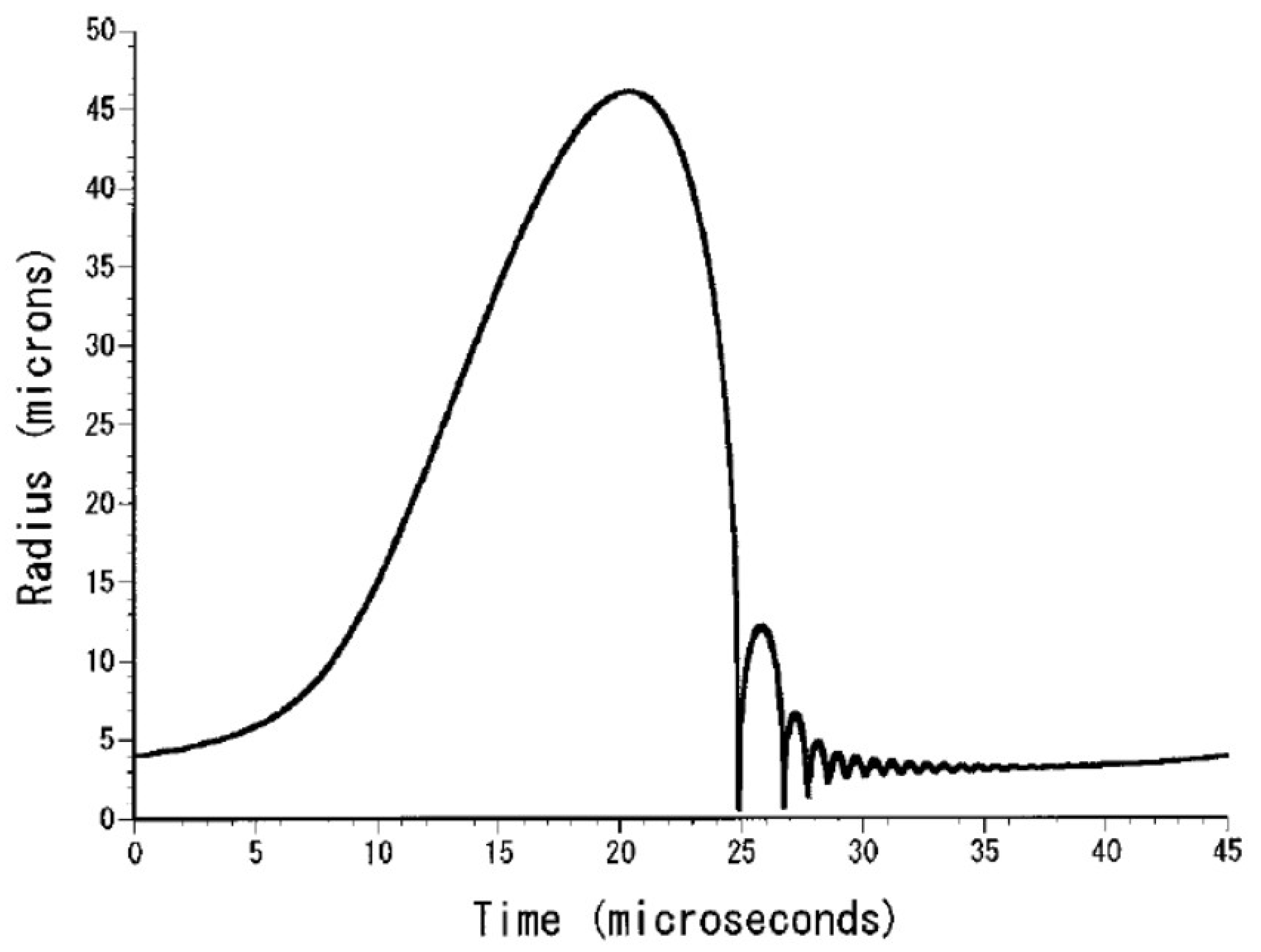
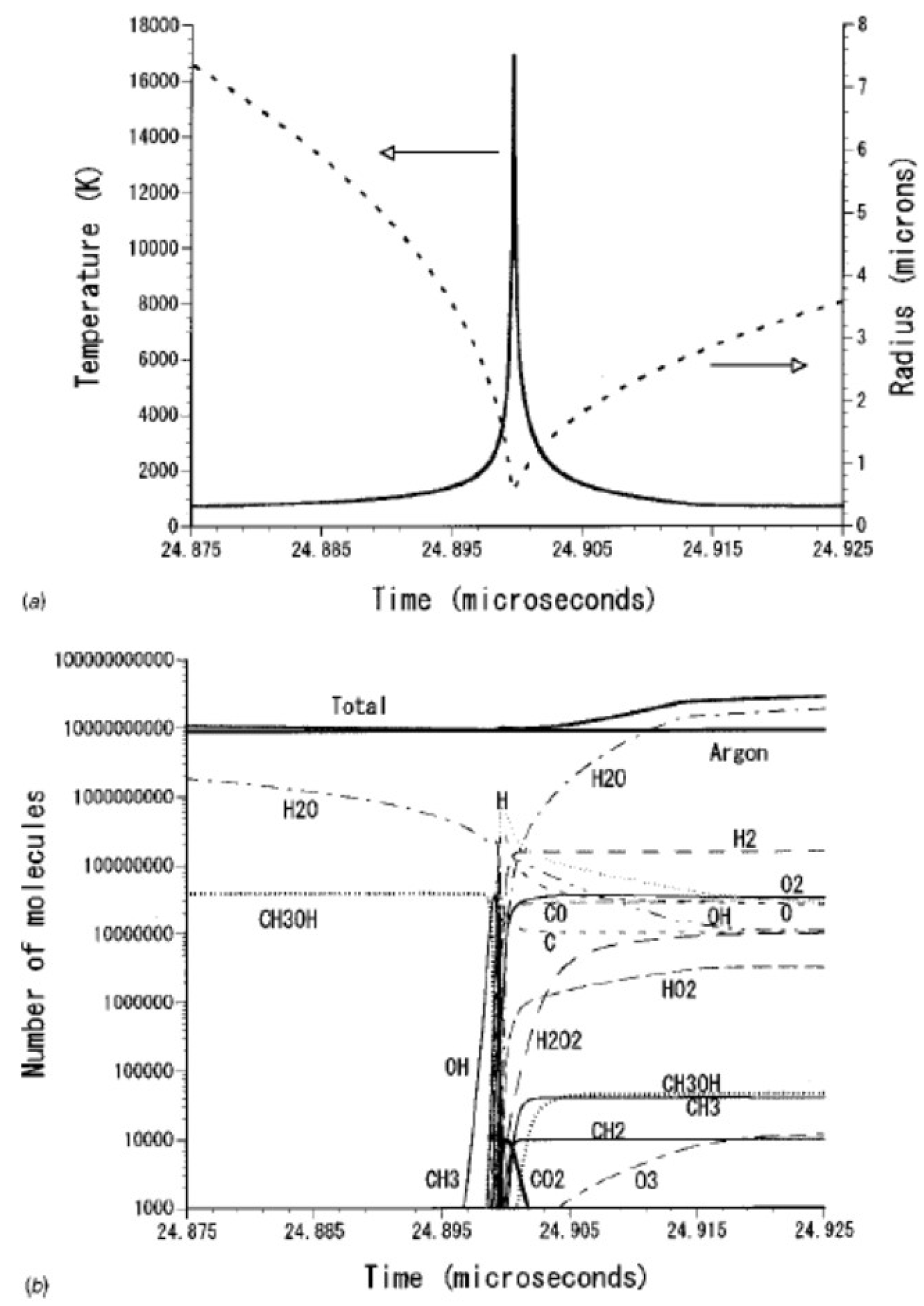
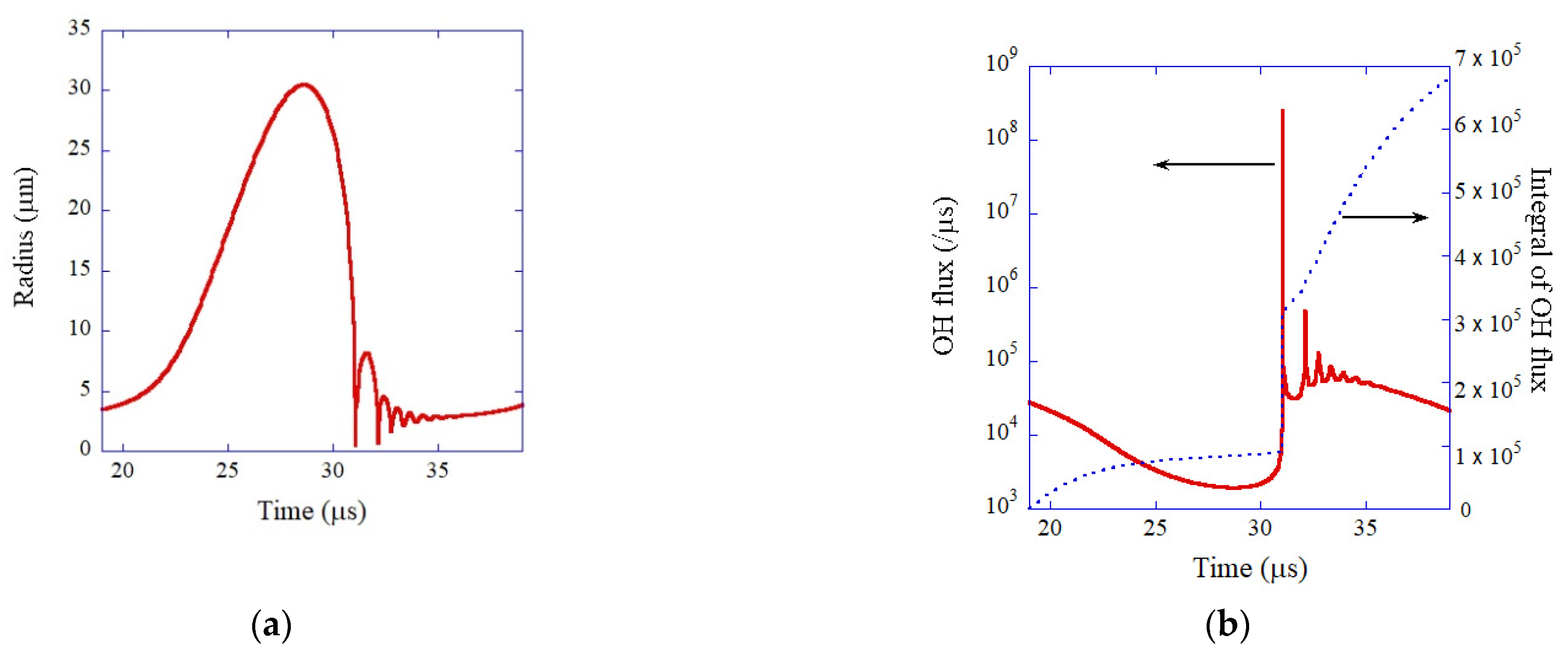
2. Theoretical Model
3. Vaporous and Gaseous Bubbles
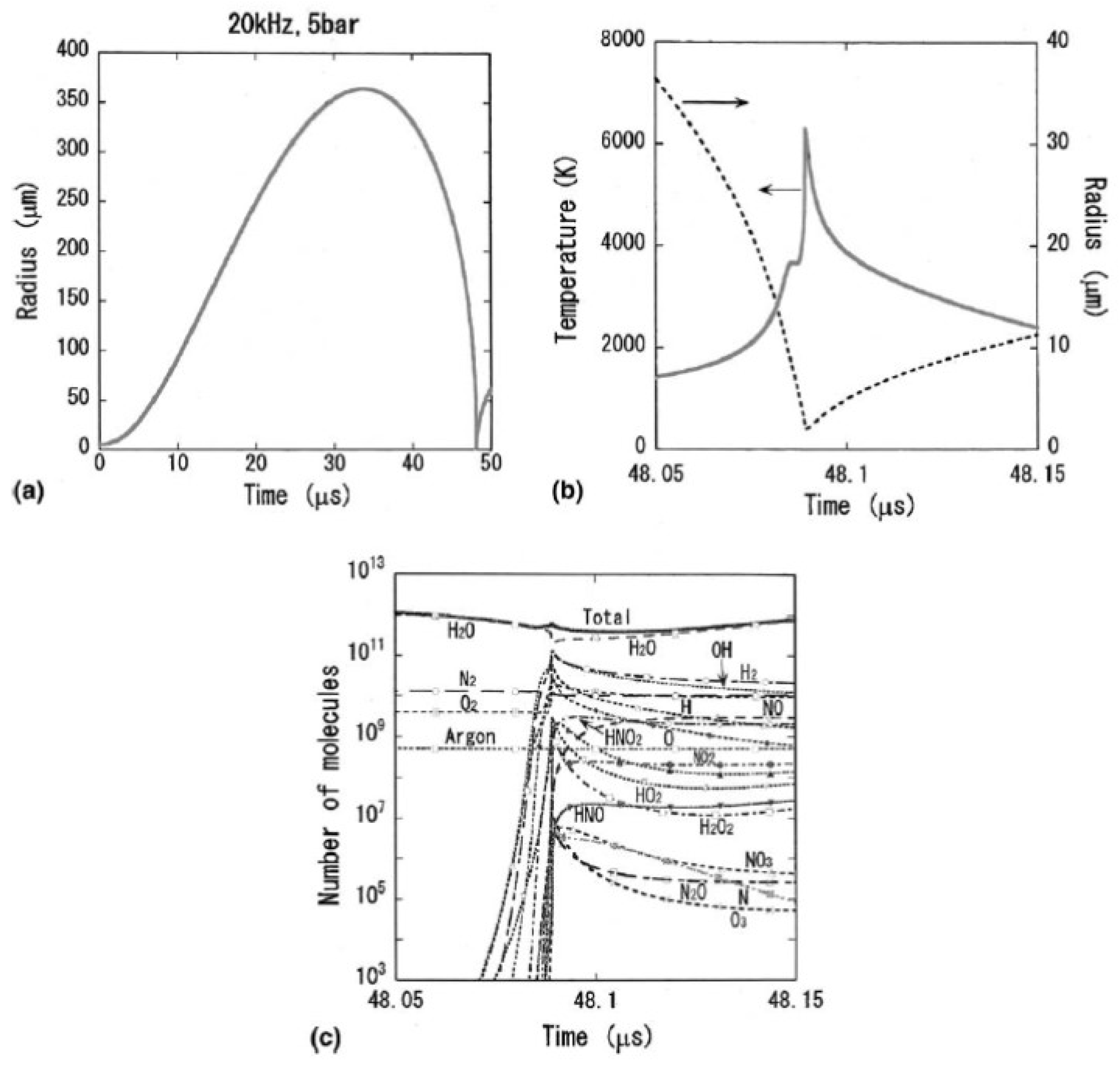
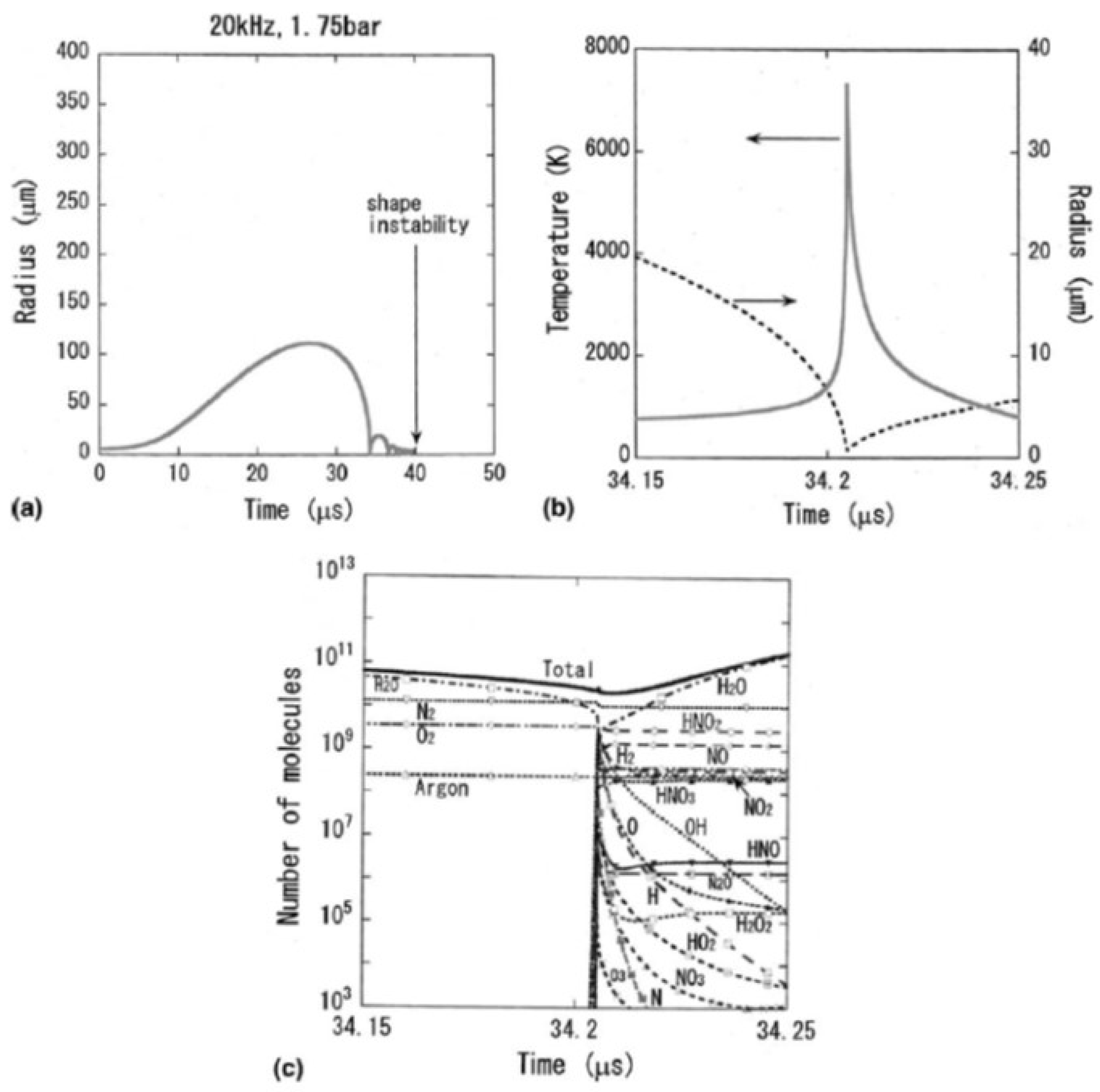
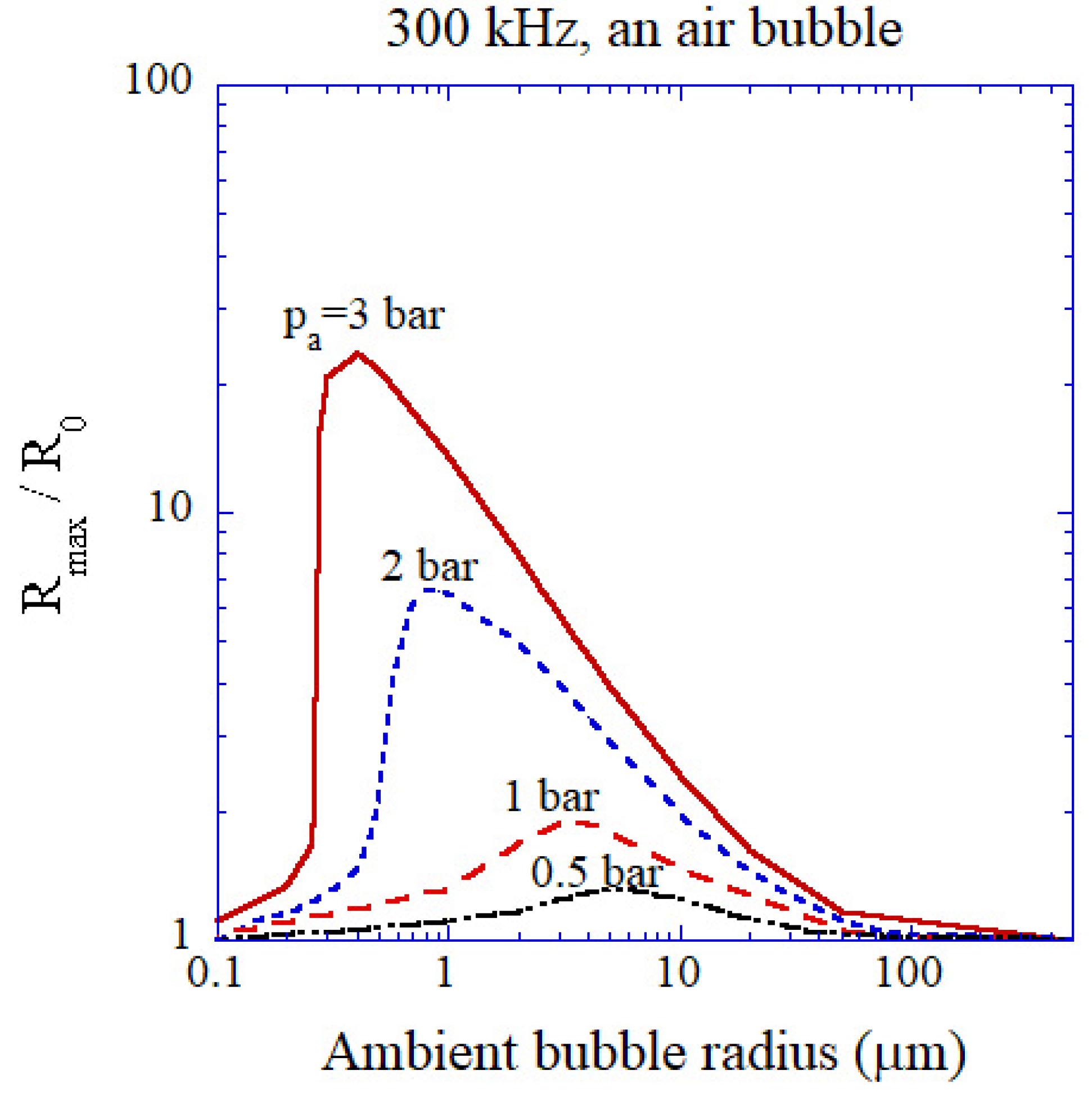
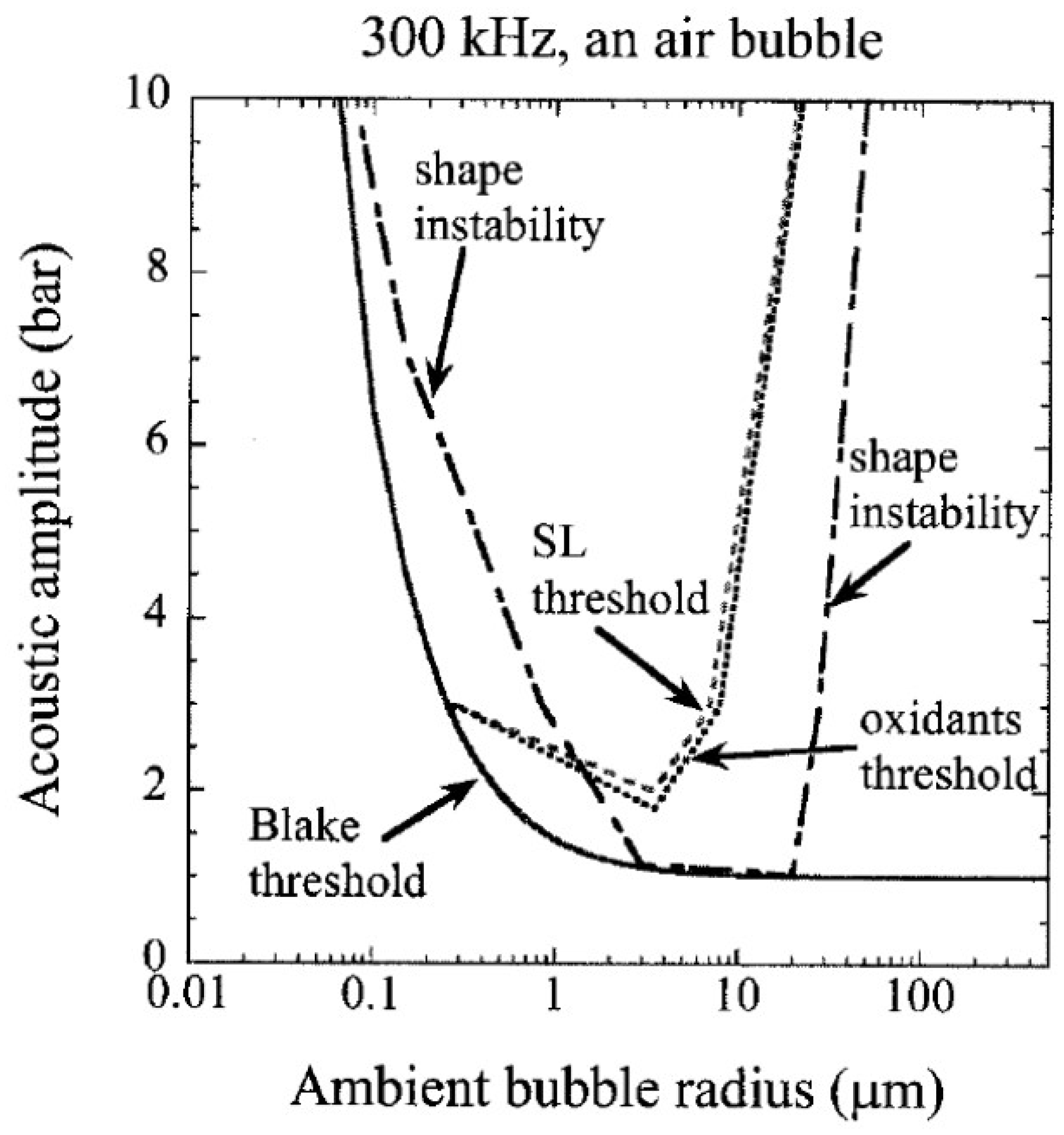
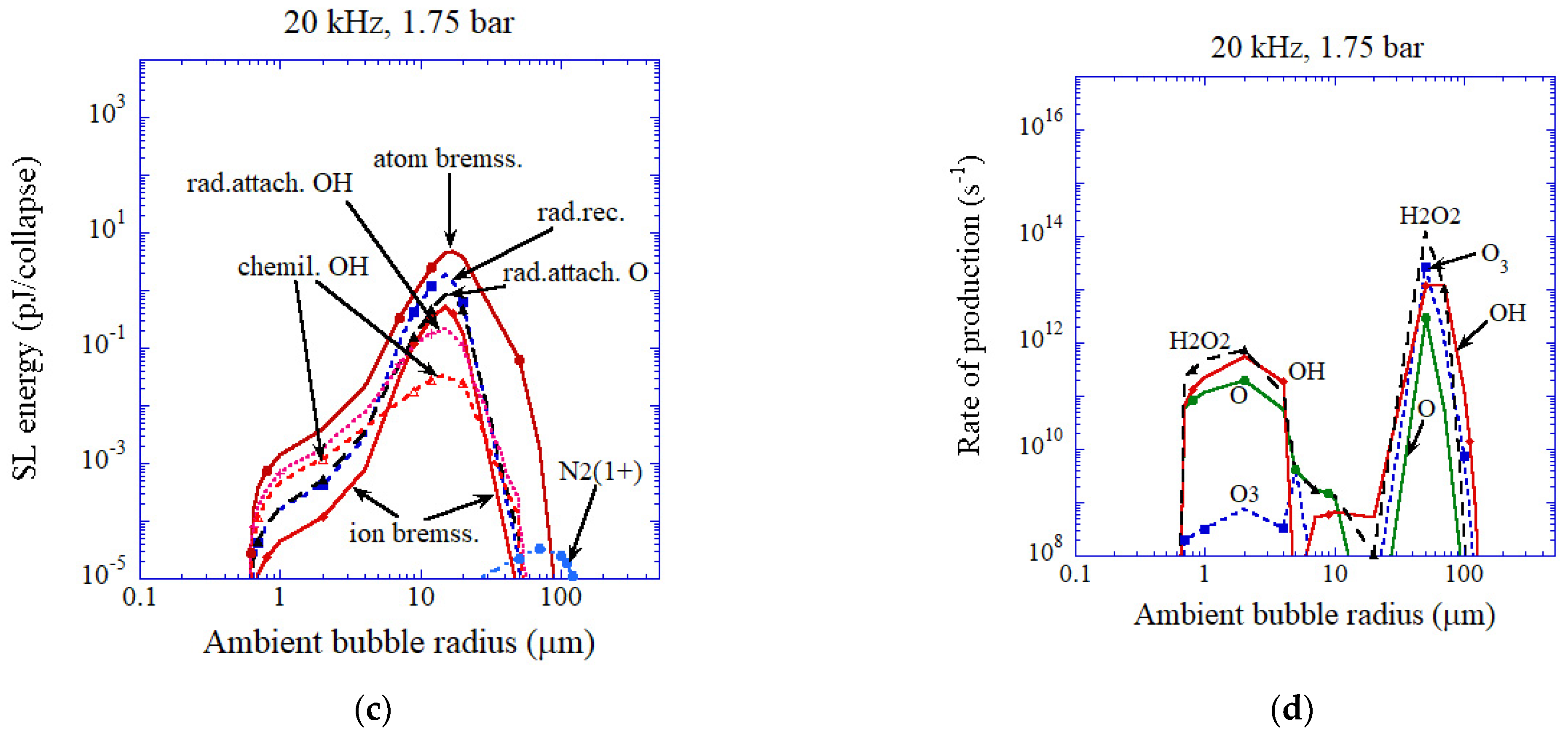
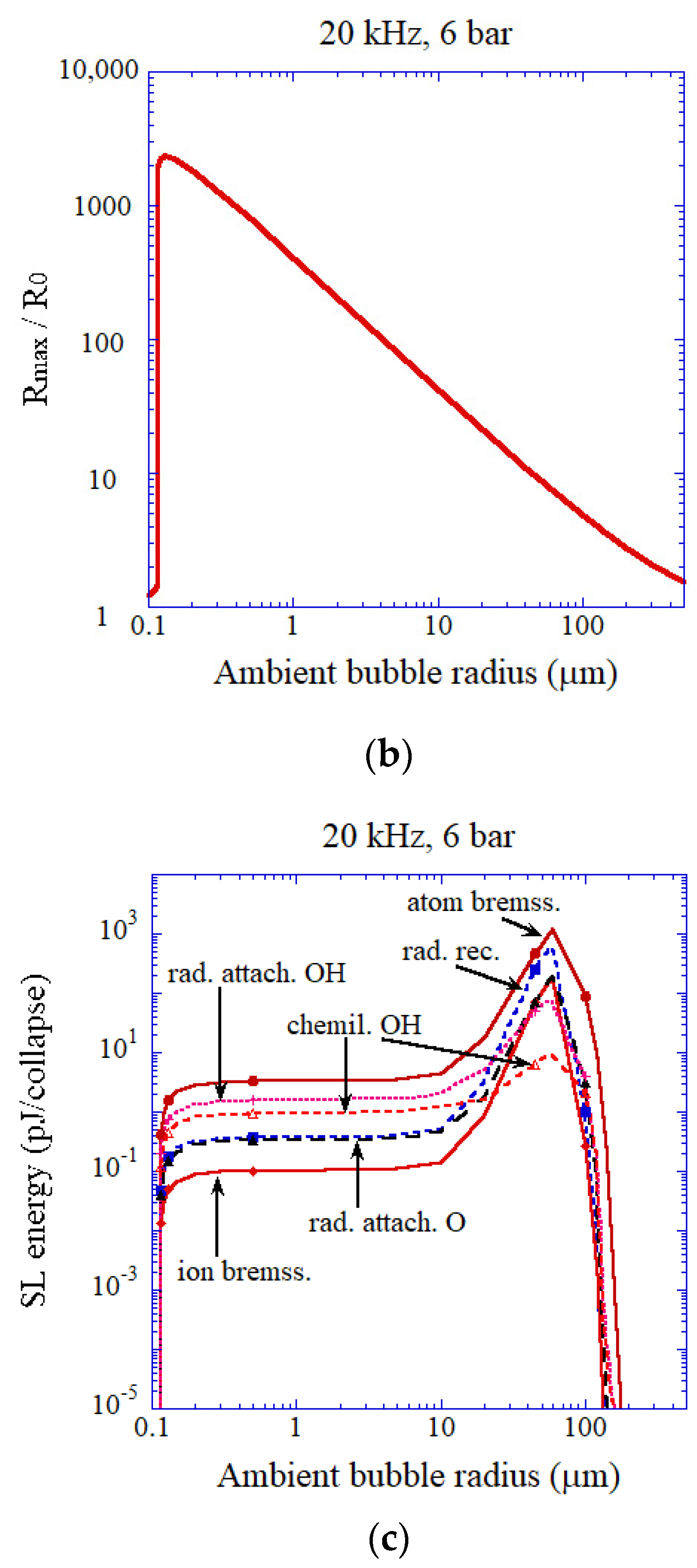
4. Influence of Bubble Size
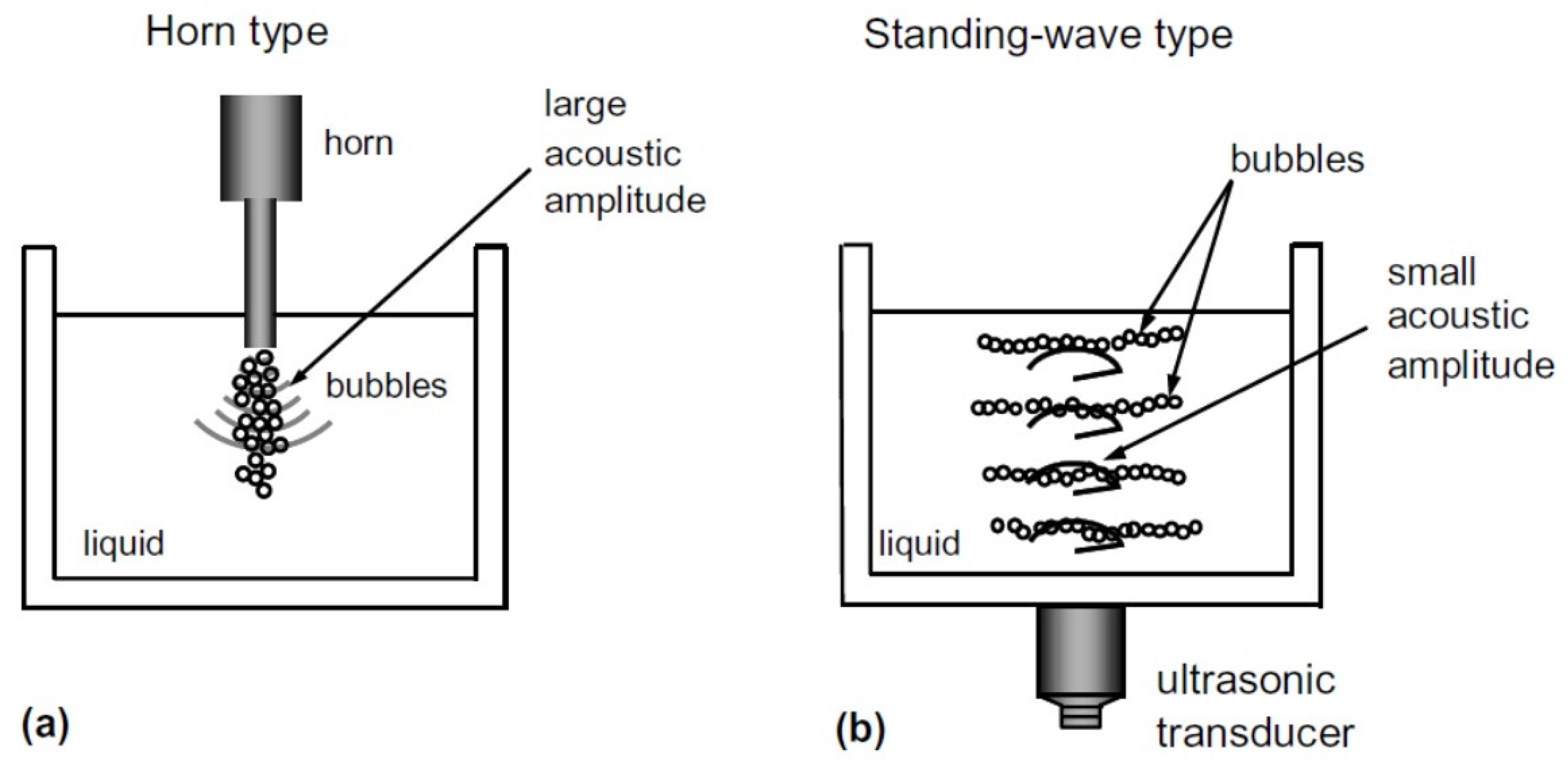
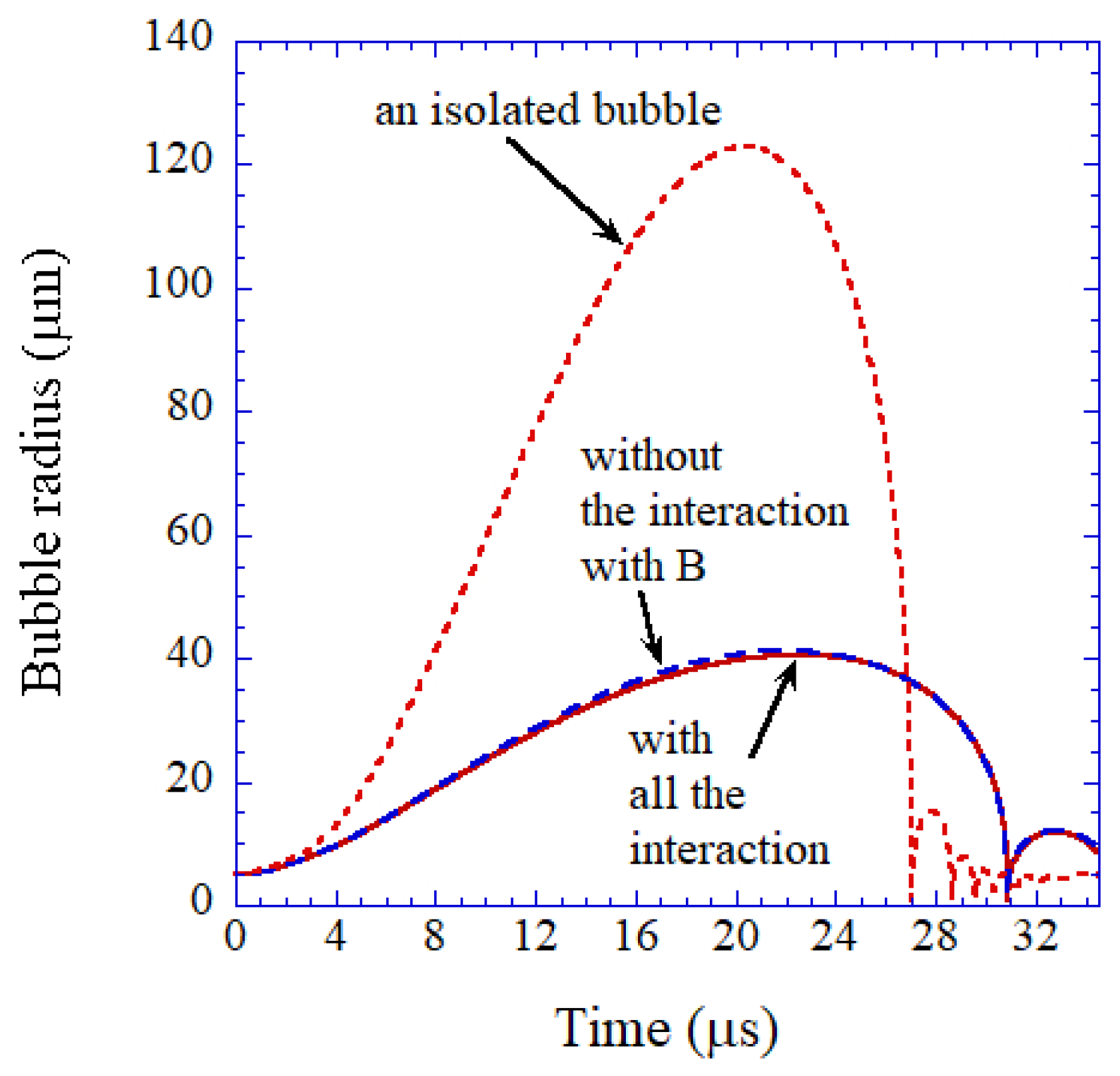
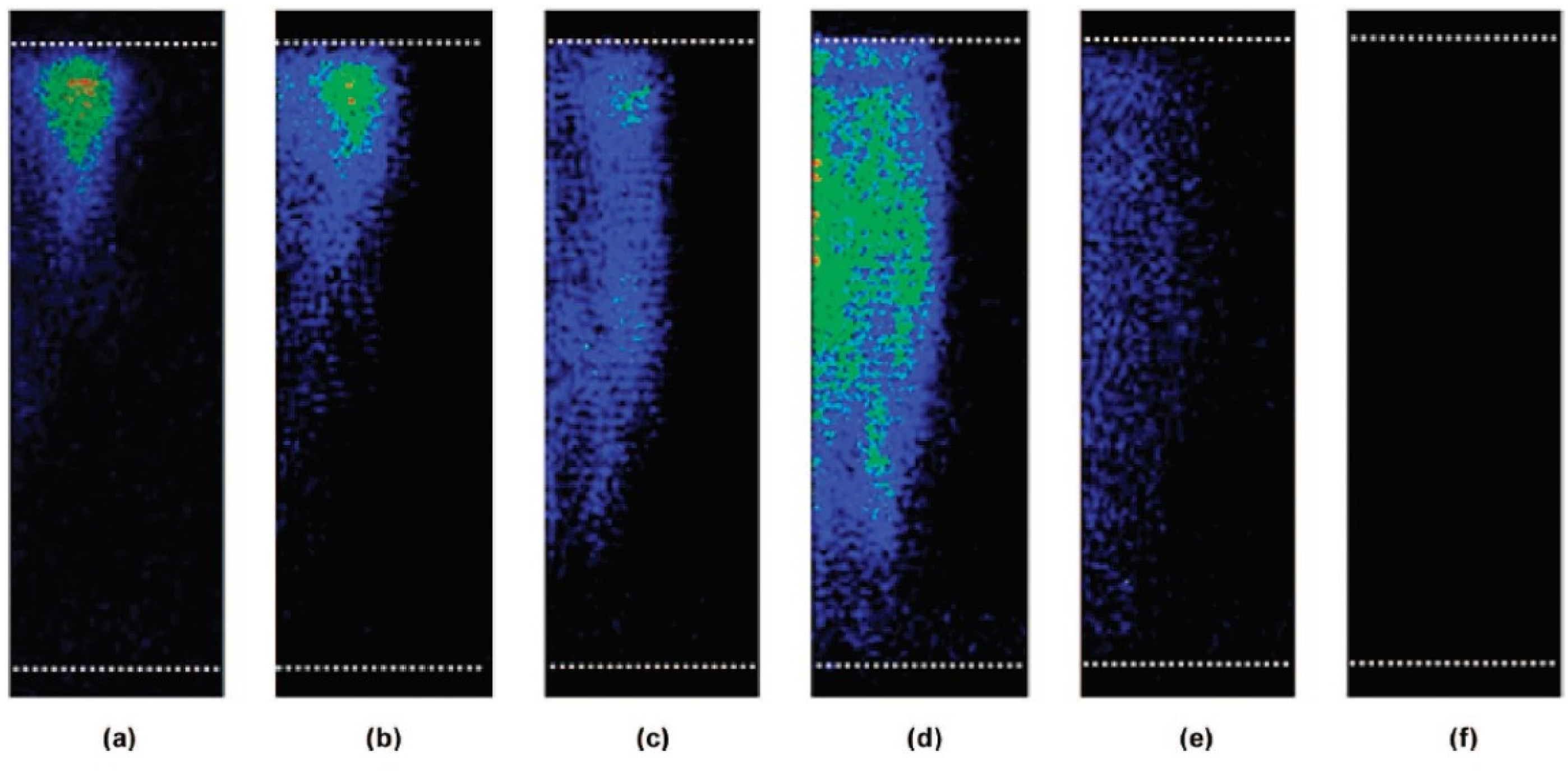
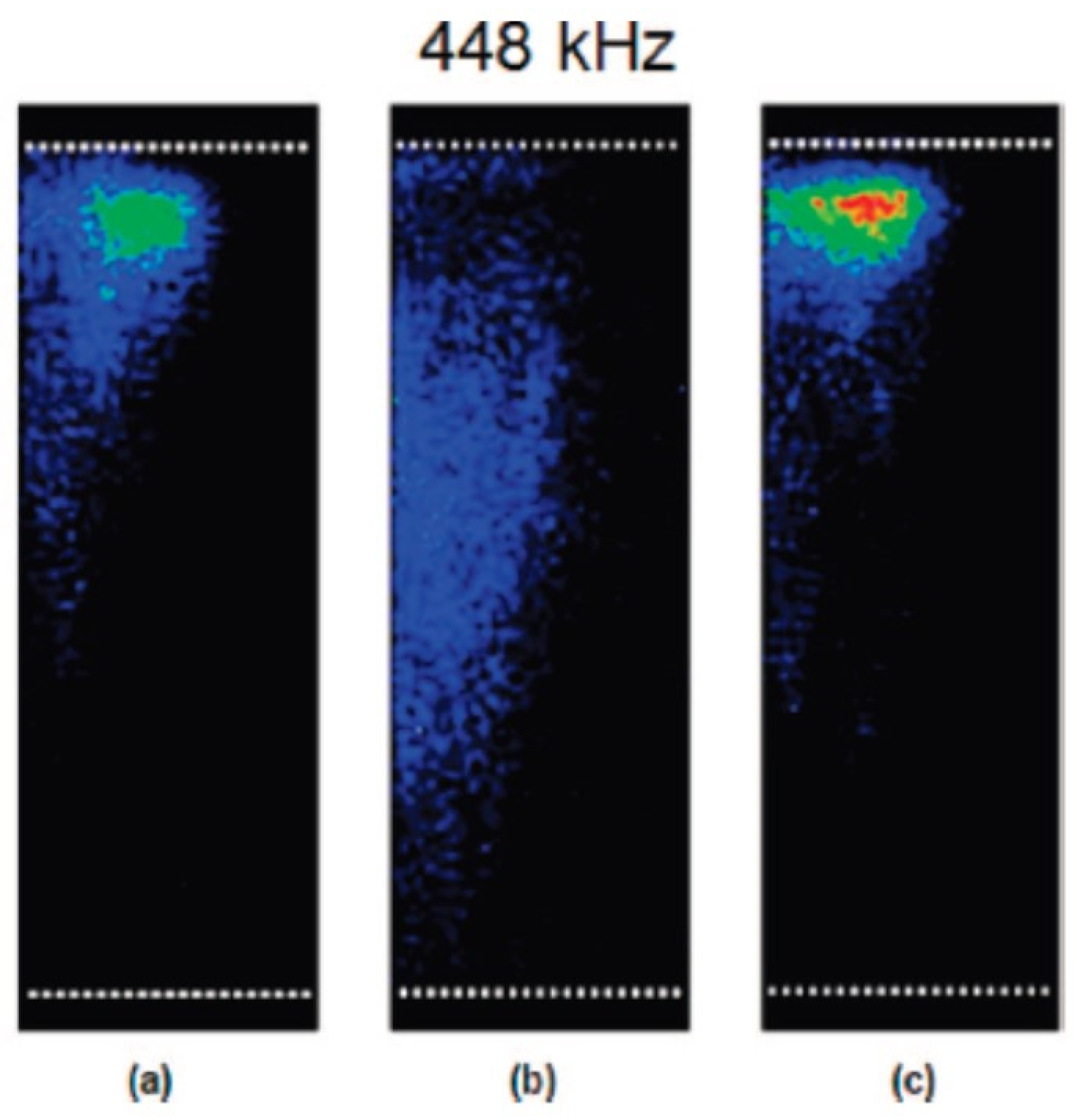
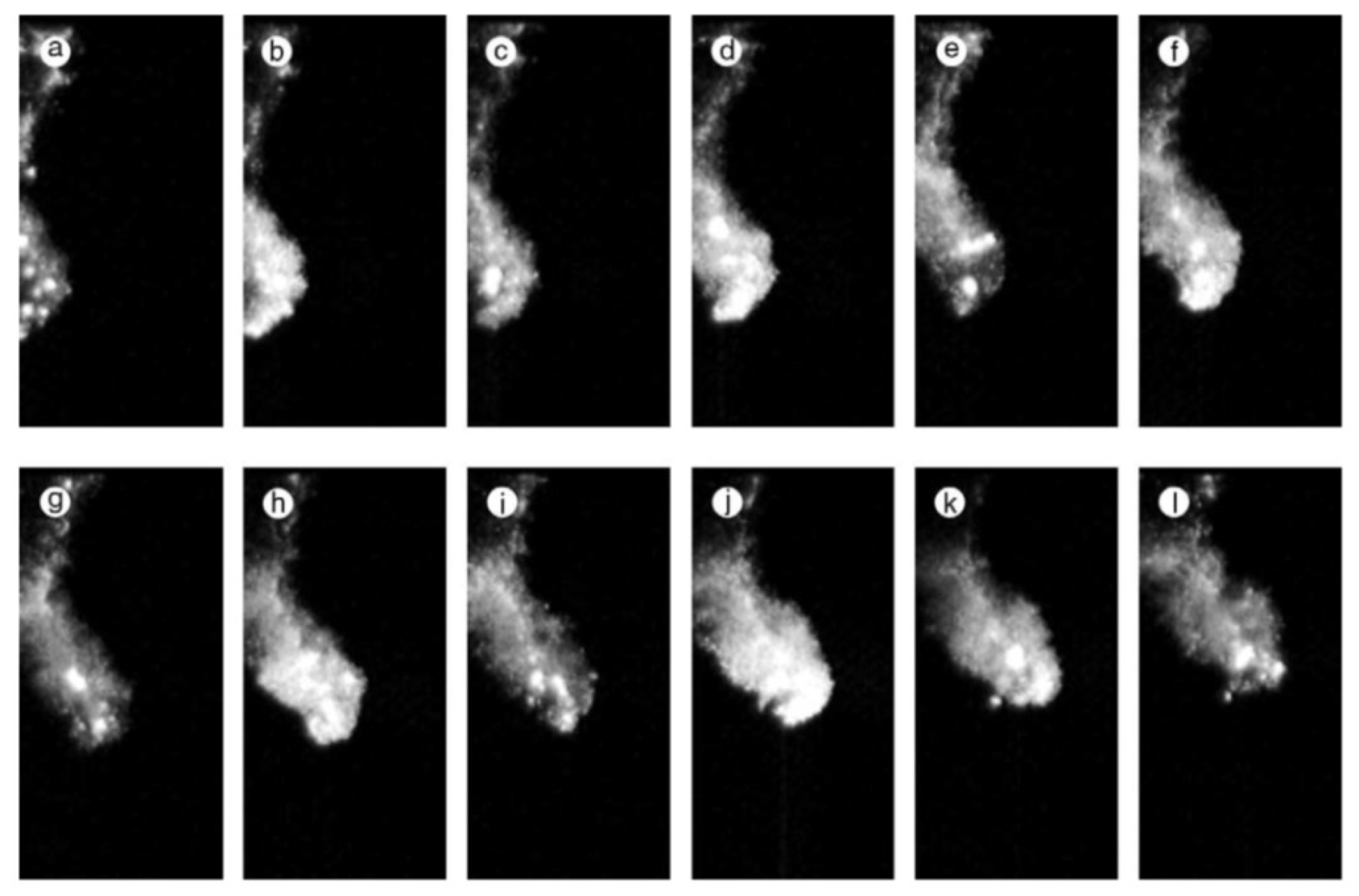
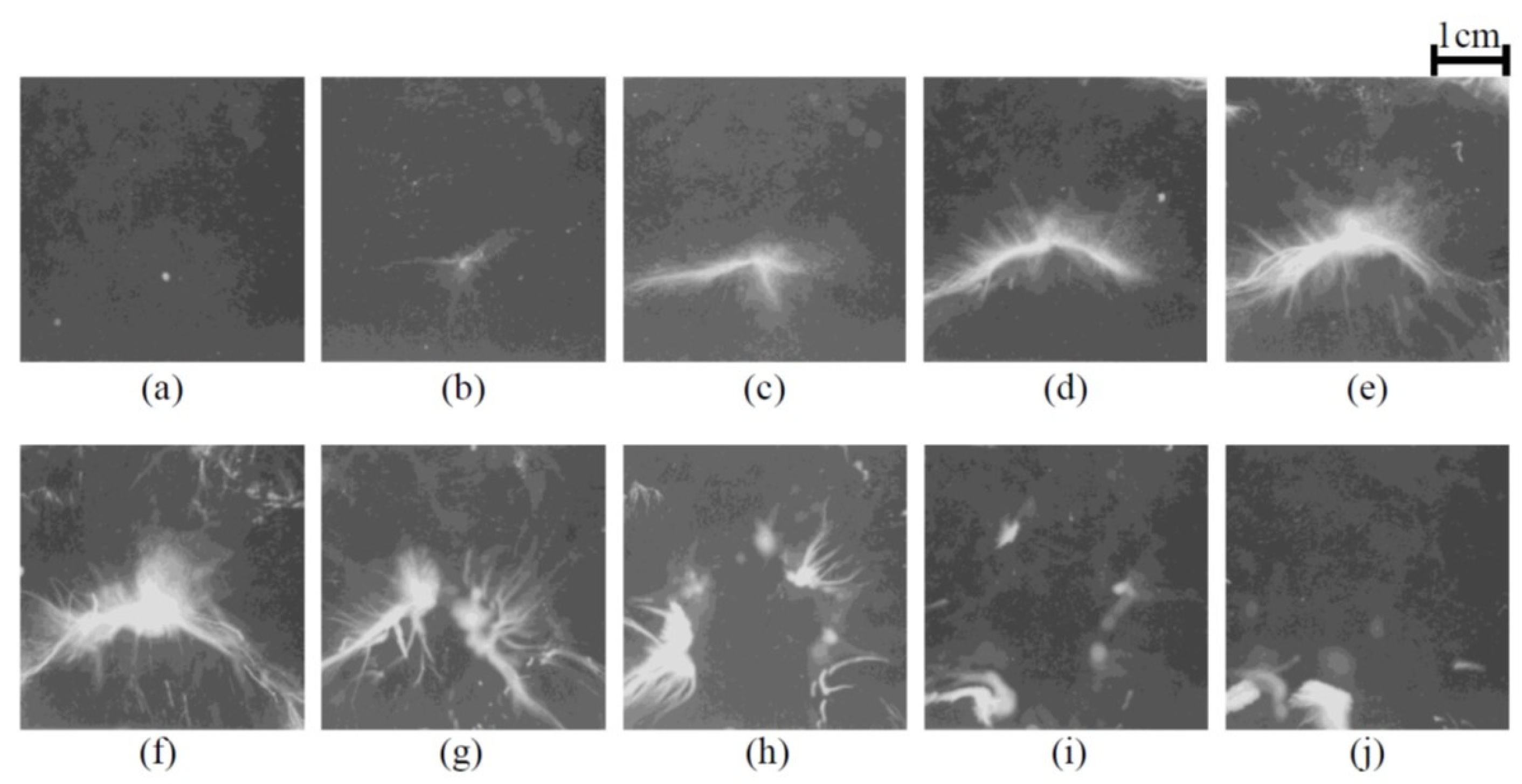
5. Bubble–Bubble Interaction
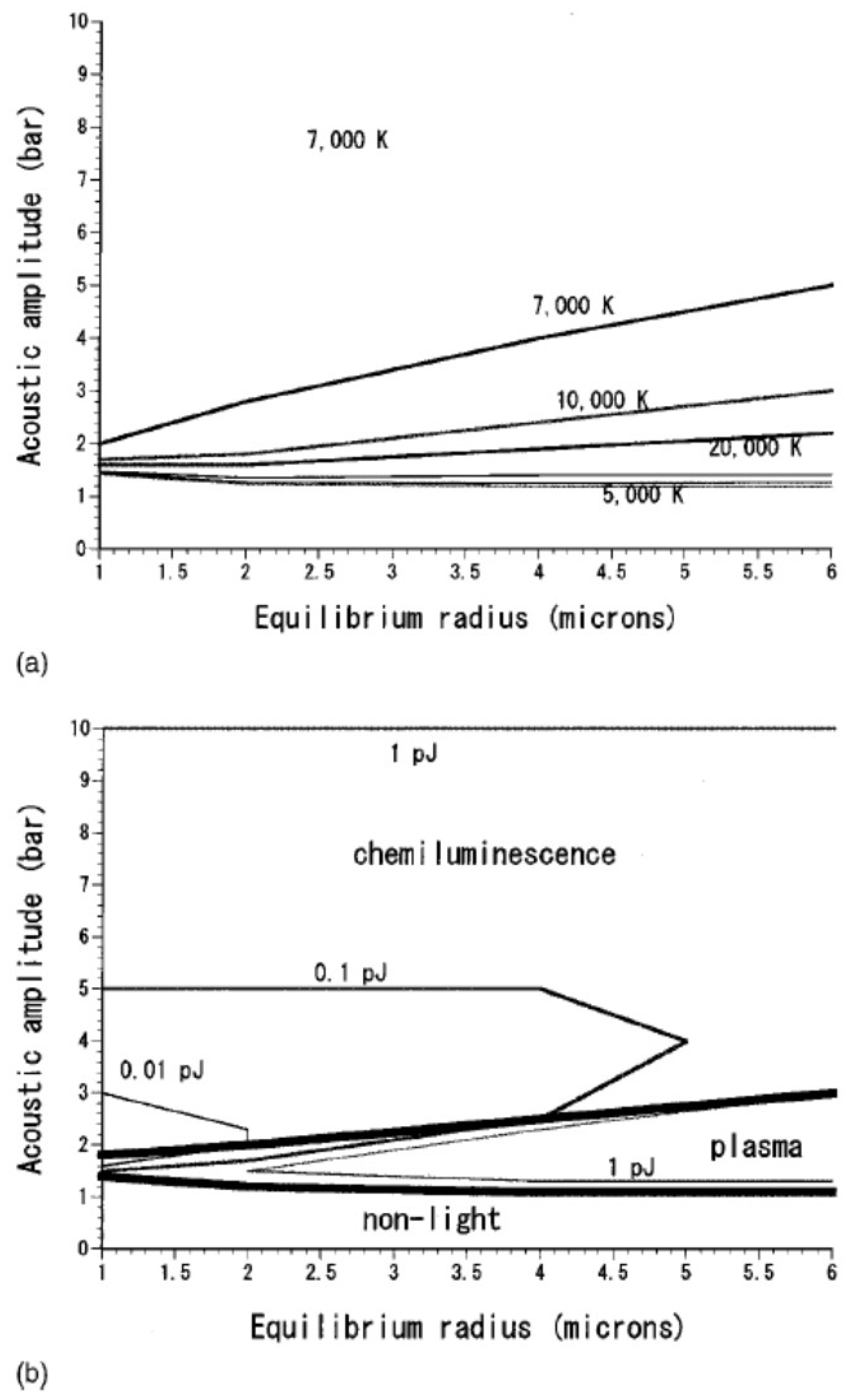
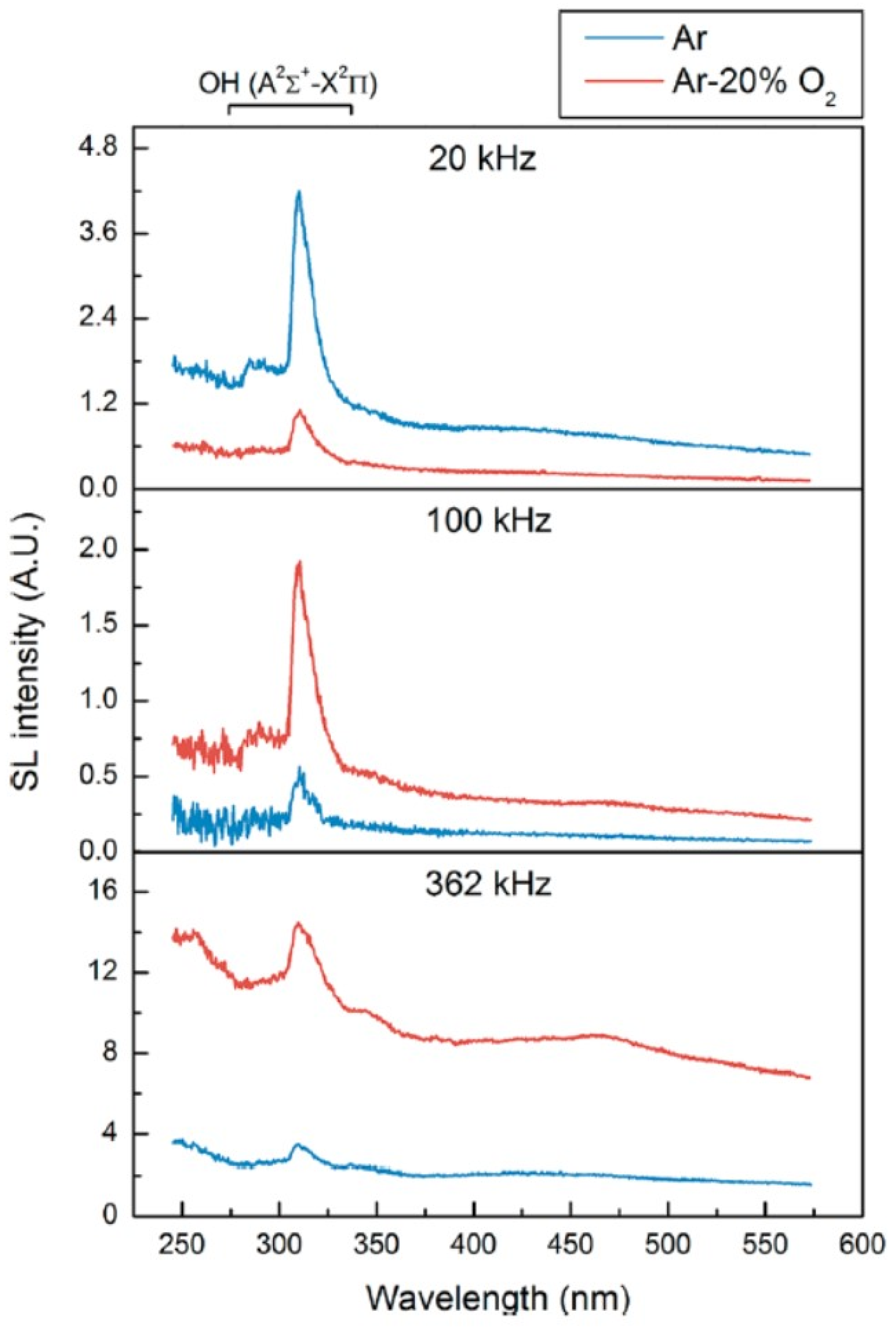
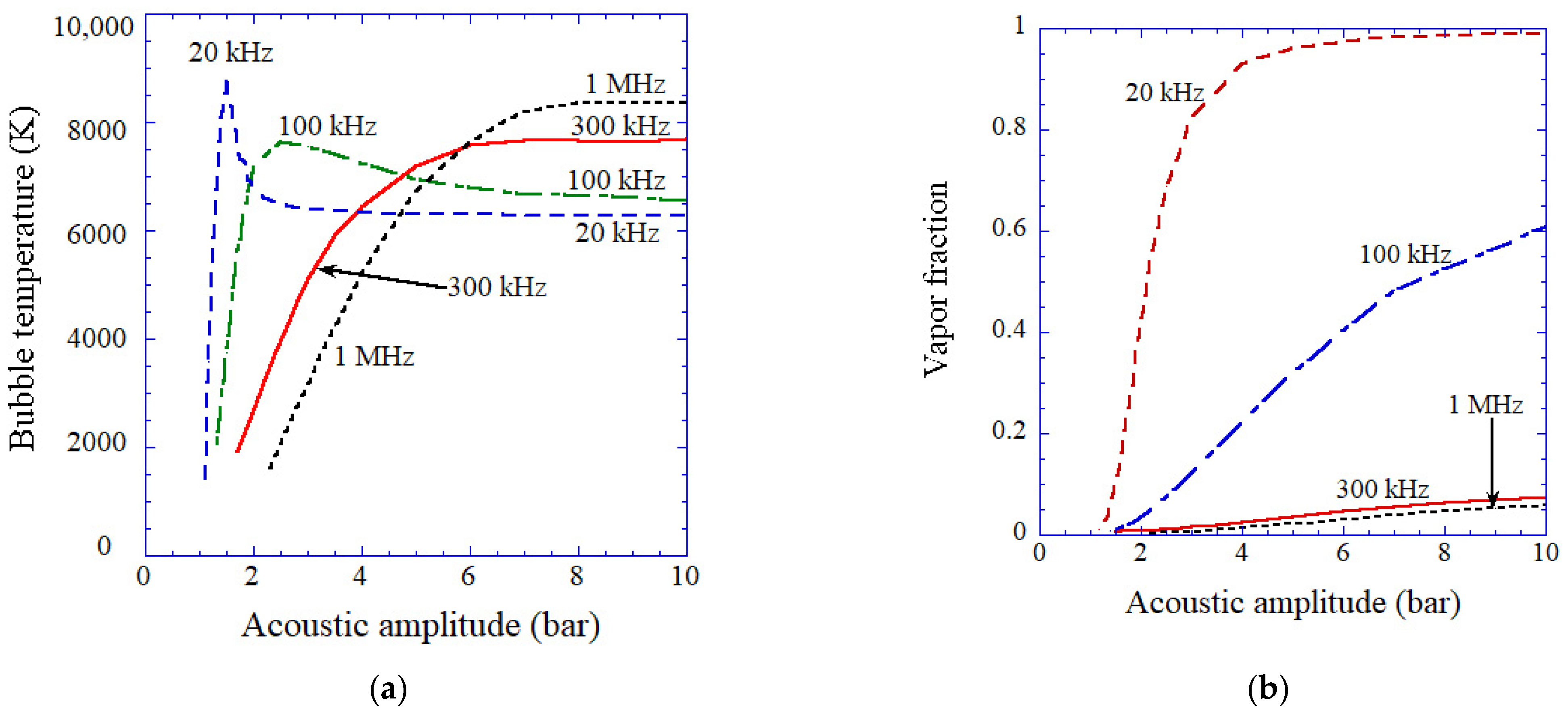
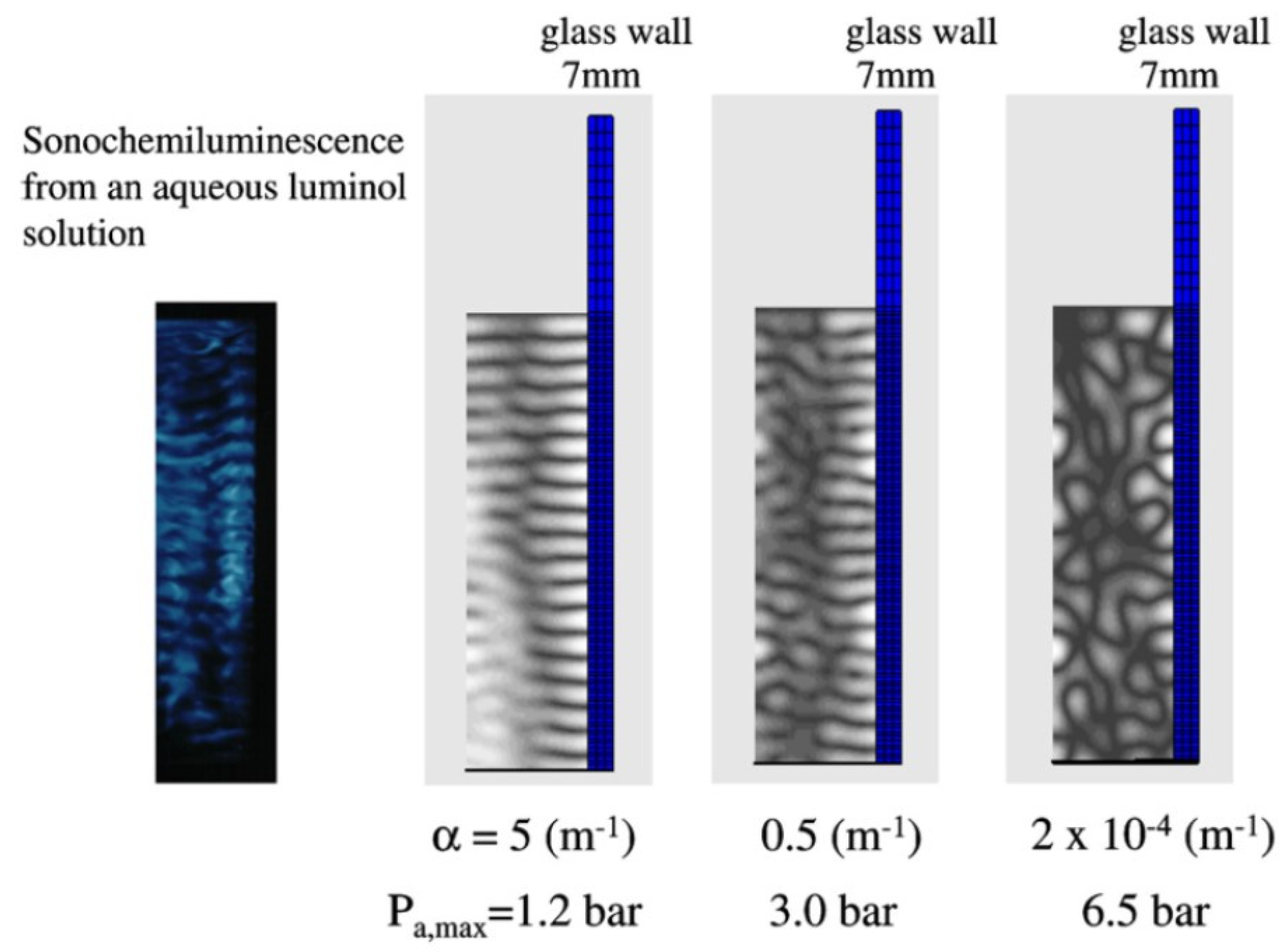
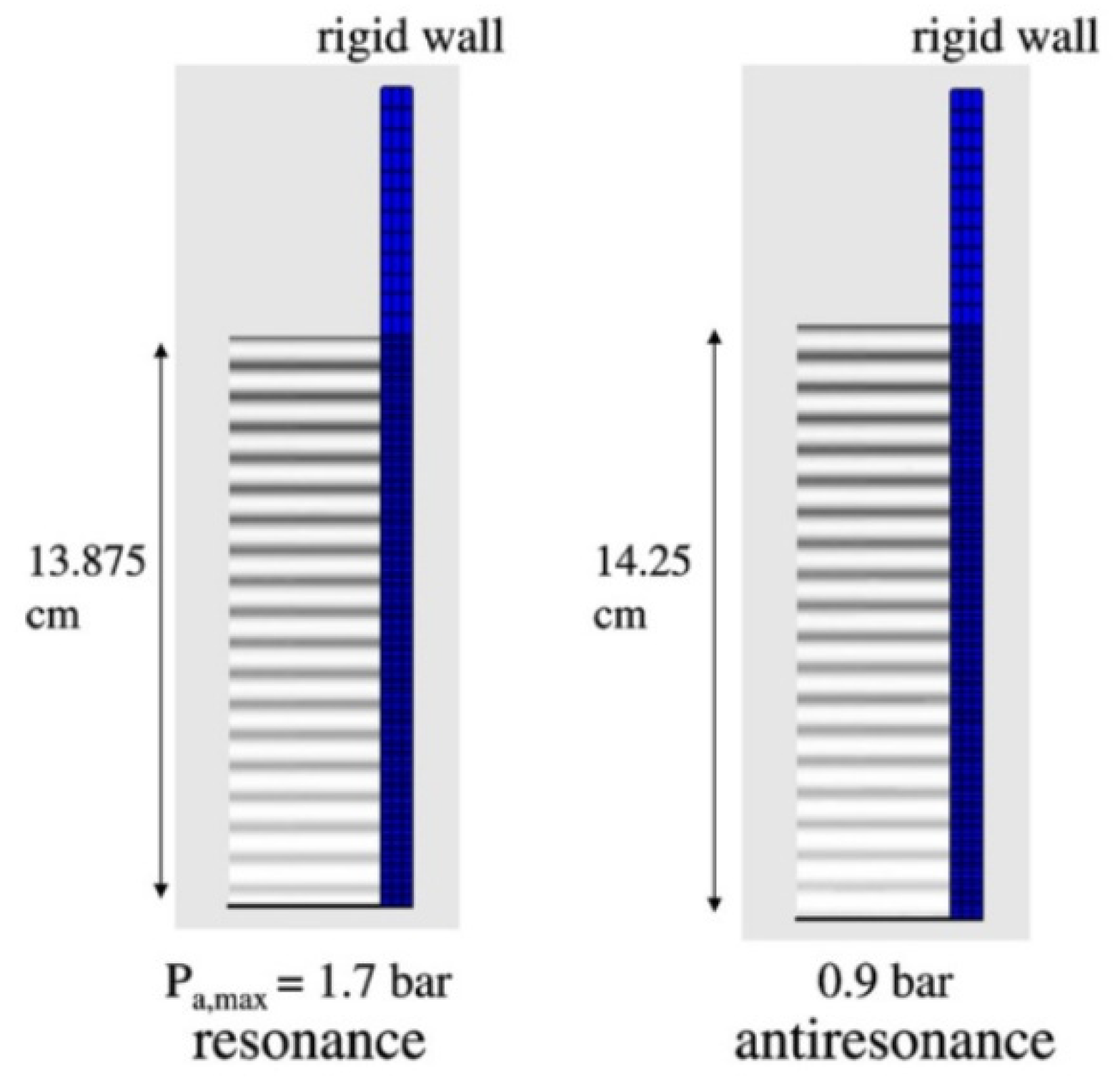
6. Acoustic Field
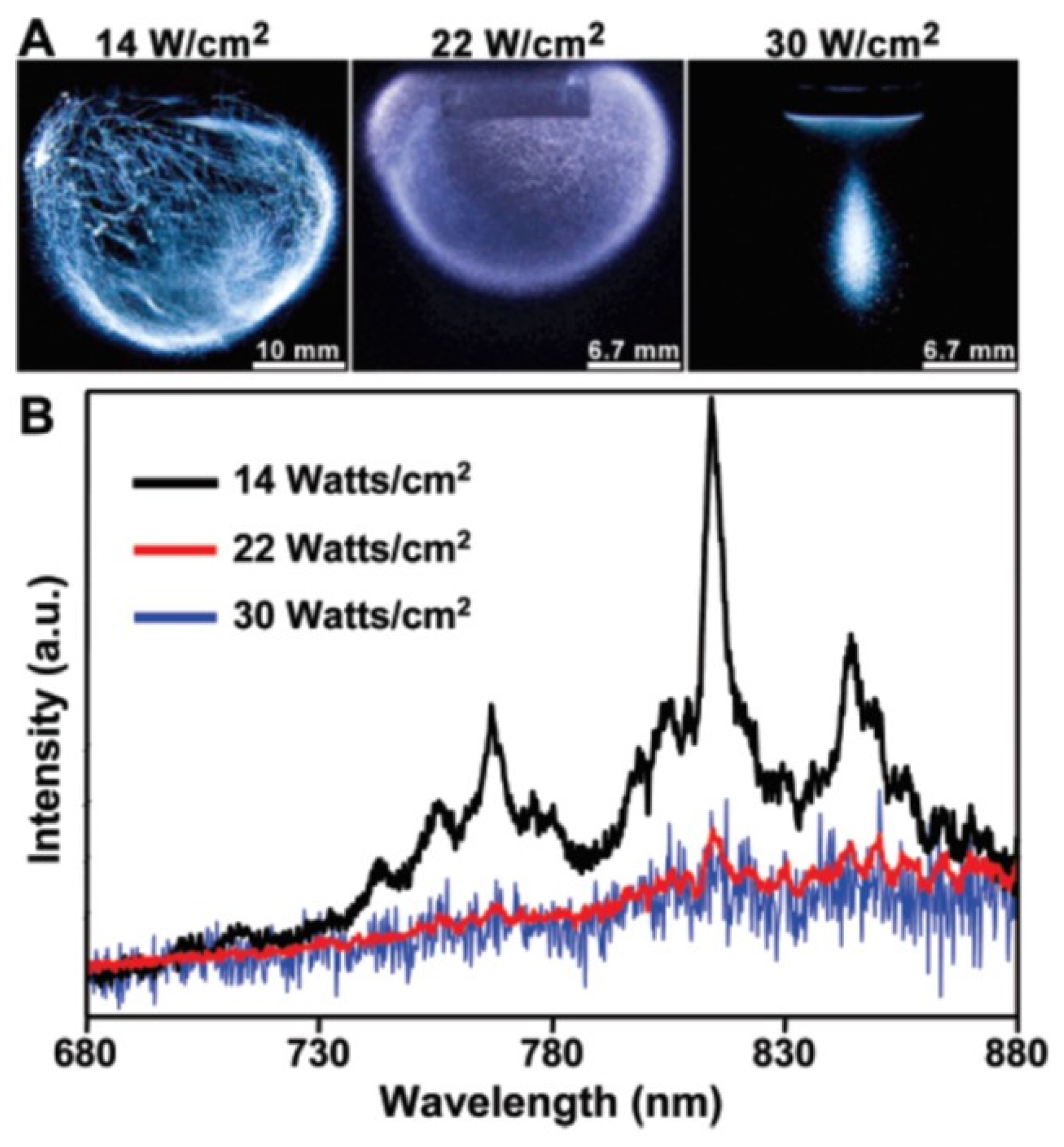
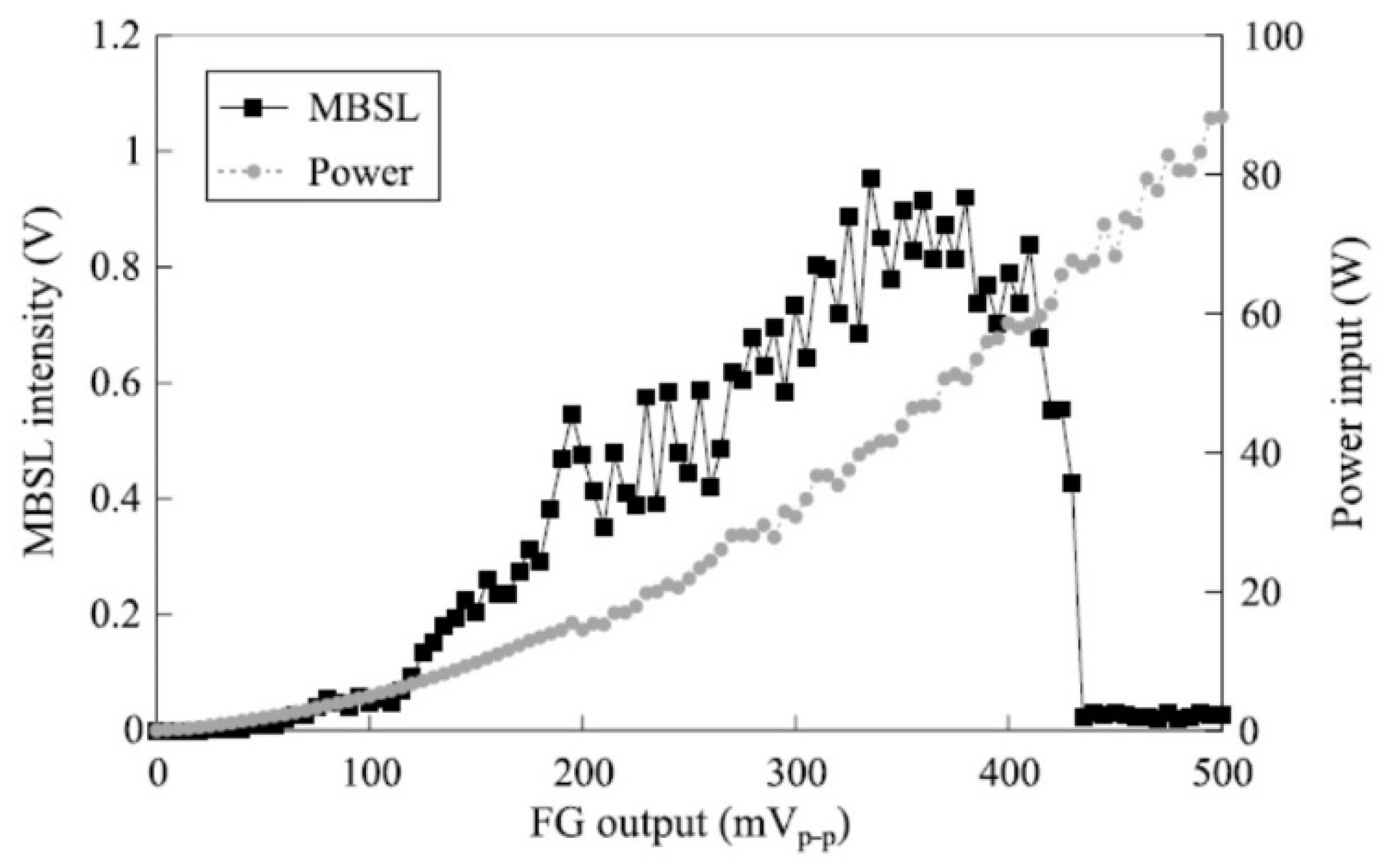
7. MBSL Quenching
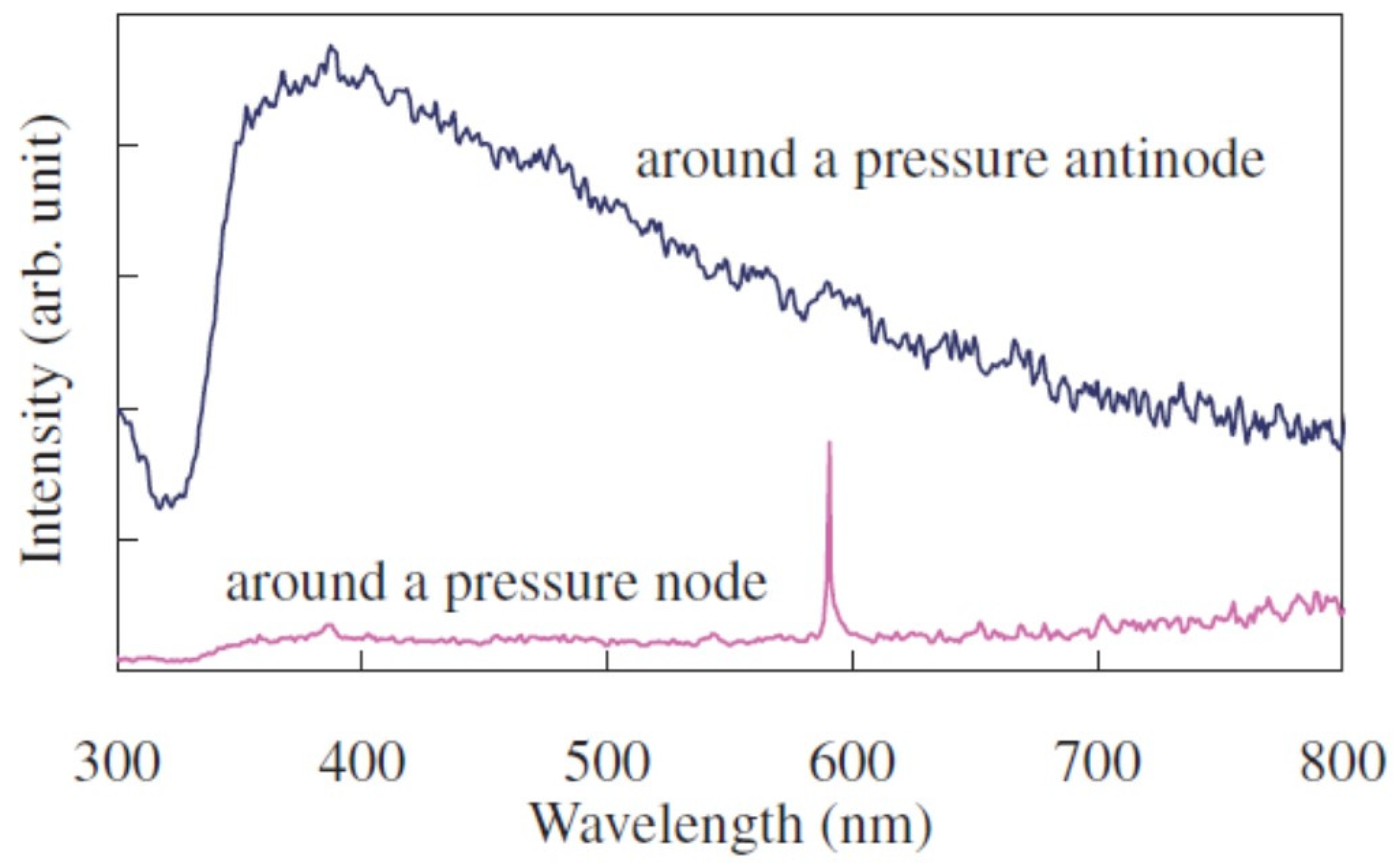
8. Na-Line Emission
9. Ultrafine Bubbles
10. Brightest MBSL
11. Applications of MBSL
12. New Development and Unsolved Problems
13. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Young, F.R. Sonoluminescence; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Yasui, K.; Tuziuti, T.; Sivakumar, M.; Iida, Y. Sonoluminescence. Appl. Spectrosc. Rev. 2004, 39, 399–436. [Google Scholar] [CrossRef]
- Hayashi, Y.; Choi, P. Two components of Na emission in sonoluminescence spectrum from surfactant aqueous solutions. Ultrason. Sonochem. 2015, 23, 333–338. [Google Scholar] [CrossRef]
- Young, F.R. Cavitation; Imperial College: London, UK, 1999. [Google Scholar]
- Yasui, K. Acoustic Cavitation and Bubble Dynamics; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Brenner, M.P.; Hilgenfeldt, S.; Lohse, D. Single-bubble sonoluminescence. Rev. Mod. Phys. 2002, 74, 425–484. [Google Scholar] [CrossRef]
- Didenko, Y.T.; McNamara, W.B., III; Suslick, K.S. Temperature of multibubble sonoluminescence in water. J. Phys. Chem. A 1999, 103, 10783–10788. [Google Scholar] [CrossRef]
- McNamara, W.B., III; Didenko, Y.T.; Suslick, K.S. Pressure during sonoluminescence. J. Phys. Chem. B 2003, 107, 7303–7306. [Google Scholar] [CrossRef]
- Bhangu, S.K.; Ashokkumar, M. Theory of sonochemistry. Top. Curr. Chem. 2016, 374, 56. [Google Scholar] [CrossRef]
- Yasui, K. Mechanism of single-bubble sonoluminescence. Phys. Rev. E 1999, 60, 1754–1758. [Google Scholar] [CrossRef]
- Marinesco, N.; Trillat, J.J. Action des ultrasons sur les plaques photographiques. Proc. R. Acad. Sci. Amst. 1933, 196, 858–860. [Google Scholar]
- Frenzel, H.; Schultes, H. Lumineszenz im ultraschall-beschickten Wasser. Z. Phys. Chem. Abt. B 1934, 27B, 421–424. [Google Scholar] [CrossRef]
- Gaitan, D.F.; Crum, L.A. Observation of sonoluminescence from a single, stable cavitation bubble in a water glycerin mixture. In Frontiers of Nonlinear Acoustics, Proceedings of the 12th ISNA, Austin, TX, USA, 27–31 August 1990; Hamilton, M.F., Blackstock, D.T., Eds.; Elsevier: London, UK, 1990; pp. 459–463. [Google Scholar]
- Yosioka, K.; Omura, A. The light emission from a single bubble driven by ultrasound and the spectra of acoustic oscillation. Proc. Annu. Meet. Acoust. Soc. Jpn. 1962, 1962, 125–126. (in Japanese). [Google Scholar]
- Barber, B.P.; Putterman, S.J. Observation of synchronous picosecond sonoluminescence. Nature 1991, 352, 318–320. [Google Scholar] [CrossRef]
- Walton, A.J.; Reynolds, G.T. Sonoluminescence. Adv. Phys. 1984, 33, 595–660. [Google Scholar] [CrossRef]
- Flannigan, D.J.; Suslick, K.S. Plasma formation and temperature measurement during single-bubble cavitation. Nature 2005, 434, 52–55. [Google Scholar] [CrossRef]
- Weninger, K.R.; Camara, C.G.; Putterman, S.J. Observation of bubble dynamics within luminescent cavitation clouds: Sonoluminescence at the nano-scale. Phys. Rev. E 2001, 63, 016310. [Google Scholar] [CrossRef]
- Yasui, K.; Iida, Y.; Tuziuti, T.; Kozuka, T.; Towata, A. Strongly interacting bubbles under an ultrasonic horn. Phys. Rev. E 2008, 77, 016609. [Google Scholar] [CrossRef]
- An, Y. Mechanism of single-bubble sonoluminescence. Phys. Rev. E 2006, 74, 026304. [Google Scholar] [CrossRef] [PubMed]
- Vuong, V.Q.; Szeri, A.J.; Young, D.A. Shock formation within sonoluminescence bubbles. Phys. Fluids 1999, 11, 10–17. [Google Scholar] [CrossRef]
- Yasui, K.; Tuziuti, T.; Iida, Y. Optimum bubble temperature for the sonochemical production of oxidants. Ultrasonics 2004, 42, 579–584. [Google Scholar] [CrossRef]
- Yasui, K. Alternative model of single-bubble sonoluminescence. Phys. Rev. E 1997, 56, 6750–6760. [Google Scholar] [CrossRef]
- Yasui, K.; Tuziuti, T.; Sivakumar, M.; Iida, Y. Theoretical study of single-bubble sonochemistry. J. Chem. Phys. 2005, 122, 224706. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K. Effect of liquid temperature on sonoluminescence. Phys. Rev. E 2001, 64, 016310. [Google Scholar] [CrossRef]
- Yasui, K. Variation of liquid temperature at bubble wall near the sonoluminescence threshold. J. Phys. Soc. Jpn. 1996, 65, 2830–2840. [Google Scholar] [CrossRef]
- Yasui, K. Effect of volatile solutes on sonoluminescence. J. Chem. Phys. 2002, 116, 2945–2954. [Google Scholar] [CrossRef]
- Lohse, D.; Brenner, M.P.; Dupont, T.F.; Hilgenfeldt, S.; Johnston, B. Sonoluminescing air bubbles rectify argon. Phys. Rev. Lett. 1997, 78, 1359–1362. [Google Scholar] [CrossRef]
- Lohse, D.; Hilgenfeldt, S. Inert gas accumulation in sonoluminescing bubbles. J. Chem. Phys. 1997, 107, 6986–6997. [Google Scholar] [CrossRef]
- Ashokkumar, M.; Crum, L.A.; Frensley, C.A.; Grieser, F.; Matula, T.J.; McNamara, W.B., III; Suslick, K.S. Effect of solutes on single-bubble sonoluminescence in water. J. Phys. Chem. A 2000, 104, 8462–8465. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1975. [Google Scholar]
- Didenko, Y.T.; Suslick, K.S. The energy efficiency of formation of photons, radicals and ions during single-bubble cavitation. Nature 2002, 418, 394–397. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K.; Tuziuti, T.; Iida, Y. Dependence of the characteristics of bubbles on types of sonochemical reactors. Ultrason. Sonochem. 2005, 12, 43–51. [Google Scholar] [CrossRef]
- Yasui, K. Temperature in multibubble sonoluminescence. J. Chem. Phys. 2001, 115, 2893–2896. [Google Scholar] [CrossRef]
- Yasui, K.; Tuziuti, T.; Kozuka, T.; Towata, A.; Iida, Y. Relationship between the bubble temperature and main oxidant created inside an air bubble under ultrasound. J. Chem. Phys. 2007, 127, 154502. [Google Scholar] [CrossRef]
- Yasui, K. Effect of non-equilibrium evaporation and condensation on bubble dynamics near the sonoluminescence threshold. Ultrasonics 1998, 36, 575–580. [Google Scholar] [CrossRef]
- Ndiaye, A.A.; Pflieger, R.; Siboulet, B.; Molina, J.; Dufreche, J.; Nikitenko, S.I. Nonequilibrium vibrational excitation of OH radicals generated during multibubble cavitation in water. J. Phys. Chem. A 2012, 116, 4860–4867. [Google Scholar] [CrossRef]
- Kappus, B.; Bataller, A.; Putterman, S.J. Energy balance for a sonoluminescence bubble yields a measure of ionization potential lowering. Phys. Rev. Lett. 2013, 111, 234301. [Google Scholar] [CrossRef] [PubMed]
- More, R.M. Electronic energy-levels in dense plasmas. J. Quant. Spectrosc. Radiat. Transf. 1982, 27, 345–357. [Google Scholar] [CrossRef]
- Zimmerman, G.B.; More, R.M. Pressure ionization in laser-fusion target simulation. J. Quant. Spectrosc. Radiat. Transf. 1980, 23, 517–522. [Google Scholar] [CrossRef]
- Flannigan, D.J.; Suslick, K.S. Inertially confined plasma in an imploding bubble. Nat. Phys. 2010, 6, 598–601. [Google Scholar] [CrossRef]
- Yasui, K.; Kato, K. Bubble dynamics and sonoluminescence from helium or xenon in mercury and water. Phys. Rev. E 2012, 86, 036320. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K.; Tuziuti, T.; Lee, J.; Kozuka, T.; Towata, A.; Iida, Y. The range of ambient radius for an active bubble in sonoluminescence and sonochemical reactions. J. Chem. Phys. 2008, 128, 184705. [Google Scholar] [CrossRef]
- Matula, T.J.; Cordry, S.M.; Roy, R.A.; Crum, L.A. Bjerknes force and bubble levitation under single-bubble sonoluminescence conditions. J. Acoust. Soc. Am. 1997, 102, 1522–1527. [Google Scholar] [CrossRef]
- Mettin, R.; Luther, S.; Ohl, C.D.; Lauterborn, W. Acoustic cavitation structures and simulations by a particle model. Ultrason. Sonochem. 1999, 6, 25–29. [Google Scholar] [CrossRef]
- Ji, R.; Pflieger, R.; Virot, M.; Nikitenko, S.I. Multibubble sonochemistry and sonoluminescence at 100 kHz: The missing link between low- and high-frequency ultrasound. J. Phys. Chem. B 2018, 122, 6989–6994. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K. Influence of ultrasonic frequency on multibubble sonoluminescence. J. Acoust. Soc. Am. 2002, 112, 1405–1413. [Google Scholar] [CrossRef]
- Hilgenfeldt, S.; Lohse, D.; Brenner, M.P. Phase diagrams for sonoluminescing bubbles. Phys. Fluids 1996, 8, 2808–2826. [Google Scholar] [CrossRef]
- Brotchie, A.; Grieser, F.; Ashokkumar, M. Effect of power and frequency on bubble-size distributions in acoustic cavitation. Phys. Rev. Lett. 2009, 102, 084302. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Ashokkumar, M.; Kentish, S.; Grieser, F. Determination of the size of sonoluminescence bubbles in a pulsed acoustic field. J. Am. Chem. Soc. 2005, 127, 16810–16811. [Google Scholar] [CrossRef] [PubMed]
- Yasui, K.; Tuziuti, T.; Iida, Y.; Mitome, H. Theoretical study of the ambient-pressure dependence of sonochemical reactions. J. Chem. Phys. 2003, 119, 346–356. [Google Scholar] [CrossRef]
- Yasui, K.; Lee, J.; Tuziuti, T.; Towata, A.; Kozuka, T.; Iida, Y. Influence of the bubble-bubble interaction on destruction of encapsulated microbubbles under ultrasound. J. Acoust. Soc. Am. 2009, 126, 973–982. [Google Scholar] [CrossRef]
- Yasui, K.; Towata, A.; Tuziuti, T.; Kozuka, T.; Kato, K. Effect of static pressure on acoustic energy radiated by cavitation bubbles in viscous liquids under ultrasound. J. Acoust. Soc. Am. 2011, 130, 3233–3242. [Google Scholar] [CrossRef]
- Yasui, K.; Tuziuti, T.; Lee, J.; Kozuka, T.; Towata, A.; Iida, Y. Numerical simulations of acoustic cavitation noise with the temporal fluctuation in the number of bubbles. Ultrason. Sonochem. 2010, 17, 460–472. [Google Scholar] [CrossRef]
- Eddingsaas, N.C.; Suslick, K.S. Evidence for a plasma core during multibubble sonoluminescence in sulfuric acid. J. Am. Chem. Soc. 2007, 129, 3838–3839. [Google Scholar] [CrossRef]
- Hatanaka, S.; Hayashi, S.; Choi, P. Sonoluminescence of alkali-metal atoms in sulfuric acid: Comparison with that in water. Jpn. J. Appl. Phys. 2010, 49, 07HE01. [Google Scholar] [CrossRef]
- Sharipov, G.L.; Abdrakhmanov, A.M.; Gainetdinov, R.K. Sonoluminescence of aqueous solutions of sulfuric acid and sulfur dioxide. Russ. Chem. Bull. Int. Ed. 2003, 52, 1966–1968. [Google Scholar] [CrossRef]
- An, Y. Formulation of multibubble cavitation. Phys. Rev. E 2011, 83, 066313. [Google Scholar] [CrossRef]
- Lee, J.; Yasui, K.; Tuziuti, T.; Kozuka, T.; Towata, A.; Iida, Y. Spatial distribution enhancement of sonoluminescence activity by altering sonication and solution conditions. J. Phys. Chem. B 2008, 112, 15333–15341, Erratum 2009, 113, 12438. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Vian, C.J.B.; Birkin, P.R.; Leighton, T.G. Cluster collapse in a cylindrical cell: Correlating multibubble sonoluminescence, acoustic pressure, and erosion. J. Phys. Chem. C 2010, 114, 16416–16425. [Google Scholar] [CrossRef]
- Thiemann, A.; Nowak, T.; Mettin, R.; Holsteyns, F.; Lippert, A. Characterization of an acoustic cavitation bubble structure at 230 kHz. Ultrason. Sonochem. 2011, 18, 595–600. [Google Scholar] [CrossRef] [PubMed]
- Hatanaka, S.; Yasui, K.; Tuziuti, T.; Mitome, H. Difference in threshold between sono- and sonochemical luminescence. Jpn. J. Appl. Phys. 2000, 39, 2962–2966. [Google Scholar] [CrossRef]
- Yasuda, K.; Torii, T.; Yasui, K.; Iida, Y.; Tuziuti, T.; Nakamura, M.; Asakura, Y. Enhancement of sonochemical reaction of terephthalate ion by superposition of ultrasonic fields of various frequencies. Ultrason. Sonochem. 2007, 14, 699–704. [Google Scholar] [CrossRef]
- Tuziuti, T.; Yasui, K.; Kozuka, T.; Towata, A.; Iida, Y. Enhancement of sonochemical reaction rate by addition of micrometer-sized air bubbles. J. Phys. Chem. A 2006, 110, 10720–10724. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, T.; Yasui, K.; Yasuda, K.; Iida, Y.; Tuziuti, T.; Torii, T.; Nakamura, M. Effect of dual frequency on sonochemical reaction rates. Res. Chem. Intermed. 2004, 30, 703–711. [Google Scholar] [CrossRef]
- Yasui, K.; Kozuka, T.; Tuziuti, T.; Towata, A.; Iida, Y.; King, J.; Macey, P. FEM calculation of an acoustic field in a sonochemical reactor. Ulrason. Sonochem. 2007, 14, 605–614. [Google Scholar] [CrossRef] [PubMed]
- Leroy, V.; Bretagne, A.; Fink, M.; Willaime, H.; Tabeling, P.; Tourin, A. Design and characterization of bubble phononic crystals. Appl. Phys. Lett. 2009, 95, 171904. [Google Scholar] [CrossRef]
- Hatanaka, S.; Yasui, K.; Kozuka, T.; Tuziuti, T.; Mitome, H. Influence of bubble clustering on multibubble sonoluminescence. Ultrasonics 2002, 40, 655–660. [Google Scholar] [CrossRef]
- Hatanaka, S.; Yasui, K.; Tuziuti, T.; Kozuka, T.; Mitome, H. Quenching mechanism of multibubble sonoluminescence at excessive sound pressure. Jpn. J. Appl. Phys. 2001, 40, 3856–3860. [Google Scholar] [CrossRef]
- Hatanaka, S.; Mitome, H.; Yasui, K.; Hayashi, S. Multibubble sonoluminescence enhancement by fluid flow. Ultrasonics 2006, 44, e435–e438. [Google Scholar] [CrossRef] [PubMed]
- Matula, T.J.; Roy, R.A.; Mourad, P.D.; McNamara, W.B., III; Suslick, K.S. Comparison of multibubble and single-bubble sonoluminescence spectra. Phys. Rev. Lett. 1995, 75, 2602–2605. [Google Scholar] [CrossRef] [PubMed]
- Abe, S.; Choi, P. Spatiotemporal separation of Na-atom emission from continuum emission in sonoluminescence. Jpn. J. Appl. Phys. 2009, 48, 07GH02. [Google Scholar] [CrossRef]
- Bremond, N.; Arora, M.; Dammer, S.M.; Lohse, D. Interaction of cavitation bubbles on a wall. Phys. Fluids 2006, 18, 121505. [Google Scholar] [CrossRef]
- Calvisi, M.L.; Lindau, O.; Blake, J.R.; Szeri, A.J. Shape stability and violent collapse of microbubbles in acoustic traveling waves. Phys. Fluids 2007, 19, 047101. [Google Scholar] [CrossRef]
- Ohl, C.D.; Arora, M.; Dijkink, R.; Janve, V.; Lohse, D. Surface cleaning from laser-induced cavitation bubbles. Appl. Phys. Lett. 2006, 89, 074102. [Google Scholar] [CrossRef]
- Plesset, M.S.; Chapman, R.B. Collapse of an initially spherical vapour cavity in the neighbourhood of a solid boundary. J. Fluid Mech. 1971, 47, 283–290. [Google Scholar] [CrossRef]
- Orthaber, U.; Zevnik, J.; Petkovsek, R.; Dular, M. Cavitation bubble collapse in a vicinity of a liquid-liquid interface—basic research into emulsification process. Ultrason. Sonochem. 2020, 68, 105224. [Google Scholar] [CrossRef]
- Pflieger, R.; Nikitenko, S.I.; Ashokkumar, M. Effect of NaCl salt on sonochemistry and sonoluminescence in aqueous solutions. Ultrason. Sonochem. 2019, 59, 104753. [Google Scholar] [CrossRef]
- Firouzi, M.; Howes, T.; Nguyen, A.V. A quantitative review of the transition salt concentration for inhibiting bubble coalescence. Adv. Colloid Interf. Sci. 2015, 222, 305–318. [Google Scholar] [CrossRef] [PubMed]
- Madanshetty, S.I.; Apfel, R.E. Acoustic microcavitation: Enhancement and applications. J. Acoust. Soc. Am. 1991, 90, 1508–1514. [Google Scholar] [CrossRef] [PubMed]
- Tuziuti, T.; Yasui, K.; Sivakumar, M.; Iida, Y.; Miyoshi, N. Correlation between acoustic cavitation noise and yield enhancement of sonochemical reaction by particle addition. J. Phys. Chem. A 2005, 109, 4869–4872. [Google Scholar] [CrossRef] [PubMed]
- Hata, T.; Yamawaki, N.; Nishiguchi, Y.; Okumura, H.; Akamatsu, S. Discrimination of ultra-fine bubbles and solid nanoparticles using the sonoluminescence effect. Bunseki Kagaku 2019, 68, 847–852. (in Japanese). [Google Scholar] [CrossRef]
- Yasui, K.; Tuziutu, T.; Kanematsu, W. Mysteries of bulk nanobubbles (ultrafine bubbles); stability and radical formation. Ultrason. Sonochem. 2018, 48, 259–266. [Google Scholar] [CrossRef] [PubMed]
- Terasaka, K.; Yasui, K.; Kanematsu, W.; Aya, N. (Eds.) Ultrafine Bubbles; Jenny Stanford: Singapore, 2021. [Google Scholar]
- Yasui, K.; Tuziuti, T.; Kanematsu, W.; Kato, K. Dynamic equilibrium model for a bulk nanobubble and a microbubble partly covered with hydrophobic material. Langmuir 2016, 32, 11101–11110. [Google Scholar] [CrossRef] [PubMed]
- Kanematsu, W.; Tuziuti, T.; Yasui, K. The influence of storage conditions and container materials on the long term stability of bulk nanobubbles—consideration from a perspective of interactions between bubbles and surroundings. Chem. Eng. Sci. 2020, 219, 115594. [Google Scholar] [CrossRef]
- Sunartio, D.; Yasui, K.; Tuziuti, T.; Kozuka, T.; Iida, Y.; Ashokkumar, M.; Grieser, F. Correlation between Na* emission and “chemically active” acoustic cavitation bubbles. ChemPhysChem 2007, 8, 2331–2335. [Google Scholar] [CrossRef]
- Kappus, B.; Khalid, S.; Putterman, S. 100-watt sonoluminescence generated by 2.5-atmosphere-pressure pulses. Phys. Rev. E 2011, 83, 056304. [Google Scholar] [CrossRef]
- Okitsu, K.; Suzuki, T.; Takenaka, N.; Bandow, H.; Nishimura, R.; Maeda, Y. Acoustic multibubble cavitation in water: A new aspect of the effect of a rare gas atmosphere on bubble temperature and its relevance to sonochemistry. J. Phys. Chem. B 2006, 110, 20081–20084. [Google Scholar] [CrossRef]
- Kazachek, M.V.; Gordeychuk, T.V. Using photon correlation counter for determining the amount of emitting bubbles and number of photons per flash of multibubble sonoluminescence. Technic. Phys. Lett. 2020, 46, 263–267. [Google Scholar] [CrossRef]
- Kerboua, K.; Hamdaoui, O. Void fraction, number density of acoustic cavitation bubbles, and acoustic frequency: A numerical investigation. J. Acoust. Soc. Am. 2019, 146, 2240–2252. [Google Scholar] [CrossRef] [PubMed]
- Yin, H.; Qiao, Y.; Cao, H.; Wan, M. Sonoluminescence and sonochemiluminescence study of cavitation field in a 1.2 MHz focused ultrasound. AIP Conf. Proc. 2017, 1816, 080006. [Google Scholar] [CrossRef]
- Yin, H.; Chang, N.; Xu, S.; Wan, M. Sonoluminescence characterization of inertial cavitation inside a BSA phantom treated by pulsed HIFU. Ulrason. Sonochem. 2016, 32, 158–164. [Google Scholar] [CrossRef]
- Matula, T.J.; Hilmo, P.R.; Bailey, M.R.; Crum, L.A. In vitro sonoluminescence and sonochemistry studies with an electrohydraulic shock-wave lithotripter. Ultrasound Med. Biol. 2002, 28, 1199–1207. [Google Scholar] [CrossRef]
- Coleman, A.J.; Choi, M.J.; Saunders, J.E.; Leighton, T.G. Acoustic emission and sonoluminescence due to cavitation at the beam focus of an electrohydraulic shock wave lithotripter. Ultrasound Med Biol. 1992, 18, 267–281. [Google Scholar] [CrossRef]
- Beguin, E.; Shrivastava, S.; Dezhkunov, N.V.; McHale, A.P.; Callan, J.F.; Stride, E. Direct evidence of multibubble sonoluminescence using therapeutic ultrasound and microbubbles. ACS Appl. Mater. Interfaces 2019, 11, 19913–19919. [Google Scholar] [CrossRef]
- Canaparo, R.; Foglietta, F.; Giuntini, F.; Francovich, A.; Serpe, L. The bright side of sound: Perspectives on the biomedical application of sonoluminescence. Photochem. Photobiol. Sci. 2020, 19, 1114–1121. [Google Scholar] [CrossRef] [PubMed]
- Suslick, K.S.; Eddingsaas, N.C.; Flannigan, D.J.; Hopkins, S.D.; Xu, H. Extreme conditions during multibubble cavitation: Sonoluminescence as a spectroscopic probe. Ultrason. Sonochem. 2011, 18, 842–846. [Google Scholar] [CrossRef]
- McNamara, W.B., III; Didenko, Y.T.; Suslick, K.S. Sonoluminescence temperatures during multi-bubble cavitation. Nature 1999, 401, 772–775. [Google Scholar] [CrossRef]
- Didenko, Y.T.; McNamara, W.B., III; Suslick, K.S. Effect of noble gases on sonoluminescence temperatures during multibubble cavitation. Phys. Rev. Lett. 2000, 84, 777–780. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Glumac, N.G.; Suslick, K.S. Temperature inhomogeneity during multibubble sonoluminescence. Angew. Chem. Int. Ed. 2010, 49, 1079–1082. [Google Scholar] [CrossRef]
- Pflieger, R.; Ndiaye, A.A.; Chave, T.; Nikitenko, S.I. Influence of ultrasonic frequency on swan band sonoluminescence and sonochemical activity in aqueous tert-butyl alcohol solutions. J. Phys. Chem. B 2015, 119, 284–290. [Google Scholar] [CrossRef]
- Pflieger, R.; Lejeune, M.; Noel, C.; Belmonte, T.; Nikitenko, S.I.; Draye, M. Diagnosing the plasma formed during acoustic cavitation in [BEPip][NTf2] ionic liquid. Phys. Chem. Chem. Phys. 2019, 21, 1183–1189. [Google Scholar] [CrossRef]
- Feder, T. Mingling art and science opens minds. Phys. Today 2021, 74, 24–29. [Google Scholar] [CrossRef]
- Cairos, C.; Mettin, R. Simultaneous high-speed recording of sonoluminescence and bubble dynamics in multibubble fields. Phys. Rev. Lett. 2017, 118, 064301. [Google Scholar] [CrossRef]
- Yu, Q.; Ma, X.; Xu, Z.; Zhao, J.; Wang, D.; Huang, Z. Thermodynamic effect of single bubble near a rigid wall. Ultrason. Sonochem. 2021, 71, 105396. [Google Scholar] [CrossRef] [PubMed]
- Gordeychuk, T.V.; Kazachek, M.V. Time-correlated photon counting for estimating the duration of Na-line and continuum emission flashes in the spectra of multi-bubble sonoluminescence. Opt. Spectrosc. 2020, 128, 1602–1610. [Google Scholar] [CrossRef]
- Lee, H.; Choi, P. Electrification of sonoluminescing single bubble. J. Phys. Chem. B 2020, 124, 3145–3151. [Google Scholar] [CrossRef]
- Takahashi, M. ξ potential of microbubbles in aqueous solutions: Electrical properties of the gas-water interface. J. Phys. Chem. B 2005, 109, 21858–21864. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Dabros, T.; Li, D.; Czarnecki, J.; Masliyah, J.H. Measurement of the zeta potential of gas bubbles in aqueous solutions by microelectrophoresis method. J. Colloid Inter. Sci. 2001, 243, 128–135. [Google Scholar] [CrossRef]
- Leroy, P.; Jougnot, D.; Revil, A.; Lassin, A.; Azaroual, M. A double layer model of the gas bubble/water interface. J. Colloid Interf. Sci. 2012, 388, 243–256. [Google Scholar] [CrossRef] [PubMed]
- Borisenok, V.A.; Sedov, S.Y. On the mechanisms of sonoluminescence in polar and nonpolar liquids. Phys. At. Nucl. 2020, 83, 1575–1584. [Google Scholar] [CrossRef]
- Yasui, K.; Itasaka, H.; Mimura, K.; Kato, K. Dynamic dielectric-response model of flexoelectric polarization from kHz to MHz range in an ordered assembly of BaTiO3 nanocubes. J. Phys. Condens. Matter 2020, 32, 495301. [Google Scholar] [CrossRef] [PubMed]
- Boyd, B.; Suslov, S.A.; Becker, S.; Greentree, A.D.; Maksymov, I.S. Beamed UV sonoluminescence by aspherical air bubble collapse near liquid-metal microparticles. Sci. Rep. 2020, 10, 1501. [Google Scholar] [CrossRef]
- Fernandez Rivas, D.; Ashokkumar, M.; Leong, T.; Yasui, K.; Tuziuti, T.; Kentish, S.; Lohse, D.; Gardeniers, H.J.G.E. Sonoluminescence and sonochemiluminescence from a microreactor. Ultrason. Sonochem. 2012, 19, 1252–1259. [Google Scholar] [CrossRef]
- Ohl, S.W.; Ohl, C.D. Acoustic cavitation in a microchannel. In Handbook of Ultrasonics and Sonochemistry; Ashokkumar, M., Ed.; Springer: Singapore, 2016; pp. 99–135. [Google Scholar] [CrossRef]
- Fernandez Rivas, D.; Kuhn, S. Synergy of microfluidics and ultrasound. Top. Curr. Chem. 2016, 374, 70. [Google Scholar] [CrossRef] [PubMed]
- Liang, J.; Wu, X.; An, Y.; Chen, W.; Wang, J. Computation and analysis of light emission in two-bubble sonoluminescence. Chin. Phys. B 2020, 29, 097801. [Google Scholar] [CrossRef]















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yasui, K. Multibubble Sonoluminescence from a Theoretical Perspective. Molecules 2021, 26, 4624. https://doi.org/10.3390/molecules26154624
Yasui K. Multibubble Sonoluminescence from a Theoretical Perspective. Molecules. 2021; 26(15):4624. https://doi.org/10.3390/molecules26154624
Chicago/Turabian StyleYasui, Kyuichi. 2021. "Multibubble Sonoluminescence from a Theoretical Perspective" Molecules 26, no. 15: 4624. https://doi.org/10.3390/molecules26154624
APA StyleYasui, K. (2021). Multibubble Sonoluminescence from a Theoretical Perspective. Molecules, 26(15), 4624. https://doi.org/10.3390/molecules26154624





