Competition of Intra- and Intermolecular Forces in Anthraquinone and Its Selected Derivatives
Abstract
:1. Introduction
2. Results and Discussion
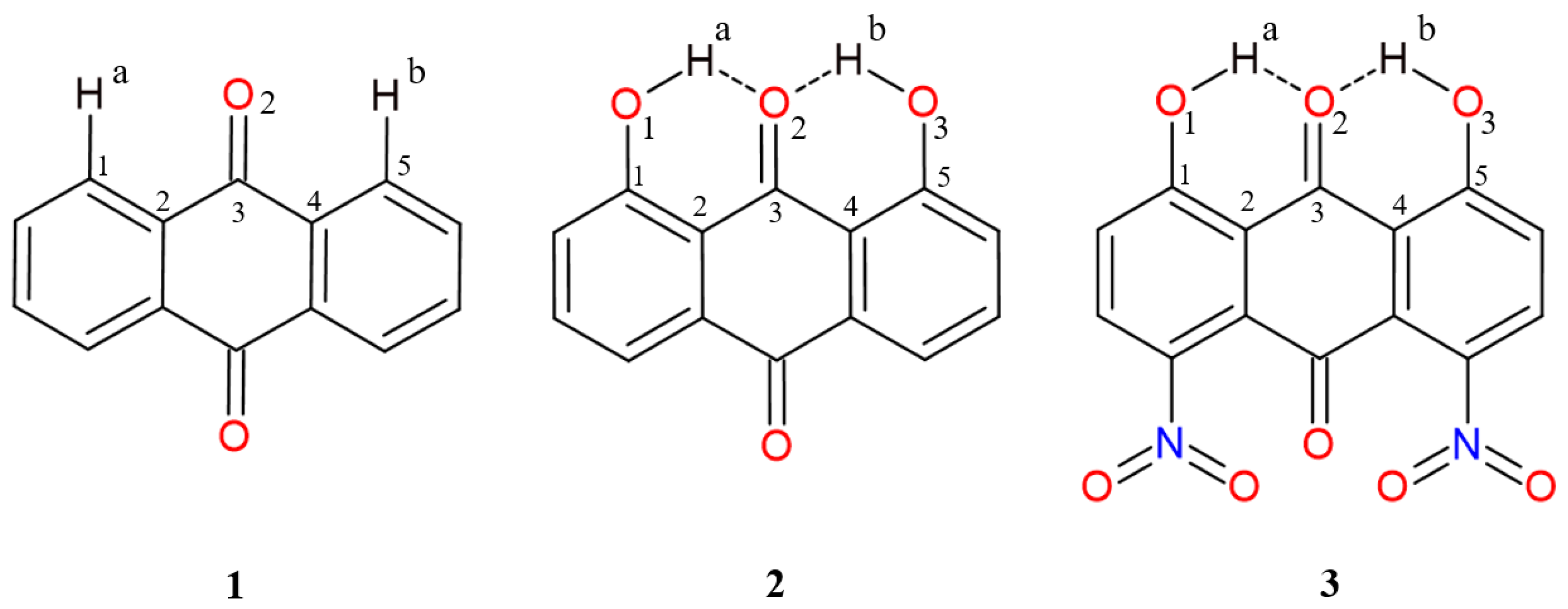
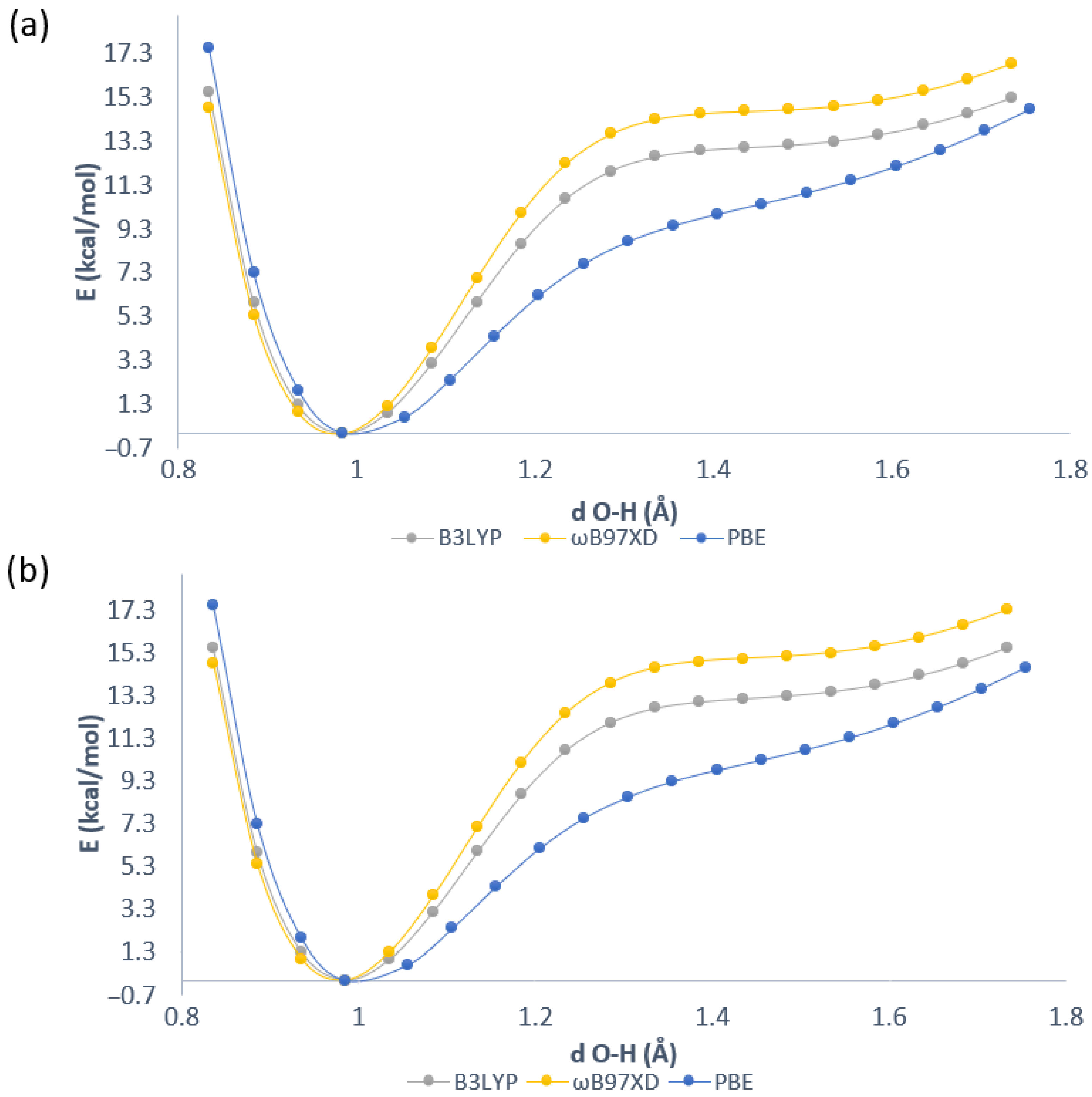
2.1. Geometric Parameters for Monomeric Forms and Proton Potential Functions
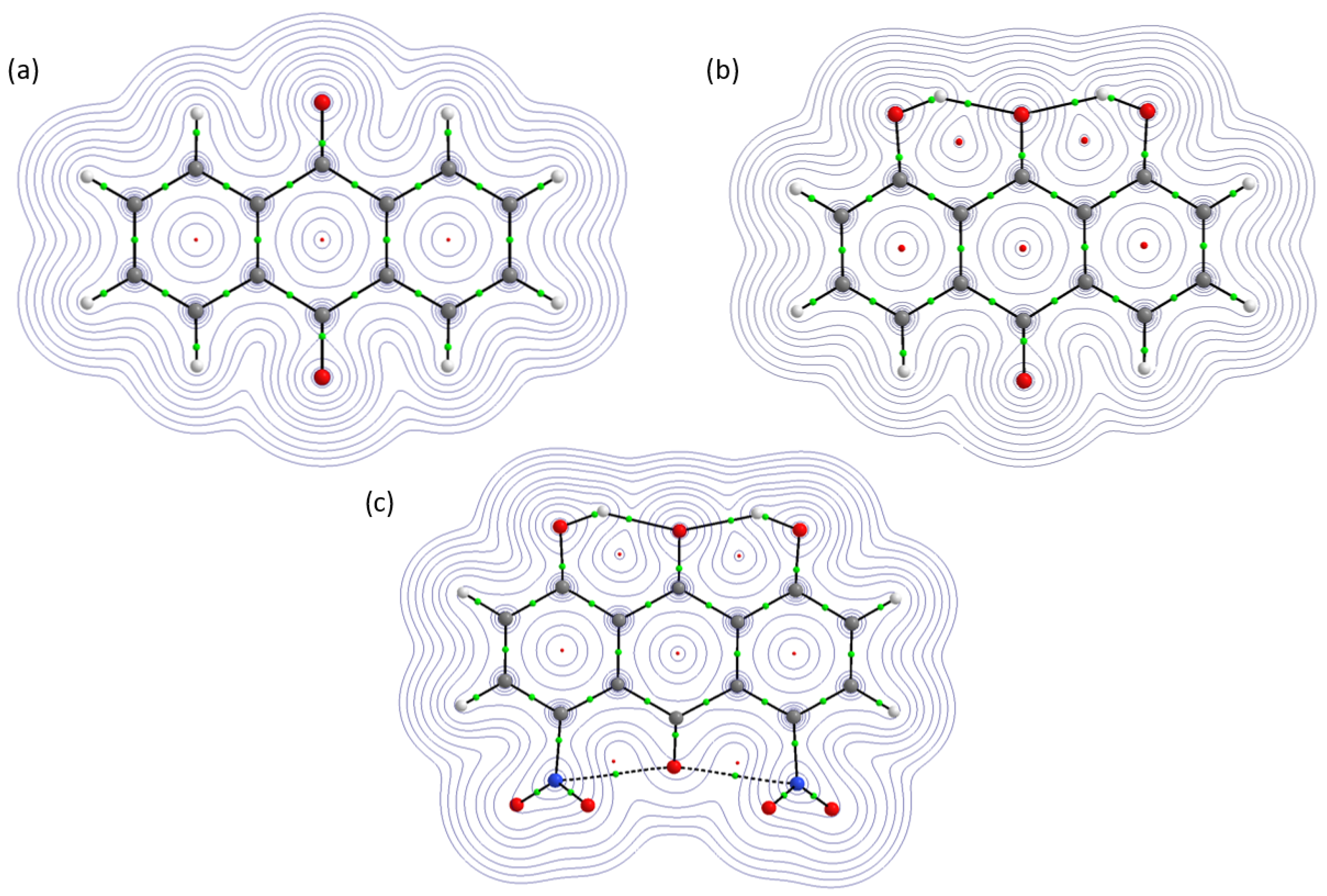
2.2. Topological Analysis of Molecular Scalar Fields—A Tool to Reveal the Pattern of Bonding
2.2.1. Atoms in Molecules (AIM)
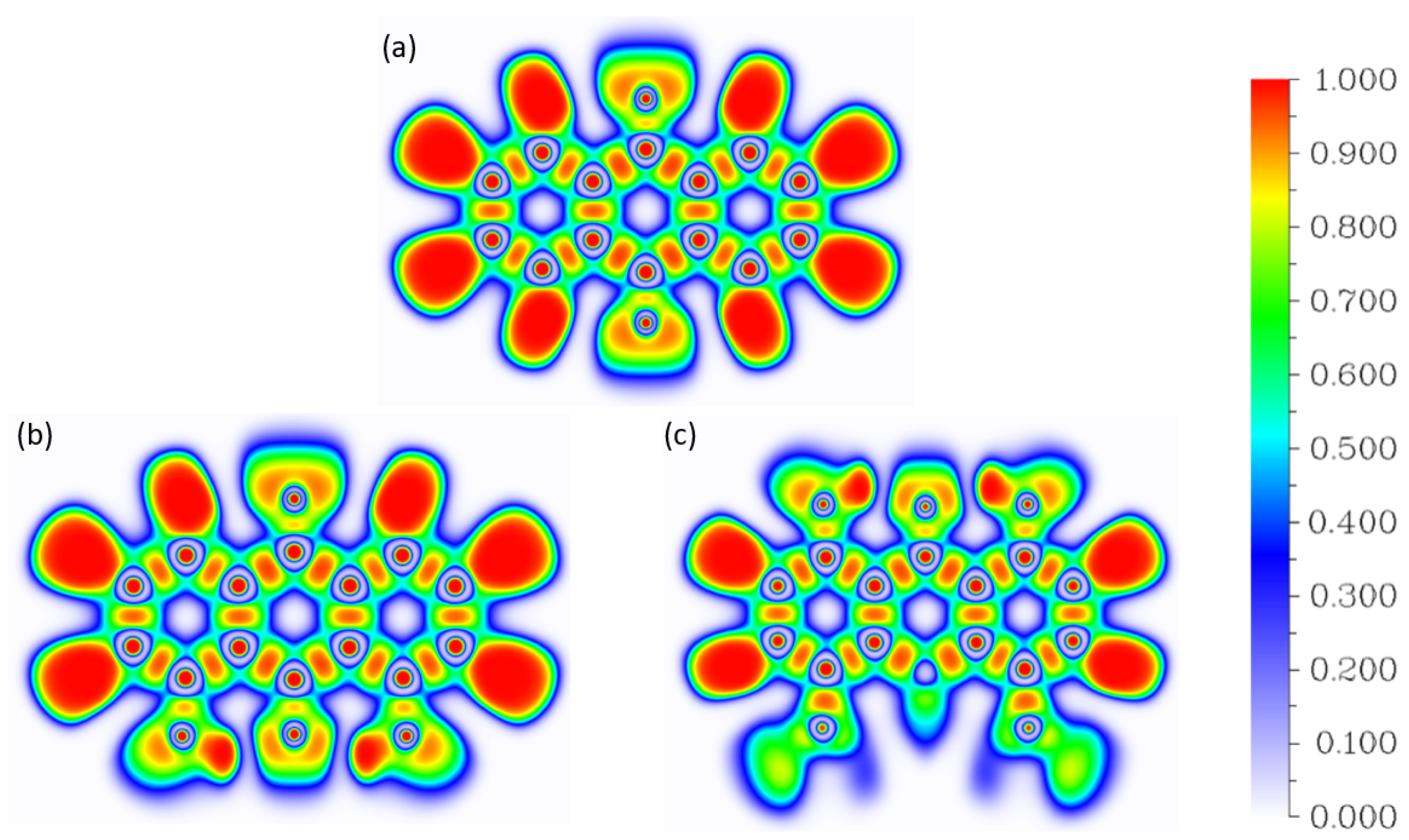
2.2.2. Electron Localization Function (ELF)
2.3. Intermolecular Forces in the Crystal Lattice: A Symmetry-Adapted Perturbation Theory Perspective
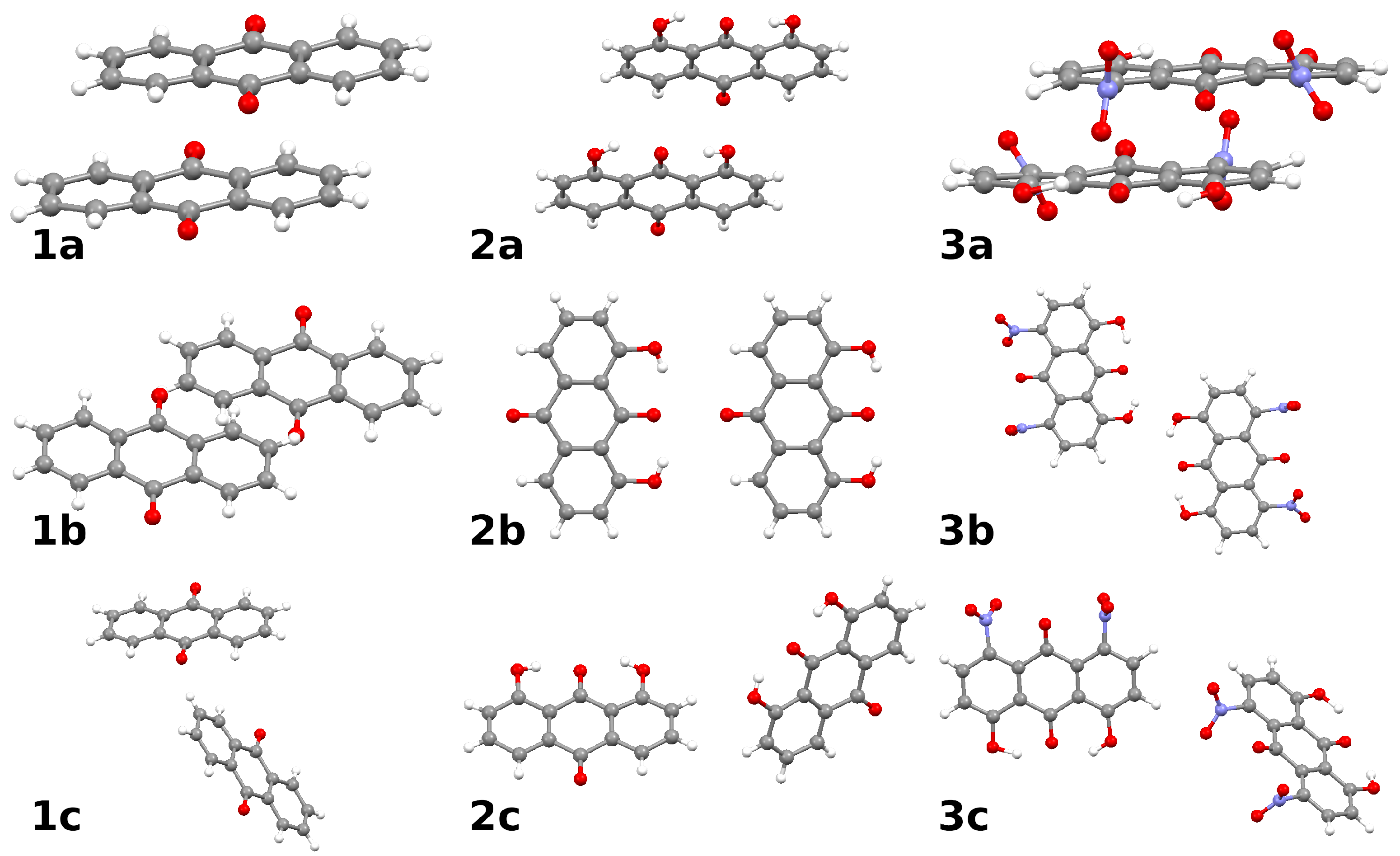
- Typical stacked structures, labeled as dimers 1a, 2a, 3a—note that, because of the substituents, the monomers in 2a and 3a are not placed directly in vertical alignment;
- Head-to-head or head-to-tail structures 1b, 2b, 3b, where 2b is head-to-tail, 3b is head-to-head, and 1b is less typical because one of the interacting molecules is raised by half of the interplanar stacking separation of 1a;
- Various forms of the C-HO interactions: in 1c the C-H bond targets the carbonyl oxygen atom, while in 2c and 3c there are lateral C-HO bonds, respectively, to the hydroxyl group or to the nitro group of the neighboring molecule.
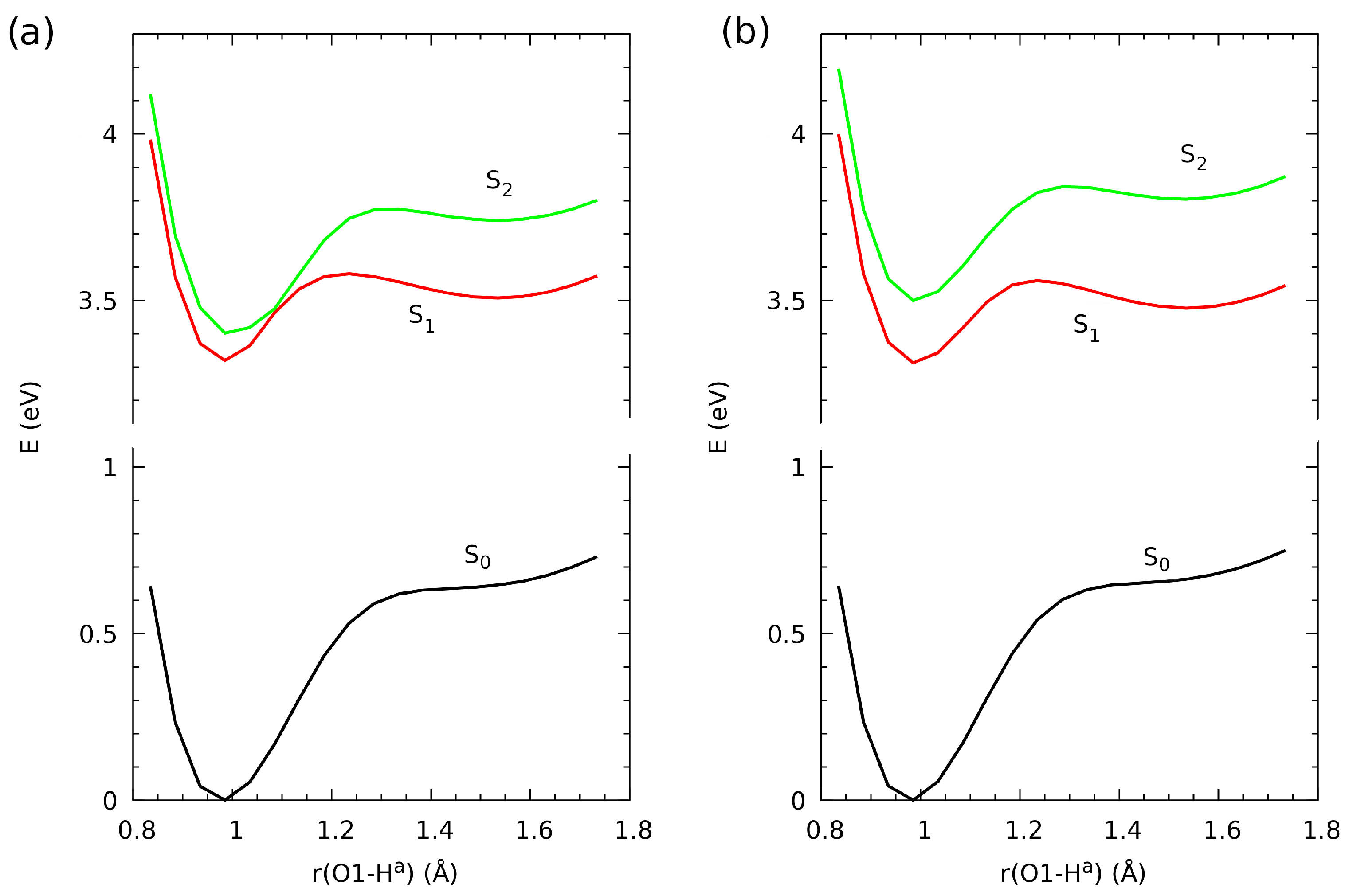
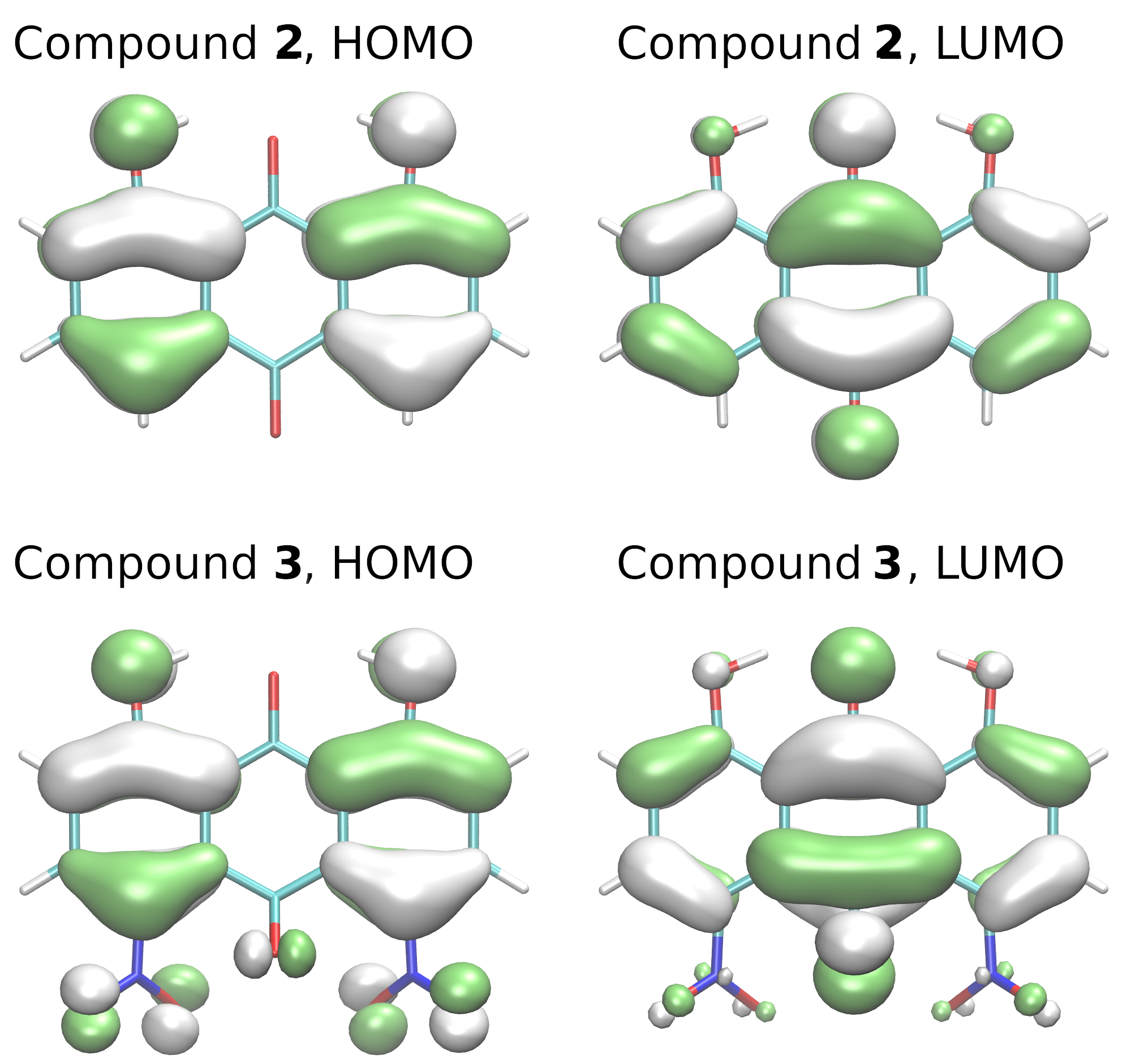
2.4. Proton Potential Functions in the Electronic Ground and Excited States
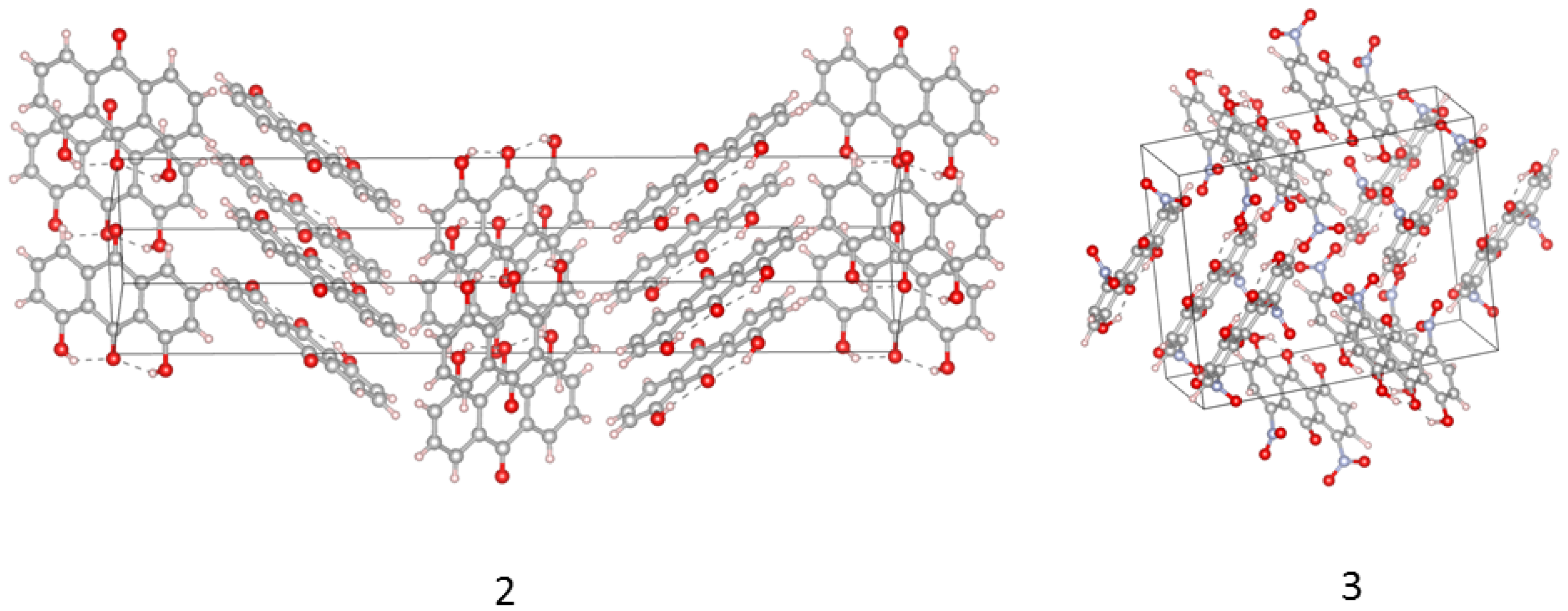
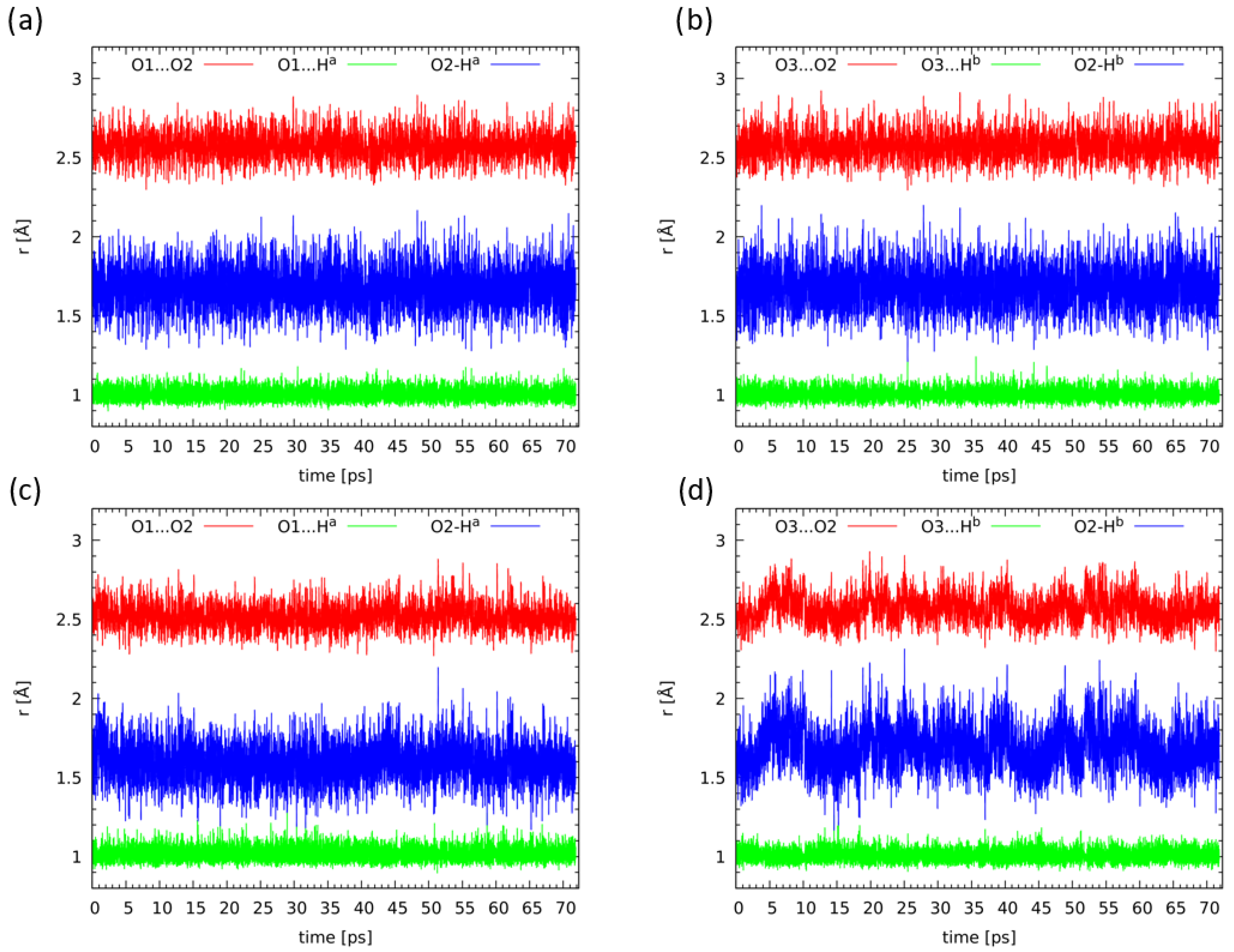
2.5. Compounds 2 and 3 in Light of the Car–Parrinello Molecular Dynamics
3. Computational Methodology
3.1. Static Electronic Ground State DFT and MP2 Models
3.2. Electronic Structure and Topological Analyses on the Basis of Atoms in Molecules (AIM) and Electron Localization Function (ELF) Theories
3.3. Symmetry-Adapted Perturbation Theory (SAPT)
3.4. Time-Dependent Density Functional Theory (TD-DFT)
3.5. Car–Parrinello Molecular Dynamics (CPMD) in the Gas Phase and Solid State
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NMR | Nuclear Magnetic Resonance spectroscopy |
| IR | Infrared spectroscopy |
| DFT | Density Functional Theory |
| MP2 | Møller–Plesset second-order perturbation theory |
| PES | Potential Energy Surface |
| AIM | Atoms in Molecules |
| ELF | Electron Localization Function |
| SAPT | Symmetry-Adapted Perturbation Theory |
| TD-DFT | Time-Dependent Density Functional Theory |
| CPMD | Car–Parrinello Molecular Dynamics |
| BCP | Bond Critical Point |
| RCP | Ring Critical Point |
| ESIPT | Excited-State Intramolecular Proton Transfer |
| HOMO | Highest Occupied Molecular Orbital |
| LUMO | Lowest Unoccupied Molecular Orbital |
| CCDC | Cambridge Crystallographic Data Centre |
| BSSE | Basis Set Superposition Error |
References
- Müller-Dethlefs, K.; Hobza, P. Noncovalent Interactions: A Challenge for Experiment and Theory. Chem. Rev. 2000, 100, 143–168. [Google Scholar] [CrossRef] [PubMed]
- Mahadevi, A.S.; Sastry, G.N. Cooperativity in Noncovalent Interactions. Chem. Rev. 2016, 116, 2775–2825. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S. New Type of Halogen Bond: Multivalent Halogen Interacting with π- and σ-Electrons. Molecules 2017, 22, 2150. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, J.; Li, Z.Z.; Wang, X.D.; Liao, L.S. Molecular-Oriented Self-Assembly of Small Organic Molecules into Uniform Microspheres. Cryst. Growth Des. 2017, 17, 4527–4532. [Google Scholar] [CrossRef]
- Scheiner, S. Understanding noncovalent bonds and their controlling forces. J. Chem. Phys. 2020, 153, 140901. [Google Scholar] [CrossRef] [PubMed]
- Lehn, J.M. Towards Complex Matter: Supramolecular Chemistry and Self-organization. Eur. Rev. 2009, 17, 263–280. [Google Scholar] [CrossRef] [Green Version]
- Mattia, E.; Otto, S. Supramolecular systems chemistry. Nat. Nanotechnol. 2015, 10, 111–119. [Google Scholar] [CrossRef] [PubMed]
- Wilson, C.J.; Bommarius, A.S.; Champion, J.A.; Chernoff, Y.O.; Lynn, D.G.; Paravastu, A.K.; Liang, C.; Hsieh, M.C.; Heemstra, J.M. Biomolecular Assemblies: Moving from Observation to Predictive Design. Chem. Rev. 2018, 118, 11519–11574. [Google Scholar] [CrossRef] [PubMed]
- Nagy, P. Competing Intramolecular vs. Intermolecular Hydrogen Bonds in Solution. Int. J. Mol. Sci. 2014, 15, 19562–19633. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ballal, D.; Chapman, W.G. Competition between Intra- and Intermolecular Association of Chain Molecules with Water-like Solvent. J. Phys. Chem. B 2015, 119, 6792–6802. [Google Scholar] [CrossRef] [PubMed]
- Sugawara, N.; Hsu, P.J.; Fujii, A.; Kuo, J.L. Competition between hydrogen bonds and van der Waals forces in intermolecular structure formation of protonated branched-chain alcohol clusters. Phys. Chem. Chem. Phys. 2018, 20, 25482–25494. [Google Scholar] [CrossRef] [PubMed]
- Macario, A.; Blanco, S.; Thomas, J.; Xu, Y.; López, J.C. Competition Between Intra- and Intermolecular Hydrogen Bonding: o-Anisic Acid···Formic Acid Heterodimer. Chem. Eur. J. 2019, 25, 12325–12331. [Google Scholar] [CrossRef] [PubMed]
- Zierkiewicz, W.; Michalczyk, M.; Scheiner, S. Competition between Intra and Intermolecular Triel Bonds. Complexes between Naphthalene Derivatives and Neutral or Anionic Lewis Bases. Molecules 2020, 25, 635. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vogel, A. Anthraquinone. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH: Weinheim, Germany, 2000; Volume 3, pp. 503–511. [Google Scholar] [CrossRef]
- Hart, P.W.; Rudie, A.W. Anthraquinone—A review of the rise and fall of a pulping catalyst. Tappi J. 2014, 13, 23–31. [Google Scholar] [CrossRef]
- Ruan, W.; Mao, J.; Chen, Q. Redox flow batteries toward more soluble anthraquinone derivatives. Curr. Opin. Electrochem. 2021, 29, 100748. [Google Scholar] [CrossRef]
- Hunger, K. (Ed.) Industrial Dyes: Chemistry, Properties, Applications; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Diaz-Muñoz, G.; Miranda, I.L.; Sartori, S.K.; de Rezende, D.C.; Diaz, M.A. Anthraquinones: An Overview. Stud. Nat. Prod. Chem. 2018, 58, 313–338. [Google Scholar] [CrossRef]
- Bien, H.; Stawitz, J.; Wunderlich, K. Anthraquinone Dyes and Intermediates. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH: Weinheim, Germany, 2000. [Google Scholar] [CrossRef]
- Chen, Y.J.; Yang, S.C.; Tsai, C.C.; Chang, K.C.; Chuang, W.H.; Chu, W.L.; Kovalev, V.; Chung, W.S. Anthryl-1, 2, 4-oxadiazole-Substituted Calix[4]arenes as Highly Selective Fluorescent Chemodosimeters for Fe3+. Chem. Asian J. 2015, 10, 1025–1034. [Google Scholar] [CrossRef] [PubMed]
- Rohl, A.L.; Moret, M.; Kaminsky, W.; Claborn, K.; McKinnon, J.J.; Kahr, B. Hirshfeld Surfaces Identify Inadequacies in Computations of Intermolecular Interactions in Crystals: Pentamorphic 1, 8-Dihydroxyanthraquinone. Cryst. Growth Des. 2008, 8, 4517–4525. [Google Scholar] [CrossRef]
- Brown, C.J.; Colclough, M.L. 1, 8-Dinitro-4, 5-dihydroxyanthraquinone, C14H6N2O8. Acta Cryst. 1983, 39, 300–302. [Google Scholar] [CrossRef] [Green Version]
- Hansch, C.; Leo, A.; Taft, R.W. A survey of Hammett substituent constants and resonance and field parameters. Chem. Rev. 1991, 91, 165–195. [Google Scholar] [CrossRef]
- Sobczyk, L.; Grabowski, S.J.; Krygowski, T.M. Interrelation between H-Bond and Pi-Electron Delocalization. Chem. Rev. 2005, 105, 3513–3560. [Google Scholar] [CrossRef] [PubMed]
- Gilli, G.; Bellucci, F.; Ferretti, V.; Bertolasi, V. Evidence for resonance-assisted hydrogen bonding from crystal-structure correlations on the enol form of the .beta.-diketone fragment. J. Am. Chem. Soc. 1989, 111, 1023–1028. [Google Scholar] [CrossRef]
- Denisov, G.S.; Mavri, J.; Sobczyk, L. Potential Energy Shape for the Proton Motion in Hydrogen Bonds Reflected in Infraredand NMR Spectra. In Hydrogen Bonding—New Insights, 1st ed.; Challenges and Advances in Computational Chemistry and Physics, 3; Grabowski, S.J., Ed.; Springer: Dordrecht, The Netherlands, 2006; pp. 377–416. [Google Scholar]
- Filarowski, A.; Koll, A. Specificity of the intramolecular hydrogen bond. The differences in spectroscopic characteristics of the intermolecular and intramolecular H-bonds. Vib. Spectrosc. 1998, 17, 123–131. [Google Scholar] [CrossRef]
- Hansen, P.E.; Spanget-Larsen, J. NMR and IR Investigations of Strong Intramolecular Hydrogen Bonds. Molecules 2017, 22, 552. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jóźwiak, K.; Jezierska, A.; Panek, J.J.; Goremychkin, E.A.; Tolstoy, P.M.; Shenderovich, I.G.; Filarowski, A. Inter- vs. Intramolecular Hydrogen Bond Patterns and Proton Dynamics in Nitrophthalic Acid Associates. Molecules 2020, 25, 4720. [Google Scholar] [CrossRef] [PubMed]
- Szatylowicz, H.; Jezuita, A.; Siodła, T.; Varaksin, K.S.; Domanski, M.A.; Ejsmont, K.; Krygowski, T.M. Toward the Physical Interpretation of Inductive and Resonance Substituent Effects and Reexamination Based on Quantum Chemical Modeling. ACS Omega 2017, 2, 7163–7171. [Google Scholar] [CrossRef] [PubMed]
- Bader, R. Atoms in Molecules: A Quantum Theory; International Series of Monographs on Chemistry; Clarendon Press: Oxford, UK, 1994. [Google Scholar]
- Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
- Jeziorski, B.; Moszynski, R.; Szalewicz, K. Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
- Koch, U.; Popelier, P.L.A. Characterization of C-H-O Hydrogen Bonds on the Basis of the Charge Density. J. Phys. Chem. 1995, 99, 9747–9754. [Google Scholar] [CrossRef]
- Hohenstein, E.G.; Sherrill, C.D. Density fitting of intramonomer correlation effects in symmetry-adapted perturbation theory. J. Chem. Phys. 2010, 133, 014101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Melikova, S.M.; Voronin, A.P.; Panek, J.; Frolov, N.E.; Shishkina, A.V.; Rykounov, A.A.; Tretyakov, P.Y.; Vener, M.V. Interplay of π-stacking and inter-stacking interactions in two-component crystals of neutral closed-shell aromatic compounds: Periodic DFT study. RSC Adv. 2020, 10, 27899–27910. [Google Scholar] [CrossRef]
- Cozza, C.; Bonomi, M.; Pietropaolo, A. A Versatile Computational Strategy To Characterize the Free-Energy Landscape of Excited States in Oligofluorenes. J. Chem. Theory Comput. 2018, 14, 5441–5445. [Google Scholar] [CrossRef] [PubMed]
- SDBSWeb. National Institute of Advanced Industrial Science and Technology, Japan. Available online: https://sdbs.db.aist.go.jp (accessed on 7 May 2021).
- CCDC Structural Database. Available online: https://www.ccdc.cam.ac.uk/ (accessed on 7 May 2021).
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef] [Green Version]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef] [Green Version]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Ernzerhof, M.; Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982–9985. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)]. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef] [Green Version]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z = 11–18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Keith, T.A.; Gristmill, T. AIMAll (Version 19.10.12); Todd A. Keith: Overland Park, KS, USA, 2019. [Google Scholar]
- Kohout, M. DGrid, Version 5.1; Max-Plack-Institut für Chemische Physik fester Stoffe: Dresden, Germany, 2019. [Google Scholar]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Goddard, T.D.; Huang, C.C.; Meng, E.C.; Pettersen, E.F.; Couch, G.S.; Morris, J.H.; Ferrin, T.E. UCSF ChimeraX: Meeting modern challenges in visualization and analysis. Protein Sci. 2018, 27, 14–25. [Google Scholar] [CrossRef] [PubMed]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef] [Green Version]
- Papajak, E.; Zheng, J.; Xu, X.; Leverentz, H.R.; Truhlar, D.G. Perspectives on Basis Sets Beautiful: Seasonal Plantings of Diffuse Basis Functions. J. Chem. Theory Comput. 2011, 7, 3027–3034. [Google Scholar] [CrossRef] [PubMed]
- Boys, S.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Parrish, R.M.; Burns, L.A.; Smith, D.G.A.; Simmonett, A.C.; DePrince, A.E.; Hohenstein, E.G.; Bozkaya, U.; Sokolov, A.Y.; Remigio, R.D.; Richard, R.M.; et al. Psi4 1.1: An Open-Source Electronic Structure Program Emphasizing Automation, Advanced Libraries, and Interoperability. J. Chem. Theory Comput. 2017, 13, 3185–3197. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD—Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993–2006. [Google Scholar] [CrossRef] [PubMed]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef] [Green Version]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Hockney, R.W. Potential Calculation and Some Applications. Methods Comput. Phys. 1970, 9, 135–211. [Google Scholar]
- Kittel, C. Introduction To Solid State Physics, 8th ed.; Wiley and Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- CPMD 3.17.1. Copyright IBM Corp. (1990–2004) Copyright MPI für Festkoerperforschung Stuttgart (1997–2001). Available online: http://www.cpmd.org/ (accessed on 12 May 2021).
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Williams, T.; Kelley, C. Gnuplot 4.4: An Interactive Plotting Program. 2010. Available online: http://gnuplot.sourceforge.net/ (accessed on 12 May 2021).

| Atomic Charge [e] | Compound 1 | Compound 2 | Compound 3 |
|---|---|---|---|
| q | 0.1013 | 0.5989 | 0.6022 |
| qO1 | — | −1.0945 | −1.0869 |
| qC1 | −0.0264 | 0.5807 | 0.6053 |
| qC2 | −0.0369 | −0.0332 | −0.0199 |
| qC3 | 0.9535 | 0.8257 | 0.8445 |
| qO2 | −1.0854 | −1.1248 | −1.1168 |
| qC4 | −0.0369 | −0.0332 | −0.0199 |
| qC5 | −0.0264 | 0.5813 | 0.6055 |
| qO3 | — | −1.0944 | −1.0869 |
| q | 0.1012 | 0.5988 | 0.6021 |
| Compound 1 | Compound 2 | Compound 3 | ||||
|---|---|---|---|---|---|---|
| BCP | ||||||
| -C1 | 0.2818 | −0.9690 | — | — | — | — |
| O2- | — | — | 0.0478 | 0.1559 | 0.0478 | 0.1570 |
| -O1 | — | — | 0.3320 | −2.2345 | 0.3316 | −2.2386 |
| O1-C1 | — | — | 0.3051 | −0.4180 | 0.3097 | −0.4160 |
| C1-C2 | 0.3068 | −0.8498 | 0.2983 | −0.8021 | 0.2970 | −0.7960 |
| C2-C3 | 02655 | −0.6622 | 0.2794 | −0.7247 | 0.2778 | −0.7160 |
| C3-O2 | 0.4013 | −0.1270 | 0.3675 | −0.3033 | 0.3707 | −0.2923 |
| C3-C4 | 0.2655 | −0.6621 | 0.2794 | −0.7247 | 0.2778 | −0.7161 |
| C4-C5 | 0.3068 | −0.8497 | 0.2983 | −0.8021 | 0.2969 | −0.7960 |
| C5- | 0.2818 | −0.9690 | — | — | — | — |
| C5-O3 | — | — | 0.3051 | −0.4180 | 0.3097 | −0.4160 |
| O3- | — | — | 0.3320 | −2.2345 | 0.3316 | −2.2384 |
| -O2 | — | — | 0.0478 | 0.1559 | 0.0479 | 0.1570 |
| Compound | Lp(O2) | Lp(O1) | V(O1-H) |
|---|---|---|---|
| 1 | 2.63 | − | − |
| 2 | 2.74 | 4.32 | 1.77 |
| 3 | 2.74 | 4.28 | 1.78 |
| Dimer Type | Elst | Exch | Ind | Disp | SAPT0 | SAPT2 |
|---|---|---|---|---|---|---|
| 1a | −5.48 | 14.10 | −1.47 | −19.17 | −11.60 | −12.01 |
| 1b | −1.63 | 2.48 | −0.65 | −3.38 | −3.98 | −3.19 |
| 1c | −2.04 | 2.10 | −0.55 | −2.63 | −4.08 | −3.12 |
| 2a | −3.10 | 7.17 | −0.78 | −9.22 | −6.19 | −5.93 |
| 2b | −0.96 | 2.82 | −0.45 | −2.68 | −0.88 | −1.27 |
| 2c | −1.55 | 1.76 | −0.32 | −1.72 | −2.06 | −1.82 |
| 3a | −4.62 | 12.69 | −1.73 | −16.85 | −10.22 | −10.51 |
| 3b | −4.25 | 5.47 | −0.62 | −2.53 | −2.33 | −1.93 |
| 3c | −2.80 | 2.65 | −0.80 | −2.15 | −4.11 | −3.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raczyński, K.; Pihut, A.; Panek, J.J.; Jezierska, A. Competition of Intra- and Intermolecular Forces in Anthraquinone and Its Selected Derivatives. Molecules 2021, 26, 3448. https://doi.org/10.3390/molecules26113448
Raczyński K, Pihut A, Panek JJ, Jezierska A. Competition of Intra- and Intermolecular Forces in Anthraquinone and Its Selected Derivatives. Molecules. 2021; 26(11):3448. https://doi.org/10.3390/molecules26113448
Chicago/Turabian StyleRaczyński, Kamil, Andrzej Pihut, Jarosław J. Panek, and Aneta Jezierska. 2021. "Competition of Intra- and Intermolecular Forces in Anthraquinone and Its Selected Derivatives" Molecules 26, no. 11: 3448. https://doi.org/10.3390/molecules26113448
APA StyleRaczyński, K., Pihut, A., Panek, J. J., & Jezierska, A. (2021). Competition of Intra- and Intermolecular Forces in Anthraquinone and Its Selected Derivatives. Molecules, 26(11), 3448. https://doi.org/10.3390/molecules26113448






