Understanding Topological Insulators in Real Space
Abstract
1. Introduction
2. Theoretical Background
2.1. The SSH Model
2.2. Localization and Delocalization in Real Space
3. Real Space Characteristics of the SSH Model
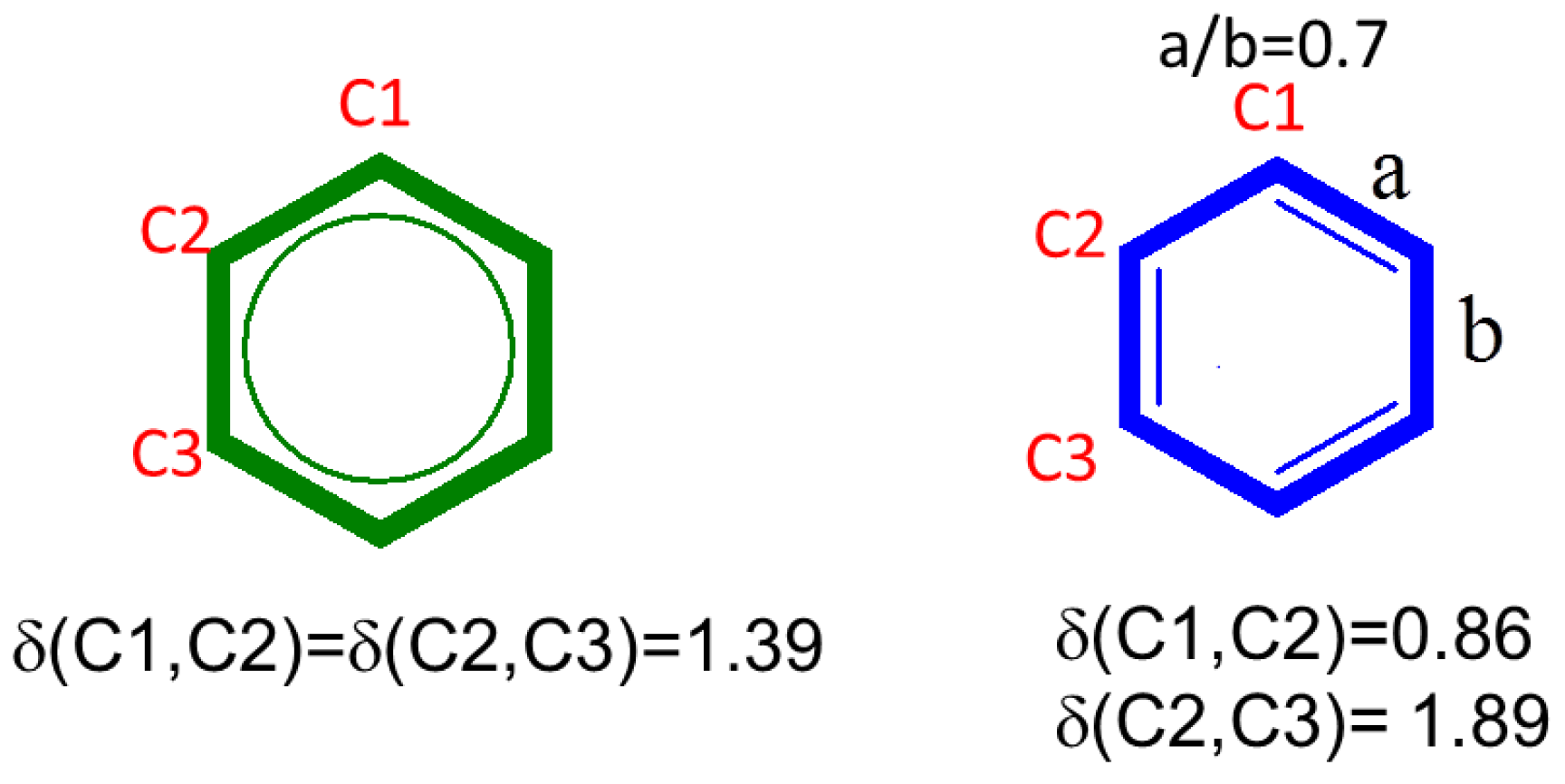
3.1. Bond Alternation and Resonance
3.2. Short vs. Long Chains: Simulating Crystalline Environments
3.3. Revealing the Breaking of Chiral Symmetry
3.3.1. The Number of Centers
3.3.2. The On-Site Energy
4. Conclusions
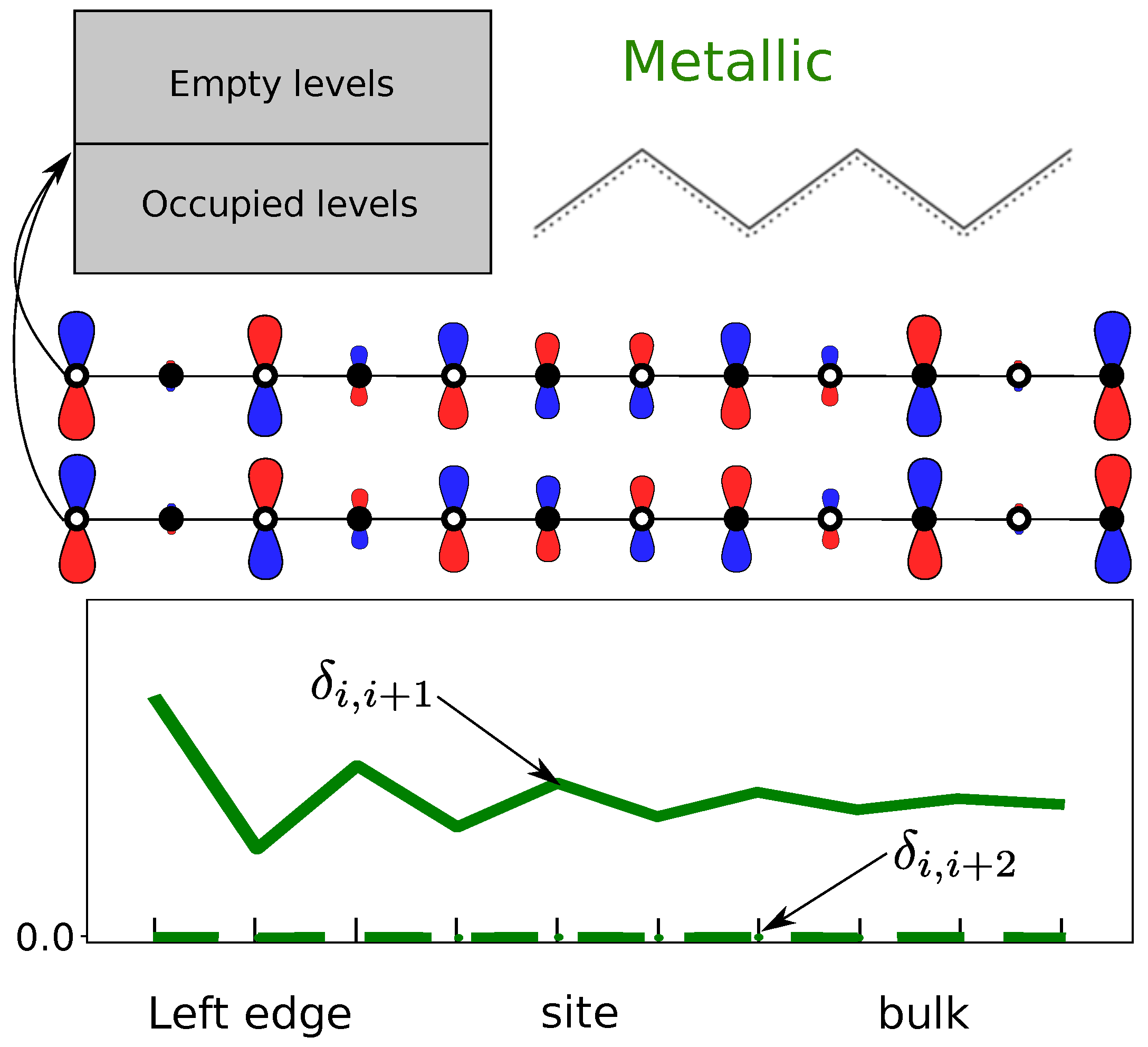
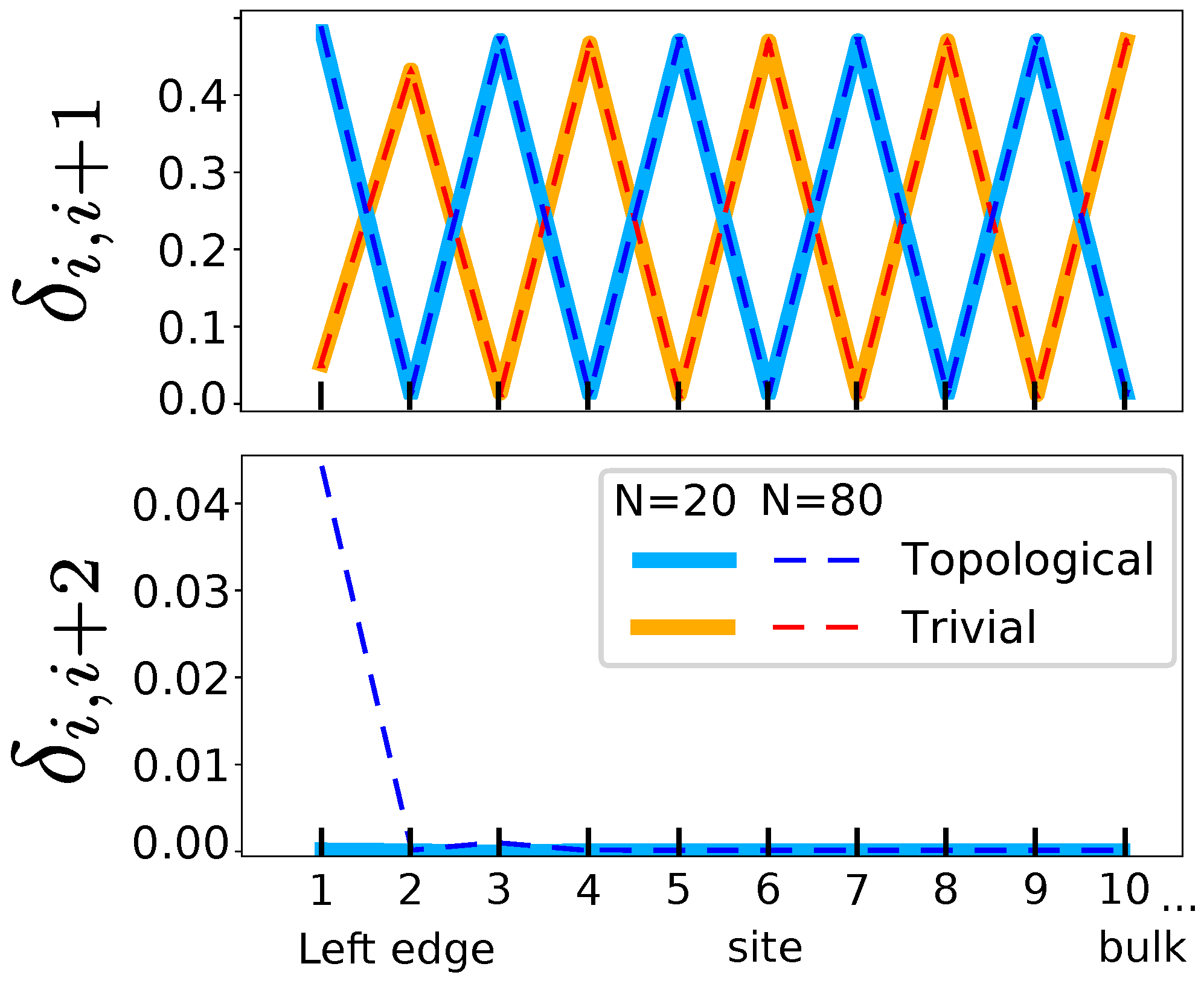
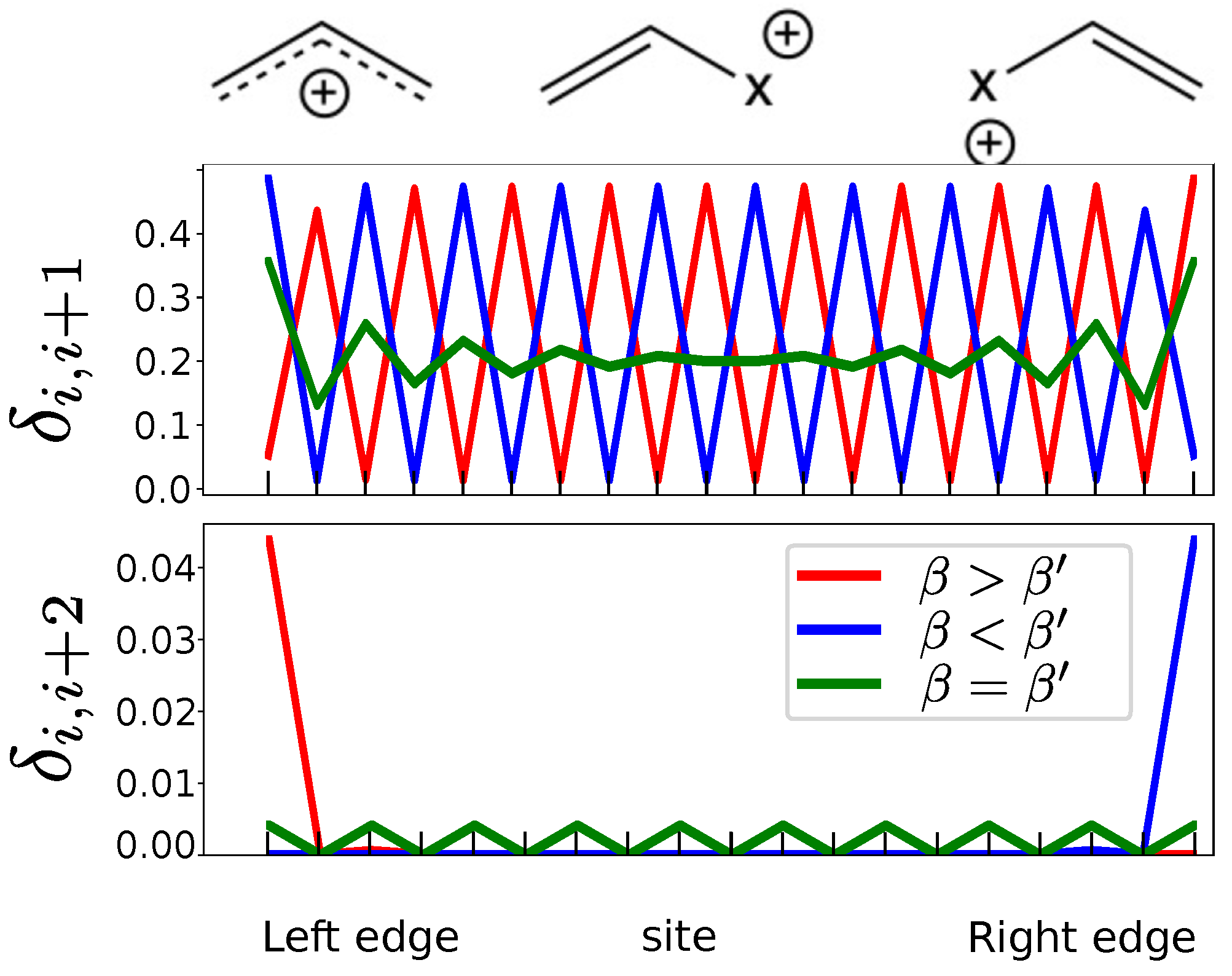
- The chiral symmetry is present if bond orders with second-neighbors, , are zero in the bulk (i.e., equivalent to the absence of delocalization in meta carbons in benzene).
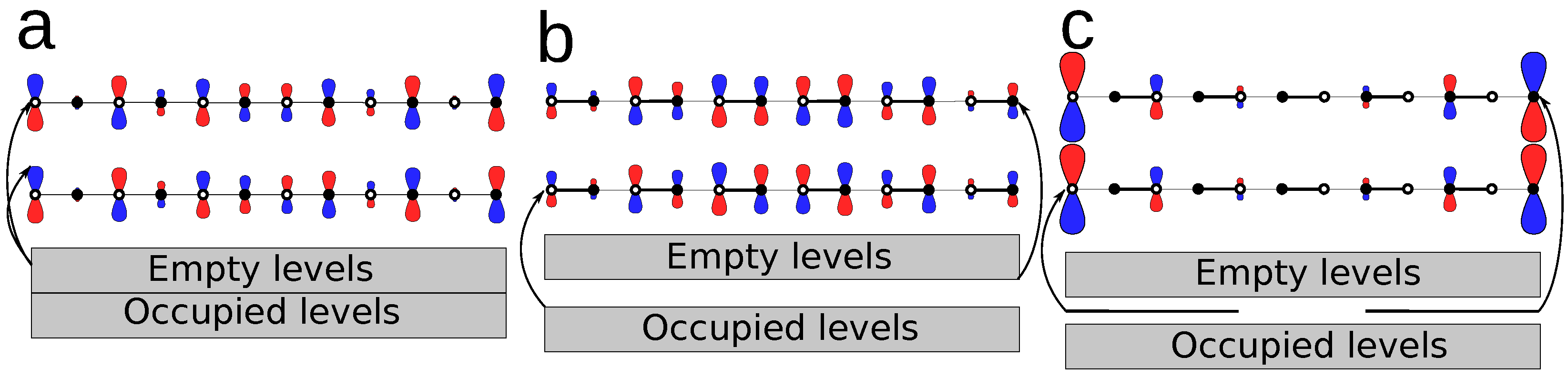
- A topological transition in the bulk can be detected by a change in the pattern of maxima and minima bond orders with first-neighbors, , which reflects the two resonance forms.
- The topological phase and its protected edge states can be detected by a non-zero second-neighbor bond order at both edges of the molecule. These bond orders decay exponentially to zero far from the edges.
- The visualization of these edge states enables the quantification of edge decoupling, i.e., of the appearance of bulk properties in linear chains.
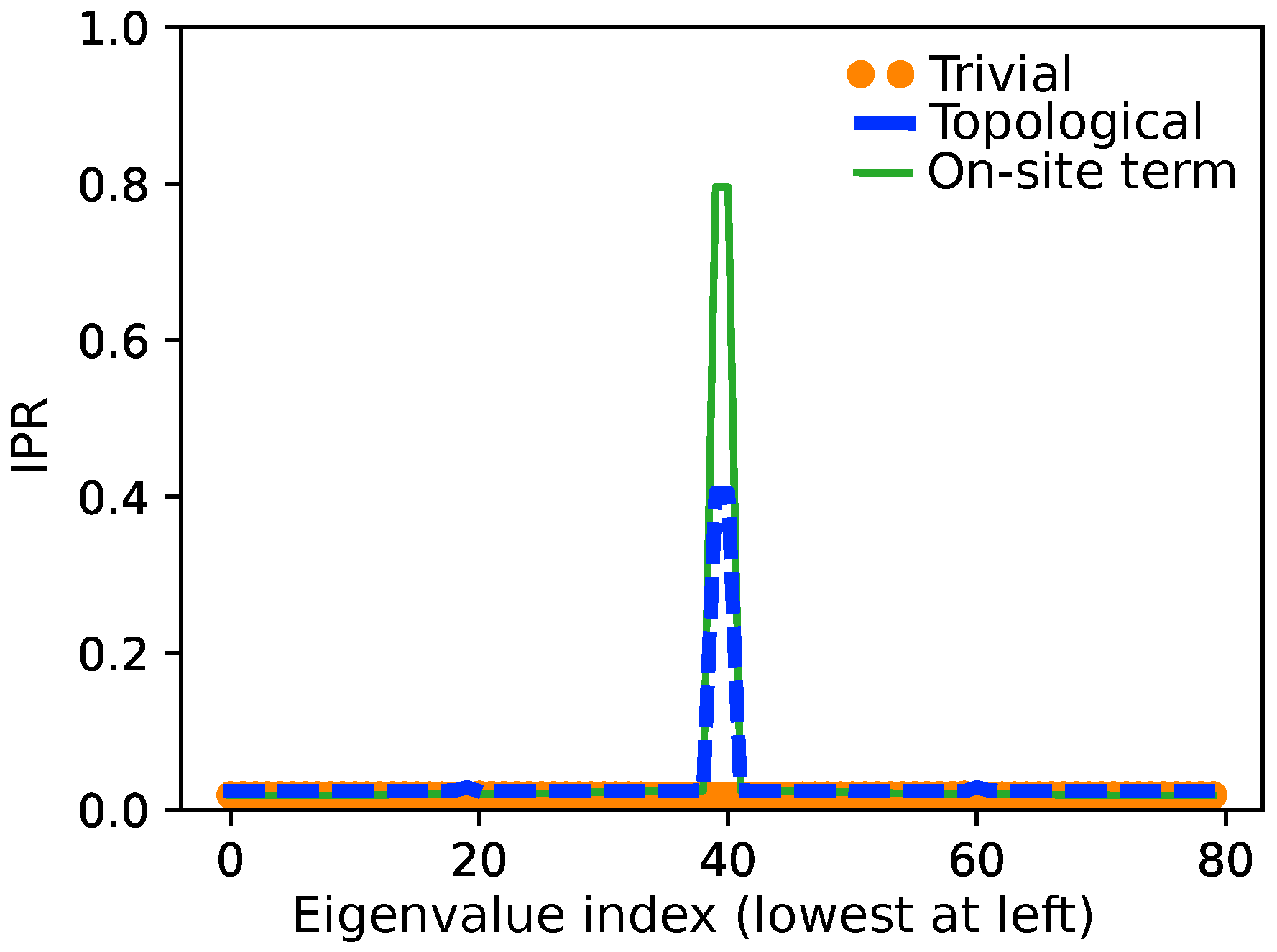
- In the case of impurities, due to the on-site .
- In the case of odd number of atoms, only one edge state appears upon changing from to , showing that both cases are equivalent, so that there is no phase transition.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Sample Availability
References
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 2006, 314, 1757–1761. [Google Scholar] [CrossRef] [PubMed]
- Bernevig, B.A.; Zhang, S.C. Quantum Spin Hall Effect. Phys. Rev. Lett. 2006, 96, 106802. [Google Scholar] [CrossRef] [PubMed]
- Kane, C.L.; Mele, E.J. Z2 Topological Order and the Quantum Spin Hall Effect. Phys. Rev. Lett. 2005, 95, 146802. [Google Scholar] [CrossRef]
- Xia, Y.; Qian, D.; Hsieh, D.; Wray, L.; Pal, A.; Lin, H.; Bansil, A.; Grauer, D.; Hor, Y.; Cava, R.; et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nat. Phys. 2009, 5, 398–402. [Google Scholar] [CrossRef]
- Chen, Y.L.; Analytis, J.G.; Chu, J.H.; Liu, Z.K.; Mo, S.K.; Qi, X.L.; Zhang, H.J.; Lu, D.H.; Dai, X.; Fang, Z.; et al. Experimental Realization of a Three-Dimensional Topological Insulator, Bi2Te3. Science 2009, 325, 178–181. [Google Scholar] [CrossRef]
- Tanaka, A.; Sasaki, T. Focus on materials science of topological insulators and superconductors. Sci. Technol. Adv. Mater. 2015, 16, 010301. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Ando, Y. Topological Insulator Materials. J. Phys. Soc. Jpn. 2013, 82, 102001. [Google Scholar] [CrossRef]
- Gupta, S.; Saxena, A. A topological twist on materials science. MRS Bull. 2014, 39, 265–279. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef]
- Xue, Q.K. Nanoelectronics: A topological twist for transistors. Nat. Nanotech. 2011, 6, 197–198. [Google Scholar] [CrossRef] [PubMed]
- Yuen-Zhou, J.; Saikin, S.K.; Yao, N.Y.; Aspuru-Guzik, A. Topologically protected excitons in porphyrin thin films. Nat. Mater. 2014, 13, 1026–1032. [Google Scholar] [CrossRef] [PubMed]
- Locane, E.; Brouwer, P.W. Current-induced switching of magnetic molecules on topological insulator surfaces. Phys. Rev. B 2017, 95, 125437. [Google Scholar] [CrossRef]
- Aguilera, E.; Jaeschke-Ubiergo, R.; Vidal-Silva, N.; Torres, L.E.F.F.; Nunez, A.S. Topological magnonics in the two-dimensional van der Waals magnet CrI3. Phys. Rev. B 2020, 102, 024409. [Google Scholar] [CrossRef]
- Hidalgo-Sacoto, R.; Gonzalez, R.I.; Vogel, E.E.; Allende, S.; Mella, J.D.; Cardenas, C.; Troncoso, R.E.; Munoz, F. Magnon valley Hall effect in CrI3-based van der Waals heterostructures. Phys. Rev. B 2020, 101, 205425. [Google Scholar] [CrossRef]
- Khanikaev, A.B.; Mousavi, S.H.; Tse, W.K.; Kargarian, M.; MacDonald, A.H.; Shvets, G. Photonic topological insulators. Nat. Mater. 2013, 12, 233–239. [Google Scholar] [CrossRef]
- Munoz, F.; Pinilla, F.; Mella, J.; Molina, M.I. Topological properties of a bipartite lattice of domain wall states. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef]
- Wang, Z.; Liu, Z.; Liu, F. Organic topological insulators in organometallic lattices. Nat. Comunn. 2013, 4, 1471. [Google Scholar] [CrossRef] [PubMed]
- Politano, A.; Chiarello, G.; Li, Z.; Fabio, V.; Wang, L.; Guo, L.; Chen, X.; Boukhvalov, D.W. Toward the effective exploitation of topological phases of matter in catalysis: Chemical reactions at the surfaces of NbAs and TaAs Weyl semimetals. Adv. Funct. Mater. 2018, 28, 1800511. [Google Scholar] [CrossRef]
- Li, G.; Felser, C. Heterogeneous catalysis at the surface of topological materials. Appl. Phys. Lett. 2020, 116, 070501. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, W.; Xiao, D.; Zhang, Z. CO oxidation facilitated by robust surface states on Au-covered topological insulators. Phys. Rev. Lett. 2011, 107, 056804. [Google Scholar] [CrossRef]
- Xiao, J.; Kou, L.; Yam, C.Y.; Frauenheim, T.; Yan, B. Toward rational design of catalysts supported on a topological insulator substrate. ACS Catal. 2015, 5, 7063–7067. [Google Scholar] [CrossRef]
- Rajamathi, C.R.; Gupta, U.; Pal, K.; Kumar, N.; Yang, H.; Sun, Y.; Shekhar, C.; Yan, B.; Parkin, S.; Waghmare, U.V.; et al. Photochemical water splitting by bismuth chalcogenide topological insulators. ChemPhysChem 2017, 18, 2322–2327. [Google Scholar] [CrossRef]
- Macedonio, F.; Politano, A.; Drioliacd, E.; Gugliuzza, A. Bi2Se3-assisted membrane crystallization. Mater. Horizons 2018, 5, 912–919. [Google Scholar] [CrossRef]
- Tang, F.; Po, H.C.; Vishwanath, A.; Wan, X. Comprehensive search for topological materials using symmetry indicators. Nature 2019, 566, 486–489. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Jiang, Y.; Song, Z.; Huang, H.; He, Y.; Fang, Z.; Weng, H.; Fang, C. Catalogue of topological electronic materials. Nature 2019, 566, 475–479. [Google Scholar] [CrossRef]
- Vergniory, M.; Elcoro, L.; Felser, C.; Regnault, N.; Bernevig, B.A.; Wang, Z. A complete catalogue of high-quality topological materials. Nature 2019, 566, 480–485. [Google Scholar] [CrossRef] [PubMed]
- Bradlyn, B.; Elcoro, L.; Cano, J.; Vergniory, M.; Wang, Z.; Felser, C.; Aroyo, M.; Bernevig, B.A. Topological quantum chemistry. Nature 2017, 547, 298–305. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Garcia-Castro, A.C.; Valencia-Jaime, I.; Mu noz, F.; Romero, A.H. Prediction and control of spin polarization in a Weyl semimetallic phase of BiSb. Phys. Rev. B 2016, 94, 161116. [Google Scholar] [CrossRef]
- Munoz, F.; Vergniory, M.; Rauch, T.; Henk, J.; Chulkov, E.V.; Mertig, I.; Botti, S.; Marques, M.A.; Romero, A. Topological crystalline insulator in a new Bi semiconducting phase. Sci. Rep. 2016, 6, 21790. [Google Scholar] [CrossRef] [PubMed]
- Otrokov, M.M.; Klimovskikh, I.I.; Bentmann, H.; Estyunin, D.; Zeugner, A.; Aliev, Z.S.; Gaß, S.; Wolter, A.; Koroleva, A.; Shikin, A.M.; et al. Prediction and observation of an antiferromagnetic topological insulator. Nature 2019, 576, 416–422. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.; Ibarra-Hernández, W.; Valencia-Jaime, I.; Avenda no-Franco, G.; Romero, A.H. Investigation of novel crystal structures of Bi–Sb binaries predicted using the minima hopping method. Phys. Chem. Chem. Phys. 2016, 18, 29771–29785. [Google Scholar] [CrossRef]
- Olsen, T.; Andersen, E.; Okugawa, T.; Torelli, D.; Deilmann, T.; Thygesen, K.S. Discovering two-dimensional topological insulators from high-throughput computations. Phys. Rev. Mater. 2019, 3, 024005. [Google Scholar] [CrossRef]
- Wan, X.; Vishwanath, A.; Savrasov, S.Y. Computational Design of Axion Insulators Based on 5 d Spinel Compounds. Phys. Rev. Lett. 2012, 108, 146601. [Google Scholar] [CrossRef]
- Marsal, Q.; Varjas, D.; Grushin, A.G. Topological Weaire–Thorpe models of amorphous matter. Proc. Natl. Acad. Sci. USA 2020, 117, 30260–30265. [Google Scholar] [CrossRef]
- Varjas, D.; Lau, A.; Pöyhönen, K.; Akhmerov, A.R.; Pikulin, D.I.; Fulga, I.C. Topological Phases without Crystalline Counterparts. Phys. Rev. Lett. 2019, 123, 196401. [Google Scholar] [CrossRef]
- Jing, Y.; Heine, T. Two-Dimensional Kagome Lattices Made of Hetero Triangulenes Are Dirac Semimetals or Single-Band Semiconductors. J. Am. Chem. Soc. 2019, 141, 743–747. [Google Scholar] [CrossRef] [PubMed]
- Springer, M.A.; Liu, T.J.; Kuc, A.; Heine, T. Topological two-dimensional polymers. Chem. Soc. Rev. 2020, 49, 2007–2019. [Google Scholar] [CrossRef]
- Galeotti, G.; De Marchi, F.; Hamzehpoor, E.; MacLean, O.; Rao, M.R.; Chen, Y.; Besteiro, L.; Dettmann, D.; Ferrari, L.; Frezza, F.; et al. Synthesis of mesoscale ordered two-dimensional π-conjugated polymers with semiconducting properties. Nat. Mater. 2020, 19, 874–880. [Google Scholar] [CrossRef]
- Cao, T.; Zhao, F.; Louie, S.G. Topological Phases in Graphene Nanoribbons: Junction States, Spin Centers, and Quantum Spin Chains. Phys. Rev. Lett. 2017, 119, 076401. [Google Scholar] [CrossRef]
- Gröning, O.; Wang, S.; Yao, X.; Pignedoli, C.A.; Barin, G.B.; Daniels, C.; Cupo, A.; Meunier, V.; Feng, X.; Narita, A.; et al. Engineering of robust topological quantum phases in graphene nanoribbons. Nature 2018, 560, 209–213. [Google Scholar] [CrossRef] [PubMed]
- Contreras-Garcia, J.; Martin-Pendas, A.; Pinilla, F.; Mella, J.D.; Cardenas, C.; Munoz, F. A Chemical Theory of Topological Insulators. Chem. Commun. 2019, 55, 12281. [Google Scholar]
- Bader, R.F. Atoms in Molecules: A Quantum Theory; Clarendon Press: Wotton-under-Edge, UK, 1990. [Google Scholar]
- Su, W.P.; Schrieffer, J.R.; Heeger, A.J. Solitons in Polyacetylene. Phys. Rev. Lett. 1979, 42, 1698–1701. [Google Scholar] [CrossRef]
- Gimarc, B.M. Molecular Structure and Bonding. The Qualitative Molecular Orbital Approach; Academic Press: New York, NY, USA, 1979. [Google Scholar]
- Mundim, K.C.; Giambiagi, M.; de Giambiagi, M.S. Multicenter bond index: Grassmann algebra and n-order density functional. J. Phys. Chem. 1994, 98, 6118–6119. [Google Scholar] [CrossRef]
- Bultinck, P.; Ponec, R.; Damme, S.V. Multicenter bond indices as a new measure of aromaticity in polycyclic aromatic hydrocarbons. J. Phys. Org. Chem. 2005, 18, 706–718. [Google Scholar] [CrossRef]
- Francisco, E.; Martín Pendás, A.; García-Revilla, M.; Álvarez Boto, R. Reduced Density Matrices: A Simpler Approach to Many-Electron Problems? Comput. Theor. Chem. 2013, 1003, 71. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Stephens, M.E. Fluctuation and correlation of electrons in molecular systems. Chem. Phys. Lett. 1974, 26, 445–449. [Google Scholar] [CrossRef]
- Pendás, Á.M.; Guevara-Vela, J.M.; Crespo, D.M.; Costales, A.; Francisco, E. An unexpected bridge between chemical bonding indicators and electrical conductivity through the localization tensor. Phys. Chem. Chem. Phys. 2017, 19, 1790–1797. [Google Scholar] [CrossRef]
- Pendás, A.M.; Blanco, M.A.; Francisco, E. Chemical fragments in real space: Definitions, properties, and energetic decompositions. J. Comput. Chem. 2006, 28, 161–184. [Google Scholar] [CrossRef]
- Kramer, B.; MacKinnon, A. Localization: Theory and experiment. Rep. Prog. Phys. 1993, 56, 1469–1564. [Google Scholar] [CrossRef]
- Gallo-Bueno, A.; Francisco, E.; Pendás, A.M. Decay rate of real space delocalization measures: A comparison between analytical and test systems. Phys. Chem. Chem. Phys. 2016, 18, 11772–11780. [Google Scholar] [CrossRef]
- Resta, R.; Sorella, S. Electron Localization in the Insulating State. Phys. Rev. Lett. 1999, 82, 370. [Google Scholar] [CrossRef]
- Gallo-Bueno, A.; Kohout, M.; Martín Pendás, A. Decay Rate of Correlated Real-Space Delocalization Measures: Insights into Chemical Bonding and Mott Transitions from Hydrogen Chains. J. Chem. Theory Comput. 2016, 12, 3053. [Google Scholar] [CrossRef]
- Lin-Liu, Y.R.; Maki, K. Two-soliton interaction energy and the soliton lattice in polyacetylene. Phys. Rev. B 1980, 22, 5754–5758. [Google Scholar] [CrossRef]
- Zhang, Y.; He, K.; Chang, C.Z.; Song, C.L.; Wang, L.L.; Chen, X.; Jia, J.F.; Fang, Z.; Dai, X.; Shan, W.Y.; et al. Crossover of the three-dimensional topological insulator Bi 2 Se 3 to the two-dimensional limit. Nat. Phys. 2010, 6, 584. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martín Pendás, A.; Muñoz, F.; Cardenas, C.; Contreras-García, J. Understanding Topological Insulators in Real Space. Molecules 2021, 26, 2965. https://doi.org/10.3390/molecules26102965
Martín Pendás A, Muñoz F, Cardenas C, Contreras-García J. Understanding Topological Insulators in Real Space. Molecules. 2021; 26(10):2965. https://doi.org/10.3390/molecules26102965
Chicago/Turabian StyleMartín Pendás, Angel, Francisco Muñoz, Carlos Cardenas, and Julia Contreras-García. 2021. "Understanding Topological Insulators in Real Space" Molecules 26, no. 10: 2965. https://doi.org/10.3390/molecules26102965
APA StyleMartín Pendás, A., Muñoz, F., Cardenas, C., & Contreras-García, J. (2021). Understanding Topological Insulators in Real Space. Molecules, 26(10), 2965. https://doi.org/10.3390/molecules26102965






