Intrinsic Dynamic and Static Nature of Halogen Bonding in Neutral Polybromine Clusters, with the Structural Feature Elucidated by QTAIM Dual-Functional Analysis and MO Calculations
Abstract
1. Introduction
2. Methodological Details in Calculations
3. Results and Discussion
3.1. Structural Optimizations of Polybromine Clusters, Br6–Br12
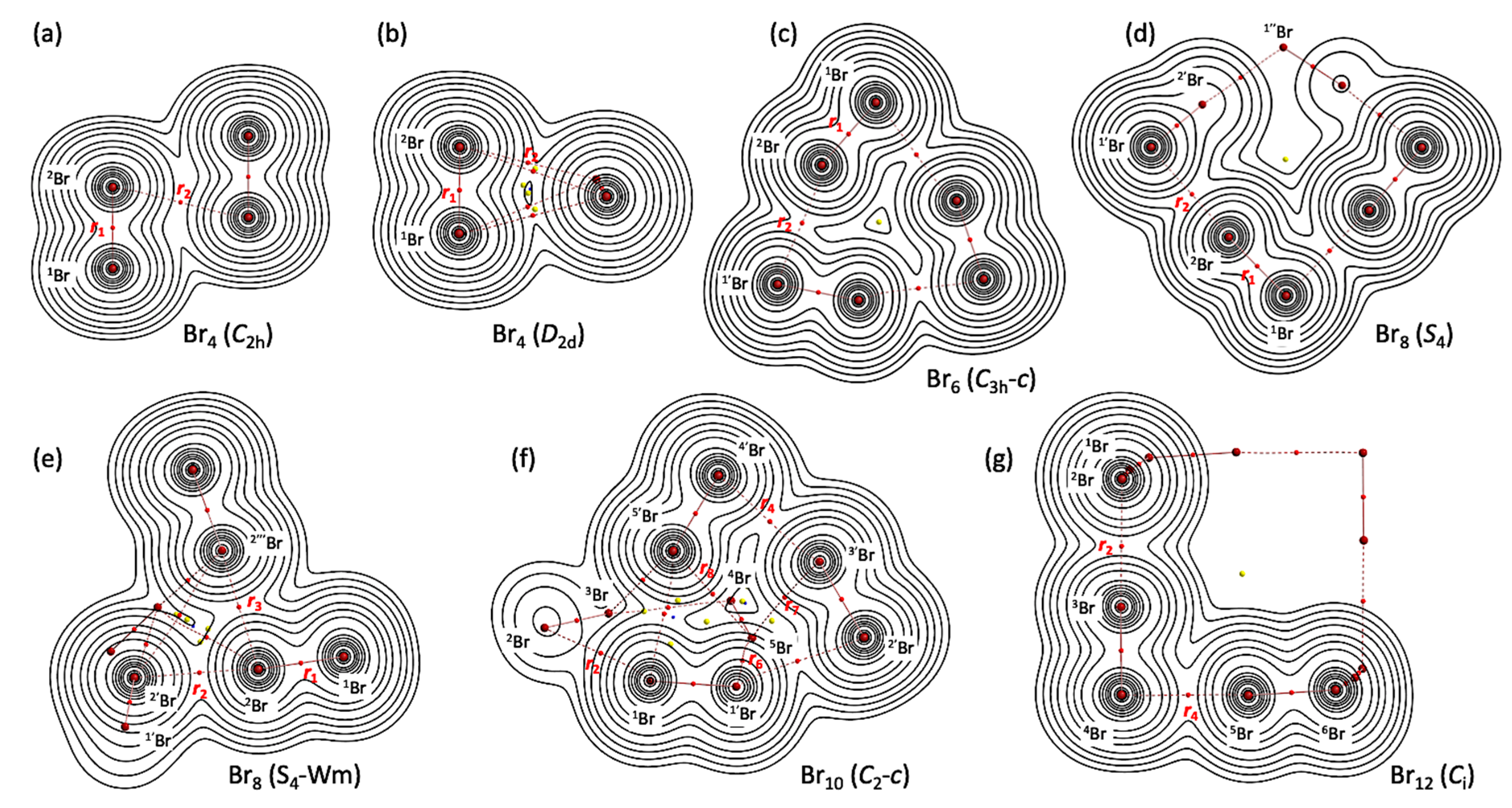
3.2. Molecular Graphs with Contour Plots of Polybromine Clusters
3.3. Survey of the Br-∗-Br Interactions in Polybromine Clusters
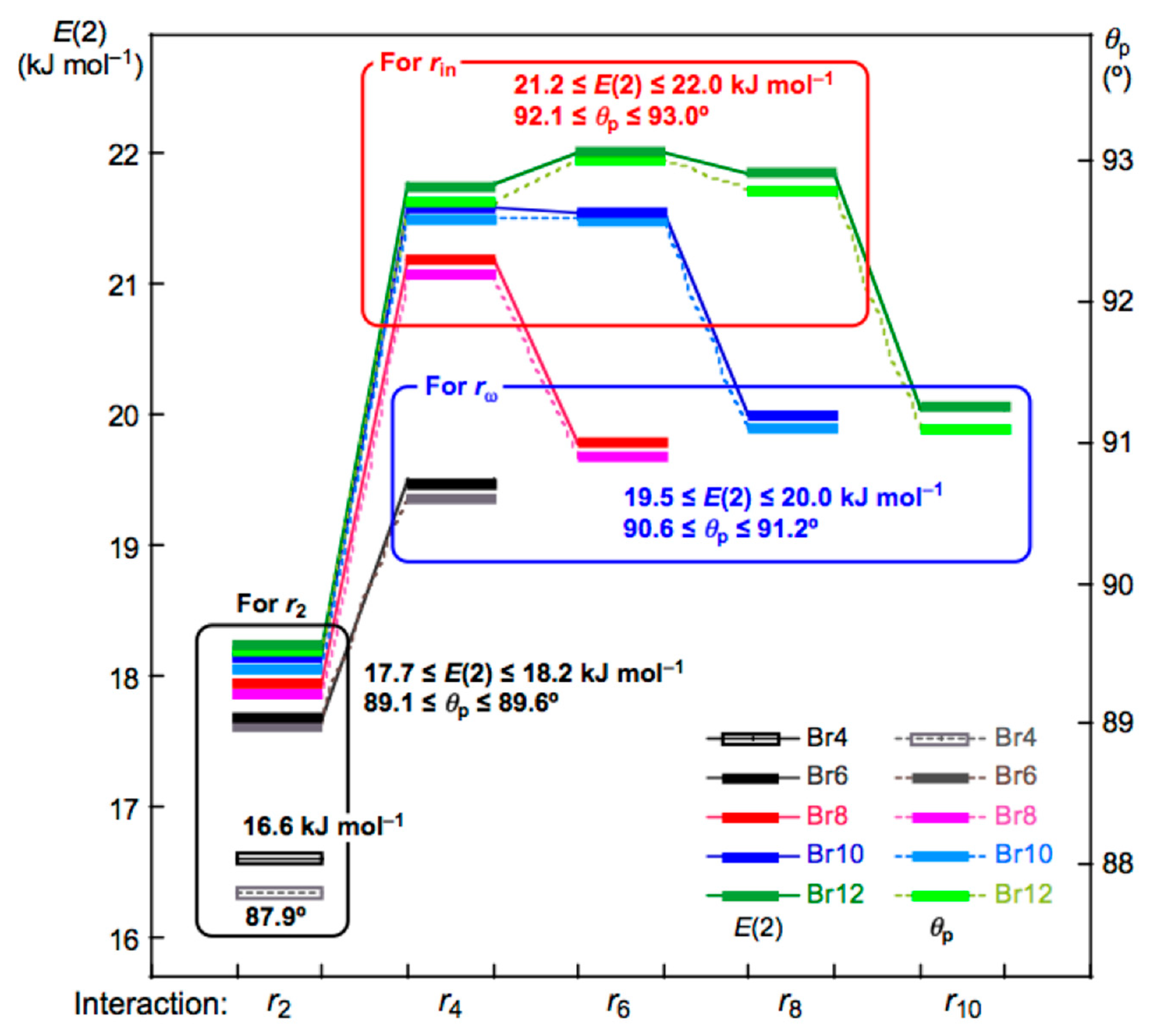
3.4. The Nature of Br-∗-Br Interactions in Polybromine Clusters
3.5. NBO Analysis for Br-∗-Br of Br4 (Cs-L1)–Br12 (Cs-L5)
3.6. MO Descriptions for Noncovalent Br-∗-Br Interactions in Br4
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References and Notes
- Colin, J.J. Sur Quelques Combinaisons de l’Iode. Ann. Chim. 1814, 91, 252–272. [Google Scholar]
- Cavallo, G.; Metrangolo, P.; Pilati, T.; Resnati, G.; Terraneo, G. Halogen Bond: A Long Overlooked Interaction. In Halogen Bonding I: Impact on Materials Chemistry and Life Sciences (Topics in Current Chemistry); Metrangolo, P., Resnati, G., Eds.; Springer: New York, NY, USA, 2015; Chapter 1; pp. 1–18. [Google Scholar]
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef]
- Bent, H.A. Structural chemistry of donor-acceptor interactions. Chem. Rev. 1968, 68, 587–648. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Parthasarathy, R. The nature of halogen halogen interactions: Are short halogen contacts due to specific attractive forces or due to close packing of nonspherical atoms? J. Am. Chem. Soc. 1989, 111, 8725–8726. [Google Scholar] [CrossRef]
- Metrangolo, P.; Resnati, G. Halogen Bonding: A Paradigm in Supramolecular Chemistry. Chem. Eur. J. 2001, 7, 2511–2519. [Google Scholar] [CrossRef]
- Erdélyi, M. Halogen bonding in solution. Chem. Soc. Rev. 2012, 41, 3547–3557. [Google Scholar] [CrossRef]
- Beale, T.M.; Chudzinski, M.G.; Sarwar, M.G.; Taylor, M.S. Halogen bonding in solution: Thermodynamics and applications. Chem. Soc. Rev. 2013, 42, 1667–1680. [Google Scholar] [CrossRef] [PubMed]
- Legon, A.C. Prereactive Complexes of Dihalogens XY with Lewis Bases B in the Gas Phase: A Systematic Case for the Halogen Analogue B⋅⋅⋅XY of the Hydrogen Bond B HX. Angew. Chem. Int. Ed. 1999, 38, 2686–2714. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other σ-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef]
- Sugibayashi, Y.; Hayashi, S.; Nakanishi, W. Behavior of Halogen Bonds of the Y–X···Type (X, Y=F, Cl, Br, I) in the Benzene p System, Elucidated by Using a Quantum Theory of Atoms in Molecules Dual-Functional Analysis. Chem. Phys. Chem. 2016, 17, 2579–2589. [Google Scholar] [CrossRef] [PubMed]
- Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
- Metrangolo, P.; Resnati, G. (Eds.) Halogen Bonding: Fundamentals and Applications; Series Structure and Bonding; Springer: New York, NY, USA, 2008. [Google Scholar]
- Gierszal, K.P.; Davis, J.G.; Hands, M.D.; Wilcox, D.S.; Slipchenko, L.V.; Ben-Amotz, D. π-Hydrogen Bonding in Liquid Water. J. Phys. Chem. Lett. 2011, 2, 2930–2933. [Google Scholar] [CrossRef]
- Categorizing Halogen Bonding and other Noncovalent Interactions Involving Halogen Atoms. a satellite event of the XXII Congress and General Assembly of the International Union of Crystallography, 2010; https://doi.org/10.1515/ci.2010.32.2.20 (accessed on 1 May 2021).
- Donohue, J.; Goodman, S.H. Interatomic distances in solid chlorine. Acta Cryst. 1965, 18, 568–569. [Google Scholar] [CrossRef]
- Powell, B.M.; Heal, K.M.; Torrie, B.H. The temperature dependence of the crystal structures of the solid halogens, bromine and chlorine. Mol. Phys. 1984, 53, 929. [Google Scholar] [CrossRef]
- Van Bolhuis, F.; Koster, P.B.; Migchelsen, T. Refinement of the crystal structure of iodine at 110° K. Acta Cryst. 1967, 23, 90–91. [Google Scholar] [CrossRef]
- Schuster, P.; Mikosch, H.; Bauer, G. All electron density functional study of neutral and ionic polybromine clusters. J. Chem. Phys. 1998, 109, 1833–1844. [Google Scholar] [CrossRef]
- Sung, D.; Park, N.; Park, W.; Hong, S. Formation of polybromine anions and concurrent heavy hole doping in carbon nanotubes. Appl. Phys. Lett. 2007, 90, 093502. [Google Scholar] [CrossRef]
- Nakanishi, W.; Hayashi, S.; Narahara, K. Polar Coordinate Representation of Hb(rc) versus (ћ2/8m)∇2ρb(rc) at BCP in AIM Analysis: Classification and Evaluation of Weak to Strong Interactions. J. Phys. Chem. A 2009, 113, 10050–10057. [Google Scholar] [CrossRef]
- Nakanishi, W.; Hayashi, S. Atoms-in-Molecules Dual Functional Analysis of Weak to Strong Interactions. Curr. Org. Chem. 2010, 14, 181–197. [Google Scholar] [CrossRef]
- Nakanishi, W.; Hayashi, S. Dynamic Behaviors of Interactions: Application of Normal Coordinates of Internal Vibrations to AIM Dual Functional Analysis. J. Phys. Chem. A 2010, 114, 7423–7430. [Google Scholar] [CrossRef]
- Nakanishi, W.; Hayashi, S.; Matsuiwa, K.; Kitamoto, M. Applications of Normal Coordinates of Internal Vibrations to Generate Perturbed Structures: Dynamic Behavior of Weak to Strong Interactions Elucidated by Atoms-in-Molecules Dual Functional Analysis. Bull. Chem. Soc. Jpn. 2012, 85, 1293–1305. [Google Scholar] [CrossRef]
- Nakanishi, W.; Hayashi, S. Role of dG/dw and dV/dw in AIM Analysis: An Approach to the Nature of Weak to Strong Interactions. J. Phys. Chem. A 2013, 117, 1795–1803. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W. Atoms in Molecules. A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Matta, C.F.; Boyd, R.J. An Introduction to the Quantum Theory of Atoms in Molecules. In The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design; WILEY-VCH: Weinheim, Germany, 2007. [Google Scholar]
- Nakanishi, W.; Hayashi, S.; Nishide, T. Intrinsic dynamic and static nature of each HB in the multi-HBs between nucleobase pairs and its behavior, elucidated with QTAIM dual functional analysis and QC calculations. RSC Adv. 2020, 10, 24730–24742. [Google Scholar] [CrossRef]
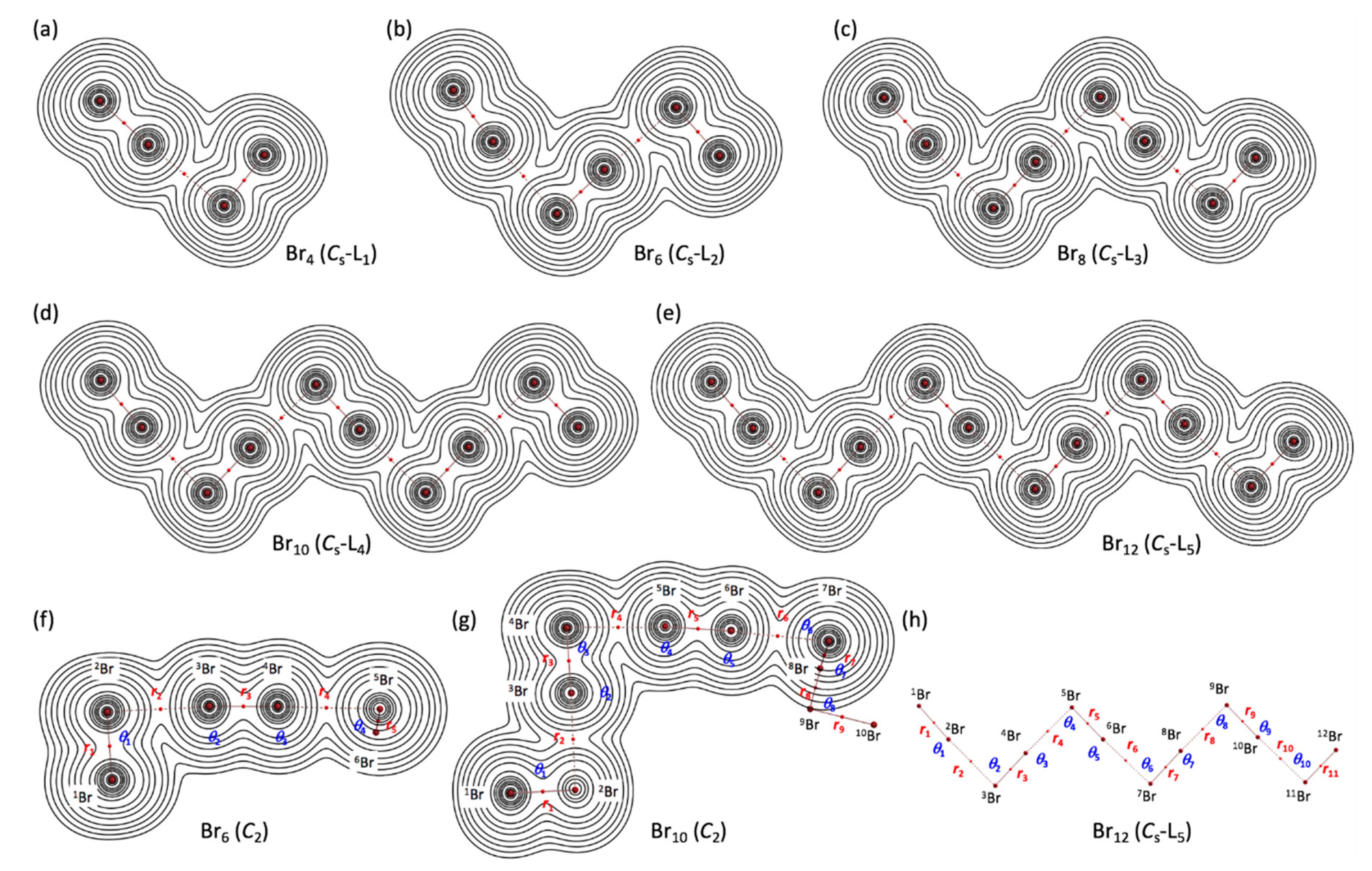
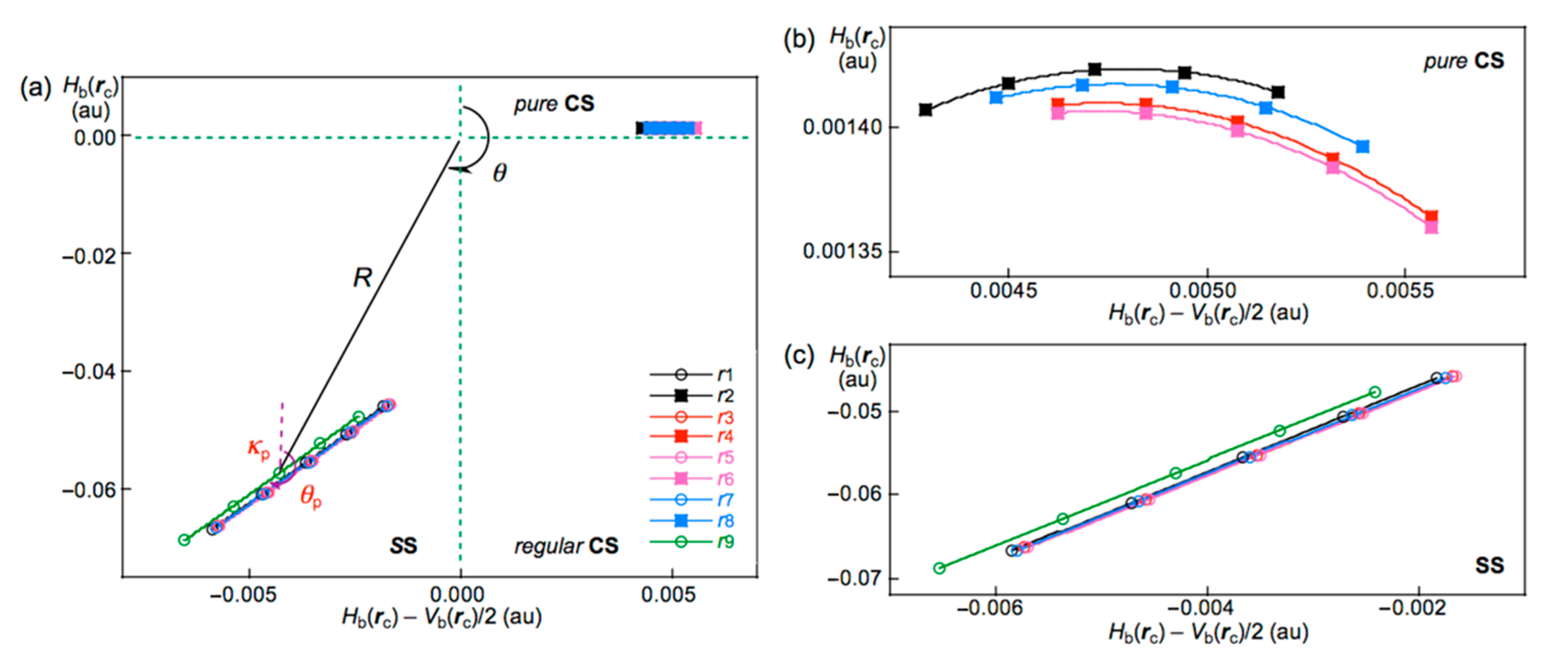
- See also Figure 5 for the definition of (R, θ) and (θp, κp), exemplified by the r9 in Br10 (Cs-L5).
- Nakanishi, W.; Hayashi, S. Perturbed structures generated using coordinates derived from compliance constants in internal vibrations for QTAIM dual functional analysis: Intrinsic dynamic nature of interactions. Int. J. Quantum Chem. 2018, 118, e25590–e25591. [Google Scholar] [CrossRef]
- The basic concept for the compliance constants was introduced by Taylor and Pitzer, followed by Konkoli and Cremer.
- Taylor, W.T.; Pitzer, K.S. Vibrational frequencies of semirigid molecules: A general method and values for ethylbenzene. J. Res. Natl. Bur. Stand. 1947, 38, 1–17. [Google Scholar] [CrossRef]
- Konkoli, Z.; Cremer, D. A new way of analyzing vibrational spectra. I. Derivation of adiabatic internal modes. Int. J. Quantum Chem. 1998, 67, 1–9. [Google Scholar] [CrossRef]
- The Cij are defined as the partial second derivatives of the potential energy due to an external force, as shown in Equations (R1), where i and j refer to internal coordinates, and the external force components acting on the system fi and fj correspond to i and j, respectively.
- Cij = ∂2E/∂fi∂fj (R1).
- The Cij Values and the Coordinates Corresponding to Cii Were Calculated by Using the Compliance 3.0.2 Program Released by Grunenberg, J. and Brandhorst, K. Available online: http://www.oc.tu-bs.de/Grunenberg/compliance.html (accessed on 1 May 2021).
- Brandhorst, K.; Grunenberg, J. Efficient computation of compliance matrices in redundant internal coordinates from Cartesian Hessians for nonstationary points. J. Chem. Phys. 2010, 132, 184101. [Google Scholar] [CrossRef]
- Brandhorst, K.; Grunenberg, J. How strong is it? The interpretation of force and compliance constants as bond strength descriptors. Chem. Soc. Rev. 2008, 37, 1558–1567. [Google Scholar] [CrossRef] [PubMed]
- Grunenberg, J. III-defined concepts in chemistry: Rigid force constants vs. compliance constants as bond strength descriptors for the triple bond in diboryne. Chem. Sci. 2015, 6, 4086–4088. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 (Revision D.01), Gaussian, Inc.: Wallingford, CT, USA, 2009.
- Binning, R.C.; Curtiss, L.A. Compact contracted basis sets for third-row atoms: Ga–Kr. J. Comput. Chem. 1990, 11, 1206–1216. [Google Scholar] [CrossRef]
- Curtiss, L.A.; McGrath, M.P.; Blaudeau, J.-P.; Davis, N.E.; Binning, R.C., Jr.; Radom, L. Extension of Gaussian-2 theory to molecules containing third-row atoms Ga–Kr. J. Chem. Phys. 1995, 103, 6104–6113. [Google Scholar] [CrossRef]
- McGrath, M.P.; Radom, L. Extension of Gaussian-1 (G1) theory to bromine-containing molecules. J. Chem. Phys. 1991, 94, 511–516. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J.; Spitznagel, G.W.; Schleyer, P.v.R. Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first-row elements, Li–F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Gauss, J. Effects of electron correlation in the calculation of nuclear magnetic resonance chemical shifts. J. Chem. Phys. 1993, 99, 3629–3643. [Google Scholar] [CrossRef]
- Gauss, J. Accurate Calculation of NMR Chemical Shifts. Ber. Bunsen-Ges. Phys. Chem. 1995, 99, 1001–1008. [Google Scholar] [CrossRef]
- Biegler-König, F.; Schönbohm, J. The AIM2000 Program (Version 2.0). Available online: http://www.aim2000.de (accessed on 1 May 2021).
- Biegler-König, F. Calculation of atomic integration data. J. Comput. Chem. 2000, 21, 1040–1048. [Google Scholar] [CrossRef]
- Keith, T.A. AIMAll (Version 17.11.14), TK Gristmill Software, Overland Park KS, USA. 2017. Available online: http://aim.tkgristmill.com (accessed on 1 May 2021).
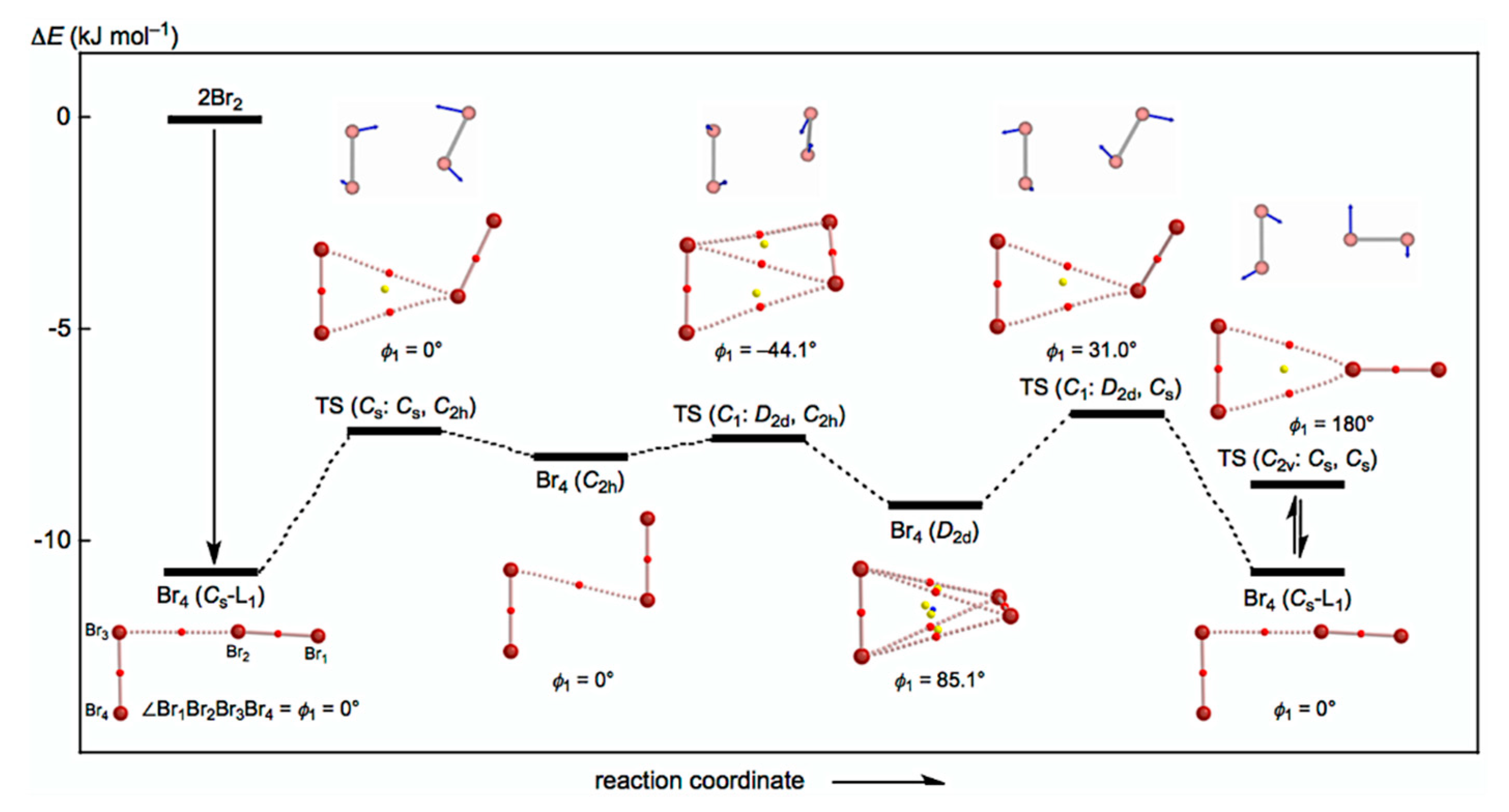
- See Figure 3 for Br4–Br12 of the L-shaped clusters in the Cs symmetry, Br4 (Cs-L1)–Br12 (Cs-L5), and Figure 4 for Br6–Br12 of the cyclic bromine clusters.
- See also Entry 1 in Table 3. http://aim.tkgristmill.com/ (accessed on 1 May 2021).
- The Br–Br distance in Br2 was optimized to be 2.2806 Å with MP2/6-311+G(3df), which was very close to the observed distance in the gas phase (2.287 Å). However, the values are shorter than that determined by the X-ray crystallographic analysis (2.491 Å) by 0.210 Å. The non-covalent Br---Br distance is 3.251 Å in crystal, which is shorter than the sum of the van der Waals radii by 0.45 Å.
- Bondi, A. van der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
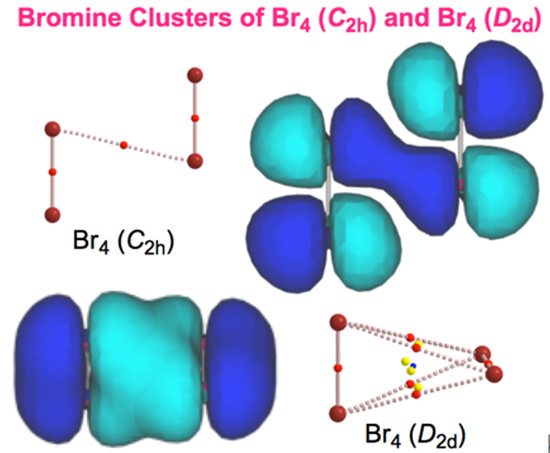
- The molecular graph for Br4 (C2h) was very complex and very different from that expected for it when calculated with MP2/6-311+G(3df)//MP2/6-311+G(3df). Some (ω,σ) = (3, −3) attractors appear in the molecular graph of Br4 (C2h), which do not correspond to bromine atoms. Therefore, the molecular graph for Br4 (C2h) were drawn with MP2/6-311+G(d)//MP2/6-311+G(3df), which was shown in Figure 2. The ρb(rc), Hb(rc) − Vb(rc)/2 (=(ћ2/8m)∇2ρb(rc)), and Hb(rc) values were calculated with the same method.
- Glendening, E.D.; Reed, A.E.; Carpenter, J.E.; Weinhold, F. NBO, Gaussian, Inc.: Pittsburgh, PA, USA, 2003; version 3.1.
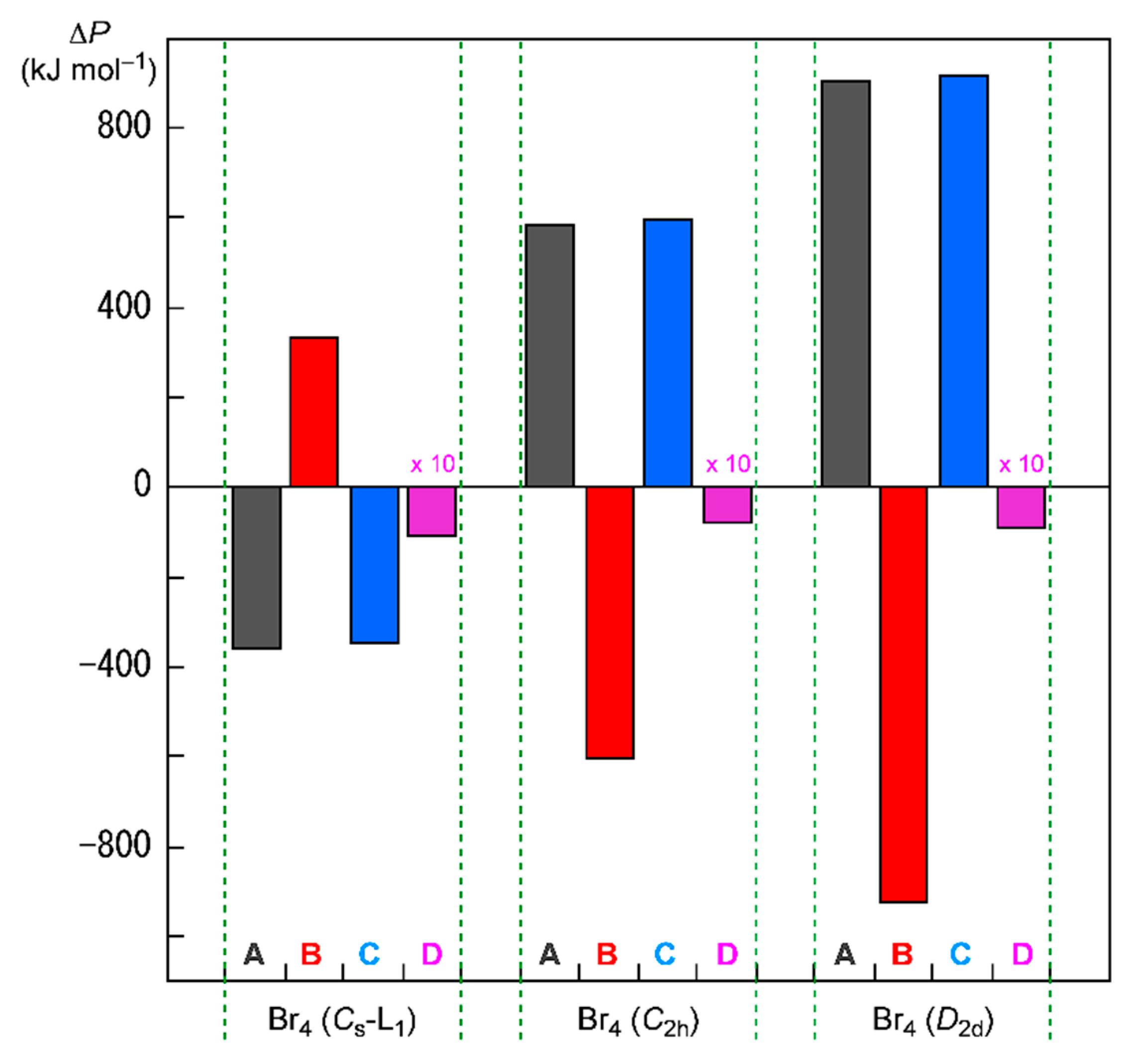
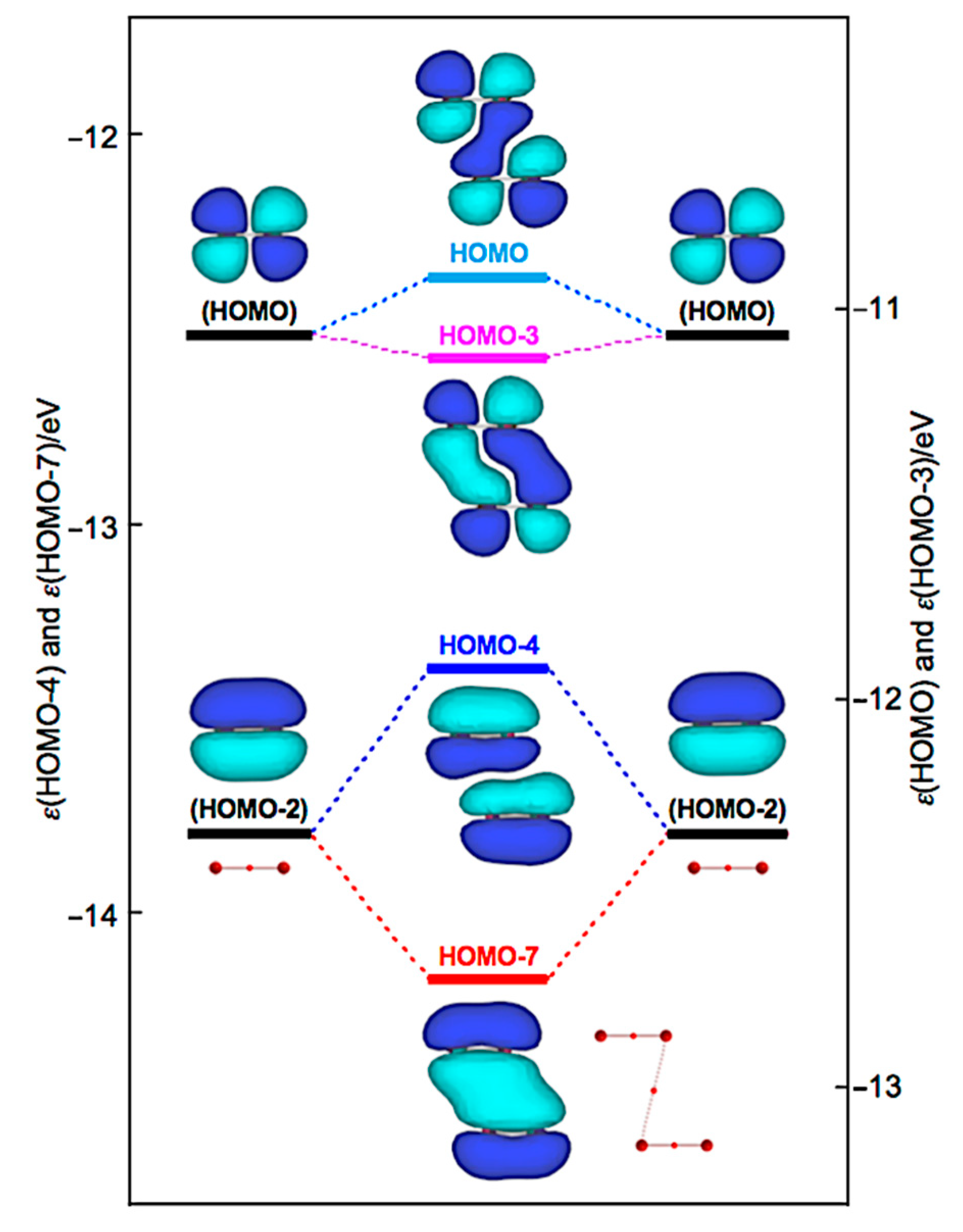
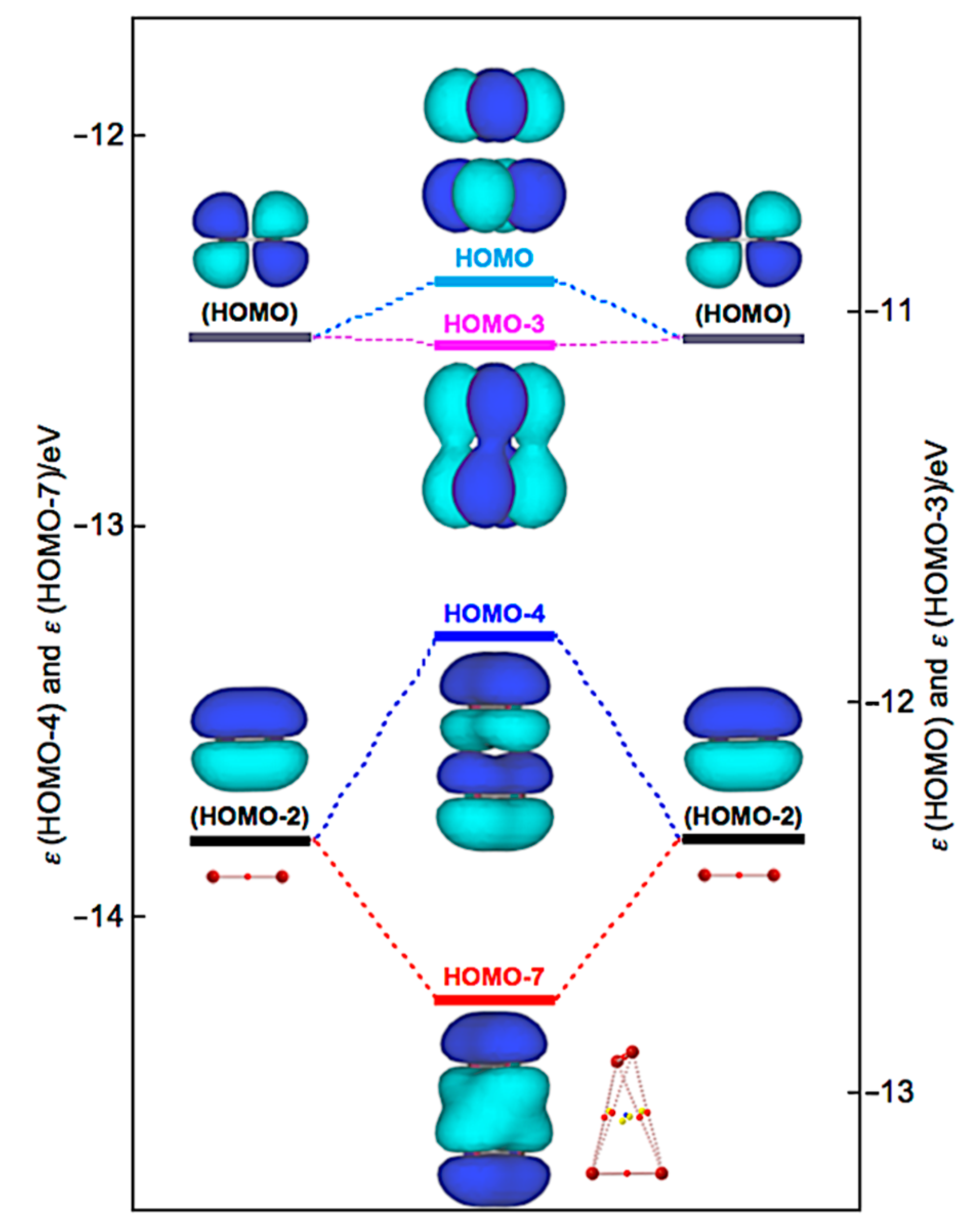
| Species | BCP on | ρb(rc) | c∇2ρb(rc) 2 | Hb(rc) | R3 | θ4 | ||
| (Symmetry) | (au) | (au) | (au) | (au) | (°) | |||
| Br4 (Cs-L1) | r2 | 0.0109 | 0.0045 | 0.0014 | 0.0048 | 72.5 | ||
| Br6 (Cs-L2) | r2 | 0.0113 | 0.0047 | 0.0014 | 0.0049 | 73.0 | ||
| Br6 (Cs-L2) | r4 | 0.0119 | 0.0049 | 0.0014 | 0.0051 | 73.7 | ||
| Br8 (Cs-L3) | r2 | 0.0114 | 0.0047 | 0.0014 | 0.0049 | 73.2 | ||
| Br8 (Cs-L3) | r4 | 0.0124 | 0.0050 | 0.0014 | 0.0052 | 74.4 | ||
| Br8 (Cs-L3) | r6 | 0.0120 | 0.0049 | 0.0014 | 0.0051 | 73.9 | ||
| Br10 (Cs-L4) | r2 | 0.0114 | 0.0047 | 0.0014 | 0.0049 | 73.2 | ||
| Br10 (Cs-L4) | r4 | 0.0125 | 0.0051 | 0.0014 | 0.0053 | 74.6 | ||
| Br10 (Cs-L4) | r6 | 0.0125 | 0.0051 | 0.0014 | 0.0053 | 74.6 | ||
| Br10 (Cs-L4) | r8 | 0.0120 | 0.0049 | 0.0014 | 0.0051 | 73.9 | ||
| Br12 (Cs-L5) | r2 | 0.0114 | 0.0047 | 0.0014 | 0.0049 | 73.2 | ||
| Br12 (Cs-L5) | r4 | 0.0126 | 0.0051 | 0.0014 | 0.0053 | 74.7 | ||
| Br12 (Cs-L5) | r6 | 0.0127 | 0.0051 | 0.0014 | 0.0053 | 74.7 | ||
| Br12 (Cs-L5) | r8 | 0.0126 | 0.0051 | 0.0014 | 0.0053 | 74.7 | ||
| Br12 (Cs-L5) | r10 | 0.0120 | 0.0049 | 0.0014 | 0.0051 | 73.9 | ||
| Br6 (C2) | r2 | 0.0104 | 0.0044 | 0.0014 | 0.0046 | 72.1 | ||
| Br10 (C2) | r2 | 0.0118 | 0.0048 | 0.0014 | 0.0050 | 73.6 | ||
| Br10 (C2) | r4 | 0.0106 | 0.0044 | 0.0014 | 0.0046 | 72.3 | ||
| Species | Cii5 | θp:CIV6 | κp:CIV7 | Predicted | ||||
| (Symmetry) | (Å mdyn−1) | (°) | (au−1) | nature | ||||
| Br4 (Cs-L1) | 15.311 | 87.8 | 121.2 | p-CS/vdW 8 | ||||
| Br6 (Cs-L2) | 14.984 | 89.0 | 124.9 | p-CS/vdW 8 | ||||
| Br6 (Cs-L2) | 14.114 | 90.6 | 127.3 | p-CS/t-HB 9 | ||||
| Br8 (Cs-L3) | 14.826 | 89.2 | 125.0 | p-CS/vdW 8 | ||||
| Br8 (Cs-L3) | 13.590 | 92.2 | 132.0 | p-CS/t-HB 9 | ||||
| Br8 (Cs-L3) | 14.048 | 90.9 | 127.1 | p-CS/t-HB 9 | ||||
| Br10 (Cs-L4) | 14.751 | 89.4 | 126.2 | p-CS/vdW 8 | ||||
| Br10 (Cs-L4) | 13.445 | 92.6 | 133.2 | p-CS/t-HB 9 | ||||
| Br10 (Cs-L4) | 13.478 | 92.6 | 132.5 | p-CS/t-HB 9 | ||||
| Br10 (Cs-L4) | 13.983 | 91.1 | 128.4 | p-CS/t-HB 9 | ||||
| Br12 (Cs-L5) | 14.719 | 89.5 | 126.9 | p-CS/vdW 8 | ||||
| Br12 (Cs-L5) | 13.376 | 92.7 | 133.3 | p-CS/t-HB 9 | ||||
| Br12 (Cs-L5) | 13.334 | 93.0 | 134.3 | p-CS/t-HB 9 | ||||
| Br12 (Cs-L5) | 13.393 | 92.8 | 132.6 | p-CS/t-HB 9 | ||||
| Br12 (Cs-L5) | 13.962 | 91.1 | 128.8 | p-CS/t-HB 9 | ||||
| Br6 (C2) | 16.025 | 86.7 | 119.2 | p-CS/vdW 8 | ||||
| Br10 (C2) | 14.218 | 90.2 | 126.7 | p-CS/t-HB 9 | ||||
| Br10 (C2) | 16.378 | 87.2 | 120.0 | p-CS/vdW 8 | ||||
| Species | BCP on | ρb(rc) | c∇2ρb(rc) 2 | Hb(rc) | R3 | θ4 | ||
| (Symmetry) | (au) | (au) | (au) | (au) | (°) | |||
| Br4 (C2h) | r2 | 0.0055 | 0.0022 | 0.0009 | 0.0024 | 67.2 | ||
| Br4 (D2d) | r2 | 0.0042 | 0.0017 | 0.0007 | 0.0018 | 66.0 | ||
| Br6 (C3h-c) | r2 | 0.0092 | 0.0038 | 0.0013 | 0.0040 | 70.7 | ||
| Br8 (S4) | r2 | 0.0128 | 0.0051 | 0.0014 | 0.0053 | 74.8 | ||
| Br8 (S4-Wm) 5 | r2 | 0.0136 | 0.0054 | 0.0013 | 0.0056 | 76.0 | ||
| Br8 (S4-Wm) 5 | r3 | 0.0038 | 0.0015 | 0.0007 | 0.0016 | 66.0 | ||
| Br10 (C2-c) | r2 | 0.0087 | 0.0035 | 0.0012 | 0.0037 | 70.5 | ||
| Br10 (C2-c) | r4 | 0.0097 | 0.0040 | 0.0014 | 0.0042 | 71.3 | ||
| Br10 (C2-c) | r6 | 0.0110 | 0.0044 | 0.0014 | 0.0046 | 73.0 | ||
| Br10 (C2-c) | r7 | 0.0049 | 0.0019 | 0.0008 | 0.0021 | 66.2 | ||
| Br10 (C2-c) | r8 | 0.0049 | 0.0018 | 0.0008 | 0.0020 | 66.6 | ||
| Br12 (Ci) | r2 | 0.0129 | 0.0052 | 0.0014 | 0.0054 | 75.0 | ||
| Br12 (Ci) | r4 | 0.0129 | 0.0052 | 0.0014 | 0.0054 | 75.0 | ||
| Species | Cii6 | θp:CIV7 | κp:CIV8 | Predicted | ||||
| (Symmetry) | (Å mdyn−1) | (°) | (au−1) | nature | ||||
| Br4 (C2h) | 24.709 | 73.6 | 122.9 | p-CS/vdW 9 | ||||
| Br4 (D2d) | 40.402 | 69.6 | 136.3 | p-CS/vdW 9 | ||||
| Br6 (C3h-c) | 25.617 | 83.3 | 121.7 | p-CS/vdW 9 | ||||
| Br8 (S4) | 13.201 | 93.5 | 139.2 | p-CS/t-HB 10 | ||||
| Br8 (S4-Wm) 5 | 11.294 | 95.3 | 139.0 | p-CS/t-HB 10 | ||||
| Br8 (S4-Wm) 5 | 52.918 | 67.5 | 204.0 | p-CS/vdW 9 | ||||
| Br10 (C2-c) | 34.402 | 81.3 | 112.7 | p-CS/vdW 9 | ||||
| Br10 (C2-c) | 23.971 | 84.7 | 122.1 | p-CS/vdW 9 | ||||
| Br10 (C2-c) | 20.831 | 87.6 | 122.6 | p-CS/vdW 9 | ||||
| Br10 (C2-c) | 29.570 | 71.5 | 118.9 | p-CS/vdW 9 | ||||
| Br10 (C2-c) | 37.855 | 71.8 | 120.4 | p-CS/vdW 9 | ||||
| Br12 (Ci) | 13.483 | 93.7 | 137.9 | p-CS/t-HB 10 | ||||
| Br12 (Ci) | 13.482 | 93.7 | 137.3 | p-CS/t-HB 10 | ||||
| Entry | Correlation | a | b | Rc2 | n |
|---|---|---|---|---|---|
| 1 | ΔEZP vs. ΔEES | 0.940 | 0.129 | 0.9999 | 20 2 |
| 2 | θ vs. R | 2595.6 | 60.70 | 0.979 | 33 |
| 3 | θp vs. R | 6449.1 | 58.19 | 0.989 | 33 |
| 4 | θp vs. θ | 2.67 | −106.26 | 0.992 | 31 3 |
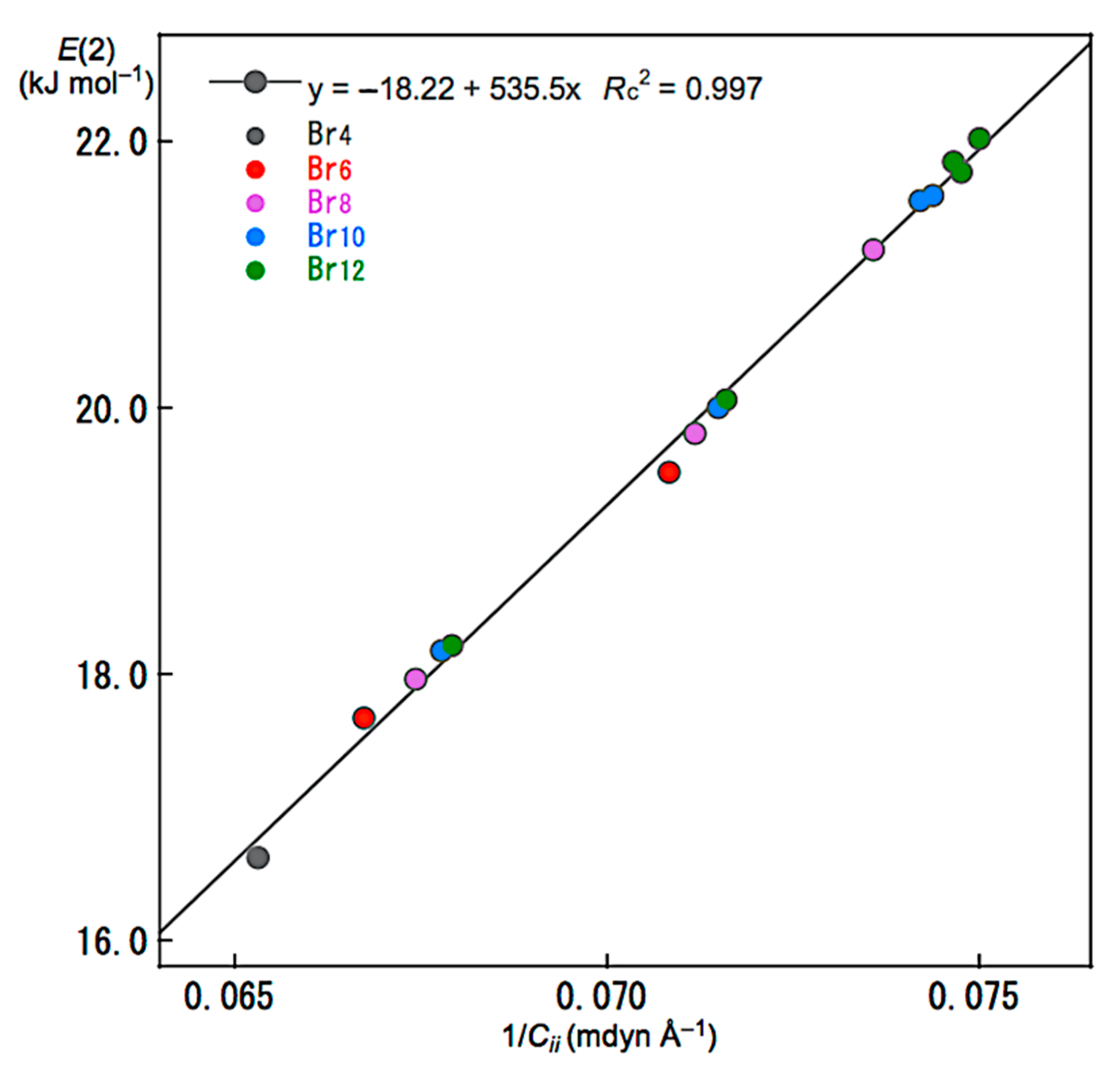
| 5 | E(2) vs. Cii−1 | 535.5 | −18.22 | 0.997 | 15 4 |
| 6 | E(2)vs. R | 9760.9 | −29.92 | 0.983 | 15 4 |
| 7 | E(2) vs θ | 2.446 | −160.88 | 0.996 | 15 4 |
| 8 | E(2) vs. θp | 1.067 | 77.17 | 0.999 | 15 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hayashi, S.; Nishide, T.; Tanaka, E.; Nakanishi, W. Intrinsic Dynamic and Static Nature of Halogen Bonding in Neutral Polybromine Clusters, with the Structural Feature Elucidated by QTAIM Dual-Functional Analysis and MO Calculations. Molecules 2021, 26, 2936. https://doi.org/10.3390/molecules26102936
Hayashi S, Nishide T, Tanaka E, Nakanishi W. Intrinsic Dynamic and Static Nature of Halogen Bonding in Neutral Polybromine Clusters, with the Structural Feature Elucidated by QTAIM Dual-Functional Analysis and MO Calculations. Molecules. 2021; 26(10):2936. https://doi.org/10.3390/molecules26102936
Chicago/Turabian StyleHayashi, Satoko, Taro Nishide, Eiichiro Tanaka, and Waro Nakanishi. 2021. "Intrinsic Dynamic and Static Nature of Halogen Bonding in Neutral Polybromine Clusters, with the Structural Feature Elucidated by QTAIM Dual-Functional Analysis and MO Calculations" Molecules 26, no. 10: 2936. https://doi.org/10.3390/molecules26102936
APA StyleHayashi, S., Nishide, T., Tanaka, E., & Nakanishi, W. (2021). Intrinsic Dynamic and Static Nature of Halogen Bonding in Neutral Polybromine Clusters, with the Structural Feature Elucidated by QTAIM Dual-Functional Analysis and MO Calculations. Molecules, 26(10), 2936. https://doi.org/10.3390/molecules26102936