A Modified Couple Stress Elasticity for Non-Uniform Composite Laminated Beams Based on the Ritz Formulation
Abstract
1. Introduction
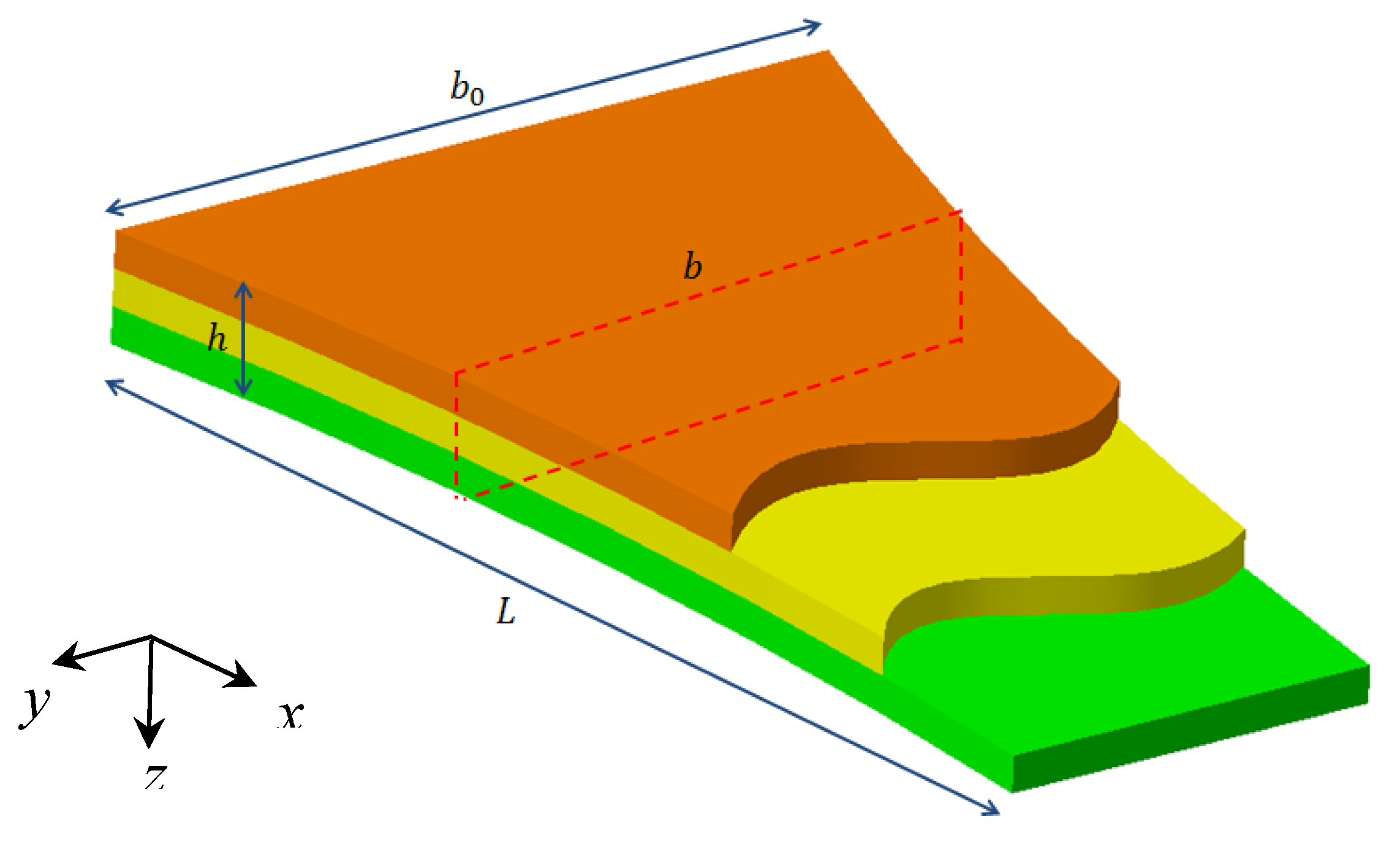
2. Theory and Mathematical Problem
3. The Rayleigh–Ritz Procedure
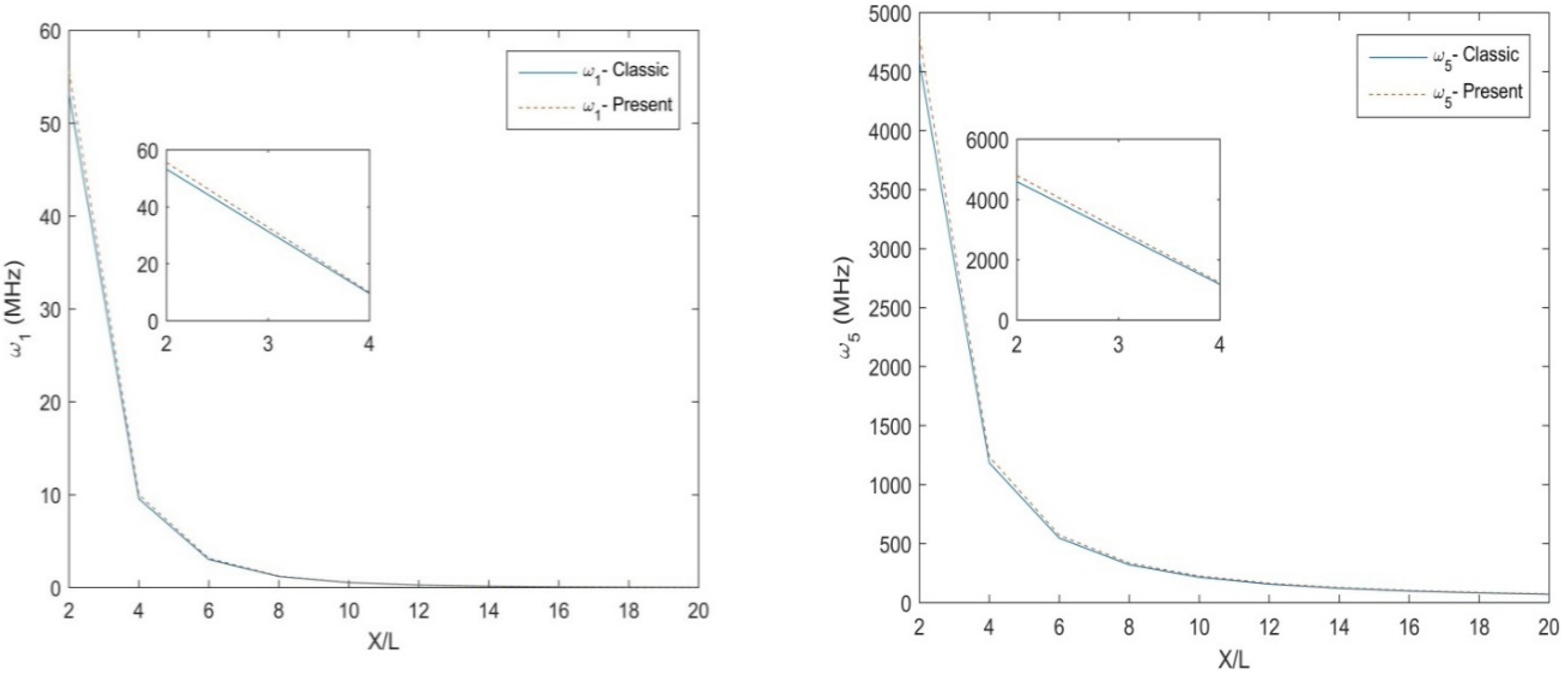
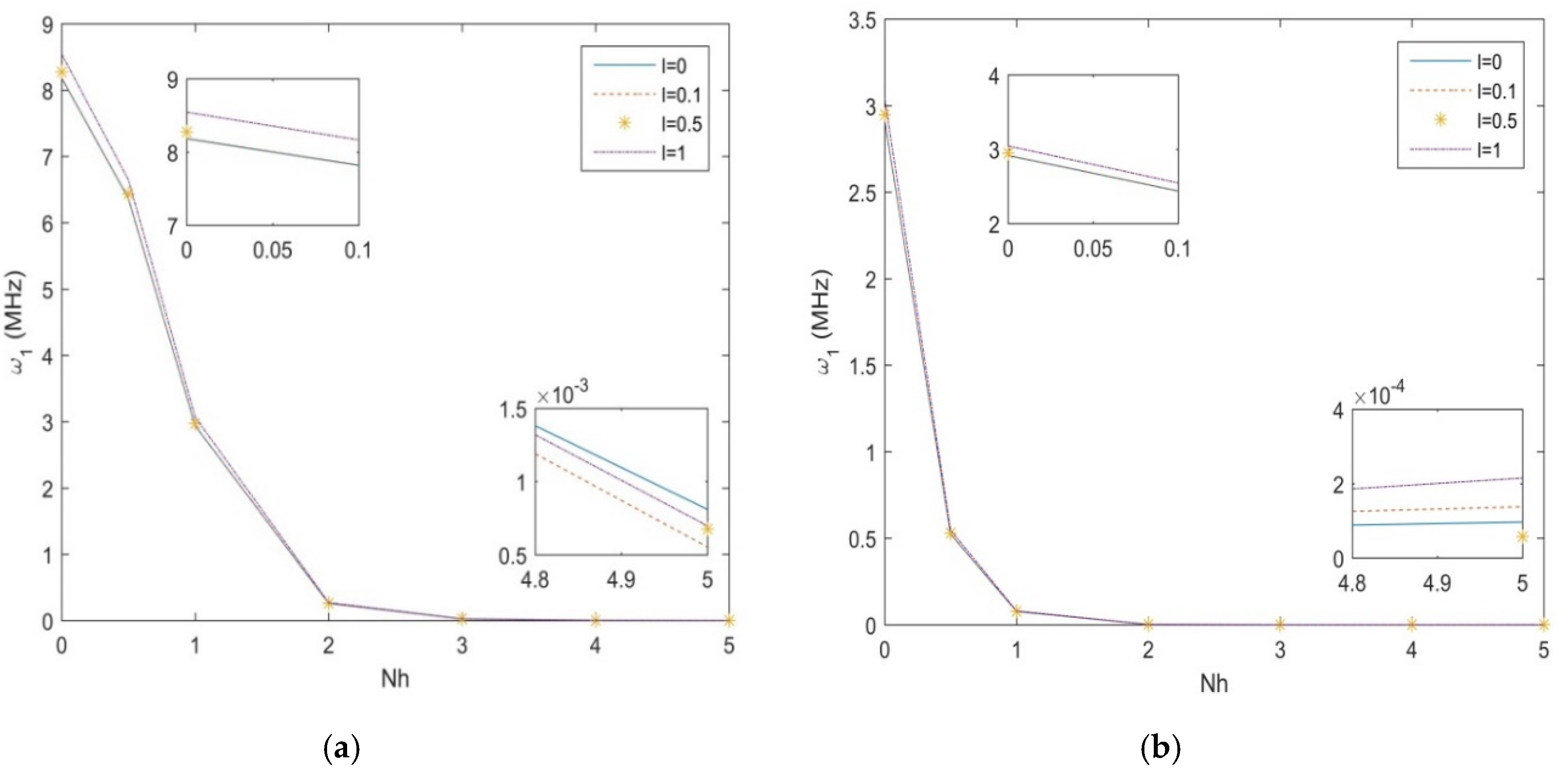
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stürzenbecher, R.; Hofstetter, K. Bending of cross-ply laminated composites: An accurate and efficient plate theory based upon models of Lekhnitskii and Ren. Compos. Struct. 2011, 93, 1078–1088. [Google Scholar] [CrossRef]
- Fleck, N.A.; Muller, G.M.; Ashby, M.F.; Hutchinson, J.W. Strain gradient plasticity: Theory and experiment. Acta Metall. Mater. 1994, 42, 475–487. [Google Scholar] [CrossRef]
- Stolken, J.S.; Evans, A.G. A microbend test method for measuring the plasticity length scale. Acta Mater. 1998, 46, 5109–5115. [Google Scholar] [CrossRef]
- Lam, D.C.C.; Yang, F.; Chong, A.C.M.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- McFarland, A.W.; Colton, J.S. Role of material microstructure in plate stiffness with relevance to microcantilever sensors. J. Micromech. Microeng. 2005, 15, 1060–1067. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Nonlinear vibration and postbuckling of functionally graded graphene reinforced porous nanocomposite beams. Compos. Sci. Technol. 2017, 142, 235–245. [Google Scholar] [CrossRef]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear bending of polymer nanocomposite beams reinforced with non-uniformly distributed graphene platelets (GPLs). Compos. Part B Eng. 2017, 110, 132–140. [Google Scholar] [CrossRef]
- Feng, C.; Kitipornchai, S.; Yang, J. Nonlinear free vibration of functionally graded polymer composite beams reinforced with graphene nanoplatelets (GPLs). Eng. Struct. 2017, 140, 110–119. [Google Scholar] [CrossRef]
- Kitipornchai, S.; Chen, D.; Yang, J. Free vibration and elastic buckling of functionally graded porous beams reinforced by graphene platelets. Mater. Des. 2017, 116, 656–665. [Google Scholar] [CrossRef]
- Sahmani, S.; Aghdam, M.M. Nonlocal strain gradient beam model for nonlinear vibration of prebuckled and postbuckled multilayer functionally graded GPLRC nanobeams. Compos. Struct. 2017, 179, 77–88. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, C.; Zhao, Z.; Yang, J. Buckling of Graphene Platelet Reinforced Composite Cylindrical Shell with Cutout. Int. J. Struct. Stab. Dyn. 2018, 18, 1850040. [Google Scholar] [CrossRef]
- Arefi, M.; Bidgoli, E.M.R.; Dimitri, R.; Tornabene, F.; Reddy, J.N. Size-Dependent Free Vibrations of FG Polymer Composite Curved Nanobeams Reinforced with Graphene Nanoplatelets Resting on Pasternak Foundations. Appl. Sci. 2019, 9, 1580. [Google Scholar] [CrossRef]
- Arefi, M.; Bidgoli, E.M.R.; Dimitri, R.; Bacciocchi, M.; Tornabene, F. Nonlocal bending analysis of curved nanobeams reinforced by graphene nanoplatelets. Compos. Part B Eng. 2019, 166, 1–12. [Google Scholar] [CrossRef]
- Jalaei, M.H.; Dimitri, R.; Tornabene, F. Dynamic stability of temperature-dependent graphene sheet embedded in an elastomeric medium. Appl. Sci. 2019, 9, 887. [Google Scholar] [CrossRef]
- Arefi, M.; Mohammadi, M.; Tabatabaeian, A.; Dimitri, R.; Tornabene, F. Two-dimensional thermo-elastic analysis of FG-CNTRC cylindrical pressure vessels. Steel Compos. Struct. 2018, 27, 525–536. [Google Scholar]
- Kiani, Y.; Dimitri, R.; Tornabene, F. Free vibration of FG-CNT reinforced composite skew cylindrical shells using the Chebyshev-Ritz formulation. Compos. Part B Eng. 2018, 147, 169–177. [Google Scholar] [CrossRef]
- Kiani, Y.; Dimitri, R.; Tornabene, F. Free vibration study of composite conical panels reinforced with FG-CNTs. Eng. Struct. 2018, 172, 472–482. [Google Scholar] [CrossRef]
- Ghasemi, A.R.; Mohandes, M.; Dimitri, R.; Tornabene, F. Agglomeration effects on the vibrations of CNTs/fiber/polymer/metal hybrid laminates cylindrical shell. Compos. Part B Eng. 2019, 167, 700–716. [Google Scholar] [CrossRef]
- Mohammadi, M.; Arefi, M.; Dimitri, R.; Tornabene, F. Higher-order thermo-elastic analysis of FG-CNTRC cylindrical vessels surrounded by a pasternak foundation. Nanomaterials 2019, 9, 79. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E. Mechanical behavior of damaged laminated composites plates and shells: Higher-order shear deformation theories. Compos. Struct. 2018, 189, 304–329. [Google Scholar] [CrossRef]
- Asadi, A.; Sheikh, A.H.; Thomsen, O.T. Buckling behaviour of thin-walled laminated composite beams having open and closed sections subjected to axial and end moment loading. Thin Walled Struct. 2019, 141, 85–96. [Google Scholar] [CrossRef]
- Karamanli, A.; Aydogdu, M. Buckling of laminated composite and sandwich beams due to axially varying in-plane loads. Compos. Struct. 2019, 210, 391–408. [Google Scholar] [CrossRef]
- Kim, K.; Choe, K.; Kim, S.; Wang, Q. A modeling method for vibration analysis of cracked laminated composite beam of uniform rectangular cross-section with arbitrary boundary condition. Compos. Struct. 2019, 208, 127–140. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M. Refined shear deformation theories for laminated composite arches and beams with variable thickness: Natural frequency analysis. Eng. Anal. Bound. Elem. 2019, 100, 24–47. [Google Scholar] [CrossRef]
- Ma, H.M.; Gao, X.-L.; Reddy, J.N. A microstructure-dependent Timoshenko beam model based on a modified couple stress theory. J. Mech. Phys. Sol. 2008, 56, 3379–3391. [Google Scholar] [CrossRef]
- Mohammadimehr, M.; Mahmudian-Najafabadi, M. Bending and Free Vibration Analysis of Nonlocal Functionally Graded Nanocomposite Timoshenko Beam Model Rreinforced by SWBNNT Based on Modified Coupled Stress Theory. J. Nanostruct. 2013, 3, 483–492. [Google Scholar]
- Akbarzadeh Khorshidi, M.; Shariati, M.; Emam, S.A. Postbuckling of functionally graded nanobeams based on modified couple stress under general beam theory. Int. J. Mech. Sci. 2016, 110, 160–169. [Google Scholar] [CrossRef]
- Ilkhani, M.R.; Hosseini-Hashemi, S.H. Size dependent vibro-buckling of rotating beam based on modified couple stress theory. Compos. Struct. 2016, 143, 75–83. [Google Scholar] [CrossRef]
- Şimşek, M. Vibration analysis of a single-walled carbon nanotube under action of a moving harmonic load based on nonlocal elasticity theory. Phys. E Low Dimens. Syst. Nanostruct. 2010, 43, 182–191. [Google Scholar] [CrossRef]
- Yas, M.H.; Heshmati, M. Dynamic analysis of functionally graded nanocomposite beams reinforced by randomly oriented carbon nanotube under the action of moving load. Appl. Math. Model. 2012, 36, 1371–1394. [Google Scholar] [CrossRef]
- Fang, J.; Gu, J.; Wang, H. Size-dependent three-dimensional free vibration of rotating functionally graded microbeams based on a modified couple stress theory. Int. J. Mech. Sci. 2018, 136, 188–199. [Google Scholar] [CrossRef]
- Jouneghani, F.Z.; Dimitri, R.; Tornabene, F. Structural response of porous FG nanobeams under hygro-thermo-mechanical loadings. Compos. Part B Eng. 2018, 152, 71–78. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Das, D. Free vibration analysis of bidirectional-functionally graded and double-tapered rotating micro-beam in thermal environment using modified couple stress theory. Compos. Struct. 2019, 215, 471–492. [Google Scholar] [CrossRef]
- Esen, I. Dynamics of size-dependant Timoshenko micro beams subjected to moving loads. Int. J. Mech. Sci. 2020, 175, 105501. [Google Scholar] [CrossRef]
- Chen, W.J.; Li, X.P. Size-dependent free vibration analysis of composite laminated Timoshenko beam based on new modified couple stress theory. Arch. Appl. Mech. 2013, 83, 431–444. [Google Scholar] [CrossRef]
- Roque, C.M.C.; Fidalgo, D.S.; Ferreira, A.J.M.; Reddy, J.N. A study of a microstructure-dependent composite laminated Timoshenko beam using a modified couple stress theory and a meshless method. Compos. Struct. 2013, 96, 532–537. [Google Scholar] [CrossRef]
- Alashti, R.A.; Abolghasemi, A.H. A size-dependent Bernoulli-Euler beam formulation based on a new model of couple stress theory. Int. J. Eng. 2014, 27, 951–960. [Google Scholar]
- Mohammad Abadi, M.; Daneshmehr, A.R. An investigation of modified couple stress theory in buckling analysis of micro composite laminated Euler–Bernoulli and Timoshenko beams. Int. J. Eng. Sci. 2014, 75, 40–53. [Google Scholar] [CrossRef]
- Romanoff, J.; Reddy, J.N. Experimental validation of the modified couple stress Timoshenko beam theory for web-core sandwich panels. Compos. Struct. 2014, 111, 130–137. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnani, A.M.; Bahrami, A. On size-dependent Timoshenko beam element based on modified couple stress theory. Int. J. Eng. Sci. 2016, 107, 134–148. [Google Scholar] [CrossRef]
- Jouneghani, F.Z.; Dashtaki, P.M.; Dimitri, R.; Bacciocchi, M.; Tornabene, F. First-order shear deformation theory for orthotropic doubly-curved shells based on a modified couple stress elasticity. Aerosp. Sci. Technol. 2018, 73, 129–147. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Modified couple stress theory in orthogonal curvilinear coordinates. Acta Mech. 2019, 230, 851–869. [Google Scholar] [CrossRef]
- Kim, J.; Żur, K.K.; Reddy, J. Bending, free vibration, and buckling of modified couples stress-based functionally graded porous micro-plates. Compos. Struct. 2019, 209, 879–888. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R. A modified nonlocal couple stress-based beam model for vibration analysis of higher-order FG nanobeams. Mech. Adv. Mater. Struct. 2018, 25, 1121–1132. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. Nonlinear mechanics of nanoscale tubes via nonlocal strain gradient theory. Int. J. Eng. Sci. 2018, 129, 84–95. [Google Scholar] [CrossRef]
- Malikan, M.; Tornabene, F.; Dimitri, R. Nonlocal three-dimensional theory of elasticity for buckling behavior of functionally graded porous nanoplates using volume integrals. Mater. Res. Exp. 2018, 5, 095006. [Google Scholar] [CrossRef]
- Zenkour, A.M. A novel mixed nonlocal elasticity theory for thermoelastic vibration of nanoplates. Compos. Struct. 2018, 185, 821–833. [Google Scholar] [CrossRef]
- Mahmoudpour, E.; Hosseini-Hashemi, S.; Faghidian, S. Nonlinear resonant behaviors of embedded thick FG double layered nanoplates via nonlocal strain gradient theory. Microsys. Technol. 2019, 25, 951–964. [Google Scholar] [CrossRef]
- Baghani, M.; Jafari-Talookolaei, R.A.; Salarieh, H. Large amplitudes free vibrations and post-buckling analysis of unsymmetrically laminated composite beams on nonlinear elastic foundation. Appl. Math. Model. 2011, 35, 130–138. [Google Scholar] [CrossRef]
- Baghani, M. Analytical study on size-dependent static pull-in voltage of microcantilevers using the modified couple stress theory. Int. J. Eng. Sci. 2012, 54, 99–105. [Google Scholar] [CrossRef]
- Lal, R.; Dangi, C. Thermomechanical vibration of bi-directional functionally graded non-uniform timoshenko nanobeam using nonlocal elasticity theory. Compos. Part B Eng. 2019, 172, 724–742. [Google Scholar] [CrossRef]
- Rajasekaran, S.; Khaniki, H.B. Bending, buckling and vibration of small-scale tapered beams. Int. J. Eng. Sci. 2017, 120, 172–188. [Google Scholar] [CrossRef]
- Akgoz, B.; Civalek, O. Buckling analysis of linearly tapered micro-columns based on strain gradient elasticity. Struct. Eng. Mech. 2013, 48, 195–205. [Google Scholar] [CrossRef]
- Khani, S.; Tabandeh, N.; Ghomshei, M. Natural frequency analysis of non-uniform smart beams with piezoelectric layers, using differential quadrature method. Compos. Part B Eng. 2014, 58, 303–311. [Google Scholar] [CrossRef]
- Mohammadimehr, M.; Monajemi, A.A.; Moradi, M. Vibration analysis of viscoelastic tapered micro-rod based on strain gradient theory resting on viscopasternak foundation using DQM. J. Mech. Sci. Technol. 2015, 29, 2297–2305. [Google Scholar] [CrossRef]
- Khaniki, H.B.; Hosseini-Hashemi, S. Buckling analysis of tapered nanobeams using nonlocal strain gradient theory and a generalized differential quadrature method. Mater. Res. Exp. 2017, 4, 065003. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Nonlinear vibration analysis of axially functionally graded shear-deformable tapered beams. Appl. Math. Model. 2018, 59, 583–596. [Google Scholar] [CrossRef]
- Khaniki, H.B.; Hosseini-Hashemi, S.; Nezamabadi, A. Buckling analysis of nonuniform nonlocal strain gradient beams using generalized differential quadrature method. Alex. Eng. J. 2018, 57, 1361–1368. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Masoodi, A.R. Exact natural frequencies and buckling load of functionally graded material tapered beam-columns considering semi-rigid connections. J. Vib. Control 2018, 24, 1787–1808. [Google Scholar] [CrossRef]
- Aranda-Ruiz, J.; Loya, J.; Fernández-Sáez, J. Bending vibrations of rotating nonuniform nanocantilevers using the Eringen nonlocal elasticity theory. Compos. Struct. 2012, 94, 2990–3001. [Google Scholar] [CrossRef]
- Eltaher, M.; Emam, S.A.; Mahmoud, F. Free vibration analysis of functionally graded size-dependent nanobeams. Appl. Math. Comput. 2012, 218, 7406–7420. [Google Scholar] [CrossRef]
- Akgöz, B.; Civalek, Ö. Free vibration analysis of axially functionally graded tapered Bernoulli–Euler microbeams based on the modified couple stress theory. Compos. Struct. 2013, 98, 314–322. [Google Scholar] [CrossRef]
- Baghani, M.; MohammadSalehi, M.; Dabaghian, P.H. Analytical Couple-stress Solution for Size-dependent Large-amplitude Vibrations of FG Tapered-nanobeams. Lat. Am. J. Solids Struct. 2016, 13, 95–118. [Google Scholar] [CrossRef][Green Version]
- Khaniki, H.B.; Hashemi, S.H. Free Vibration Analysis of Nonuniform Microbeams Based on Modified Couple Stress Theory: An Analytical Solution. Int. J. Eng. Trans. B Appl. 2017, 30, 311. [Google Scholar]
- Aydogdu, M. Buckling analysis of cross-ply laminated beams with general boundary conditions by Ritz method. Compos. Sci. Technol. 2006, 66, 1248–1255. [Google Scholar] [CrossRef]
- Şimşek, M. Static analysis of a functionally graded beam under a uniformly distributed load by Ritz method. Int. J. Appl. Sci. Eng. 2009, 1, 1–11. [Google Scholar]
- Şimşek, M. Non-linear vibration analysis of a functionally graded Timoshenko beam under action of a moving harmonic load. Compos. Struct. 2010, 92, 2532–2546. [Google Scholar] [CrossRef]
- Mantari, J.; Canales, F. Free vibration and buckling of laminated beams via hybrid Ritz solution for various penalized boundary conditions. Compos. Struct. 2016, 152, 306–315. [Google Scholar] [CrossRef]
- Fakher, M.; Hosseini-Hashemi, S. Bending and free vibration analysis of nanobeams by differential and integral forms of nonlocal strain gradient with Rayleigh-Ritz method. Mater. Res. Exp. 2017, 4, 125025. [Google Scholar] [CrossRef]
- Nguyen, T.-K.; Nguyen, N.-D.; Vo, T.P.; Thai, H.-T. Trigonometric-series solution for analysis of laminated composite beams. Compos. Struct. 2017, 160, 142–151. [Google Scholar] [CrossRef]
- Mazanoglu, K. Natural frequency analyses of segmented Timoshenko–Euler beams using the Rayleigh–Ritz method. J. Vib. Control 2017, 23, 2135–2154. [Google Scholar] [CrossRef]
- Nguyen, N.D.; Nguyen, T.K.; Thai, H.T.; Vo, T.P. A Ritz type solution with exponential trial functions for laminated composite beams based on the modified couple stress theory. Compos. Struct. 2018, 191, 154–167. [Google Scholar] [CrossRef]
- Nguyen, N.-D.; Nguyen, T.-K.; Nguyen, T.-N.; Thai, H.-T. New Ritz-solution shape functions for analysis of thermo-mechanical buckling and vibration of laminated composite beams. Compos. Struct. 2018, 184, 452–460. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are not available from the authors. |


| m | ||||||
|---|---|---|---|---|---|---|
| classic | 2 | 5.285 | 21.142 | - | - | - |
| 3 | 5.285 | 21.142 | 47.569 | - | - | |
| 4 | 5.285 | 21.142 | 47.569 | 84.566 | - | |
| 5 | 5.2854 | 21.142 | 47.569 | 84.566 | 132.13 | |
| Ref. [35] | 5.28539 | 21.1416 | 47.5686 | 84.5663 | 132.135 | |
| = 0.1 | 2 | 5.2857 | 21.143 | - | - | - |
| 3 | 5.2857 | 21.143 | 47.571 | - | - | |
| 4 | 5.2857 | 21.143 | 47.571 | 84.57 | - | |
| 5 | 5.2857 | 21.143 | 47.571 | 84.57 | 132.14 | |
| Ref. [35] | 5.28544 | 21.1417 | 47.569 | 84.5671 | 132.136 |
| l = 0.1 | 5.2857 | 21.143 | 47.571 | 84.57 | 132.14 |
| Ref [35] | 5.28544 | 21.1417 | 47.569 | 84.5671 | 132.136 |
| l = 1 | 5.3105 | 21.242 | 47.795 | 84.968 | 132.76 |
| Ref [35] | 5.28959 | 21.1583 | 47.6063 | 84.6334 | 132.24 |
| l = 3 | 5.5074 | 22.03 | 49.566 | 88.118 | 137.68 |
| Ref [35] | 5.32304 | 21.2922 | 47.9073 | 85.1685 | 133.076 |
| Natural Frequency (MHz) | |||||||
|---|---|---|---|---|---|---|---|
| 2 | 0 | 0 | 204.5367 | 818.1467 | 1840.83 | 3272.587 | 5113.417 |
| 0.1 | 204.6292 | 818.5169 | 1841.663 | 3274.067 | 5115.730 | ||
| 0.5 | 206.8380 | 827.3519 | 1861.542 | 3309.408 | 5170.949 | ||
| 1 | 213.5932 | 854.3726 | 1922.338 | 3417.491 | 5339.829 | ||
| 0.5 | 0 | 202.5349 | 820.068 | 1844.083 | 3276.601 | 5136.471 | |
| 0.1 | 202.6265 | 820.4391 | 1844.917 | 3278.083 | 5138.795 | ||
| 0.5 | 204.8136 | 829.2948 | 1864.831 | 3313.467 | 5194.263 | ||
| 1 | 211.5027 | 856.379 | 1925.735 | 3421.682 | 5363.904 | ||
| 1 | 0 | 196.6233 | 825.9774 | 1853.967 | 3289.191 | 5205.040 | |
| 0.1 | 196.7123 | 826.3511 | 1854.806 | 3290.679 | 5207.395 | ||
| 0.5 | 198.8356 | 835.2707 | 1874.827 | 3326.199 | 5263.603 | ||
| 1 | 205.3294 | 862.5501 | 1936.057 | 3434.83 | 5435.509 | ||
| 5 | 0 | 73.49691 | 1116.877 | 2251.706 | 3894.916 | 7160.348 | |
| 0.1 | 73.53017 | 1117.382 | 2252.725 | 3896.679 | 7163.588 | ||
| 0.5 | 74.32385 | 1129.443 | 2277.041 | 3938.739 | 7240.911 | ||
| 1 | 76.75122 | 1166.33 | 2351.407 | 4067.376 | 7477.394 | ||
| 10 | 0 | 0 | 8.181467 | 32.72587 | 73.63320 | 130.9035 | 204.5367 |
| 0.1 | 8.185169 | 32.74067 | 73.66652 | 130.9627 | 204.6292 | ||
| 0.5 | 8.273519 | 33.09407 | 74.46167 | 132.3763 | 206.8380 | ||
| 1 | 8.543726 | 34.17491 | 76.89354 | 136.6996 | 213.5932 | ||
| 0.5 | 0 | 6.365682 | 34.93440 | 77.13089 | 135.8051 | 226.6082 | |
| 0.1 | 6.368563 | 34.95020 | 77.16579 | 135.8666 | 226.7108 | ||
| 0.5 | 6.437305 | 35.32745 | 77.99871 | 137.3331 | 229.1579 | ||
| 1 | 6.647543 | 36.48122 | 80.54610 | 141.8183 | 236.6420 | ||
| 1 | 0 | 2.939876 | 44.67508 | 90.06824 | 155.7967 | 286.4139 | |
| 0.1 | 2.941207 | 44.69529 | 90.109 | 155.8672 | 286.5435 | ||
| 0.5 | 2.972954 | 45.17773 | 91.08163 | 157.5496 | 289.6364 | ||
| 1 | 3.070049 | 46.6532 | 94.05629 | 162.695 | 299.0958 | ||
| 5 | 0 | 0.000810 | 562.0597 | 709.8402 | 1031.638 | 2059.529 | |
| 0.1 | 0.000553 | 562.0737 | 709.3336 | 1030.639 | 2059.634 | ||
| 0.5 | 0.000677 | 568.0907 | 716.7862 | 1041.347 | 2081.615 | ||
| 1 | 0.000698 | 587.0221 | 741.525 | 1077.762 | 2150.972 | ||
| 20 | 0 | 0 | 2.045367 | 8.181467 | 18.40830 | 32.72587 | 51.13417 |
| 0.1 | 2.046292 | 8.185169 | 18.41663 | 32.74067 | 51.15730 | ||
| 0.5 | 2.068380 | 8.273519 | 18.61542 | 33.09408 | 51.70949 | ||
| 1 | 2.135932 | 8.543726 | 19.22338 | 34.17491 | 53.39829 | ||
| 0.5 | 0 | 0.734969 | 11.16877 | 22.51706 | 38.94916 | 71.60348 | |
| 0.1 | 0.735302 | 11.17382 | 22.52725 | 38.96679 | 71.63588 | ||
| 0.5 | 0.743238 | 11.29443 | 22.77041 | 39.38739 | 72.40911 | ||
| 1 | 0.767512 | 11.66330 | 23.51407 | 40.67376 | 74.77394 | ||
| 1 | 0 | 0.065155 | 25.58565 | 39.19111 | 62.86697 | 125.5065 | |
| 0.1 | 0.065185 | 25.59722 | 39.20884 | 62.89541 | 125.5632 | ||
| 0.5 | 0.065888 | 25.87351 | 39.63205 | 63.57429 | 126.9186 | ||
| 1 | 0.068040 | 26.71853 | 40.92641 | 65.65059 | 131.0636 | ||
| 5 | 0 | 0.000225 | 8.265543 | 424.5829 | 633.7069 | 1295.298 | |
| 0.1 | 0.000162 | 7.726310 | 425.0330 | 634.0109 | 1295.894 | ||
| 0.5 | 0.000228 | 15.30474 | 429.4644 | 640.8440 | 1309.876 | ||
| 1 | 1.66 × 10−5 | 21.26517 | 443.7296 | 661.7879 | 1352.664 | ||
| Natural Frequency (MHz) | |||||||
|---|---|---|---|---|---|---|---|
| 2 | 0 | 0 | 72.88189 | 457.6423 | 1290.903 | 2536.334 | 4475.916 |
| 0.1 | 72.91487 | 457.8494 | 1291.487 | 2537.481 | 4477.941 | ||
| 0.5 | 73.70190 | 462.7914 | 1305.428 | 2564.871 | 4526.275 | ||
| 1 | 76.10896 | 477.9059 | 1348.062 | 2648.638 | 4674.101 | ||
| 0.5 | 0 | 53.20652 | 417.1568 | 1258.329 | 2512.959 | 4589.336 | |
| 0.1 | 53.23060 | 417.3456 | 1258.898 | 2514.097 | 4591.412 | ||
| 0.5 | 53.80516 | 421.8504 | 1272.486 | 2541.234 | 4640.972 | ||
| 1 | 55.56241 | 435.6277 | 1314.045 | 2624.229 | 4792.543 | ||
| 1 | 0 | 38.22259 | 379.7801 | 1234.672 | 2504.318 | 4735.686 | |
| 0.1 | 38.23989 | 379.9519 | 1235.231 | 2505.451 | 4737.829 | ||
| 0.5 | 38.65265 | 384.0531 | 1248.564 | 2532.495 | 4788.969 | ||
| 1 | 39.91502 | 396.5960 | 1289.341 | 2615.205 | 4945.374 | ||
| 5 | 0 | 1.919722 | 145.8122 | 1431.766 | 3013.441 | 6965.49 | |
| 0.1 | 1.920590 | 145.8782 | 1432.414 | 3014.804 | 6968.642 | ||
| 0.5 | 1.941321 | 147.4528 | 1447.876 | 3047.346 | 7043.861 | ||
| 1 | 2.004724 | 152.2685 | 1495.162 | 3146.870 | 7273.909 | ||
| 10 | 0 | 0 | 2.915276 | 18.30569 | 51.63613 | 101.4534 | 179.0366 |
| 0.1 | 2.916595 | 18.31398 | 51.65949 | 101.4993 | 179.1176 | ||
| 0.5 | 2.948076 | 18.51166 | 52.21710 | 102.5948 | 181.0510 | ||
| 1 | 3.044358 | 19.11623 | 53.92248 | 105.9455 | 186.9640 | ||
| 0.5 | 0 | 0.523811 | 11.20938 | 48.88157 | 102.9362 | 214.2888 | |
| 0.1 | 0.524048 | 11.21445 | 48.90369 | 102.9828 | 214.3857 | ||
| 0.5 | 0.529704 | 11.33550 | 49.43155 | 104.0944 | 216.6998 | ||
| 1 | 0.547004 | 11.70571 | 51.04596 | 107.4941 | 223.7771 | ||
| 1 | 0 | 0.076789 | 5.832488 | 57.27066 | 120.5376 | 278.6196 | |
| 0.1 | 0.076824 | 5.835127 | 57.29657 | 120.5922 | 278.7457 | ||
| 0.5 | 0.077653 | 5.898111 | 57.91503 | 121.8938 | 281.7544 | ||
| 1 | 0.080189 | 6.090739 | 59.80650 | 125.8748 | 290.9564 | ||
| 5 | 0 | 9.66 × 10−5 | 0.014512 | 591.1270 | 855.0637 | 1978.064 | |
| 0.1 | 0.000138 | 0.014404 | 591.3888 | 855.4374 | 1978.953 | ||
| 0.5 | 5.77 × 10−5 | 0.014593 | 597.7759 | 864.6805 | 2000.319 | ||
| 1 | 0.000215 | 0.015137 | 617.2996 | 892.9213 | 2065.648 | ||
| 20 | 0 | 0 | 0.728819 | 4.576423 | 12.90903 | 25.36334 | 44.75916 |
| 0.1 | 0.729149 | 4.578494 | 12.91487 | 25.37481 | 44.77941 | ||
| 0.5 | 0.737019 | 4.627914 | 13.05428 | 25.64871 | 45.26275 | ||
| 1 | 0.761090 | 4.779059 | 13.48062 | 26.48638 | 46.74101 | ||
| 0.5 | 0 | 0.019197 | 1.458122 | 14.31766 | 30.13441 | 69.65490 | |
| 0.1 | 0.019206 | 1.458782 | 14.32414 | 30.14804 | 69.68642 | ||
| 0.5 | 0.019413 | 1.474528 | 14.47876 | 30.47346 | 70.43861 | ||
| 1 | 0.020047 | 1.522685 | 14.95162 | 31.46870 | 72.73909 | ||
| 1 | 0 | 0.000505 | 0.257315 | 28.78270 | 50.96007 | 123.7777 | |
| 0.1 | 0.000505 | 0.257432 | 28.79573 | 50.98313 | 123.8337 | ||
| 0.5 | 0.000511 | 0.260210 | 29.10654 | 51.53344 | 125.1703 | ||
| 1 | 0.000528 | 0.268709 | 30.05715 | 53.21649 | 129.2583 | ||
| 5 | 0 | 3 × 10−5 | 0.000409 | 47.09510 | 652.2625 | 1516.248 | |
| 0.1 | 6.75 × 10−5 | 0.000338 | 47.13148 | 652.5578 | 1516.935 | ||
| 0.5 | 3.73 × 10−5 | 0.000278 | 47.53909 | 659.6012 | 1533.308 | ||
| 1 | 3.23 × 10−5 | 0.000304 | 49.23231 | 681.1439 | 1583.385 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jouneghani, F.Z.; Babamoradi, H.; Dimitri, R.; Tornabene, F. A Modified Couple Stress Elasticity for Non-Uniform Composite Laminated Beams Based on the Ritz Formulation. Molecules 2020, 25, 1404. https://doi.org/10.3390/molecules25061404
Jouneghani FZ, Babamoradi H, Dimitri R, Tornabene F. A Modified Couple Stress Elasticity for Non-Uniform Composite Laminated Beams Based on the Ritz Formulation. Molecules. 2020; 25(6):1404. https://doi.org/10.3390/molecules25061404
Chicago/Turabian StyleJouneghani, Farajollah Zare, Hamidraza Babamoradi, Rossana Dimitri, and Francesco Tornabene. 2020. "A Modified Couple Stress Elasticity for Non-Uniform Composite Laminated Beams Based on the Ritz Formulation" Molecules 25, no. 6: 1404. https://doi.org/10.3390/molecules25061404
APA StyleJouneghani, F. Z., Babamoradi, H., Dimitri, R., & Tornabene, F. (2020). A Modified Couple Stress Elasticity for Non-Uniform Composite Laminated Beams Based on the Ritz Formulation. Molecules, 25(6), 1404. https://doi.org/10.3390/molecules25061404









