Physical Properties of Molecules and Condensed Materials Governed by Onsite Repulsion, Spin-Orbit Coupling and Polarizability of Their Constituent Atoms
Abstract
1. Introduction
2. Inadequacy of the Aufbau Principle
2.1. Low-Spin vs. High-Spin States
2.2. Extension of Hund’s Rule
2.3. Limits of the One-Electron Picture
1e = (xy, x2-y2) = (|2, 2〉, |2, -2〉)
2e = (xz, yz) = (|2, 1〉, |2, -1〉)
3. Effect of Onsite Repulsion on the relative Stabilities of Metallic and Magnetic Insulating States
3.1. One-Electron Approximation
3.2. Magnetic Insulating State Induced by Onsite Repulsion
3.3. Need to Consider beyond Onsite Repulsion
4. Effect of Spin-Orbit Coupling
4.1. Energy of SOC
4.2. Dependence of the SOC Energy on the Spin Orientation
4.3. Magnetic Insulating State Induced by Spin-Orbit Coupling and Onsite Repulsion
4.4. Singlet to Triplet Transition
5. Polarizability
5.1. Induced Polarization, Polarizability and Second Harmonic Generation
5.2. Polarizabilities of Cations and Anions
6. Experimental Trends
6.1. Ionic Sizes and Oxidation States
6.2. Onsite Repulsion and d-Electron. Count
6.3. Onsite Repulsion and Spin Orbit Coupling
7. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- For Comprehensive Details on the History of the Periodic Table. Available online: https://en.wikipedia.org/wiki/History_of_the_periodic_table (accessed on 30 December 2019).
- Whangbo, M.-H. Mott-Hubbard conditions for electron localization in the Hartree-Fock band theory. J. Chem. Phys. 1979, 70, 4963. [Google Scholar] [CrossRef]
- Hay, P.J.; Thibeault, J.C.; Hoffmann, R. Orbital interactions in metal dimer complexes. J. Am. Chem. Soc. 1975, 97, 4884–4899. [Google Scholar] [CrossRef]
- Brasseur, G.P.; Solomon, S. Aeronomy of the Middle Atmosphere: Chemistry and Physics of the Stratosphere and Mesosphere; Springer: Dordrecht, The Netherlands, 2005. [Google Scholar]
- Hirai, K.; Itoh, T.; Tomioka, H. Persistent triplet carbenes. Chem. Rev. 2009, 109, 3275–3332. [Google Scholar] [CrossRef] [PubMed]
- Koo, H.-J.; Kasapbasi, E.E.; Whitten, J.L.; Whangbo, M.-H. The conceptual dilemma of the one-electron picture in describing the uniaxial magnetism at linear coordination sites. Eur. J. Inorg. Chem. 2019, 2630–2634. [Google Scholar] [CrossRef]
- Whangbo, M.-H.; Xiang, H.J.; Koo, H.-J.; Gordon, E.E.; Whitten, J.L. Electronic and structural factors controlling the spin orientations of magnetic Ions. Inorg. Chem. 2019, 58, 11854–11874. [Google Scholar] [CrossRef]
- Dai, D.; Whangbo, M.-H. Analysis of the uniaxial magnetic properties of high-spin d6 ions at trigonal prism and linear two-coordinate sites: Uniaxial magnetic properties of Ca3Co2O6 and Fe[C(SiMe3)3]2. Inorg. Chem. 2005, 44, 4407–4414. [Google Scholar] [CrossRef]
- Reiff, W.M.; LaPointe, A.M.; Witten, E.H. Virtual free ion magnetism and the absence of Jahn−Teller distortion in a linear two-coordinate complex of high-spin Iron(II). J. Am. Chem. Soc. 2004, 126, 10206–10207. [Google Scholar] [CrossRef]
- Zadrozny, J.M.; Xiao, D.J.; Atanasov, M.; Long, G.J.; Grandjean, F.; Neese, F.; Long, J.R. Magnetic blocking in a linear iron(I) complex. Nat. Chem. 2013, 5, 577–581. [Google Scholar] [CrossRef]
- Bunting, P.C.; Atanasov, M.; Damgaard-Møller, E.; Perfetti, M.; Grassee, I.; Orlita, M.; Overgaard, J.; van Slageren, J.; Neese, F.; Long, J.R. A linear Co(II) complex with maximal orbital angular momentum from non-Aufbau ground state. Science 2018, 362, 1378. [Google Scholar] [CrossRef]
- Atanasov, M.; Aravena, D.; Suturina, E.; Bill, E.; Magana, D.; Neese, F. First principles approach to the electronic structure, magnetic anisotropy and spin relaxation in mononuclear 3d-transition metal single molecule magnets. Coord. Chem. Rev. 2015, 289–290, 177–214. [Google Scholar] [CrossRef]
- Mott, N.F. Metal–Insulator Transition; Taylor & Francis Ltd.: London, UK, 1974. [Google Scholar]
- Xiang, H.J.; Whangbo, M.-H. Cooperative effect of electron correlation and spin-orbit coupling on the electronic and magnetic properties of Ba2NaOsO6. Phys. Rev. B. 2007, 75, 052407. [Google Scholar] [CrossRef]
- Erickson, A.S.; Misra, S.; Miller, G.J.; Gupta, R.R.; Schlesinger, Z.; Harrison, W.A.; Kim, J.M.; Fisher, I.R. Ferromagnetism in the Mott Insulator Ba2NaOsO6. Phys. Rev. Lett. 2007, 99, 016404. [Google Scholar] [CrossRef] [PubMed]
- Dai, D.; Xiang, H.J.; Whangbo, M.-H. Effects of spin-orbit coupling on magnetic properties of discrete and extended magnetic systems. J. Comput. Chem. 2008, 29, 2187–2209. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Yan, D.; Yesudhas, S.; Deng, H.; Xiao, H.; Chen, B.; Sereika, R.; Yin, X.; Yi, C.; Shi, Y.; et al. Lattice frustration in spin-orbit Mott insulator Sr3Ir2O7 at high pressure. NJP Quantum Mater. 2019, 4, 23. [Google Scholar] [CrossRef]
- Albright, T.A.; Burdett, J.K.; Whangbo, M.-H. Orbital Interactions in Chemistry, 2nd ed.; Wiley: New York, NY, USA, 2013. [Google Scholar]
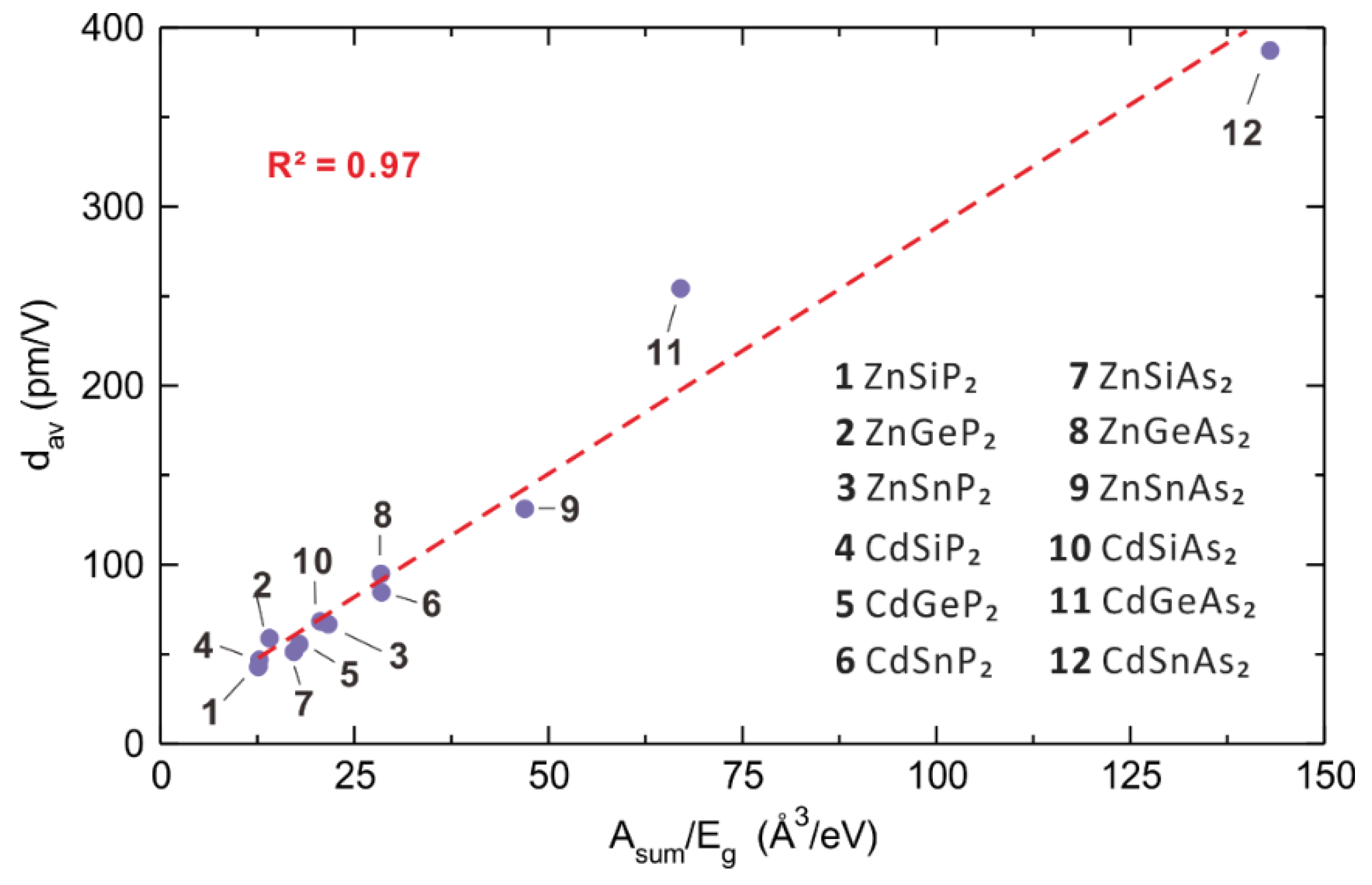
- Cheng, X.Y.; Whangbo, M.-H.; Hong, M.C.; Deng, S. Dependence of the second-harmonic generation response on the cell volume to bandgap ratio. Inorg. Chem. 2019, 58, 9572–9575. [Google Scholar] [CrossRef]
- Miller, R.C. Optical second harmonic generation in piezoelectric crystals. Appl. Phys. Lett. 1964, 5, 17. [Google Scholar] [CrossRef]
- Shannon, R.D.; Fischer, R.X. Empirical electronic polarizabilities of ions for the prediction and interpretation of refractive indices: Oxides and oxysalts. Am. Mineral. 2016, 101, 2288–2300. [Google Scholar] [CrossRef]
- Sadlej, A.J. Static dipole polarizability of the fluoride ion. J. Phys. Chem. 1979, 83, 1653–1957. [Google Scholar] [CrossRef]
- Qi, J.; Xue, D.; Ratajczak, H.; Ning, G. Electronic polarizability of the oxide ion and density of binary silicate, borate and phosphate oxide glasses. Phys. B: Condensed Matter 2004, 349, 265–269. [Google Scholar] [CrossRef]
- Wilson, J.N.; Curtis, R.M. Dipole polarizabilities of ions in alkali halide crystals. J. Phys. Chem. 1970, 1, 187–196. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. A. 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Cheng, X.Y.; Li, Z.H.; Wu, X.-T.; Hong, M.C.; Whangbo, M.-H.; Deng, S. Key factors leading to large second harmonic generation in nonlinear optical materials. ACS Appl. Mater. Interface 2020. [Google Scholar] [CrossRef] [PubMed]
- Witczak-Krempa, W.; Chen, G.; Kim, Y.B.; Balents, L. Correlated quantum phenomena in the strong spin-orbit regime. Annu. Rev. Condens. Matter Phys. 2014, 5, 57–82. [Google Scholar] [CrossRef]








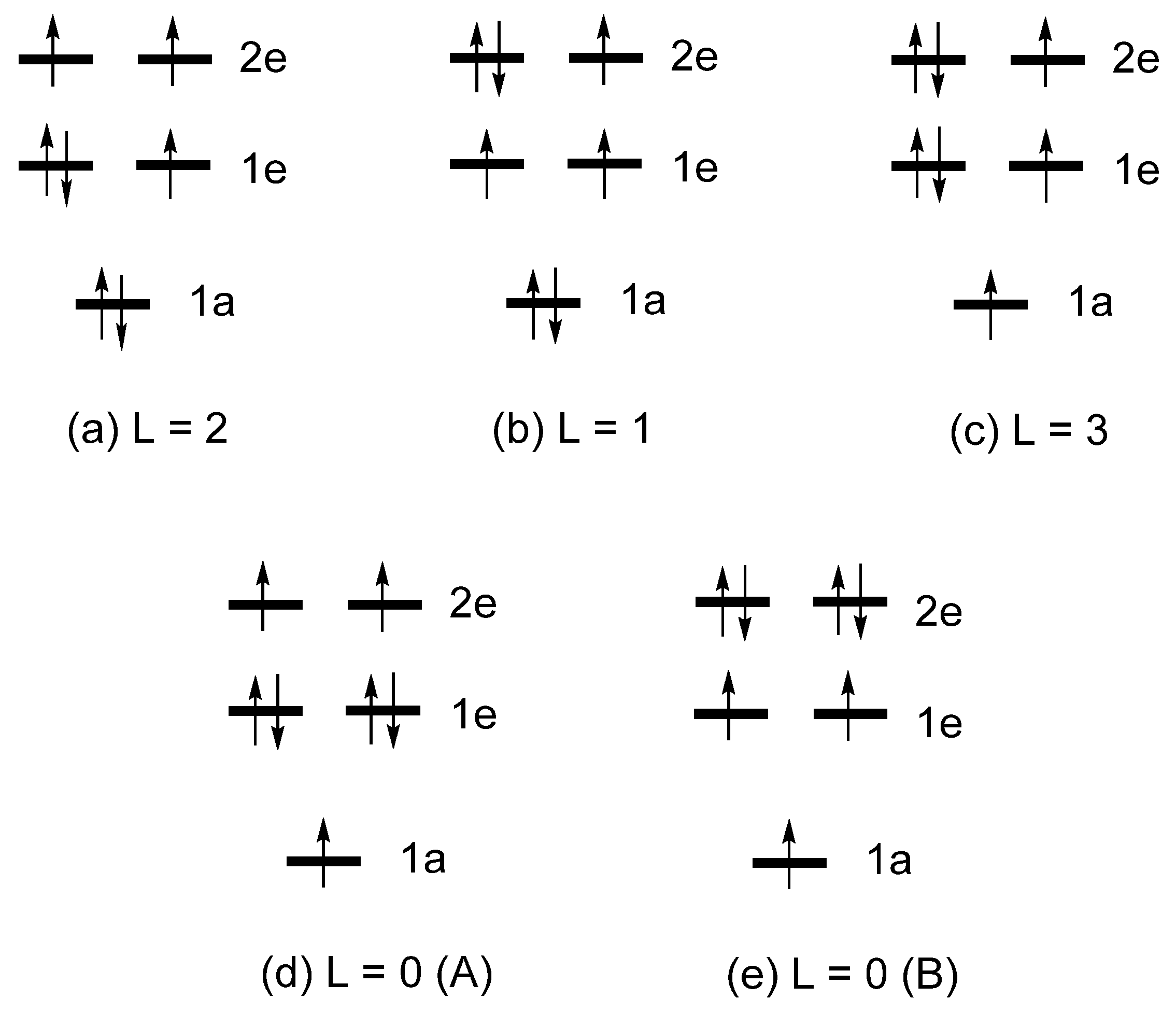















© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maggard, P.A.; Cheng, X.; Deng, S.; Whangbo, M.-H. Physical Properties of Molecules and Condensed Materials Governed by Onsite Repulsion, Spin-Orbit Coupling and Polarizability of Their Constituent Atoms. Molecules 2020, 25, 867. https://doi.org/10.3390/molecules25040867
Maggard PA, Cheng X, Deng S, Whangbo M-H. Physical Properties of Molecules and Condensed Materials Governed by Onsite Repulsion, Spin-Orbit Coupling and Polarizability of Their Constituent Atoms. Molecules. 2020; 25(4):867. https://doi.org/10.3390/molecules25040867
Chicago/Turabian StyleMaggard, Paul A., Xiyue Cheng, Shuiquan Deng, and Myung-Hwan Whangbo. 2020. "Physical Properties of Molecules and Condensed Materials Governed by Onsite Repulsion, Spin-Orbit Coupling and Polarizability of Their Constituent Atoms" Molecules 25, no. 4: 867. https://doi.org/10.3390/molecules25040867
APA StyleMaggard, P. A., Cheng, X., Deng, S., & Whangbo, M.-H. (2020). Physical Properties of Molecules and Condensed Materials Governed by Onsite Repulsion, Spin-Orbit Coupling and Polarizability of Their Constituent Atoms. Molecules, 25(4), 867. https://doi.org/10.3390/molecules25040867








