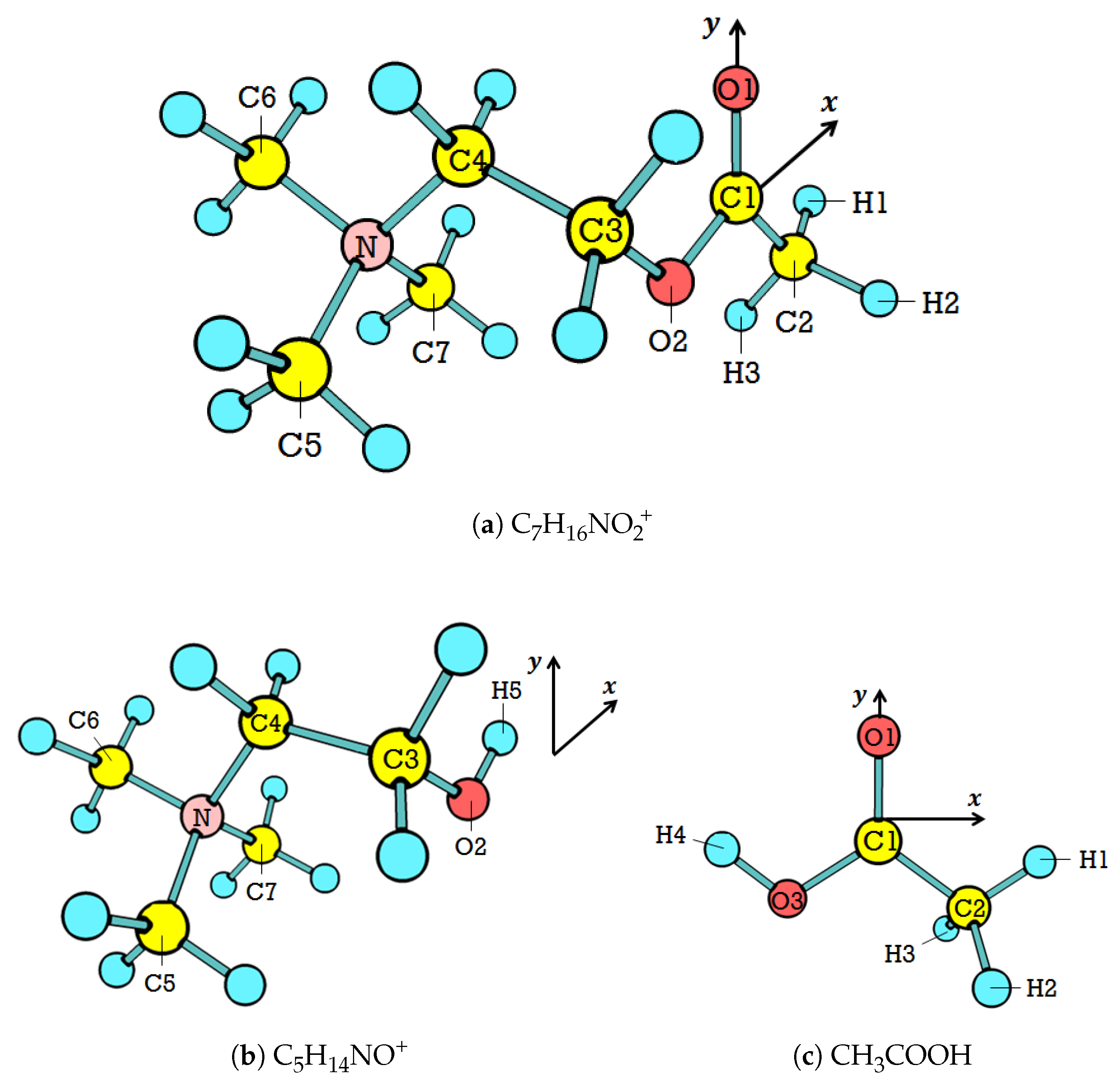
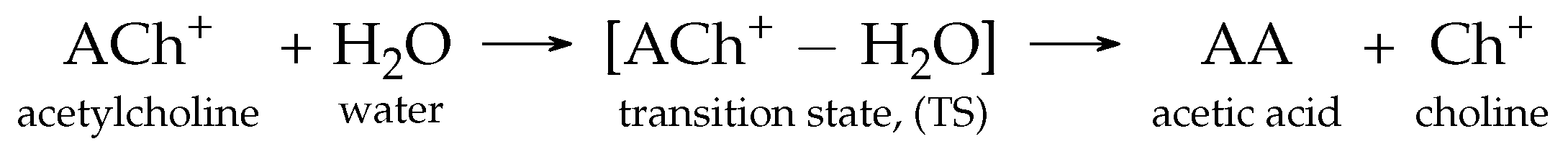3.1. The Ground-State Structure
Table 2 presents the discrepancy in geometry between the experimental value and our calculations for
in the ground state. The experimental values are from the crystal structure [
29], which is comparable to our calculations in the gas phase. Overall, the values of
are within the accuracy limit, according to Young [
38]. It implies that B3LYP functional and the 6-311++G(d,p) basis set are appropriate for studying
.
The optimization routine calculations predict the stable conformer for both
and
. The cartesian coordinates of the stable conformers are given in the
Supplementary Materials. Only seven out of 64 potential
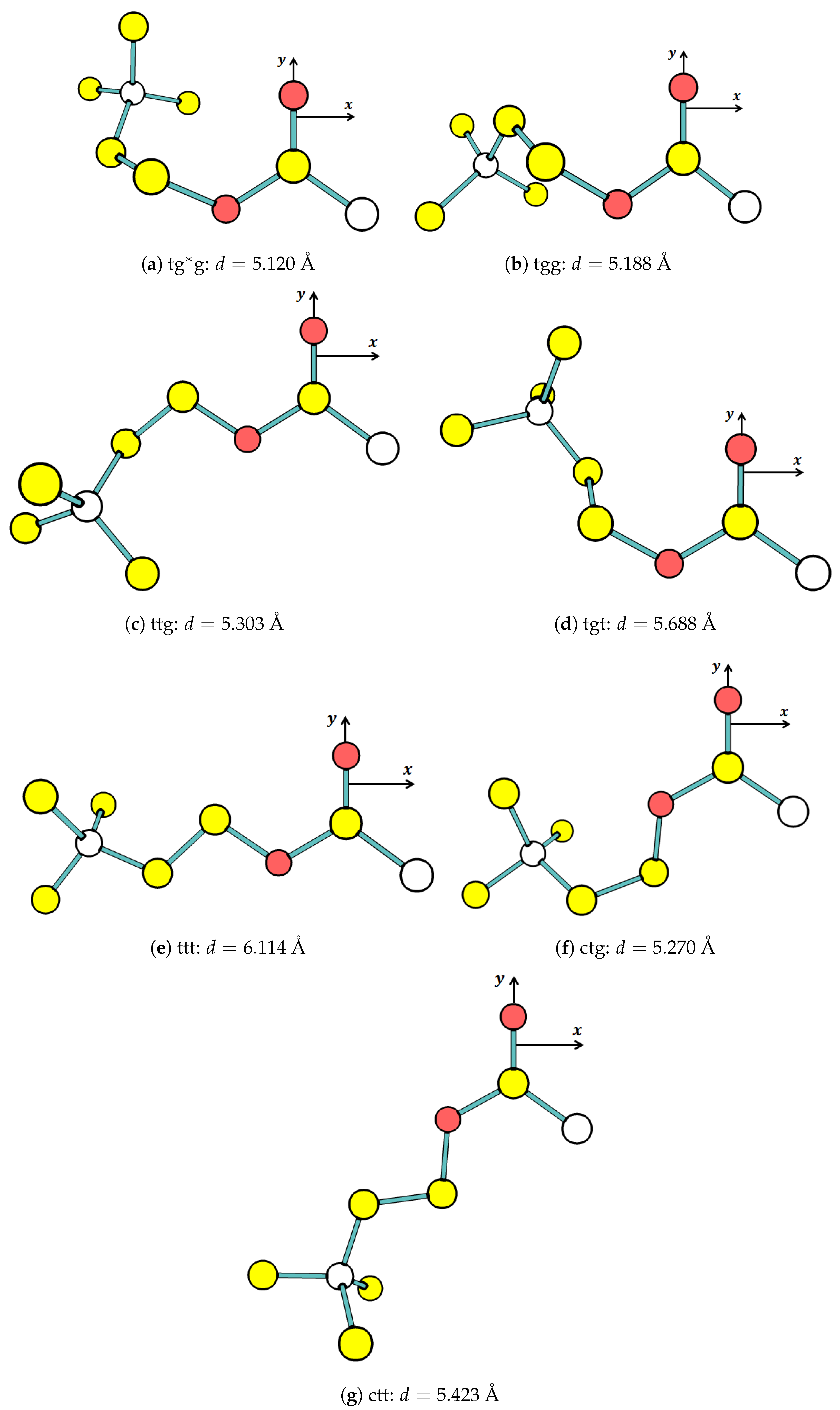
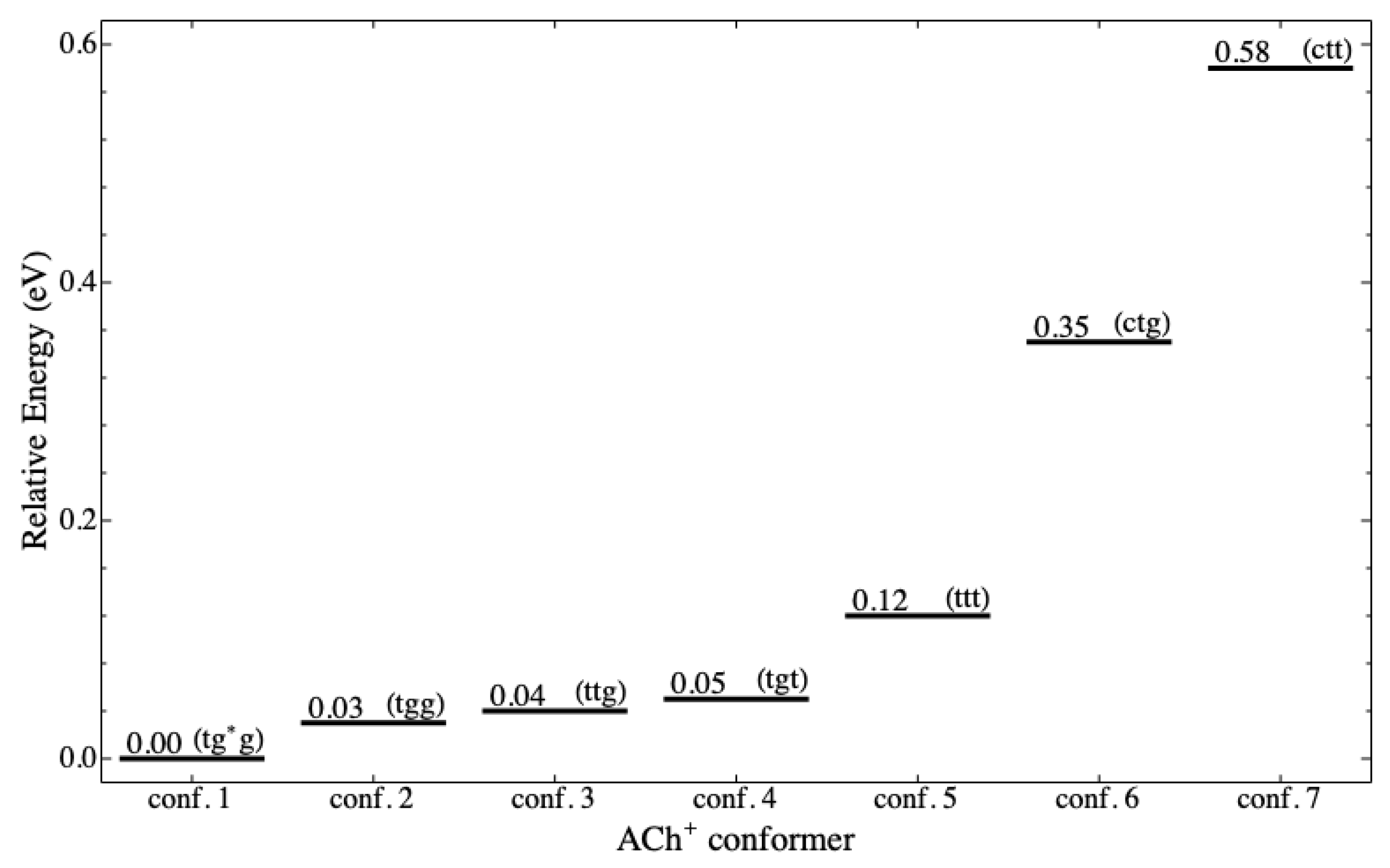
conformers are stable in the ground state, as shown in
Figure 3. For
, there are only two possible out of 16 potential conformers.
Table 3 and
Table 4 resume the results for
and
, respectively. In both
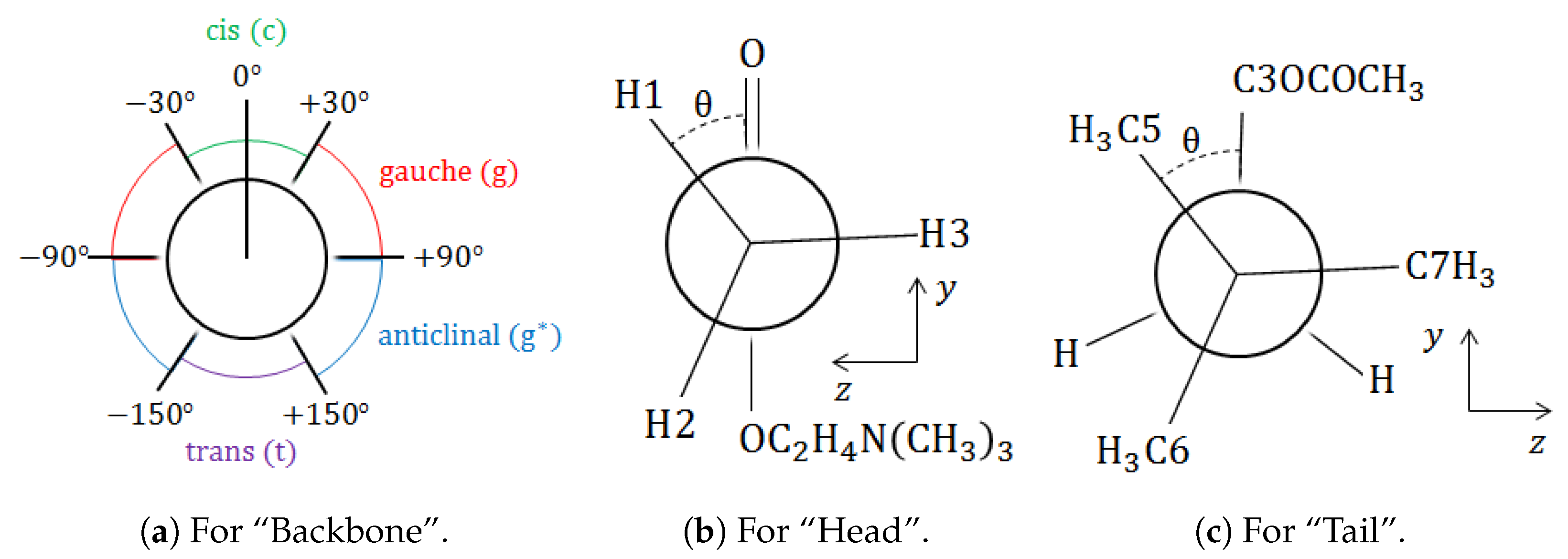
and
, the spans of the dihedral angle are more significant than those of bond lengths and bond angles, which is as expected. That is to say that the backbone determines the conformation, whereas the head (for
only) is always eclipsed and the tail is always staggered.
Figure 4 shows the energy level diagram (ELD) for the seven stable
conformers in eV (1 eV ≈ 23.06 kcal/mol). It is clear from the energy level that there are two groups of conformers, which are low and high level. The low-level group is more stable than the high-level group. The five
conformers (tg*g, tgg, ttg, tgt, and ttt) are in the low-level group (
Figure 3a–e), and the other two conformers (ctg and ctt) are in the high-level group (
Figure 3f,g). Other computational studies [
20,
23,
39,
40] also conclude the stability of the five low-level conformers. It is important to note that our results support the experiments that observed
(tg*g), (tgg), and (ttg) in their stable states [
29,
41,
42].
The ELD displays three noticeable patterns of the conformation related to stability as individual molecules. The first is that gauche conformation at cannot achieve stability, whereas trans and cis can. The second is that cis at and cannot achieve the stability, whereas trans and gauche (and anticlinal) can. The second pattern is as expected because the cis conformation causes two bulky groups (acetyl and trimethylamine) to be ecliptic, leading to a repulsive interaction among atoms of the two groups. The third is that gauche conformation at and makes more stable than when they are trans; therefore, at the same , it is possible to arrange the order of stability (based on and ), from the most to the least stable, as gg, tg, gt, and tt. In addition to the third pattern, it appears that the stability is more dependent on than .
Charge distributions align with this pattern. The overall NBO calculations determine that more electrons are distributed in the head, resulting in the tail being positively charged (see
Table 5). It agrees with the typical
structure [
43]. The shorter the head–tail distance, the stronger the coulombic interaction and, consequently, the more stable the conformer. Therefore, the backbone and the tail must curl up in order to shorten the head–tail distance. Such curling behavior does not only exist in gas phase but also in solvent [
18,
20,
23,
27]. The
gauche conformation at
and
meets the condition, particularly at
, where the head–tail distance is the shortest.
Figure 3 depicts the circumstance, in which the distance gradually increases from the shortest in the g*g conformation to the longest in the tt conformation for the low-level group and from the shortest tg to the longest tt for the high-level group.
Additionally, the charge distribution shown in
Table 5 indicates an electrophilic site of all
stable conformers. It is in the backbone, where C1 is located. This site is typical for the ester family. According to our study on ethyl acetate neutral hydrolysis [
28], the activated complex (
–water) forms between C1 and O3, the nucleophilic site of water.
The electrophilic site of the
conformers gives a hint to the cleaving location during the hydrolysis. The cleaving location shall be the C1–O2 bond. Therefore, we extracted the C1–O2 bonding atomic orbital from the NBO calculations as listed in
Table 6. All conformers have an average bonding orbital of 0.5464 C
+ 0.8375 O
. This bonding is relatively weaker than the C1–O2 bond of ethyl acetate, which is 0.5898 C
+ 0.8076 O
[
28]. It suggests that the neutral hydrolysis of
is easier than that of ethyl acetate.
3.2. The Transition State Structure
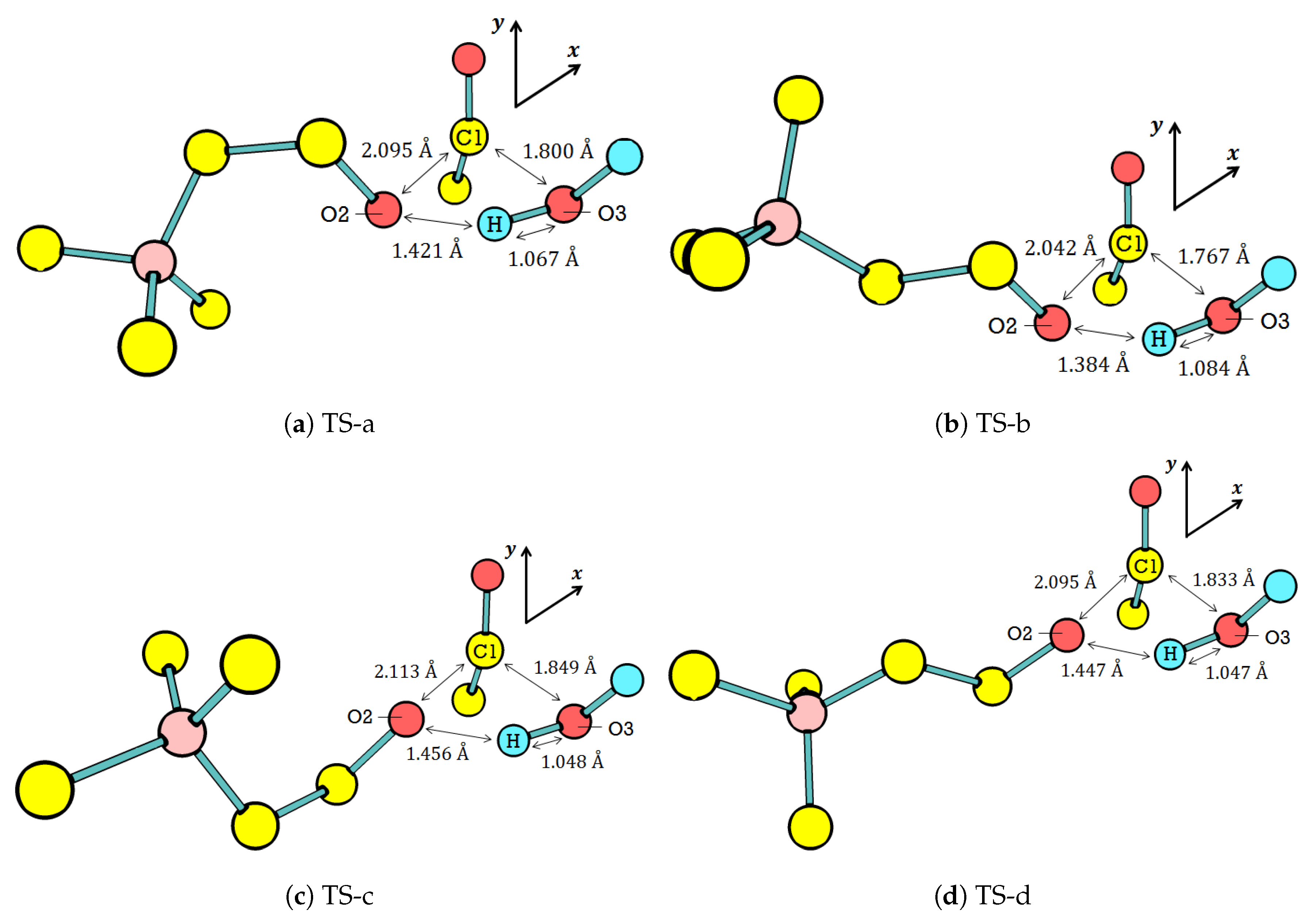
The calculations narrow down the TS geometry from seven possible reactants to four [
–water] activated complexes. The cartesian coordinates of the four activated complexes are given in the
Supplementary Materials.
Table 7 lists the seven possible reactants (codes Re1–Re7).
Figure 5 displays the optimized activated complex of these four [
–water]. The overall orientation of water with respect to
is similar to our previous study on [ethyl acetate–water] activated complex [
28]. This similarity suggests that
neutral hydrolysis resembles base-induced ester hydrolysis.
The
–water interaction in all four possible TSs elongates C1–O2, which makes it an important parameter since it is the cleaving location, as we have discussed in
Table 6. The elongation of C1–O2 is around 50% (from 1.40 Å (
Table 3) to 2.10 Å (
Figure 5)). It is significantly larger than that of the C1–O2 in ethyl acetate–water interaction, which is around 33% [
28]. The large C1–O2 elongation is explainable according to the bonding orbital of C1–O2 described in
Table 6. The bond in
is weaker than that in ethyl acetate; therefore, the bond is easier to break in
relative to ethyl acetate. Consequently,
neutral hydrolysis is expected be faster than that of ethyl acetate. This expectation agrees with the experimental data showing that, at room temperature, the rate constant of the former is
/s [
44], whereas that of the latter is
/s [
45].
In addition to the C1–O2 elongation, there are two other similarities among the four TS geometries. First, the elongation is large enough to split the acetyl group from the rest of . For comparison, the generalization of C–O bond lengths in saturated molecules, like , has been widely assumed as 1.43 Å. Meanwhile, the O3 of water is still too far from C1 to form a covalent bond. The activated complex thus consists of three groups: water, acetyl, and choline. The three groups interact with each other through noncovalent interactions to form the activated complex, which lies on the TS. Second, prefers the curling and in the presence of water. The curling and relates the in the TS to the one in the ground state: (ttg), (tgt), (ctg), and (ctt). Since the curling, and also affect the C2–N distance and the seven conformers are grouped into three curling levels. The levels are extreme (d < 5.20 Å), medium (5.30 < d < 5.70 Å), and low (d > 5.70 Å). Accordingly, all TS geometries require the medium curling level of conformers.
Among the four TS geometries, TS-b is the most favorable one for product formation. Generally, the product formation requires the elongation of C1–O2 and O3–H in the TS with respect to the ground state, as well as shortening the distances of C1–O3 and O2–H (distances between groups in the activated complex). The shortened C1–O3 and O2–H promote the formation of and , respectively. TS-b meets most of the requirements for product formation as its O3–H is the longest, whereas its C1–O3 and O2–H are the shortest among the four TS geometries.
3.3. The Reaction Coordinate
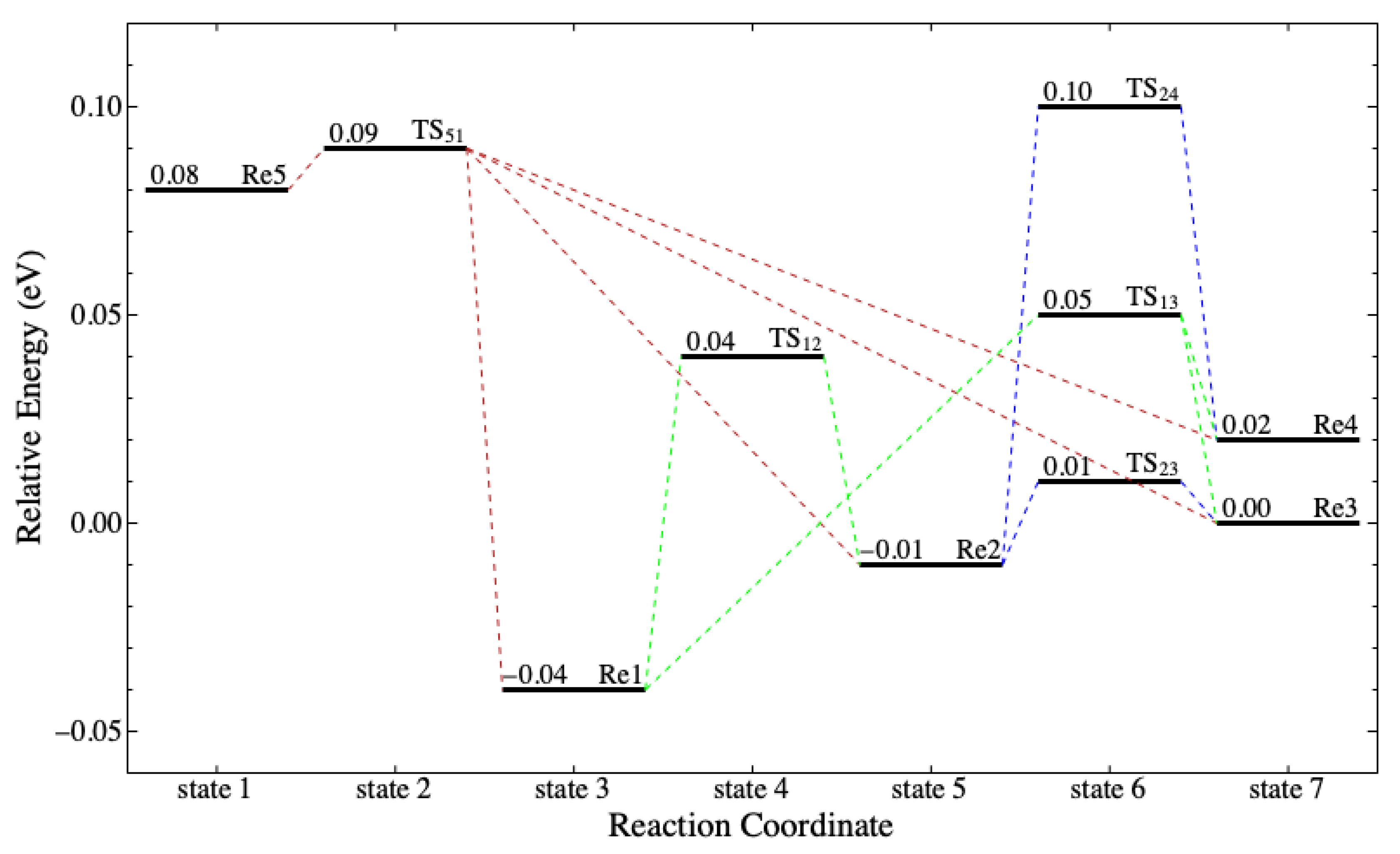
Figure 6 shows the neutral hydrolysis reaction coordinate in the ELD. The ELD involves four out of the seven potential reactants (see
Table 7) capable of forming the activated complex at the TS through a one-step mechanism. The possible reactants are Re3, Re4, Re6, and Re7, which are related to the aforementioned
curling levels. The possible products are Pr1 and Pr2, which comprise
(tg) and
(tt) from
Table 4. Although the TS depends on the curling levels of
and
of the
conformers, the products depend only on
. Since
does not contain the electrophilic site, it does not change when
is hydrolyzed into
.
Figure 7 shows the pre-hydrolysis reaction coordinate in the ELD. There are three out of seven potential reactants that require a pre-hydrolysis process (Re1, Re2, and Re5). These reactants need to undergo conformational isomerization to form either
(ttg) or (tgt) with the energy barriers at no more than 0.11 eV. It implies that the conformational isomerization can occur by thermal energy. Together with
Figure 6,
Figure 7 suggests that all seven potential reactants can perform hydrolysis in four pathways. The reactants with the low-level group of
conformers go through Re3 or Re4 before going to either TS-a or TS-b. Both pathways are possible because the energy barrier to form Re3 and Re4 is no more than 0.11 eV. Meanwhile, the reactants with the high-level group of
conformers go directly to TS-c and TS-d.
Table 8 shows the
for all possible reaction coordinates in
Figure 6 and
Figure 7. The calculations of
suggest that reactants with the high-level
conformers are always exothermic and go toward either Pr1 or Pr2. Meanwhile, reactants from the low-level group are exothermic if they go toward Pr1, but they are endothermic if they go toward Pr2. Experimentally, the reaction is endothermic, with
being
kcal/mol [
46]. According to our results, Pr2 is mostly the product of the hydrolysis. In particular, the experiment observed mostly reactions (viii) or (ix), suggesting that the practically preferred
conformer undergoes neutral hydrolysis, which is (tgt) or (ttt). It is worthwhile to mention that our results are in line with the study of Zhorov et al. [
47], which suggest that
with
and
being
trans is productive for the
hydrolysis catalyzed by acetylcholinesterase (AChE), as well as the study of Chothia and Pauling [
48], which suggests that the
conformation relevant for its interaction with AChE is the one with
,
, and
being
trans.
In addition to
,
Table 8 shows
. As expected,
of reactants with the high-level
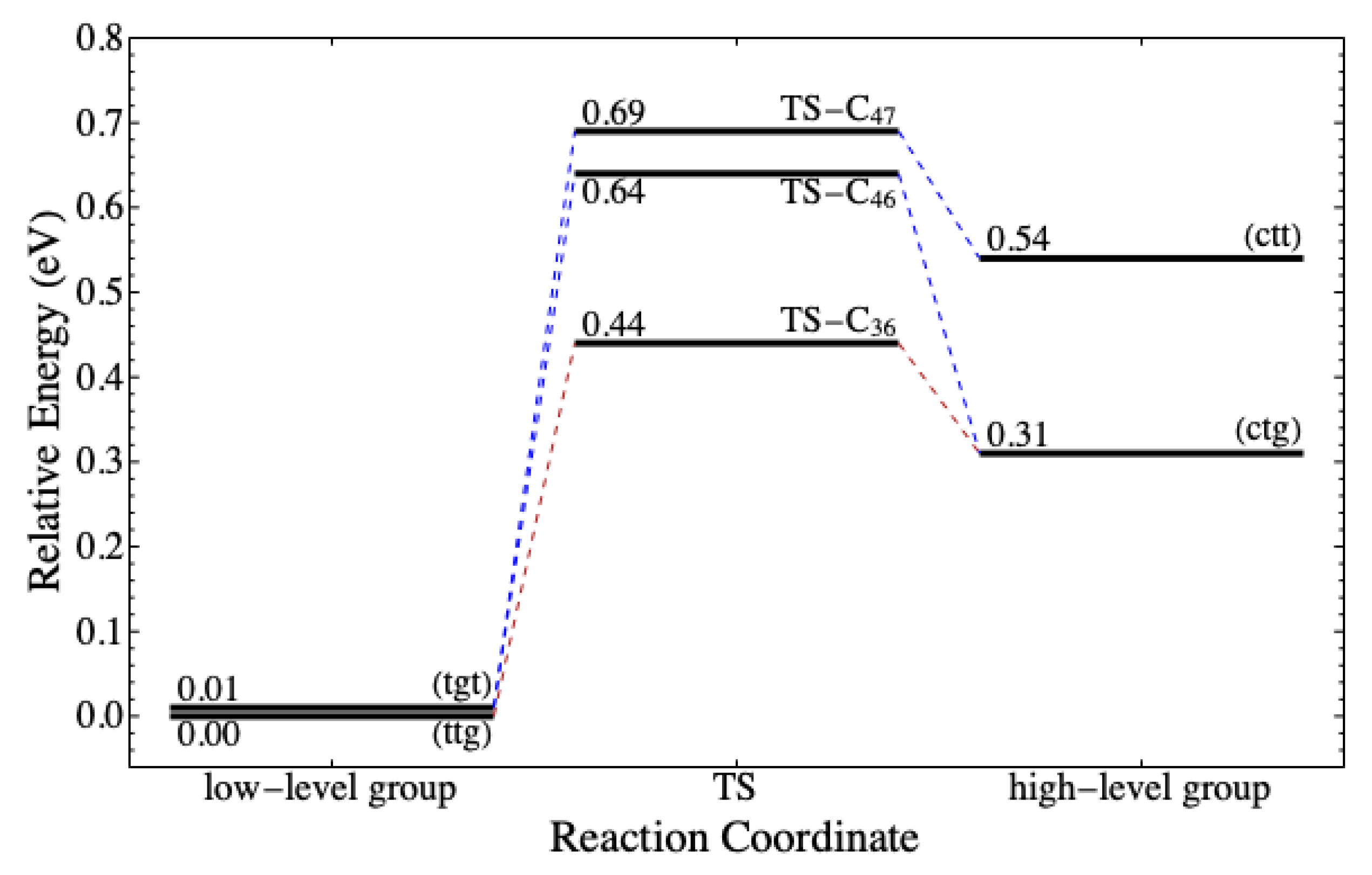
conformers are lower than that of reactants with the low-level conformers. Consequently, reactions (v) and (x) are favorable to occur due to the low activation energy and the high exothermicity. However, the energy level of both
(ctt) and (ctg) are more than 0.30 eV higher than the most stable conformer. They can transform to
(tgt) and (ttg) via conformational isomerization according to the reaction coordinate depicted in
Figure 8. The energy barrier is no more than 0.33 eV, which is still in the order of thermal energy. It implies that, despite a low
, the number of
(ctt) and (ctg) in nature is likely lower than that in the low-level group.