Memory Effect in the Spatial Series Based on Diamond and Graphite Crystals
Abstract
1. Introduction
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gaite, J. The fractal geometry of the cosmic web and its formation. Adv. Astron. 2019, 6587138. [Google Scholar] [CrossRef]
- Grizzi, F.; Castello, A.; Qehajaj, D.; Russo, C.; Lopci, E. The complexity and fractal geometry of nuclear medicine images. Mol. Imaging Biol. 2019, 21, 401–409. [Google Scholar] [CrossRef] [PubMed]
- Quaranta, G.; Lacarbonara, W.; Masri, S.F. A review on computational intelligence for identification of nonlinear dynamical systems. Nonlinear Dyn. 2020, 99, 1709–1761. [Google Scholar] [CrossRef]
- Covas, E. Spatial-temporal forecasting the sunspot diagram. Astron. Astrophys. 2017, 605, A44. [Google Scholar] [CrossRef]
- Ma, K.; Guo, L.; Liu, W. Investigation of the spatial clustering properties of seismic time series: A comparative study from shallow to intermediate-depth earthquakes. Complexity 2018, 7169482. [Google Scholar] [CrossRef]
- Roca, J.L.; Rodríguez-Bermúdez, G.; Fernández-Martínez, M. Fractal-based techniques for physiological time series: An updated approach. Open Phys. 2018, 16, 741–750. [Google Scholar] [CrossRef]
- Krzyszczak, J.; Baranowski, P.; Zubik, M.; Kazandjiev, V.; Georgieva, V.; Sławiński, C.; Siwek, K.; Kozyra, J.; Nieróbca, A. Multifractal characterization and comparison of meteorological time series from two climatic zones. Theor. Appl. Climatol. 2019, 137, 1811–1824. [Google Scholar] [CrossRef]
- Jiang, Z.-Q.; Xie, W.-J.; Zhou, W.-X.; Sornette, D. Multifractal analysis of financial markets: A review. Rep. Prog. Phys. 2019, 82, 125901. [Google Scholar] [CrossRef]
- Karain, W.I. Detecting transitions in protein dynamics using a recurrence quantification analysis based bootstrap method. BMC Bioinform. 2017, 18, 525. [Google Scholar] [CrossRef]
- Cramer, J.A.; Booksh, K.S. Chaos theory in chemistry and chemometrics: A review. J. Chemom. 2006, 20, 447–454. [Google Scholar] [CrossRef]
- Mandelbrot, B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed]
- Eke, A.; Herman, P.; Kocsis, L.; Kozak, L.R. Fractal characterization of complexity in temporal physiological signals. Physiol. Meas. 2002, 23, R1–R38. [Google Scholar] [CrossRef] [PubMed]
- Kristoufek, L. How are rescaled range analyses affected by different memory and distributional properties? A Monte Carlo study. Physica A 2012, 391, 4252–4260. [Google Scholar] [CrossRef]
- Hurst, H. Long term storage capacity of reservoirs. Trans. Am. Soc. Civil. Eng. 1951, 116, 770–799. [Google Scholar]
- Peng, C.-K.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Quantification of scaling exponents and crossover phenomena in nonstationary heartbeat time series. Chaos 1995, 5, 82–87. [Google Scholar] [CrossRef]
- Shiomi, K.; Sato, H.; Ohtake, M. Broad-band power-law spectra of well-log data in Japan. Geophys. J. Int. 1997, 130, 57–64. [Google Scholar] [CrossRef]
- Simonsen, I.; Hansen, A.; Nes, O.M. Determination of the Hurst exponent by use of wavelet transforms. Phys. Rev. E 1998, 58, 2779–2787. [Google Scholar] [CrossRef]
- Grigorev, V.; Raevskii, O. Fractal dimension of the interatomic distance histogram: New 3D descriptor of molecular structure. Russ. J. Gen. Chem. 2011, 81, 449–455. [Google Scholar] [CrossRef]
- Grigorev, V.Y.; Grigoreva, L.D. Long-term memory effect in spatial series of model peptides composed of glycine and alanine. Mosc. Univ. Chem. Bull. 2019, 74, 216–222. [Google Scholar] [CrossRef]
- Grigorev, V.Y.; Grigoreva, L.D. The study of molecular histograms of interatomic distances in organic homologs on the basis of R/S analysis. Mosc. Univ. Chem. Bull. 2017, 72, 144–148. [Google Scholar] [CrossRef]
- Falcao, E.H.L.; Wudl, F. Carbon allotropes: Beyond graphite and diamond. J. Chem. Technol. Biotechnol. 2007, 82, 524–531. [Google Scholar] [CrossRef]
- Malamud, B.D.; Turcotte, D.L. Self-affine time series: I. Generation and analyses. Adv. Geophys. 1999, 40, 1–90. [Google Scholar] [CrossRef]
- Lopez-Lambrano, A.A.; Fuentes, C.; Lopez-Ramos, A.A.; Mata-Ramirez, J.; Lopez-Lambrano, M. Spatial and temporal Hurst exponent variability of rainfall series based on the climatological distribution in a semiarid region in Mexico. Atmosfera 2018, 31, 199–219. [Google Scholar] [CrossRef]
- Muratov, E.N.; Bajorath, J.; Sheridan, R.P.; Tetko, I.V.; Filimonov, D.; Poroikov, V.; Oprea, T.I.; Baskin, I.I.; Varnek, A.; Roitberg, A.; et al. QSAR without borders. Chem. Soc. Rev. 2020, 49, 3525–3564. [Google Scholar] [CrossRef]
- HyperChem. Available online: http://www.hyper.com (accessed on 10 October 2020).
- CrystalMaker. Available online: http://www.crystalmaker.com/index.html (accessed on 10 October 2020).
- AMCSD. Available online: http://rruff.geo.arizona.edu/AMS/minerals (accessed on 10 October 2020).
- CCDC. Available online: https://www.ccdc.cam.ac.uk (accessed on 10 October 2020).
- arXiv. Available online: https://arxiv.org/abs/0804.0747 (accessed on 10 October 2020).
- IMSL. Available online: https://docs.roguewave.com/en/imsl-main (accessed on 10 October 2020).

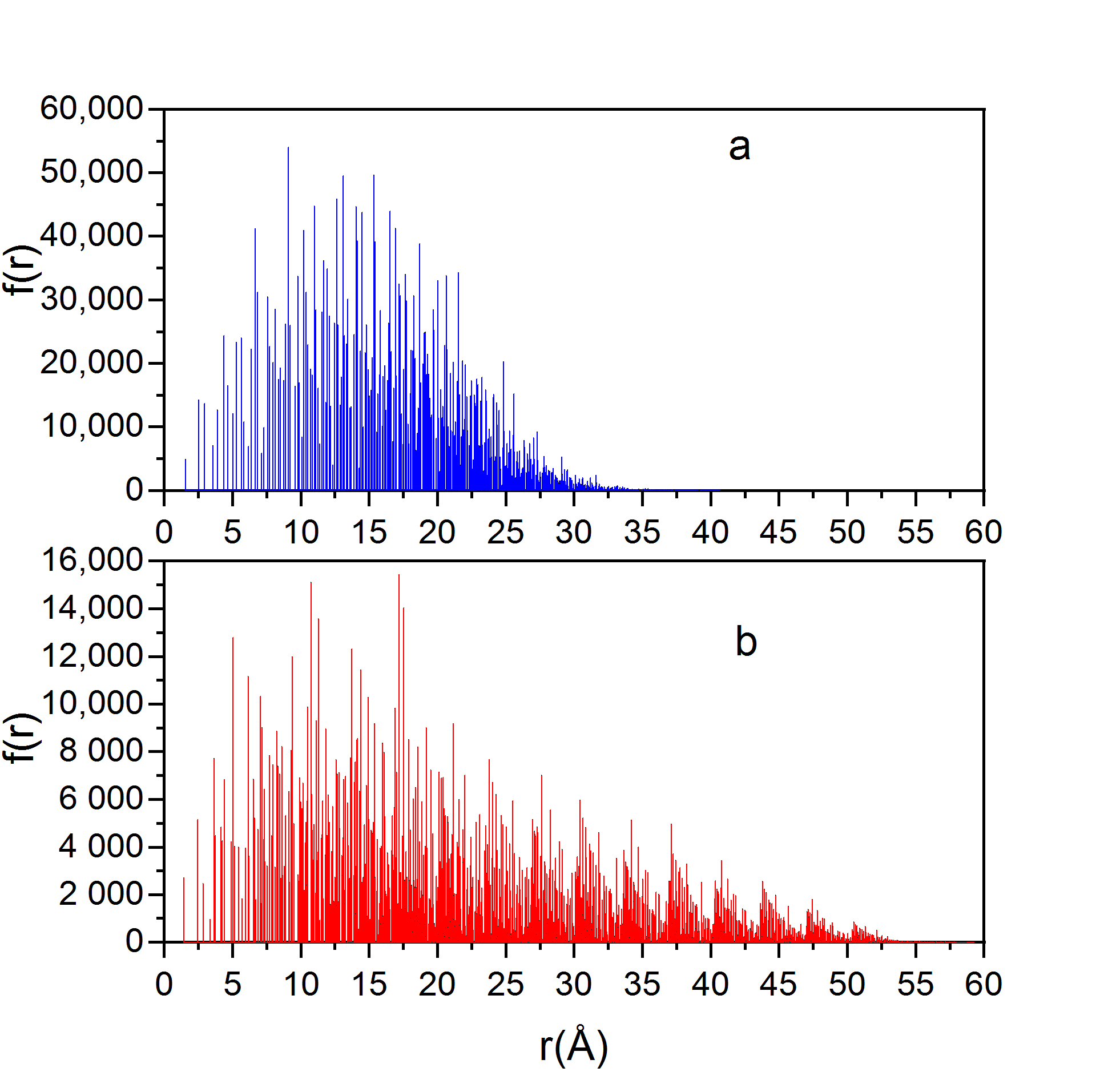
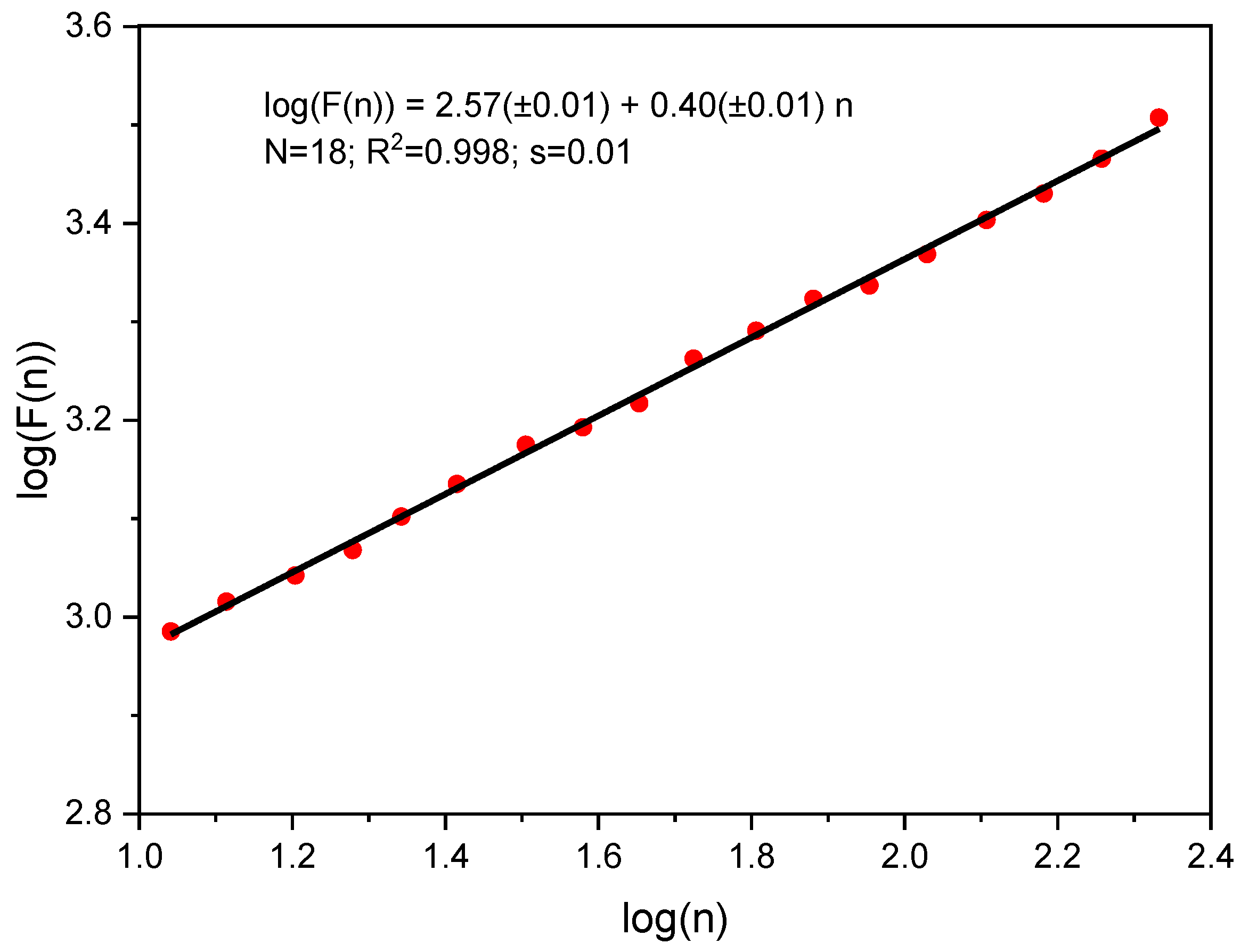
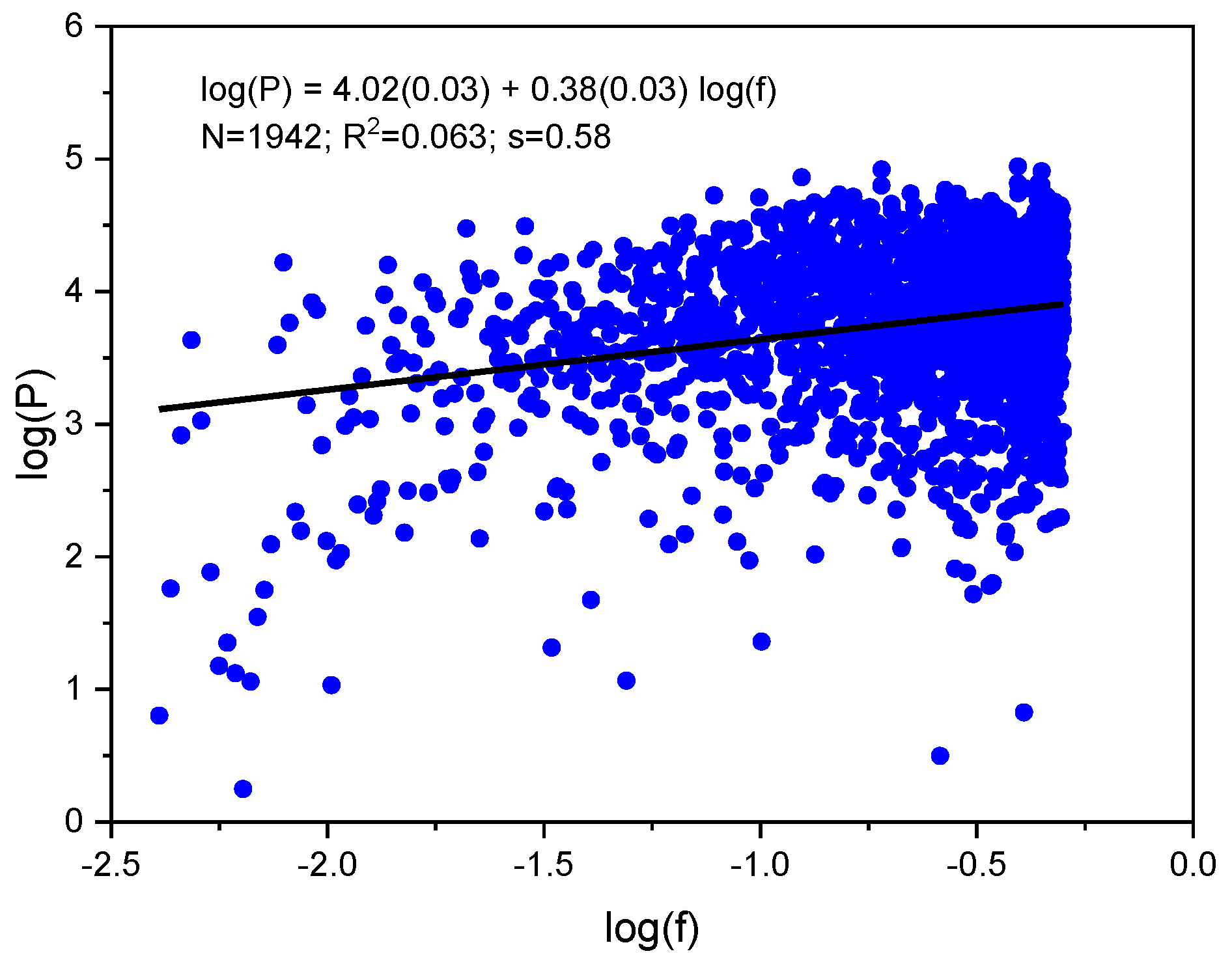
| Crystal | α ± Δ | Hα ± Δ | Hαrand ± Δ | −β ± Δ | Hβ ± Δ | Hβrand ± Δ |
|---|---|---|---|---|---|---|
| D1 | 0.27 ± 0.01 | 0.27 ± 0.01 | 0.50 ± 0.02 | 0.37 ± 0.03 | 0.32 ± 0.02 | 0.51 ± 0.02 |
| D2 | 0.27 ± 0.01 | 0.27 ± 0.01 | 0.49 ± 0.02 | 0.38 ± 0.03 | 0.31 ± 0.02 | 0.50 ± 0.01 |
| G1 | 0.40 ± 0.01 | 0.40 ± 0.01 | 0.49 ± 0.02 | 0.26 ± 0.03 | 0.37 ± 0.01 | 0.50 ± 0.01 |
| G2 | 0.39 ± 0.01 | 0.39 ± 0.01 | 0.51 ± 0.02 | 0.17 ± 0.03 | 0.42 ± 0.01 | 0.51 ± 0.01 |
Sample Availability: Samples of the compounds D1, D2, G1 and G2 are not available from the authors. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grigoreva, L.; Razdolsky, A.; Kazachenko, V.; Strakhova, N.; Grigorev, V. Memory Effect in the Spatial Series Based on Diamond and Graphite Crystals. Molecules 2020, 25, 5387. https://doi.org/10.3390/molecules25225387
Grigoreva L, Razdolsky A, Kazachenko V, Strakhova N, Grigorev V. Memory Effect in the Spatial Series Based on Diamond and Graphite Crystals. Molecules. 2020; 25(22):5387. https://doi.org/10.3390/molecules25225387
Chicago/Turabian StyleGrigoreva, Ludmila, Alexander Razdolsky, Vladimir Kazachenko, Nadezhda Strakhova, and Veniamin Grigorev. 2020. "Memory Effect in the Spatial Series Based on Diamond and Graphite Crystals" Molecules 25, no. 22: 5387. https://doi.org/10.3390/molecules25225387
APA StyleGrigoreva, L., Razdolsky, A., Kazachenko, V., Strakhova, N., & Grigorev, V. (2020). Memory Effect in the Spatial Series Based on Diamond and Graphite Crystals. Molecules, 25(22), 5387. https://doi.org/10.3390/molecules25225387






