Intermolecular Interaction in Methylene Halide (CH2F2, CH2Cl2, CH2Br2 and CH2I2) Dimers
Abstract
1. Introduction
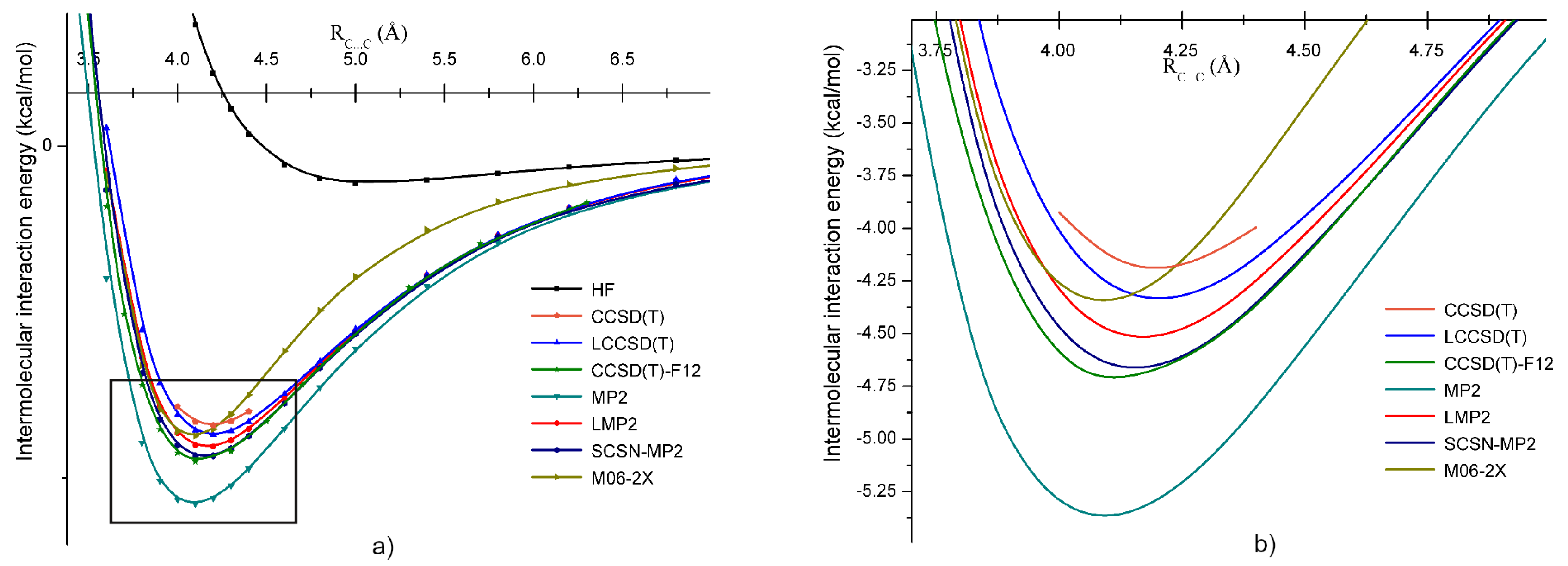
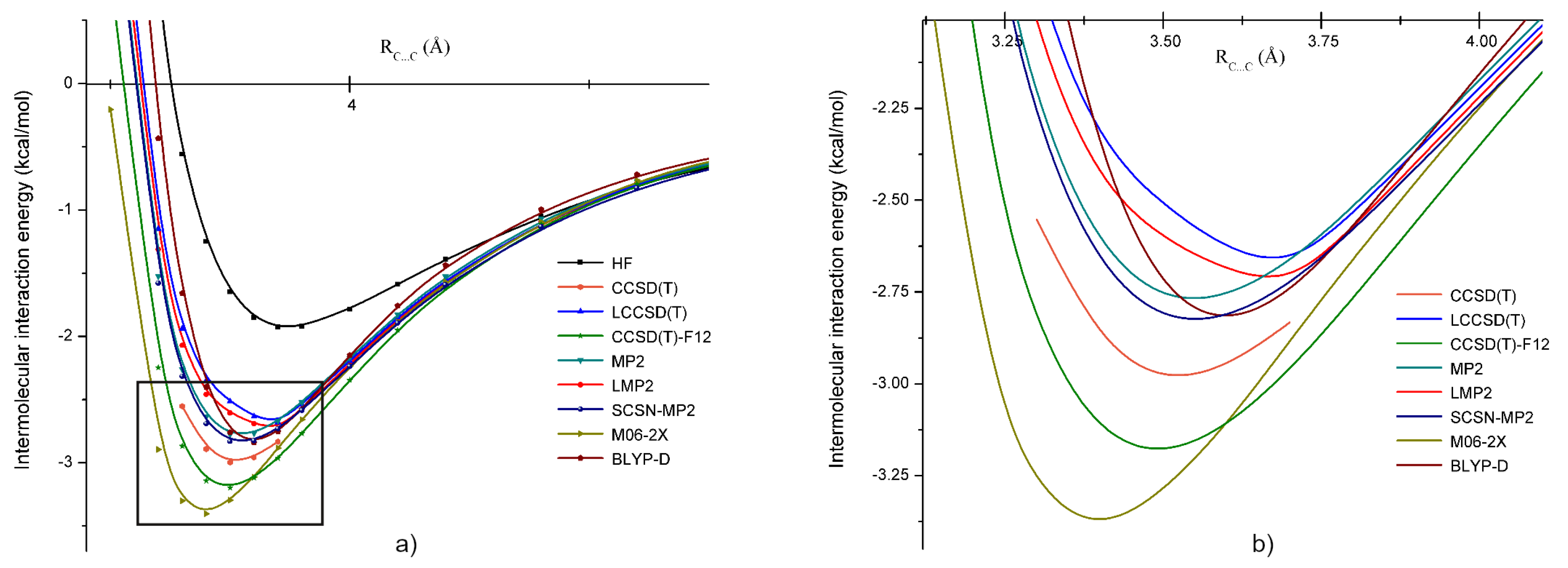
2. Computational Methods
3. Intermolecular Interactions and Dimer Structures
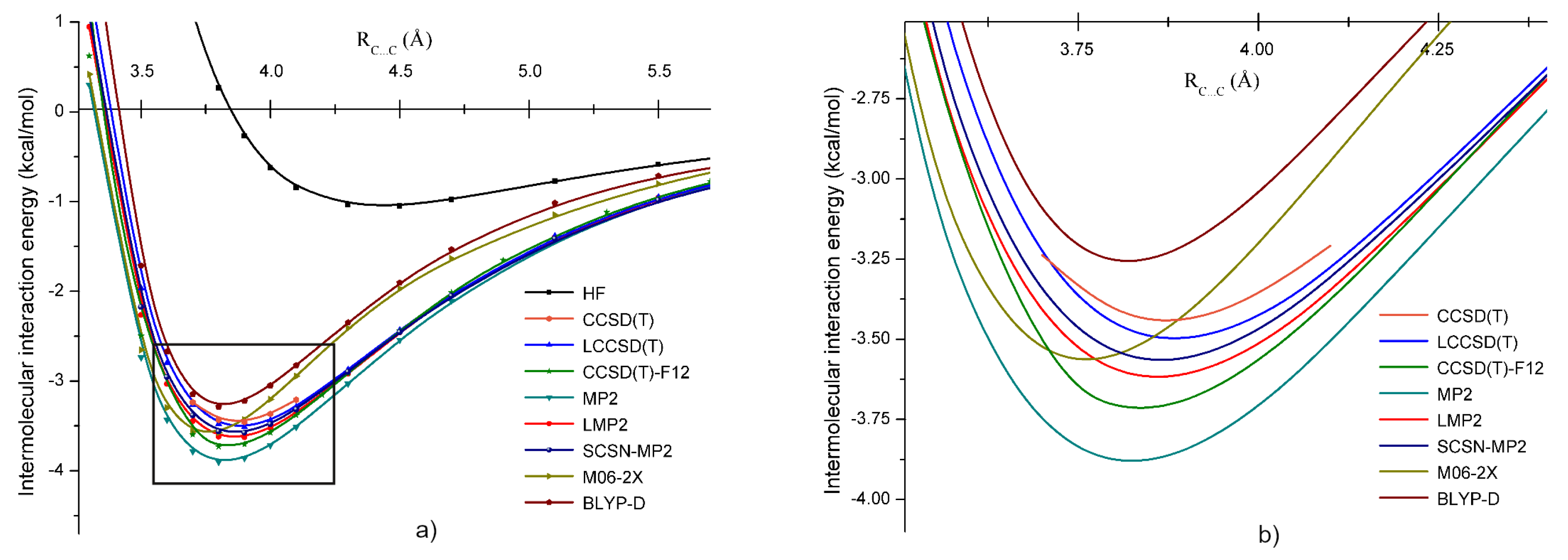
3.1. Methylene Chloride ()
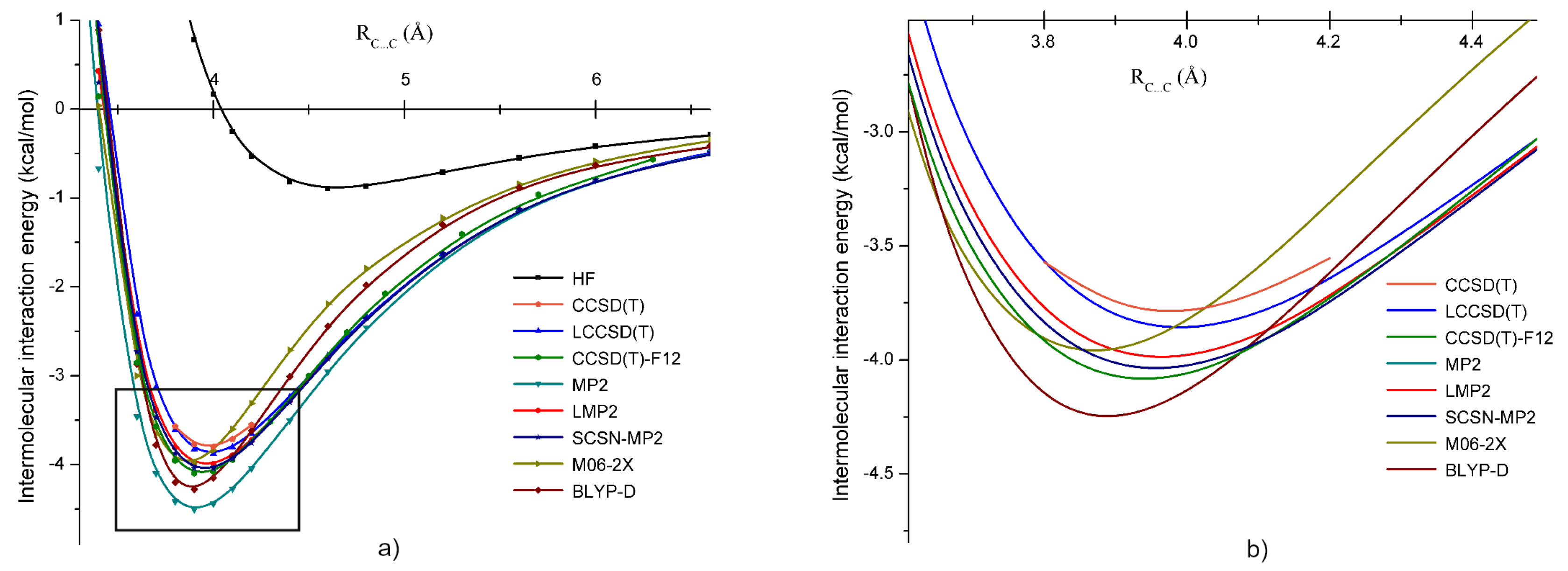
3.2. Methylene Bromide ()
3.3. Methylene Iodide ()
3.4. Methylene Fluoride ()
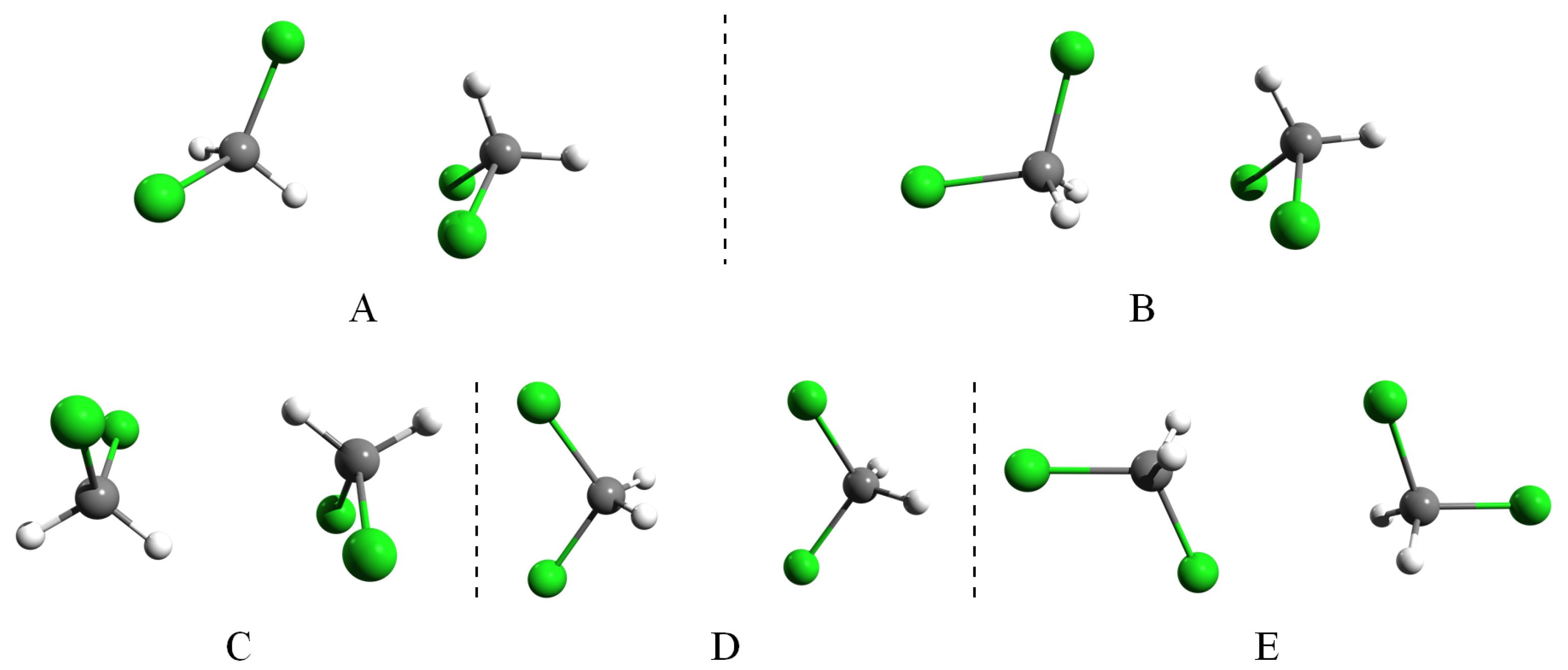
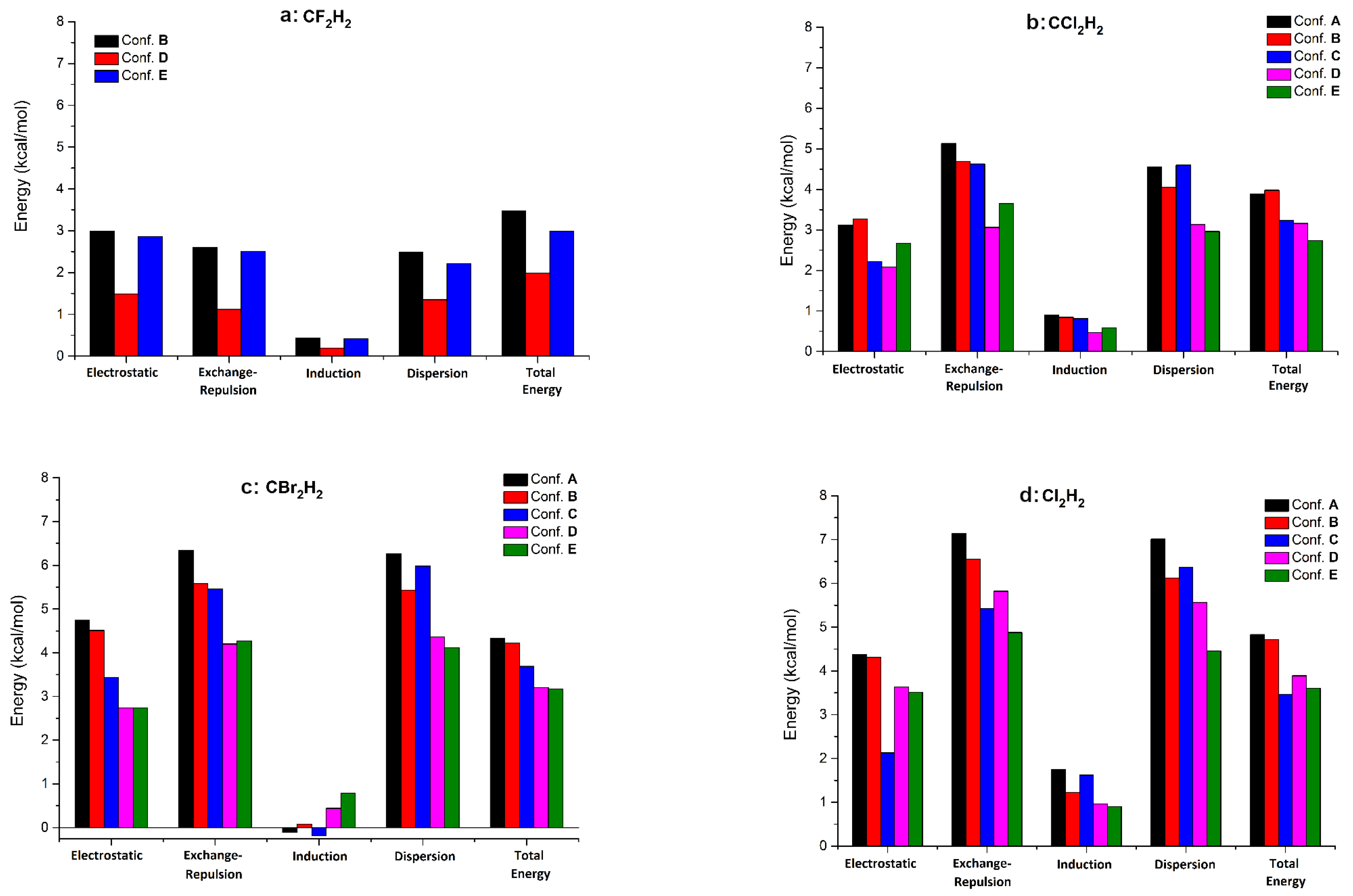
3.5. Intermolecular Interaction in Methylene Halide Dimers
4. Orientational Correlations in the Liquid Phase
5. Comparison of Nearest Neighbor Orientations in the Liquid and in the Gas Phase
- “Dipolar effects, although they are visible, do not have a decisive role in forming pairwise molecular arrangements in liquids. Steric effects, on the other hand, are more important.” Comparing the five calculated configurations, we see that fully-antiparallel dipole orientations appear in Structures C and E, while a parallel dipole orientation is only seen for Structure D. In the remaining two structures with strongest binding, the dipole vectors are nearly perpendicular. Thus, it can be seen that also for the dimers in a vacuum, the dipolar forces are weak, and the attraction of the molecules is rather due to vdW interactions (which are often referred to as steric forces when discussing RMC computer modeling). The weak contribution of the electrostatic forces in molecular liquids and was also confirmed in molecular dynamics simulations with Coulomb interactions turned off [99,100].
- “The most frequent orientation of molecules is of the 2:2 (edge-to-edge) type over the entire distance range in each liquid. Within the 2:2 original group, the H,X-H,X subgroup is the most prominent, apart from the short range orientations in where the H,H-H,Cl arrangement is the most frequent.” As mentioned above, we can attribute the dominance of the edge-to-edge orientations to the optimal intermediately-compact arrangement of the molecules. The only 2:2-type mutual orientation occurs in the weakly-bound D-type dimer, in which the molecules are aligned with parallel dipole moments, the corresponding subgroup being H,H-X,X. This orientation however does not appear in the liquid, indicating that the dipole interaction is too weak to orient the neighboring molecules.
- “The structure of liquid methylene chloride appears to be different from the structure of the other two materials. The origin of structural differences is the significant size difference between and / molecules”.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rajput, L.; Biradha, K. Robust hydrogen bonding synthon in one-dimensional and two-dimensional coordination polymers of pyridine-appended reverse amides and amides. CrystEngComm 2009, 11, 1220–1222. [Google Scholar] [CrossRef]
- Verdan, S.; Melich, X.; Bernardinelli, G.; Williams, A.F. Molecular bricklaying II. CrystEngComm 2009, 11, 1416–1426. [Google Scholar] [CrossRef]
- Jérome, D.; Shulz, H.J. Organic conductors and superconductors. Adv. Phys. 1982, 31, 299–490. [Google Scholar] [CrossRef]
- Hunter, C.A.; Singh, J.; Thornton, J.M. π − π interactions: The geometry and energetics of phenylalanine-phenylalanine interactions in proteins. J. Mol. Biol. 1991, 218, 837–846. [Google Scholar] [CrossRef]
- Saenger, W. Principles of Nucleic Acid Structure; Springer: New York, NY, USA, 1984. [Google Scholar]
- Hobza, P. Theoretical studies of hydrogen bonding. Annu. Rep. Prog. Chem. Sect. C Phys. Chem. 2004, 100, 3–27. [Google Scholar] [CrossRef]
- Grimme, S. Do special noncovalent π − π stacking interactions really exist? Angew. Chem. Int. Ed. 2008, 47, 3430–3434. [Google Scholar] [CrossRef]
- Tsuzuki, S.; Honda, K.; Uchimaru, T.; Mikami, M. Estimated MP2 and CCSD(T) interaction energies of n-alkane dimers at the basis set limit: Comparison of the methods of Helgaker et al. and Feller. J. Chem. Phys. 2006, 124, 114304. [Google Scholar] [CrossRef]
- Li, Q.; Xu, X.; Liu, T.; Jing, B.; Li, W.; Cheng, J.; Gong, B.; Sun, J. Competition between hydrogen bond and halogen bond in complexes of formaldehyde with hypohalous acids. Phys. Chem. Chem. Phys. 2010, 12, 6837–6843. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zeng, Y.; Li, X.; Meng, L.; Zheng, S. Comparison in the complexes of oxygen-containing σ-electron donor with hydrogen halide and dihalogen molecules. J. Mol. Struct. Theochem. 2010, 950, 27–35. [Google Scholar] [CrossRef]
- Cukiernik, F.D.; Zelcer, A.; Garland, M.T.; Baggio, R. Halogen bonding in 1,2-dibromo-4,5-dimethoxybenzene and 1,2-diiodo-4,5-dimethoxybenzene. Acta Cryst. 2008, C64, o604–o608. [Google Scholar] [CrossRef]
- Cukiernik, F.D.; Cecchi, F.; Baggio, R. Comparison of halogen bonding and van der Waals and π − π interactions in 4,5-dibromo-2-hexylphenol. Acta Cryst. 2009, C65, o233–o236. [Google Scholar]
- Zhou, P.; Lv, J.; Zou, J.; Tian, F.; Shang, Z. Halogen–water–hydrogen bridges in biomolecules. J. Struct Biol. 2010, 169, 172–182. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Wang, Y.; Zhu, W. Nonbonding interactions of organic halogens in biological systems: Implications for drug discovery and biomolecular design. Phys. Chem. Chem. Phys. 2010, 12, 4543–4551. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.M.T.; Peeters, J.; Zeegers-Huyskens, T. Theoretical study of the blue-shifting hydrogen bonds between CH2X2 and CHX3 (X = F, Cl, Br) and hydrogen peroxide. J. Mol. Struct. 2006, 792–793, 16–22. [Google Scholar] [CrossRef]
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The σ-hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Lane, P.; Concha, M.C.; Ma, Y.; Murray, J.S. An overview of halogen bonding. J. Mol. Model. 2007, 13, 305–311. [Google Scholar] [CrossRef] [PubMed]
- Torii, H.; Yoshida, M. Properties of halogen atoms for representing intermolecular electrostatic interactions related to halogen bonding and their substituent effects. J. Comput. Chem. 2010, 31, 107–116. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Halogen Bonding: An Interim Discussion. ChemPhysChem 2013, 14, 278–294. [Google Scholar] [CrossRef] [PubMed]
- Blanco, S.; López, J.C.; Lesarri, A.; Alonso, J.L. A molecular-beam Fourier transform microwave study of difluoromethane dimer. J. Mol. Struct. 2002, 612, 255–260. [Google Scholar] [CrossRef]
- Lago, A.F.; Kercher, J.P.; Böldi, A.; Sztáray, B.; Miller, B.; Wurzelmann, D.; Baer, T. Dissociative Photoionization and Thermochemistry of Dihalomethane Compounds Studied by Threshold Photoelectron Photoion Coincidence Spectroscopy. J. Phys. Chem. A 2005, 109, 1802–1809. [Google Scholar] [CrossRef] [PubMed]
- Makogon, O.; Flyunt, R.; Tobien, T.; Naumov, S.; Bonifačić, M. Dimethylselenide as a Probe for Reactions of Halogenated Alkoxyl Radicals in Aqueous Solution. Degradation of Dichloro- and Dibromomethane. J. Phys. Chem. A 2008, 112, 5908–5916. [Google Scholar] [CrossRef]
- Hauchecorne, F.; Herrebout, W.A. Experimental Characterization of C–X⋯Y–C (X = Br, I; Y = F, Cl) Halogen–Halogen Bonds. J. Phys. Chem. A 2013, 117, 11548–11557. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, K.; da Silva, J.F. Halogen and Hydrogen Bonding Interplay in the Crystal Packing of Halometallocenes. Molecules 2018, 23, 2959. [Google Scholar] [CrossRef] [PubMed]
- Gilday, L.C.; Robinson, S.W.; Barendt, T.A.; Langton, M.J.; Mullaney, B.R.; Beer, P.D. Halogen Bonding in Supramolecular Chemistry. Chem. Rev. 2015, 115, 7118–7195. [Google Scholar] [CrossRef] [PubMed]
- Pothoczki, S.; Temleitner, L.; Pusztai, L. Structure of Neat Liquids Consisting of (Perfect and Nearly) Tetrahedral Molecules. Chem. Rev. 2015, 115, 13308–13361. [Google Scholar] [CrossRef]
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Wang, W.; Jin, W.J. σ-Hole Bond vs π-Hole Bond: A Comparison Based on Halogen Bond. Chem. Rev. 2016, 116, 5072–5104. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
- Legon, A.C. Prereactive Complexes of Dihalogens XY with Lewis Bases B in the Gas Phase: A Systematic Case for the Halogen Analogue B⋯XY of the Hydrogen Bond B⋯HX. Angew. Chem. Int. Ed. 1999, 38, 2686–2714. [Google Scholar] [CrossRef]
- Karpfen, A. The intermolecular interaction in the charge-transfer complexes between amines and halogens. Theor. Chem. Acc. 2003, 110, 1–10. [Google Scholar] [CrossRef]
- Rosokha, S.V.; Neretin, I.S.; Rosokha, T.Y.; Hecht, J.; Kochi, J.K. Charge-Transfer Character of Halogen Bonding: Molecular Structures and Electronic Spectroscopy of Carbon Tetrabromide and Bromoform Complexes with Organic σ- and π-Donors. Heteroatom Chem. 2006, 17, 449–459. [Google Scholar] [CrossRef]
- Awwadi, F.F.; Willett, R.D.; Peterson, K.A.; Twamley, B. The Nature of Halogen⋯Halide Synthons: Theoretical and Crystallographic Studies. J. Phys. Chem. A 2007, 111, 2319–2328. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Hobza, P. Origin of the X-Hal (Hal = Cl, Br) Bond-Length Change in the Halogen-Bonded Complexes. J. Phys. Chem. A 2008, 112, 4114–4119. [Google Scholar] [CrossRef] [PubMed]
- Torii, H. Atomic quadrupolar effect in intermolecular electrostatic interactions of chloroalkanes: the cases of chloroform and dichloromethane. J. Mol. Liq. 2005, 119, 31–39. [Google Scholar] [CrossRef]
- Metrangolo, P.; Resnati, G. Type II halogen⋯halogen contacts are halogen bonds. IUCrJ 2014, 1, 5–7. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.L.; Horton, P.N.; Hursthouse, M.B.; Legon, A.C.; Bruce, D.W. Halogen bonding: A new interaction for liquid crystal formation. J. Am. Chem. Soc. 2003, 126, 16–17. [Google Scholar] [CrossRef] [PubMed]
- Osuna, R.M.; Hernández, V.; Navarrete, J.T.L.; D’Oria, E.; Novoa, J.J. Theoretical evaluation of the nature and strength of the F⋯F intermolecular interactions present in fluorinated hydrocarbons. Theor. Chem. Acc. 2011, 128, 541–553. [Google Scholar] [CrossRef]
- Price, S.L.; Stone, A.J.; Lucas, J.; Rowland, R.S.; Thornley, A.E. The Nature of -Cl⋯Cl- Intermolecular Interactions. J. Am. Chem. Soc. 1994, 116, 4910–4918. [Google Scholar] [CrossRef]
- Hyla-Kryspin, I.; Haufe, G.; Grimme, S. Weak Hydrogen Bridges: A Systematic Theoretical Study on the Nature and Strength of C–H⋯F–C Interactions. Chem. Eur. J. 2004, 10, 3411–3422. [Google Scholar] [CrossRef] [PubMed]
- Rednic, M.I.; Varga, R.A.; Bende, A.; Grosu, I.G.; Miclăuş, M.; Hădade, N.D.; Terec, A.; Bogdan, B.; Grosu, I. Supramolecular anion recognition by β-HCH. Chem. Commun. 2016, 52, 12322–12325. [Google Scholar] [CrossRef]
- Grosu, I.G.; Rednic, M.I.; Miclăuş, M.; Grosu, I.; Bende, A. The nature of intermolecular interactions in pyridinium–anion–β-hexachlorocyclohexane molecular crystals. Phys. Chem. Chem. Phys. 2017, 19, 20691–20698. [Google Scholar] [CrossRef]
- Novák, M.; Marek, R.; Foroutan-Nejad, C. Anti-Electrostatic CH–Ion Bonding in Decorated Graphanes. Chem. Eur. J. 2017, 23, 14931–14936. [Google Scholar]
- Varadwaj, A.; Marques, H.M.; Varadwaj, P.R. Is the Fluorine in Molecules Dispersive? Is Molecular Electrostatic Potential a Valid Property to Explore Fluorine-Centered Non-Covalent Interactions? Molecules 2019, 24, 379. [Google Scholar] [CrossRef] [PubMed]
- Hobza, P.; Špirko, V.; Selzle, H.L.; Schlag, E.W. Anti-Hydrogen Bond in the Benzene Dimer and Other Carbon Proton Donor Complexes. J. Phys. Chem. A 1998, 102, 2501–2504. [Google Scholar] [CrossRef]
- Cubero, E.; Orozco, M.; Hobza, P.; Luque, F.J. Hydrogen Bond versus Anti-Hydrogen Bond: A Comparative Analysis. J. Phys. Chem. A 1999, 103, 6394–6401. [Google Scholar] [CrossRef]
- Van der Veken, B.; Herrebout, W.A.; Szostak, R.; Shchepkin, D.N.; Havlas, Z.; Hobza, P. The Nature of Improper, Blue-Shifting Hydrogen Bonding Verified Experimentally. J. Am. Chem. Soc. 2001, 123, 12290–12293. [Google Scholar] [CrossRef]
- Hobza, P.; Havlas, Z. Improper, blue-shifting hydrogen bond. Theor. Chem. Acc. 2002, 108, 325–334. [Google Scholar] [CrossRef]
- Kryachko, E.; Scheiner, S. CH⋯F Hydrogen Bonds. Dimers of Fluoromethanes. J. Phys. Chem. A 2004, 108, 2527–2535. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Roohi, H.; Habibi, S.M. The characterization of stationary points in the potential energy surface of difluoromethane dimer. J. Mol. Struct. (THEOCHEM) 2004, 684, 87–93. [Google Scholar] [CrossRef]
- Zierkiewicz, W.; Michalska, D.; Havlas, Z.; Hobza, P. Study of the Nature of Improper Blue-Shifting Hydrogen Bonding and Standard Hydrogen Bonding in the X3CH⋯OH2 and XH⋯OH2 Complexes (X = F, Cl, Br, I): A Correlated Ab Initio Study. ChemPhysChem 2002, 3, 511–518. [Google Scholar] [CrossRef]
- Pulay, P. Localizability of dynamic electron correlation. Chem. Phys. Lett. 1983, 100, 151–154. [Google Scholar] [CrossRef]
- Saebø, S.; Pulay, P. Local treatment of electron correlation. Annu. Rev. Phys. Chem. 1993, 44, 213–236. [Google Scholar] [CrossRef]
- Hampel, C.; Werner, H.-J. Local treatment of electron correlation in coupled cluster theory. J. Chem. Phys. 1996, 104, 6286–6297. [Google Scholar] [CrossRef]
- Hetzer, G.; Schütz, M.; Stoll, H.; Werner, H.-J. Low-order scaling local correlation methods II: Splitting the Coulomb operator in linear scaling local second-order Møller–Plesset perturbation theory. J. Chem. Phys. 2000, 113, 9443–9455. [Google Scholar] [CrossRef]
- Schütz, M. Low-order scaling local electron correlation methods. III. Linear scaling local perturbative triples correction (T). J. Chem. Phys. 2000, 113, 9986–10001. [Google Scholar] [CrossRef]
- Schütz, M.; Werner, H.-J. Low-order scaling local electron correlation methods. IV. Linear scaling local coupled-cluster (LCCSD). J. Chem. Phys. 2001, 114, 661–681. [Google Scholar] [CrossRef]
- Vahtras, O.; Almlöf, J.; Feyereisen, M.W. Integral approximations for LCAO-SCF calculations. Chem. Phys. Lett. 1993, 213, 514–518. [Google Scholar] [CrossRef]
- Hill, J.G.; Platts, J.A.; Werner, H.-J. Calculation of intermolecular interactions in the benzene dimer using coupled-cluster and local electron correlation methods. Phys. Chem. Chem. Phys. 2006, 8, 4072–4078. [Google Scholar] [CrossRef]
- Grimme, S. Improved second-order Møller–Plesset perturbation theory by separate scaling of parallel- and antiparallel-spin pair correlation energies. J. Chem. Phys. 2003, 118, 9095–9102. [Google Scholar] [CrossRef]
- Hill, J.G.; Platts, J.A. Spin-Component Scaling Methods for Weak and Stacking Interactions. J. Chem. Theory Comput. 2007, 3, 80–85. [Google Scholar] [CrossRef]
- Jurečka, P.; Šponer, J.; Cerný, J.; Hobza, P. Benchmark database of accurate (MP2 and CCSD(T) complete basis set limit) interaction energies of small model complexes, DNA base pairs, and amino acid pairs. Phys. Chem. Chem. Phys. 2006, 8, 1985–1993. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Kutzelnigg, W. r12-Dependent terms in the wave function as closed sums of partial wave amplitudes for large l. Theor. Chim. Acta 1985, 68, 445–469. [Google Scholar] [CrossRef]
- Klopper, W.; Manby, F.R.; Ten-No, S.; Valeev, E.F. R12 methods in explicitly correlated molecular electronic structure theory. Int. Rev. Phys. Chem. 2006, 25, 427–468. [Google Scholar] [CrossRef]
- Noga, J.; Kedžuch, S.; Šimunek, J.; Ten-No, S. Explicitly correlated coupled cluster F12 theory with single and double excitations. J. Chem. Phys. 2008, 128, 174103. [Google Scholar] [CrossRef]
- Adler, T.B.; Knizia, G.; Werner, H.-J. A simple and efficient CCSD(T)-F12 approximation. J. Chem. Phys. 2007, 127, 221106. [Google Scholar] [CrossRef]
- May, A.J.; Manby, F.R. An explicitly correlated second order Møller–Plesset theory using a frozen Gaussian geminal. J. Chem. Phys. 2004, 121, 4479–4485. [Google Scholar] [CrossRef]
- Jeziorski, B.; Moszyński, R.; Szalewicz, K. Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes. Chem. Rev. 1994, 94, 1887–1930. [Google Scholar] [CrossRef]
- Bende, A.; Almásy, L. Weak intermolecular bonding in N,N’-dimethylethyleneurea dimers and N,N’-dimethylethyleneurea–water systems: The role of the dispersion effects in intermolecular interaction. Chem. Phys. 2008, 354, 202–210. [Google Scholar] [CrossRef]
- Werner, H.-J.; Knowles, P.J.; Lindh, R.; Manby, F.R.; Schütz, M.; Celani, P.; Korona, T.; Mitrushenkov, A.; Rauhut, G.; Adler, T.B.; et al. MOLPRO, Version 2010.1, a Package of ab Initio Programs. Available online: http://www.molpro.net (accessed on 9 May 2019).
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. III. The atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
- Wilson, A.K.; Woon, D.E.; Peterson, K.A.; Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. IX. The atoms gallium through krypton. J. Chem. Phys. 1999, 110, 7667–7676. [Google Scholar] [CrossRef]
- Peterson, K.A.; Shepler, B.C.; Figgen, D.; Stoll, H. On the Spectroscopic and Thermochemical Properties of ClO, BrO, IO, and Their Anions. J. Phys. Chem. A 2006, 110, 13877–13883. [Google Scholar] [CrossRef] [PubMed]
- Pipek, J.; Mezey, P.G. A fast intrinsic localization procedure applicable for ab initio and semiempirical linear combination of atomic orbital wave functions. J. Chem. Phys. 1989, 90, 4916–4926. [Google Scholar] [CrossRef]
- Schütz, M.; Rauhut, G.; Werner, H.-J. Local Treatment of Electron Correlation in Molecular Clusters: Structures and Stabilities of (H2O)n, n = 2–4. J. Phys. Chem. A 1998, 102, 5997–6003. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06 Functionals and Twelve Other Functionals. Theo. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Grimme, S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Bylaska, E.J.; de Jong, W.A.; Govind, N.; Kowalski, K.; Straatsma, T.P.; Valiev, M.; Wang, D.; Apra, E.; Windus, T.L.; Hammond, J.; et al. NWChem, A Computational Chemistry Package for Parallel Computers, Version 6.1; Pacific Northwest National Laboratory: Richland, WA, USA, 2009.
- Bauzá, A.; Alkorta, I.; Frontera, A.; Elguero, J. On the Reliability of Pure and Hybrid DFT Methods for the Evaluation of Halogen, Chalcogen, and Pnicogen Bonds Involving Anionic and Neutral Electron Donors. J. Chem. Theory Comput. 2013, 9, 5201–5210. [Google Scholar] [CrossRef]
- Heßelmann, A.; Jansen, G. The helium dimer potential from a combined density functional theory and symmetry-adapted perturbation theory approach using an exact exchange–correlation potential. Phys. Chem. Chem. Phys. 2003, 5, 5010–5014. [Google Scholar] [CrossRef]
- Allouche, A.-R. Gabedit—A graphical user interface for computational chemistry softwares. J. Comput. Chem. 2011, 32, 174–182. [Google Scholar] [CrossRef]
- Almásy, L.; Bende, A. Ab initio structures of interacting methylene chloride molecules with comparison to the liquid phase. J. Mol. Liq. 2011, 158, 205–207. [Google Scholar] [CrossRef][Green Version]
- Bende, A.; Grosu, I.; Turcu, I. Molecular Modeling of Phenothiazine Derivatives: Self-Assembling Properties. J. Phys. Chem. A 2010, 114, 12479–12489. [Google Scholar] [CrossRef]
- Riley, K.E.; Hobza, P. The relative roles of electrostatics and dispersion in the stabilization of halogen bonds. Phys. Chem. Chem. Phys. 2013, 15, 17742–17751. [Google Scholar] [CrossRef]
- Stone, A.J. Are Halogen Bonded Structures Electrostatically Driven? J. Am. Chem. Soc. 2013, 135, 7005–7009. [Google Scholar] [CrossRef]
- Hill, J.G.; Legon, A.C. On the directionality and non-linearity of halogen and hydrogen bonds. Phys. Chem. Chem. Phys. 2015, 17, 858–867. [Google Scholar] [CrossRef]
- Pothoczki, S.; Kohara, S.; Pusztai, L. Partial radial distribution functions of methylene halide molecular liquids. J. Mol. Liq. 2010, 153, 112–116. [Google Scholar] [CrossRef]
- Pothoczki, S.; Temleitner, L.; Pusztai, L. Extended orientational correlation study for molecular liquids containing distorted tetrahedral molecules: Application to methylene halides. J. Chem. Phys. 2010, 132, 164511. [Google Scholar] [CrossRef]
- Rey, R. Quantitative characterization of orientational order in liquid carbon tetrachloride. J. Chem. Phys. 2007, 126, 164506. [Google Scholar] [CrossRef]
- Caminati, W.; Melandri, S.; Moreschini, P.; Favero, P.G. The C-F⋯H-C “anti-hydrogen bond” in the gas phase: Microwave structure of the difluoromethane dimer. Angew. Chem. Int. Ed. 1999, 38, 2924–2925. [Google Scholar] [CrossRef]
- Lu, T.; Chen, J.; Zhang, J.; Gou, Q.; Xia, Z.; Feng, G. Conformational landscape of the weakly bound difluoromethane-1,1-difluoroethane dimer explored by rotational spectroscopy and quantum chemical calculations. J. Mol. Spectr. 2019, 357, 32–37. [Google Scholar] [CrossRef]
- Blanco, S.; Melandri, S.; Ottaviani, P.; Caminati, W. Shapes and Noncovalent Interactions of Oligomers: The Rotational Spectrum of the Difluoromethane Trimer. J. Am. Chem. Soc. 2007, 129, 2700–2703. [Google Scholar] [CrossRef] [PubMed]
- Feng, G.; Evangelisti, L.; Cacelli, I.; Carbonaro, L.; Prampolini, G.; Caminati, W. Oligomers based on weak hydrogen bond networks: A rotational study of the tetramer of difluoromethane. ChemComm 2014, 50, 171–173. [Google Scholar] [CrossRef]
- Prampolini, G.; Carbonaro, L.; Feng, G.; Evangelisti, L.; Caminati, W.; Cacelli, I. Computational Screening of Weak Hydrogen Bond Networks: Predicting Stable Structures for Difluoromethane Oligomers. J. Chem. Theor. Comp. 2014, 10, 2204–2211. [Google Scholar] [CrossRef] [PubMed]
- Pothoczki, S.; Ottochian, A.; Rovira-Esteva, M.; Pardo, L.C.; Tamarit, J.L.; Cuello, G.J. Role of steric and electrostatic effects in the short-range order of quasitetrahedral molecular liquids. Phys. Rev. B 2012, 85, 014202. [Google Scholar] [CrossRef]
- Karnes, J.J.; Benjamin, I. On the local intermolecular ordering and dynamics of liquid chloroform. J. Mol. Liq. 2017, 248, 121–126. [Google Scholar] [CrossRef]
- Megyes, T.; Bálint, S.; Grósz, T.; Radnai, T.; Bakó, I.; Almásy, L. Structure of liquid nitromethane: Comparison of simulation and diffraction studies. J. Chem. Phys. 2007, 126, 164507. [Google Scholar] [CrossRef]
- Cabaco, M.I.; Danten, Y.; Besnard, M.; Guissani, Y.; Guillot, B. Evidence of dimer formation in neat liquid 1,3,5-trifluorobenzene. Chem. Phys. Lett. 1996, 262, 120–124. [Google Scholar] [CrossRef]
- Podsiadło, M.; Dziubek, K.; Katrusiak, A. In situ high-pressure crystallization and compression of halogen contacts in dichloromethane. Acta Cryst. 2005, B61, 595–600. [Google Scholar] [CrossRef]
- Podsiadło, M.; Dziubek, K.; Szafranski, M.; Katrusiak, A. Molecular interactions in crystalline dibromomethane and diiodomethane, and the stabilities of their high-pressure and low-temperature phases. Acta Cryst. 2006, B62, 1090–1098. [Google Scholar] [CrossRef]
- Li, A.H.-T.; Huang, S.-C.; Chao, S.D. Molecular dynamics simulation of liquid carbon tetrachloride using ab initio force field. J. Chem. Phys. 2010, 132, 024506. [Google Scholar] [CrossRef] [PubMed]
- Yin, C.-C.; Li, A.H.-T.; Chao, S.D. Liquid chloroform structure from computer simulation with a full ab initio intermolecular interaction potential. J. Chem. Phys. 2013, 139, 194501. [Google Scholar] [CrossRef] [PubMed]
| Dimer | Unit | A | B | C | D | E |
|---|---|---|---|---|---|---|
| d(C⋯C) | Å | 3.91 | 3.85 | 3.65 | 4.09 | 4.28 |
| kcal/mol | 0.57 | −0.04 | 1.27 | −0.70 | −1.02 | |
| kcal/mol | −3.72 | −3.64 | −3.34 | −2.81 | −2.55 | |
| kcal/mol | −3.86 | −3.35 | −4.00 | −2.53 | −2.56 | |
| kcal/mol | −3.58 | −3.51 | −3.18 | −2.72 | −2.47 | |
| kcal/mol | −3.89 | −3.98 | −3.23 | −3.16 | −2.73 | |
| kcal/mol | −4.56 | −4.05 | −4.60 | −3.13 | −2.96 | |
| kcal/mol | - | 0.08 | 0.37 | 1.15 | 1.39 |
| Dimer | Unit | A | B | C | D | E |
|---|---|---|---|---|---|---|
| d(C⋯C) | Å | 4.04 | 3.96 | 3.71 | 4.39 | 4.25 |
| kcal/mol | 1.17 | 0.40 | 1.96 | 0.62 | 0.17 | |
| kcal/mol | −4.15 | −3.98 | −3.57 | −3.06 | −3.01 | |
| kcal/mol | −4.60 | −3.90 | −4.63 | −3.27 | −2.92 | |
| kcal/mol | −4.00 | −3.86 | −3.40 | −2.97 | −2.93 | |
| kcal/mol | −4.33 | −3.85 | −3.69 | −3.20 | −3.17 | |
| kcal/mol | −6.26 | −4.22 | −5.98 | −4.36 | −4.12 | |
| kcal/mol | - | 0.14 | 0.59 | 1.01 | 1.07 |
| Dimer | Unit | A | B | C | D | E |
|---|---|---|---|---|---|---|
| d(C⋯C) | Å | 4.25 | 4.16 | 3.80 | 4.53 | 4.56 |
| kcal/mol | 2.14 | 1.36 | 2.86 | 1.64 | 0.81 | |
| kcal/mol | −4.82 | −4.54 | −3.90 | −3.85 | −3.31 | |
| kcal/mol | −5.82 | −4.97 | −5.54 | −4.59 | −3.59 | |
| kcal/mol | −4.61 | −4.34 | −3.68 | −3.67 | −3.17 | |
| kcal/mol | −4.83 | −4.72 | −3.46 | −3.89 | −3.61 | |
| kcal/mol | −7.01 | −6.12 | −6.37 | −5.56 | −4.46 | |
| kcal/mol | - | 0.25 | 0.92 | 0.90 | 1.41 |
| Dimer | Unit | B | D | E |
|---|---|---|---|---|
| d(C⋯C) | Å | −3.54 | −3.98 | −3.61 |
| kcal/mol | −1.75 | −1.02 | −1.50 | |
| kcal/mol | −2.62 | −1.67 | −2.08 | |
| kcal/mol | −1.58 | −1.37 | −0.90 | |
| kcal/mol | −2.53 | −1.63 | −1.99 | |
| kcal/mol | −3.47 | −1.99 | −2.99 | |
| kcal/mol | −2.48 | −1.35 | −2.21 | |
| kcal/mol | - | 0.55 | 0.87 |
| Configuration | Complex | E | E | E | E | E | E |
|---|---|---|---|---|---|---|---|
| A | CClH | −3.12 | 5.13 | −0.90 | −4.56 | 0.57 | −3.89 |
| CBrH | −4.74 | 6.34 | 0.11 | −6.26 | 1.17 | −4.33 | |
| CIH | −4.38 | 7.14 | −1.75 | −7.01 | 2.79 | −4.83 | |
| B | CFH | −2.99 | 2.60 | −0.44 | −2.48 | −1.75 | −3.47 |
| CClH | −3.27 | 4.69 | −0.84 | −4.05 | −0.04 | −3.98 | |
| CBrH | −4.51 | 5.58 | −0.08 | −5.43 | 0.40 | −4.22 | |
| CIH | −4.31 | 6.55 | −1.23 | −6.12 | 2.27 | −4.72 | |
| C | CClH | −2.22 | 4.63 | −0.81 | −4.60 | 1.27 | −3.23 |
| CBrH | −3.44 | 5.46 | 0.18 | −5.98 | 1.96 | −3.69 | |
| CIH | −2.13 | 5.43 | −1.62 | −6.37 | 3.32 | −3.46 | |
| D | CFH | −1.49 | 1.12 | −0.19 | −1.35 | −1.02 | −1.99 |
| CClH | −2.08 | 3.06 | −0.46 | −3.13 | 0.23 | −3.16 | |
| CBrH | −2.74 | 4.20 | −0.44 | −4.36 | 0.62 | −3.20 | |
| CIH | −3.64 | 5.82 | −0.96 | −5.56 | 2.22 | −3.89 | |
| E | CFH | −2.86 | 2.50 | −0.42 | −2.21 | −1.50 | −2.99 |
| CClH | −2.67 | 3.65 | −0.58 | −2.96 | −0.07 | −2.73 | |
| CBrH | −2.74 | 4.27 | −0.79 | −4.12 | 0.17 | −3.17 | |
| CIH | −3.51 | 4.88 | −0.90 | −4.46 | 1.39 | −3.61 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almásy, L.; Bende, A. Intermolecular Interaction in Methylene Halide (CH2F2, CH2Cl2, CH2Br2 and CH2I2) Dimers. Molecules 2019, 24, 1810. https://doi.org/10.3390/molecules24091810
Almásy L, Bende A. Intermolecular Interaction in Methylene Halide (CH2F2, CH2Cl2, CH2Br2 and CH2I2) Dimers. Molecules. 2019; 24(9):1810. https://doi.org/10.3390/molecules24091810
Chicago/Turabian StyleAlmásy, László, and Attila Bende. 2019. "Intermolecular Interaction in Methylene Halide (CH2F2, CH2Cl2, CH2Br2 and CH2I2) Dimers" Molecules 24, no. 9: 1810. https://doi.org/10.3390/molecules24091810
APA StyleAlmásy, L., & Bende, A. (2019). Intermolecular Interaction in Methylene Halide (CH2F2, CH2Cl2, CH2Br2 and CH2I2) Dimers. Molecules, 24(9), 1810. https://doi.org/10.3390/molecules24091810







