Calibration Transfer Based on Affine Invariance for NIR without Transfer Standards
Abstract
1. Introduction
2. Results and Discussion
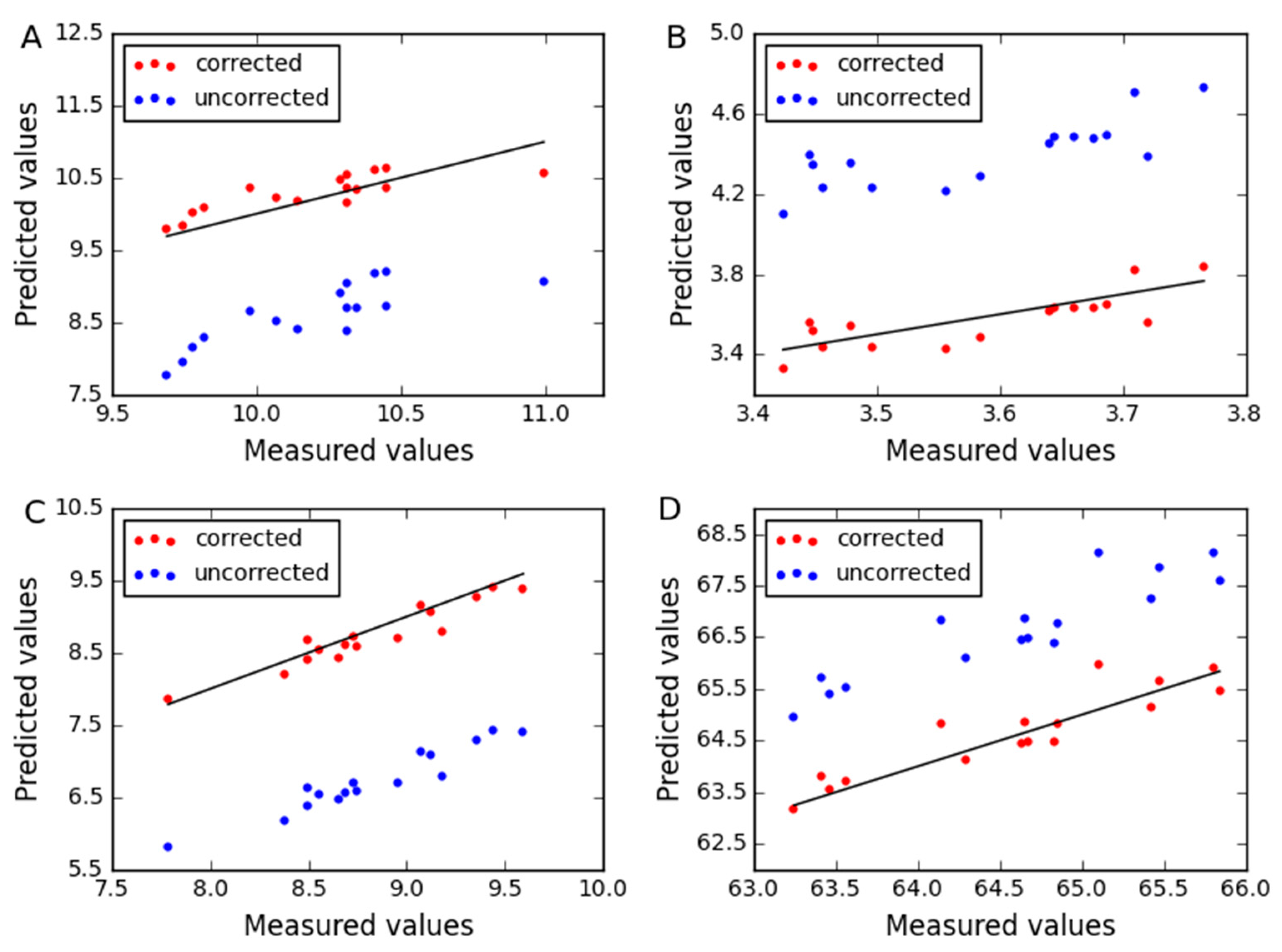
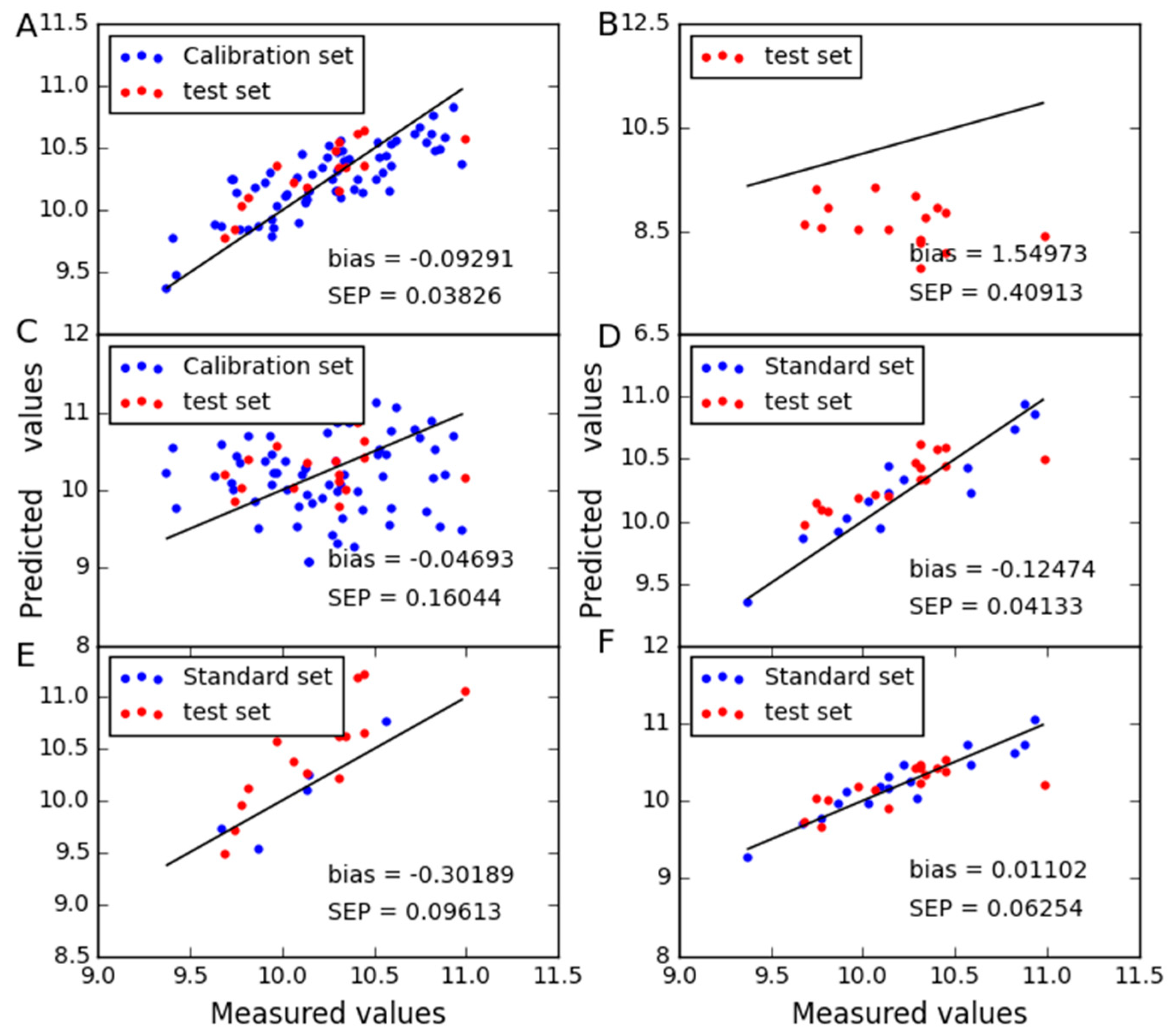
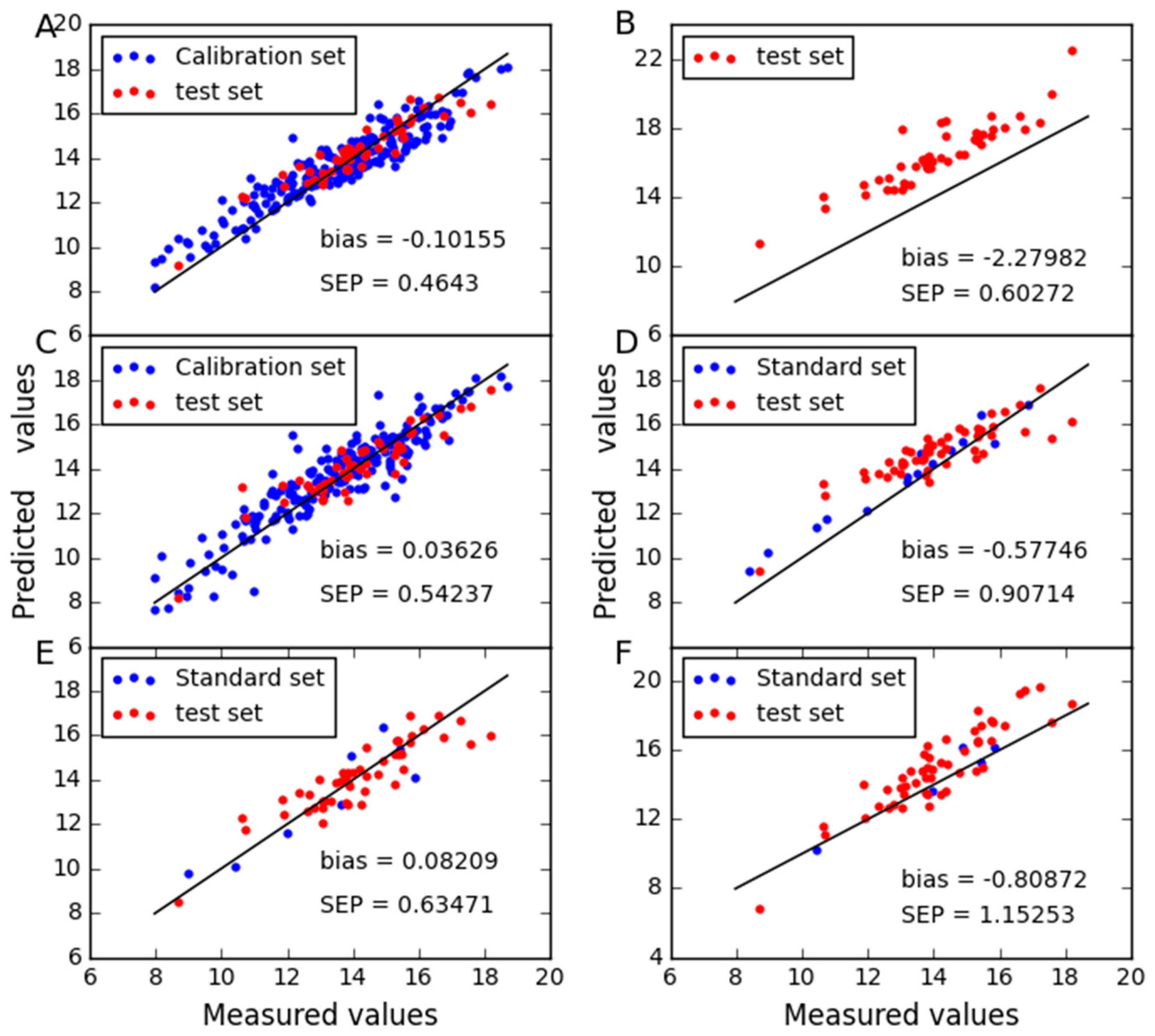
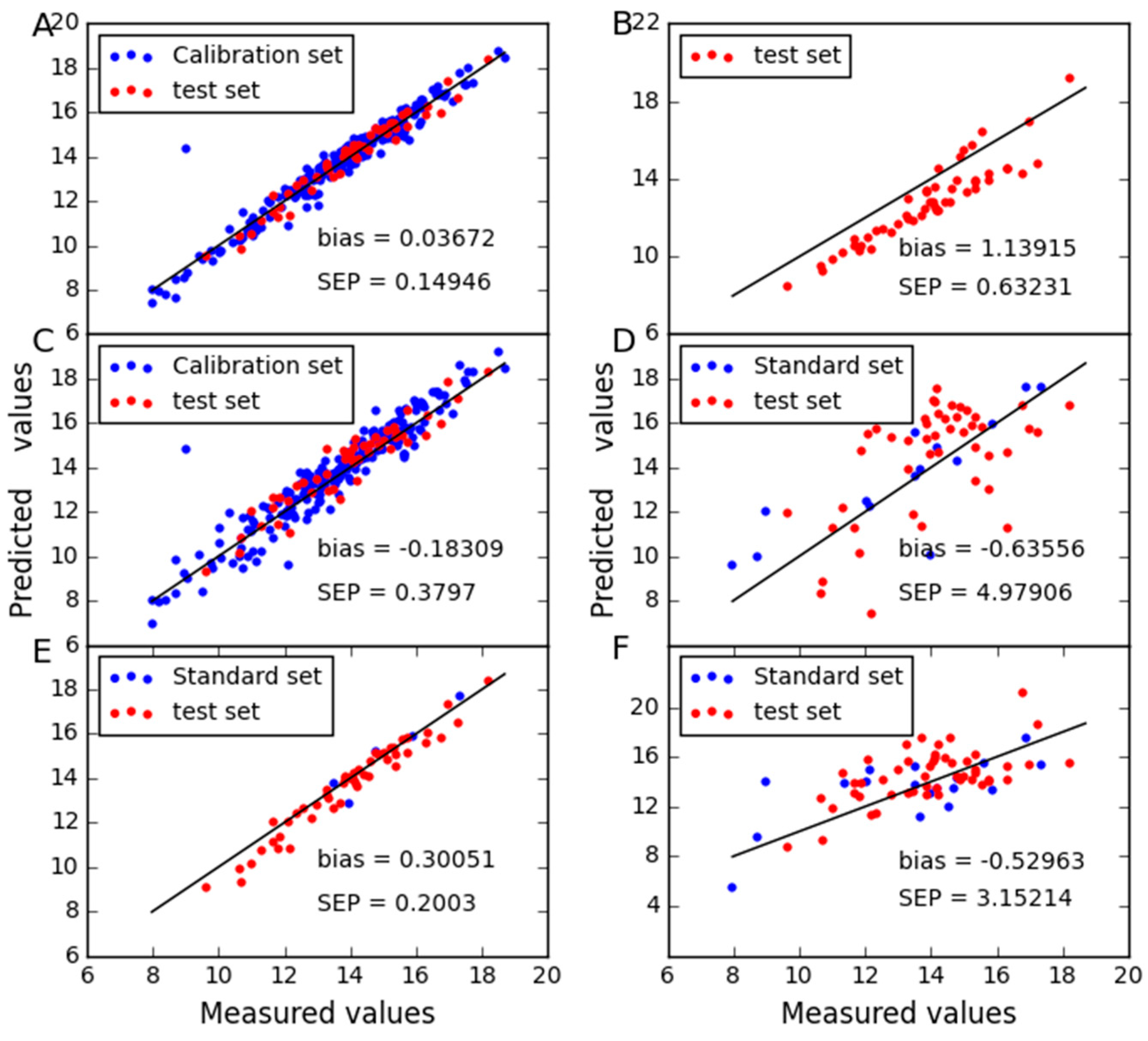
2.1. Analysis of the Corn Dataset
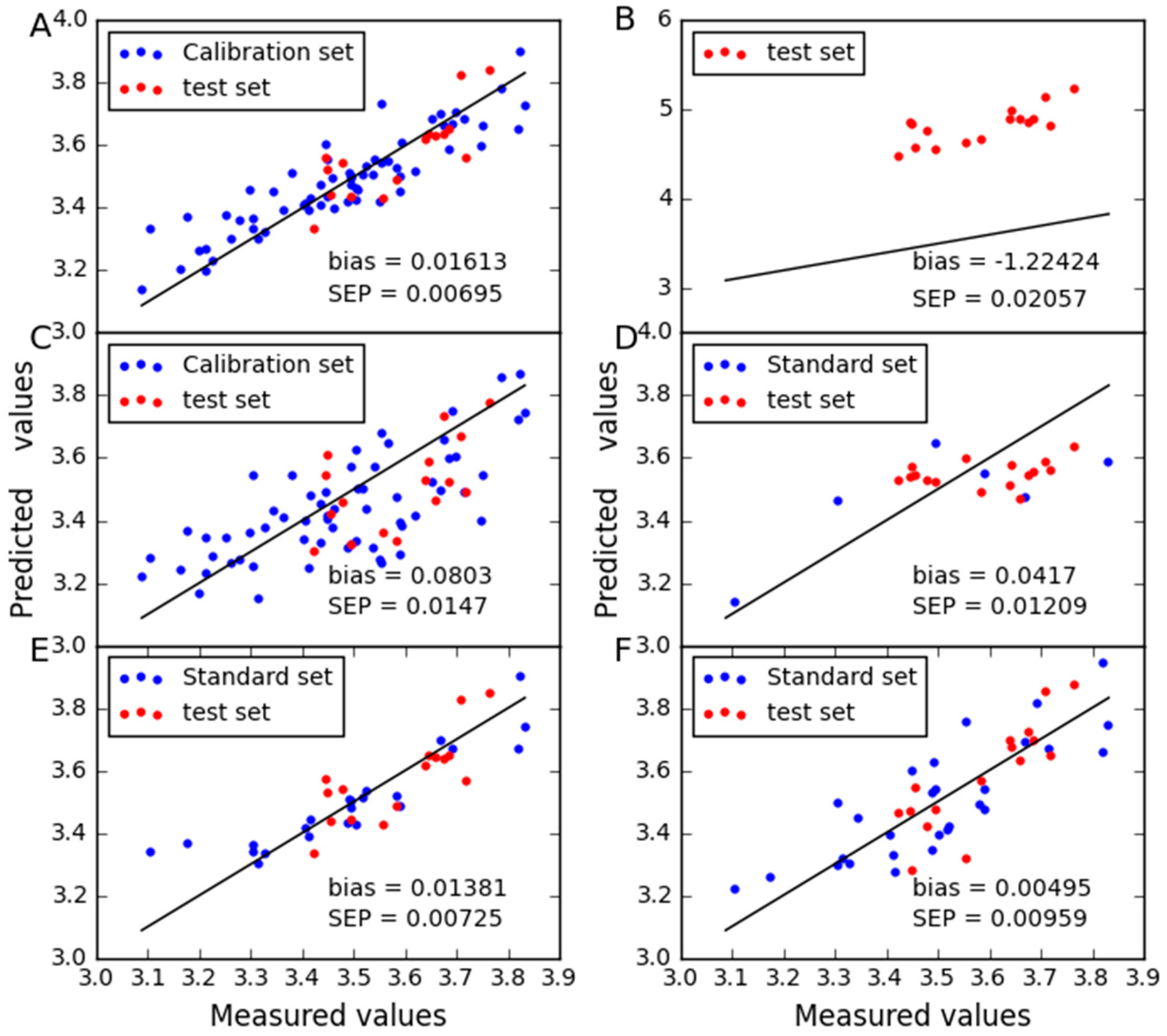
2.2. Analysis of the Wheat Dataset
3. Materials and Methods
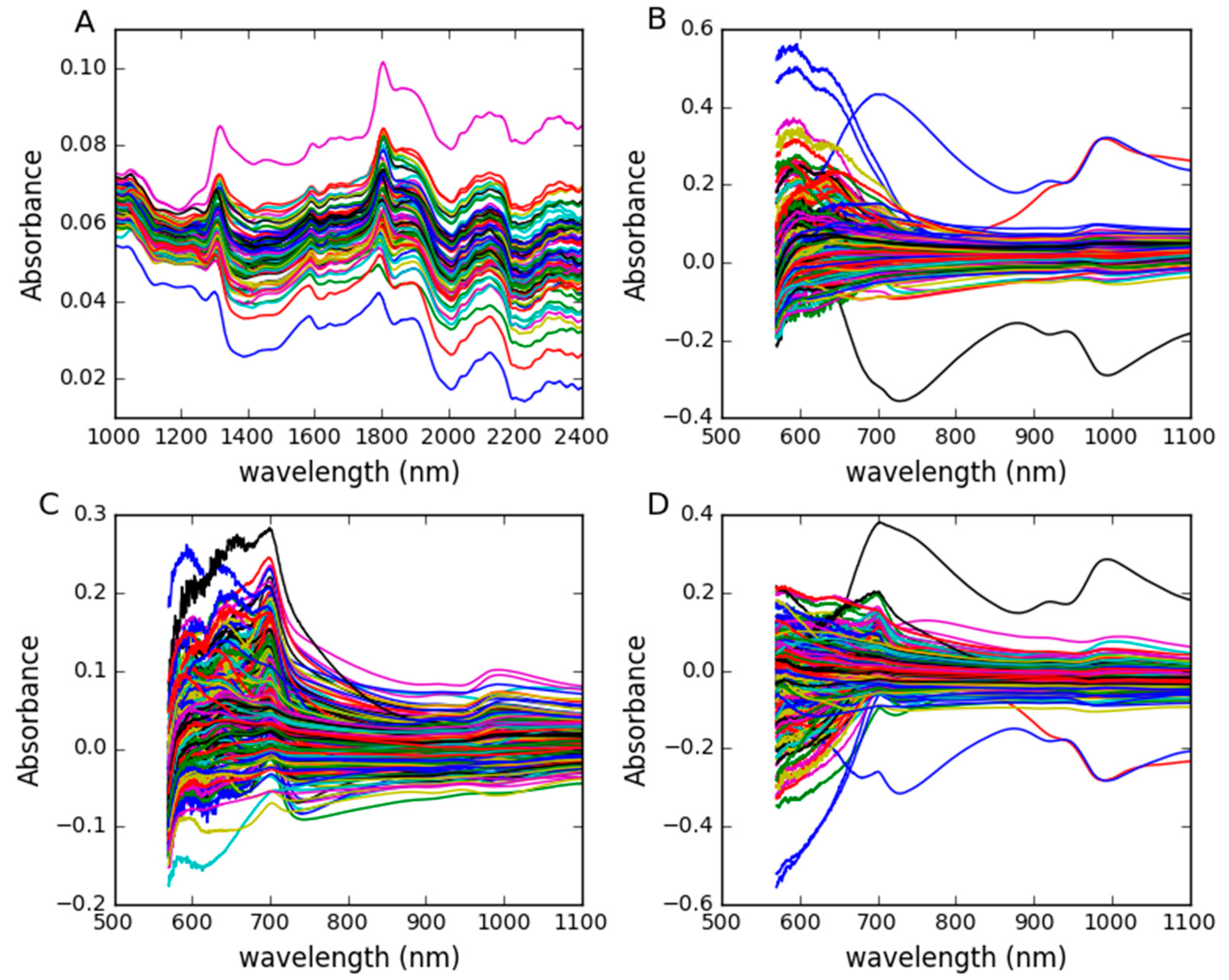
3.1. Dataset Description
3.1.1. Corn Dataset
3.1.2. Wheat Dataset
3.2. Determination of the Optimal Parameters
3.3. Model Performance Evaluation
3.4. Computational Environment
3.5. Calibration Transfer
3.5.1. Notation
3.5.2. Overview of PLS
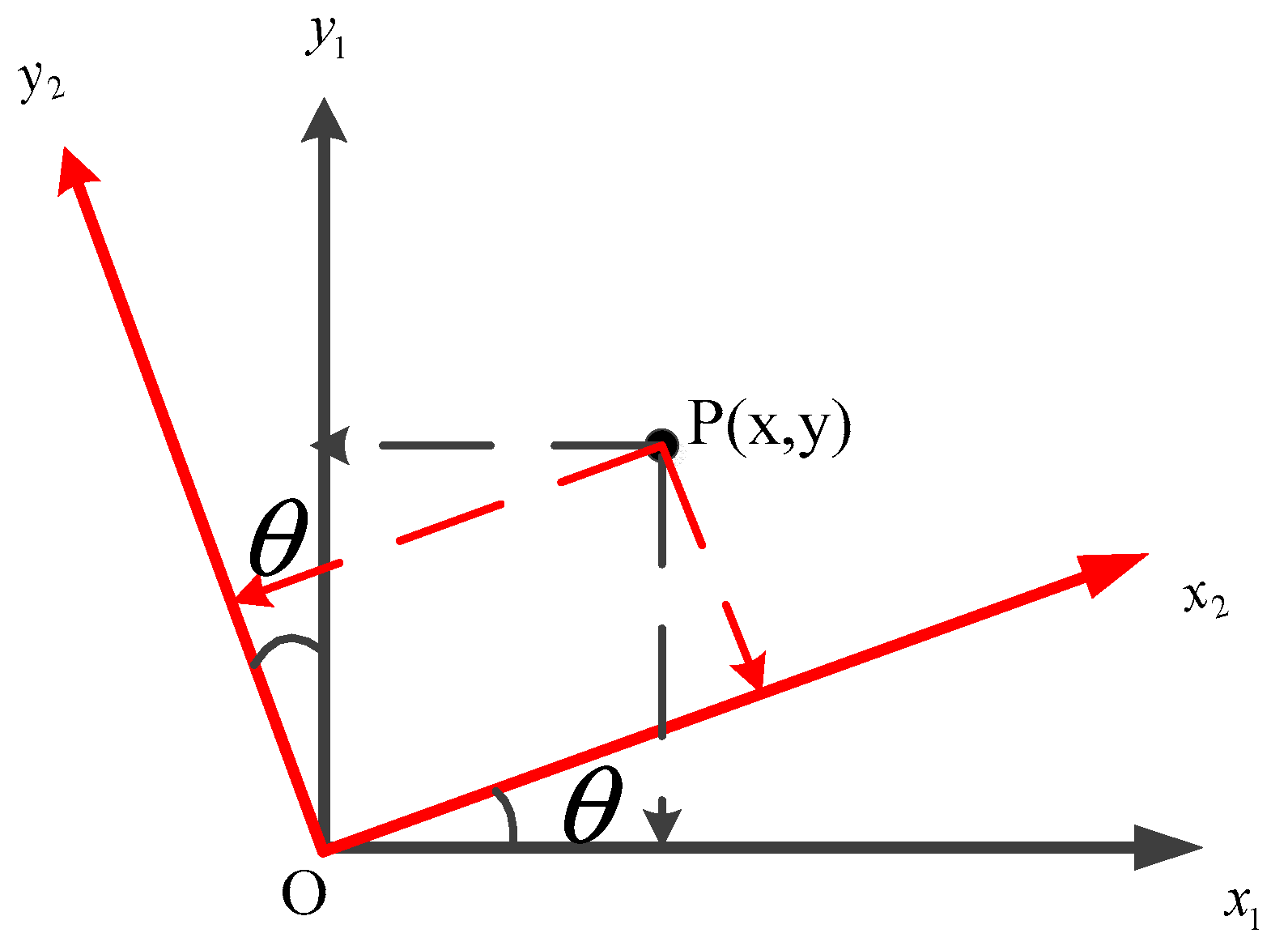
3.5.3. Affine Transformation
3.5.4. Calibration Transfer Method based on Affine Transformation
3.5.5. Summary of CTAI
Given calibration set of the master , calibration set of the slave and test set .
|
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, H.; Yu, H.; Xu, H.; Ying, Y. Near infrared spectroscopy for on/in-line monitoring of quality in foods and beverages: A review. J. Food Eng. 2008, 87, 303–313. [Google Scholar] [CrossRef]
- Roggo, Y.; Chalus, P.; Maurer, L.; Lema-Martinez, C.; Edmond, A.; Jent, N. A review of near infrared spectroscopy and chemometrics in pharmaceutical technologies. J. Pharm. Biomed. Anal. 2007, 44, 683–700. [Google Scholar] [CrossRef]
- Martinez, J.C.; Guzmán-Sepúlveda, J.R.; Bolañoz Evia, G.R.; Córdova, T.; Guzmán-Cabrera, R. Enhanced Quality Control in Pharmaceutical Applications by Combining Raman Spectroscopy and Machine Learning Techniques. Int. J. Thermophys. 2018, 39, 79. [Google Scholar] [CrossRef]
- Porep, J.U.; Kammerer, D.R.; Carle, R. On-line application of near infrared (NIR) spectroscopy in food production. Trends Food Sci. Tech. 2015, 46, 211–230. [Google Scholar] [CrossRef]
- Geladi, P.; Esbensen, K. Regression on multivariate images: Principal component regression for modeling, prediction and visual diagnostic tools. J. Chemom. 1991, 5, 97–111. [Google Scholar] [CrossRef]
- Næs, T.; Martens, H. Principal component regression in NIR analysis: View-points, background details and selection of components. J. Chemom. 1988, 2, 155–167. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Sijmen, D.J. SIMPLS: An alternative approach to partial least squares regression. Chemom. Intell. Lab. Syst. 1993, 18, 251–263. [Google Scholar]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Matthew, B.; Rayens, W. Partial least squares for discrimination. J. Chemometrics. 2012, 30, 446–452. [Google Scholar]
- Workman, J.J. A Review of Calibration Transfer Practices and Instrument Differences in Spectroscopy. Appl. Spectrosc. 2018, 72, 340–365. [Google Scholar] [CrossRef]
- Bouveresse, E.; Hartmann, C.; Massart, D.L.; Last, I.R.; Prebble, K.A. Standardization of near-infrared spectrometric instruments. Anal. Chem. 1996, 68, 982–990. [Google Scholar] [CrossRef]
- Feudale, R.N.; Woody, N.A.; Tan, H.; Myles, A.J.; Brown, S.D.; Ferré, J. Transfer of multivariate calibration models: A review. Chemom. Intell. Lab. Syst. 2002, 64, 181–192. [Google Scholar] [CrossRef]
- Wang, Y.; Veltkamp, D.J.; Kowalski, B.R. Multivariate instrument standardization. Anal. Chem. 1991, 63, 2750–2756. [Google Scholar] [CrossRef]
- Wang, Y.; Michael, J.L.; Kowalski, B.R. Improvement of multivariate calibration through instrument standardization. Anal. Chem. 1992, 64, 562–564. [Google Scholar] [CrossRef]
- Bouveresse, E.; Massart, D. Improvement of the piecewise direct standardisation procedure for the transfer of NIR spectra for multivariate calibration. Chemom. Intell. Lab. Syst. 1996, 32, 201–213. [Google Scholar] [CrossRef]
- Wang, Z.; Thomas, D.; Kowalski, B.R. Additive background correction in multivariate instrument standardization. Anal. Chem. 1995, 67, 2379–2385. [Google Scholar] [CrossRef]
- Tan, H.-W.; Brown, S.D. Wavelet hybrid direct standardization of near-infrared multivariate calibrations. J. Chemometrics. 2001, 15, 647–663. [Google Scholar] [CrossRef]
- Fan, W.; Liang, Y.; Yuan, D.; Wang, J. Calibration model transfer for near-infrared spectra based on canonical correlation analysis. Anal. Chim. Acta 2008, 623, 22–29. [Google Scholar] [CrossRef] [PubMed]
- Zheng, K.; Zhang, X.; Iqbal, J.; Fan, W.; Wu, Ti.; Du, Y.; Liang, Y. Calibration transfer of near-infrared spectra for extraction of informative components from spectra with canonical correlation analysis. J. Chemometrics. 2014, 28, 773–784. [Google Scholar] [CrossRef]
- Melzer, T.; Reiter, M.; Bischof, H. Appearance models based on kernel canonical correlation analysis. Pattern Recognit. 2003, 36, 1961–1971. [Google Scholar] [CrossRef]
- Leng, L.; Zhang, T.; Kleinman, L.; Zhu, W. Ordinary least square regression, orthogonal regression, geometric mean regression and their applications in aerosol science. J. Phys. Conf. Ser. 2007, 78, 012084. [Google Scholar] [CrossRef]
- Donald, C.; Orcutt, G.H. Application of least squares regression to relationships containing auto-correlated error terms. J. Amer. Stat. Assoc. 1949, 44, 32–61. [Google Scholar]
- Chen, W.-R.; Bin, J.; Lu, H.-M.; Zhang, Z.-M.; Liang, Y.-Z. Calibration transfer via an extreme learning machine auto-encoder. Analyst 2016, 141, 1973–1980. [Google Scholar] [CrossRef] [PubMed]
- Wise, B.M.; Martens, H.; Høy, M.; Bro, R.; Brockhoff, P.B. Calibration Transfer by Generalized Least Squares. In Proceedings of the Seventh Scandinavian Symposium on Chemometrics (SSC7), Copenhagen, Denmark, 19–23 August 2001. [Google Scholar]
- Du, W.; Chen, Z.-P.; Zhong, L.-J.; Wang, S.-X.; Yu, R.-Q.; Nordon, A.; Littlejohn, D.; Holden, M. Maintaining the predictive abilities of multivariate calibration models by spectral space transformation. Anal. Chim. Acta. 2011, 690, 64–70. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.P.; Li, L.M.; Yu, R.Q.; Littlejohn, D.; Nordon, A.; Morris, J.; Dann, A.S.; Jeffkins, P.A.; Richardson, M.D.; Stimpson, S.L. Systematic prediction error correction: A novel strategy for maintaining the predictive abilities of multivariate calibration models. Analyst. 2010, 136, 98–106. [Google Scholar] [CrossRef] [PubMed]
- Kramer, K.E.; Morris, R.E.; Rose-Pehrsson, S.L. Comparison of two multiplicative signal correction strategies for calibration transfer without standards. Chemom. Intell. Lab. Syst. 2008, 92, 33–43. [Google Scholar] [CrossRef]
- Preisner, O.; Lopes, J.A.; Guiomar, R.; Machado, J.; José, C.M. Fourier transform infrared (FT-IR) spectroscopy in bacteriology: towards a reference method for bacteria discrimination. Anal. Bioanal. Chem. 2007, 387, 1739–1748. [Google Scholar] [CrossRef] [PubMed]
- Isaksson, T.; Næs, T. The effect of multiplicative scatter correction (MSC) and linearity improvement in NIR spectroscopy. Appl. Spectrosc. 1988, 42, 1273–1284. [Google Scholar] [CrossRef]
- Blank, T.B.; Sum, S.T.; Brown, S.D.; Monfre, S.L. Transfer of near-infrared multivariate calibrations without standards. Anal. Chem. 1996, 68, 2987–2995. [Google Scholar] [CrossRef]
- Wold, S.; Antti, H.; Lindgren, F.; Öhman, J. Orthogonal signal correction of near infrared spectra. Chemom. Intell. Lab. Syst. 1998, 44, 175–185. [Google Scholar] [CrossRef]
- Sjöblom, J.; Svensson, O.; Josefson, M.; Kullberg, H.; Wold, S. An evaluation of orthogonal signal correction applied to calibration transfer of near infrared spectra. Chemom. Intell. Lab. Syst. 1998, 44, 229–244. [Google Scholar] [CrossRef]
- Malli, B.; Birlutiu, A.; Natschläger, T. Standard-free calibration transfer-An evaluation of different techniques. Chemom. Intell. Lab. Syst. 2017, 161, 49–60. [Google Scholar] [CrossRef]
- Pan, S.J.; Tsang, I.; Kwok, J.; Yang, Q. Domain adaptation via transfer component analysis. IEEE Trans. Neural Netw. 2011, 22, 199–210. [Google Scholar] [CrossRef] [PubMed]
- Schölkopf, B.; Smola, A.; Müller, K.R. Kernel principal component analysis. In Artificial Neural Networks — ICANN’97, Proceeding of 7th International Conference Lausanne, Lausanne, Switzerland, 8–10 October 1997; Springer: Berlin/Heidelberg, Germany, 1997; pp. 583–588. [Google Scholar]
- Schölkopf, B.; Smola, A.; Müller, K.-R. Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Muandet, K.; Balduzzi, D.; Schölkopf, B. Domain generalization via invariant feature representation. In Proceedings of the 30th International Conference on Machine Learning (ICML-13), Atlanta, GA, USA, 16–21 June 2013; pp. 10–18. [Google Scholar]
- Bloomenthal, J.; Jon, R. Homogeneous coordinates. Visual Computer. 1994, 11, 15–26. [Google Scholar] [CrossRef]
Sample Availability: Samples are not available from the authors. |
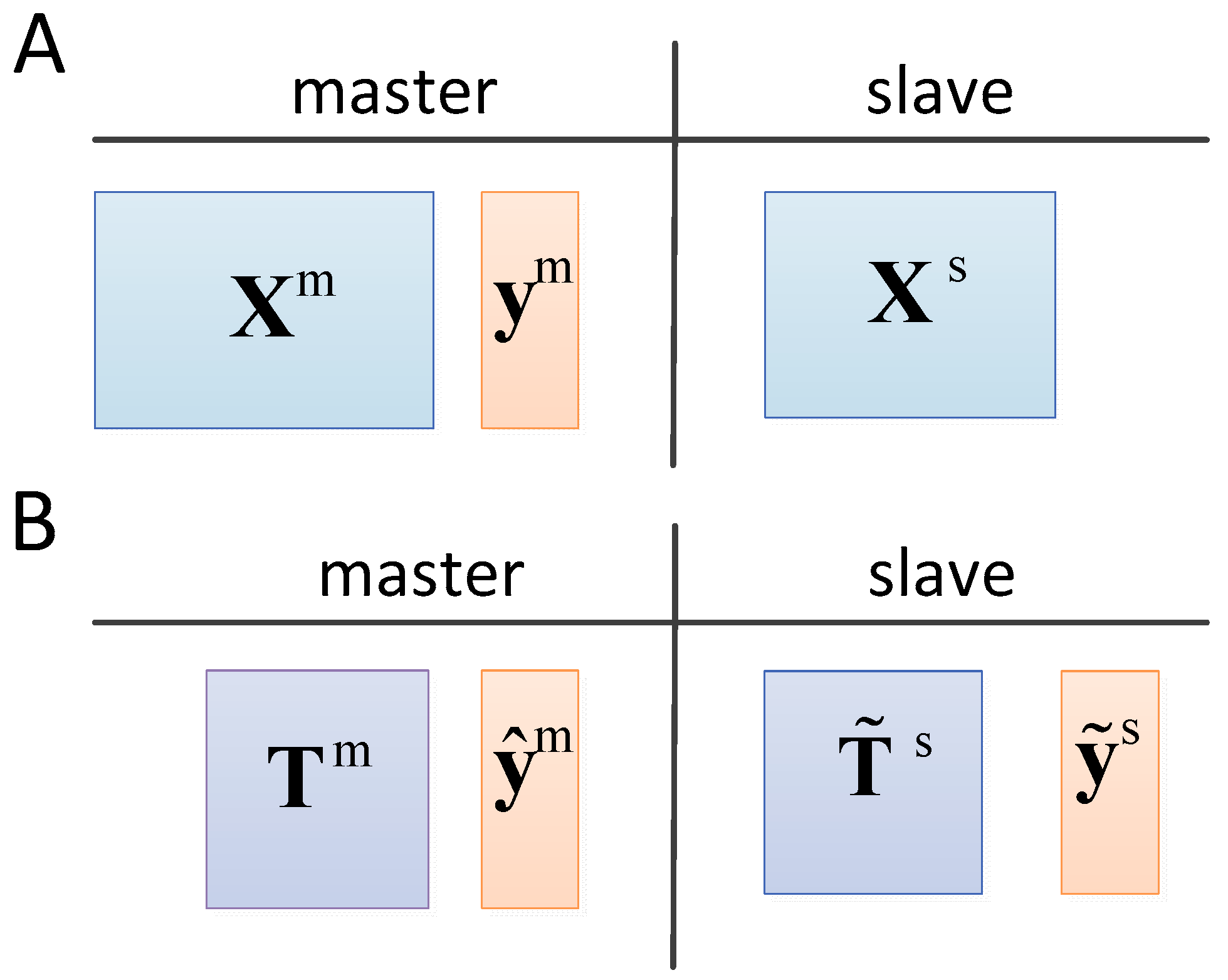
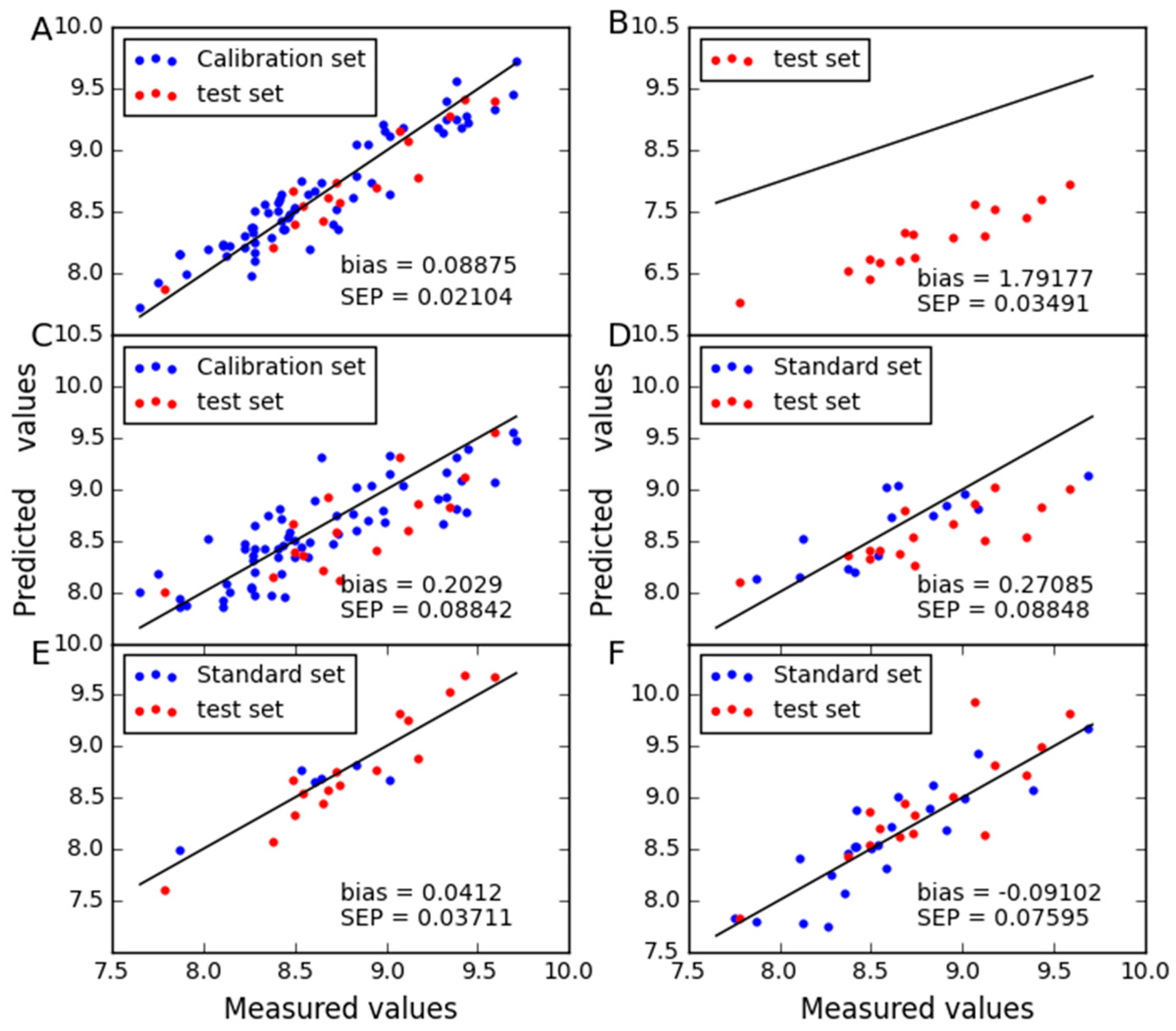
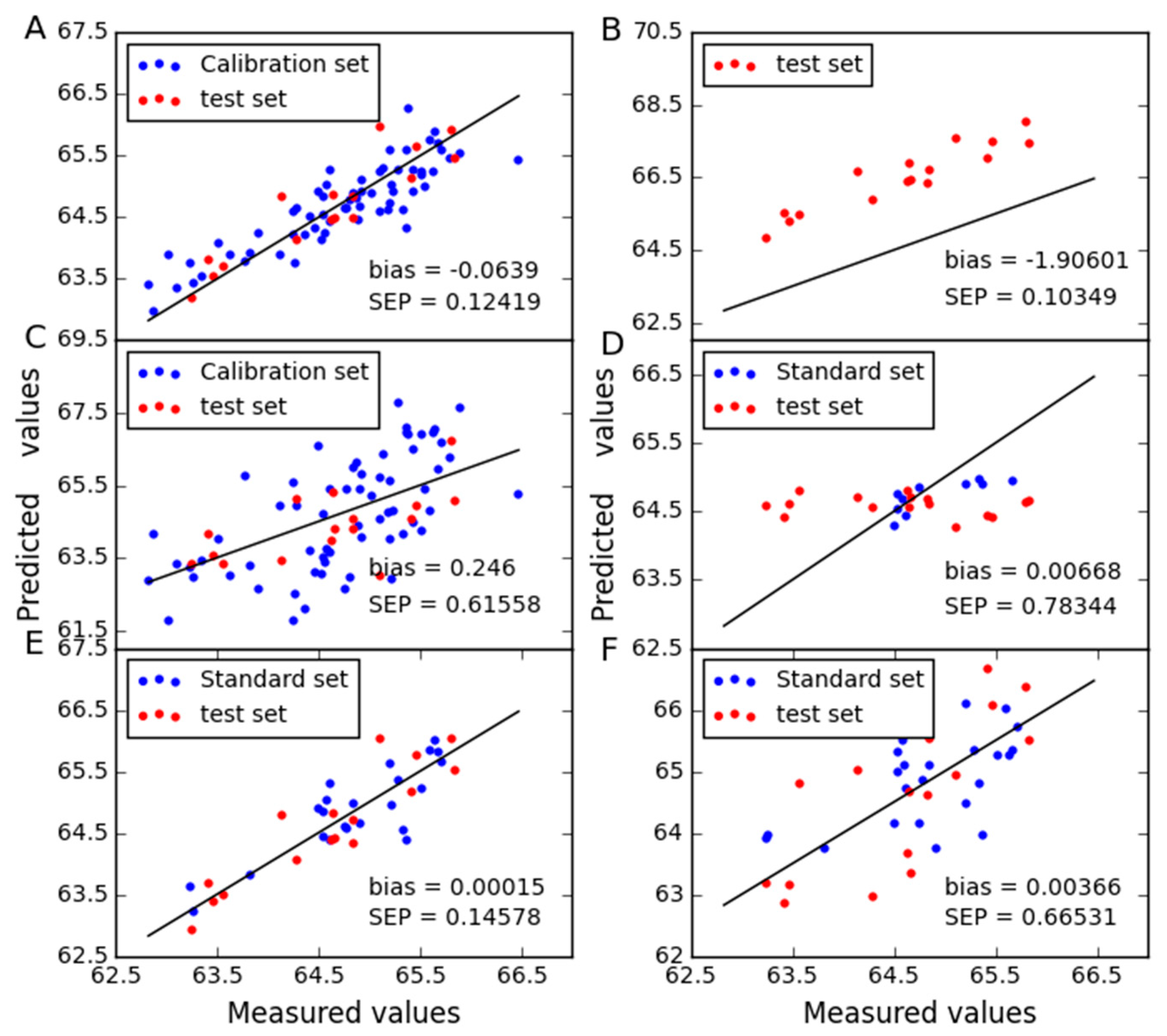
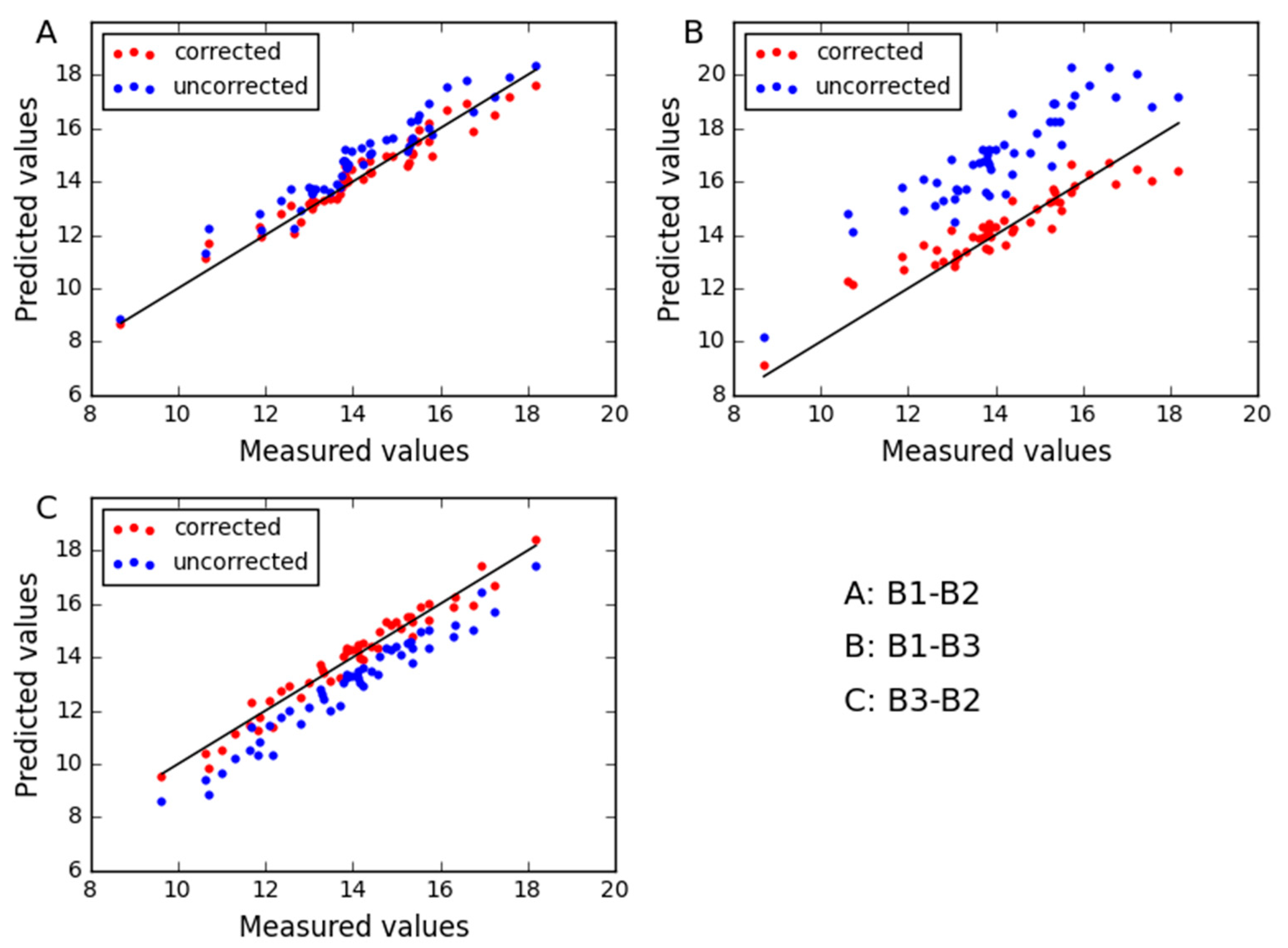
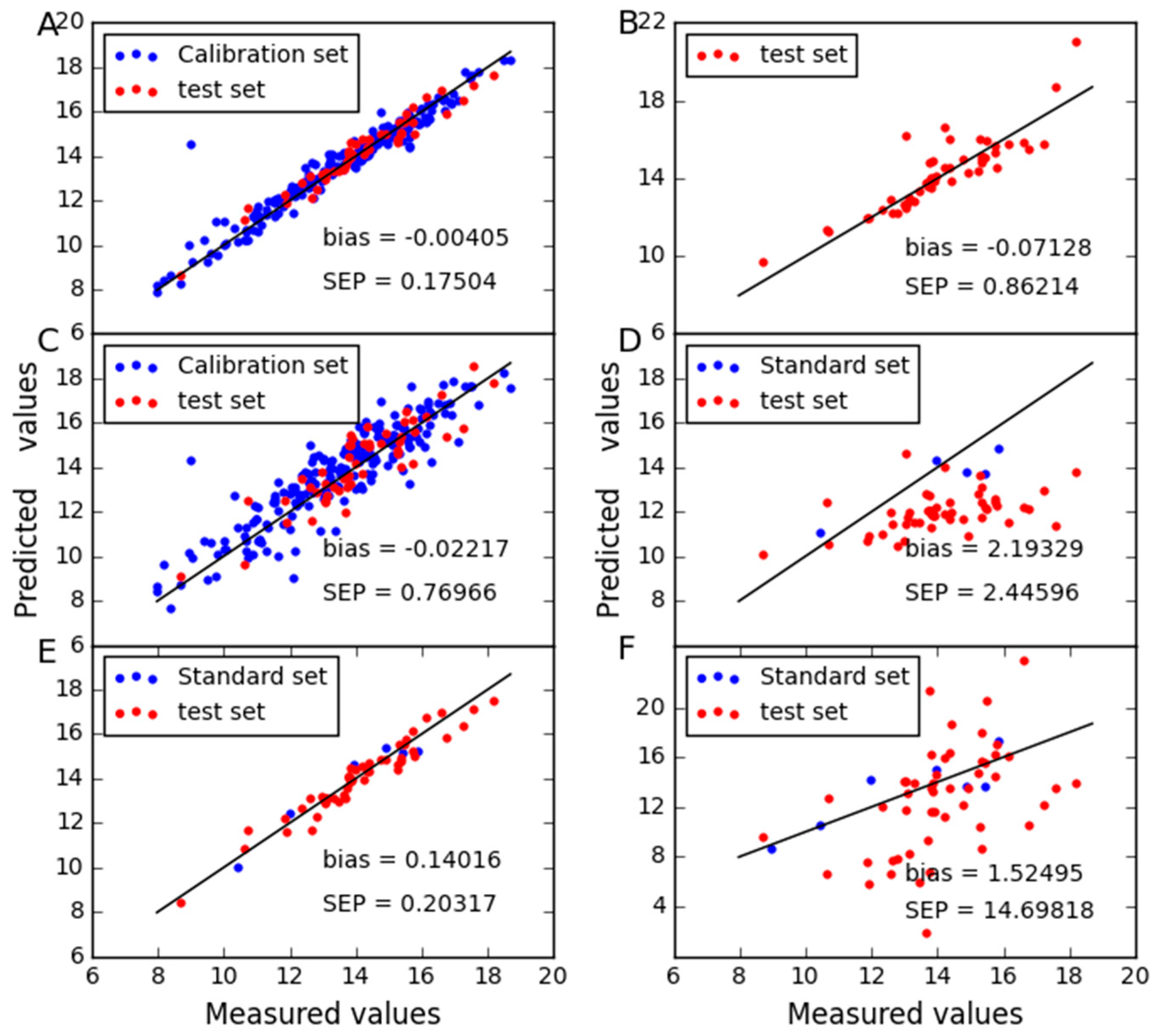

| Instrument | Reference Values | RMSECm | RMSEPm | RMSECVmin (LV) | Biasm | rm | pm |
|---|---|---|---|---|---|---|---|
| m5spec | moisture | 0.00599 | 0.00764 | 0.01066(14) | 0.0008 | 0.99973 | 2.6 × 10−24 |
| m5spec | oil | 0.02686 | 0.05664 | 0.05049(15) | −0.01327 | 0.9332 | 1.3 × 10−7 |
| m5spec | protein | 0.0507 | 0.10066 | 0.11012(15) | 0.02814 | 0.97632 | 1 × 10−10 |
| m5spec | starch | 0.09539 | 0.18993 | 0.19227(15) | 0.01789 | 0.97464 | 1.6 × 10−10 |
| mp6spec | moisture | 0.09991 | 0.15637 | 0.14775(10) | −0.02678 | 0.92083 | 4.2 × 10−7 |
| mp6spec | oil | 0.06052 | 0.09098 | 0.09872(12) | 0.01868 | 0.87697 | 8.2 × 10−6 |
| mp6spec | protein | 0.10101 | 0.13338 | 0.15043(12) | 0.02128 | 0.96659 | 1.1 × 10−9 |
| mp6spec | starch | 0.27636 | 0.26723 | 0.35978(9) | 0.02124 | 0.93136 | 1.6 × 10−7 |
| B1 | protein | 0.3288 | 0.33254 | 0.50337(15) | 0.00906 | 0.98508 | 2.3 × 10−38 |
| B2 | protein | 0.21636 | 0.83755 | 0.32441(15) | −0.13124 | 0.8485 | 7.2 × 10−15 |
| B3 | protein | 0.30288 | 0.51567 | 0.43896(15) | −0.034 | 0.96009 | 3.2 × 10−28 |
| Instrument Reference Values | m5spec*-mp6spec | B1*-B2 | B1*-B3 | B3*-B2 | ||||
|---|---|---|---|---|---|---|---|---|
| Moisture | Oil | Protein | Starch | Protein | ||||
| RMSEPupre | 1.60705 | 0.7989 | 2.06797 | 2.11743 | 0.69894 | 2.92541 | 1.23368 | |
| RMSEPpre | 0.21255 | 0.06922 | 0.13195 | 0.33358 | 0.31537 | 0.62632 | 0.65398 | |
| kpre | 0.6498 | 0.77129 | 0.94553 | 0.82527 | 0.88809 | 0.76290 | 0.86909 | |
| rpre | 0.81644 | 0.89598 | 0.96286 | 0.92197 | 0.97594 | 0.87695 | 0.93715 | |
| ppre | 1.1 × 10−4 | 2.6 × 10−6 | 2.3 × 10−9 | 3.8 × 10−7 | 2 × 10−33 | 6.8 × 10−17 | 1.3 × 10−23 | |
| tpre | −15.429 | 19.335 | −19.147 | 8.838 | 2.292 | 10.684 | -3.826 | |
| RMSEPu | 1.60762 | 0.81532 | 2.09665 | 2.10291 | 0.71977 | 2.90011 | 1.08008 | |
| RMSEP | 0.21095 | 0.08233 | 0.16614 | 0.34714 | 0.41419 | 0.68215 | 0.38446 | |
| k | 0.65191 | 0.53297 | 0.98736 | 0.79329 | 0.96898 | 0.85693 | 0.93896 | |
| r | 0.81922 | 0.78858 | 0.95844 | 0.91487 | 0.96770 | 0.89517 | 0.97796 | |
| p | 1.0 × 10−4 | 2.8 × 10−4 | 5.1 × 10−9 | 6.9 × 10−7 | 2.2 × 10−30 | 1.8 × 10−18 | 2.5 × 10−34 | |
| t | −15.437 | 19.657 | −19.408 | 8.762 | 2.256 | 10.649 | −3.701 | |
| tcritical_value | 2.131 | 2.131 | 2.131 | 2.131 | 2.01 | 2.01 | 2.01 | |
| Method | CTAI | MSC | TCR | CCA | SBC | PDS | |
|---|---|---|---|---|---|---|---|
| moisture | RMSEC | 0.22646 | 1.92839 | 0.61873 | 0.15996(14a) | 0.18506(5a) | 0.14742(17a) |
| RMSEP | 0.21095 | 1.6689 | 0.39066 | 0.23304(14a) | 0.42574(5a) | 0.24238(17a) | |
| oil | RMSEC | 0.08141 | 1.21647 | 0.14543 | 0.15764(6a) | 0.08423(23a) | 0.10794(28a) |
| RMSEP | 0.08233 | 1.23209 | 0.14225 | 0.11432(6a) | 0.08361(23a) | 0.09495(28a) | |
| protein | RMSEC | 0.17247 | 1.77294 | 0.28297 | 0.27860(14a) | 0.17422(6a) | 0.24662(23a) |
| RMSEP | 0.16614 | 1.80087 | 0.35223 | 0.39535(14a) | 0.19101(6a) | 0.28193(23a) | |
| starch | RMSEC | 0.39517 | 1.89165 | 1.21093 | 0.33937(10a) | 0.38426(23a) | 0.62099(23a) |
| RMSEP | 0.34714 | 1.93129 | 0.79852 | 0.85704(10a) | 0.36969(23a) | 0.78977(23a) | |
| B1*-B2 | RMSEC | 0.55682 | 1.31153 | 0.99246 | 1.11889(5a) | 0.48509(6a) | 1.3676(7a) |
| RMSEP | 0.41419 | 0.92194 | 0.86881 | 2.68469(5a) | 0.4677(6a) | 4.09019(7a) | |
| B1*-B3 | RMSEC | 0.81895 | 2.91695 | 0.84682 | 0.68529(15a) | 1.00007(8a) | 0.57858(5a) |
| RMSEP | 0.68215 | 2.40587 | 0.72996 | 1.10564(15a) | 0.79294(8a) | 1.33547(5a) | |
| B3*-B2 | RMSEC | 0.54753 | 1.25096 | 0.76972 | 1.57073(14a) | 0.56236(5a) | 2.1039(8a) |
| RMSEP | 0.38446 | 1.38468 | 0.63689 | 2.29856(14a) | 0.53534(5a) | 1.83564(8a) | |
| MSC | TCR | CCA | SBC | PDS | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| h(%) | p | h(%) | p | h(%) | p | h(%) | p | h(%) | p | |
| moisture | 87.35 | 4.3 × 10 −4 | 46 | 0.53 | 9.48 | 0.43 | 50.45 | 0.01 | 12.96 | 0.04 |
| oil | 93.31 | 4.3 × 10 −4 | 42.12 | 0.01 | 27.98 | 0.32 | 1.52 | 0.23 | 13.28 | 0.46 |
| protein | 90.77 | 4.3 × 10 −4 | 52.83 | 0.09 | 57.97 | 0.03 | 13.02 | 0.23 | 41.06 | 0.01 |
| starch | 82.02 | 4.3 × 10 −4 | 56.52 | 0.23 | 59.49 | 0.83 | 6.09 | 0.02 | 56.04 | 0.75 |
| B1*-B2 | 55.07 | 0.11 | 52.32 | 0.79 | 84.57 | 5.3 × 10 −9 | 11.44 | 2.6 × 10 −9 | 89.87 | 9.2 × 10 −3 |
| B1*-B3 | 71.64 | 7.5 × 10 −10 | 6.55 | 0.11 | 38.3 | 1.8 × 10 −5 | 13.97 | 1 × 10 −5 | 48.92 | 9.8 × 10 −5 |
| B3*-B2 | 72.23 | 3.1 × 10−9 | 39.63 | 4.6 × 10−3 | 83.27 | 0.02 | 28.18 | 7.5 × 10 −10 | 79.05 | 0.06 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Zhao, Z.; Shan, P.; Peng, S.; Yu, J.; Gao, S. Calibration Transfer Based on Affine Invariance for NIR without Transfer Standards. Molecules 2019, 24, 1802. https://doi.org/10.3390/molecules24091802
Zhao Y, Zhao Z, Shan P, Peng S, Yu J, Gao S. Calibration Transfer Based on Affine Invariance for NIR without Transfer Standards. Molecules. 2019; 24(9):1802. https://doi.org/10.3390/molecules24091802
Chicago/Turabian StyleZhao, Yuhui, Ziheng Zhao, Peng Shan, Silong Peng, Jinlong Yu, and Shuli Gao. 2019. "Calibration Transfer Based on Affine Invariance for NIR without Transfer Standards" Molecules 24, no. 9: 1802. https://doi.org/10.3390/molecules24091802
APA StyleZhao, Y., Zhao, Z., Shan, P., Peng, S., Yu, J., & Gao, S. (2019). Calibration Transfer Based on Affine Invariance for NIR without Transfer Standards. Molecules, 24(9), 1802. https://doi.org/10.3390/molecules24091802






