Intrinsic Flexibility of the EMT Zeolite Framework under Pressure
Abstract
1. Introduction
2. Results and Discussion
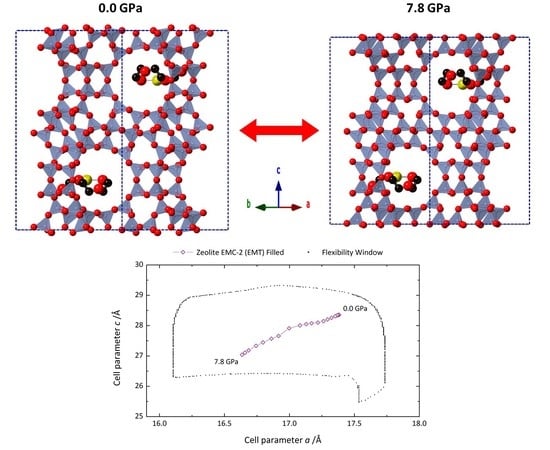
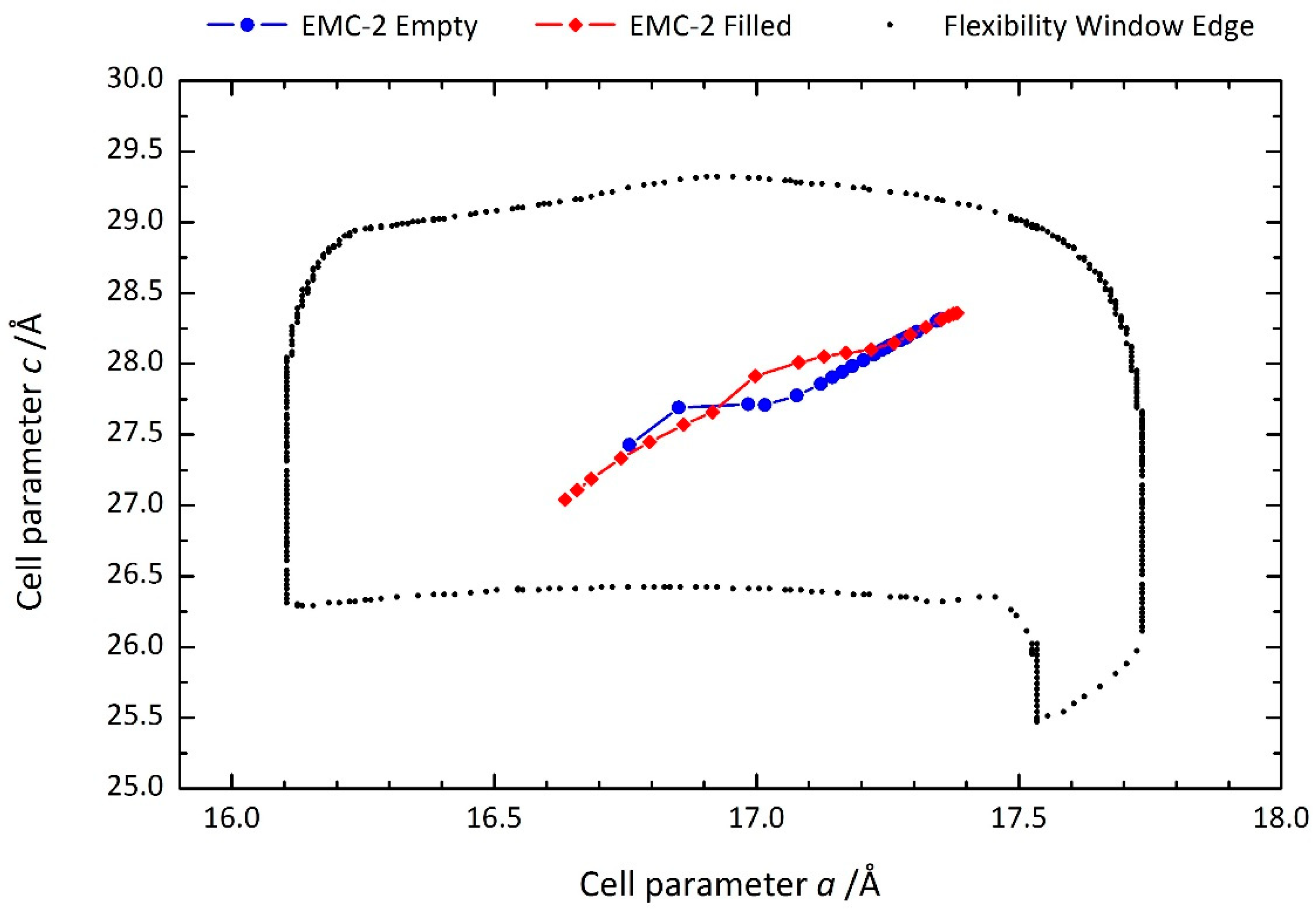
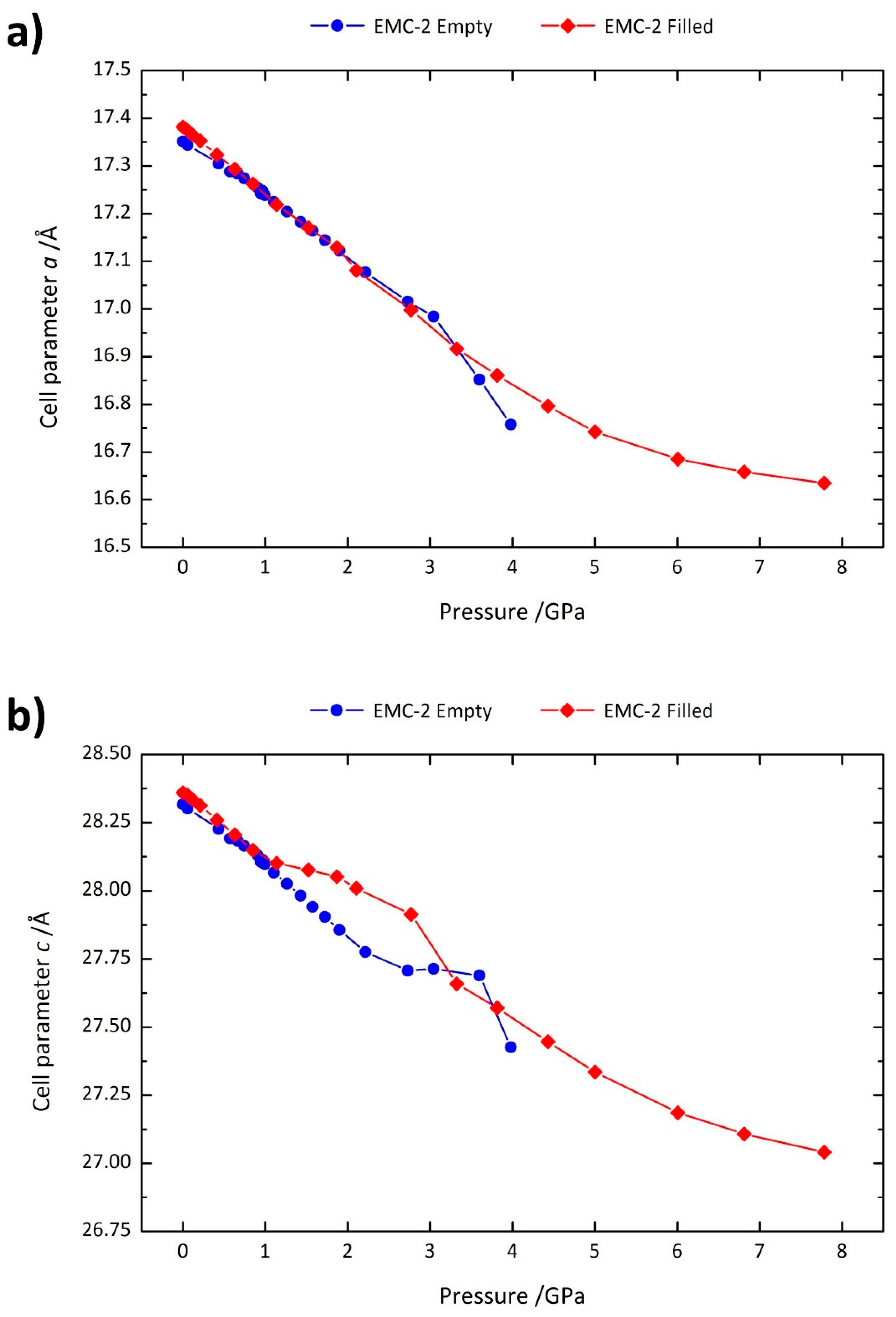
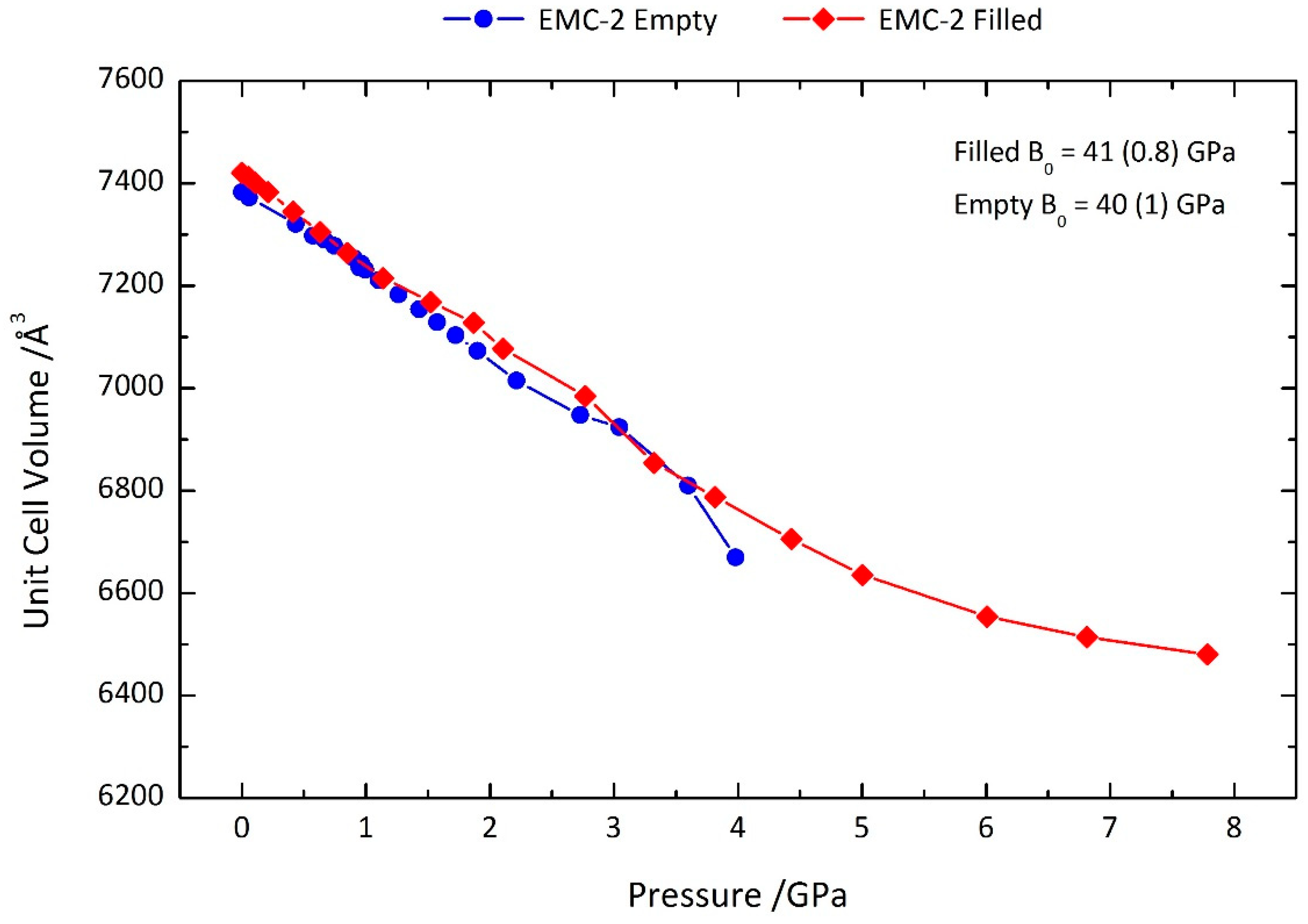
2.1. High-Pressure Powder X-ray Diffraction
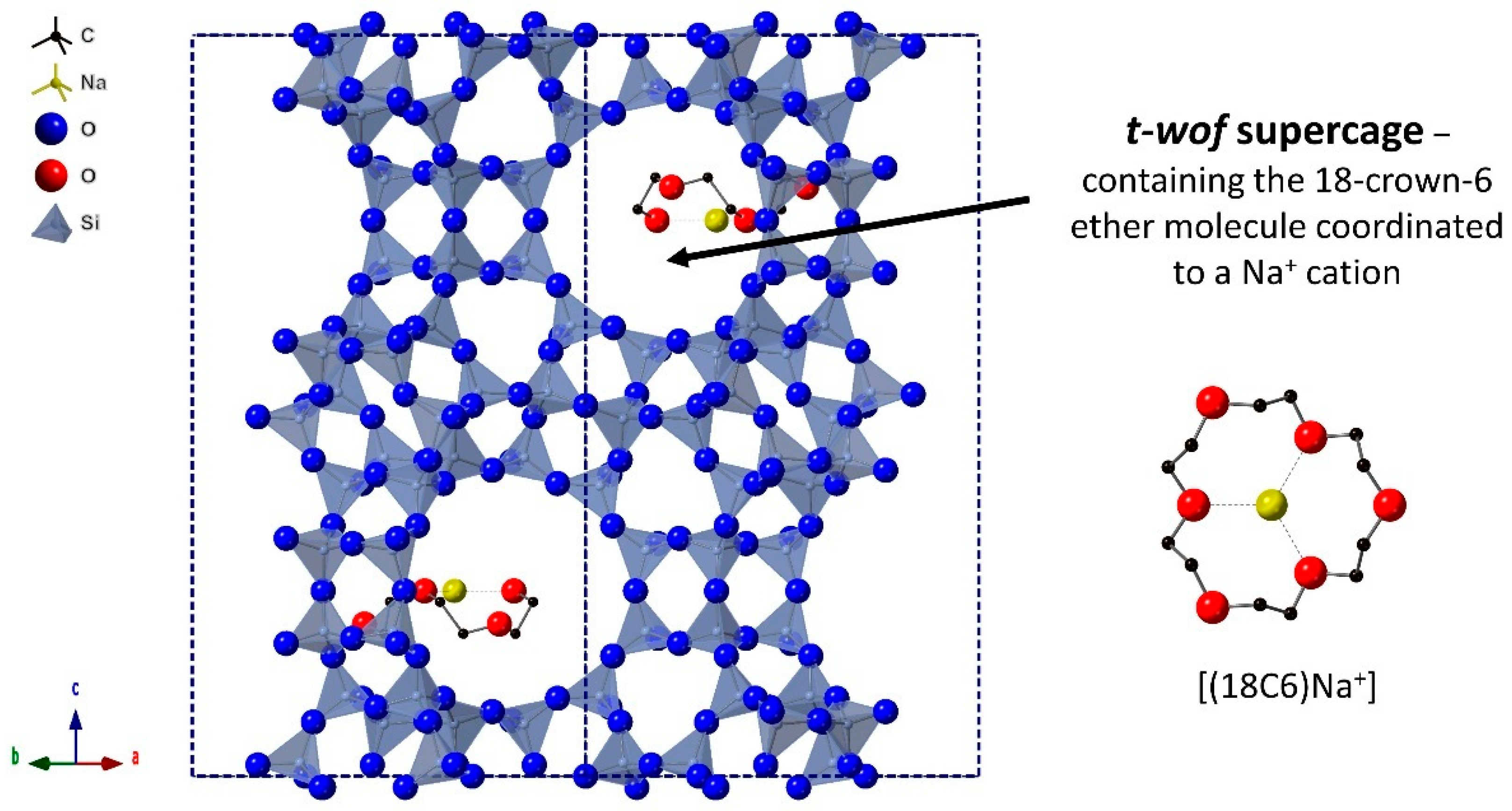
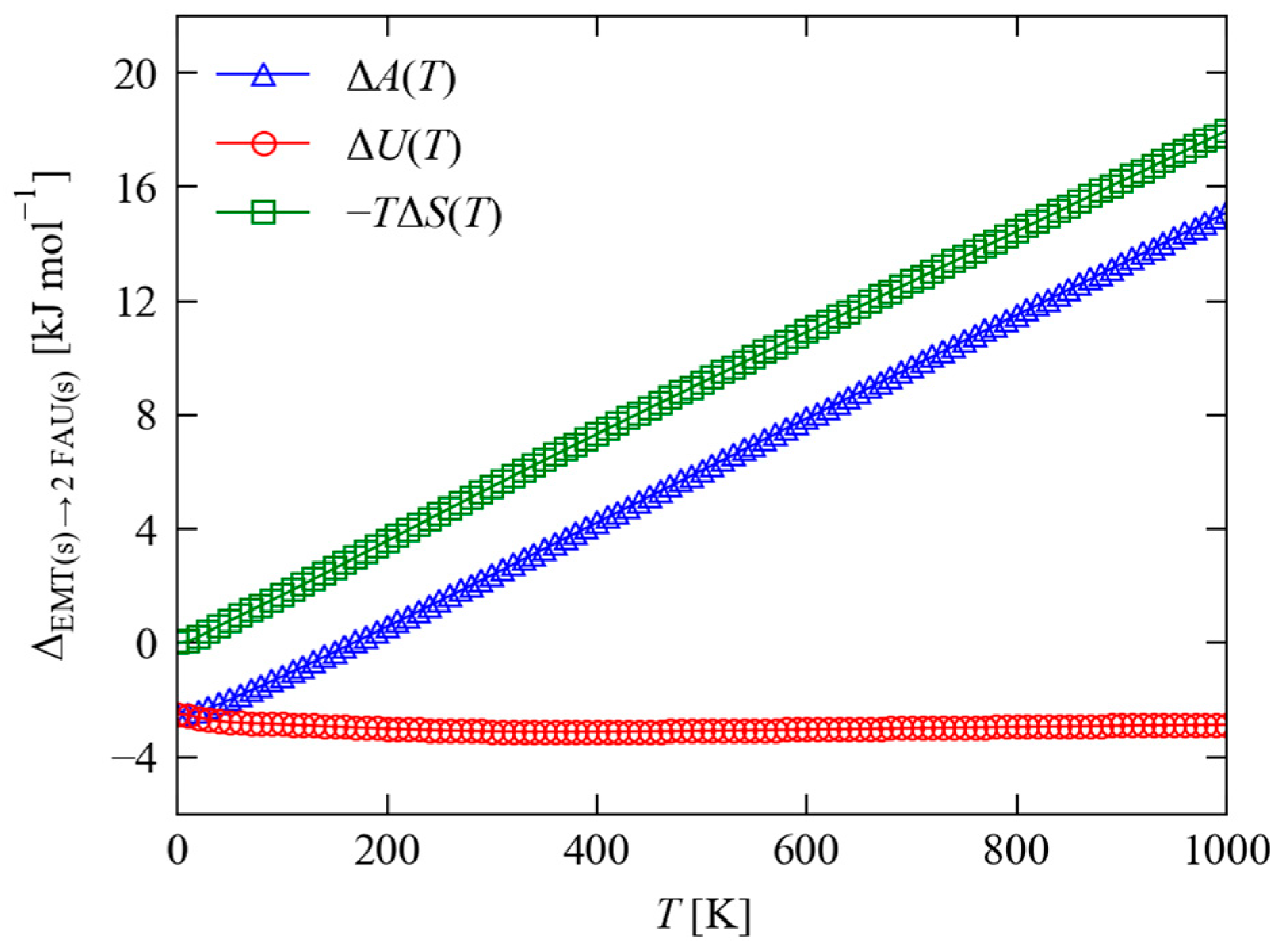
2.2. Computational Modelling
3. Materials and Methods
3.1. Sample Preparation
3.2. High-Pressure Powder X-ray Diffraction
3.3. Computational Modelling
3.4. Data Availability
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Breck, D.W. Zeolite Molecular Sieves: Structure, Chemistry and Use, 6th ed.; R.E. Krieger: Malabar, FL, USA, 1984. [Google Scholar]
- Dyer, A. Ion exchange properties of zeolites and related materials. In Introduction to Zeolite Science and Practice, 3rd ed.; Elsevier Science B.V.: Amsterdam, The Netherlands, 2007; pp. 525–554. [Google Scholar]
- Bhatia, S. Zeolite Catalysts: Principles and Applications; CRC press: Boca Raton, FL, USA, 1989. [Google Scholar]
- Sartbaeva, A.; Wells, S.A.; Treacy, M.; Thorpe, M. The flexibility window in zeolites. Nat. Mater. 2006, 5, 962. [Google Scholar] [CrossRef] [PubMed]
- Baerlocher, C.; McCusker, L.B.; Olson, D.H. Atlas of Zeolite Framework Types, 6th ed.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Jacobs, P.A.; Flanigen, E.M.; Jansen, J.C.; van Bekkum, H. Introduction to Zeolite Science and Practice; Elsevier Science B.V.: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Lee, Y.; Hriljac, J.A.; Vogt, T.; Parise, J.B.; Edmondson, M.J.; Anderson, P.A.; Corbin, D.R.; Nagai, T. Phase transition of zeolite RHO at high-pressure. J. Am. Chem. Soc. 2001, 123, 8418–8419. [Google Scholar] [CrossRef] [PubMed]
- Gatta, G.; Lee, Y. Zeolites at high pressure: A review. Mineral. Mag. 2014, 78, 267–291. [Google Scholar] [CrossRef]
- Cundy, C.S.; Cox, P.A. The hydrothermal synthesis of zeolites: Precursors, intermediates and reaction mechanism. Microporous Mesoporous Mater. 2005, 82, 1–78. [Google Scholar] [CrossRef]
- Nearchou, A.; Sartbaeva, A. Influence of alkali metal cations on the formation of zeolites under hydrothermal conditions with no organic structure directing agents. Crystengcomm 2015, 17, 2496–2503. [Google Scholar] [CrossRef]
- Lobo, R.F.; Zones, S.I.; Davis, M.E. Structure-direction in zeolite synthesis. In Inclusion Chemistry with Zeolites: Nanoscale Materials by Design; Herron, N., Corbin, D.R., Eds.; Springer: Heidelberg, Germany, 1995; pp. 47–78. [Google Scholar]
- Davis, M.E.; Lobo, R.F. Zeolite and molecular sieve synthesis. Chem. Mater. 1992, 4, 756–768. [Google Scholar] [CrossRef]
- Flanigen, E.M.; Bennett, J.; Grose, R.; Cohen, J.; Patton, R.; Kirchner, R.; Smith, J. Silicalite, a new hydrophobic crystalline silica molecular sieve. Nature 1978, 271, 512–516. [Google Scholar] [CrossRef]
- Ilyushin, G. Theory of cluster self-organization of crystal-forming systems: Geometrical–topological modeling of nanocluster precursors with a hierarchical structure. Struct. Chem. 2012, 23, 997–1043. [Google Scholar] [CrossRef]
- Chatelain, T.; Patarin, J.; Brendle, E.; Dougnier, F.; Guth, J.L.; Schulz, P. Synthesis of high-silica FAU-, EMT-, RHO- and KFI-type zeolites in the presence of 18-crown-6 ether. Stud. Surf. Sci. Catal. 1997, 105, 173–180. [Google Scholar] [CrossRef]
- Lewis, D.W.; Willock, D.J.; Catlow, C.R.A.; Thomas, J.M.; Hutchings, G.J. De novo design of structure-directing agents for the synthesis of microporous solids. Nature 1996, 382, 604–606. [Google Scholar] [CrossRef]
- Lewis, D.W.; Freeman, C.M.; Catlow, C.R.A. Predicting the templating ability of organic additives for the synthesis of microporous materials. J. Phys. Chem. 1995, 99, 11194–11202. [Google Scholar] [CrossRef]
- Stevens, A.P.; Gorman, A.M.; Freeman, C.M.; Cox, P.A. Prediction of template location via a combined Monte Carlo–simulated annealing approach. J. Chem. Soc. Faraday Trans. 1996, 92, 2065–2073. [Google Scholar] [CrossRef]
- Casci, J. Zeolite Synthesis Using Catalytic Amounts of Template: Structure Blocking Effects and Stoichiometric Syntheses. Stud. Surf. Sci. Catal. 1994, 84, 133–140. [Google Scholar] [CrossRef]
- Cox, P.A.; Casci, J.; Stevens, A. Molecular modelling of templated zeolite synthesis. Faraday Discuss. 1997, 106, 473–487. [Google Scholar] [CrossRef]
- Sartbaeva, A.; Wells, S.A. Framework flexibility and rational design of new zeolites for catalysis. Appl. Petrochem. Res. 2012, 2, 69–72. [Google Scholar] [CrossRef]
- Liu, H.J.; Secco, R.A.; Huang, Y.N. Pressure-induced amorphization of hydrated Na-X zeolite. PhysChemComm 2001, 4, 37–39. [Google Scholar] [CrossRef]
- Seoung, D.; Lee, Y.; Kim, S.J.; Lee, H.-H.; Ahn, D.; Shin, N.-S.; Vogt, T.; Lee, Y. Pressure-induced hydration and cation migration in a Cs+ exchanged gallosilicate zeolite LTL: Synchrotron X-ray powder diffraction study at ambient and high pressures. Microporous Mesoporous Mater. 2010, 136, 75–82. [Google Scholar] [CrossRef]
- Wells, S.A.; Leung, K.M.; Edwards, P.P.; Tucker, M.G.; Sartbaeva, A. Defining the flexibility window in ordered aluminosilicate zeolites. R. Soc. Open Sci. 2017, 4, 170757. [Google Scholar] [CrossRef]
- Fletcher, R.E.; Wells, S.A.; Leung, K.M.; Edwards, P.P.; Sartbaeva, A. Intrinsic flexibility of porous materials; theory, modelling and the flexibility window of the EMT zeolite framework. Acta Crystallogr. B 2015, 71, 641–647. [Google Scholar] [CrossRef]
- Wells, S.A.; Sartbaeva, A. GASP: Software for geometric simulations of flexibility in polyhedral and molecular framework structures. Mol. Simulat. 2015, 41, 1409–1421. [Google Scholar] [CrossRef]
- Wells, S.A.; Sartbaeva, A. Template-based geometric simulation of flexible frameworks. Materials 2012, 5, 415–431. [Google Scholar] [CrossRef] [PubMed]
- Baerlocher, C.; McCusker, L.B.; Chiappetta, R. Location of the 18-crown-6 ether template in EMC-2 (EMT) Rietveld refinement of the calcined and as-synthesised forms. Microporous Mater. 1994, 2, 269–280. [Google Scholar] [CrossRef]
- Delprato, F.; Delmotte, L.; Guth, J.L.; Huve, L. Synthesis of new silica-rich cubic and hexagonal faujasites using crown-ether-based supramolecules as templates. Zeolites 1990, 10, 546–552. [Google Scholar] [CrossRef]
- Feijen, E.J.P.; Matthijs, B.; Grobet, P.J.; Martens, J.A.; Jacobs, P.A. Structure directing role of Na+ and TMA(+) cations in 18-crown-6 ether mediated crystallization of EMT, MAZ and SOD aluminosilicate zeolites. Stud. Surf. Sci. Catal. 1997, 105, 165–172. [Google Scholar] [CrossRef]
- Feijen, E.J.P.; Devadder, K.; Bosschaerts, M.H.; Lievens, J.L.; Martens, J.A.; Grobet, P.J.; Jacobs, P.A. Role of 18-crown-6 and 15-crown-5 ethers in the crystallization of polytype faujasite zeolites. J. Am. Chem. Soc. 1994, 116, 2950–2957. [Google Scholar] [CrossRef]
- Burkett, S.L.; Davis, M.E. Structure-directing effects in the crown ether-mediated syntheses of FAU and EMT zeolites. Microporous Mater. 1993, 1, 265–282. [Google Scholar] [CrossRef]
- Ohsuna, T.; Terasaki, O.; Alfredsson, V.; Bovin, J.O.; Watanabe, D.; Carr, S.W.; Anderson, M.W. Observations on the role of crown ether templates in the formation of hexagonal and cubic polymorphs of zeolite Y. Proc. R. Soc. A 1996, 452, 715–740. [Google Scholar] [CrossRef]
- Nearchou, A.; Raithby, P.R.; Sartbaeva, A. Systematic approaches towards template-free synthesis of EMT-type zeolites. Microporous Mesoporous Mater. 2018, 255, 261–270. [Google Scholar] [CrossRef]
- Sartbaeva, A.; Haines, J.; Cambon, O.; Santoro, M.; Gorelli, F.; Levelut, C.; Garbarino, G.; Wells, S.A. Flexibility windows and compression of monoclinic and orthorhombic silicalites. Phys. Rev. B 2012, 85, 064109. [Google Scholar] [CrossRef]
- Angel, R.J.; Bujak, M.; Zhao, J.; Gatta, G.D.; Jacobsen, S.D. Effective hydrostatic limits of pressure media for high-pressure crystallographic studies. J. Appl. Crystallogr. 2007, 40, 26–32. [Google Scholar] [CrossRef]
- Cliffe, M.J.; Goodwin, A.L. PASCal: A principal axis strain calculator for thermal expansion and compressibility determination. J. Appl. Crystallogr. 2012, 45, 1321–1329. [Google Scholar] [CrossRef]
- Colligan, M.; Forster, P.M.; Cheetham, A.K.; Lee, Y.; Vogt, T.; Hriljac, J.A. Synchrotron X-ray powder diffraction and computational investigation of purely siliceous zeolite Y under pressure. J. Am. Chem. Soc. 2004, 126, 12015–12022. [Google Scholar] [CrossRef] [PubMed]
- Baerlocher, C.; McCusker, L.B. Database of Zeolite Structures. Available online: http://izasc.ethz.ch/fmi/xsl/IZA-SC/ft.xsl (accessed on 1 September 2016).
- Mathew, K.; Sundararaman, R.; Letchworth-Weaver, K.; Arias, T.; Hennig, R.G. Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways. J. Chem. Phys. 2014, 140, 084106. [Google Scholar] [CrossRef]
- Mathew, K.; Hennig, R.G. Implicit self-consistent description of electrolyte in plane-wave density-functional theory. arXiv preprint. 2016. Available online: https://arxiv.org/abs/1601.03346 (accessed on 4 February 2019).
- Pallipurath, A.R.; Skelton, J.M.; Warren, M.R.; Kamali, N.; McArdle, P.; Erxleben, A. Sulfamerazine: Understanding the influence of slip planes in the polymorphic phase transformation through X-ray crystallographic studies and ab initio lattice dynamics. Mol. Pharm. 2015, 12, 3735–3748. [Google Scholar] [CrossRef] [PubMed]
- Butler, K.T.; Svane, K.; Kieslich, G.; Cheetham, A.K.; Walsh, A. Microscopic origin of entropy-driven polymorphism in hybrid organic-inorganic perovskite materials. Phys. Rev. B 2016, 94, 180103. [Google Scholar] [CrossRef]
- Skelton, J.M.; Burton, L.A.; Oba, F.; Walsh, A. Chemical and Lattice Stability of the Tin Sulfides. J. Phys. Chem. C 2017, 121, 6446–6454. [Google Scholar] [CrossRef] [PubMed]
- Structure Commission of the International Zeolite Association. Verified Syntheses of Zeolitic Materials, Second Revised ed.; Robson, H., Ed.; Elsevier Science B.V.: Amsterdam, The Netherland, 2001; p. 265. [Google Scholar]
- Bell, P.; Mao, H. Absolute Pressure Measurements and Their Comparison with the Ruby Fluorescence (R1) Pressure Scale to 1.5 Mbar. Carnegie Institution of Washington Year Book; Carnegie Institution: Washington, DC, USA, 1979; pp. 665–669. [Google Scholar]
- Hammersley, A.; Svensson, S.; Hanfland, M.; Fitch, A.; Hausermann, D. Two-dimensional detector software: From real detector to idealised image or two-theta scan. High Press. Res. 1996, 14, 235–248. [Google Scholar] [CrossRef]
- Prescher, C.; Prakapenka, V.B. DIOPTAS: A program for reduction of two-dimensional X-ray diffraction data and data exploration. High Press. Res. 2015, 35, 223–230. [Google Scholar] [CrossRef]
- Coelho, A.A. TOPAS and TOPAS-Academic: An optimization program integrating computer algebra and crystallographic objects written in C++. J. Appl. Crystallogr. 2018, 51, 210–218. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Le Page, Y.; Saxe, P. Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress. Phys. Rev. B 2002, 65, 104104. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Gajdoš, M.; Hummer, K.; Kresse, G.; Furthmüller, J.; Bechstedt, F. Linear optical properties in the projector-augmented wave methodology. Phys. Rev. B 2006, 73, 045112. [Google Scholar] [CrossRef]
- Skelton, J.M.; Burton, L.A.; Jackson, A.J.; Oba, F.; Parker, S.C.; Walsh, A. Lattice dynamics of the tin sulphides SnS 2, SnS and Sn 2 S 3: Vibrational spectra and thermal transport. Phys. Chem. Chem. Phys. 2017, 19, 12452–12465. [Google Scholar] [CrossRef]
- Skelton, J.M. SpectroscoPy Package. Available online: https://github.com/JMSkelton/Phonopy-Spectroscopy (accessed on 31 January 2019).
- Nearchou, A.; Cornelius, M.U.; Skelton, J.M. Dataset for “Intrinsic flexibility of the EMT zeolite framework under pressure”. University of Bath Research Data Archive. Available online: https://researchdata.bath.ac.uk/ (accessed on 31 January 2019).
Sample Availability: Samples of the compounds are available from the authors. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nearchou, A.; Cornelius, M.-L.U.; Skelton, J.M.; Jones, Z.L.; Cairns, A.B.; Collings, I.E.; Raithby, P.R.; Wells, S.A.; Sartbaeva, A. Intrinsic Flexibility of the EMT Zeolite Framework under Pressure. Molecules 2019, 24, 641. https://doi.org/10.3390/molecules24030641
Nearchou A, Cornelius M-LU, Skelton JM, Jones ZL, Cairns AB, Collings IE, Raithby PR, Wells SA, Sartbaeva A. Intrinsic Flexibility of the EMT Zeolite Framework under Pressure. Molecules. 2019; 24(3):641. https://doi.org/10.3390/molecules24030641
Chicago/Turabian StyleNearchou, Antony, Mero-Lee U. Cornelius, Jonathan M. Skelton, Zöe L. Jones, Andrew B. Cairns, Ines E. Collings, Paul R. Raithby, Stephen A. Wells, and Asel Sartbaeva. 2019. "Intrinsic Flexibility of the EMT Zeolite Framework under Pressure" Molecules 24, no. 3: 641. https://doi.org/10.3390/molecules24030641
APA StyleNearchou, A., Cornelius, M.-L. U., Skelton, J. M., Jones, Z. L., Cairns, A. B., Collings, I. E., Raithby, P. R., Wells, S. A., & Sartbaeva, A. (2019). Intrinsic Flexibility of the EMT Zeolite Framework under Pressure. Molecules, 24(3), 641. https://doi.org/10.3390/molecules24030641