5-Fluorouracil—Complete Insight into Its Neutral and Ionised Forms
Abstract
1. Introduction
2. Methodology
2.1. Geometry Optimisations
2.2. Methods of the pKa Evaluations
3. Results and Discussion
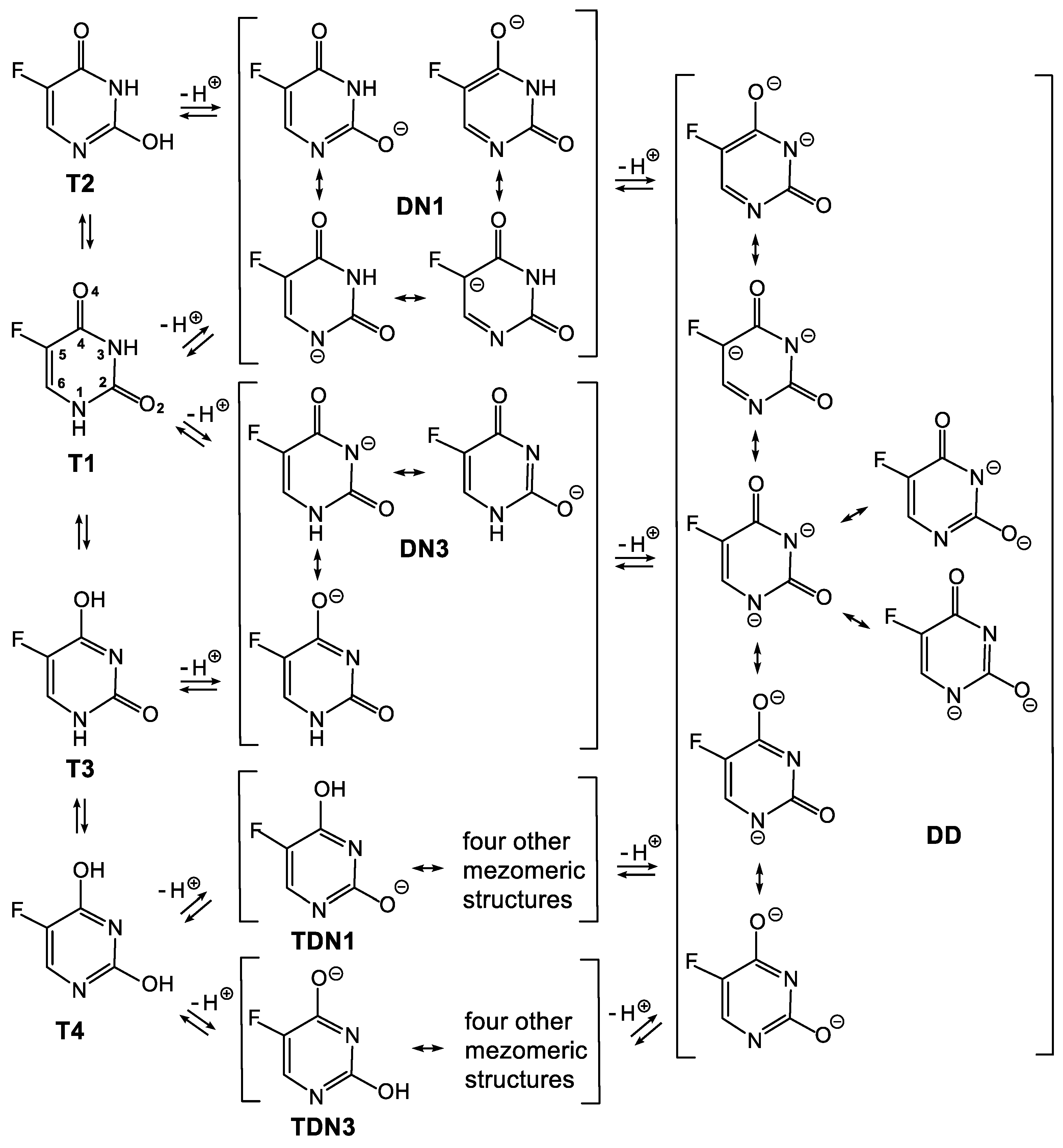
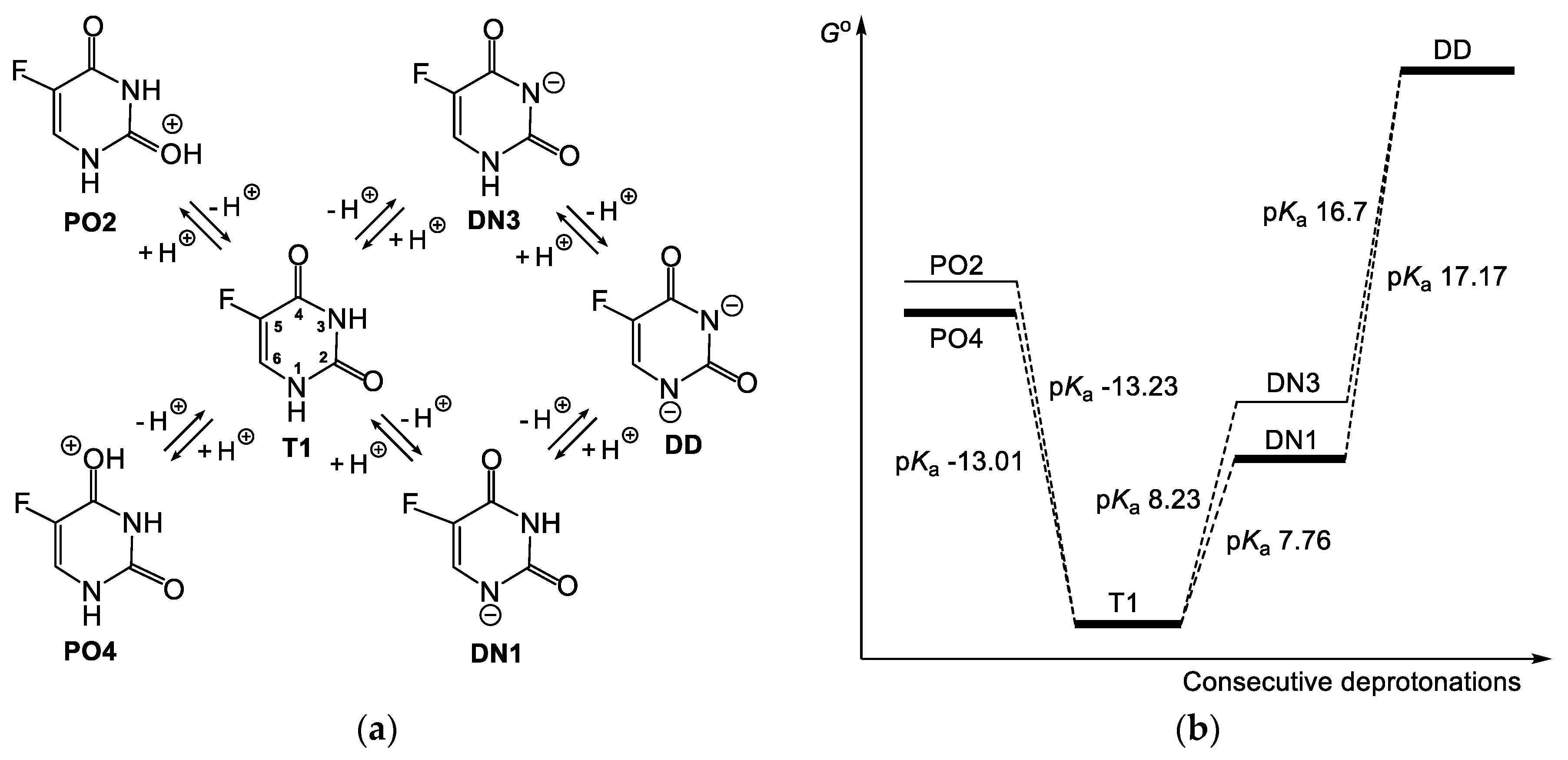
3.1. Relationship between Tautomeric, Deprotonated and Protonated forms of 5FU
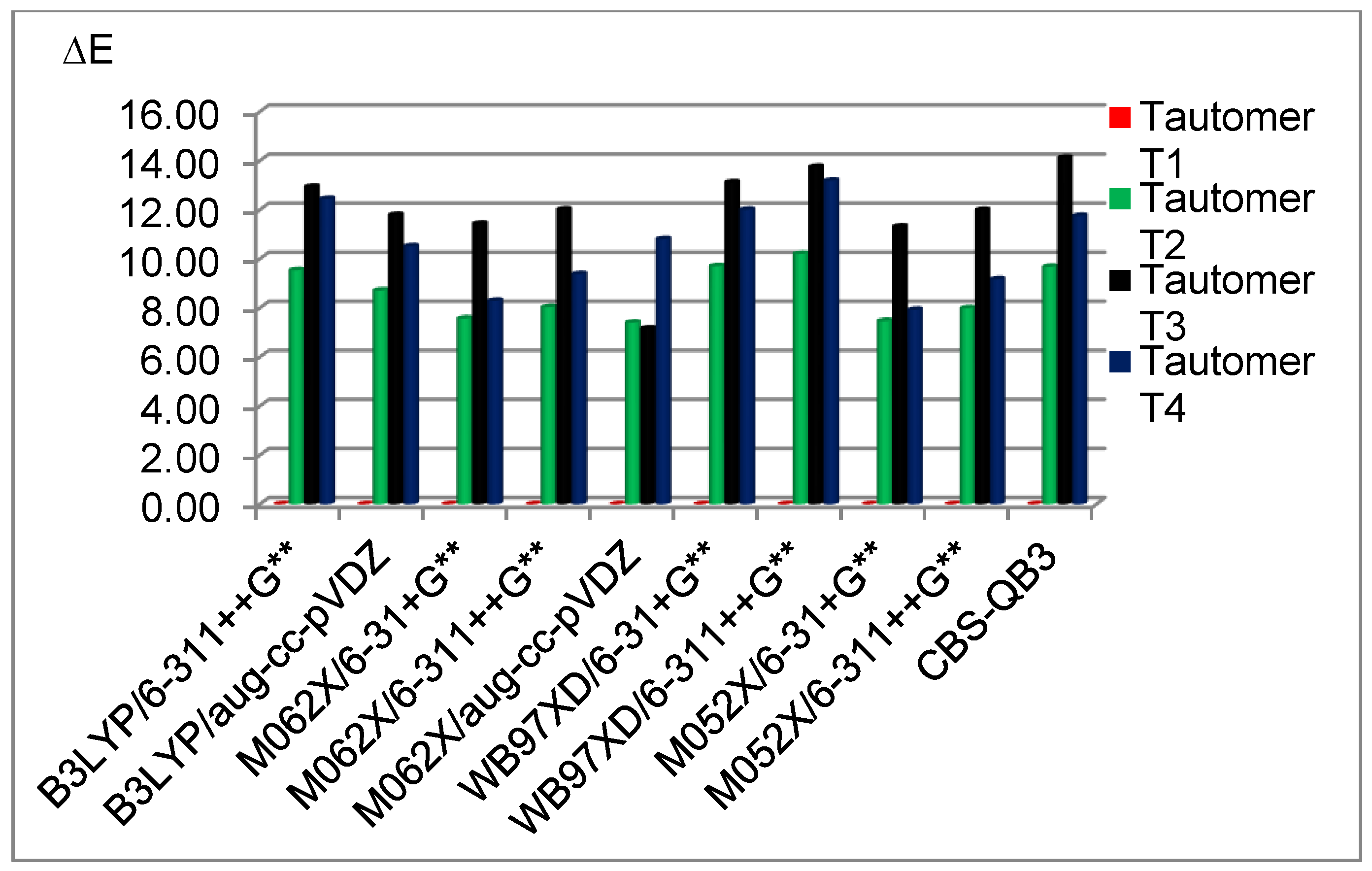
3.2. Stability of the Tautomeric Forms of 5FU
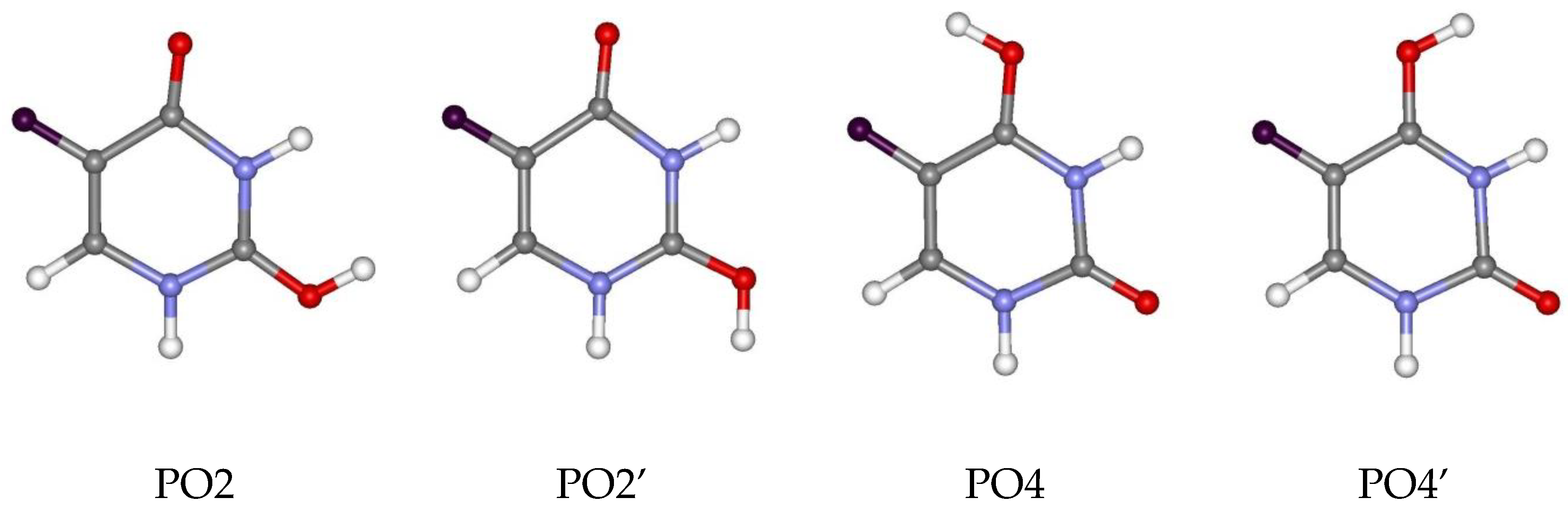
3.3. Deprotonated and Protonated Forms of 5FU in the Gas Phase
3.4. Deprotonated and Protonated Forms of 5FU in Water
3.5. Calculations of the pKa Values
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Toolaram, A.P.; Kümmerer, K.; Schneider, M. Environmental Risk Assessment of Anti-Cancer Drugs and Their Transformation Products: A Focus on Their Genotoxicity Characterization-State of Knowledge and Short Comings. Mutat. Res. Rev. Mutat. Res. 2014, 760, 18–35. [Google Scholar] [CrossRef] [PubMed]
- Mioduszewska, K.; Maszkowska, J.; Białk-Bielińska, A.; Krüger, O.; Kalbe, U.; Liberek, B.; Łukaszewicz, P.; Stepnowski, P. The Leaching Behavior of Cyclophosphamide and Ifosfamide from Soil in the Presence of Co-Contaminant—Mixture Sorption Approach. Sci. Total Environ. 2016, 542, 915–922. [Google Scholar] [CrossRef] [PubMed]
- Grem, J.L. 5-Fluorouracil: Forty-plus and Still Ticking. A Review of Its Preclinical and Clinical Development. Investig. New Drugs 2000, 18, 299–313. [Google Scholar] [CrossRef]
- Longley, D.B.; Harkin, D.P.; Johnston, P.G. 5-Fluorouracil: Mechanisms of Action and Clinical Strategies. Nat. Rev. Cancer 2003, 3, 330–338. [Google Scholar] [CrossRef] [PubMed]
- Odds, F.C.; Brown, A.J.P.; Gow, N.A.R. Antifungal Agents: Mechanisms of Action. Trends Microbiol. 2003, 11, 272–279. [Google Scholar] [CrossRef]
- Privat, E.J.; Sowers, L.C. A Proposed Mechanism for the Mutagenicity of 5-Formyluracil. Mutat. Res. Fundam. Mol. Mech. Mutagen. 1996, 354, 151–156. [Google Scholar] [CrossRef]
- Şanli, N.; Şanli, S.; Alsancak, G. Determination of Dissociation Constants of Folinic Acid (Leucovorin), 5-Fluorouracil, and Irinotecan in Hydro-Organic Media by a Spectrophotometry Method. J. Chem. Eng. Data 2010, 55, 2695–2699. [Google Scholar] [CrossRef]
- Fallingborg, J. Intraluminal pH of the human gastrointestinal tract. Dan. Med. Bull. 1999, 46, 183–196. [Google Scholar]
- Kosjek, T.; Heath, E. Occurrence, Fate and Determination of Cytostatic Pharmaceuticals in the Environment. Trends Anal. Chem. 2011, 30, 1065–1087. [Google Scholar] [CrossRef]
- Tesseromatis, C.; Alevizou, A. The Role of the Protein-Binding on the Mode of Drug Action as Well the Interactions with Other Drugs. Eur. J. Drug Metab. Pharmacokinet. 2008, 33, 225–230. [Google Scholar] [CrossRef]
- Neuhoff, S.; Ungell, A.L.; Zamora, I.; Artursson, P. PH-Dependent Passive and Active Transport of Acidic Drugs across Caco-2 Cell Monolayers. Eur. J. Pharm. Sci. 2005, 25, 211–220. [Google Scholar] [CrossRef] [PubMed]
- Krämer, S.D.; Lombardi, D.; Primorac, A.; Thomae, A.V.; Wunderli-Allenspach, H. Lipid-Bilayer Permeation of Drug-Like Compounds. Chem. Biodivers. 2009, 6, 1900–1916. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.; Artursson, P.; Avdeef, A.; Di, L.; Ecker, G.F.; Faller, B.; Houston, J.B.; Kansy, M.; Kerns, E.H.; Krämer, S.D.; et al. Passive Lipoidal Diffusion and Carrier-Mediated Cell Uptake Are Both Important Mechanisms of Membrane Permeation in Drug Disposition. Mol. Pharm. 2014, 11, 1727–1738. [Google Scholar] [CrossRef] [PubMed]
- Wojtkowiak, J.W.; Verduzco, D.; Schramm, K.J.; Gillies, R.J. Drug Resistance and Cellular Adaptation to Tumor Acidic pH Microenvironment. Mol. Pharm. 2011, 8, 2032–2038. [Google Scholar] [CrossRef] [PubMed]
- Swietach, P.; Hulikova, A.; Patiar, S.; Vaughan-Jones, R.D.; Harris, A.L. Importance of Intracellular pH in Determining the Uptake and Efficacy of the Weakly Basic Chemotherapeutic Drug, Doxorubicin. PLoS ONE 2012, 7, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Prescott, D.M.; Charles, H.C.; Poulson, J.M.; Page, R.L.; Thrall, D.E.; Vujaskovic, Z.; Dewhirst, M.W. The Relationship between Intracellular and Extracellular pH in Spontaneous Canine Tumors. Clin. Cancer Res. 2000, 6, 2501–2505. [Google Scholar]
- Lin, H.H.H.; Lin, A.Y.C. Photocatalytic Oxidation of 5-Fluorouracil and Cyclophosphamide via UV/TiO2 in an Aqueous Environment. Water Res. 2014, 48, 559–568. [Google Scholar] [CrossRef]
- Yu, H.; Eritja, R.; Bloom, L.B.; Goodman, M.F. Ionization of Bromouracil and Fluorouracil Stimulates Base Mispairing Frequencies with Guanine. J. Biol. Chem. 1993, 268, 15935–15943. [Google Scholar]
- Jang, Y.H.; Sowers, L.C.; Çaǧin, T.; Goddard, W.A. First Principles Calculation of pKa Values for 5-Substituted Uracils. J. Phys. Chem. A 2001, 105, 274–280. [Google Scholar] [CrossRef]
- Chandra, A.K.; Uchimaru, T.; Zeegers-Huyskens, T. Theoretical Study on Protonated and Deprotonated 5-Substituted Uracil Derivatives and Their Complexes with Water. J. Mol. Struct. 2002, 605, 213–220. [Google Scholar] [CrossRef]
- Markova, N.; Enchev, V.; Ivanova, G. Tautomeric Equilibria of 5-Fluorouracil Anionic Species in Water. J. Phys. Chem. A 2010, 114, 13154–13162. [Google Scholar] [CrossRef] [PubMed]
- Mioduszewska, K.; Dołżonek, J.; Wyrzykowski, D.; Kubik, Ł.; Wiczling, P.; Sikorska, C.; Toński, M.; Kaczyński, Z.; Stepnowski, P.; Białk-Bielińska, A. Overview of Experimental and Computational Methods for the Determination of the pKa Values of 5-Fluorouracil, Cyclophosphamide, Ifosfamide, Imatinib and Methotrexate. Trends Anal. Chem. 2017, 97, 283–296. [Google Scholar] [CrossRef]
- Pavel, I.; Cota, S.; Cinta-Pinzaru, S.; Kiefer, W. Raman, Surface Enhanced Raman Spectroscopy, and DFT Calculations: A Powerful Approach for the Identification and Characterization of 5-Fluorouracil Anticarcinogenic Drug Species. J. Phys. Chem. A 2005, 109, 9945–9952. [Google Scholar] [CrossRef] [PubMed]
- Sardo, M.; Ruano, C.; Castro, J.L.; López-Tocón, I.; Soto, J.; Ribeiro-Claro, P.; Otero, J.C. Surface-Enhanced Raman Scattering of 5-Fluorouracil Adsorbed on Silver Nanostructures. Phys. Chem. Chem. Phys. 2009, 11, 7437–7443. [Google Scholar] [CrossRef] [PubMed]
- Abdrakhimova, G.S.; Ovchinnikov, M.Y.; Lobov, A.N.; Spirikhin, L.V.; Ivanov, S.P.; Khursan, S.L. 5-Fluorouracil Solutions: NMR Study of Acid-Base Equilibrium in Water and DMSO. J. Phys. Org. Chem. 2014, 27, 876–883. [Google Scholar] [CrossRef]
- Booker, V.; Halsall, C.; Llewellyn, N.; Johnson, A.; Williams, R. Prioritising Anticancer Drugs for Environmental Monitoring and Risk Assessment Purposes. Sci. Total Environ. 2014, 473–474, 159–170. [Google Scholar] [CrossRef]
- Schaftenaar, G.; Noordik, J.H. Molden: A Pre-and Post-Processing Program for Molecular and Electronic Structures. J. Comput. Aided Mol. Des. 2000, 14, 123–134. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 09; Revision D.01; Gaussian, Inc.: Pittsburgh, PA, USA, 2013. [Google Scholar]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2006, 2, 364–382. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 Suite of Density Functionals for Main Group Thermochemistry, Thermochemical Kinetics, Noncovalent Interactions, Excited States, and Transition Elements: Two New Functionals and Systematic Testing of Four M06-Class Functionals and 12 Other Function. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-Range Corrected Hybrid Density Functionals with Damped Atom–atom Dispersion Corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, J.A.; Frisch, M.J.; Ochterski, J.W.; Petersson, G.A. A Complete Basis Set Model Chemistry. VII. Use of the Minimum Population Localization Method. J. Chem. Phys. 2000, 112, 6532–6542. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Unviersal Solvation Modle Based on Solute Electron Density and a Contiuum Model of the Solvent Defind by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Lim, C.; Bashford, D.; Karplus, M. Absolute pKa Calculations with Continuum Dielectric Methods. J. Phys. Chem. 1991, 95, 5610–5620. [Google Scholar] [CrossRef]
- Kallies, B.; Mitzner, R. pKa Values of Amines in Water from Quantum Mechanical Calculations Using a Polarized Dielectric Continuum Representation of the Solvent. J. Phys. Chem. B 1997, 101, 2959–2967. [Google Scholar] [CrossRef]
- Shapley, W.A.; Bacskay, G.B.; Warr, G.G. Ab Initio Quantum Chemical Studies of the pKa’s of Hydroxybenzoic Acids in Aqueous Solution with Special Reference to the Hydrophobicity of Hydroxybenzoates and Their Binding to Surfactants. J. Phys. Chem. B 1998, 102, 1938–1944. [Google Scholar] [CrossRef]
- Fan, L.; Yang, X.; Tian, Z.; Zhao, X.; Li, R.; Xue, Y. Theoretical Calculations of the pKa Values of 1-Aryl-4-Propylpiperazine Drugs in Aqueous Solution. Chem. Res. Chin. Univ. 2014, 30, 455–460. [Google Scholar] [CrossRef]
- Ho, J. Are Thermodynamic Cycles Necessary for Continuum Solvent Calculation of pKa’s and Reduction Potentials? Phys. Chem. Chem. Phys. 2015, 17, 2859–2868. [Google Scholar] [CrossRef]
- Besler, B.H.; Merz, K.M., Jr.; Kolman, P.A. Atomic Charges Derived from Semiempirical Methods. J. Comput. Chem. 1990, 11, 431–439. [Google Scholar] [CrossRef]
- Glendening, D.E.; Reed, A.E.; Carpenter, J.E.; Weinhold, F. NBO Version 3.1; Gaussian, Inc.: Pittsburgh, PA, USA, 2003. [Google Scholar]
- Toth, A.M.; Liptak, M.D.; Phillips, D.L.; Shields, G.C. Accurate Relative pKa Calculations for Carboxylic Acids Using Complete Basis Set and Gaussian-n Models Combined with Continuum Solvation Methods. J. Chem. Phys. 2001, 114, 4595–4606. [Google Scholar] [CrossRef]
- Liptak, M.D.; Gross, K.C.; Seybold, P.G.; Feldgus, S.; Shields, G.C. Absolute pKa Determinations for Substituted Phenols. J. Am. Chem. Soc. 2002, 124, 6421–6427. [Google Scholar] [CrossRef] [PubMed]
- Gao, D.; Svoronos, P.; Wong, P.K.; Maddalena, D.; Hwang, J.; Walker, H. pKa of Acetate in Water: A Computational Study. J. Phys. Chem. A 2005, 109, 10776–10785. [Google Scholar] [CrossRef]
- Król, M.; Wrona, M.; Page, C.S.; Bates, P.A. Macroscopic pKa Calculations for Fluorescein and Its Derivatives. J. Chem. Theory Comput. 2006, 2, 1520–1529. [Google Scholar] [CrossRef]
- Charif, I.E.; Mekelleche, S.M.; Villemin, D.; Mora-Diez, N. Correlation of Aqueous pKa Values of Carbon Acids with Theoretical Descriptors: A DFT Study. J. Mol. Struct. THEOCHEM 2007, 818, 1–6. [Google Scholar] [CrossRef]
- Kelly, C.P.; Cramer, C.J.; Truhlar, D.G. Adding Explicit Solvent Molecules to Continuum Solvent Calculations for the Calculation of Aqueous Acid Dissociation Constants. J. Phys. Chem. A 2006, 110, 2493–2499. [Google Scholar] [CrossRef]
- Liptak, M.D.; Shields, G.C. Accurate pKa Calculations for Carboxylic Acids Using Complete Basis Set and Gaussian-n Models Combined with CPCM Continuum Solvation Methods. J. Am. Chem. Soc. 2001, 123, 7314–7319. [Google Scholar] [CrossRef]
- Kelly, C.P.; Cramer, C.J.; Truhlar, D.G. Aqueous Solvation Free Energies of Ions and Ion—Water Clusters Based on an Accurate Value for the Absolute Aqueous Solvation Free Energy of the Proton. J. Phys. Chem. B 2006, 110, 16066–16081. [Google Scholar] [CrossRef]
- Ho, J.; Coote, M.L. A Universal Approach for Continuum Solvent pKa Calculations: Are We There Yet? Theor. Chem. Acc. 2010, 125, 3–21. [Google Scholar] [CrossRef]
- Casasnovas, R.; Fernández, D.; Ortega-Castro, J.; Frau, J.; Donoso, J.; Muñoz, F. Avoiding Gas-Phase Calculations in Theoretical pKa Predictions. Theor. Chem. Acc. 2011, 130, 1–13. [Google Scholar] [CrossRef]
- Sastre, S.; Casasnovas, R.; Muñoz, F.; Frau, J. Isodesmic Reaction for pKa Calculations of Common Organic Molecules. Theor. Chem. Acc. 2013, 132, 1–8. [Google Scholar] [CrossRef]
- Poliak, P. The DFT Calculations of pKa Values of the Cationic Acids of Aniline and Pyridine Derivatives in Common Solvents. Acta Chim. Slovaca 2014, 7, 25–30. [Google Scholar] [CrossRef]
- Sastre, S.; Casasnovas, R.; Muñoz, F.; Frau, J. Isodesmic Reaction for Accurate Theoretical pKa Calculations of Amino Acids and Peptides. Phys. Chem. Chem. Phys. 2016, 18, 11202–11212. [Google Scholar] [CrossRef] [PubMed]
- Namazian, M.; Halvani, S.M.; Noorbala, M.R. Density Functional Theory Response to the Calculations of pKa values of Some Carboxylic Acids in Aqueous Solution. J. Mol. Struct. THEOCHEM 2004, 711, 13–18. [Google Scholar] [CrossRef]
- Markova, N.; Enchev, V.; Timtcheva, I. Oxo-Hydroxy Tautomerism of 5-Fluorouracil: Water-Assisted Proton Transfer. J. Phys. Chem. A 2005, 109, 1981–1988. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Samples of the compounds are not available from the authors. |

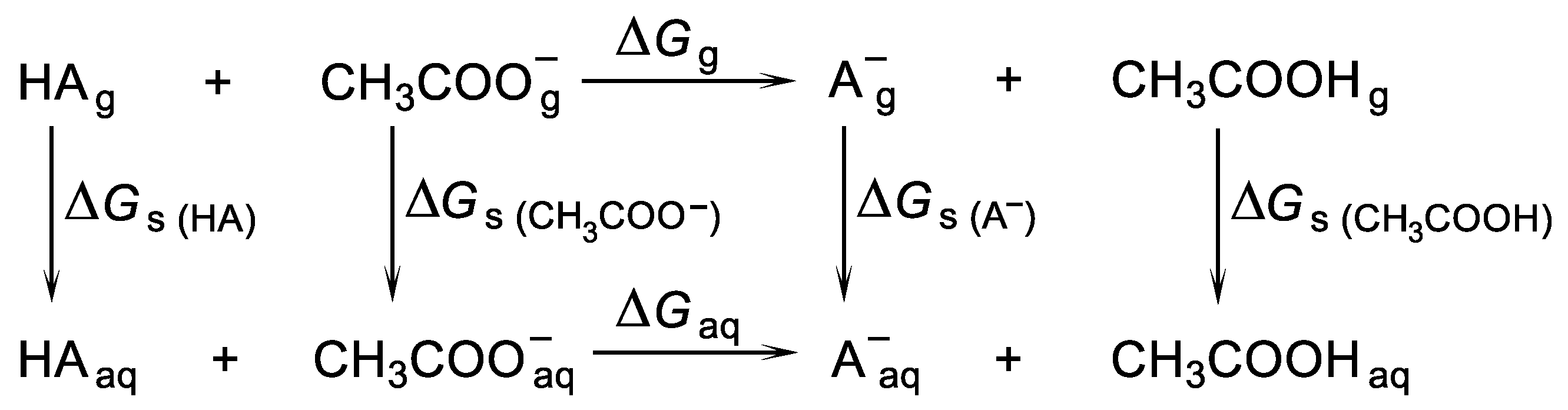

| Gas Phase | Water | |||||
|---|---|---|---|---|---|---|
| Method a | Tautomer | ΔGT | Method | Solvation Model (α) b | Tautomer | ΔGT |
| B3LYP/ | T1 | 0.00 | B3LYP/ | pcm (1,2) | T1 | 0.00 |
| 6-311++G** | T2 | 9.70 | 6-311++G** | (1a) | T2 | 11.68 |
| (1) | T3 | 13.00 | T3 | 12.50 | ||
| T4 | 12.71 | T4 | 16.70 | |||
| B3LYP/ | T1 | 0.00 | B3LYP/ | pcm (1,2) | T1 | 0.00 |
| aug-cc-pVDZ | T2 | 8.83 | aug-cc-pVDZ | (2a) | T2 | 10.86 |
| (2) | T3 | 11.83 | T3 | 11.49 | ||
| T4 | 10.71 | T4 | 14.98 | |||
| M062X/ | T1 | 0.00 | M062X/ | pcm (1,2) | T1 | 0.00 |
| 6-311++G** | T2 | 8.25 | 6-311++G** | (3a) | T2 | 10.16 |
| (3) | T3 | 12.13 | T3 | 11.39 | ||
| T4 | 9.71 | T4 | 13.46 | |||
| M062X/ | T1 | 0.00 | M062X/ | pcm (1,2) | T1 | 0.00 |
| aug-cc-pVDZ | T2 | 7.32 | aug-cc-pVDZ | (4a) | T2 | 9.27 |
| (4) | T3 | 10.88 | T3 | 10.32 | ||
| T4 | 7.64 | T4 | 11.63 | |||
| WB97XD/ | T1 | 0.00 | WB97XD/ | smd (1,2) | T1 | 0.00 |
| 6-31+G** | T2 | 9.85 | 6-31+G** | (5b) | T2 | 8.53 |
| (5) | T3 | 13.19 | T3 | 8.93 | ||
| T4 | 12.25 | T4 | 10.67 | |||
| WB97XD/ | T1 | 0.00 | WB97XD/ | smd (1,2) | T1 | 0.00 |
| 6-311++G** | T2 | 10.38 | 6-311++G** | (6b) | T2 | 8.99 |
| (6) | T3 | 13.82 | T3 | 9.60 | ||
| T4 | 13.47 | T4 | 11.71 | |||
| M052X/ | T1 | 0.00 | M052X/ | smd (1,2) | T1 | 0.00 |
| 6-31+G** | T2 | 7.67 | 6-31+G** | (7b) | T2 | 6.48 |
| (7) | T3 | 11.40 | T3 | 7.09 | ||
| T4 | 8.20 | T4 | 6.89 | |||
| M052X/ | T1 | 0.00 | M052X/ | smd (1,2) | T1 | 0.00 |
| 6-311++G** | T2 | 8.19 | 6-311++G** | (8b) | T2 | 6.95 |
| (8) | T3 | 12.09 | T3 | 7.81 | ||
| T4 | 9.48 | T4 | 7.99 | |||
| CBS-QB3 | T1 | 0.00 | ||||
| (9) | T2 | 10.01 | ||||
| T3 | 13.33 | |||||
| T4 | 13.19 | |||||
| Method a | Anions | Cations | ||
|---|---|---|---|---|
| Form | ΔGA | Form | ΔGC | |
| B3LYP/ | DN1 | 0.00 | PO4 | 0.00 |
| 6-311++G** | DN3 | 10.89 | PO4’ | 4.91 |
| (1) | PO2 | 7.84 | ||
| PO2’ | 8.95 | |||
| B3LYP/ | DN1 | 0.00 | PO4 | 0.00 |
| aug-cc-pVDZ | DN3 | 10.80 | PO4’ | 4.76 |
| (2) | PO2 | 7.81 | ||
| PO2’ | 8.82 | |||
| M062X/ | DN1 | 0.00 | PO4 | 0.00 |
| 6-311++G** | DN3 | 11.48 | PO4’ | 5.06 |
| (3) | PO2 | 7.03 | ||
| PO2’ | 8.09 | |||
| M062X/ | DN1 | 0.00 | PO4 | 0.00 |
| aug-cc-pVDZ | DN3 | 10.42 | PO4’ | 4.91 |
| (4) | PO2 | 6.96 | ||
| PO2’ | 7.92 | |||
| WB97XD/ | DN1 | 0.00 | PO4 | 0.00 |
| 6-31+G** | DN3 | 11.29 | PO4’ | 5.44 |
| (5) | PO2 | 7.91 | ||
| PO2’ | 8.92 | |||
| WB97XD/ | DN1 | 0.00 | PO4 | 0.00 |
| 6-311++G** | DN3 | 10.96 | PO4’ | 5.28 |
| (6) | PO2 | 7.59 | ||
| PO2’ | 8.56 | |||
| M052X/ | DN1 | 0.00 | PO4 | 0.00 |
| 6-31+G** | DN3 | 11.11 | PO4’ | 5.31 |
| (7) | PO2 | 7.84 | ||
| PO2’ | 8.85 | |||
| M052X/ | DN1 | 0.00 | PO4 | 0.00 |
| 6-311++G** | DN3 | 9.93 | PO4’ | 5.24 |
| (8) | PO2 | 7.56 | ||
| PO2’ | 8.61 | |||
| CBS-QB3 | DN1 | 0.00 | ||
| (9) | DN3 | 12.32 | ||
| Atom | B3LYP/6-311++G** (1) | M062X/6-311++G** (3) | ||||||
|---|---|---|---|---|---|---|---|---|
| DN1 | DN3 | DN1 | DN3 | |||||
| NBO | ESP | NBO | ESP | NBO | ESP | NBO | ESP | |
| N1 | −0.64160 | −0.87928 | −0.62546 | −0.67064 | −0.65680 | −0.87076 | −0.65107 | −0.68324 |
| C2 | 0.75691 | 1.14084 | 0.74969 | 1.06060 | 0.78306 | 1.12004 | 0.78291 | 1.03724 |
| O2 | −0.71649 | −0.79926 | −0.72704 | −0.79611 | −0.72892 | −0.78939 | −0.74066 | −0.78536 |
| N3 | −0.63861 | −0.86443 | −0.66903 | −0.96868 | −0.66353 | −0.87699 | −0.69441 | −0.95796 |
| C4 | 0.56819 | 0.82014 | 0.54955 | 0.93854 | 0.59520 | 0.81466 | 0.57438 | 0.91704 |
| O4 | −0.69612 | −0.71467 | −0.67777 | −0.74247 | −0.70419 | −0.70408 | −0.68767 | −0.72959 |
| C5 | 0.17966 | −0.11270 | 0.26282 | 0.02598 | 0.16543 | −0.12635 | 0.26248 | 0.02735 |
| C6 | 0.01039 | 0.19541 | −0.06090 | −0.11183 | 0.01927 | 0.18140 | −0.05630 | −0.12355 |
| F | −0.37576 | −0.25392 | −0.36543 | −0.25231 | −0.37704 | −0.24870 | −0.36861 | −0.24879 |
| HC a | 0.16596 | 0.09509 | 0.18129 | 0.16590 | 0.17319 | 0.11285 | 0.18983 | 0.18207 |
| HN a | 0.38746 | 0.37278 | 0.38228 | 0.35103 | 0.39434 | 0.38734 | 0.38911 | 0.36479 |
| Atom | B3LYP/6-311++G** (1) | M062X/6-311++G** (3) | ||||||
|---|---|---|---|---|---|---|---|---|
| PO2 | PO4 | PO2 | PO4 | |||||
| NBO | ESP | NBO | ESP | NBO | ESP | NBO | ESP | |
| N1 | −0.52172 | −0.37637 | −0.54624 | −0.44314 | −0.54561 | −0.39133 | −0.57441 | −0.47095 |
| C2 | 0.82453 | 0.71708 | 0.79747 | 0.72929 | 0.85539 | 0.73047 | 0.82381 | 0.73340 |
| O2 | −0.58743 | −0.53626 | −0.49825 | −0.45452 | −0.60298 | −0.54483 | −0.50598 | −0.44923 |
| N3 | −0.59010 | −0.56479 | −0.55623 | −0.46815 | −0.61740 | −0.59039 | −0.58116 | −0.48926 |
| C4 | 0.60941 | 0.63068 | 0.61677 | 0.53756 | 0.63262 | 0.63635 | 0.64624 | 0.55605 |
| O4 | −0.45348 | −0.40000 | −0.56529 | −0.45044 | −0.45754 | −0.39176 | −0.58214 | −0.46086 |
| C5 | 0.33519 | 0.21267 | 0.24963 | 0.08462 | 0.33339 | 0.20824 | 0.23501 | 0.06382 |
| C6 | −0.01754 | −0.16055 | 0.10877 | 0.05337 | −0.01960 | −0.17216 | 0.12090 | 0.06358 |
| F | −0.27028 | −0.12250 | −0.29963 | −0.14171 | −0.27896 | −0.12694 | −0.30502 | −0.14267 |
| HC a | 0.25859 | 0.26240 | 0.26027 | 0.23840 | 0.26595 | 0.27593 | 0.26711 | 0.24881 |
| HN1 a | 0.45185 | 0.42961 | 0.44978 | 0.40651 | 0.44843 | 0.41084 | 0.46509 | 0.43472 |
| HN3 a | 0.44031 | 0.39876 | 0.45650 | 0.42280 | 0.45973 | 0.43911 | 0.45746 | 0.41824 |
| HO a | 0.52067 | 0.50927 | 0.52645 | 0.48541 | 0.52659 | 0.51647 | 0.53309 | 0.49435 |
| Method | Solvation Model (α) a | Anions | Cations | ||
|---|---|---|---|---|---|
| Form | ΔGA | Form | ΔGC | ||
| B3LYP/ | pcm (1,2) | DN1 | 0.00 | PO4 | 0.00 |
| 6-311++G** | (1a) | DN3 | 4.10 | PO4’ | 2.59 |
| 1 | PO2’ | 3.13 | |||
| PO2 | 3.73 | ||||
| smd (1,0) | DN1 | 0.00 | PO4 | 0.00 | |
| (1c) | DN3 | 1.39 | PO2’ | 0.37 | |
| PO2 | 0.99 | ||||
| B3LYP/ | pcm (1,2) | DN1 | 0.00 | PO4 | 0.00 |
| aug-cc-pVDZ | (2a) | DN3 | 3.86 | PO4’ | 2.64 |
| 2 | PO2’ | 3.53 | |||
| PO2 | 3.82 | ||||
| M062X/ | pcm (1,2) | DN1 | 0.00 | PO4 | 0.00 |
| 6-311++G** | (3a) | DN3 | 3.63 | PO2’ | 2.51 |
| 3 | PO4’ | 2.58 | |||
| PO2 | 2.90 | ||||
| smd (1,0) | DN1 | 0.00 | PO4 | 0.00 | |
| (3c) | DN3 | 0.91 | PO2 | 1.00 | |
| M062X/ | pcm (1,2) | DN1 | 0.00 | PO4 | 0.00 |
| aug-cc-pVDZ | (4a) | DN3 | 3.38 | PO4’ | 2.65 |
| 4 | PO2’ | 2.75 | |||
| PO2 | 2.95 | ||||
| WB97XD/ | smd (1,2) | DN1 | 0.00 | PO4 | 0.00 |
| 6-31+G** | (5b) | DN3 | 1.93 | PO4’ | 0.80 |
| 5 | PO2’ | 0.94 | |||
| PO2 | 0.97 | ||||
| smd (1,0) | DN1 | 0.00 | PO4 | 0.00 | |
| (5c) | DN3 | 0.86 | PO2 | 1.46 | |
| WB97XD/ | smd (1,2) | DN1 | 0.00 | PO4 | 0.00 |
| 6-311++G** | (6b) | DN3 | 2.03 | PO4’ | 0.71 |
| 6 | PO2 | 0.78 | |||
| PO2’ | 0.79 | ||||
| smd (1,0) | DN1 | 0.00 | PO4 | 0.00 | |
| (6c) | DN3 | 0.98 | PO2 | 1.30 | |
| M052X/ | smd (1,2) | DN1 | 0.00 | PO4 | 0.00 |
| 6-31+G** | (7b) | DN3 | 1.63 | PO2’ | 0.76 |
| 7 | PO4’ | 0.77 | |||
| PO2 | 0.79 | ||||
| smd (1,0) | DN1 | 0.00 | PO4 | 0.00 | |
| (7c) | DN3 | 0.56 | PO2 | 1.31 | |
| M052X/ | smd (1,2) | DN1 | 0.00 | PO4 | 0.00 |
| 6-311++G** | (8b) | DN3 | 1.81 | PO2 | 0.56 |
| 8 | PO2’ | 0.61 | |||
| PO4’ | 0.66 | ||||
| Method | Solvation Model (α) a | Anion | pKa T1→A b | pKa A→DD | Cation | pKa C c→T1 | |||
|---|---|---|---|---|---|---|---|---|---|
| A | met. D | met. R | met. D | met. R | C | met. D | met. R | ||
| B3LYP/ | pcm (1,2) | DN1 | 11.07 | 5.48 | 29.08 | 23.55 | PO4 | −19.09 | −24.32 |
| 6-311++G** | 1a | DN3 | 13.25 | 7.67 | 26.90 | 21.37 | PO2 | −21.38 | −27.07 |
| smd (1,0) | DN1 | 9.22 | 4.80 | 18.97 | 14.58 | PO4 | −12.25 | −16.73 | |
| 1c | DN3 | 9.33 | 4.91 | 18.86 | 14.47 | PO2 | −12.46 | −16.94 | |
| B3LYP | pcm (1,2) | DN1 | 5.29 | 23.36 | PO4 | −23.23 | |||
| aug-cc-pVDZ | 2a | DN3 | 7.75 | 20.90 | PO2 | −26.23 | |||
| M062X | pcm (1,2) | DN1 | 9.98 | 2.59 | 27.92 | 20.58 | PO4 | −20.50 | −27.99 |
| 6-311++G** | 3a | DN3 | 12.55 | 5.17 | 25.35 | 18.01 | PO2 | −22.23 | −29.72 |
| smd (1,0) | DN1 | 7.76 | 1.75 | 17.17 | 11.19 | PO4 | −13.01 | −19.08 | |
| 3c | DN3 | 8.23 | 2.22 | 16.70 | 10.72 | PO2 | −13.23 | −19.31 | |
| M062X | pcm (1,2) | DN1 | 2.09 | 20.10 | PO4 | −27.28 | |||
| aug-cc-pVDZ | 4a | DN3 | 4.25 | 17.94 | PO2 | −29.13 | |||
| WB97XD | smd (1,2) | DN1 | 11.17 | 7.51 | 21.95 | 18.71 | PO4 | 8.24 | 4.96 |
| 6-31+G** | 5b | DN3 | 12.02 | 8.75 | 21.10 | 17.86 | PO2 | 7.63 | 4.34 |
| smd (1,0) | DN1 | 10.79 | 8.03 | 19.98 | 17.25 | PO4 | 7.65 | 4.88 | |
| 5c | DN3 | 10.80 | 8.04 | 19.97 | 17.24 | PO2 | 7.03 | 4.25 | |
| WB97XD | smd (1,2) | DN1 | 11.49 | 8.18 | 22.21 | 18.93 | PO4 | 7.63 | 4.30 |
| 6-311++G** | 6b | DN3 | 12.24 | 8.92 | 21.47 | 18.18 | PO2 | 7.16 | 3.83 |
| smd (1,0) | DN1 | 11.11 | 8.25 | 20.24 | 17.44 | PO4 | 7.14 | 4.30 | |
| 6c | DN3 | 11.02 | 8.20 | 20.32 | 17.53 | PO2 | 6.64 | 3.80 | |
| M052X | smd (1,2) | DN1 | 8.15 | 6.40 | 19.00 | 17.29 | PO4 | −11.72 | −13.53 |
| 6-31+G** | 7b | DN3 | 8.80 | 7.05 | 18.35 | 16.64 | PO2 | −12.17 | −13.98 |
| smd (1,0) | DN1 | 6.65 | 6.56 | 16.92 | 15.77 | PO4 | −12.14 | −13.66 | |
| 7c | DN3 | 6.44 | 6.34 | 17.13 | 15.98 | PO2 | −13.19 | −14.11 | |
| M052X | smd (1,2) | DN1 | 7.77 | 6.66 | 18.64 | 17.67 | PO4 | −12.71 | −13.88 |
| 6-311++G** | 8b | DN3 | 7.66 | 6.55 | 18.75 | 17.78 | PO2 | −13.02 | −14.20 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wielińska, J.; Nowacki, A.; Liberek, B. 5-Fluorouracil—Complete Insight into Its Neutral and Ionised Forms. Molecules 2019, 24, 3683. https://doi.org/10.3390/molecules24203683
Wielińska J, Nowacki A, Liberek B. 5-Fluorouracil—Complete Insight into Its Neutral and Ionised Forms. Molecules. 2019; 24(20):3683. https://doi.org/10.3390/molecules24203683
Chicago/Turabian StyleWielińska, Justyna, Andrzej Nowacki, and Beata Liberek. 2019. "5-Fluorouracil—Complete Insight into Its Neutral and Ionised Forms" Molecules 24, no. 20: 3683. https://doi.org/10.3390/molecules24203683
APA StyleWielińska, J., Nowacki, A., & Liberek, B. (2019). 5-Fluorouracil—Complete Insight into Its Neutral and Ionised Forms. Molecules, 24(20), 3683. https://doi.org/10.3390/molecules24203683






