Structural and Optical Properties of Metal-Nitrosyl Complexes †
Abstract
1. Introduction
2. Computational Details
3. Structural and Electronic Properties
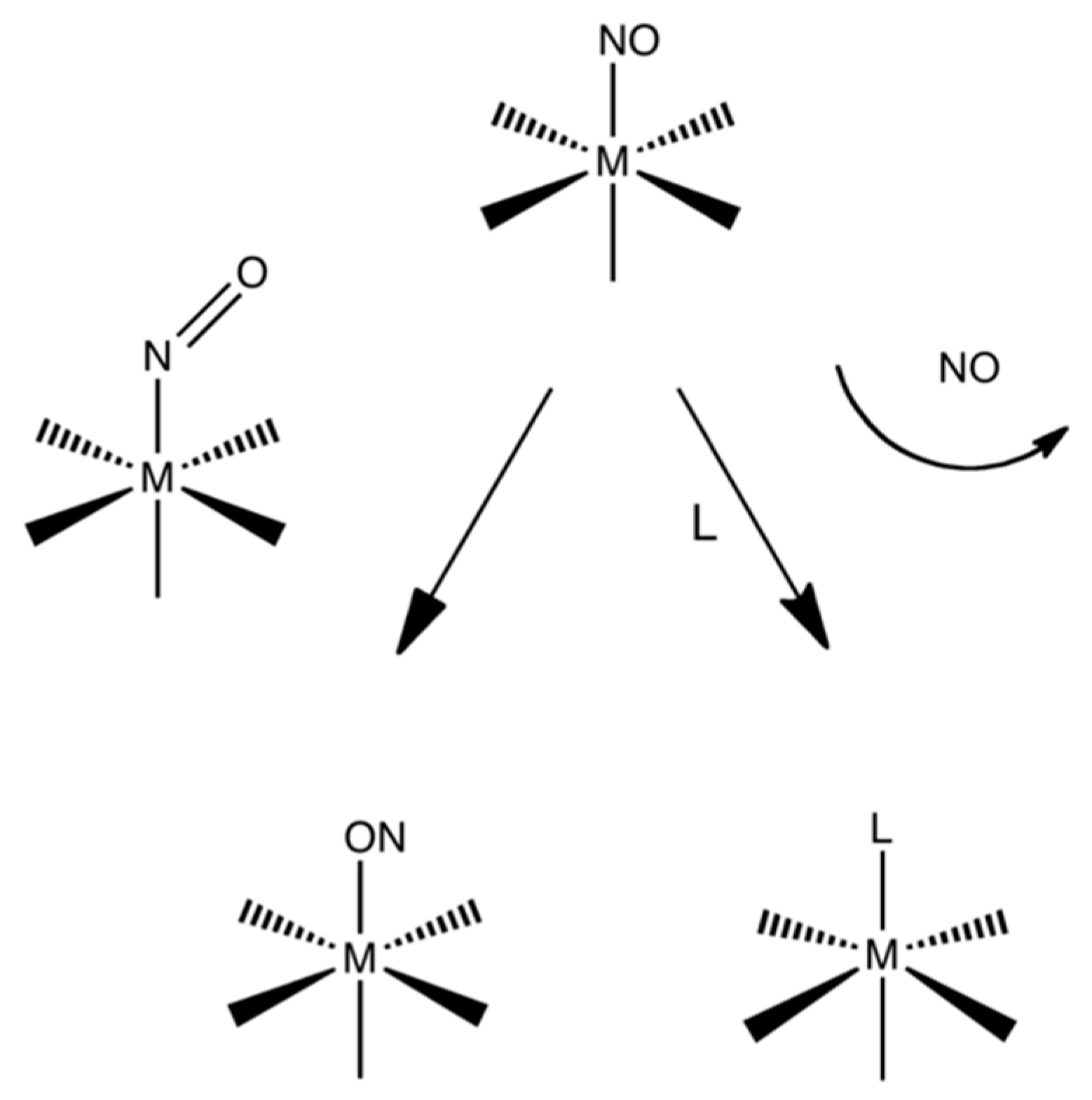
3.1. Structures
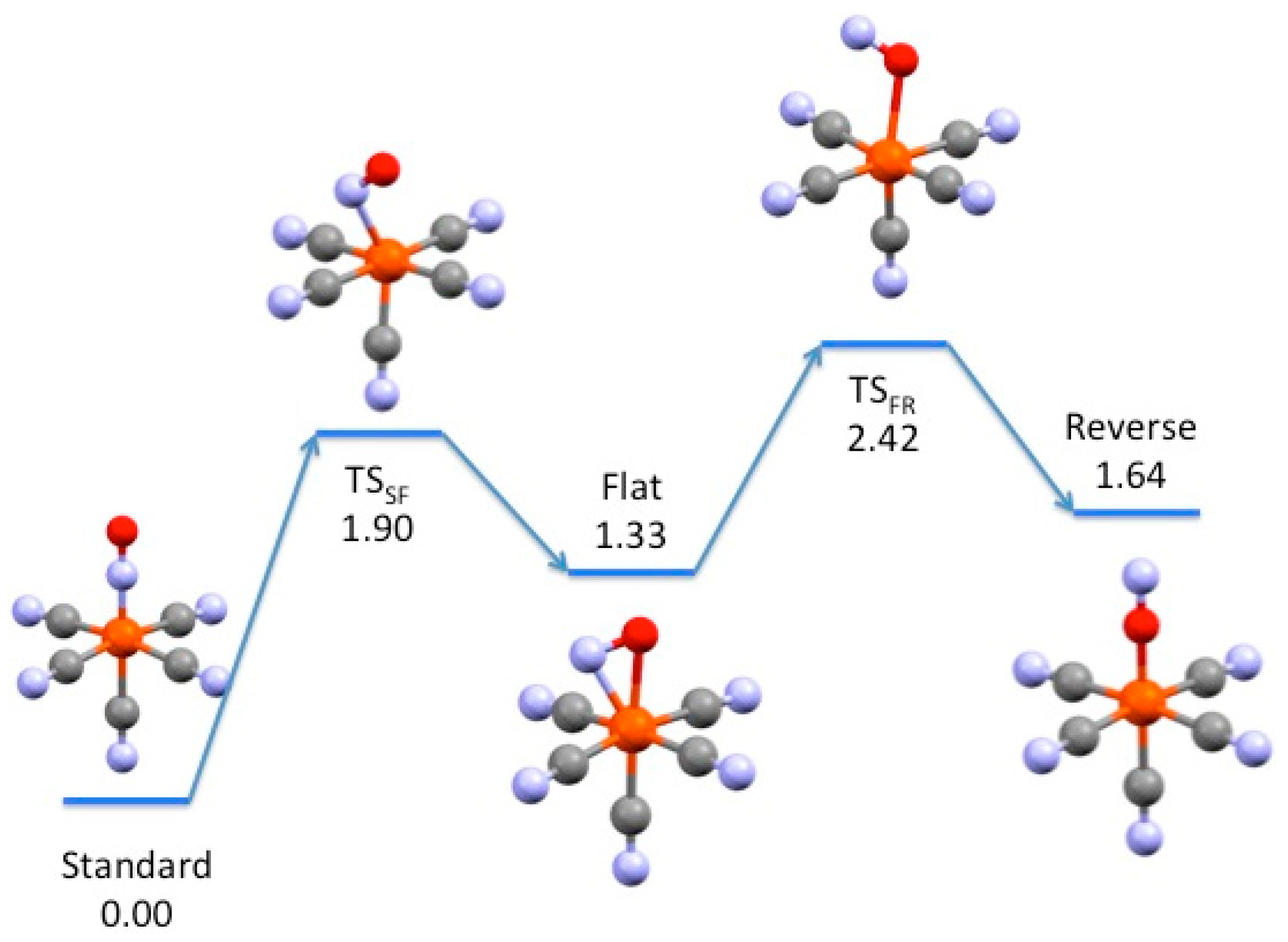
3.2. Electronic Structures and Potential Energy Profiles
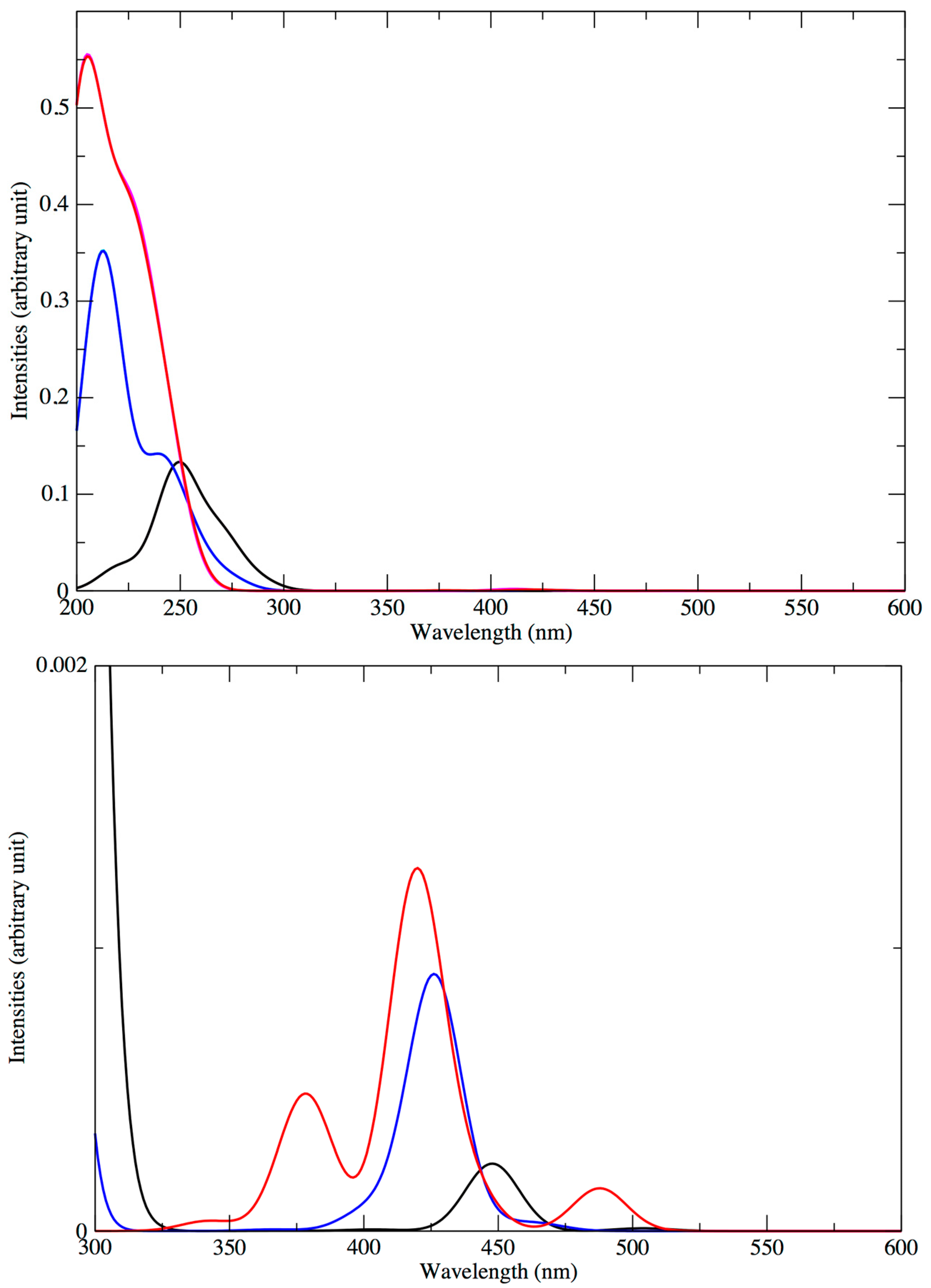
4. Optical Properties
4.1. Absorption Spectra of the Standard Structures
4.2. Low-Lying Singlet and Triplet States
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Awasabisah, D.; Richter-Addo, G.B. NOx Related Chemistry. In Advances in Inorganic Chemistry, 1st ed.; Van Eldik, R., Olabe, J.A., Eds.; Academic Press: Cambridge, MA, USA, 2015; Volume 67, pp. 1–86. [Google Scholar]
- Daniel, C.; Gourlaouen, C. Chemical Bonding Alteration Upon Electronic Excitation in Transition Metal Complexes. Coord. Chem. Rev. 2017, 344, 131–149. [Google Scholar] [CrossRef]
- Ford, P.C.; Bourassa, J.; Miranda, K.; Lee, B.; Lorkovic, I.; Boggs, S.; Kudo, S.; Laverman, L. Photochemistry of metal nitrosyl complexes. Delivery of nitric oxide to biological targets. Coord. Chem. Rev. 1998, 171, 185–202. [Google Scholar] [CrossRef]
- Rose, M.J.; Mascharak, P.K. Photoactive ruthenium nitrosyls: Effects of light and potential application as NO donors. Coord. Chem. Rev. 2008, 252, 2093–2114. [Google Scholar] [CrossRef] [PubMed]
- Ford, P.C. Polychromophoric Metal Complexes for Generating the Bioregulatory Agent Nitric Oxide by Single- and Two-Photon Excitation. Acc. Chem. Res. 2008, 41, 190–200. [Google Scholar] [CrossRef] [PubMed]
- Ford, P.C. Photochemical Deliverey of Nitric Oxides. Nitride Oxide 2013, 34, 56–64. [Google Scholar] [CrossRef] [PubMed]
- de Boer, T.R.; Mascharak, P.K. NOx Related Chemistry. In Advances in Inorganic Chemistry, 1st ed.; Van Eldik, R., Olabe, J.A., Eds.; Academic Press: Cambridge, MA, USA, 2015; Volume 67, pp. 145–170. [Google Scholar]
- Hauser, U.; Oestreich, V.; Rohrweck, H.D. On optical dispersion in transparent molecular systems. Z. Phys. A 1977, 280, 17–25, 125–130. [Google Scholar] [CrossRef]
- Coppens, P.; Novozhilova, I.; Kovalevsky, A. Photoinduced Linkage Isomers of Transition-Metal Nitrosyl Compounds and Related Complexes. Chem. Rev. 2002, 102, 861–884. [Google Scholar] [CrossRef] [PubMed]
- Lynch, M.S.; Cheng, M.; Van Kuiken, B.E.; Khalil, M. Probing the Photoinduced Metal−Nitrosyl Linkage Isomerism of Sodium Nitroprusside in Solution Using Transient Infrared Spectroscopy. J. Am. Chem. Soc. 2011, 133, 5255–5262. [Google Scholar] [CrossRef] [PubMed]
- Boulet, P.; Chermette, H.; Weber, J. Photochemistry of the CpNiNO Complex. A Theoretical Study Using Density Functional Theory. Inorg. Chem. 2001, 40, 7032–7039. [Google Scholar] [CrossRef]
- Furtado Andriani, K.; Finoto Caramori, G.; Gorzoni Doro, F.; Tame Parreira, R.L. Ru-NO and Ru-NO2 bonding linkage isomerism in cis-[Ru(NO)(NO)(bpy)2]2+ complexes—A theoretical insight. Dalton Trans. 2014, 43, 8792–8804. [Google Scholar] [CrossRef]
- Sanz García, J.; Alary, F.; Boggio-Pasqua, M.; Dixon, I.M.; Malfant, I.; Heully, J.-L. Establishing the Two-Photon Linkage Isomerization Mechanism in the Nitrosyl Complex trans-[RuCl(NO)(py)4](2+) by DFT and TDDFT. Inorg. Chem. 2015, 54, 8310–8318. [Google Scholar] [CrossRef] [PubMed]
- Bitterwolf, E. Photochemical nitrosyl linkage isomerism/metastable states. Coord. Chem. Rev. 2006, 250, 1196–1207. [Google Scholar] [CrossRef]
- Kostin, G.A.; Borodin, A.O.; Mikhailov, A.A.; Kuratieva, N.V.; Kolesov, B.A.; Pishchur, D.P.; Woike, T.; Schaniel, D. Photocrystallographic, Spectroscopic, and Calorimetric Analysis of Light-Induced Linkage NO Isomers in [RuNO(NO2)2(pyridine)2OH]. Eur. J. Inorg. Chem. 2015, 29, 4905–4913. [Google Scholar] [CrossRef]
- Thornley, A.; Bitterwolf, T.E. Photolysis of Isoelectronic Ruthenium Nitrosyl and Diazonium Complexes in Frozen PVC Matrices: Retention of Dinitrogen on Ruthenium Following Photochemical Phenyl Radical Loss. Eur. J. Inorg. Chem. 2016, 4, 464–468. [Google Scholar] [CrossRef]
- Klein, A.; von Mering, Y.; Uthe, A.; Butsch, K.; Schaniel, D.; Mockus, N.; Woike, T. Oxidation States and Photoinduced Metastable States in [Fe(CO)2 (NO)2]. Polyhedron 2010, 29, 2553–2559. [Google Scholar] [CrossRef]
- Delcey, M.G.; Freitag, L.; Bondo Pedersen, T.; Aquilante, F.; Lindh, R.; González, L. Analytical gradients of complete active space self-consistent field energies using Cholesky decomposition: Geometry optimization and spin-state energetics of a ruthenium nitrosyl complex. J. Chem. Phys. 2014, 140, 174103. [Google Scholar] [CrossRef] [PubMed]
- Freitag, L.; Knecht, S.; Keller, S.F.; Delcey, M.G.; Aquilante, F.; Bondo Pedersen, T.; Lindh, R.; Reiher, M.; Gonzàlez, L. Orbital Entanglement and CASSCF Analysis of the Ru–NO bond in a Ruthenium Nitrosyl Complex. Phys. Chem. Chem. Phys. 2015, 17, 14383–14392. [Google Scholar] [CrossRef] [PubMed]
- Finoto Caramori, G.; Guilherme Kunitz, A.; Furtado Andriani, K.; Gorzoni Doro, F.; Frenking, G.; Tfouni, E. The nature of Ru–NO bonds in ruthenium tetraazamacrocycle nitrosyl complexes—A computational study. Dalton Trans. 2012, 41, 7327–7339. [Google Scholar] [CrossRef] [PubMed]
- Caramori, G.F.; Frenking, G. The Nature of the Ru−NO Bond in Ruthenium Tetraammine Nitrosyl Complexes. Organometallics 2007, 26, 5815–5825. [Google Scholar] [CrossRef]
- Boulet, P.; Buchs, M.; Chermette, H.; Daul, C.; Furet, E.; Gilardoni, F.; Rogemond, F.; Schläpfer, C.W.; Weber, J. DFT Investigation of Metal Complexes Containing a Nitrosyl Ligand. 2. Excited States. J. Phys. Chem. A 2001, 105, 8999–9003. [Google Scholar] [CrossRef]
- Boulet, P.; Buchs, M.; Chermette, H.; Daul, C.; Gilardoni, F.; Rogemond, F.; Schläpfer, C.W.; Weber, J. DFT Investigation of Metal Complexes Containing a Nitrosyl Ligand. 1. Ground State and Metastable States. J. Phys. Chem. A 2001, 105, 8991–8998. [Google Scholar] [CrossRef]
- Schaniel, D.; Mockus, N.; Woike, T.; Klein, A.; Sheptyakov, D.; Todorova, T.; Delley, B. Reversible photoswitching between nitrito-N and nitrito-O isomers in trans-[Ru(py)(4)(NO(2))(2)]. Phys. Chem. Chem. Phys. 2010, 12, 6171–6178. [Google Scholar] [CrossRef] [PubMed]
- Schaniel, D.; Schefer, J.; Delley, B.; Imlau, M.; Woike, T. Light-induced absorption changes by excitation of metastable states in Na2[Fe(CN)5NO]2H2O single crystals. Phys. Rev. B 2002, 66, 085103. [Google Scholar] [CrossRef]
- Ishikawa, T.; Tanaka, K. Theoretical study of the photoinduced transfer among the ground state and two metastable states in [Fe(CN)5NO]2−. J. Chem. Phys. 2005, 122, 074314. [Google Scholar] [CrossRef] [PubMed]
- te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comp. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Fonseca Guerra, C.; Snijders, J.G.; te Velde, G.; Baerends, E.J. Towards an order-N DFT method. Theor. Chem. Acc. 1998, 99, 391–403. [Google Scholar] [CrossRef]
- ADF2013, SCM, Theoretical Chemistry. Vrije Universiteit: Amsterdam, The Netherlands. Available online: http://www.scm.com (accessed on 29 September 2019).
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. B 1964, 136, 864–871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. A 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- van Lenthe, E.; Baerends, E.J. Optimized Slater-type basis sets for the elements 1–118. J. Comp. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef]
- van Lenthe, E.; Ehlers, A.E.; Baerends, E.J. Geometry optimization in the Zero Order Regular Approximation for relativistic effects. J. Chem. Phys. 1999, 110, 8943–8953. [Google Scholar] [CrossRef]
- Pye, C.C.; Ziegler, T. An implementation of the conductor-like screening model of solvation within the Amsterdam density functional package. Theor. Chem. Acc. 1999, 101, 396–408. [Google Scholar] [CrossRef]
- Gross, E.K.U.; Dobson, J.F.; Petersilka, M. Density Functional Theory; Nalewajski, R.F., Ed.; Springer: Heidelberg, Germany, 1996. [Google Scholar]
- Wang, F.; Ziegler, T. A simplified relativistic time-dependent density-functional theory formalism for the calculations of excitation energies including spin-orbit coupling effect. J. Chem. Phys. 2005, 123, 154102. [Google Scholar] [CrossRef] [PubMed]
- Hirata, S.; Head-Gordon, M. Time-dependent density functional theory within the Tamm-Dancoff approximation. Chem. Phys. Lett. 1999, 314, 291–299. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. Self-Consistent Molecular Orbital Methods. 9. Extended Gaussian-type basis for molecular-orbital studies of organic molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
- Fuentealba, P.; Preuss, H.; Stoll, H.; Szentpály, L. A Proper Account of Core-polarization with Pseudopotentials—Single Valence-Electron Alkali Compounds. Chem. Phys. Lett. 1982, 89, 418–422. [Google Scholar] [CrossRef]
- Miertuš, S.; Scrocco, E.; Tomasi, J. Electrostatic Interaction of a Solute with a Continuum. A Direct Utilization of ab initio Molecular Potentials for the Prevision of Solvent Effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar]
- Roos, B.O. The multiconfigurational (MC) self-consistent field (SCF) theory. In Lecture Notes in Quantum Chemistry; Springer: Berlin, Germany, 1992; Volume 58, pp. 177–254. [Google Scholar]
- Finley, J.; Malmqvist, P.-Å.; Roos, B.O.; Serrano-Andrés, L. The multi-state CASPT2 method. Chem. Phys. Lett. 1998, 288, 299–306. [Google Scholar] [CrossRef]
- Roos, B.O.; Veryazov, V.; Widmark, P.-O. Relativistic atomic natural orbital type basis sets for the alkaline and alkaline-earth atoms applied to the ground-state potentials for the corresponding dimers. Theor. Chem. Acc. 2004, 111, 345–351. [Google Scholar] [CrossRef]
- Aquilante, F.; Autschbach, J.; Carlson, R.K.; Chibotaru, L.F.; Delcey, M.G.; De Vico, L.; Galván, I.F.; Ferré, N.; Frutos, L.M.; Gagliardi, L.; et al. Molcas 8: New capabilities for multiconfigurational quantum chemical calculations across the periodic table. J. Comp. Chem. 2016, 37, 506–541. [Google Scholar] [CrossRef]
- Soria, D.B.; Chacón Villalba, M.E.; Piro, O.E.; Aymonino, P.J. Crystal and molecular structure and photoisomerization of nitropentaamminecobalt(III) nitroprusside sesquihydrate, [Co(NH3)5NO2][Fe(CN)5NO]·1.5H2O. Polyhedron 2002, 21, 1767–1774. [Google Scholar] [CrossRef]
- Peresypkina, E.V.; Samsonenko, D.G.; Vostrikova, K.E. Heterobimetallic coordination polymers involving 3d metal complexes and heavier transition metals cyanometallates. J. Solid. State Chem. 2015, 224, 107–114. [Google Scholar] [CrossRef]
- Hopmann, K.H.; Ghosh, A.; Noodleman, N. Density Functional Theory Calculations on Mössbauer Parameters of Nonheme Iron Nitrosyls. Inorg. Chem. 2009, 48, 9155–9165. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Samples of the compounds are not available from the authors. |
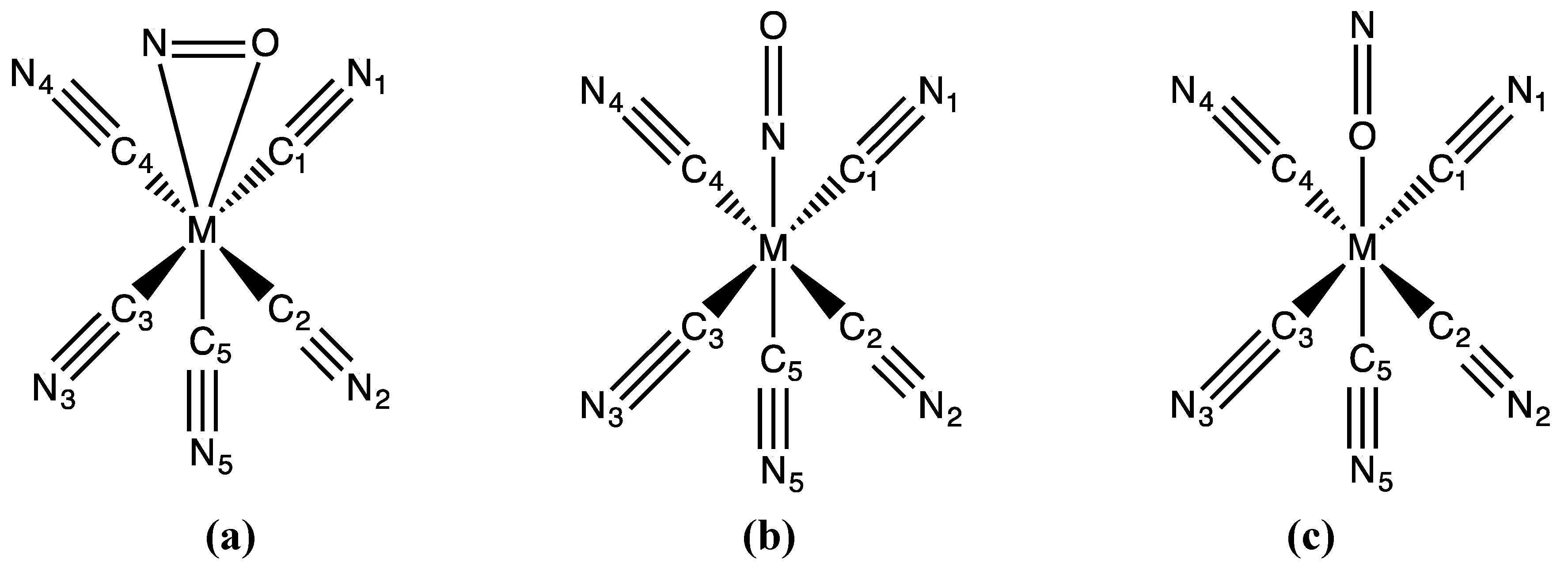
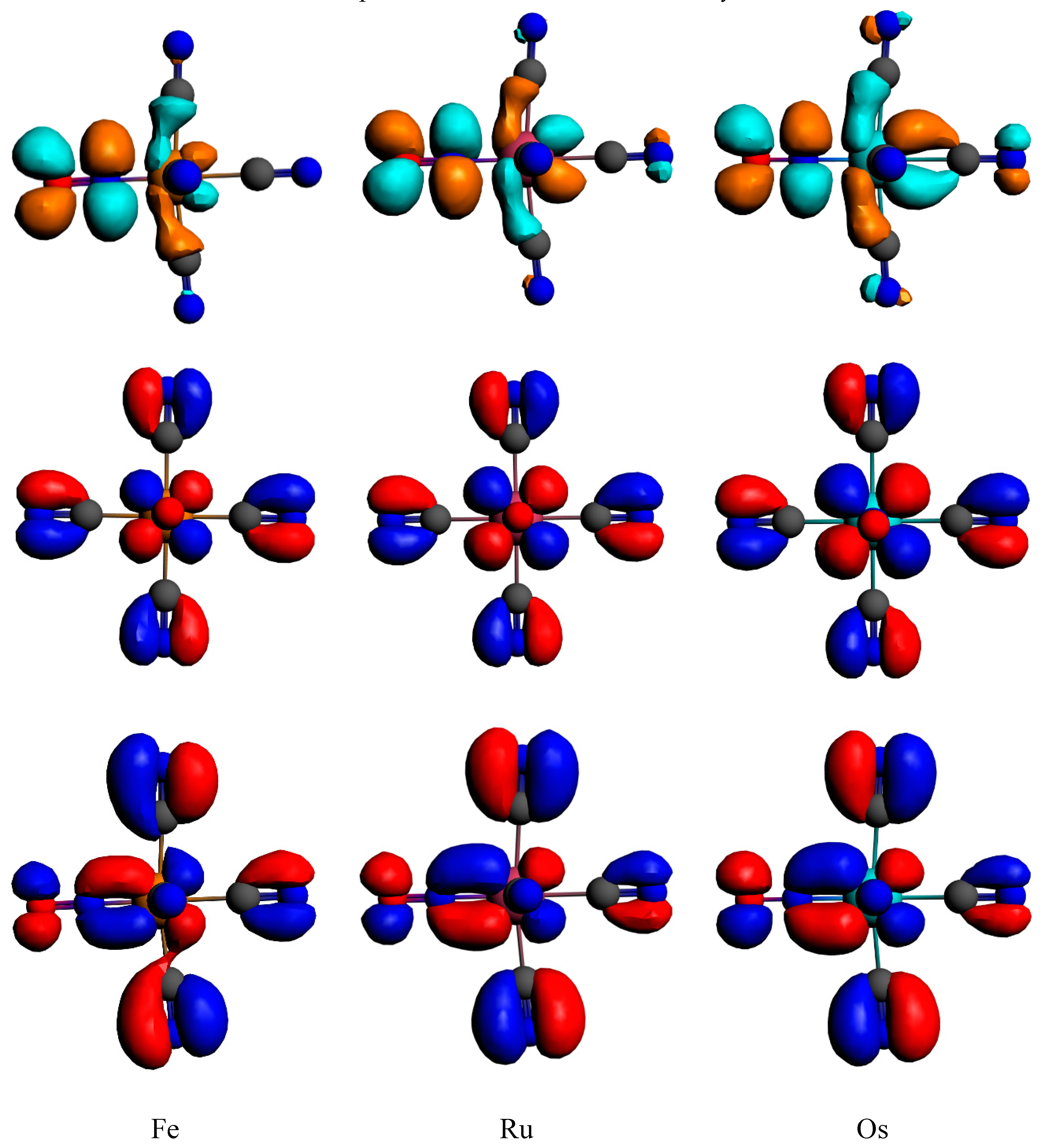
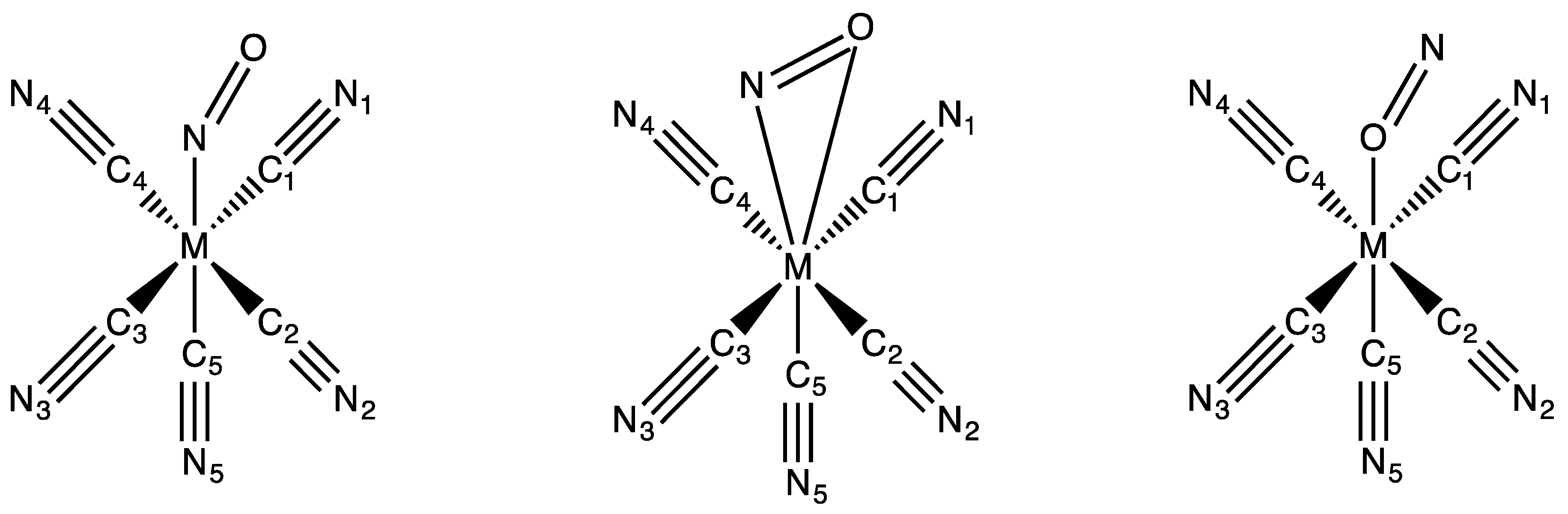
| Bonds Angles | Fe | Fe (RX) a | Ru | Ru (RX) b | Os |
|---|---|---|---|---|---|
| M-N | 1.66 | 1.65 | 1.81 | 1.75 | 1.79 |
| M-C1 | 1.96 | 1.93 | 2.09 | 2.07 | 2.08 |
| M-C2 | 1.96 | 1.93 | 2.09 | 2.07 | 2.08 |
| M-C3 | 1.96 | 1.93 | 2.09 | 2.07 | 2.08 |
| M-C4 | 1.96 | 1.94 | 2.09 | 2.07 | 2.08 |
| M-C5 | 1.95 | 1.93 | 2.08 | 2.07 | 2.10 |
| NO | 1.13 | 1.13 | 1.14 | 1.15 | 1.14 |
| M-N-O | 179.8 | 178.2 | 179.9 | 177.0 | 179.9 |
| N-M-C1 | 94.1 | 95.9 | 94.1 | 94.3 | 94.2 |
| N-M-C2 | 94.0 | 95.5 | 94.1 | 93.3 | 94.1 |
| N-M-C3 | 93.9 | 94.1 | 94.1 | 95.9 | 94.0 |
| N-M-C4 | 94.0 | 96.1 | 94.1 | 95.3 | 94.1 |
| Bonds Angles | Fe | Ru | Os | ||||
|---|---|---|---|---|---|---|---|
| Flat S0 | Reverse S0 | Reverse a T1 | Flat S0 | Reverse S0 | Flat S0 | Reverse S0 | |
| M-N | 1.92 | 2.04 | 2.01 | ||||
| M-O | 2.04 | 1.77 | 2.28 | 2.21 | 1.95 | 2.20 | 1.92 |
| M-C1 | 1.96 | 1.96 | 1.96 | 2.09 | 2.08 | 2.09 | 2.08 |
| M-C2 | 1.97 | 1.96 | 1.96 | 2.09 | 2.08 | 2.08 | 2.08 |
| M-C3 | 1.95 | 1.96 | 1.95 | 119.3 | 2.08 | 2.08 | 2.08 |
| M-C4 | 1.97 | 1.96 | 1.96 | 2.09 | 2.08 | 2.08 | 2.08 |
| M-C5 | 1.91 | 1.91 | 1.89 | 2.01 | 2.02 | 2.02 | 2.02 |
| NO | 1.15 | 1.11 | 1.15 | 1.16 | 1.12 | 1.18 | 1.13 |
| M-N-O | 79.3 | 82.8 | 82.9 | ||||
| M-O-N | 67.0 | 179.8 | 128.2 | 65.9 | 179.8 | 64.9 | 179.9 |
| N-M-C1 | 79.7 | 92.6 | 87.3 | 78.0 | 92.6 | 77.8 | 92.0 |
| N-M-C2 | 91.0 | 92.6 | 87.2 | 91.5 | 92.4 | 90.9 | 92.0 |
| N-M-C3 | 120.4 | 92.7 | 90.5 | 119.3 | 92.5 | 119.4 | 92.0 |
| N-M-C4 | 91.0 | 92.6 | 88.4 | 91.5 | 92.6 | 90.9 | 92.1 |
| EDFT | 1.46 | 1.65 | 1.49 | 1.33 | 1.67 | 1.59 | 2.05 |
| Metal | Standard | TSSF | Flat | TSFR | Reverse |
|---|---|---|---|---|---|
| Fe | 0.0 | 1.90 | 1.33 | 2.42 | 1.64 |
| Fe (triplet) | 0.42 | 0.87 | |||
| Ru | 0.0 | 2.00 | 1.33 | ||
| Os | 0.0 | 2.30 | 1.54 | 3.01 | 2.02 |
| States | Fe | Fe a | Ru | Os |
|---|---|---|---|---|
| T1A’ | 2.45 | 2.41 | 2.70 | 2.82 |
| T1A” | 2.45 | 2.33 | 2.70 | 2.82 |
| T2A’ | 2.31 | 2.76 | 2.99 | |
| S1A’ | 2.79 | 2.92 | 3.03 | |
| S1A” | 2.79 | 2.92 | 3.03 |
| Structure | Standard | Flat | Reverse | NO-bent | MNO-bent | ON-bent |
|---|---|---|---|---|---|---|
| S0 | 0.0 | 1.46 | 1.65 | 2.09 a | 2.20 b | |
| S1 (A’) | 2.42 | 3.41 | 2.99 | |||
| T1 (A’) | 2.12 | -NO | 2.62 | |||
| T2 (A’) | 1.77 | 1.86 a | 2.10 b | |||
| S1 (A”) | - | 2.85 | 2.22 | 2.65 | ||
| T1 (A”) | - | 1.75 | 2.25 | 2.45 |
| Structure | Standard | Flat | Reverse | NO-bent | MNO-bent |
|---|---|---|---|---|---|
| S0 | 0.0 | 1.33 | 1.67 | ||
| S1 (A’) | 2.54 | 3.22 | 3.10 | ||
| T1 (A’) | - | - | |||
| T2 (A’) | 2.19 | 2.58 | |||
| S1 (A”) | - | -NO | 2.37 | ||
| T1 (A”) | - | 2.83 | 2.13 | 2.66 |
| Structure | Standard | Flat | Reverse | NO-bent | MNO-bent | ON-bent |
|---|---|---|---|---|---|---|
| S0 | 0.0 | 1.59 | 2.05 | |||
| S1 (A’) | 2.69 | 3.41 | 3.56 | |||
| T1 (A’) | 2.50 | 3.08 | - | |||
| T2 (A’) | - | - | 3.03 | |||
| S1 (A”) | - | -NO | 2.54 | 3.31 | ||
| T1 (A”) | - | - | 2.33 | 3.09 | 3.31 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daniel, C.; Gourlaouen, C. Structural and Optical Properties of Metal-Nitrosyl Complexes. Molecules 2019, 24, 3638. https://doi.org/10.3390/molecules24203638
Daniel C, Gourlaouen C. Structural and Optical Properties of Metal-Nitrosyl Complexes. Molecules. 2019; 24(20):3638. https://doi.org/10.3390/molecules24203638
Chicago/Turabian StyleDaniel, Chantal, and Christophe Gourlaouen. 2019. "Structural and Optical Properties of Metal-Nitrosyl Complexes" Molecules 24, no. 20: 3638. https://doi.org/10.3390/molecules24203638
APA StyleDaniel, C., & Gourlaouen, C. (2019). Structural and Optical Properties of Metal-Nitrosyl Complexes. Molecules, 24(20), 3638. https://doi.org/10.3390/molecules24203638





