Theoretical Analysis of Efficiency of Multi-Layer Core-Shell Stationary Phases in the High Performance Liquid Chromatography of Large Biomolecules
Abstract
1. Introduction
2. Theory
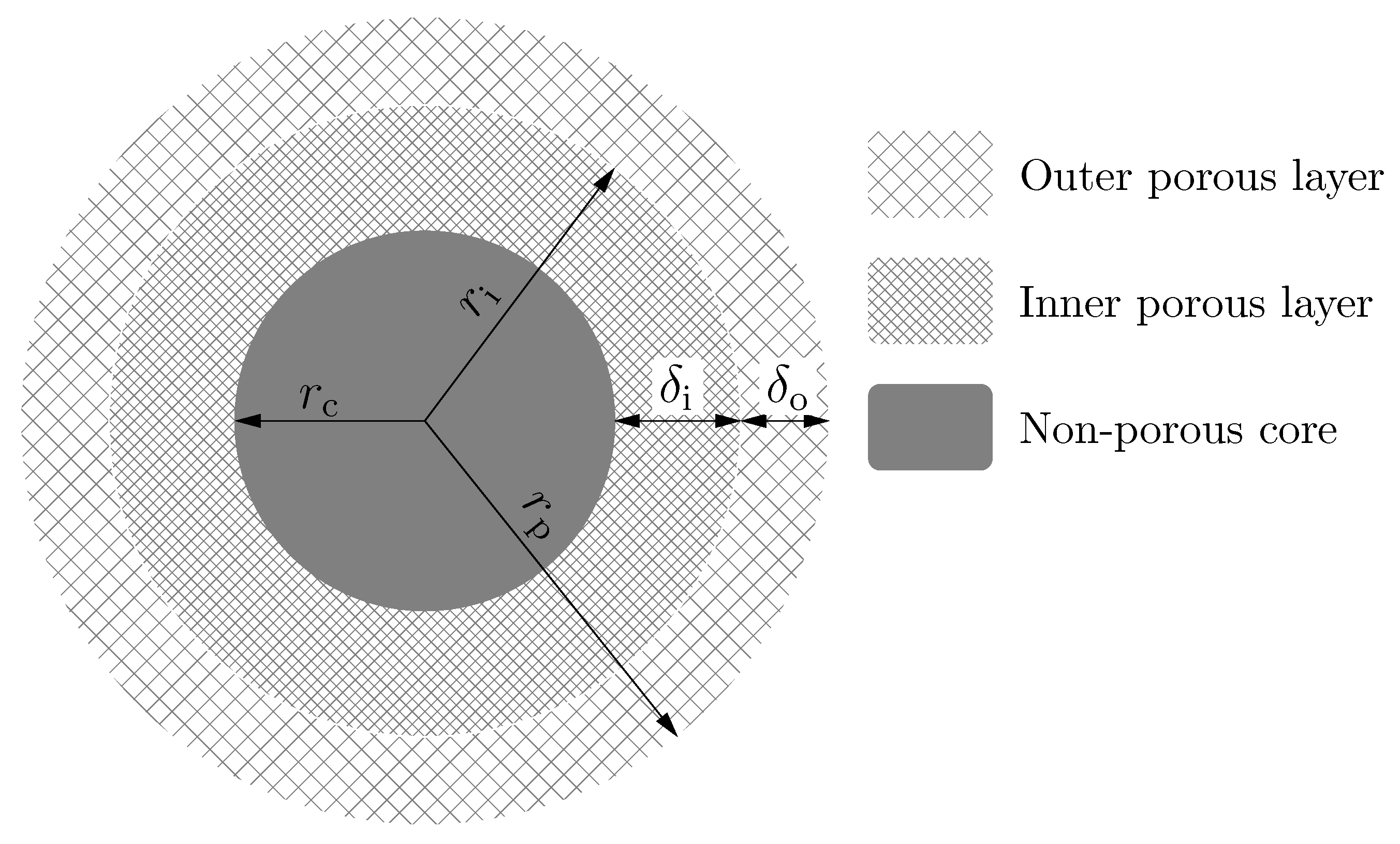
2.1. Structure of Multi-Layer Core-Shell Particles
- A non-porous core with a radius :where is the radius of particle (Figure 1) and is the factor of proportonality between the radius of the inner solid core and the radius of the particle. This region is impermeable to the compounds analyzed and to the molecules of eluent. Note that, if is equal to 0, there is no solid core inside the particle, while, in the case of , the whole particle is non-porous, such as the Kovasil phases [22]. Accordingly, .
- A porous inner layer with a thickness "where is the radius of the outer surface of the inner porous layer (Figure 1) and is the factor of proportonality between and . This layer has a given porosity () and surface chemistry. Note that, if is equal to or 1, the particle has only one porous layer. If , the particle has two porous layers.
- A porous outer layer with a tickness :Depending on the manufacturer, this layer may or may not have different porosity () and surface chemistry than the inner porous layer.
2.2. General Rate Model for Multi-Layer Core-Shell Particles
2.3. Height Equivalent to a Theoretical Plate of Chromatographic Columns
3. Methods
4. Results and Discussions
4.1. General Solution of the GR Model
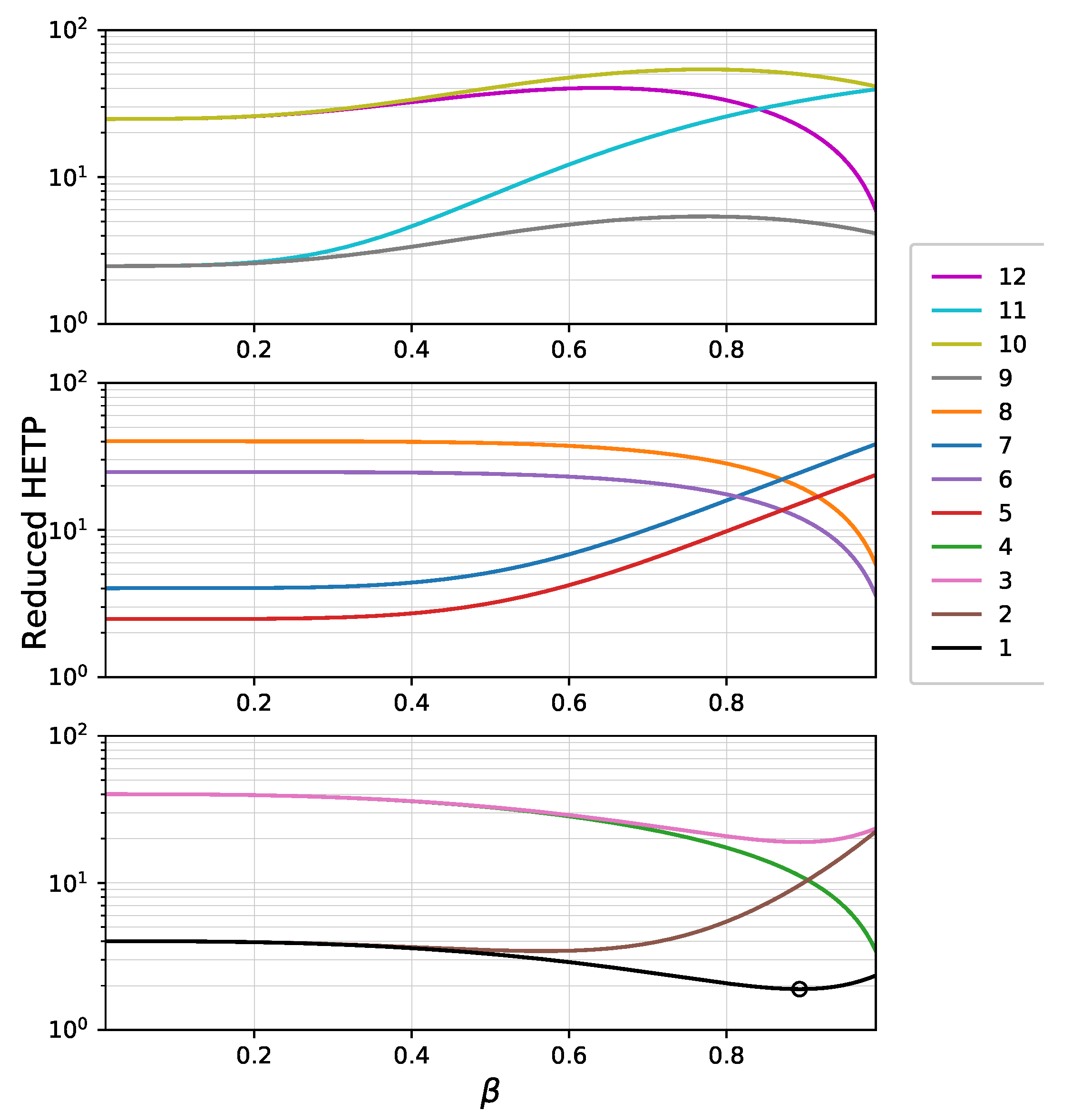
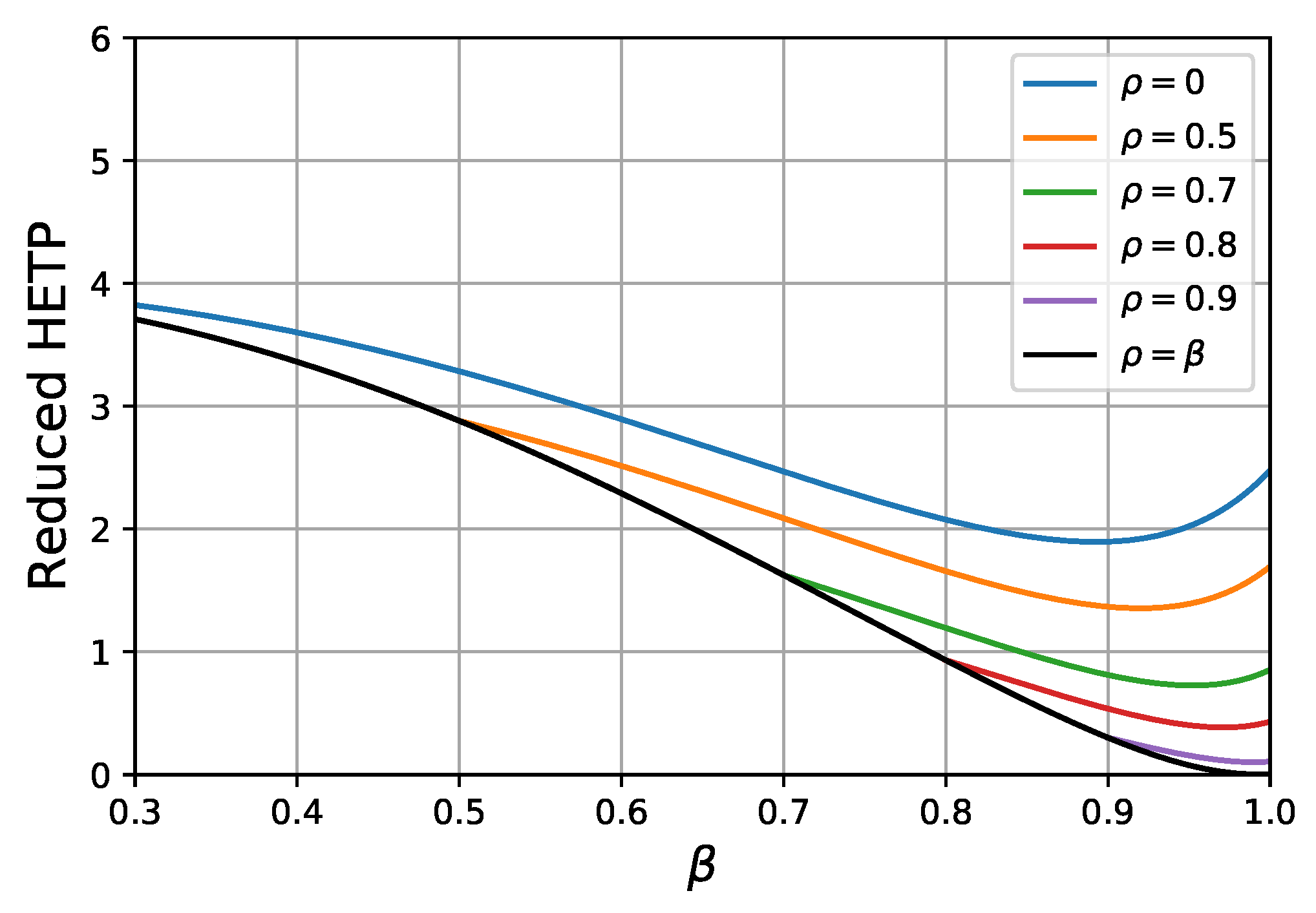
4.2. Separation Efficiency of Bi-Layer Fully Porous Particles
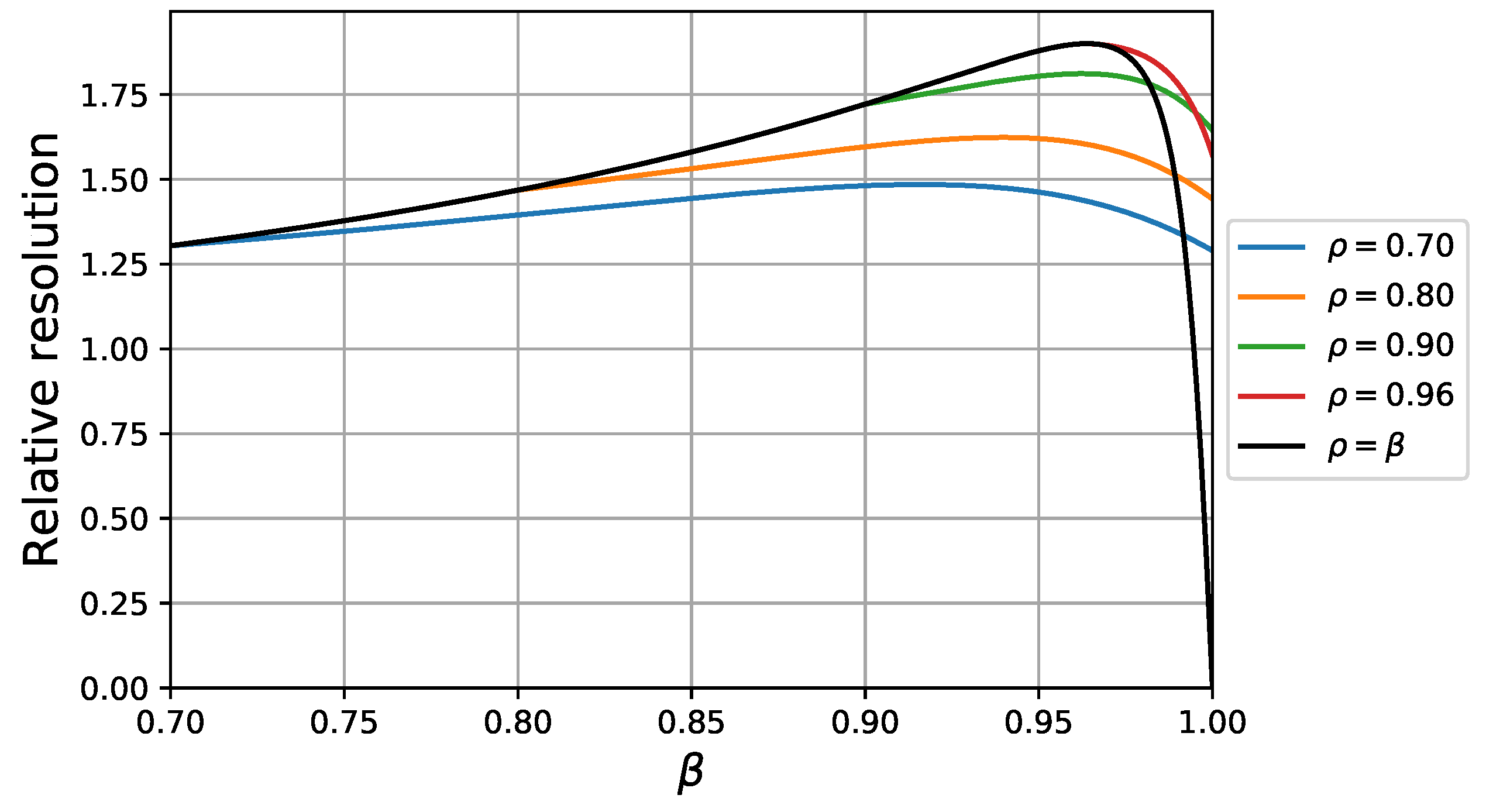
4.3. Separation Efficiency of Bi-Layer Core-Shell Particles
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| HPLC | High pressure liquid chromatography |
| HETP | Height equivalent to a theoretical plate |
| GRM | General rate model |
| SPP | Superficially porous particle |
| TPP | Totally porous particle |
| particle radius | |
| core radius | |
| radius of the outer surface of the inner porous layer | |
| factor of proportonality between the and | |
| factor of proportonality between and | |
| thickness of the inner porous layer | |
| thickness of the outer porous layer | |
| total porosity of the porous shells | |
| porosity of the inner porous layer | |
| porosity of the outer porous layer | |
| external porosity of the column | |
| total porosity of the column | |
| interstitial velocity of the eluent | |
| F | phase ratio |
| axial dispersion coefficient | |
| concentration of the solute in the interstitial volume | |
| concentration of the solute within the pores at the outer perimeter of the particle | |
| q | concentration of solute adsorbed on the surface of stationary phase |
| q averaged over the entire particle | |
| external mass transfer coefficient | |
| concentration of the solute in the stagnant mobile phase of pores in the inner layer | |
| concentration of the solute in the stagnant mobile phase of pores in the outer layer | |
| pore diffusion coefficient of solute in the inner layer | |
| pore diffusion coefficient of solute in the outer layer | |
| Henry coefficient of the solute in the inner layer | |
| Henry coefficient of the solute in the outer layer | |
| first normalized moment of the peak | |
| second centralized moment of the peak | |
| L | column length |
| Laplace transform of the elution profile at the outlet of the column | |
| column diameter | |
| particle diameter | |
| contribution of axial dispersion to the variance of peak eluted | |
| contribution of external film mass transfer to the variance of peak eluted | |
| contribution of intra-particle diffusion to the variance of peak eluted | |
| contribution of axial dispersion to the HETP | |
| contribution of external film mass transfer to the HETP | |
| contribution of intra-particle diffusion to the HETP | |
| zone retention coefficient of the inner layer | |
| zone retention coefficient of the outer layer | |
| zone retention coefficient, sum of and | |
| retention parameter of the outer layer | |
| retention parmeter of the outer layer | |
| k | apparent retention factor |
| retention time | |
| hold-up time of the column | |
| z | spatial variable |
| s | Laplace variable |
| r | radial variable |
| t | time |
References
- Fekete, S.; Oláh, E.; Fekete, J. Fast liquid chromatography: The domination of core-shell and very fine particles. J. Chromatogr. A 2012, 1228, 57–71. [Google Scholar] [CrossRef]
- Hayes, R.; Ahmed, A.; Edge, T.; Zhang, H. Core-shell particles: Preparation, fundamentals and applications in high performance liquid chromatography. J. Chromatogr. A 2014, 1357, 36–52. [Google Scholar] [CrossRef] [PubMed]
- Žuvela, P.; Skoczylas, M.; Jay Liu, J.; Baçzek, T.; Kaliszan, R.; Wong, M.W.; Buszewski, B. Column Characterization and Selection Systems in Reversed-Phase High-Performance Liquid Chromatography. Chem. Rev. 2019, 119, 3674–3729. [Google Scholar] [CrossRef]
- Kirkland, J.; Langlois, T.; DeStefano, J. Fused core particles for HPLC columns. Am. Labor. 2007, 39, 18–21. [Google Scholar]
- DeStefano, J.J.; Langlois, T.J.; Kirkland, J.J. Characteristics of superficially-porous silica particles for fast HPLC: Some performance comparisons with sub-2-mu m particles. J. Chromatogr. Sci. 2008, 46, 254. [Google Scholar] [CrossRef] [PubMed]
- DeStefano, J.; Boyes, B.; Schuster, S.; Miles, W.; Kirkland, J. Are sub-2μm particles best for separating small molecules? An alternative. J. Chromatogr. A 2014, 1368, 163–172. [Google Scholar] [CrossRef] [PubMed]
- Fekete, S.; Fekete, J.; Ganzler, K. Characterization of new types of stationary phases for fast liquid chromatographic applications. J. Pharm. Biomed. Anal. 2009, 50, 703–709. [Google Scholar] [CrossRef]
- Knox, J.H.; Saleem, M. Kinetic conditions for optimum speed and resolution in column chromatography. J. Chromatogr. Sci. 1969, 7, 614–622. [Google Scholar] [CrossRef]
- Horváth, K.; Horváth, S.; Lukács, D. Effect of axial temperature gradient on chromatographic efficiency under adiabatic conditions. J. Chromatogr. A 2017, 1483, 80–85. [Google Scholar] [CrossRef] [PubMed]
- Gritti, F.; Guiochon, G. Measurement of the axial and radial temperature profiles of a chromatographic column. Influence of thermal insulation on column efficiency. J. Chromatogr. A 2007, 1138, 141–157. [Google Scholar] [CrossRef] [PubMed]
- Gritti, F.; Guiochon, G. Complete temperature profiles in ultra-high-pressure liquid chromatography columns. Anal. Chem. 2008, 80, 5009–5020. [Google Scholar] [CrossRef] [PubMed]
- Horváth, C.G.; Preiss, B.A.; Lipsky, S.L. Fast liquid chromatography. Investigation of operating parameters and the separation of nucleotides on pellicular ion exchangers. Anal. Chem. 1967, 39, 1422–1428. [Google Scholar] [CrossRef] [PubMed]
- Horváth, C.G.; Lipsky, S.L. Column Design in High Pressure Liquid Chromatography. J. Chromatogr. Sci. 1969, 7, 109–116. [Google Scholar] [CrossRef]
- Fekete, S.; Guillarme, D.; Dong, M.W. Superficially Porous Particles: Perspectives, Practices, and Trends. LC GC 2014, 32, 420–433. [Google Scholar]
- Guiochon, G.; Gritti, F. Shell particles, trials, tribulations and triumphs. J. Chromatogr. A 2011, 1218, 1915–1938. [Google Scholar] [CrossRef]
- Cabooter, D.; Fanigliulo, A.; Bellazzi, G.; Allieri, B.; Desmet, G. Relationship between the particle size distribution of commercial fully porous and superficially porous high-performance liquid chromatography column packings and their chromatographic performance. J. Chromatogr. A 2010, 1217, 7074–7081. [Google Scholar] [CrossRef] [PubMed]
- González-Ruiz, V.; Olives, A.I.; Martín, M.A. Core-shell particles lead the way to renewing high-performance liquid chromatography. Trends Anal. Chem. 2015, 64, 17–28. [Google Scholar] [CrossRef]
- Deridder, S.; Catani, M.; Cavazzini, A.; Desmet, G. A theoretical study on the advantage of core-shell particles with radially-oriented mesopores. J. Chromatogr. A 2016, 1456, 137–144. [Google Scholar] [CrossRef]
- Pirok, B.W.; Breuer, P.; Hoppe, S.J.; Chitty, M.; Welch, E.; Farkas, T.; van der Wal, S.; Peters, R.; Schoenmakers, P.J. Size-exclusion chromatography using core-shell particles. J. Chromatogr. A 2017, 1486, 96–102. [Google Scholar] [CrossRef]
- Horváth, K.; Gritti, F.; Fairchild, J.N.; Guiochon, G. On the optimization of the shell thickness of superficially porous particles. J. Chromatogr. A 2010, 1217, 6373–6381. [Google Scholar] [CrossRef]
- Gritti, F.; Horváth, K.; Guiochon, G. How changing the particle structure can speed up protein mass transfer kinetics in liquid chromatography. J. Chromatogr. A 2012, 1263, 84–98. [Google Scholar] [CrossRef] [PubMed]
- Ohmacht, R.; Kiss, I. Application of a New Non-Porous Stationary Phase (Kovasil-H) for the Fast Separation of Peptides by HPLC. Chromatographia 1996, 42, 595–598. [Google Scholar] [CrossRef]
- Kulsing, C.; Yang, Y.; Munera, C.; Tse, C.; Matyska, M.T.; Pesek, J.J.; Boysen, R.I.; Hearn, M.T. Correlations between the zeta potentials of silica hydride-based stationary phases, analyte retention behaviour and their ionic interaction descriptors. Anal. Chim. Acta 2014, 817, 48–60. [Google Scholar] [CrossRef] [PubMed]
- Forssén, P.; Multia, E.; Samuelsson, J.; Andersson, M.; Aastrup, T.; Altun, S.; Wallinder, D.; Wallbing, L.; Liangsupree, T.; Riekkola, M.L.; et al. Reliable Strategy for Analysis of Complex Biosensor Data. Anal. Chem. 2018, 90, 5366–5374. [Google Scholar] [CrossRef] [PubMed]
- Kaczmarski, K.; Guiochon, G. Modeling of the Mass-Transfer Kinetics in Chromatographic Columns Packed with Shell and Pellicular Particles. Anal. Chem. 2007, 79, 4648–4656. [Google Scholar] [CrossRef] [PubMed]
- Guiochon, G.; Felinger, A.; Shirazi, D.G.; Katti, A.M. Fundamentals of Preparative and Nonlinear Chromatography; Academic Press: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Kučera, E. Contribution to the theory of chromatography: Linear non-equilibrium elution chromatography. J. Chromatogr. A 1965, 19, 237–248. [Google Scholar] [CrossRef]
- Cavazzini, A.; Gritti, F.; Kaczmarski, K.; Marchetti, N.; Guiochon, G. Mass-transfer kinetics in a shell packing material for chromatography. Anal. Chem. 2007, 79, 5972. [Google Scholar] [CrossRef] [PubMed]
- Fekete, S.; Berky, R.; Fekete, J.; Veuthey, J.L.; Guillarme, D. Evaluation of a new wide pore core-shell material (AerisTM WIDEPORE) and comparison with other existing stationary phases for the analysis of intact proteins. J. Chromatogr. A 2012, 1236, 177–188. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Python codes used for the calculations are available from the authors. |
| Parameter | Value |
|---|---|
| Column length (L) | 10 cm |
| Column diameter () | 0.3 cm |
| Particle diameter () | 2.7 m |
| External porosity () | 0.4 |
| Interstitial mobile phase velocity () | 5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Horváth, S.; Gritti, F.; Kormány, R.; Horváth, K. Theoretical Analysis of Efficiency of Multi-Layer Core-Shell Stationary Phases in the High Performance Liquid Chromatography of Large Biomolecules. Molecules 2019, 24, 2849. https://doi.org/10.3390/molecules24152849
Horváth S, Gritti F, Kormány R, Horváth K. Theoretical Analysis of Efficiency of Multi-Layer Core-Shell Stationary Phases in the High Performance Liquid Chromatography of Large Biomolecules. Molecules. 2019; 24(15):2849. https://doi.org/10.3390/molecules24152849
Chicago/Turabian StyleHorváth, Szabolcs, Fabrice Gritti, Róbert Kormány, and Krisztián Horváth. 2019. "Theoretical Analysis of Efficiency of Multi-Layer Core-Shell Stationary Phases in the High Performance Liquid Chromatography of Large Biomolecules" Molecules 24, no. 15: 2849. https://doi.org/10.3390/molecules24152849
APA StyleHorváth, S., Gritti, F., Kormány, R., & Horváth, K. (2019). Theoretical Analysis of Efficiency of Multi-Layer Core-Shell Stationary Phases in the High Performance Liquid Chromatography of Large Biomolecules. Molecules, 24(15), 2849. https://doi.org/10.3390/molecules24152849





