Metadevices with Potential Practical Applications
Abstract
1. Introduction
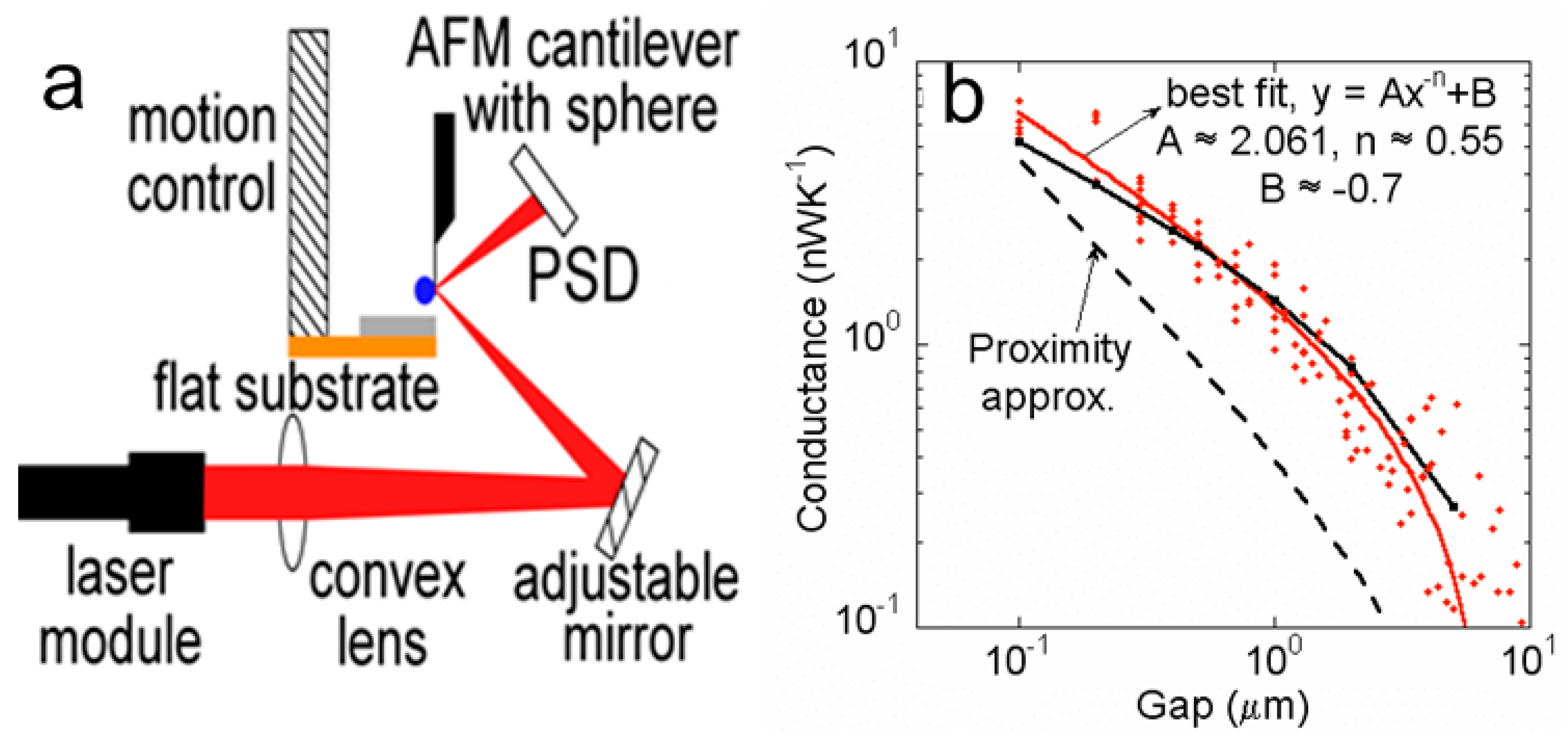
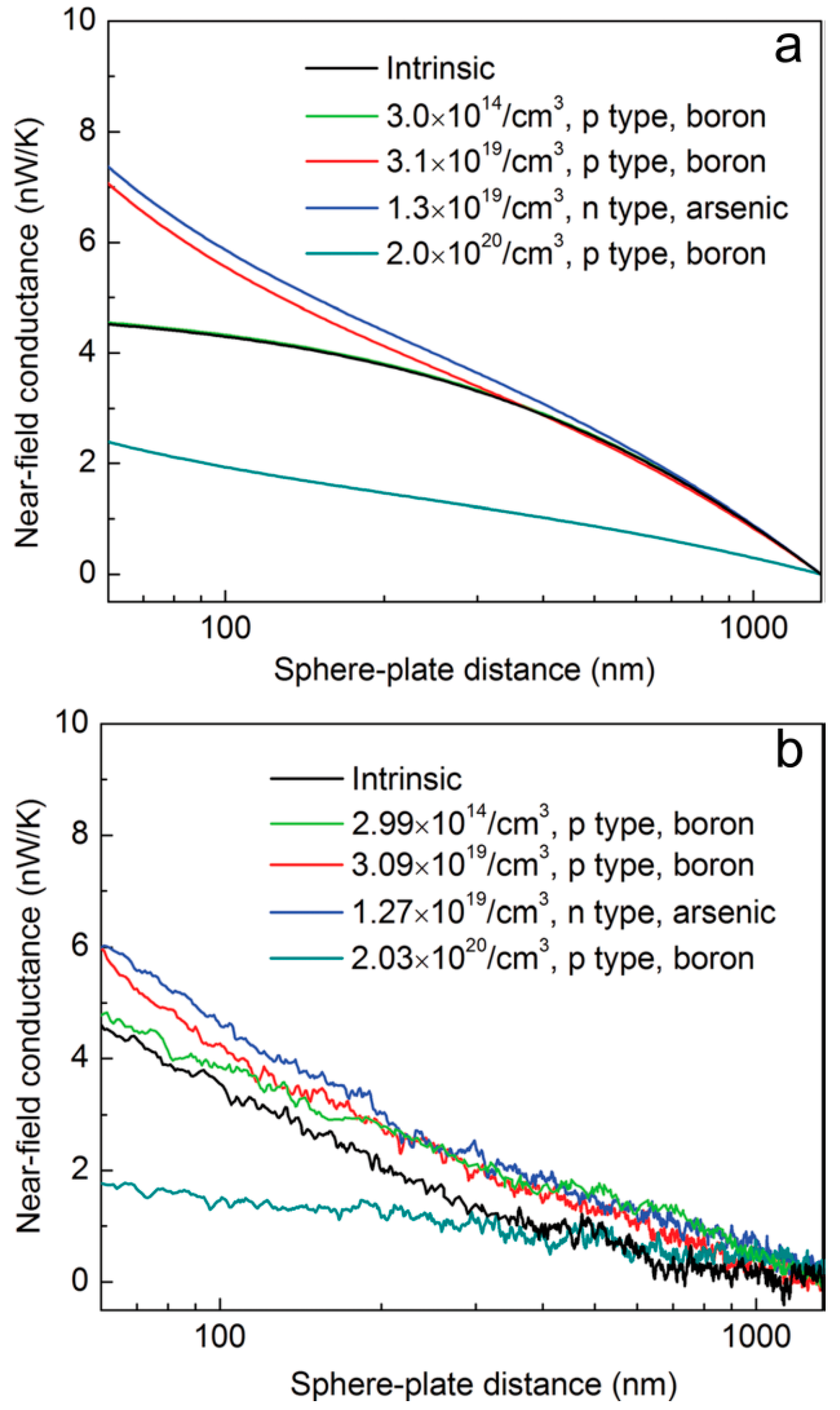
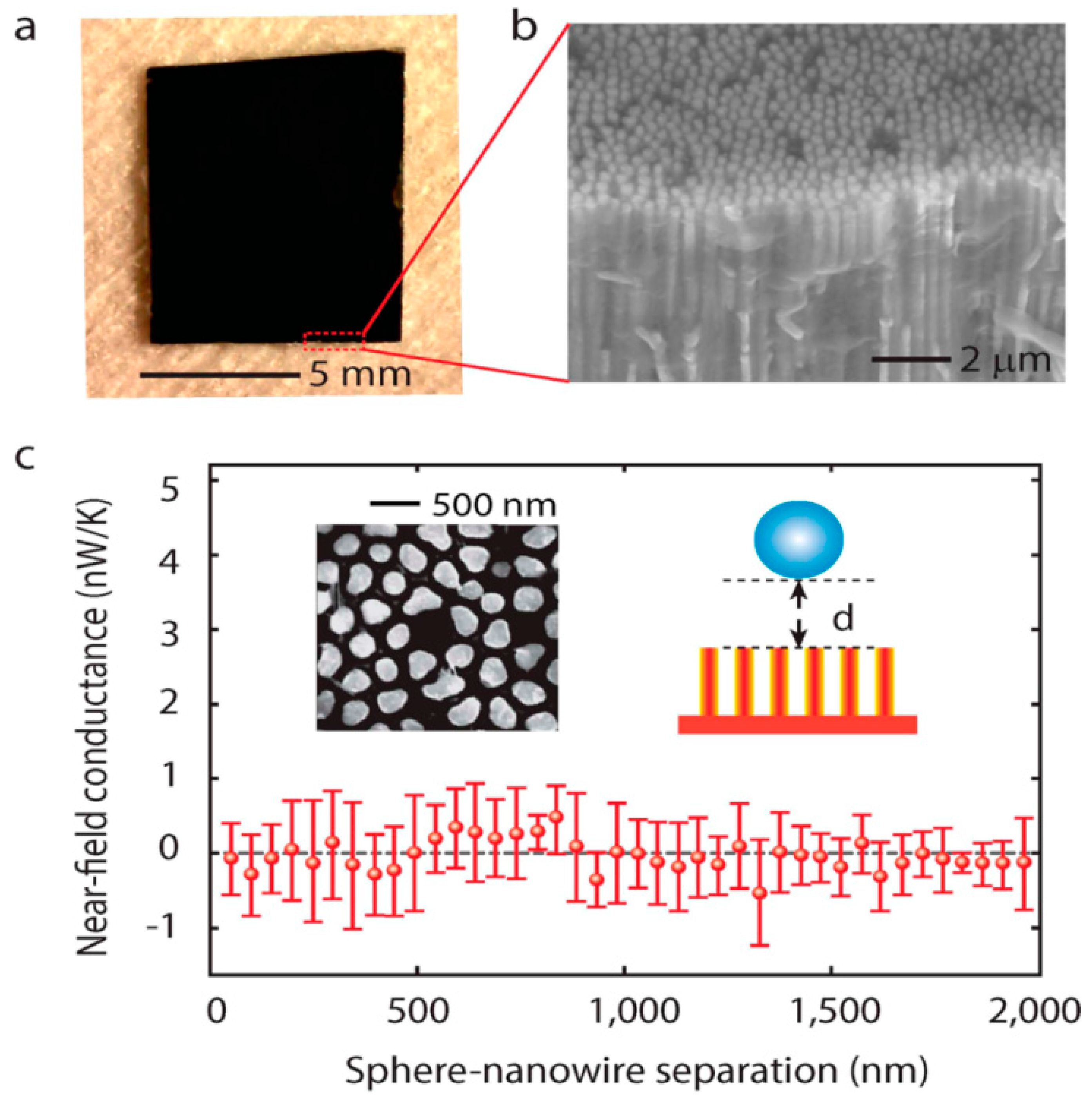
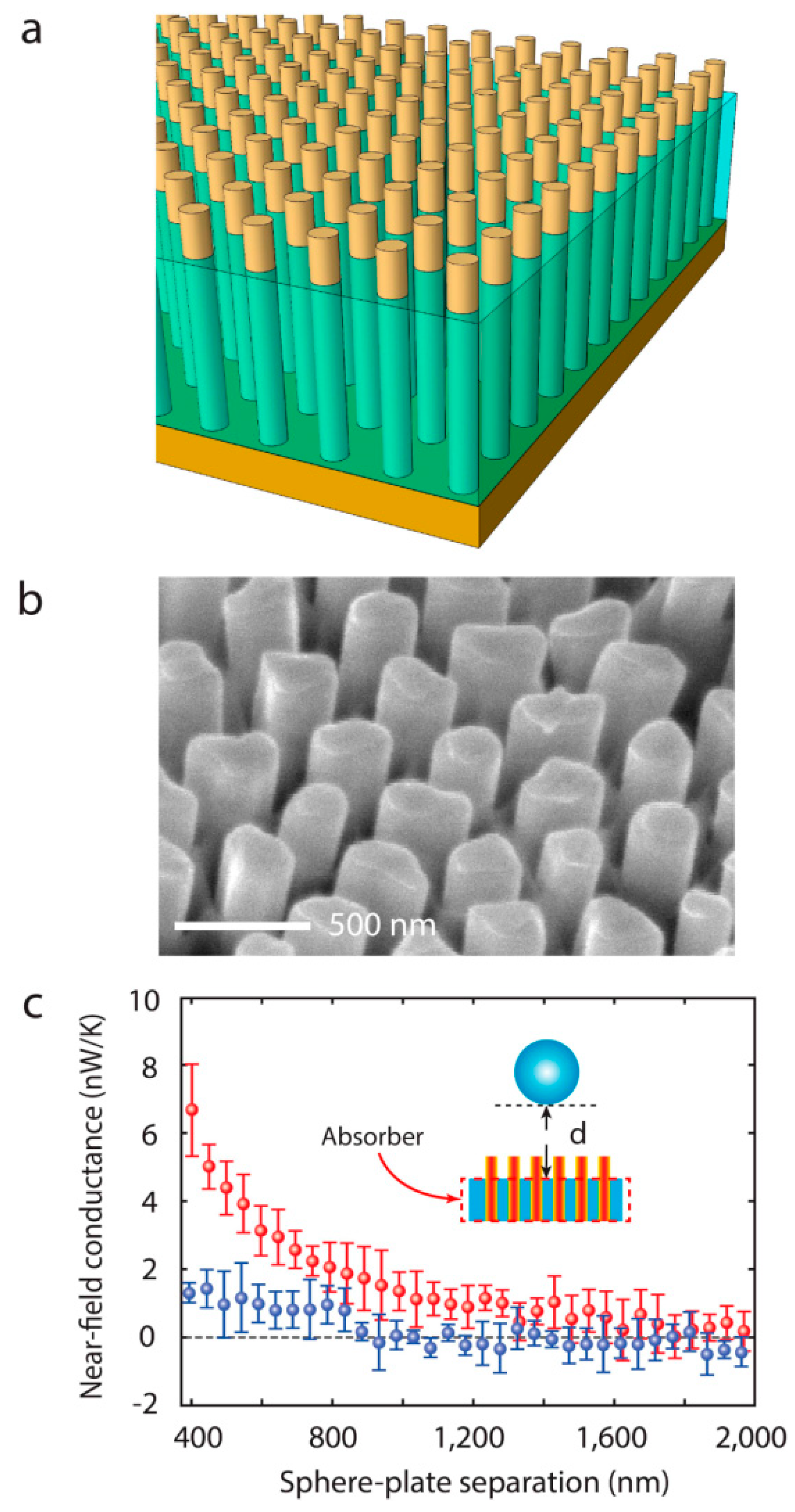
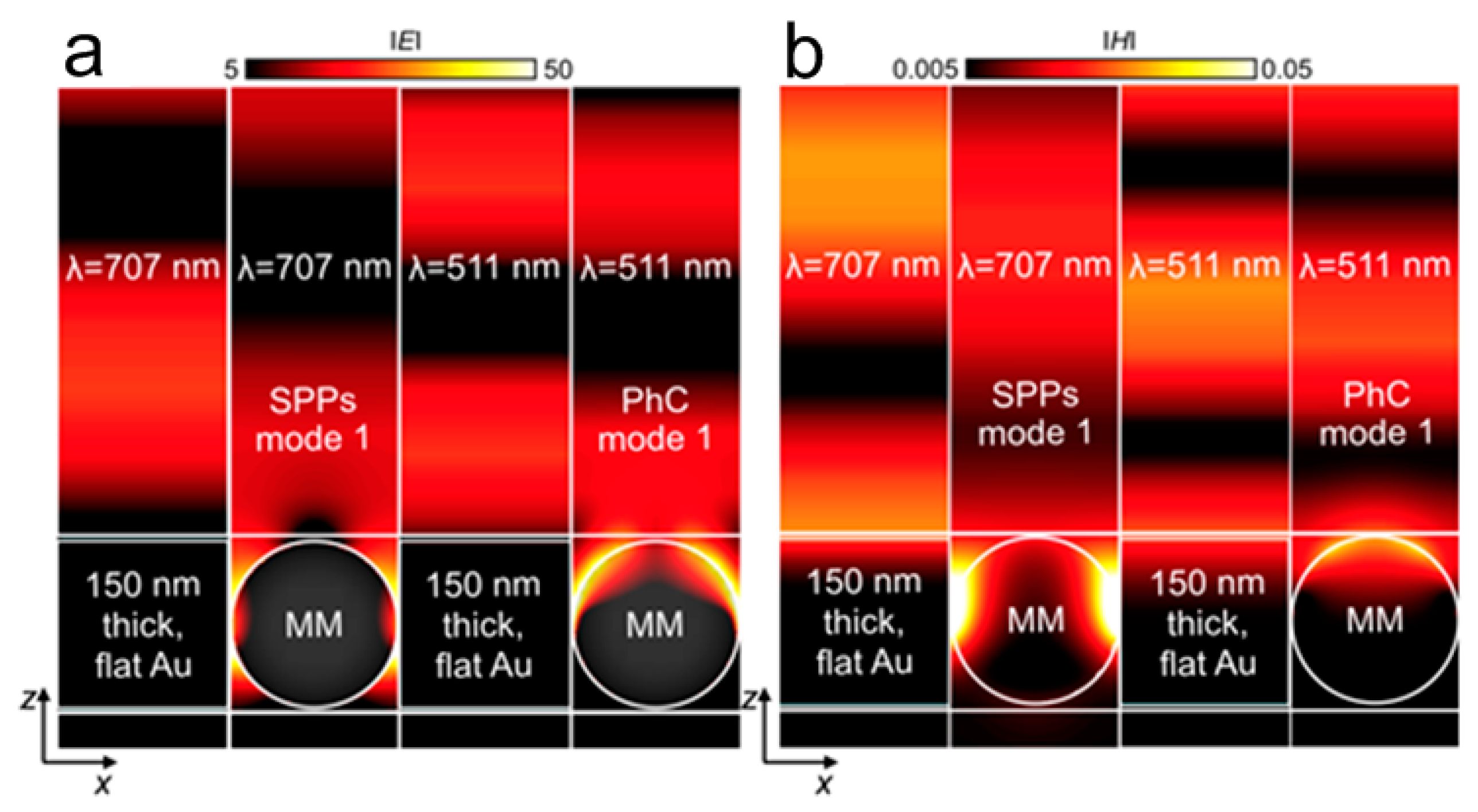
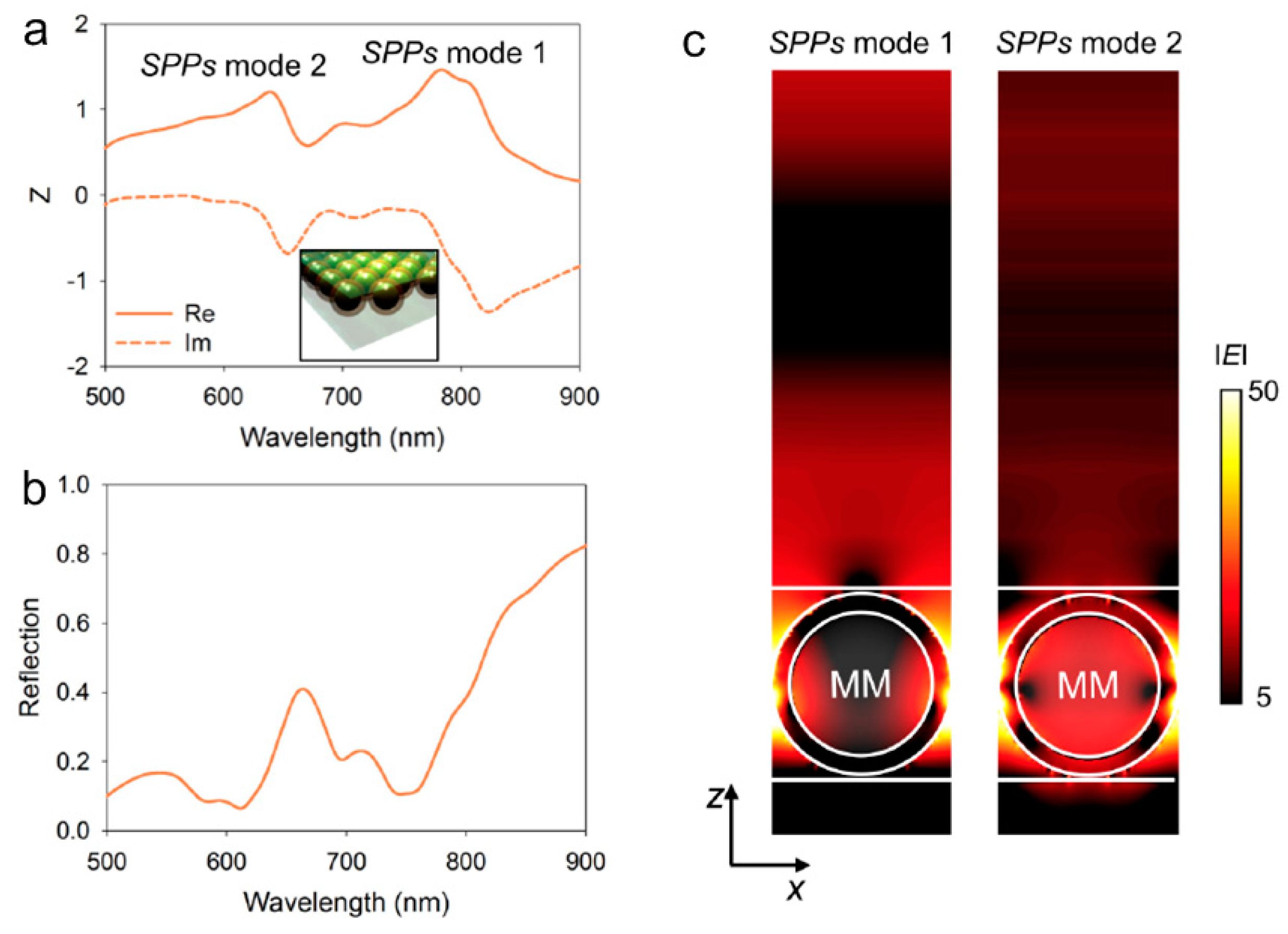
2. Near-Field Energy Transfer Devices
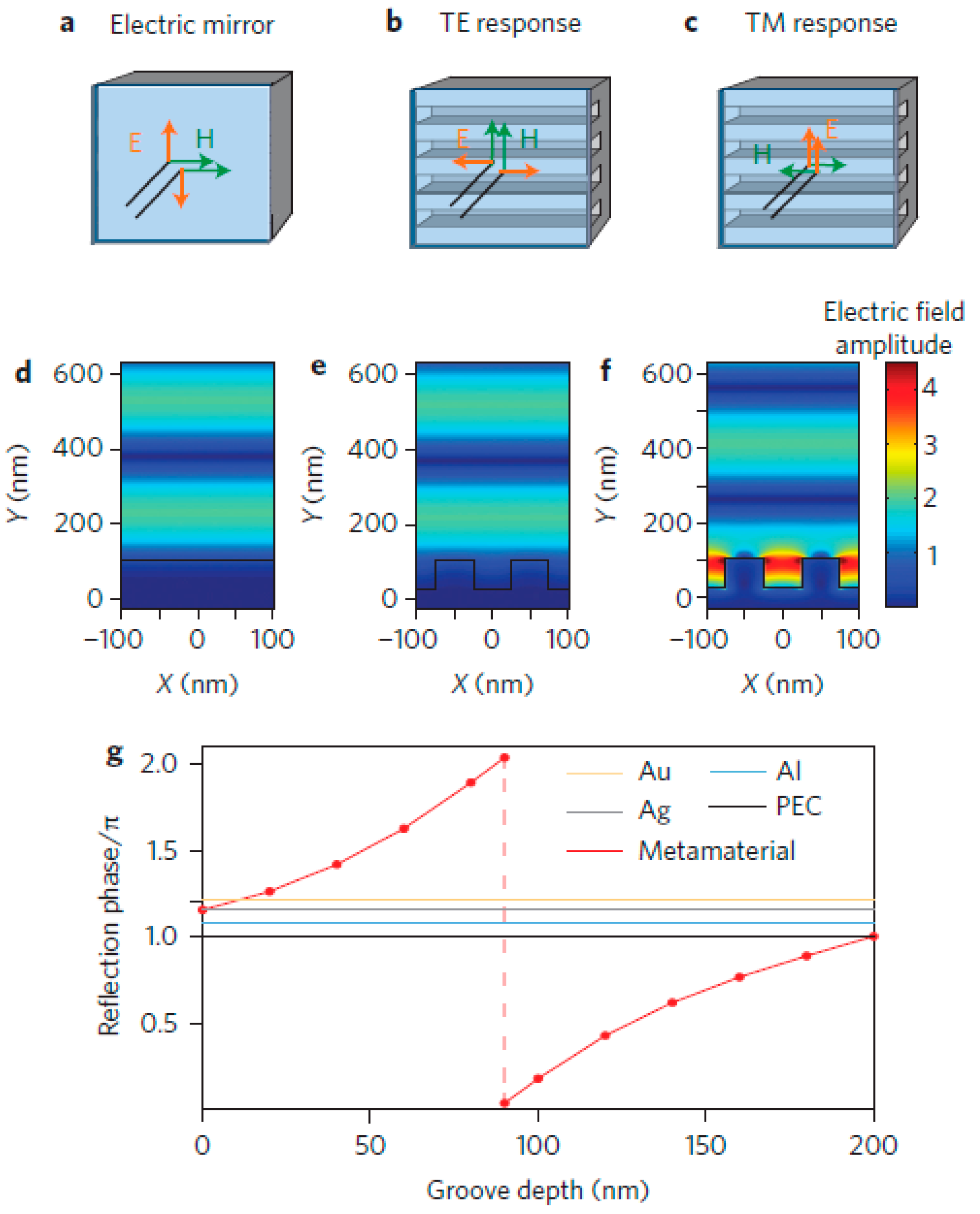
3. Metamaterial Mirrors
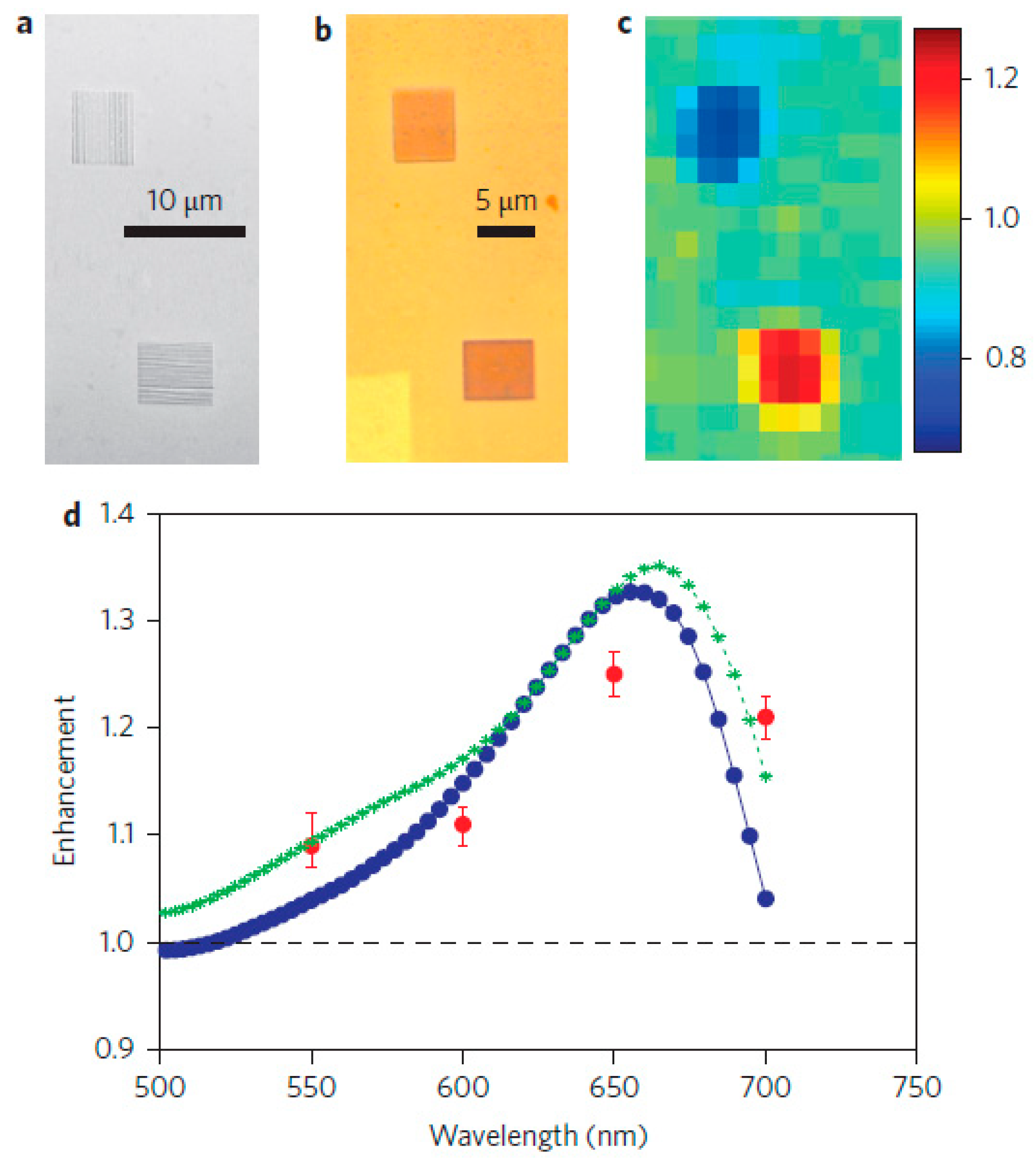
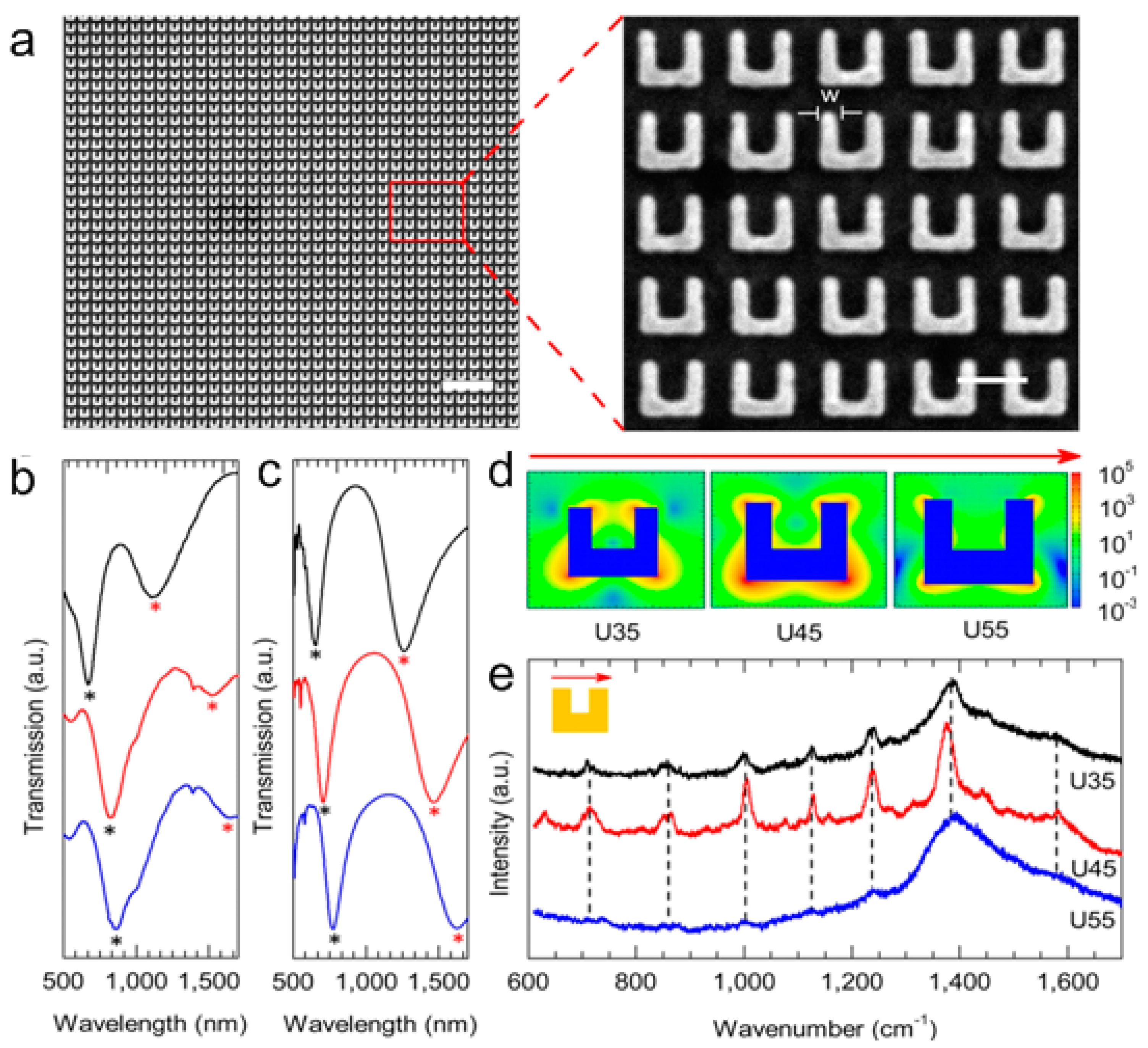
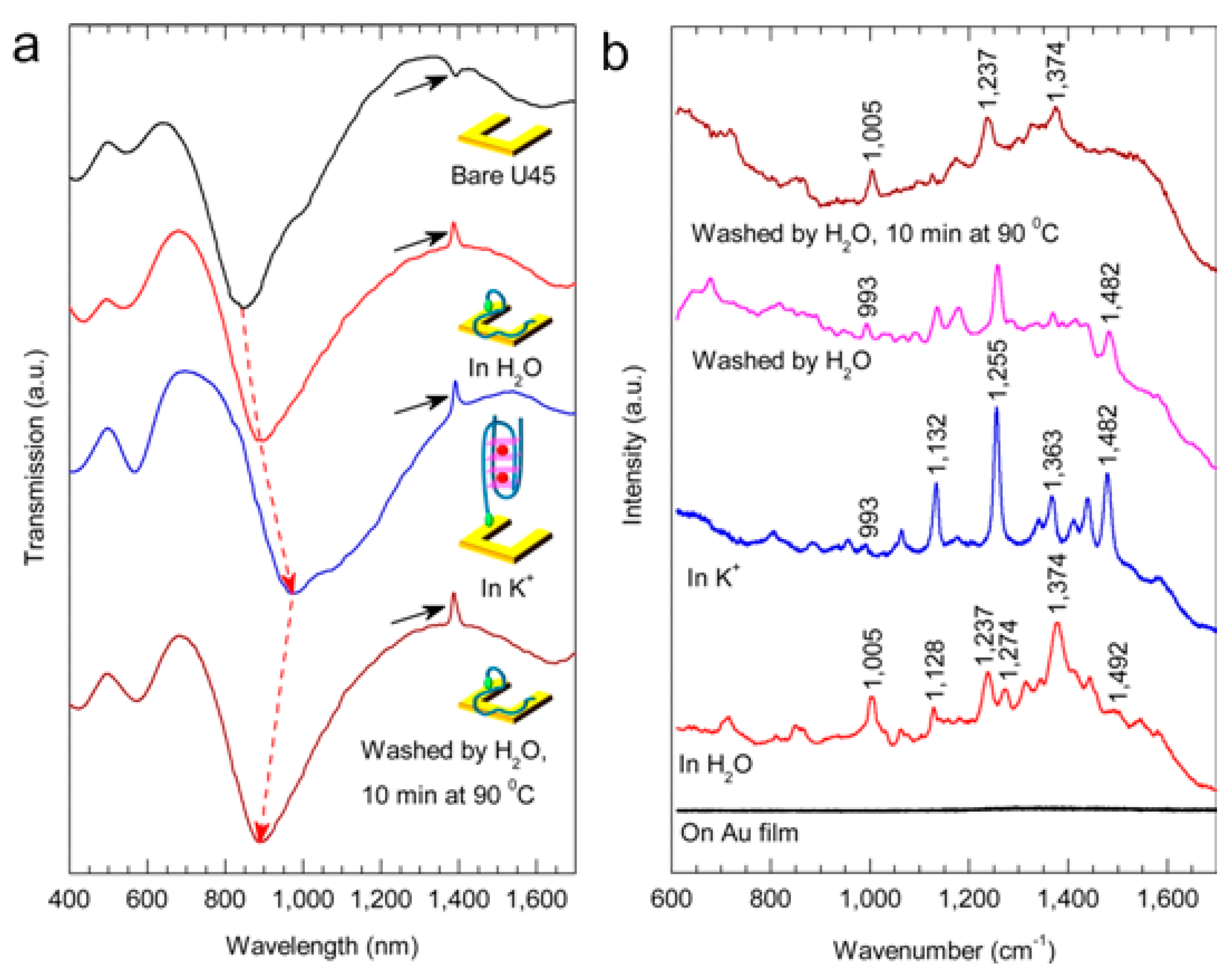
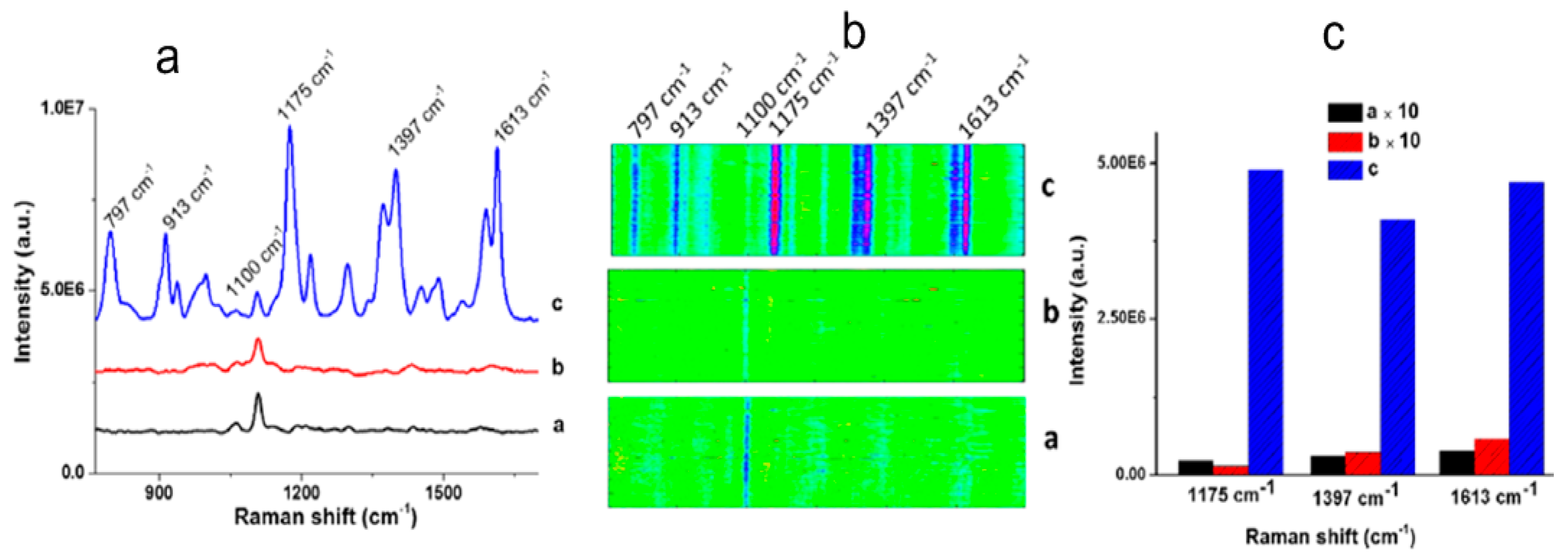
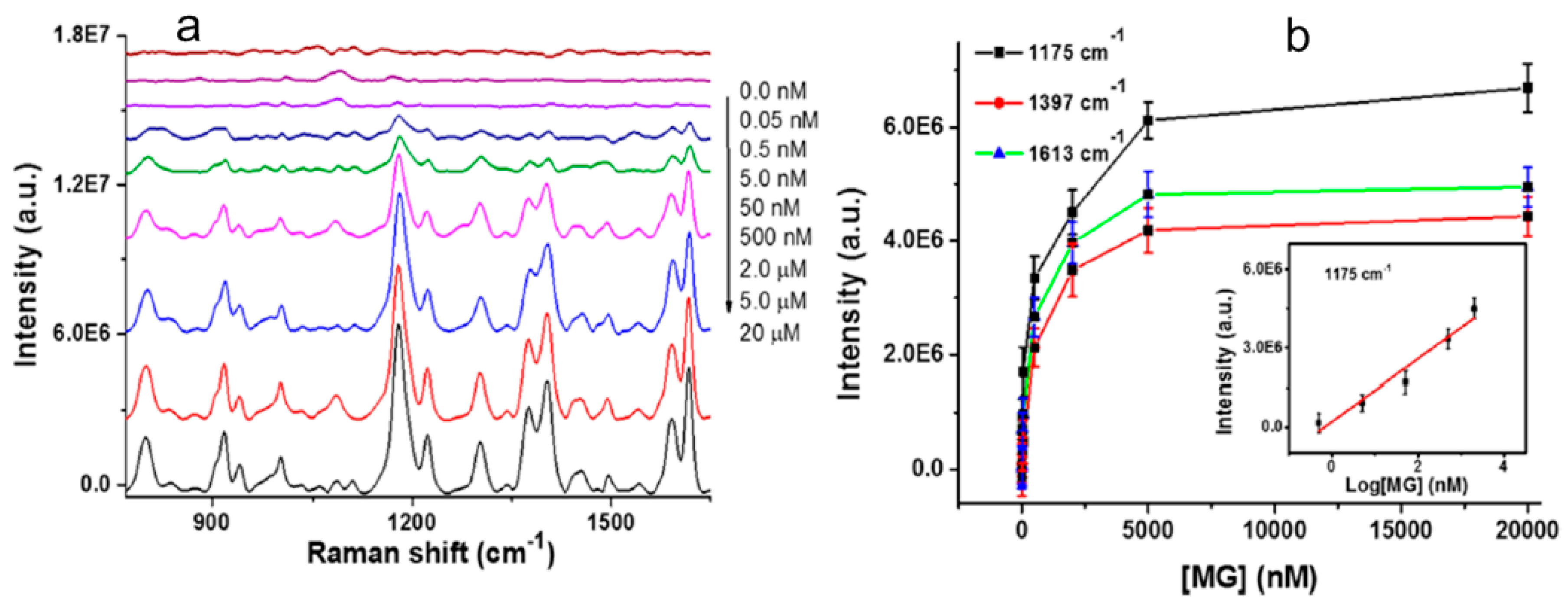
4. Metamaterial Biosensors
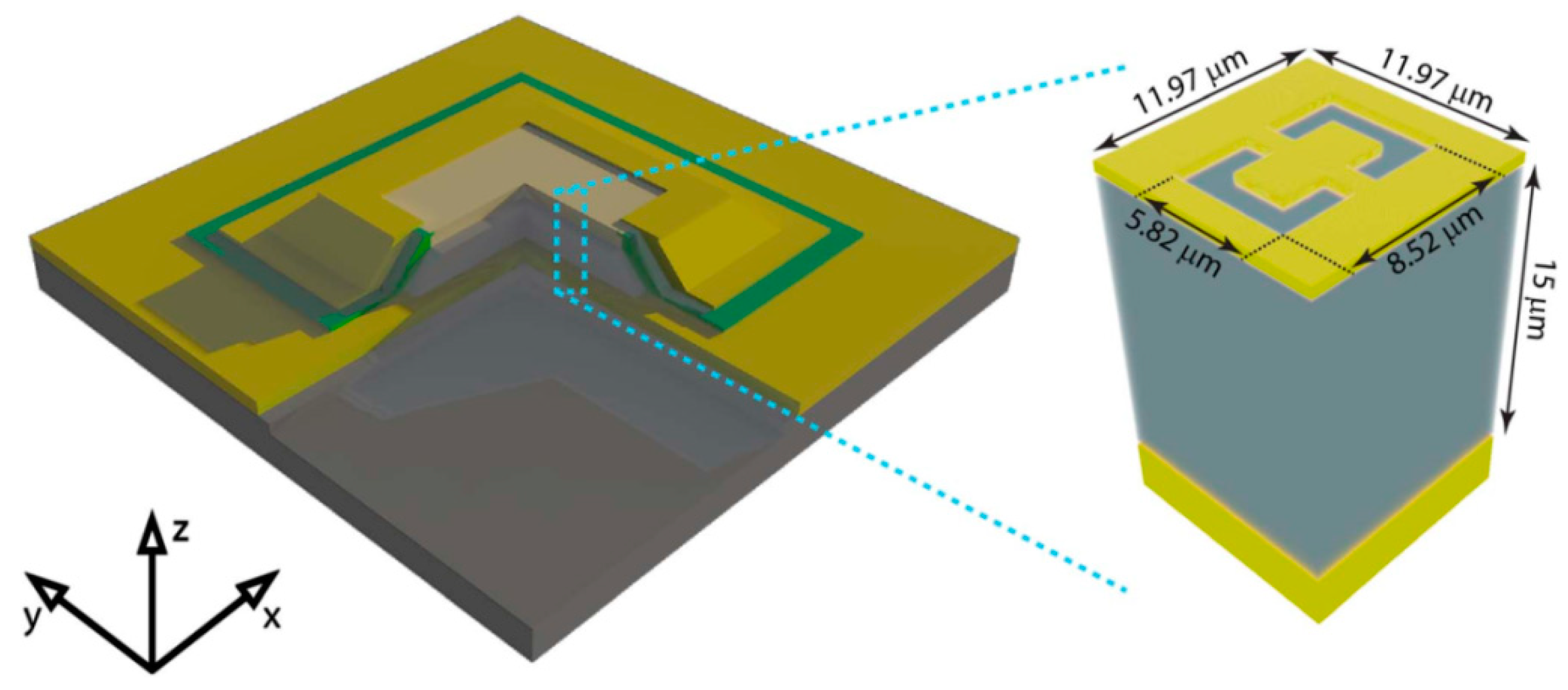
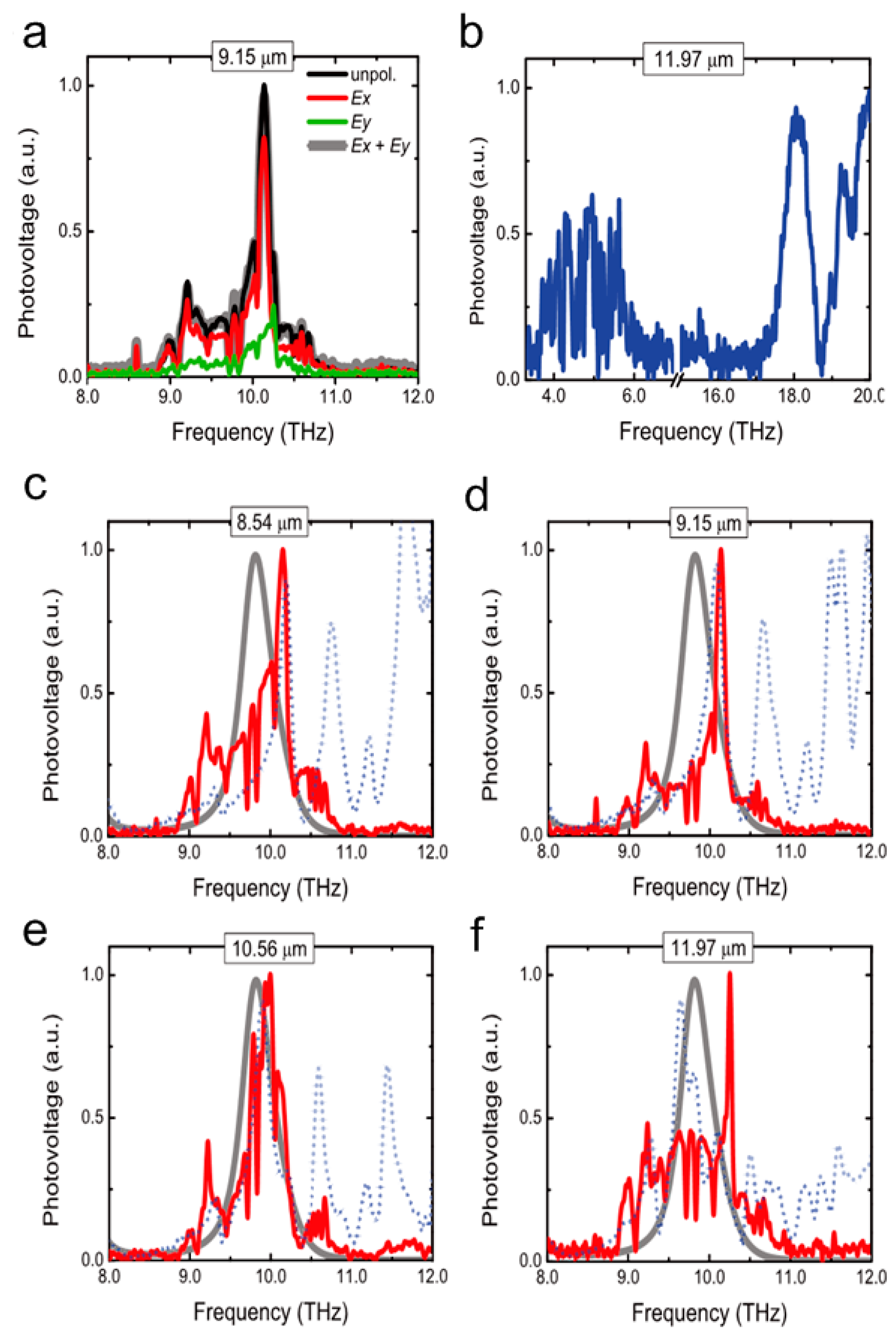
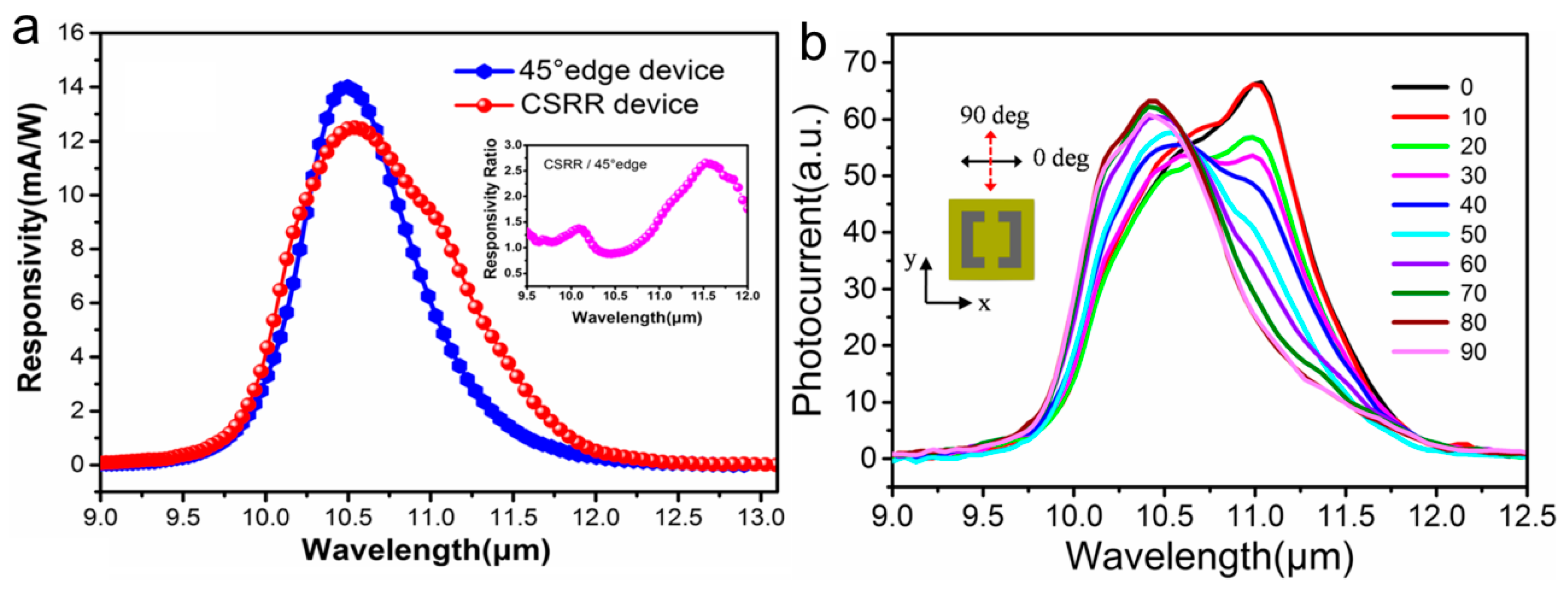
5. Metamaterial Detectors
6. Conclusion and Outlook
Funding
Conflicts of Interest
References
- Ishihara, K.; Suzuki, T. Metamaterial Demonstrates Both a High Refractive Index and Extremely Low Reflection in the 0.3-THz Band. J. Infrared Millim. Terahertz Waves 2017, 38, 1130–1139. [Google Scholar] [CrossRef]
- Yoo, S.; Park, Q.-H. Metamaterials and Chiral Sensing: A Review of Fundamentals and Applications. Nanophotonics 2019, 8, 249–261. [Google Scholar] [CrossRef]
- Gholipur, R.; Bahari, A. Preparation and Characterization Silver/Zirconium Nickel Oxide Nanocomposites with Negative Electromagnetic Parameters. Opt. Laser Technol. 2017, 91, 166–174. [Google Scholar] [CrossRef]
- Ling, F.; Zhong, Z.Q.; Huang, R.S.; Zhang, B. A Broadband Tunable Terahertz Negative Refractive Index Metamaterial. Sci. Rep. 2018, 8, 9843. [Google Scholar] [CrossRef] [PubMed]
- Fegadolli, W.S.; Pavarelli, N.; O’Brien, P.; Njoroge, S.; Almeida, V.R.; Scherer, A. Thermally Controllable Silicon Photonic Crystal Nanobeam Cavity Without Surface Cladding for Sensing Applications. ACS Photonics 2015, 2, 470–474. [Google Scholar] [CrossRef]
- Gu, C.; Zhang, X. A Novel Structure of Left-Handed Material with Equal Magnetic and Electric Resonant Frequency. IEEE T. Magn. 2017, 53, 2800504. [Google Scholar] [CrossRef]
- Chang, S.Y.; Guo, X.X.; Ni, X.J. Optical Metasurfaces: Progress and Applications. Annu. Rev. Mater. Res. 2018, 48, 279–302. [Google Scholar] [CrossRef]
- Hoa, N.T.Q.; Lam, P.H.; Tung, P.D.; Tuan, T.S.; Nguyen, H. Numerical Study of An Efficient Broadband Metamaterial Absorber In Visible Light Region. IEEE Photonics J. 2019, 11, 4600810. [Google Scholar] [CrossRef]
- Fan, Y.W.; Singer, S.B.; Bergstrom, R.; Regan, B.C. Probing Planck’s Law with Incandescent Light Emission from a Single Carbon Nanotube. Phys. Rev. Lett. 2009, 102, 187402. [Google Scholar] [CrossRef]
- Yu, Z.F.; Sergeant, N.P.; Skauli, T.; Zhang, G.; Wang, H.L.; Fan, S.H. Enhancing Far-Field Thermal Emission with Thermal Extraction. Nat. Commun. 2013, 4, 1730. [Google Scholar] [CrossRef]
- Kim, K.; Song, B.; Fernández-Hurtado, V.; Lee, W.; Jeong, W.; Cui, L.; Thompson, D.; Feist, J.; Reid, M.T.H.; García-Vidal, F.J.; et al. Radiative Heat Transfer in the Extreme Near Field. Nature 2015, 528, 387–391. [Google Scholar] [CrossRef] [PubMed]
- Messina, R.; Ben-Abdallah, P. Graphene-Based Photovoltaic Cells for Near-Field Thermal Energy Conversion. Sci. Rep. 2013, 3, 1383. [Google Scholar] [CrossRef] [PubMed]
- Guha, B.; Otey, C.; Poitras, C.B.; Fan, S.H.; Lipson, M. Near-Field Radiative Cooling of Nanostructures. Nano Lett. 2012, 12, 4546–4550. [Google Scholar] [CrossRef] [PubMed]
- Watts, C.M.; Shrekenhamer, D.; Montoya, J.; Lipworth, G.; Hunt, J.; Sleasman, T.; Krishna, S.; Smith, D.R.; Padilla, W.J. Terahertz Compressive Imaging with Metamaterial Spatial Light Modulators. Nat. Photonics 2014, 8, 605–609. [Google Scholar] [CrossRef]
- Challener, W.A.; Peng, C.B.; Itagi, A.V.; Karns, D.; Peng, W.; Peng, Y.G.; Yang, X.M.; Zhu, X.B.; Gokemeijer, N.J.; Hsia, Y.-T.; et al. Heat-Assisted Magnetic Recording by a Near-field Transducer with Efficient Optical Energy Transfer. Nat. Photonics 2009, 3, 220–224. [Google Scholar] [CrossRef]
- Enoch, J.M. History of Mirrors Dating Back 8000 Years. Optom. Vis. Sci. 2006, 83, 775–781. [Google Scholar] [CrossRef] [PubMed]
- Si, G.; Zhao, Y.; Lv, J.; Wang, F.; Liu, H.; Teng, J.; Liu, Y.J. Direct and Accurate Patterning of Plasmonic Nanostructures with Ultrasmall Gaps. Nanoscale 2013, 5, 4309–4313. [Google Scholar] [CrossRef]
- Bogue, R. Sensing with Metamaterials: A Review of Recent Developments. Sensor Rev. 2017, 37, 305–311. [Google Scholar] [CrossRef]
- Luukkonen, O.; Simovski, C.; Granet, G.; Goussetis, G.; Lioubtchenko, D.; Räisänen, A.V.; Tretyakov, S.A. Simple and Accurate Analytical Model of Planar Grids and High-Impedance Surfaces Comprising Metal Strips or Patches. IEEE Trans. Antennas Propag. 2008, 56, 1624–1632. [Google Scholar] [CrossRef]
- Si, G.; Jiang, X.; Lv, J.; Gu, Q.; Wang, F. Fabrication and Characterization of Well-Aligned Plasmonic Nanopillars with Ultrasmall Separations. Nanoscale Res. Lett. 2014, 9, 299. [Google Scholar] [CrossRef]
- Moreau, A.; Ciracì, C.; Mock, J.J.; Hill, R.T.; Wang, Q.; Wiley, B.J.; Chilkoti, A.; Smith, D.R. Controlled- Reflectance Surfaces with Film-Coupled Colloidal Nanoantennas. Nature 2012, 492, 86–89. [Google Scholar] [CrossRef] [PubMed]
- Si, G.; Zhao, Y.; Lv, J.; Lu, M.; Wang, F.; Liu, H.; Xiang, N.; Huang, T.J.; Danner, A.J.; Teng, J.; et al. Reflective Plasmonic Color Filters Based on Lithographically Patterned Silver Nanorod Arrays. Nanoscale 2013, 5, 6243–6248. [Google Scholar] [CrossRef] [PubMed]
- Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Planar Photonics with Metasurfaces. Science 2013, 339, 1232009. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.R.; Li, S.C.; Gu, C.D.; Anwar, S.; Hou, B.; Lai, Y. Electromagnetic Characteristics of Hilbert Curve- Based Metamaterials. Appl. Phys. A-Mater. 2014, 117, 445–450. [Google Scholar] [CrossRef]
- Si, G.; Wang, Q.; Lv, J.; Miao, L.; Wang, F.; Peng, S. Interference Lithography Patterned Large Area Plasmonic Nanodisks for Infrared Detection. Mater. Lett. 2014, 128, 373–375. [Google Scholar] [CrossRef]
- Naheed, M.; Faryad, M.; Mackay, T.G. Electromagnetic Surface Waves Guided by the Planar Interface of Isotropic Chiral Materials. J. Opt. Soc. Am. B 2019, 36, F1–F8. [Google Scholar] [CrossRef]
- Lv, J.; Leong, E.S.P.; Jiang, X.; Kou, S.; Dai, H.; Lin, J.; Liu, Y.J.; Si, G. Plasmon-Enhanced Sensing: Current Status and Prospects. J. Nanomater. 2015, 2015, 474730. [Google Scholar] [CrossRef]
- Zhang, X.; Fan, Y.C.; Qi, L.M.; Li, H.Q. Broadband Plasmonic Metamaterial Absorber with Fish-Scale Structure at Visible Frequencies. Opt. Mater. Express 2016, 6, 2448–2457. [Google Scholar] [CrossRef]
- Fedotov, V.A.; Rogacheva, A.V.; Zheludev, N.I.; Mladyonov, P.L.; Prosvirnin, S.L. Mirror that Does Not Change the Phase of Reflected Waves. Appl. Phys. Lett. 2006, 88, 091119. [Google Scholar] [CrossRef]
- Si, G.; Leong, E.S.P.; Pan, W.; Chum, C.C.; Liu, Y.J. Plasmon-Induced Transparency in Coupled Triangle- Rod Arrays. Nanotechnology 2015, 26, 025201. [Google Scholar] [CrossRef]
- Ni, X.J.; Emani, N.K.; Kildishev, A.V.; Boltasseva, A.; Shalaev, V.M. Broadband Light Bending with Plasmonic Nanoantennas. Science 2012, 335, 427. [Google Scholar] [CrossRef] [PubMed]
- Si, G.; Zhao, Y.; Leong, E.S.P.; Lv, J.; Liu, Y.J. Incident-Angle Dependent Color Tuning from a Single Plasmonic Chip. Nanotechnology 2014, 25, 455203. [Google Scholar] [CrossRef] [PubMed]
- Jiang, X.; Leong, E.S.P.; Liu, Y.J.; Si, G. Tuning Plasmon Resonance in Depth-Variant Plasmonic Nanostructures. Mater. Des. 2016, 96, 64–67. [Google Scholar] [CrossRef]
- Hu, J.Y.; Ghosh, M.; Miller, M.J.; Bohn, P.W. Whole-Cell Biosensing by Siderophore-Based Molecular Recognition and Localized Surface Plasmon Resonance. Anal. Methods 2019, 11, 296–302. [Google Scholar] [CrossRef]
- Anker, J.N.; Hall, W.P.; Lyandres, O.; Shah, N.C.; Zhao, J.; Van Duyne, R.P. Biosensing with Plasmonic Nanosensors. Nat. Mater. 2008, 7, 442–453. [Google Scholar] [CrossRef] [PubMed]
- Hall, W.P.; Modica, J.; Anker, J.; Lin, Y.; Mrksich, M.; Van Duyne, R.P. A Conformation- and Ion-Sensitive Plasmonic Biosensor. Nano Lett. 2011, 11, 1098–1105. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Ma, C.; Zhang, L.; Chen, B.; Chen, L.Y.; Zeng, H.P. Tuning Localized Surface Plasmon Resonance of Nanoporous Gold with a Silica Shell for Surface Enhanced Raman Scattering. Nanomaterials 2019, 9, 251. [Google Scholar] [CrossRef] [PubMed]
- Špringer, T.; Piliarik, M.; Homola, J. Real-Time Monitoring of Biomolecular Interactions in Blood Plasma Using a Surface Plasmon Resonance Biosensor. Anal. Bioanal. Chem. 2010, 398, 1955–1961. [Google Scholar] [CrossRef]
- Ochsenküehn, M.A.; Campbell, C.J. Probing Biomolecular Interactions Using Surface Enhanced Raman Spectroscopy: Label-Free Protein Detection Using a G-Quadruplex DNA Aptamer. Chem. Commun. 2010, 46, 2799–2801. [Google Scholar] [CrossRef][Green Version]
- Rusciano, G.; De Luca, A.C.; Pesce, G.; Sasso, A.; Oliviero, G.; Amato, J.; Borbone, N.; D’Errico, S.; Piccialli, V.; Piccialli, G.; et al. Label-Free Probing of G-Quadruplex Formation by Surface-Enhanced Raman Scattering. Anal. Chem. 2011, 83, 6849–6855. [Google Scholar] [CrossRef]
- Lim, D.-K.; Jeon, K.-S.; Hwang, J.-H.; Kim, H.; Kwon, S.; Suh, Y.D.; Nam, J.-M. Highly Uniform and Reproducible Surface-Enhanced Raman Scattering from DNA-Tailorable Nanoparticles with 1-nm Interior Gap. Nat. Nanotechnol. 2011, 6, 452–460. [Google Scholar] [CrossRef] [PubMed]
- Andrey, L.; Igor, B.; Vladimir, C.; Alexander, E.; Andrey, F.; Andrey, I.; Ilya, K.; Sergey, K.; Alexander, L.; Dmitriy, N.; et al. SERS-Active Dielectric Metamaterials Based on Periodic Nanostructures. Opt. Express 2016, 24, 7133–7150. [Google Scholar]
- Clark, A.W.; Glidle, A.; Cumming, D.R.S.; Cooper, J.M. Plasmonic Split-Ring Resonators as Dichroic Nanophotonic DNA Biosensors. J. Am. Chem. Soc. 2009, 131, 17615–17619. [Google Scholar] [CrossRef] [PubMed]
- Hendry, E.; Carpy, T.; Johnston, J.; Popland, M.; Mikhaylovskiy, R.V.; Lapthorn, A.J.; Kelly, S.M.; Barron, L.D.; Gadegaard, N.; Kadodwala, M. Ultrasensitive Detection and Characterization of Biomolecules Using Superchiral Fields. Nat. Nanotechnol. 2010, 5, 783–787. [Google Scholar] [CrossRef] [PubMed]
- Kabashin, A.V.; Evans, P.; Pastkovsky, S.; Hendren, W.; Wurtz, G.A.; Atkinson, R.; Pollard, R.; Podolskiy, V.A.; Zayats, A.V. Plasmonic Nanorod Metamaterials for Biosensing. Nat. Mater. 2009, 8, 867–871. [Google Scholar] [CrossRef] [PubMed]
- Pryce, I.M.; Kelaita, Y.A.; Aydin, K.; Atwater, H.A. Compliant Metamaterials for Resonantly Enhanced Infrared Absorption Spectroscopy and Refractive Index Sensing. ACS Nano. 2011, 5, 8167–8174. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.H.; Khanikaev, A.B.; Adato, R.; Arju, N.; Yanik, A.A.; Altug, H.; Shvets, G. Fano-Resonant Asymmetric Metamaterials for Ultrasensitive Spectroscopy and Identification of Molecular Monolayers. Nat. Mater. 2012, 11, 69–75. [Google Scholar] [CrossRef]
- Demir, S.M.; Yüksek, Y.; Sabah, C. Investigation of Graphene-Integrated Tunable Metamaterials in THz Regime. Pramana-J. Phys. 2018, 90, 65. [Google Scholar] [CrossRef]
- Meng, Q.L.; Zhang, Y.; Zhong, Z.Q.; Zhang, B. Optically Tuneable Broadband Terahertz Metamaterials Using Photosensitive Semiconductor Material. J. Mod. Opt. 2018, 65, 2086–2092. [Google Scholar] [CrossRef]
- Xu, X.L.; Peng, B.; Li, D.H.; Zhang, J.; Wong, L.M.; Zhang, Q.; Wang, S.J.; Xiong, Q.H. Flexible Visible-Infrared Metamaterials and Their Applications in Highly Sensitive Chemical and Biological Sensing. Nano Lett. 2011, 11, 3232–3238. [Google Scholar] [CrossRef]
- Soukoulis, C.M.; Linden, S.; Wegener, M. Negative Refractive Index at Optical Wavelengths. Science 2007, 315, 47–49. [Google Scholar] [CrossRef] [PubMed]
- Adato, R.; Yanik, A.A.; Amsden, J.J.; Kaplan, D.L.; Omenetto, F.G.; Hong, M.K.; Erramilli, S.; Altug, H. Ultra-Sensitive Vibrational Spectroscopy of Protein Monolayers with Plasmonic Nanoantenna Arrays. Proc. Natl. Acad. Sci. USA 2009, 106, 19227–19232. [Google Scholar] [CrossRef] [PubMed]
- Benz, A.; Krall, M.; Schwarz, S.; Dietze, D.; Detz, H.; Andrews, A.M.; Schrenk, W.; Strasser, G.; Unterrainer, K. Resonant Metamaterial Detectors Based on THz Quantum-Cascade Structures. Sci. Rep. 2014, 4, 4269. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Zhai, S.-Q.; Wang, F.-J.; Liu, J.-Q.; Liu, S.-M.; Zhuo, N.; Zhang, C.-J.; Wang, L.-J.; Liu, F.-Q.; Wang, Z.-G. A Polarization-Dependent Normal Incident Quantum Cascade Detector Enhanced Via Metamaterial Resonator. Nanoscale Res. Lett. 2016, 11, 536. [Google Scholar] [CrossRef] [PubMed]
- Rogalski, A.; Antoszewski, J.; Faraone, L. Third-Generation Infrared Photodetector Arrays. J. Appl. Phys. 2009, 105, 091101. [Google Scholar] [CrossRef]
- Levine, B.F. Quantum Well Infrared Photodetectors. J. Appl. Phys. 1993, 74, R1–R81. [Google Scholar] [CrossRef]
- Liu, H.C.; Li, J.M.; Buchanan, M.; Wasilewski, Z.R. High-Frequency Quantum-Well Infrared Photodetectors Measured by Microwave-Rectification Technique. IEEE J. Quantum Elect. 1996, 32, 1024–1028. [Google Scholar] [CrossRef]
- Zhang, S.Y.; Revin, D.G.; Cockburn, J.W.; Kennedy, K.; Krysa, A.B.; Hopkinson, M. λ ∼ 3.1 μm Room Temperature InGaAs/AlAsSb/InP Quantum Cascade Lasers. Appl. Phys. Lett. 2009, 94, 031106. [Google Scholar] [CrossRef]
- Walther, C.; Fischer, M.; Scalari, G.; Terazzi, R.; Hoyler, N.; Faist, J. Quantum Cascade Lasers Operating From 1.2 to 1.6 THz. Appl. Phys. Lett. 2007, 91, 131122. [Google Scholar] [CrossRef]
- Wang, X.F.; Kim, S.-S.; Roßbach, R.; Jetter, M.; Michler, P.; Mizaikoff, B. Ultra-sensitive Mid-infrared Evanescent Field Sensors Combining Thin-Film Strip Waveguides with Quantum Cascade Lasers. Analyst 2012, 137, 2322. [Google Scholar] [CrossRef]
- Benz, A.; Deutsch, C.; Brandstetter, M.; Andrews, A.M.; Klang, P.; Detz, H.; Schrenk, W.; Strasser, G.; Unterrainer, K. Terahertz Active Photonic Crystals for Condensed Gas Sensing. Sensors 2011, 11, 6003–6014. [Google Scholar] [CrossRef] [PubMed]
- Gendron, L.; Carras, M.; Huynh, A.; Ortiz, V.; Koeniguer, C.; Berger, V. Quantum Cascade Photodetector. Appl. Phys. Lett. 2004, 85, 2824–2826. [Google Scholar] [CrossRef]
- Giorgetta, F.R.; Baumann, E.; Graf, M.; Yang, Q.K.; Manz, C.; Köhler, K.; Beere, H.E.; Ritchie, D.A.; Linfield, E.; Davies, A.G.; et al. Quantum Cascade Detectors. IEEE J. Quantum Elect. 2009, 45, 1039–1052. [Google Scholar] [CrossRef]
- Ravikumar, A.P.; De Jesus, J.; Tamargo, M.C.; Gmachl, C.F. High Performance, Room Temperature, Broadband II-VI Quantum Cascade Detector. Appl. Phys. Lett. 2015, 107, 141105. [Google Scholar] [CrossRef]
- Ravikumar, A.P.; Sivco, D.; Gmachl, C.F. Wavelength Independent Normal Incident Quantum Cascade Detectors. Opt. Express 2016, 24, 25269–25276. [Google Scholar] [CrossRef] [PubMed]
- Harrer, A.; Szedlak, R.; Schwarz, B.; Moser, H.; Zederbauer, T.; MacFarland, D.; Detz, H.; Andrews, A.M.; Schrenk, W.; Lendl, B.; et al. Mid-Infrared Surface Transmitting and Detecting Quantum Cascade Device for Gas-Sensing. Sci. Rep. 2016, 6, 21795. [Google Scholar] [CrossRef] [PubMed]
- Graf, M.; Hoyler, N.; Giovannini, M.; Faist, J.; Hofstetter, D. InP-Based Quantum Cascade Detectors in the Mid-Infrared. Appl. Phys. Lett. 2006, 88, 241118. [Google Scholar] [CrossRef]
- Hinds, S.; Buchanan, M.; Dudek, R.; Haffouz, S.; Laframboise, S.; Wasilewski, Z.; Liu, H.C. Near-Room- Temperature Mid-Infrared Quantum Well Photodetector. Adv. Mater. 2011, 23, 5536–5539. [Google Scholar] [CrossRef]
- Wang, X.J.; Liu, J.Q.; Zhai, S.Q.; Liu, F.Q.; Wang, Z.G. Room Temperature Quantum Cascade Detector Operating at 4.3 μm. J. Semicond. 1040, 35, 104009. [Google Scholar] [CrossRef]
- Narayanaswamy, A.; Shen, S.; Chen, G. Near-Field Radiative Heat Transfer between a Sphere and a Substrate. Phys. Rev. B 2008, 78, 115303. [Google Scholar] [CrossRef]
- Narayanaswamy, A.; Chen, G. Thermal Near-Field Radiative Transfer between Two Spheres. Phys. Rev. B 2008, 77, 075125. [Google Scholar] [CrossRef]
- Shen, S.; Narayanaswamy, A.; Chen, G. Surface Phonon Polaritons Mediated Energy Transfer between Nanoscale Gaps. Nano Lett. 2009, 9, 2909–2913. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.W.; Li, P.F.; Liu, B.A.; Shen, S. Tuning Near Field Radiation by Doped Silicon. Appl. Phys. Lett. 2013, 102, 183114. [Google Scholar] [CrossRef]
- Basu, S.; Francoeur, M. Near-Field Radiative Transfer Based Thermal Rectification Using Doped Silicon. Appl. Phys. Lett. 2011, 98, 113106. [Google Scholar] [CrossRef]
- Dedkov, G.V.; Kyasov, A.A. Radiative Heat Exchange of Spherical Particles with Plates of a Metal and an Insulator. Phys. Solid State + 2011, 53, 669–678. [Google Scholar] [CrossRef]
- Dyakov, S.A.; Dai, J.; Yan, M.; Qiu, M. Near Field Thermal Memory Device. arXiv 2014, arXiv:1408.5831. [Google Scholar]
- Zhang, Z.J.; Liang, Y.Z.; Xu, T. Research Advances of Hyperbolic Metamaterials and Metasurfaces. Opto- Elec. Eng. 2017, 44, 276–288. [Google Scholar]
- Forati, E.; Hanson, G.W.; Yakovlev, A.B.; Alu, A. Planar Hyperlens Based on a Modulated Graphene Monolayer. Phys. Rev. B 2014, 89, 081410. [Google Scholar] [CrossRef]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic Metamaterials. Nat. Photonics 2013, 7, 948–957. [Google Scholar] [CrossRef]
- Liu, B.A.; Shen, S. Broadband Near-Field Radiative Thermal Emitter/Absorber Based on Hyperbolic Metamaterials: Direct Numerical Simulation by the Wiener Chaos Expansion Method. Phys. Rev. B 2013, 87, 115403. [Google Scholar] [CrossRef]
- Yao, J.; Wang, Y.; Tsai, K.-T.; Liu, Z.W.; Yin, X.B.; Bartal, G.; Stacy, A.M.; Wang, Y.-L.; Zhang, X. Design, Fabrication and Characterization of Indefinite Metamaterials of Nanowires. Philos. Trans. A. Math. Phys. Eng. Sci. 2011, 369, 3434–3446. [Google Scholar] [CrossRef] [PubMed]
- Qiao, F.; Liang, Q.C.; Yang, J.; Chen, Z.Y.; Xu, Q. A Facile Approach of Fabricating Various ZnO Microstructures via Electrochemical Deposition. J. Electron. Mater. 2019, 48, 2338–2342. [Google Scholar] [CrossRef]
- Chen, R.K.; Lu, M.-C.; Srinivasan, V.; Wang, Z.J.; Cho, H.H.; Majumdar, A. Nanowires for Enhanced Boiling Heat Transfer. Nano Lett. 2009, 9, 548–553. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.W.; Liu, B.A.; Li, P.F.; Ng, L.Y.; Shen, S. Near-Field Energy Extraction with Hyperbolic Metamaterials. Nano Lett. 2015, 15, 1217–1221. [Google Scholar] [CrossRef] [PubMed]
- Schwanecke, A.S.; Fedotov, V.A.; Khardikov, V.V.; Prosvirnin, S.L.; Chen, Y.; Zheludev, N.I. Rapid Communication: Optical Magnetic Mirrors. J. Opt. A-Pure Appl. Op. 2007, 9, 1–2. [Google Scholar] [CrossRef]
- Esfandyarpour, M.; Garnett, E.C.; Cui, Y.; McGehee, M.D.; Brongersma, M.L. Metamaterial Mirrors in Optoelectronic Devices. Nat. Nanotechnol. 2014, 9, 542–547. [Google Scholar] [CrossRef]
- Lee, S.; Kim, J. Design of Optical Metamaterial Mirror with Metallic Nanoparticles for Floating-Gate Graphene Optoelectronic Devices. Opt. Express 2015, 23, 21809–21818. [Google Scholar] [CrossRef]
- Sievenpiper, D.; Zhang, L.J.; Broas, R.F.J.; Alexópolous, N.G.; Yablonovitch, E. High-Impedance Electromagnetic Surfaces with a Forbidden Frequency Band. IEEE T. Microw. Theory 1999, 47, 2059–2074. [Google Scholar] [CrossRef]
- Jang, S.; Hwang, E.; Lee, Y.; Lee, S.; Cho, J.H. Multifunctional Graphene Optoelectronic Devices Capable of Detecting and Storing Photonic Signals. Nano Lett. 2015, 15, 2542–2547. [Google Scholar] [CrossRef]
- Girvan, A.C.; Teng, Y.; Casson, L.K.; Thomas, S.D.; Jüliger, S.; Ball, M.W.; Klein, J.B.; Pierce Jr, W.M.; Barve, S.S.; Bates, P.J. AGRO100 Inhibits Activation of Nuclear Factor-ĸB (NF-ĸB) by Forming a Complex with NF-ĸB Essential Modulator (NEMO) and Nucleolin. Mol. Cancer Ther. 2006, 5, 1790–1799. [Google Scholar] [CrossRef]
- Bhasikuttan, A.C.; Mohanty, J. Targeting G-Quadruplex Structures with Extrinsic Fluorogenic Dyes: Promising Fluorescence Sensors. Chem. Commun. 2015, 51, 7581–7597. [Google Scholar] [CrossRef] [PubMed]
- Biffi, G.; Di Antonio, M.; Tannahill, D.; Balasubramanian, S. Visualization and Selective Chemical Targeting of RNA G-Quadruplex Structures in the Cytoplasm of Human Cells. Nat. Chem. 2014, 6, 75–80. [Google Scholar] [CrossRef]
- Muller, S.; Kumari, S.; Rodriguez, R.; Balasubramanian, S. Small-Molecule-Mediated G-Quadruplex Isolation from Human Cells. Nat.Chem. 2010, 2, 1095–1098. [Google Scholar] [CrossRef]
- Olejko, L.; Cywinski, P.J.; Bald, I. Ion-Selective Formation of a Guanine Quadruplex on DNA Origami Structures. Angew. Chem. Int. Ed. 2015, 54, 673–677. [Google Scholar] [CrossRef]
- Koirala, D.; Dhakal, S.; Ashbridge, B.; Sannohe, Y.; Rodriguez, R.; Sugiyama, H.; Balasubramanian, S.; Mao, H.B. A Single-Molecule Platform for Investigation of Interactions between G-Quadruplexes and Small-Molecule Ligands. Nat. Chem. 2011, 3, 782–787. [Google Scholar] [CrossRef] [PubMed]
- He, H.Z.; Chan, D.S.; Leung, C.H.; Ma, D.L. G-Quadruplexes for Luminescent Sensing and Logic Gates. Nucleic Acids Res. 2013, 41, 4345–4359. [Google Scholar] [CrossRef]
- Soundararajan, S.; Wang, L.; Sridharan, V.; Chen, W.W.; Courtenay-Luck, N.; Jones, D.; Spicer, E.K.; Fernandes, D.J. Plasma Membrane Nucleolin is a Receptor for the Anticancer Aptamer AS1411 in MV4-11 Leukemia Cells. Mol. Pharmacol. 2009, 76, 984–991. [Google Scholar] [CrossRef] [PubMed]
- Hanakahi, L.A.; Sun, H.; Maizels, N. High Affinity Interactions of Nucleolin with G-G-Paired rDNA. J. Biol. Chem. 1999, 274, 15908–15912. [Google Scholar] [CrossRef] [PubMed]
- Bates, P.J.; Laber, D.A.; Miller, D.M.; Thomas, S.D.; Trent, J.O. Discovery and Development of the G-Rich Oligonucleotide AS1411 as a Novel Treatment for Cancer. Exp. Mol. Pathol. 2009, 86, 151–164. [Google Scholar] [CrossRef] [PubMed]
- Cao, C.; Zhang, J.; Wen, X.L.; Dodson, S.L.; Dao, N.T.; Wong, L.M.; Wang, S.J.; Li, S.Z.; Phan, A.T.; Xiong, Q.H. Metamaterials-Based Label-Free Nanosensor for Conformation and Affinity Biosensing. ACS Nano 2013, 7, 7583–7591. [Google Scholar] [CrossRef]
- Zheludev, N.I. The Road Ahead for Metamaterials. Science 2010, 328, 582–583. [Google Scholar] [CrossRef]
- Qiu, H.S.; Kurihara, T.; Harada, H.; Kato, K.; Takano, K.; Suemoto, T.; Tani, M.; Sarukura, N.; Yoshimura, M.; Nakajima, M. Enhancing Terahertz Magnetic Near Field Induced by a Micro-Split-Ring Resonator with a Tapered Waveguide. Opt. Lett. 2018, 43, 1658–1661. [Google Scholar] [CrossRef]
- Nasarov, M.M.; Zarubin, A.N.; Sarkisov, S.Y.; Tolbanov, O.P.; Tyazhev, A.V. Influence of Split-Ring Resonators on the Terahertz Transmission of a Planar Waveguide. Russ. Phys. J. 2015, 58, 562–566. [Google Scholar] [CrossRef]
- Haes, A.J.; Zou, S.L.; Schatz, G.C.; Van Duyne, R.P. Nanoscale Optical Biosensor: Short Range Distance Dependence of the Localized Surface Plasmon Resonance of Noble Metal Nanoparticles. J. Phys. Chem. B 2004, 108, 6961–6968. [Google Scholar] [CrossRef]
- Rossi, S.; Gazzola, E.; Capaldo, P.; Borile, G.; Romanato, F. Grating-Coupled Surface Plasmon Resonance (GC-SPR) Optimization for Phase-Interrogation Biosensing in a Microfluidic Chamber. Sensors 2018, 18, 1621. [Google Scholar] [CrossRef]
- Rahman, M.S.; Rikta, K.A.; Bin Bashar, L.; Anower, M.S. Numerical Analysis of Graphene Coated Surface Plasmon Resonance Biosensors for Biomedical Applications. Optik - Int. J. Light Electron Opt. 2018, 156, 384–390. [Google Scholar] [CrossRef]
- Chen, S.N.; Dong, L.J.; Yan, M.; Dai, Z.X.; Sun, C.H.; Li, X. Rapid and Sensitive Biomaker Detection Using Molecular Imprinting Polymer Hydrogel and Surface-Enhanced Raman Scattering. R. Soc. Open Sci. 2018, 5, 171488. [Google Scholar] [CrossRef]
- Raphael, M.P.; Christodoulides, J.A.; Delehanty, J.B.; Long, J.P.; Pehrsson, P.E.; Byers, J.M. Quantitative LSPR Imaging for Biosensing with Single Nanostructure Resolution. Biophys. J. 2013, 104, 30–36. [Google Scholar] [CrossRef][Green Version]
- Pagba, C.V.; Lane, S.M.; Wachsmann-Hogiu, S. Conformational Changes in Quadruplex Oligonucleotide Structures Probed by Raman Spectroscopy. Biomed. Opt. Express 2011, 2, 207–217. [Google Scholar] [CrossRef]
- Wei, C.Y.; Jia, G.Q.; Yuan, J.L.; Feng, Z.C.; Li, C. A Spectroscopic Study on the Interactions of Porphyrin with G-Quadruplex DNAs. Biochemistry 2006, 45, 6681–6691. [Google Scholar] [CrossRef] [PubMed]
- Chan, C.-Y.; Umar, M.I.; Kwok, C.K. Spectroscopic Analysis Reveals the Effect of a Single Nucleotide Bulge on G-Quadruplex Structures. Chem. Commun. 2019, 55, 2616–2619. [Google Scholar] [CrossRef] [PubMed]
- Di Fonzo, S.; Bottari, C.; Brady, J.W.; Tavagnacco, L.; Caterino, M.; Petraccone, L.; Amato, J.; Giancola, C.; Cesàro, A. Crowding and Conformation Interplay on Human DNA G-Quadruplex by Ultraviolet Resonant Raman Scattering. Phys.Chem. Chem. Phys. 2019, 21, 2093–2101. [Google Scholar] [CrossRef] [PubMed]
- Qiu, S.Y.; Zhao, F.S.; Zenasni, O.; Li, J.T.; Shih, W.-C. Nanoporous Gold Disks Functionalized with Stabilized G-Quadruplex Moieties for Sensing Small Molecules. ACS Appl. Mater. Interfaces 2016, 8, 29968–29976. [Google Scholar] [CrossRef] [PubMed]
- Mohanty, J.; Barooah, N.; Dhamodharan, V.; Harikrishna, S.; Pradeepkumar, P.I.; Bhasikuttan, A.C. Thioflavin T as an Efficient Inducer and Selective Fluorescent Sensor for the Human Telomeric G-Quadruplex DNA. J. Am. Chem. Soc. 2013, 135, 367–376. [Google Scholar] [CrossRef] [PubMed]
- Das, J.; Ivanov, I.; Montermini, L.; Rak, J.; Sargent, E.H.; Kelley, S.O. An Electrochemical Clamp Assay for Direct, Rapid Analysis of Circulating Nucleic Acids in Serum. Nat. Chem. 2015, 7, 569–575. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Y.; Yu, W.S.; Pei, L.; Lai, K.Q.; Rasco, B.A.; Huang, Y.Q. Rapid Analysis of Malachite Green and Leucomalachite Green in Fish Muscles with Surface-Enhanced Resonance Raman Scattering. Food Chem. 2015, 169, 80–84. [Google Scholar] [CrossRef] [PubMed]
- Pedireddy, S.; Lee, H.K.; Tjiu, W.W.; Phang, I.Y.; Tan, H.R.; Chua, S.Q.; Troadec, C.; Ling, X.Y. One-Step Synthesis of Zero-Dimensional Hollow Nanoporous Gold Nanoparticles with Enhanced Methanol Electrooxidation Performance. Nat. Commun. 2014, 5, 4947. [Google Scholar] [CrossRef]
- Niu, S.Z.; Liu, J.Q.; Zhao, Y.; Cheng, F.M.; Zhang, J.C.; Wang, L.J.; Liu, S.M.; Liu, F.Q.; Wang, Z.G.; Wei, Z.P.; et al. High-Performance Bound-to-Continuum Quantum Cascade Lasers at λ~8 μm. J. Nanosci. Nanotechno. 2018, 18, 7498–7501. [Google Scholar] [CrossRef]
- Borri, S.; Insero, G.; Santambrogio, G.; Mazzotti, D.; Cappelli, F.; Galli, I.; Galzerano, G.; Marangoni, M.; Laporta, P.; Di Sarno, V.; et al. High-Precision Molecular Spectroscopy in the Mid-Infrared Using Quantum Cascade Lasers. Appl. Phys. B 2019, 125, 18. [Google Scholar] [CrossRef]
- Scalari, G.; Maissen, C.; Turčinková, D.; Hagenmüller, D.; De Liberato, S.; Ciuti, C.; Reichl, C.; Schuh, D.; Wegscheider, W.; Beck, M.; et al. Ultrastrong Coupling of the Cyclotron Transition of a 2D Electron Gas to a THz Metamaterial. Science 2012, 335, 1323–1326. [Google Scholar] [CrossRef]
- Geiser, M.; Walther, C.; Scalari, G.; Beck, M.; Fischer, M.; Nevou, L.; Faist, J. Strong Light-Matter Coupling at Terahertz Frequencies at Room Temperature in Electronic LC Resonators. Appl. Phys. Lett. 2010, 97, 191107. [Google Scholar] [CrossRef]
- Dietze, D.; Benz, A.; Strasser, G.; Unterrainer, K.; Darmo, J. Terahertz Meta-Atoms Coupled to a Quantum Well Intersubband Transition. Opt. Express 2011, 19, 13700–13706. [Google Scholar] [CrossRef] [PubMed]
- Albo, A.; Fekete, D.; Bahir, G. Photocurrent Spectroscopy of Intersubband Transitions in GaInAsN/(Al)GaAs Asymmetric Quantum Well Infrared Photodetectors. J. Appl. Phys. 2012, 112, 084502. [Google Scholar] [CrossRef]
- Choi, K.-K.; Sun, J.; Olver, K.A.; Fu, R. Parameter Study of Resonator-Quantum Well Infrared Photodetectors. IEEE J. Quantum Elect. 2017, 53, 4000410. [Google Scholar] [CrossRef]
- Ravikumar, A.P.; Chen, G.P.; Zhao, K.L.; Tian, Y.; Prucnal, P.; Tamargo, M.C.; Gmachl, C.F.; Shen, A.D. Room Temperature and High Responsivity Short Wavelength II-VI Quantum Well Infrared Photodetector. Appl. Phys. Lett. 2013, 102, 161107. [Google Scholar] [CrossRef]
- Sakr, S.; Giraud, E.; Dussaigne, A.; Tchernycheva, M.; Grandjean, N.; Julien, F.H. Two-Color GaN/AlGaN Quantum Cascade Detector at Short Infrared Wavelengths of 1 and 1.7 μm. Appl. Phys. Lett. 2012, 100, 181103. [Google Scholar] [CrossRef]
- Barve, A.V.; Krishna, S. Photovoltaic Quantum Dot Quantum Cascade Infrared Photodetector. Appl. Phys. Lett. 2012, 100, 021105. [Google Scholar] [CrossRef]
- Zhai, S.Q.; Liu, J.Q.; Wang, X.J.; Zhuo, N.; Liu, F.Q.; Wang, Z.G.; Liu, X.H.; Li, N.; Lu, W. 19 μm Quantum Cascade Infrared Photodetectors. Appl. Phys. Lett. 2013, 102, 191120. [Google Scholar] [CrossRef]
- Sakr, S.; Crozat, P.; Gacemi, D.; Kotsar, Y.; Pesach, A.; Quach, P.; Isac, N.; Tchernycheva, M.; Vivien, L.; Bahir, G.; et al. GaN/AlGaN Waveguide Quantum Cascade Photodetectors at λ ≈ 1.55 μm with Enhanced Responsivity and 40 GHz Frequency Bandwidth. Appl. Phys. Lett. 2013, 102, 011135. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Lv, J.; Gu, Q.; Hu, S.; Li, Z.; Jiang, X.; Ying, Y.; Si, G. Metadevices with Potential Practical Applications. Molecules 2019, 24, 2651. https://doi.org/10.3390/molecules24142651
Li Y, Lv J, Gu Q, Hu S, Li Z, Jiang X, Ying Y, Si G. Metadevices with Potential Practical Applications. Molecules. 2019; 24(14):2651. https://doi.org/10.3390/molecules24142651
Chicago/Turabian StyleLi, Yafei, Jiangtao Lv, Qiongchan Gu, Sheng Hu, Zhigang Li, Xiaoxiao Jiang, Yu Ying, and Guangyuan Si. 2019. "Metadevices with Potential Practical Applications" Molecules 24, no. 14: 2651. https://doi.org/10.3390/molecules24142651
APA StyleLi, Y., Lv, J., Gu, Q., Hu, S., Li, Z., Jiang, X., Ying, Y., & Si, G. (2019). Metadevices with Potential Practical Applications. Molecules, 24(14), 2651. https://doi.org/10.3390/molecules24142651




