Adaptive QM/MM for Molecular Dynamics Simulations: 5. On the Energy-Conserved Permuted Adaptive-Partitioning Schemes
Abstract
1. Introduction
2. Materials and Methods
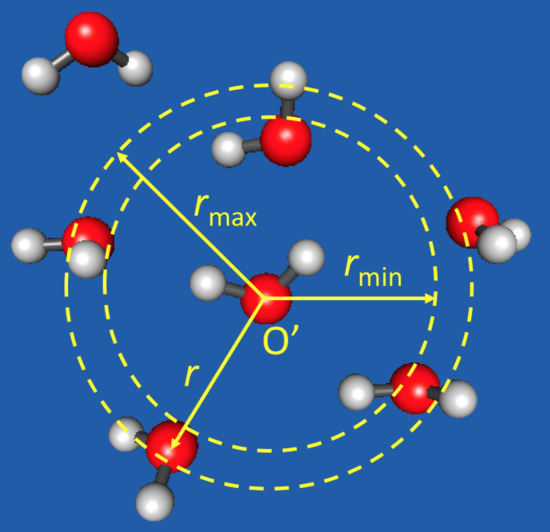
2.1. The PAP Algorithm
2.2. HAMBC Expression for PAP
2.2.1. A Mean-Field Treatment of the Individual Group Corrections
2.2.2. Calculations of and
2.2.3. Many-Body Contributions to
2.2.4. Effects Due to Truncation in mPAP Hamiltonian
2.3. Simulation Details
3. Results
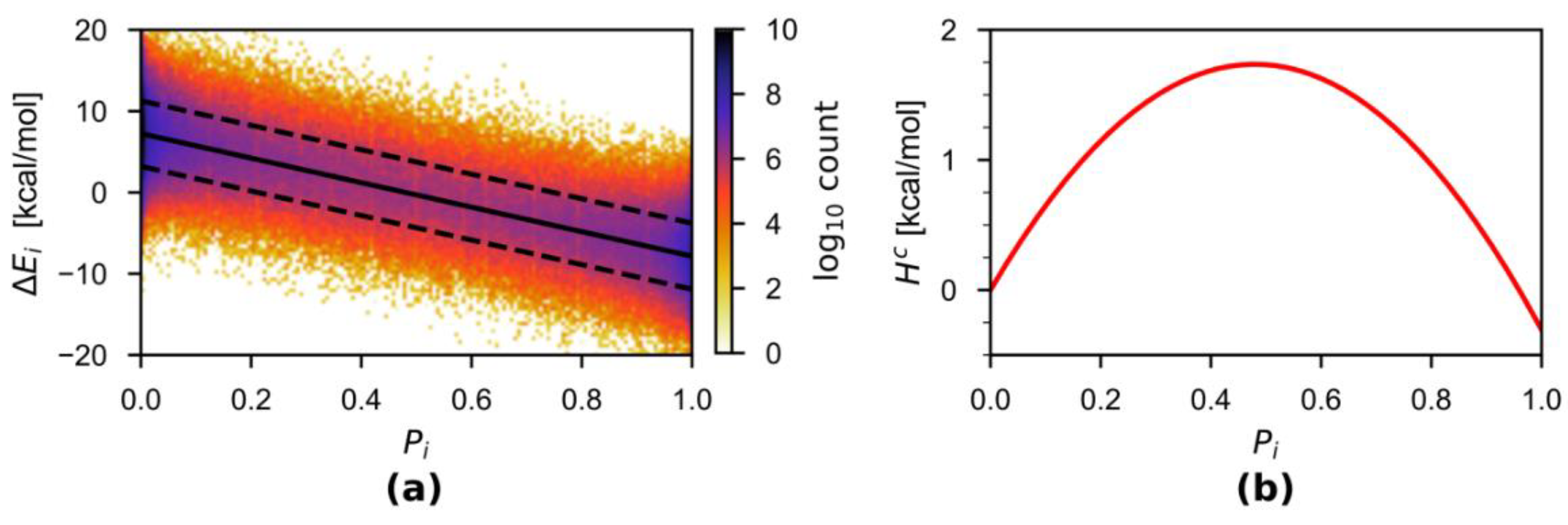
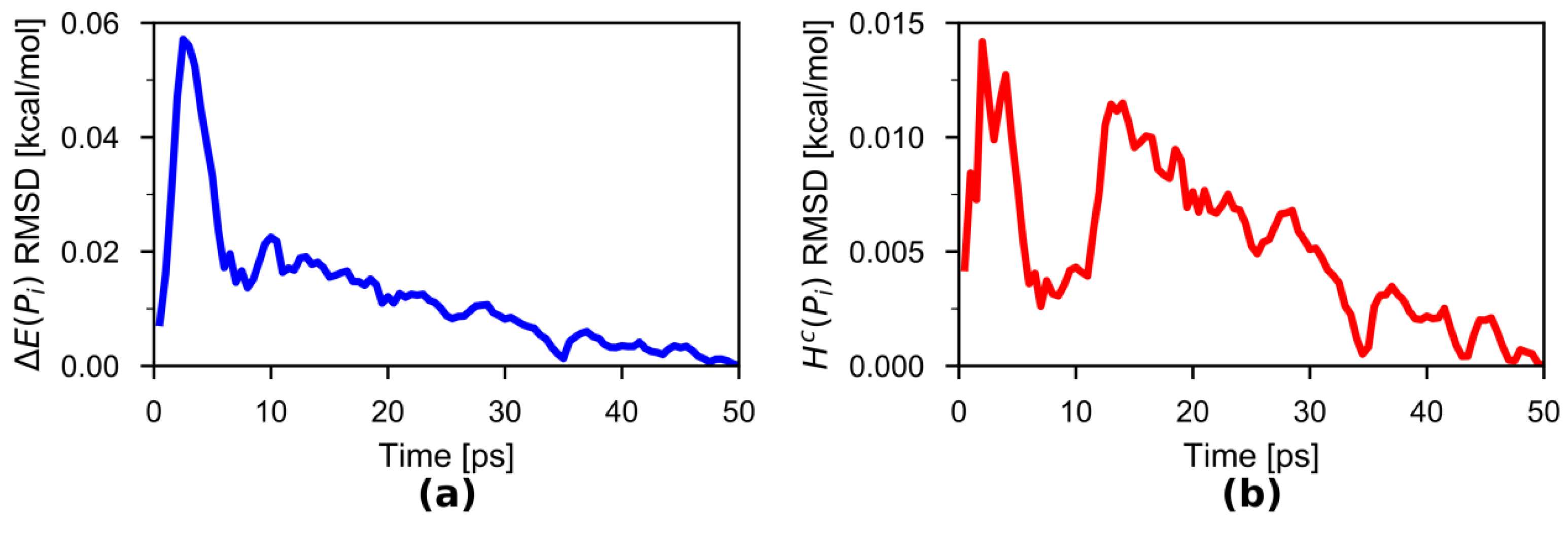
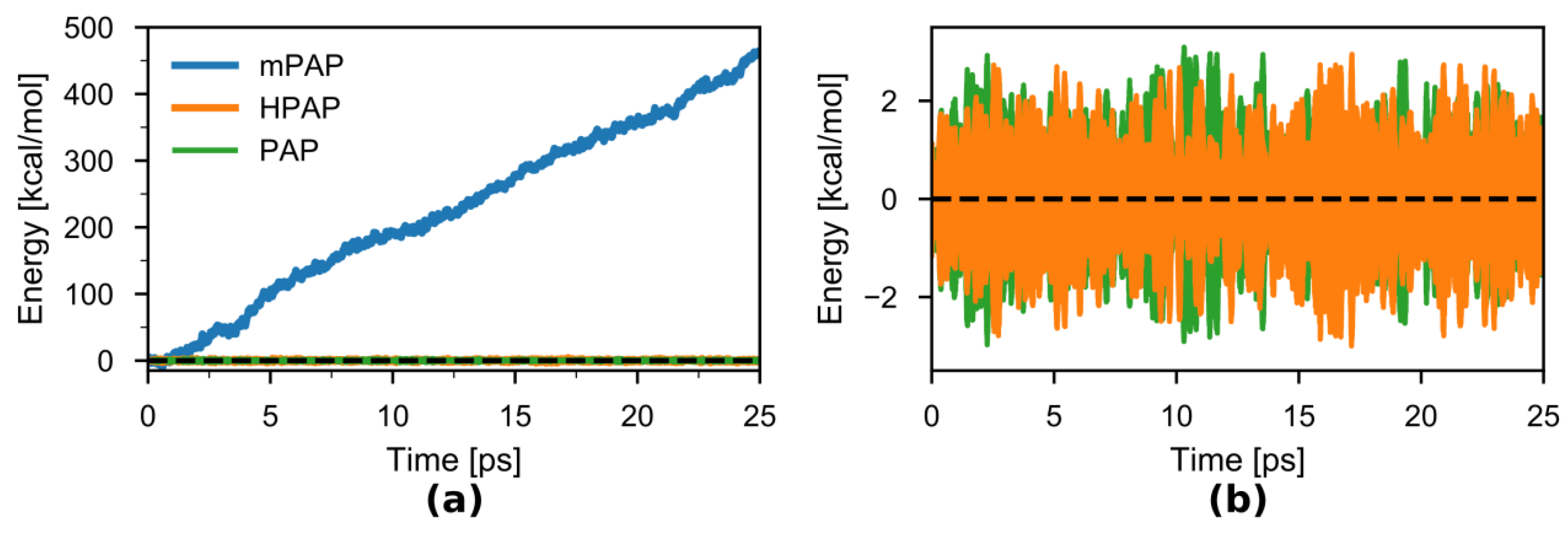
3.1. HAMBC Correction Term
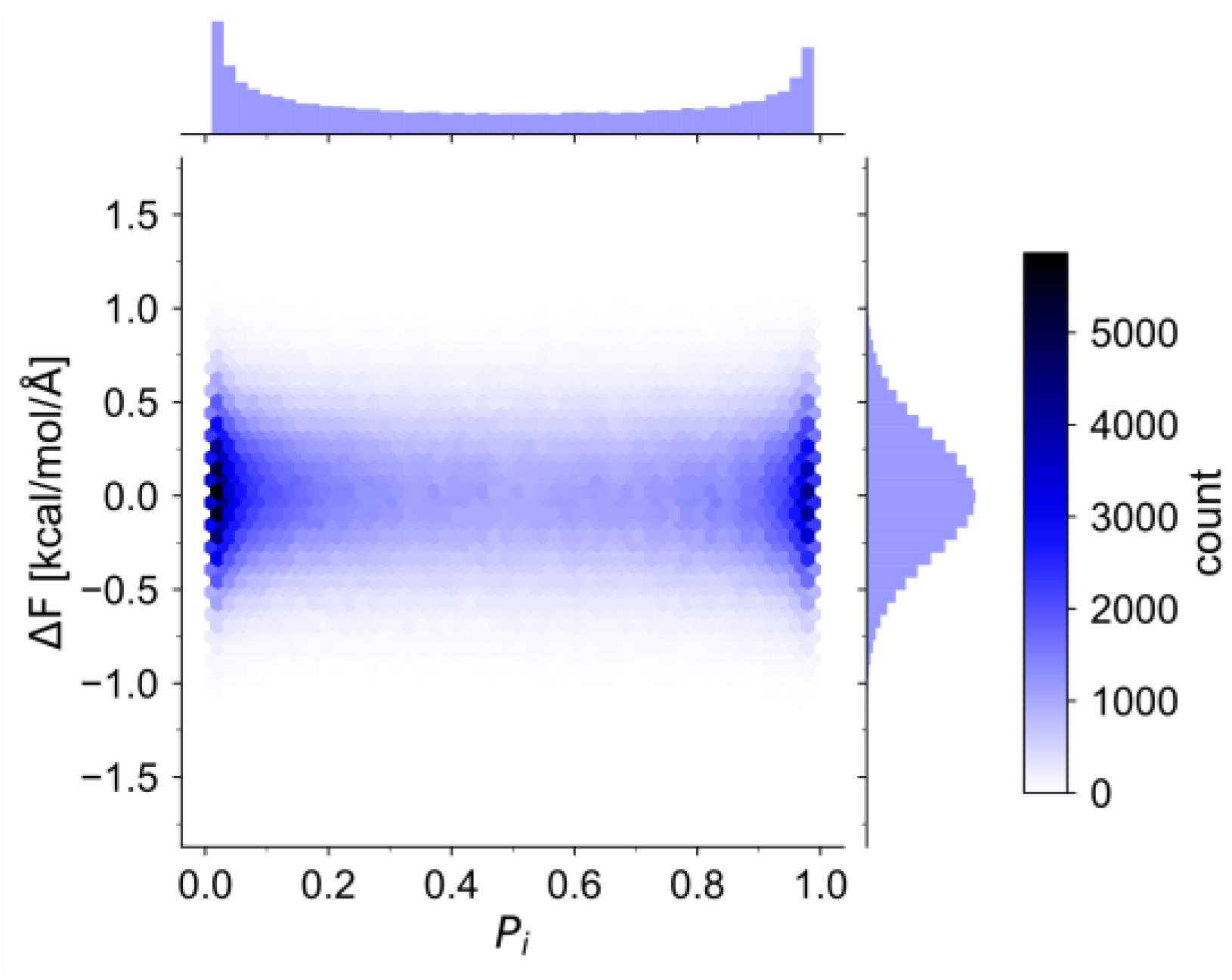
3.2. Solvation Structures
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Warshel, A.; Levitt, M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol. 1976, 103, 227–249. [Google Scholar] [CrossRef]
- Singh, U.C.; Kollmann, P.A. A combined ab initio quantum mechanical and molecular mechanical method for carrying out simulations on complex molecular systems: Applications to the CH3Cl + Cl− exchange reaction and gas phase protonation of polyethers. J. Comput. Chem. 1986, 7, 718–730. [Google Scholar] [CrossRef]
- Field, M.J.; Bash, P.A.; Karplus, M. A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations. J. Comput. Chem. 1990, 11, 700–733. [Google Scholar] [CrossRef]
- Gao, J. Methods and applications of combined quantum mechanical and molecular mechanical potentials. Rev. Comput. Chem. 1996, 7, 119–185. [Google Scholar]
- Monard, G.; Merz, K.M., Jr. Combined quantum mechanical/molecular mechanical methodologies applied to biomolecular systems. Acc. Chem. Res. 1999, 32, 904–911. [Google Scholar] [CrossRef]
- Hammes-Schiffer, S. Theoretical perspectives on proton-coupled electron transfer reactions. Acc. Chem. Res. 2000, 34, 273–281. [Google Scholar] [CrossRef]
- Sherwood, P. Hybrid quantum mechanics/molecular mechanics approaches. In Modern Methods and Algorithms of Quantum Chemistry; Grotendorst, J., Ed.; John von Neumann-Instituts: Jülich, German, 2000; Volume 3, pp. 285–305. [Google Scholar]
- Gao, J.; Truhlar, D.G. Quantum mechanical methods for enzyme kinetics. Annu. Rev. Phys. Chem. 2002, 53, 467–505. [Google Scholar] [CrossRef] [PubMed]
- Riccardi, D.; Schaefer, P.; Yang, Y.; Yu, H.; Ghosh, N.; Prat-Resina, X.; König, P.; Li, G.; Xu, D.; Guo, H.; et al. Development of effective quantum mechanical/molecular mechanical (QM/MM) methods for complex biological process. J. Phys. Chem. B 2006, 110, 6458–6469. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Truhlar, D.G. QM/MM: What have we learned, where are we, and where do we go from here? Theor. Chem. Acc. 2007, 117, 185–199. [Google Scholar] [CrossRef]
- Senn, H.M.; Thiel, W. QM/MM methods for biological systems. Top. Curr. Chem. 2007, 268, 173–290. [Google Scholar]
- Hu, H.; Yang, W. Free energies of chemical reactions in solution and in enzymes with ab initio quantum mechanics/molecular mechanics methods. Annu. Rev. Phys. Chem. 2008, 59, 573–601. [Google Scholar] [CrossRef] [PubMed]
- Sherwood, P.; Brooks, B.R.; Sansom, M.S.P. Multiscale methods for macromolecular simulations. Curr. Opin. Struct. Biol. 2008, 18, 630–640. [Google Scholar] [CrossRef] [PubMed]
- Sabin, J.R.; Brändas, E. Combining Quantum Mechanics and Molecular Mechanics. Some Recent Progresses in QM/MM Methods; Academic Press: San Diego, CA, USA, 2010; pp. 1–416. [Google Scholar]
- Ferrer, S.; Ruiz-Pernia, J.; Marti, S.; Moliner, V.; Tunon, I.; Bertran, J.; Andres, J. Hybrid schemes based on quantum mechanics/molecular mechanics simulations: Goals to success, problems, and perspectives. In Advances in Protein Chemistry and Structural Biology, Vol. 85: Computational Chemistry Methods in Structural Biology; Christov, C., Ed.; Elsevier Academic Press Inc.: San Diego, CA, USA, 2011; Volume 85, pp. 81–142. [Google Scholar]
- Menikarachchi, L.C.; Gascon, J.A. QM/MM approaches in medicinal chemistry research. Curr. Top. Med. Chem. 2010, 10, 46–54. [Google Scholar] [CrossRef] [PubMed]
- Wallrapp, F.H.; Guallar, V. Mixed quantum mechanics and molecular mechanics methods: Looking inside proteins. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 315–322. [Google Scholar] [CrossRef]
- Woodcock, H.L.; Miller, B.T.; Hodoscek, M.; Okur, A.; Larkin, J.D.; Ponder, J.W.; Brooks, B.R. MSCALE: A general utility for multiscale modeling. J. Chem. Theory Comput. 2011, 7, 1208–1219. [Google Scholar] [CrossRef] [PubMed]
- Chung, L.W.; Hirao, H.; Li, X.; Morokuma, K. The ONIOM method: Its foundation and applications to metalloenzymes and photobiology. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 327–350. [Google Scholar] [CrossRef]
- Lonsdale, R.; Harvey, J.N.; Mulholland, A.J. A practical guide to modelling enzyme-catalysed reactions. Chem. Soc. Rev. 2012, 41, 3025–3038. [Google Scholar] [CrossRef] [PubMed]
- Monari, A.; Rivail, J.-L.; Assfeld, X. Theoretical modeling of large molecular systems. Advances in the local self consistent field method for mixed quantum mechanics/molecular mechanics calculations. Acc. Chem. Res. 2012, 46, 596–603. [Google Scholar] [CrossRef] [PubMed]
- Wu, R.; Cao, Z.; Zhang, Y. Computational simulations of zinc enzyme: Challenges and recent advances. Prog. Chem. 2012, 24, 1175–1184. [Google Scholar]
- Mennucci, B. Modeling environment effects on spectroscopies through QM/classical models. Phys. Chem. Chem. Phys. 2013, 15, 6583–6594. [Google Scholar] [CrossRef] [PubMed]
- Meier, K.; Choutko, A.; Dolenc, J.; Eichenberger, A.P.; Riniker, S.; van Gunsteren, W.F. Multi-resolution simulation of biomolecular systems: A review of methodological issues. Angew. Chem. Int. Ed. 2013, 52, 2820–2834. [Google Scholar] [CrossRef] [PubMed]
- Pezeshki, S.; Lin, H. Recent developments in QM/MM methods towards open-boundary multi-scale simulations. Mol. Simulat. 2015, 41, 168–189. [Google Scholar] [CrossRef]
- Duarte, F.; Amrein, B.A.; Blaha-Nelson, D.; Kamerlin, S.C.L. Recent advances in QM/MM free energy calculations using reference potentials. BBA-Gen. Subj. 2015, 1850, 954–965. [Google Scholar] [CrossRef] [PubMed]
- Kerdcharoen, T.; Liedl, K.R.; Rode, B.M. A QM/MM simulation method applied to the solution of Li+ in liquid ammonia. Chem. Phys. 1996, 211, 313–323. [Google Scholar] [CrossRef]
- Kerdcharoen, T.; Morokuma, K. ONIOM-XS: An extension of the ONIOM method for molecular simulation in condensed phase. Chem. Phys. Lett. 2002, 355, 257–262. [Google Scholar] [CrossRef]
- Heyden, A.; Lin, H.; Truhlar, D.G. Adaptive partitioning in combined quantum mechanical and molecular mechanical calculations of potential energy functions for multiscale simulations. J. Phys. Chem. B 2007, 111, 2231–2241. [Google Scholar] [CrossRef] [PubMed]
- Bulo, R.E.; Ensing, B.; Sikkema, J.; Visscher, L. Toward a practical method for adaptive QM/MM simulations. J. Chem. Theory Comput. 2009, 5, 2212–2221. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, S.O.; Bulo, R.E.; Moore, P.B.; Ensing, B. Recent progress in adaptive multiscale molecular dynamics simulations of soft matter. Phys. Chem. Chem. Phys. 2010, 12, 12401–12414. [Google Scholar] [CrossRef] [PubMed]
- Pezeshki, S.; Lin, H. Adaptive-partitioning redistributed charge and dipole schemes for QM/MM dynamics simulations: On-the-fly relocation of boundaries that pass through covalent bonds. J. Chem. Theory Comput. 2011, 7, 3625–3634. [Google Scholar] [CrossRef] [PubMed]
- Takenaka, N.; Kitamura, Y.; Koyano, Y.; Nagaoka, M. The number-adaptive multiscale QM/MM molecular dynamics simulation: Application to liquid water. Chem. Phys. Lett. 2012, 524, 56–61. [Google Scholar] [CrossRef]
- Bulo, R.E.; Michel, C.; Fleurat-Lessard, P.; Sautet, P. Multiscale modeling of chemistry in water: Are we there yet? J. Chem. Theory Comput. 2013, 9, 5567–5577. [Google Scholar] [CrossRef] [PubMed]
- Pezeshki, S.; Davis, C.; Heyden, A.; Lin, H. Adaptive-partitioning QM/MM dynamics simulations: 3. Solvent molecules entering and leaving protein binding sites. J. Chem. Theory Comput. 2014, 10, 4765–4776. [Google Scholar] [PubMed]
- Waller, M.P.; Kumbhar, S.; Yang, J. A density-based adaptive quantum mechanical/molecular mechanical method. ChemPhysChem 2014, 15, 3218–3225. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, H.C.; Kubař, T.; Elstner, M. Size-consistent multipartitioning QM/MM: A stable and efficient adaptive QM/MM method. J. Chem. Theory Comput. 2014, 10, 4242–4252. [Google Scholar] [CrossRef] [PubMed]
- Böckmann, M.; Doltsinis, N.L.; Marx, D. Adaptive switching of interaction potentials in the time domain: An extended lagrangian approach tailored to transmute force field to QM/MM simulations and back. J. Chem. Theory Comput. 2015, 11, 2429–2439. [Google Scholar] [CrossRef] [PubMed]
- Jiang, T.; Boereboom, J.M.; Michel, C.; Fleurat-Lessard, P.; Bulo, R.E. Proton transfer in aqueous solution: Exploring the boundaries of adaptive QM/MM. In Quantum Modeling of Complex Molecular Systems; Rivail, J.-L., Ruiz-Lopez, M., Assfeld, X., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 51–91. [Google Scholar]
- Pezeshki, S.; Lin, H. Adaptive-partitioning QM/MM for molecular dynamics simulations: 4. Proton hopping in bulk water. J. Chem. Theory Comput. 2015, 11, 2398–2411. [Google Scholar] [CrossRef] [PubMed]
- Pezeshki, S.; Lin, H. Recent developments in adaptive QM/MM. In Quantum Modeling of Complex Molecular Systems; Rivail, J.-L., Ruiz-Lopez, M., Assfeld, X., Eds.; Springer: New York, NY, USA, 2015; pp. 93–113. [Google Scholar]
- Boereboom, J.M.; Potestio, R.; Donadio, D.; Bulo, R.E. Toward Hamiltonian adaptive QM/MM: Accurate solvent structures using many-body potentials. J. Chem. Theory Comput. 2016, 12, 3441–3448. [Google Scholar] [CrossRef] [PubMed]
- Duster, A.; Garza, C.; Lin, H. Adaptive partitioning QM/MM dynamics simulations for substrate uptake, product release, and solvent exchange. In Computational Approaches for Studying Enzyme Mechanism; Voth, G.A., Ed.; Elsevier: Cambridge, UK, 2016; pp. 342–358. [Google Scholar]
- Zheng, M.; Waller, M.P. Adaptive quantum mechanics/molecular mechanics methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2016, 6, 369–385. [Google Scholar] [CrossRef]
- Dohm, S.; Spohr, E.; Korth, M. Developing adaptive QM/MM computer simulations for electrochemistry. J. Comput. Chem. 2017, 38, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Duster, A.W.; Wang, C.-H.; Garza, C.M.; Miller, D.E.; Lin, H. Adaptive quantum/molecular mechanics: What have we learned, where are we, and where do we go from here? Wiley Interdiscip. Rev. Comput. Mol. Sci. 2017, 7, e1310. [Google Scholar] [CrossRef]
- Field, M.J. An algorithm for adaptive QC/MM simulations. J. Chem. Theory Comput. 2017, 13, 2342–2351. [Google Scholar] [CrossRef] [PubMed]
- Zheng, M.; Kuriappan, J.A.; Waller, M.P. Toward more efficient density-based adaptive QM/MM methods. Int. J. Quantum Chem. 2017, 117, e25336. [Google Scholar] [CrossRef]
- Boereboom, J.M.; Fleurat-Lessard, P.; Bulo, R.E. Explicit solvation matters: Performance of QM/MM solvation models in nucleophilic addition. J. Chem. Theory Comput. 2018, 14, 1841–1852. [Google Scholar] [CrossRef] [PubMed]
- Hofer, T.S.; Hünenberger, P.H. Absolute proton hydration free energy, surface potential of water, and redox potential of the hydrogen electrode from first principles: QM/MM MD free-energy simulations of sodium and potassium hydration. J. Chem. Phys. 2018, 148, 222814. [Google Scholar] [CrossRef] [PubMed]
- Zheng, M.; Waller, M.P. Yoink: An interaction-based partitioning API. J. Comput. Chem. 2018, 39, 799–806. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, H. Improvement of performance, stability and continuity by modified size-consistent multipartitioning quantum mechanical/molecular mechanical method. Molecules 2018, 23, 1882. [Google Scholar] [CrossRef] [PubMed]
- Potestio, R.; Fritsch, S.; Español, P.; Delgado-Buscalioni, R.; Kremer, K.; Everaers, R.; Donadio, D. Hamiltonian adaptive resolution simulation for molecular liquids. Phys. Rev. Lett. 2013, 110, 108301. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Zhang, Y.; Pezeshki, S.; Duster, A.; Truhlar, D.G. QMMM, Version 2.2.8.CO; University of Minnesota: Minneapolis, MN, USA, 2017.
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
- Thiel, W. MNDO2005, Version 7.0; Max-Planck-Institut für Kohlenforschung: Müheim an der Ruhr, Germany, 2005.
- Schmitt, U.W.; Voth, G.A. The computer simulation of proton transport in water. J. Chem. Phys. 1999, 111, 9361–9381. [Google Scholar] [CrossRef]
- Wu, Y.; Tepper, H.L.; Voth, G.A. Flexible simple point-charge water model with improved liquid-state properties. J. Chem. Phys. 2006, 124, 024503. [Google Scholar] [CrossRef] [PubMed]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Cisneros, G.A.; Wikfeldt, K.T.; Ojamäe, L.; Lu, J.; Xu, Y.; Torabifard, H.; Bartók, A.P.; Csányi, G.; Molinero, V.; Paesani, F. Modeling molecular interactions in water: From pairwise to many-body potential energy functions. Chem. Rev. 2016, 116, 7501–7528. [Google Scholar] [CrossRef] [PubMed]
- Jiang, T.; Simko, S.; Bulo, R.E. Accurate QM/MM simulation of aqueous solutions with tailored MM models. J. Chem. Theory Comput. 2018, 14, 3943–3954. [Google Scholar] [CrossRef] [PubMed]

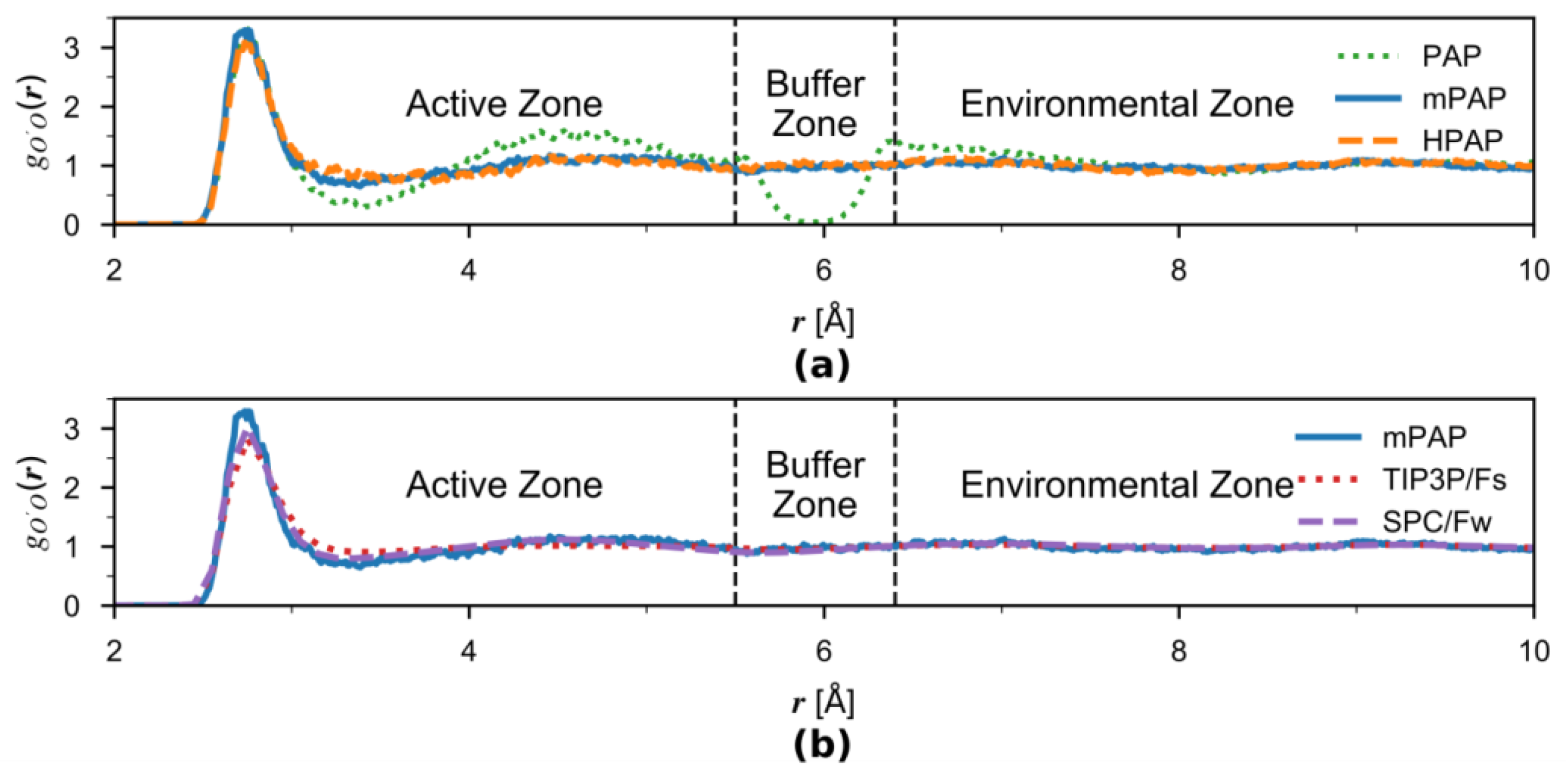

| Interaction | Parameter | TIP3P/Fs 1 | SPC/Fw 2 |
|---|---|---|---|
| O-H stretching | kb [kcal/mol/Å2] | 1059.162 | 1059.162 |
| B0 [Å] | 0.960 | 1.012 | |
| H-O-H bending | kθ [kcal/mol/rad2] | 68.097 | 75.900 |
| θ0 [deg] | 104.500 | 113.24 | |
| Electrostatic | qH [e] | 0.417 | 0.41 |
| qO [e] | −0.834 | −0.82 | |
| van der Waals (O only) | Rmin/2 [Å] | 1.7682 | 1.7767 |
| ε [kcal/mol] | −0.1522 | −0.1524 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duster, A.W.; Wang, C.-H.; Lin, H. Adaptive QM/MM for Molecular Dynamics Simulations: 5. On the Energy-Conserved Permuted Adaptive-Partitioning Schemes. Molecules 2018, 23, 2170. https://doi.org/10.3390/molecules23092170
Duster AW, Wang C-H, Lin H. Adaptive QM/MM for Molecular Dynamics Simulations: 5. On the Energy-Conserved Permuted Adaptive-Partitioning Schemes. Molecules. 2018; 23(9):2170. https://doi.org/10.3390/molecules23092170
Chicago/Turabian StyleDuster, Adam W., Chun-Hung Wang, and Hai Lin. 2018. "Adaptive QM/MM for Molecular Dynamics Simulations: 5. On the Energy-Conserved Permuted Adaptive-Partitioning Schemes" Molecules 23, no. 9: 2170. https://doi.org/10.3390/molecules23092170
APA StyleDuster, A. W., Wang, C.-H., & Lin, H. (2018). Adaptive QM/MM for Molecular Dynamics Simulations: 5. On the Energy-Conserved Permuted Adaptive-Partitioning Schemes. Molecules, 23(9), 2170. https://doi.org/10.3390/molecules23092170