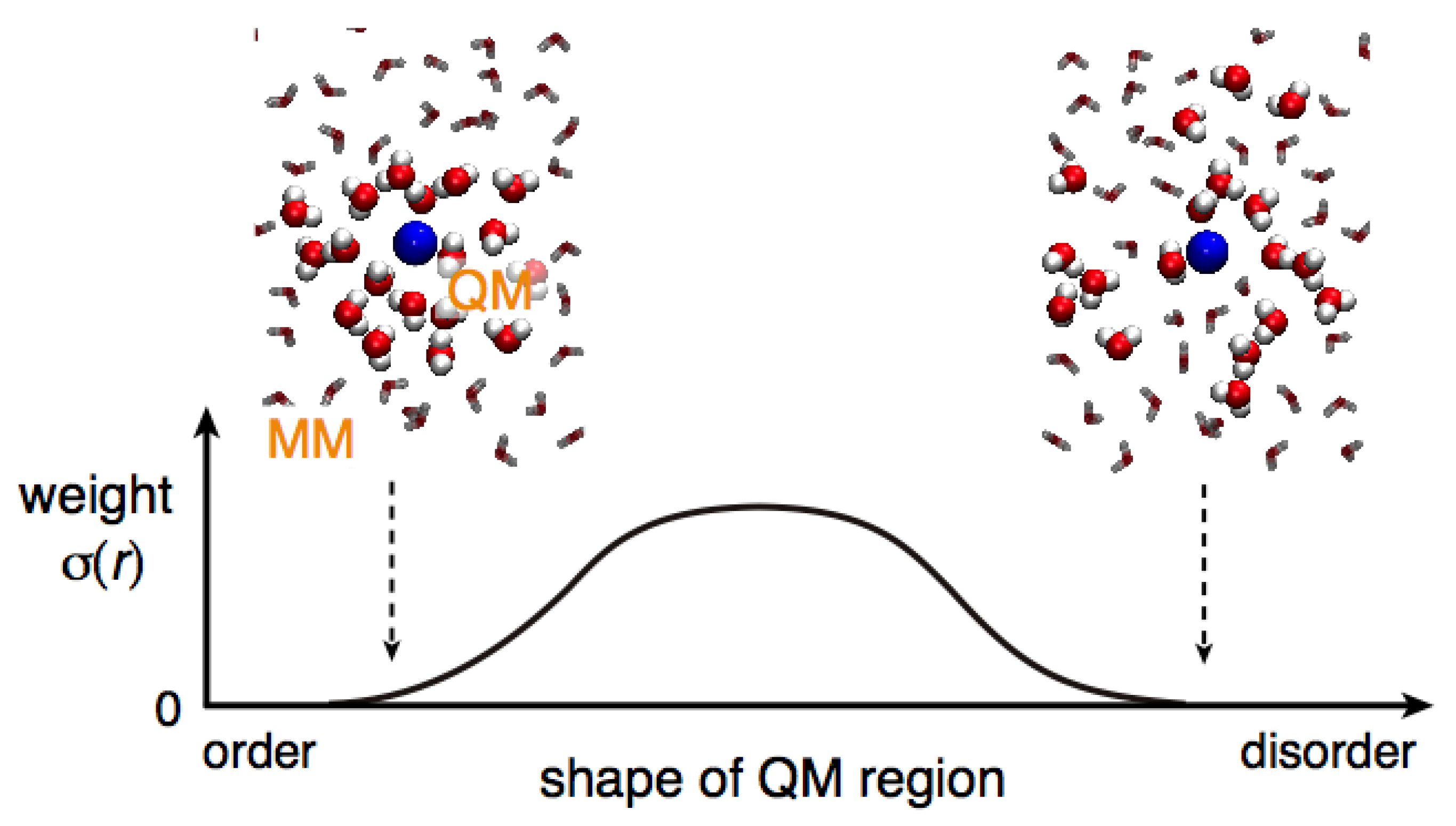
1. Introduction
In molecular simulations, the choice of molecular models has been a major concern and always a product of compromise between accuracy and computational cost. To optimize this balance, multiscale simulations, which combine more than two molecular models, have been proposed by many research groups. Among the various multiscale techniques, the quantum-mechanical (QM)/molecular-mechanical (MM) method has been the most popular and successful one. While QM methods are transferable and accurate because they explicitly treat the electronic structure, they require massive computation time and resources. Therefore, they have severe limitations regarding the size of the systems that can be treated and the simulation times that can be achieved. In the contrast, the QM/MM method makes partial electronic structures of gigantic systems available with moderate computational load. Thus, it has been widely applied to investigate reactions in biomolecules and solutions. To apply QM/MM methods within a molecular dynamics (MD) simulation framework, there are two possible options. The first one is to define only the solute molecule as QM and the rest as MM. The second option is to expand the QM region to the surrounding solvent molecules. Apparently and intuitively, the latter option seems to yield a more reasonable and natural picture of the molecular structure and dynamics because of the incorporation of environmental quantum chemical effects. Regarding dynamics simulations, however, mobile solvent molecules diffuse away from the QM solute in course of time. As a result, the solvent quantum effect is lost, although the computational cost remains substantially larger than in the former setting, which treats all solvent molecules as MM. Therefore, in conventional QM/MM MD simulations, quantum chemical solvent effects cannot be taken into consideration.
To overcome this limitation, various corrective approaches have been proposed by several research groups in the last two decades [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11]. These approaches are categorized into two groups: “constrained” and “adaptive” QM/MM methods. The constrained methods, such as “flexible inner region ensemble separator” (FIRES) [
1], “boundary based on exchange symmetry theory” (BEST) [
2] and “boundary constraint with correction” (BCC) [
3], employ constraints on QM (and MM) solvent molecules to prevent their diffusion. These methods are relatively stable, in particular the Hamiltonian is well conserved in BCC. In addition, their computational cost is moderate compared to that of the methods belonging to the other group because a particular division of the molecular system into QM and MM regions, which is termed a QM/MM partitioning, is fixed during the simulation. Since the “constrained” methods do not allow the exchange of solvent molecules through the QM/MM border, their dynamics is not realistic. Instead, they are designed to investigate solvation structures (e.g., through the calculation of radial distribution functions) using ensemble averages. These methods are controversial because they assume that ensemble averages are rigorously accurate only if there is a symmetric exchange between QM and MM solvent molecules; that is, they suppose that QM and MM solvent molecules are energetically identical.
In contrast to the constrained methods, adaptive QM/MM methods employ a flexible molecular definition and allow exchanges between QM and MM molecules. To this end, most adaptive QM/MM methods exploit a multipartitioning approach, which considers various QM/MM partitionings whose QM regions consist of different sets of solvent molecules. Based on the respective partitionings, potential energies and forces are individually calculated and then the effective energy and forces, which are used to update the coordinates along the MD simulation, are obtained as a weighted average. The adaptive QM/MM methods, such as ONIOM-XS [
5], buffered-force [
6], permuted adaptive partitioning (PAP) [
7], modified PAP (mPAP) [
8], sorted adaptive partitioning (SAP) [
7], difference-based adaptive solvation (DAS) [
9], scaled interaction single partition adaptive (SISPA) [
10] and size-consistent multipartitioning (SCMP) [
11], vary in the definition of the partitioning scheme and weight function. For comparison, most constrained and adaptive methods are also termed “single-partitioning” and “multipartitioning” methods, respectively. Since the computational cost to calculate energy and forces depends on the number of QM/MM partitionings, adaptive QM/MM methods require substantial computational resources except in the case of SISPA, which is based on a single-partitioning approach.
In the adaptive QM/MM methods, the stability of the simulations is a major concern. To have stable simulations, an adequate choice of weight function is key and the conservation of the Hamiltonian is an important index. Because of solvent diffusion, in adaptive methods, partitionings have to be redefined to keep the solute of interest surrounded by QM solvent molecules, although the abrupt update of partitionings can cause a discontinuity in the potential energy surface. Thus, a weight function is introduced to silence contributions from updated partitionings. However, in some adaptive methods, the weight function cannot completely remove the aforementioned discontinuity (denoted as temporal discontinuity), although the weight function is differentiable. In ONIOM-XS, two QM partitionings are considered, where one partitioning has a smaller QM region that does not include the solvent in transition region, while the other partitioning has a larger QM region that include them [
5]. For instance, if a solvent molecule moves across the border, the forces acting on the solvent molecules in the inner layer become discontinuous, because the weight function cannot remove the contribution from the partitioning with smaller QM region, which abruptly changes the number of QM solvent molecules. In the SAP and DAS methods, temporal discontinuities appear, when the solvent number in the active zone (QM region) changes. For instance, when a solvent molecule moves from the active zone to the transition zone, an additional partitioning seems to abruptly appear with non-zero weight [
7,
9]. The PAP method theoretically realizes perfect continuity by taking into account all possible partitionings. However, it requires massive computation and thus is not feasible in reality [
7]. To reduce the computational cost in PAP, modified PAP (mPAP) truncates the series expansion at around fifth order, although it faces the temporal discontinuity problem again [
8]. In many cases, these deficiency in the weight functions result in drastic temperature drifts under microcanonical (
NVE) conditions, as reviewed by Bulo et al. [
12]. To keep a constant temperature and stabilize the MD simulations, a system may be linked to a thermostat (
NVT ensemble). However, if the Hamiltonian is not conserved, the MD simulation does not yield accurate
NVT ensemble. In other words, averaged observables are not physically accurate even though the temperature is moderately controlled. We proposed the size-consistent multipartitioning (SCMP) QM/MM method in 2014 [
11], which numerically conserve Hamiltonian and lead to stable MD simulations over hundreds of pico seconds.
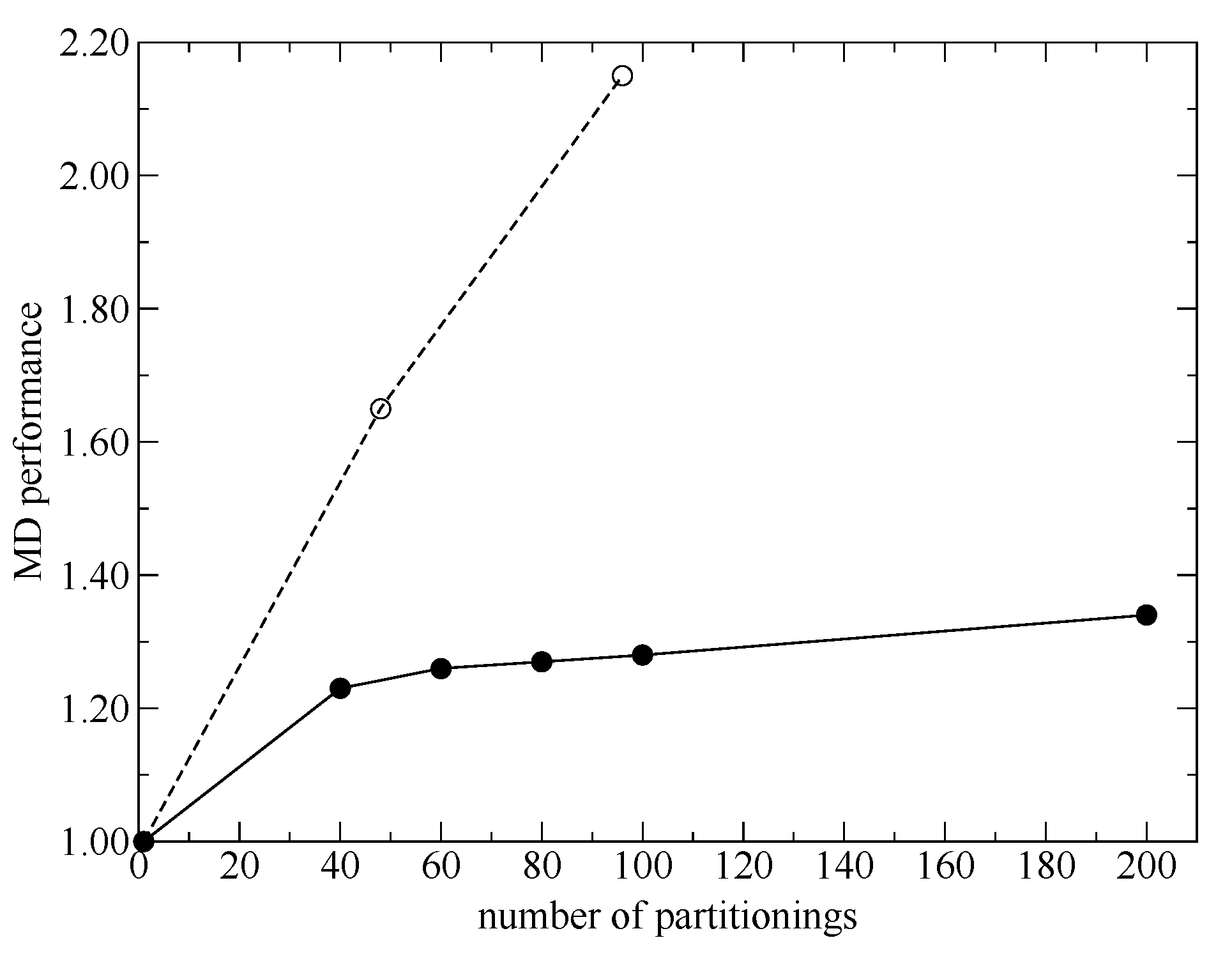
Because the force and energy calculations for each partitioning are independent in multipartitioning methods, adaptive QM/MM methods can be trivially parallelized. However, most of them are based on multiscale multipartitioning, in which the size of the QM regions varies among partitionings. Therefore, the computational loads due to the energy and force calculations are inhomogeneous among the respective partitioning, which causes idle time at several computational nodes. In contrast, all partitionings in the SCMP method have the same number of QM solvent molecules; thus, the SCMP method has high affinity with parallel computing.
As practical applications, we have employed the SCMP methods to evaluate physicochemical properties of water and monoatomic cation solutions [
13,
14]. Then, we demonstrated that quantum chemical solvent effects exert a great impact on the solvation structure and dynamics of these systems by evaluating their radial distribution function, infrared spectrum and diffusion coefficient.
Although the SCMP method has shown high performance and potential, it still has vulnerability because of the weight functions, where all the weights can be zero for certain situations, and, as a result, MD simulations can crash. Furthermore, in previous studies, we also confirmed that the SCMP can connect the QM and MM regions continuously on time average but the spatial continuity is not necessarily ensured at every MD time step. Moreover, the importance of the instantaneous spatial continuity has not been discussed yet. Additionally, although the SCMP method theoretically should keep its MD performance even for highly parallelized computing, the potential was not fully elicited in a previous study [
14]. Thus, in the present study, we propose modification of the SCMP theoretical framework to increase MD performance, simulation stability and spatial continuity. Then, we carry out benchmark simulations for pure water and demonstrate the updated performance.
3. Modification of the Update Protocol
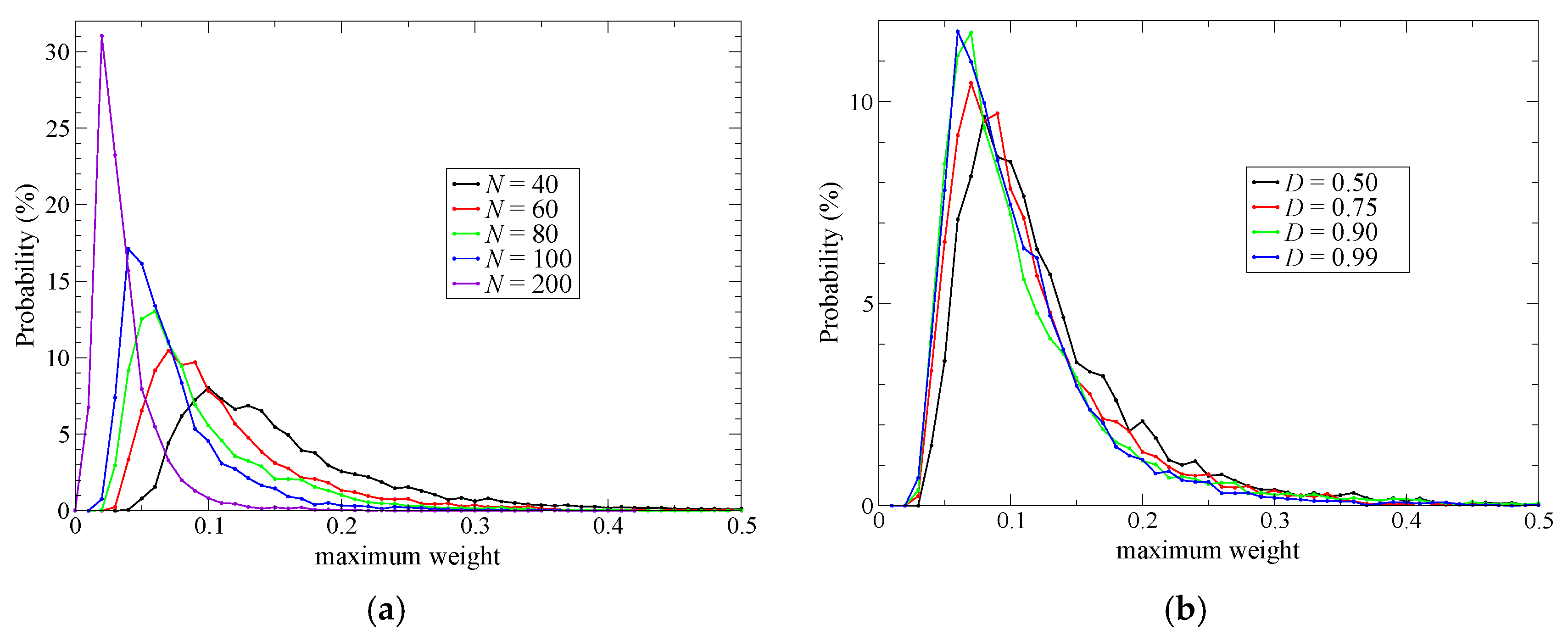
The MD stability problem arises from the character of the SCMP weight function; the weight functions can become zero in limit of ordered or disordered partitioning. In addition, the number of partitionings to be considered is limited in practice. As a result, it is possible to have only a small number of partitionings with large weights, which would cause problems of stability and spatial continuity.
To better understand the stability problem, consider a solvent molecule that is defined as QM in all the weighted partitionings. If the QM solvent molecules diffuse beyond
tQM from a QM solute molecule, all the partitionings can have simultaneously a weight of zero, which would result in the collapse of the MD simulation. This would also be the case for the solvent molecules that are defined as MM in all the weighted partitionings. Therefore, to achieve the stability of the MD simulations, the partitionings should have variety in the selection of the QM solvent molecules and as many partitionings as possible should have nonzero weight. To assess simulation stability, let us define
σmax as
Note that σmax ranges from 1/N to 1, where N represents the total number of partitionings. To achieve stable simulations, σmax should be kept as small as possible.
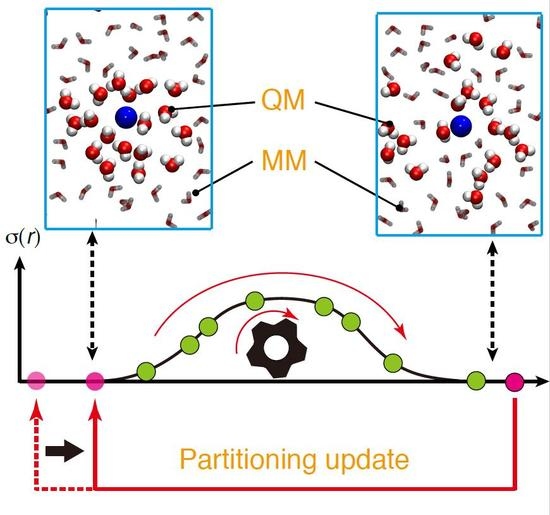
Spatial continuity denotes a smooth connection between QM and MM regions. In other words, solvent models are smoothly alternated when solvent molecules cross the QM/MM border. To intuitively understand spatial continuity, in a previous study [
11], we introduced a useful measure: the instantaneous QM profile
ωt(
j)
where
and
ωt(
j) describes how much a solvent molecule that is the
j-th nearest neighbor to the QM solute behaves as a QM molecule at time
t [
11].
Since
σ(n) is normalized in Equation (8), a QM profile ranges from 0 to 1 where the values of unity or zero indicate that the solvent molecule corresponds to a perfectly QM or MM model, respectively. Thus, as a solvent molecule approaches the QM solute, the QM profile should become larger and vice versa. Therefore, to have a smooth connection between the QM and MM regions, the QM profiles should gradually and monotonically decrease as the molecular number
j increases. Then, the time-averaged QM profile
ω(
j) is written as
Then, we evaluated the standard deviation of the QM profile of the
j-th solvent molecule as
3.1. Partitioning Update Types
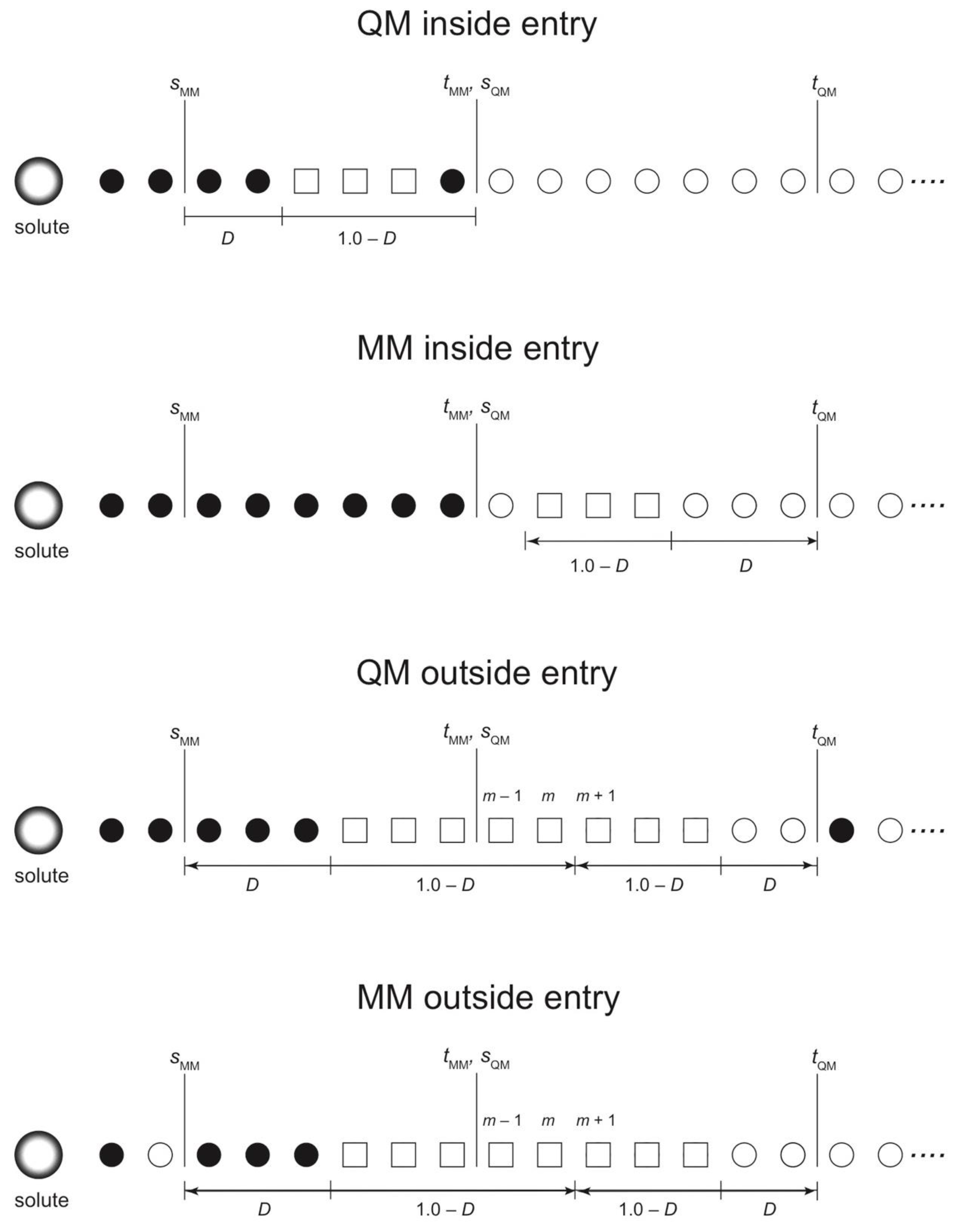
In this section, we discuss the SCMP update types and modify the previous update scheme for efficiency. Let a QM inside entry be a process where a partitioning with σ = 0, because of either IQM = 0 or IMM = 0, at a certain MD step becomes effectively weighted at the next MD step. Likewise, let MM inside entry be a process where a partitioning has nonzero weight because IMM > 0. Here, we note that inside updates are not always available depending on the range parameters s and t. For example, suppose all partitionings have consistently m QM solvent molecules. Let dj be the distance between the QM solute and the j-th nearest solvent molecule. Note that IQM = 0 for sQM ≥ dm and IMM = 0 for dm+1 ≥ tMM. Since dj fluctuates during the MD simulations, if tMM > sQM, there can be a moment in which tMM > dm+1 ≥ dm > sQM. In this case, partitionings satisfying either IQM = 0 or IMM = 0 do not exist. If sQM ≥ tMM, in contrast, there always exists at least one zero-weighted partitioning satisfying either IQM = 0 or IMM = 0 regardless of dm. To make the update available at every MD time step, we assume sQM ≥ tMM hereafter.
Next, let us compare the conditions sQM = tMM and sQM > tMM. To have stable simulations, ideally, partitionings should have nonzero weights immediately after the update. Suppose that an updated partitioning with σ = 0 has IQM = 0 for sQM > dm. Because of the diffusion of the QM solvent molecules, sooner or later, the updated partitioning by inside entry will have a nonzero weight, when sQM < dm. However, if sQM >> dm, it would take time for the partitioning to have a nonzero weight; as a result, a small number of partitionings would have large weights, making the simulation unstable. Thus, sQM should be as small as possible. For the same reason, tMM should be as large as possible. Therefore, we assume that sQM = tMM is the most efficient situation to suppress σmax and this will be the condition that we will apply for efficient update unless otherwise stated.
Let a QM outside entry be a process where a disordered partitioning with σ = 0 because OQM = 0 happens to be reweighted again. For instance, suppose that a QM solvent molecule diffuses beyond tQM and accordingly OQM = 0. Then, the diffused QM solvent molecule may happen to come back within tQM again, leading to σ > 0 with OQM > 0. Likewise, let an MM outside entry be a process where σ > 0 when an MM solvent molecule moves beyond sMM of the QM solute. In contrast to the QM entries, the MM entries are always available regardless of range parameters s and t.
Note that partitionings updated by any of the four types, in particular MM inside and QM outside entries, may not necessarily be weighted again. For instance, while waiting for σ > 0 by a QM outside entry, the MM fade-out functions can become OMM = 0. In such case, it is less likely that this partitioning can have a nonzero weight again in the limited simulation time. Thus, partitionings updated should be carefully checked to see if there are better candidates with nonzero weights among other possible partitionings. In contrast, a QM outside entry seems to happen more frequently because the sphere surface at r = tQM is larger than those at r = sMM and sQM and therefore, the frequency of solvent molecules crossing the surface is also higher.
We also note that, in previous studies, we made only use of the inside entry for partitioning update. In this case, limited partitionings are available for update, which seems to be inefficient, if many partitionings have to be updated at the same time because of partitioning overlap. In the present study, we propose to exploit the outside entries to effectively control σmax. For efficiency, when a partitioning becomes disordered (σ = 0 by either OQM = 0 or OMM = 0), we make the partitioning partially-ordered by tuning the solvent molecules irrelevant to O = 0. Otherwise, as previously mentioned, the outside-entered partitioning is highly likely to become disordered again.
3.2. Degree of Order
Under the condition that the range parameters sQM = tMM, the perfectly ordered partitioning whose QM region consists of the nearest m solvent molecules has always zero weight as described in the previous section. Using this property, in a previous study, we employed a minimum update protocol where the partitioning to be updated is always replaced by the perfectly ordered partitioning, namely the QM region consists of the nearest solvent molecules. Note that when the minimum update is once performed, the partitioning update is not available until solvent diffusion occurs to some extent. Otherwise, more than one partitioning can become identical. As a result, idling times can happen between partitioning updates, which can cause an increase of the maximum weight σmax and destabilize the MD simulation. Thus, the minimum update protocol is inefficient.
Here, we make the partitioning update more flexible by introducing an index, degree of order (
D). Note that either
IQMOQM or
IMMOMM is zero in a new partitioning, while the nonzero one is arbitrary. Thus, keeping
σ = 0, new partitionings can be disordered to some extent. The degree of order
D indicates how ordered a new partitioning is. If
D = 1, the fade-in function
I = 0 (
O = 1) and the scenario is equivalent to that of the minimum update. If
D = 0,
I = 1 (
O = 0), which indicates that the partitioning is already completely disordered. The four types of update protocols in combination with the degree of order are visualized in
Scheme 2 and detailed in
Appendix A. We assume that the optimal value of
D makes the updated partitionings to become effectively weighted after an entry. Although the optimal value of
D is not trivial, it should obviously be between
D = 0 and
D = 1. Thus, we assessed the optimal value of
D in the section below.
6. Conclusions
The SCMP method enables to incorporate quantum chemical solvent effects in MD simulations. First, in the present study, we proposed a simple form for the score functions used in the weight evaluations and discussed an additional parallelization scheme. Then, we benchmarked the MD performance and demonstrated that the SCMP potential efficiency was well elicited even for highly parallel computations.
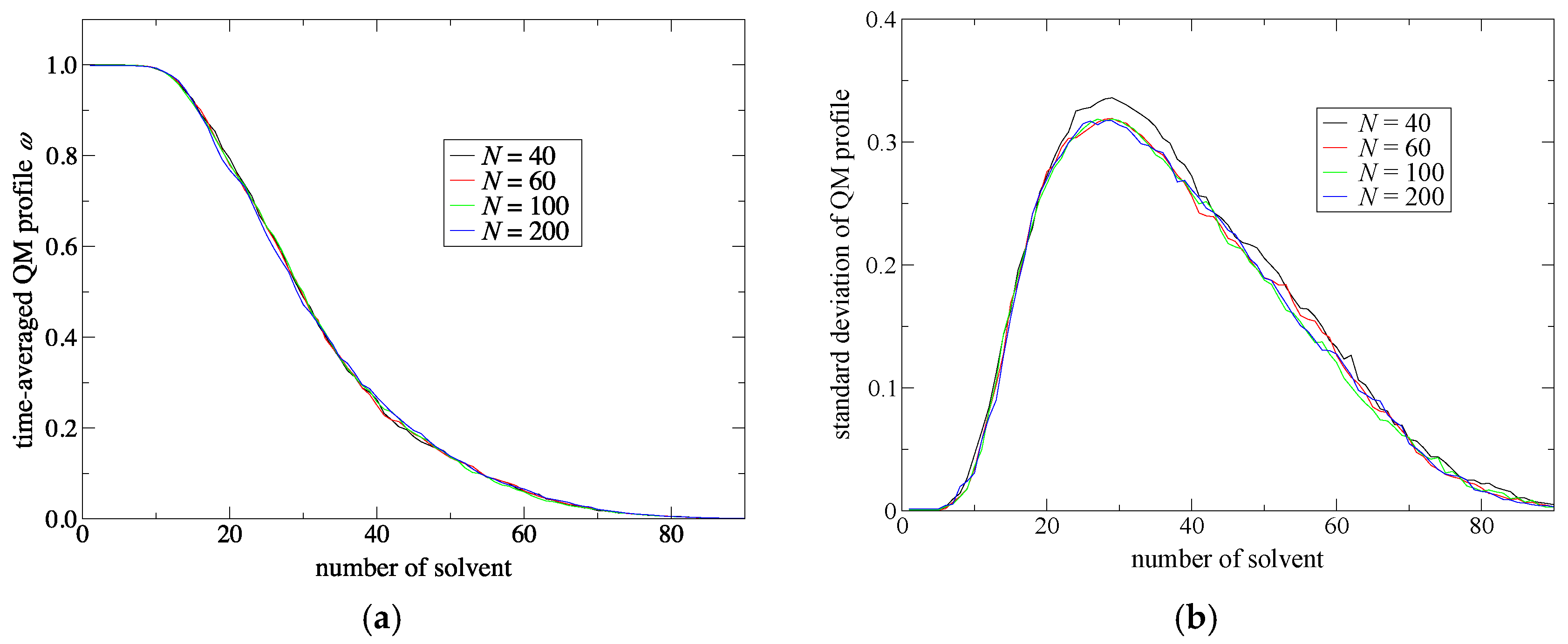
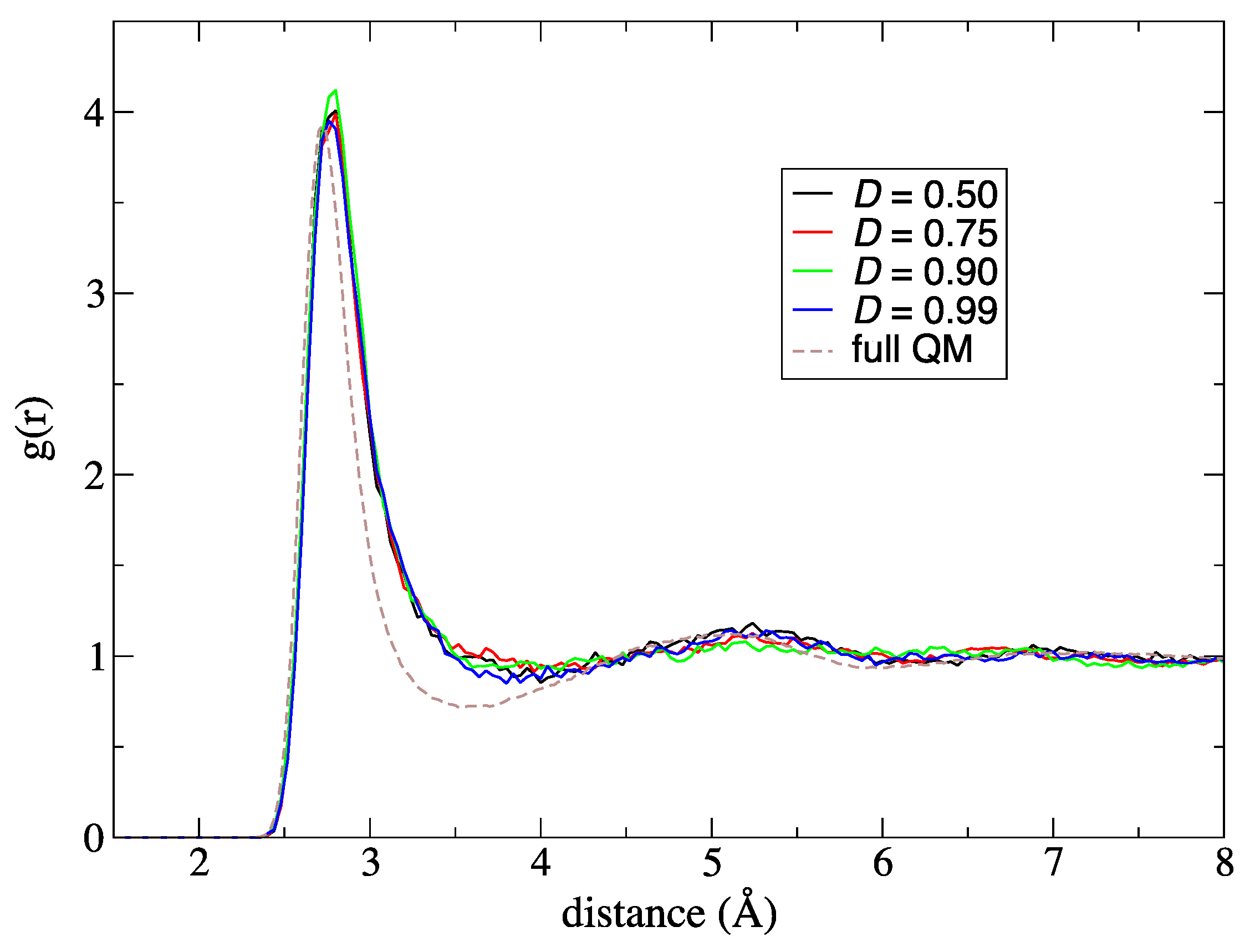
Next, to improve simulation stability and spatial continuity, we proposed new protocols for the partitioning update and introduced an index, degree of order. We focused on the maximum weight at every MD time step as a measure of the stability of the simulations. Then, we found an extended partitioning update protocol that increases the simulation stability; as a result, we did not face any collapse in the MD simulation performed in the present study. We also demonstrated that the number of partitionings is directly connected to the simulation stability. In addition to the extended update protocol, we introduced the degree of order, which affects simulation stability to some extent too. Benchmark simulations showed that there is an optimal value for the degree of order, which presumably depends on the simulation condition. For spatial continuity, we used the QM profile as an index and demonstrated that the present simulations achieved spatial continuity on time average over MD simulations regardless of the number of partitionings (at least in a range from 40 to 200). Notably, however, instantaneous spatial continuity at every MD time step was not necessarily satisfactory containing large errors. While the number of partitionings, which saturates around 60 partitionings, is not crucial to achieve instantaneous spatial continuity, the degree of order in the partitioning update protocol seems to be influential. Concerning the degree of order, notably, the optimal values to achieve spatial continuity and simulation stability do not necessarily match. Because RDFs are also obtained by time-averaged analysis, we could not observe any distinct difference in RDFs in what regards to instantaneous spatial continuity. There still remains room for further research on evaluating spatial continuity.