Detailed Analysis of 17β-Estradiol-Aptamer Interactions: A Molecular Dynamics Simulation Study
Abstract
1. Introduction
2. Results
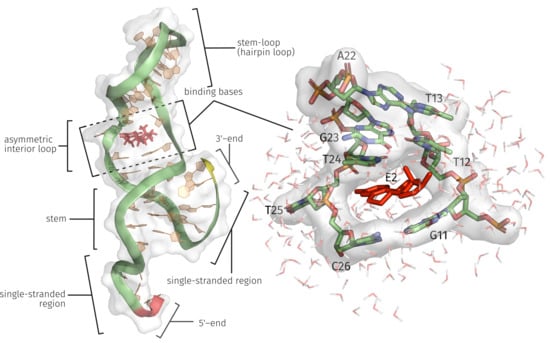
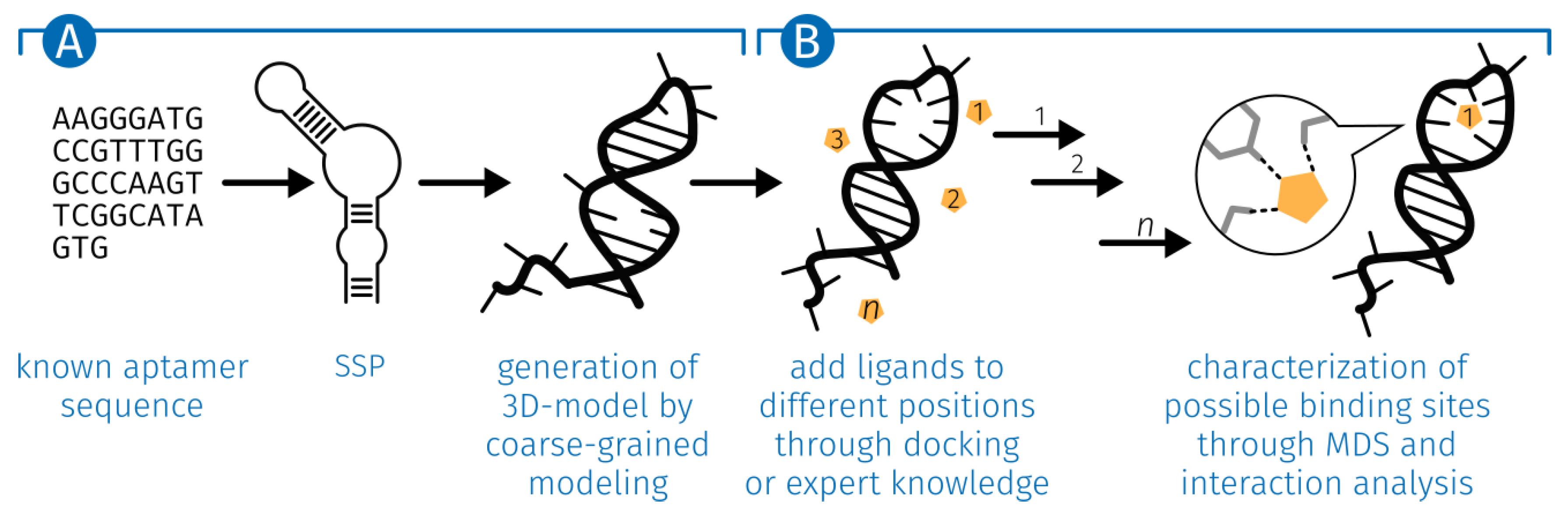
2.1. Generation of the ssDNA Aptamer Structure
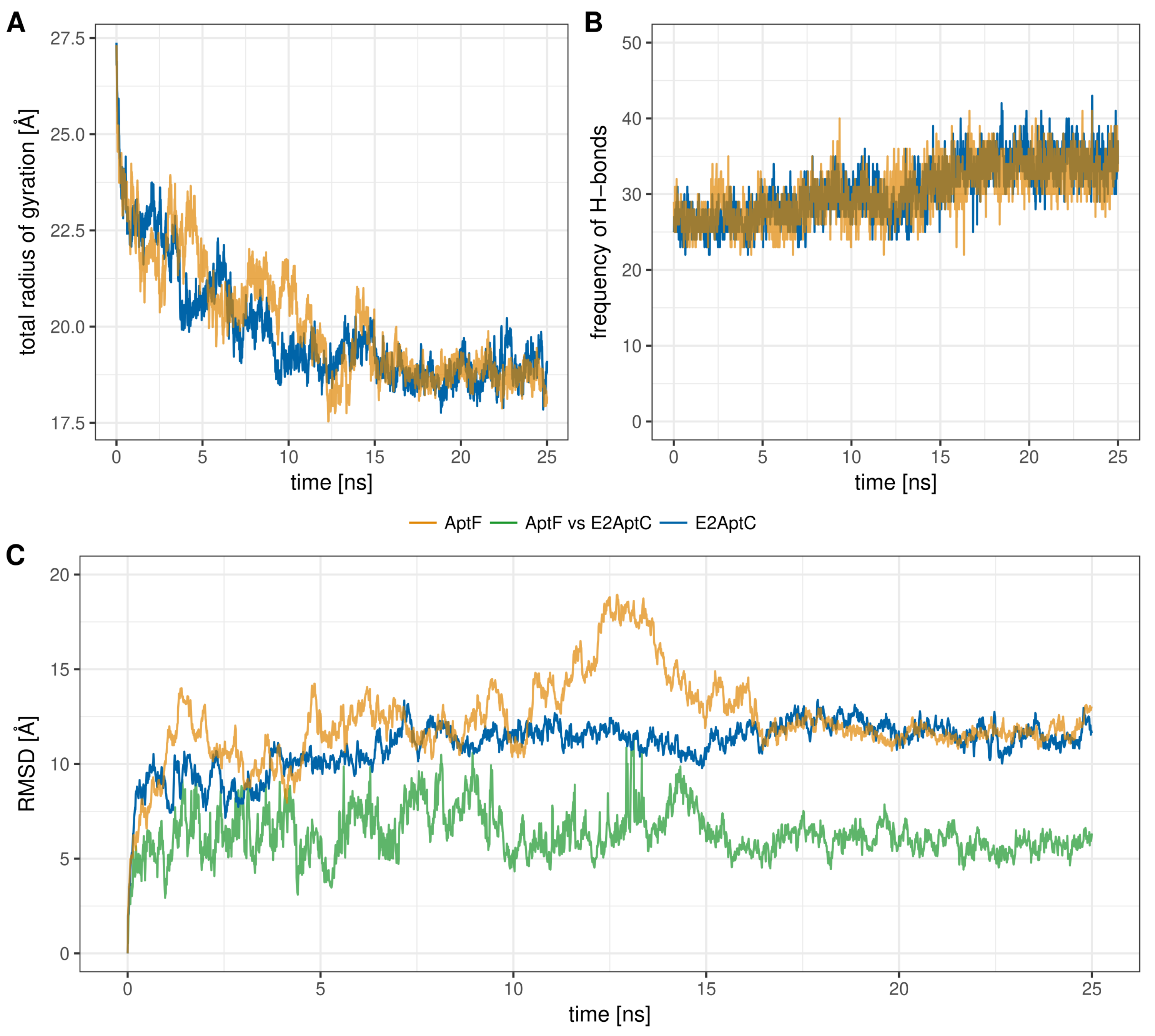
2.2. MD Analysis
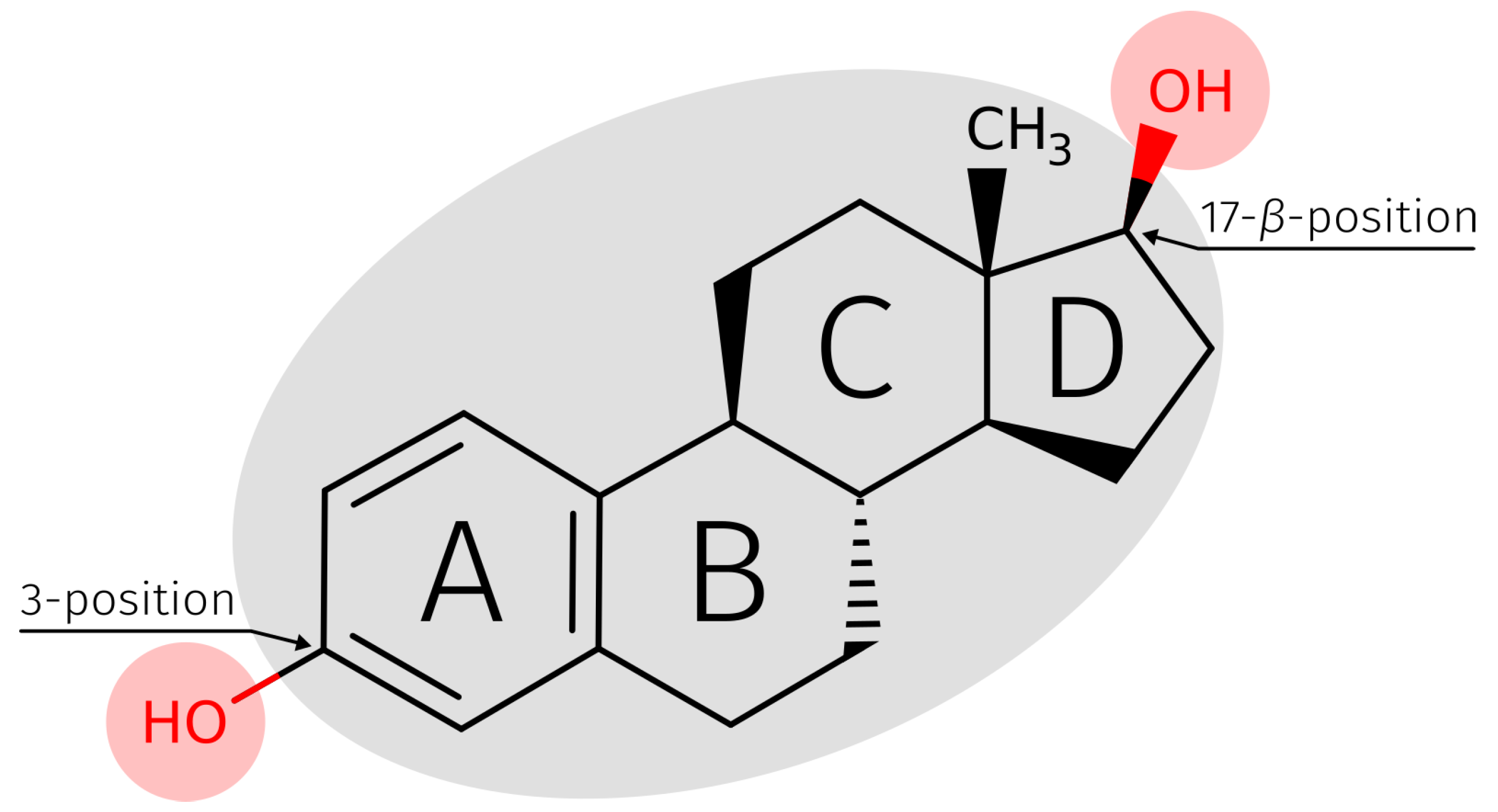
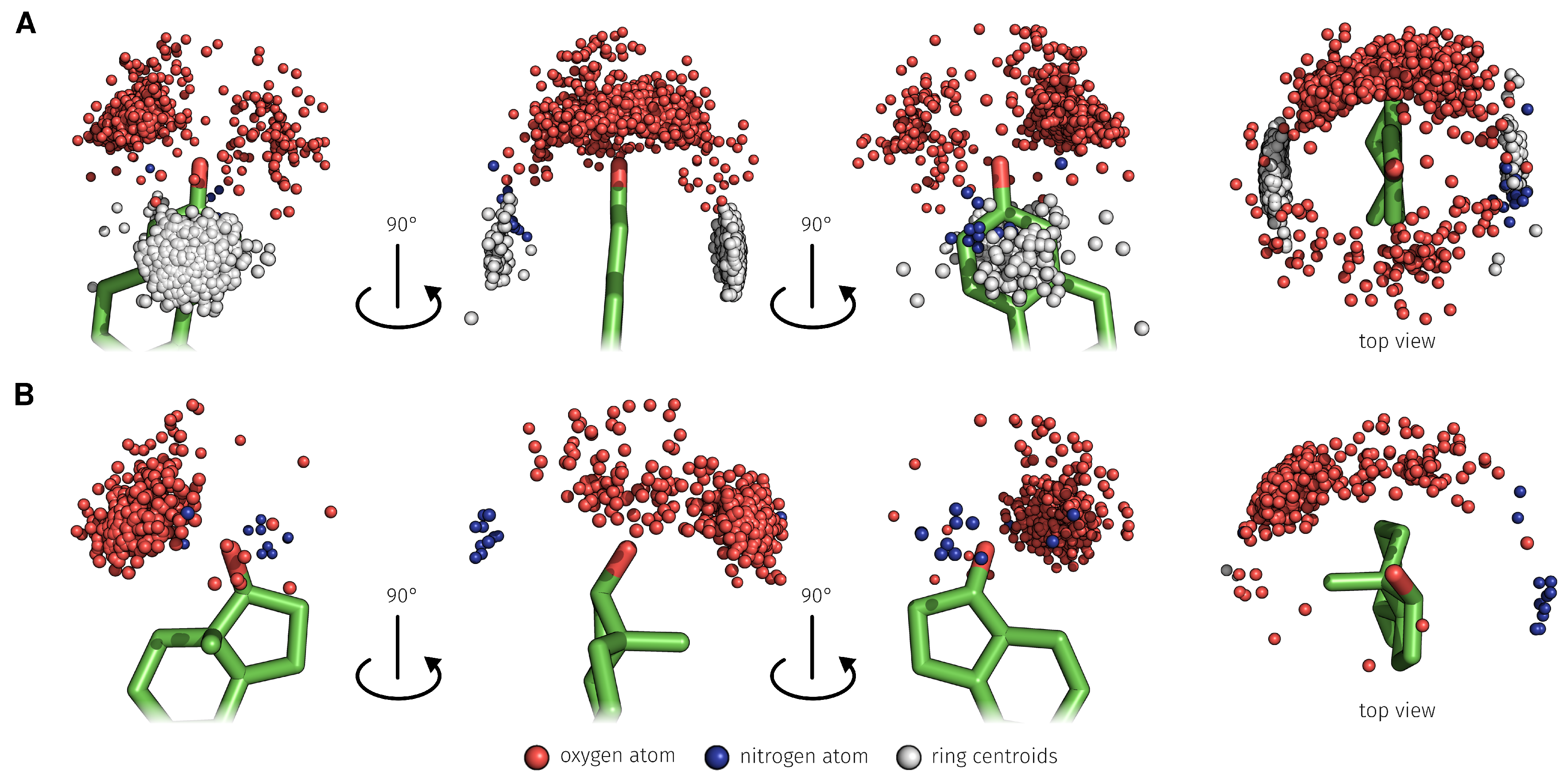
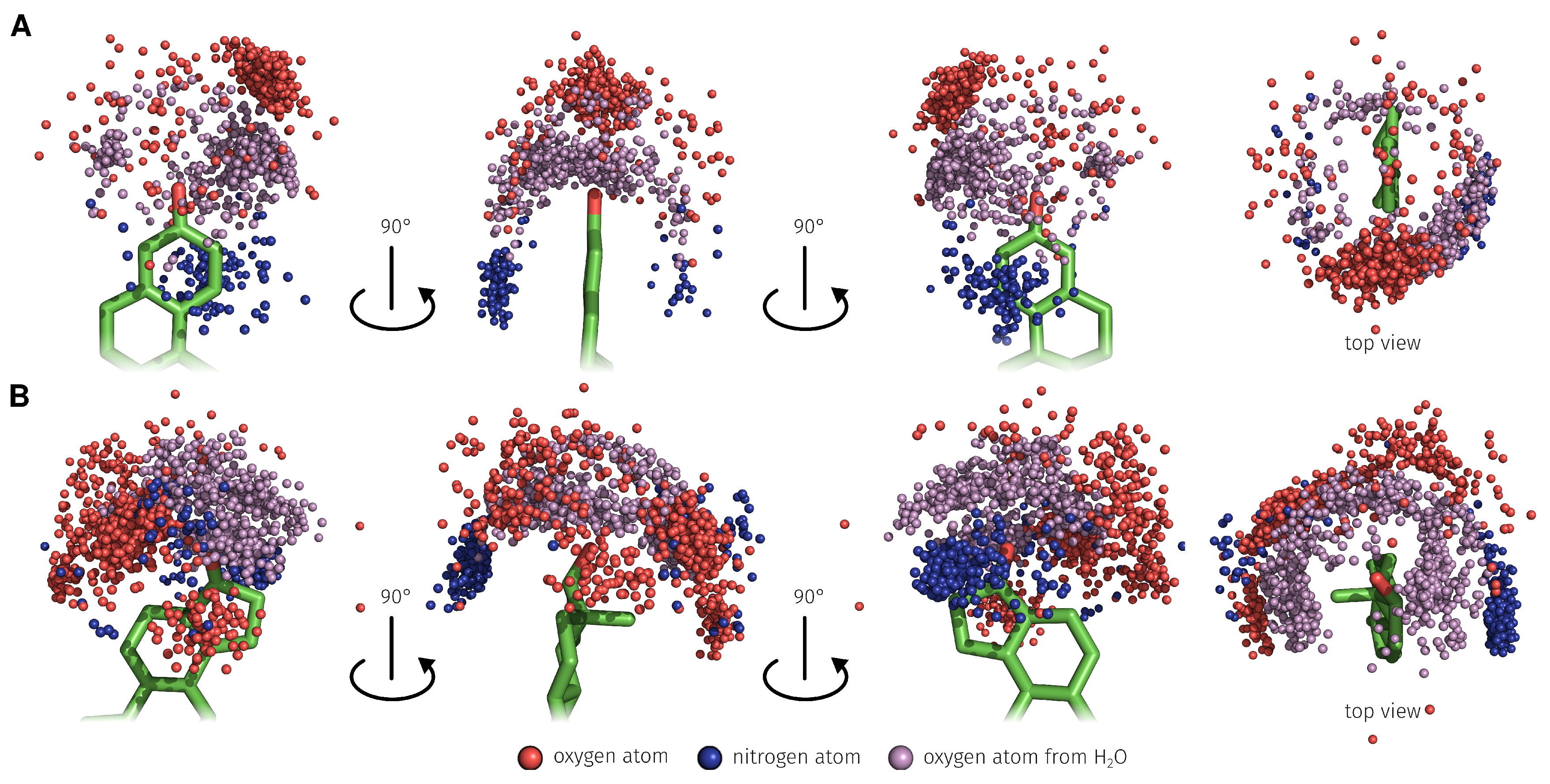
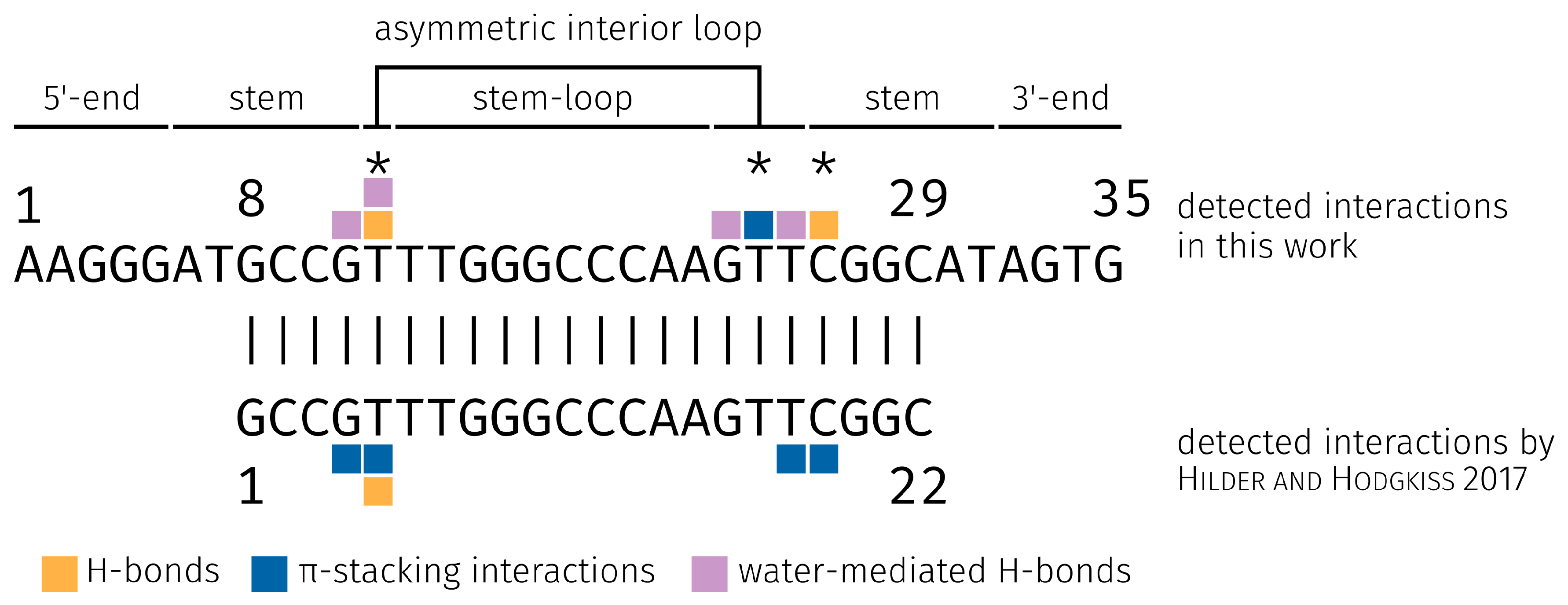
2.3. E2-Interaction Analysis
3. Discussion
3.1. Generation of the ssDNA Aptamer Structure
3.2. MD Analysis
3.3. E2-Interaction Analysis
4. Conclusions
5. Methods
5.1. Generation of the ssDNA Aptamer Structure
5.2. MD Simulation
5.3. E2-Interaction Analysis
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ACPYPE | AnteChamber PYthon Parser interfacE |
| AIL | asymmetric interior loop |
| AptF | aptamer-free |
| E2 | 17-Estradiol |
| E2AptC | E2-aptamer complex |
| FEP | free energy perturbation |
| GROMACS | Groningen Machine for Chemical Simulations |
| H-bond | hydrogen bond |
| HL | hairpin loop |
| MMB | MacroMoleculeBuilder |
| MD | molecular dynamics |
| MM/PBSA | molecular mechanics Poisson–Boltzmann surface area |
| NPT | constant number (N), pressure (P), and temperature (T) |
| NVT | constant number (N), volume (V), and temperature (T) |
| PLIP | Protein–Ligand Interaction Profiler |
| R | Radius of gyration |
| RMSD | root mean square deviation |
| RMSF | root mean square fluctuation |
| SELEX | systematic evolution of ligands by exponential enrichment process |
| SR | stem region |
| ssDNA | single stranded DNA |
| SSE | secondary structure element |
| SSP | secondary structure prediction |
References
- Valcarcel, Y.; Valdehita, A.; Becerra, E.; Lopez de Alda, M.; Gil, A.; Gorga, M.; Petrovic, M.; Barcelo, D.; Navas, J.M. Determining the presence of chemicals with suspected endocrine activity in drinking water from the Madrid region (Spain) and assessment of their estrogenic, androgenic and thyroidal activities. Chemosphere 2018, 201, 388–398. [Google Scholar] [CrossRef] [PubMed]
- Leusch, F.D.L.; Neale, P.A.; Arnal, C.; Aneck-Hahn, N.H.; Balaguer, P.; Bruchet, A.; Escher, B.I.; Esperanza, M.; Grimaldi, M.; Leroy, G.; et al. Analysis of endocrine activity in drinking water, surface water and treated wastewater from six countries. Water Res. 2018, 139, 10–18. [Google Scholar] [CrossRef] [PubMed]
- De Assis, S.; Warri, A.; Cruz, M.I.; Laja, O.; Tian, Y.; Zhang, B.; Wang, Y.; Huang, T.H.; Hilakivi-Clarke, L. High-fat or ethinyl-oestradiol intake during pregnancy increases mammary cancer risk in several generations of offspring. Nat. Commun. 2012, 3, 1053. [Google Scholar] [CrossRef] [PubMed]
- Irwin, L.K.; Gray, S.; Oberdorster, E. Vitellogenin induction in painted turtle, Chrysemys picta, as a biomarker of exposure to environmental levels of estradiol. Aquat. Toxicol. 2001, 55, 49–60. [Google Scholar] [CrossRef]
- Ying, G.G.; Kookana, R.S.; Ru, Y.J. Occurrence and fate of hormone steroids in the environment. Environ. Int. 2002, 28, 545–551. [Google Scholar] [CrossRef]
- Huy, G.D.; Jin, N.; Yin, B.C.; Ye, B.C. A novel separation and enrichment method of 17β-estradiol using aptamer-anchored microbeads. Bioprocess Biosyst. Eng. 2011, 34, 189–195. [Google Scholar] [PubMed]
- Delbes, G.; Levacher, C.; Habert, R. Estrogen effects on fetal and neonatal testicular development. Reproduction 2006, 132, 527–538. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez-Mozaz, S.; de Alda, M.J.; Barcelo, D. Monitoring of estrogens, pesticides and bisphenol A in natural waters and drinking water treatment plants by solid-phase extraction-liquid chromatography-mass spectrometry. J. Chromatogr. A 2004, 1045, 85–92. [Google Scholar] [CrossRef] [PubMed]
- Westerhoff, P.; Yoon, Y.; Snyder, S.; Wert, E. Fate of endocrine-disruptor, pharmaceutical, and personal care product chemicals during simulated drinking water treatment processes. Environ. Sci. Technol. 2005, 39, 6649–6663. [Google Scholar] [CrossRef] [PubMed]
- Adeel, M.; Song, X.; Wang, Y.; Francis, D.; Yang, Y. Environmental impact of estrogens on human, animal and plant life: A critical review. Environ. Int. 2017, 99, 107–119. [Google Scholar] [CrossRef] [PubMed]
- Pessoa, G.P.; de Souza, N.C.; Vidal, C.B.; Alves, J.A.; Firmino, P.I.M.; Nascimento, R.F.; dos Santos, A.B. Occurrence and removal of estrogens in Brazilian wastewater treatment plants. Sci. Total Environ. 2014, 490, 288–295. [Google Scholar] [CrossRef] [PubMed]
- Hamid, H.; Eskicioglu, C. Fate of estrogenic hormones in wastewater and sludge treatment: A review of properties and analytical detection techniques in sludge matrix. Water Res. 2012, 46, 5813–5833. [Google Scholar] [CrossRef] [PubMed]
- Panter, G.; Thompson, R.; Sumpter, J. Adverse reproductive effects in male fathead minnows (Pimephales promelas) exposed to environmentally relevant concentrations of the natural oestrogens, oestradiol and oestrone. Aquat. Toxicol. 1998, 42, 243–253. [Google Scholar] [CrossRef]
- Pfeiffer, F.; Mayer, G. Selection and Biosensor Application of Aptamers for Small Molecules. Front. Chem. 2016, 4, 25. [Google Scholar] [CrossRef] [PubMed]
- Ellington, A.D.; Szostak, J.W. In vitro selection of RNA molecules that bind specific ligands. Nature 1990, 346, 818–822. [Google Scholar] [CrossRef] [PubMed]
- Alsager, O.A.; Kumar, S.; Zhu, B.; Travas-Sejdic, J.; McNatty, K.P.; Hodgkiss, J.M. Ultrasensitive colorimetric detection of 17β-estradiol: The effect of shortening DNA aptamer sequences. Anal. Chem. 2015, 87, 4201–4209. [Google Scholar] [CrossRef] [PubMed]
- Joeng, C.B.; Niazi, J.H.; Lee, S.J.; Gu, M.B. ssDNA aptamers that recognize diclofenac and 2-anilinophenylacetic acid. Bioorg. Med. Chem. 2009, 17, 5380–5387. [Google Scholar] [CrossRef] [PubMed]
- Beier, R.; Pahlke, C.; Quenzel, P.; Henseleit, A.; Boschke, E.; Cuniberti, G.; Labudde, D. Selection of a DNA aptamer against norovirus capsid protein VP1. FEMS Microbiol. Lett. 2014, 351, 162–169. [Google Scholar] [CrossRef] [PubMed]
- Deng, B.; Lin, Y.; Wang, C.; Li, F.; Wang, Z.; Zhang, H.; Li, X.F.; Le, X.C. Aptamer binding assays for proteins: The thrombin example—A review. Anal. Chim. Acta 2014, 837, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Kim, S. Nucleic acid aptamer which specifically binds to bisphenol A. US Patent 8,410,256, 2 April 2013. [Google Scholar]
- Stoltenburg, R.; Reinemann, C.; Strehlitz, B. SELEX–a (r)evolutionary method to generate high-affinity nucleic acid ligands. Biomol. Eng. 2007, 24, 381–403. [Google Scholar] [CrossRef] [PubMed]
- Stoltenburg, R.; Strehlitz, B. Refining the Results of a Classical SELEX Experiment by Expanding the Sequence Data Set of an Aptamer Pool Selected for Protein A. Int. J. Mol. Sci. 2018, 19, 642. [Google Scholar] [CrossRef] [PubMed]
- Tuerk, C.; Gold, L. Systematic evolution of ligands by exponential enrichment: RNA ligands to bacteriophage T4 DNA polymerase. Science 1990, 249, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Sherlock, M.E.; Sudarsan, N.; Breaker, R.R. Riboswitches for the alarmone ppGpp expand the collection of RNA-based signaling systems. Proc. Natl. Acad. Sci. USA 2018, 115, 6052–6057. [Google Scholar] [CrossRef] [PubMed]
- Dunn, M.R.; Jimenez, R.M.; Chaput, J.C. Analysis of aptamer discovery and technology. Nat. Rev. Chem. 2017, 1, 0076. [Google Scholar] [CrossRef]
- Beier, R.; Boschke, E.; Labudde, D. New strategies for evaluation and analysis of SELEX experiments. Biomed. Res. Int. 2014, 2014, 849743. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Guo, L.; He, J.; Xu, H.; Xie, J. Stepping Library-Based Post-SELEX Strategy Approaching to the Minimized Aptamer in SPR. Anal. Chem. 2017, 89, 6559–6566. [Google Scholar] [CrossRef] [PubMed]
- Hermann, T.; Patel, D.J. Adaptive recognition by nucleic acid aptamers. Science 2000, 287, 820–825. [Google Scholar] [CrossRef] [PubMed]
- Svobodová, M.; Skouridou, V.; Botero, M.L.; Jauset-Rubio, M.; Schubert, T.; Bashammakh, A.S.; El-Shahawi, M.S.; Alyoubi, A.O.; O’Sullivan, C.K. The characterization and validation of 17β-estradiol binding aptamers. J. Steroid Biochem. Mol. Biol. 2017, 167, 14–22. [Google Scholar] [CrossRef] [PubMed]
- Alder, B.J.; Wainwright, T.E. Studies in molecular dynamics. I. General method. J. Chem. Phys. 1959, 31, 459–466. [Google Scholar] [CrossRef]
- Chen, M.; Qin, X.; Zeng, G. Biodegradation of Carbon Nanotubes, Graphene, and Their Derivatives. Trends Biotechnol. 2017, 35, 836–846. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Zeng, G.; Xu, P.; Yan, M.; Xiong, W.; Zhou, S. Interaction of carbon nanotubes with microbial enzymes: Conformational transitions and potential toxicity. Environ. Sci. Nano 2017, 4, 1954–1960. [Google Scholar] [CrossRef]
- Flores, S.C.; Sherman, M.A.; Bruns, C.M.; Eastman, P.; Altman, R.B. Fast flexible modeling of RNA structure using internal coordinates. IEEE/ACM Trans. Comput. Biol. Bioinform. 2011, 8, 1247–1257. [Google Scholar] [CrossRef] [PubMed]
- Jiang, F.; Kumar, R.A.; Jones, R.A.; Patel, D.J. Structural basis of RNA folding and recognition in an AMP-RNA aptamer complex. Nature 1996, 382, 183–186. [Google Scholar] [CrossRef] [PubMed]
- Hilder, T.A.; Hodgkiss, J.M. The Bound Structures of 17β-Estradiol-Binding Aptamers. ChemPhysChem 2017, 18, 1881–1887. [Google Scholar] [CrossRef] [PubMed]
- Ruan, M.; Seydou, M.; Noel, V.; Piro, B.; Maurel, F.; Barbault, F. Molecular Dynamics Simulation of a RNA Aptasensor. J. Phys. Chem. B 2017, 121, 4071–4080. [Google Scholar] [CrossRef] [PubMed]
- Warfield, B.M.; Anderson, P.C. Molecular simulations and Markov state modeling reveal the structural diversity and dynamics of a theophylline-binding RNA aptamer in its unbound state. PLoS ONE 2017, 12, e0176229. [Google Scholar] [CrossRef] [PubMed]
- Salentin, S.; Schreiber, S.; Haupt, V.J.; Adasme, M.F.; Schroeder, M. PLIP: Fully automated protein-ligand interaction profiler. Nucleic Acids Res. 2015, 43, W443–W447. [Google Scholar] [CrossRef] [PubMed]
- Wishart, D.S.; Feunang, Y.D.; Guo, A.C.; Lo, E.J.; Marcu, A.; Grant, J.R.; Sajed, T.; Johnson, D.; Li, C.; Sayeeda, Z.; et al. DrugBank 5.0: A major update to the DrugBank database for 2018. Nucleic Acids Res. 2018, 46, D1074–D1082. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J. Studies on the structural stability of rabbit prion probed by molecular dynamics simulations. J. Biomol. Struct. Dyn. 2009, 27, 159–162. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, B.; Mohr, P.; Stahl, M. Intramolecular hydrogen bonding in medicinal chemistry. J. Med. Chem. 2010, 53, 2601–2611. [Google Scholar] [CrossRef] [PubMed]
- Perez-Cano, L.; Eliahoo, E.; Lasker, K.; Wolfson, H.J.; Glaser, F.; Manor, H.; Bernado, P.; Fernandez-Recio, J. Conformational transitions in human translin enable nucleic acid binding. Nucleic Acids Res. 2013, 41, 9956–9966. [Google Scholar] [CrossRef] [PubMed]
- Byeon, I.J.; Ahn, J.; Mitra, M.; Byeon, C.H.; Hercik, K.; Hritz, J.; Charlton, L.M.; Levin, J.G.; Gronenborn, A.M. NMR structure of human restriction factor APOBEC3A reveals substrate binding and enzyme specificity. Nat. Commun. 2013, 4, 1890. [Google Scholar] [CrossRef] [PubMed]
- Marklund, E.G.; Mahmutovic, A.; Berg, O.G.; Hammar, P.; van der Spoel, D.; Fange, D.; Elf, J. Transcription-factor binding and sliding on DNA studied using micro- and macroscopic models. Proc. Natl. Acad. Sci. USA 2013, 110, 19796–19801. [Google Scholar] [CrossRef] [PubMed]
- Ouldridge, T.E.; Louis, A.A.; Doye, J.P. DNA nanotweezers studied with a coarse-grained model of DNA. Phys. Rev. Lett. 2010, 104, 178101. [Google Scholar] [CrossRef] [PubMed]
- Maffeo, C.; Ngo, T.T.; Ha, T.; Aksimentiev, A. A Coarse-Grained Model of Unstructured Single-Stranded DNA Derived from Atomistic Simulation and Single-Molecule Experiment. J. Chem. Theory Comput. 2014, 10, 2891–2896. [Google Scholar] [CrossRef] [PubMed]
- Popenda, M.; Szachniuk, M.; Antczak, M.; Purzycka, K.J.; Lukasiak, P.; Bartol, N.; Blazewicz, J.; Adamiak, R.W. Automated 3D structure composition for large RNAs. Nucleic Acids Res. 2012, 40, e112. [Google Scholar] [CrossRef] [PubMed]
- Das, R.; Baker, D. Automated de novo prediction of native-like RNA tertiary structures. Proc. Natl. Acad. Sci. USA 2007, 104, 14664–14669. [Google Scholar] [CrossRef] [PubMed]
- Jonikas, M.A.; Radmer, R.J.; Laederach, A.; Das, R.; Pearlman, S.; Herschlag, D.; Altman, R.B. Coarse-grained modeling of large RNA molecules with knowledge-based potentials and structural filters. RNA 2009, 15, 189–199. [Google Scholar] [CrossRef] [PubMed]
- Rendek, K.N.; Fromme, R.; Grotjohann, I.; Fromme, P. Crystallization of a self-assembled three-dimensional DNA nanostructure. Acta Crystallogr. Sect. F Struct. Biol. Cryst. Commun. 2013, 69, 141–146. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
- Wang, J.; Cieplak, P.; Kollman, P.A. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? J. Comput. Chem. 2000, 21, 1049–1074. [Google Scholar] [CrossRef]
- Brooks, B.R.; Brooks, C.L.; Mackerell, A.D.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Cheatham, T.E.; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef] [PubMed]
- Perez, A.; Marchan, I.; Svozil, D.; Sponer, J.; Cheatham, T.E.; Laughton, C.A.; Orozco, M. Refinement of the AMBER force field for nucleic acids: Improving the description of alpha/gamma conformers. Biophys. J. 2007, 92, 3817–3829. [Google Scholar] [CrossRef] [PubMed]
- Duan, Y.; Wu, C.; Chowdhury, S.; Lee, M.C.; Xiong, G.; Zhang, W.; Yang, R.; Cieplak, P.; Luo, R.; Lee, T.; et al. A point-charge force field for molecular mechanics simulations of proteins based on condensed-phase quantum mechanical calculations. J. Comput. Chem. 2003, 24, 1999–2012. [Google Scholar] [CrossRef] [PubMed]
- Oostenbrink, C.; Villa, A.; Mark, A.E.; Van Gunsteren, W.F. A biomolecular force field based on the free enthalpy of hydration and solvation: The GROMOS force-field parameter sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656–1676. [Google Scholar] [CrossRef] [PubMed]
- Foloppe, N.; MacKerell, A.D., Jr. All-atom empirical force field for nucleic acids: I. Parameter optimization based on small molecule and condensed phase macromolecular target data. J. Comput. Chem. 2000, 21, 86–104. [Google Scholar] [CrossRef]
- Chakraborty, K.; Mantha, S.; Bandyopadhyay, S. Molecular dynamics simulation of a single-stranded DNA with heterogeneous distribution of nucleobases in aqueous medium. J. Chem. Phys. 2013, 139, 075103. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Zhang, L.; Xiao, X.; Jiang, Y.; Guo, Y.; Yu, X.; Pu, X.; Li, M. Unfolding mechanism of thrombin-binding aptamer revealed by molecular dynamics simulation and Markov State Model. Sci. Rep. 2016, 6, 24065. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Wang, M.L.; Cranford, S.W. Ranking of Molecular Biomarker Interaction with Targeted DNA Nucleobases via Full Atomistic Molecular Dynamics. Sci. Rep. 2016, 6, 18659. [Google Scholar] [CrossRef] [PubMed]
- Koshland, D.E. The key–lock theory and the induced fit theory. Angew. Chem. Int. Ed. 1995, 33, 2375–2378. [Google Scholar] [CrossRef]
- Lin, P.H.; Tsai, C.W.; Wu, J.W.; Ruaan, R.C.; Chen, W.Y. Molecular dynamics simulation of the induced-fit binding process of DNA aptamer and L-argininamide. Biotechnol. J. 2012, 7, 1367–1375. [Google Scholar] [CrossRef] [PubMed]
- Sonoda, M.T.; Martinez, L.; Webb, P.; Skaf, M.S.; Polikarpov, I. Ligand dissociation from estrogen receptor is mediated by receptor dimerization: Evidence from molecular dynamics simulations. Mol. Endocrinol. 2008, 22, 1565–1578. [Google Scholar] [CrossRef] [PubMed]
- Jereva, D.; Fratev, F.; Tsakovska, I.; Alov, P.; Pencheva, T.; Pajeva, I. Molecular dynamics simulation of the human estrogen receptor alpha: Contribution to the pharmacophore of the agonists. Math. Comput. Simul. 2017, 133, 124–134. [Google Scholar] [CrossRef]
- Hilder, T.A.; Hodgkiss, J.M. Molecular Mechanism of Binding between 17β-Estradiol and DNA. Comput. Struct. Biotechnol. J. 2017, 15, 91–97. [Google Scholar] [CrossRef] [PubMed]
- Jubb, H.C.; Higueruelo, A.P.; Ochoa-Montano, B.; Pitt, W.R.; Ascher, D.B.; Blundell, T.L. Arpeggio: A Web Server for Calculating and Visualising Interatomic Interactions in Protein Structures. J. Mol. Biol. 2017, 429, 365–371. [Google Scholar] [CrossRef] [PubMed]
- Zwanzig, R.W. High-temperature equation of state by a perturbation method. I. nonpolar gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
- Kollman, P.A.; Massova, I.; Reyes, C.; Kuhn, B.; Huo, S.; Chong, L.; Lee, M.; Lee, T.; Duan, Y.; Wang, W.; et al. Calculating structures and free energies of complex molecules: Combining molecular mechanics and continuum models. Acc. Chem. Res. 2000, 33, 889–897. [Google Scholar] [CrossRef] [PubMed]
- Genheden, S.; Ryde, U. The MM/PBSA and MM/GBSA methods to estimate ligand-binding affinities. Expert Opin. Drug Discov. 2015, 10, 449–461. [Google Scholar] [CrossRef] [PubMed]
- Kar, P.; Lipowsky, R.; Knecht, V. Importance of polar solvation and configurational entropy for design of antiretroviral drugs targeting HIV-1 protease. J. Phys. Chem. B 2013, 117, 5793–5805. [Google Scholar] [CrossRef] [PubMed]
- Foloppe, N.; Nilsson, L. Toward a full characterization of nucleic acid components in aqueous solution: Simulations of nucleosides. J. Phys. Chem. B 2005, 109, 9119–9131. [Google Scholar] [CrossRef] [PubMed]
- Perez, A.; Lankas, F.; Luque, F.J.; Orozco, M. Towards a molecular dynamics consensus view of B-DNA flexibility. Nucleic Acids Res. 2008, 36, 2379–2394. [Google Scholar] [CrossRef] [PubMed]
- Levinson, N.M.; Boxer, S.G. A conserved water-mediated hydrogen bond network defines bosutinib’s kinase selectivity. Nat. Chem. Biol. 2014, 10, 127–132. [Google Scholar] [CrossRef] [PubMed]
- Rudling, A.; Orro, A.; Carlsson, J. Prediction of Ordered Water Molecules in Protein Binding Sites from Molecular Dynamics Simulations: The Impact of Ligand Binding on Hydration Networks. J. Chem. Inf. Model. 2018, 58, 350–361. [Google Scholar] [CrossRef] [PubMed]
- Panigrahi, S.K. Strong and weak hydrogen bonds in protein-ligand complexes of kinases: A comparative study. Amino Acids 2008, 34, 617–633. [Google Scholar] [CrossRef] [PubMed]
- Case, D.; Darden, T.; Cheatham, T., III; Simmerling, C.; Wang, J.; Duke, R.; Luo, R.; Walker, R.; Zhang, W.; Merz, K.; et al. AmberTools 16; University of California: San Francisco, CA, USA, 2016. [Google Scholar]
- Sousa da Silva, A.W.; Vranken, W.F. ACPYPE—sAnteChamber PYthon Parser interfacE. BMC Res. Notes 2012, 5, 367. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Kumari, R.; Kumar, R.; Lynn, A. g_mmpbsa—A GROMACS tool for high-throughput MM-PBSA calculations. J. Chem. Inf. Model. 2014, 54, 1951–1962. [Google Scholar] [CrossRef] [PubMed]
- Verma, S.; Grover, S.; Tyagi, C.; Goyal, S.; Jamal, S.; Singh, A.; Grover, A. Hydrophobic Interactions Are a Key to MDM2 Inhibition by Polyphenols as Revealed by Molecular Dynamics Simulations and MM/PBSA Free Energy Calculations. PLoS ONE 2016, 11, e0149014. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhang, L.; Xu, Y.; Jiang, S.; Shao, Y. Deciphering the binding behavior of flavonoids to the cyclin dependent kinase 6/cyclin D complex. PLoS ONE 2018, 13, e0196651. [Google Scholar] [CrossRef] [PubMed]
- Patra, M.C.; Kwon, H.K.; Batool, M.; Choi, S. Computational Insight Into the Structural Organization of Full-Length Toll-Like Receptor 4 Dimer in a Model Phospholipid Bilayer. Front. Immunol. 2018, 9, 489. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Not available. |
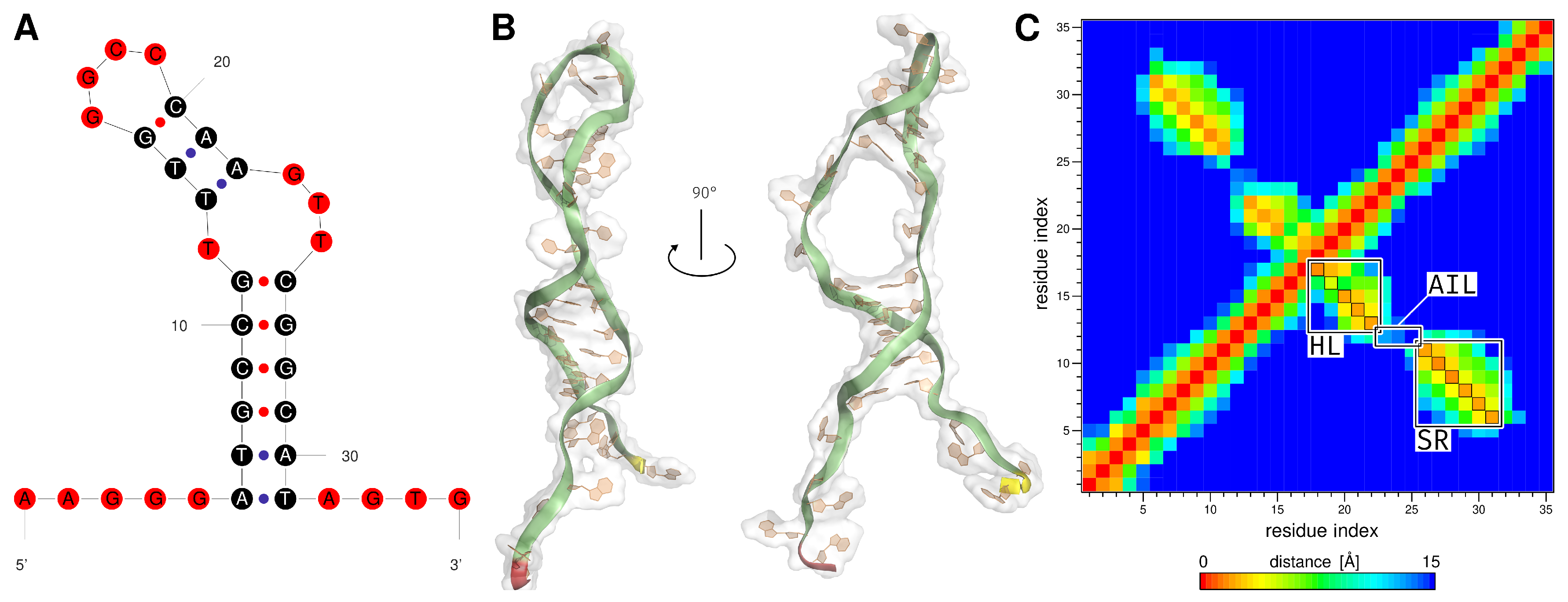
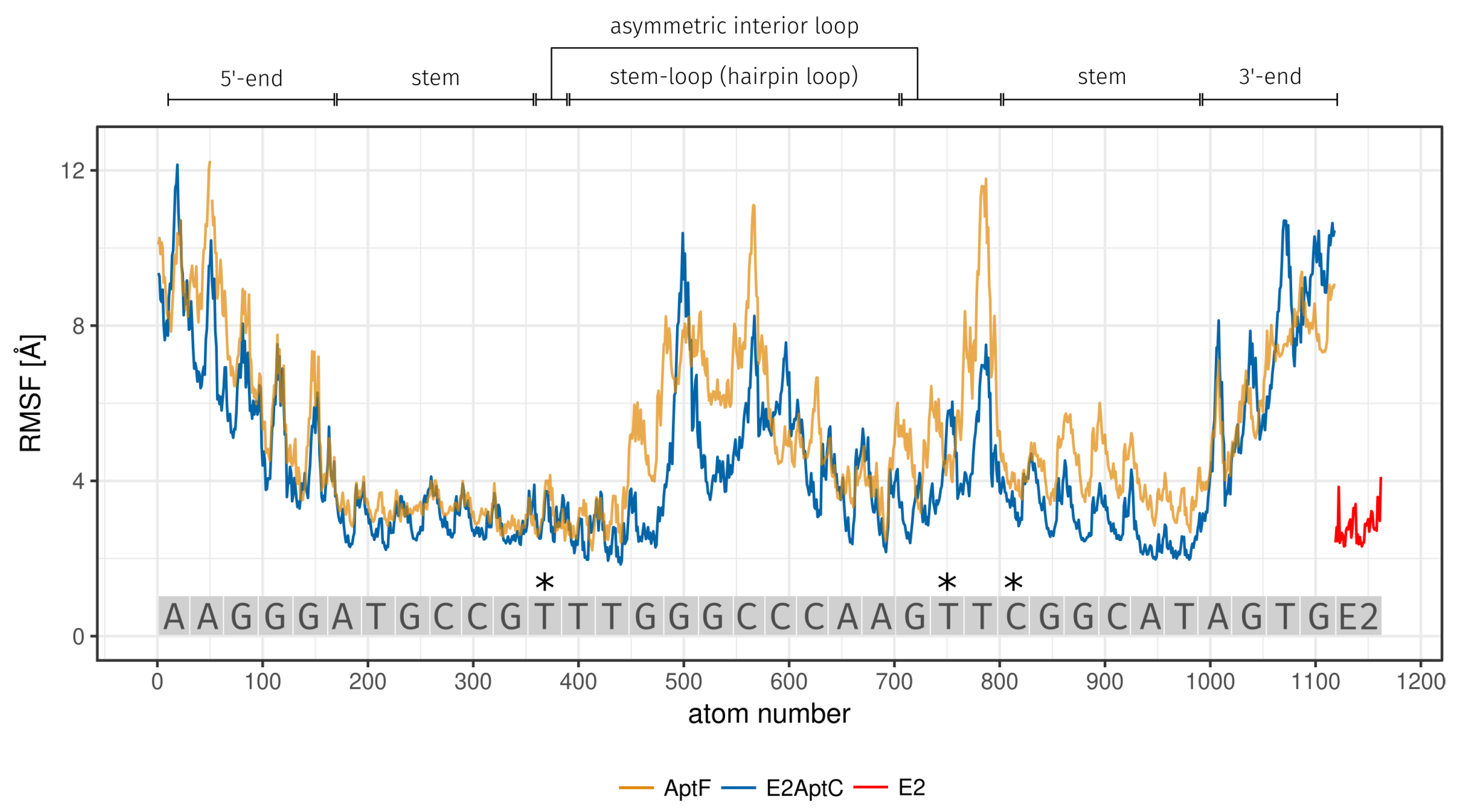
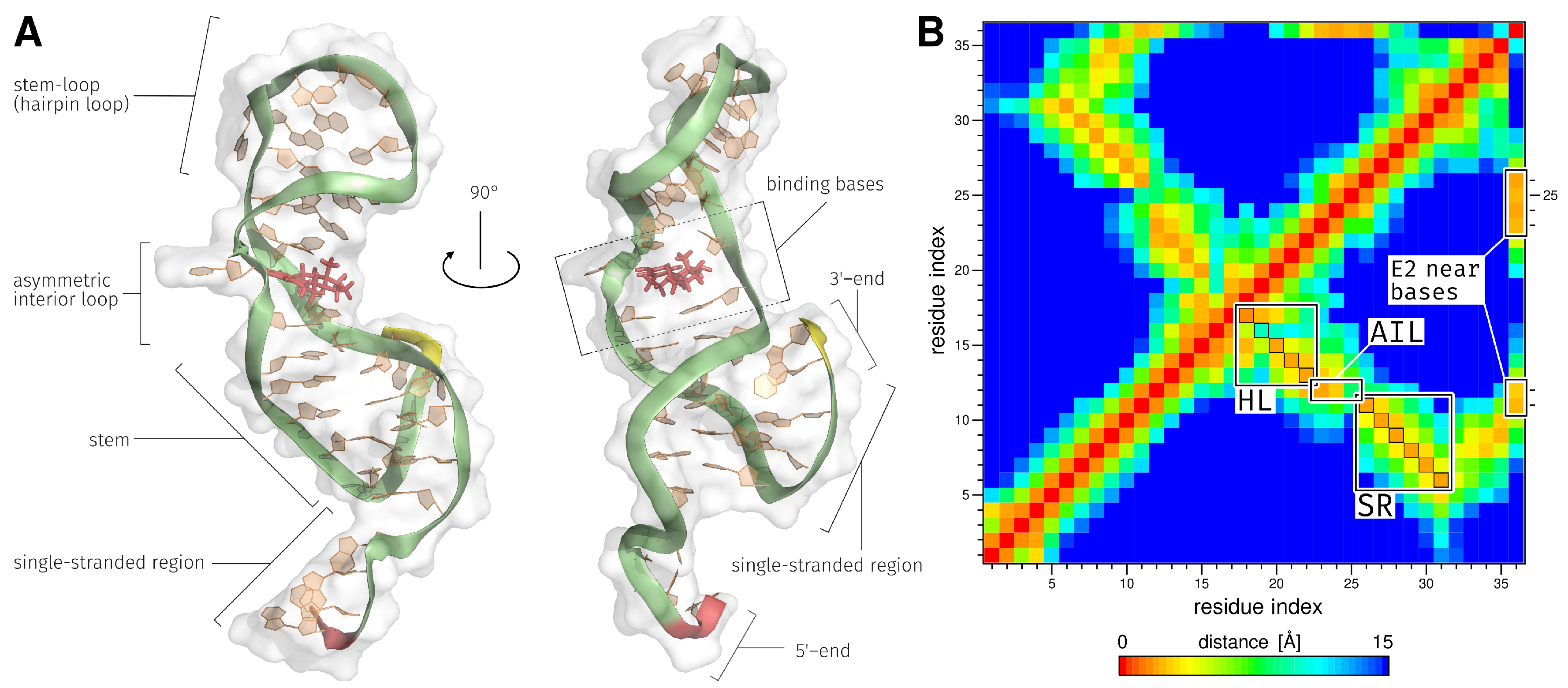
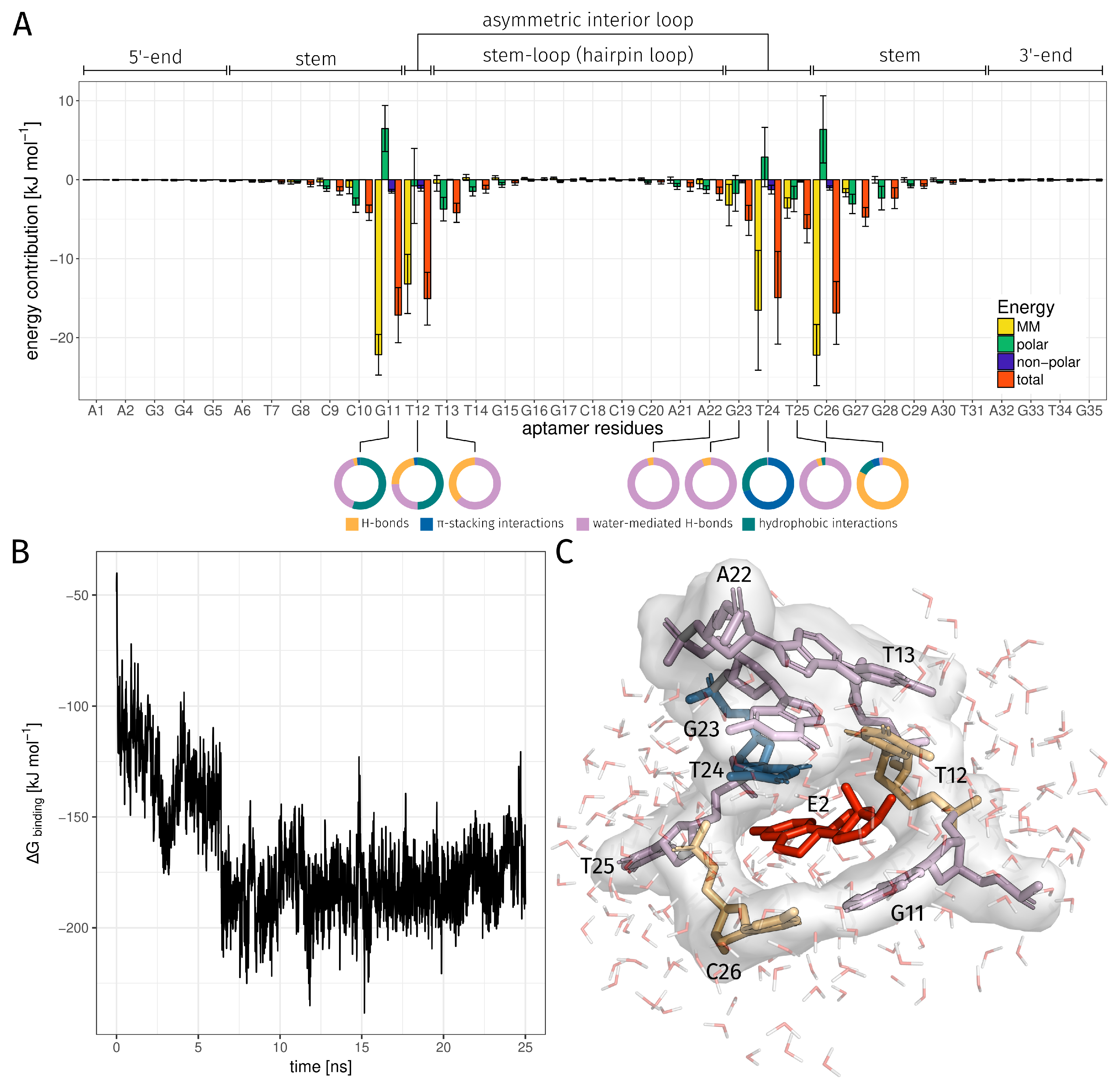
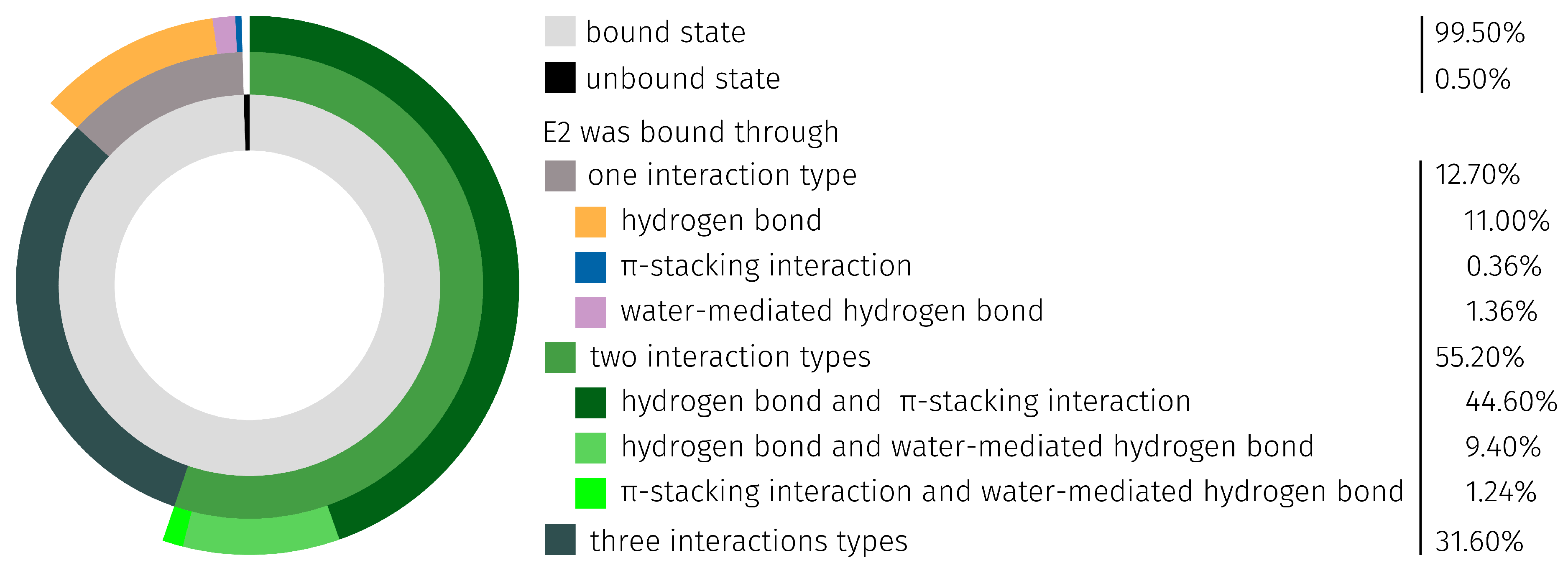
| Region | Base Range | RMSF [Å] of AptF | RMSF [Å] of E2AptC |
|---|---|---|---|
| 5-end | A1 to G5 | 7.34 | 6.43 |
| stem | A6 to G11 and C26 to T31 | 3.72 | 3.02 |
| asymmetric interior loop | T12 and G23 to T25 | 5.61 | 3.99 |
| hairpin loop | T13 to A22 | 5.14 | 4.24 |
| 3-end | A32 to G35 | 6.57 | 6.96 |
| 3*E2 binding site | T12 (asymmetric interior loop) | 3.18 | 3.10 |
| T24 (asymmetric interior loop) | 5.20 | 4.31 | |
| C26 (stem) | 4.20 | 3.61 | |
| E2 | - | - | 2.81 |
| Binding Bases | H-Bond rel. [%] | -Stacking int. rel. [%] | Water-Mediated H-Bond rel. [%] | Hydrophobic int. rel. [%] | Total rel. [%] |
|---|---|---|---|---|---|
| DG11 | 1.00 | 0.80 | 15.44 | 21.08 | 33.44 |
| DT12 | 17.68 | 1.92 | 19.04 | 38.64 | 60.96 |
| DT13 | 0.32 | 0.00 | 0.48 | 0.00 | 0.68 |
| DA22 | 0.04 | 0.00 | 0.96 | 0.00 | 1.00 |
| DG23 | 0.24 | 0.00 | 3.92 | 0.00 | 4.16 |
| DT24 | 0.04 | 70.56 | 0.56 | 29.76 | 76.44 |
| DT25 | 0.36 | 0.00 | 10.24 | 0.28 | 10.84 |
| DC26 | 94.36 | 5.76 | 2.68 | 11.16 | 98.00 |
| E2 Position | H-Bond abs./rel. [%] | Water-Mediated H-Bond abs./rel. [%] | Total abs./rel. [%] |
|---|---|---|---|
| 3 | 2415/84.65 | 494/33.40 | 2909/67.15 |
| 17- | 438/15.35 | 985/66.60 | 1423/32.85 |
| ∑ | 2853/100.00 | 1479/100.00 | 4332/100.00 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eisold, A.; Labudde, D. Detailed Analysis of 17β-Estradiol-Aptamer Interactions: A Molecular Dynamics Simulation Study. Molecules 2018, 23, 1690. https://doi.org/10.3390/molecules23071690
Eisold A, Labudde D. Detailed Analysis of 17β-Estradiol-Aptamer Interactions: A Molecular Dynamics Simulation Study. Molecules. 2018; 23(7):1690. https://doi.org/10.3390/molecules23071690
Chicago/Turabian StyleEisold, Alexander, and Dirk Labudde. 2018. "Detailed Analysis of 17β-Estradiol-Aptamer Interactions: A Molecular Dynamics Simulation Study" Molecules 23, no. 7: 1690. https://doi.org/10.3390/molecules23071690
APA StyleEisold, A., & Labudde, D. (2018). Detailed Analysis of 17β-Estradiol-Aptamer Interactions: A Molecular Dynamics Simulation Study. Molecules, 23(7), 1690. https://doi.org/10.3390/molecules23071690