Gold Nanoparticles as a Photothermal Agent in Cancer Therapy: The Thermal Ablation Characteristic Length
Abstract
:1. Introduction
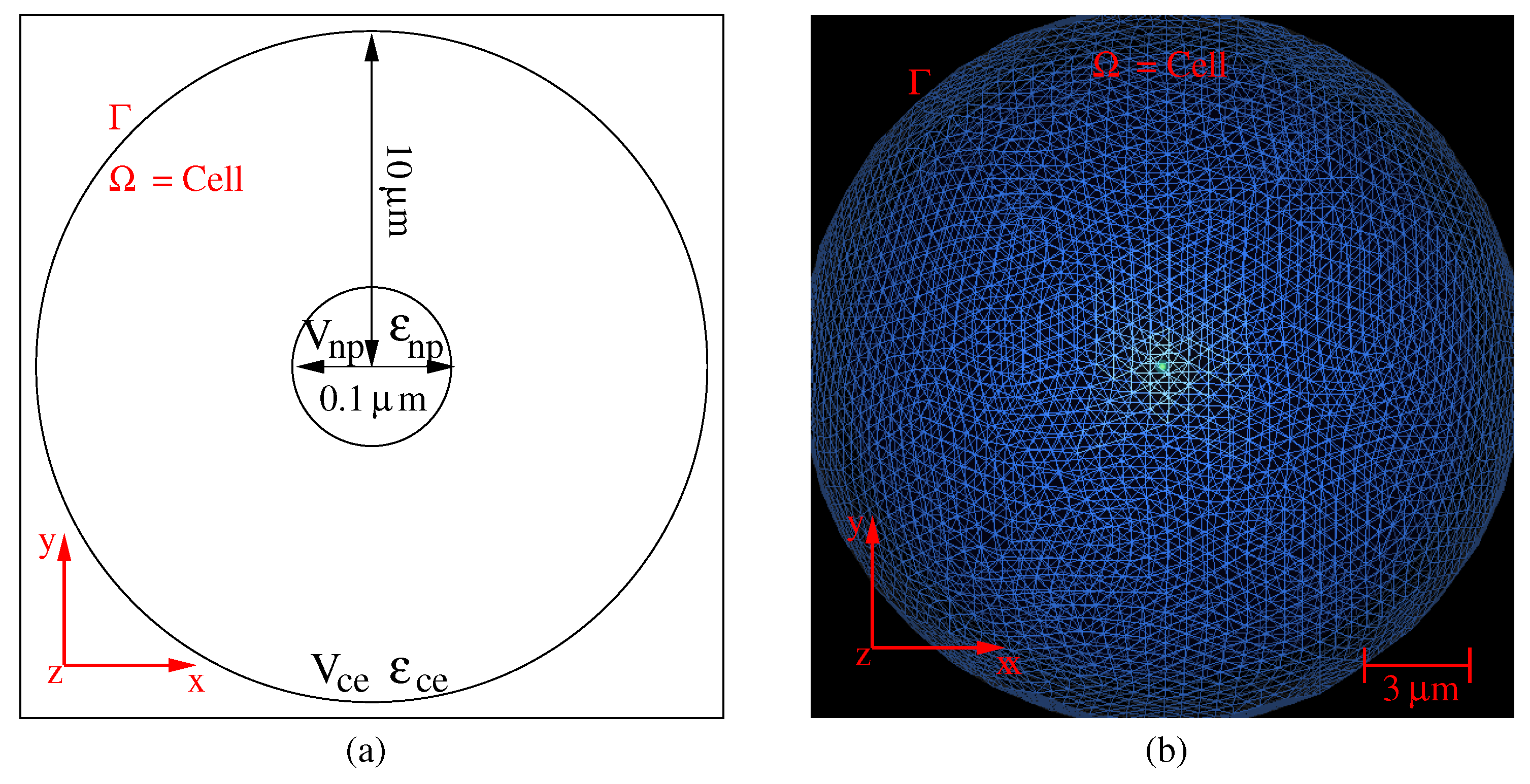
2. Photothermal Model
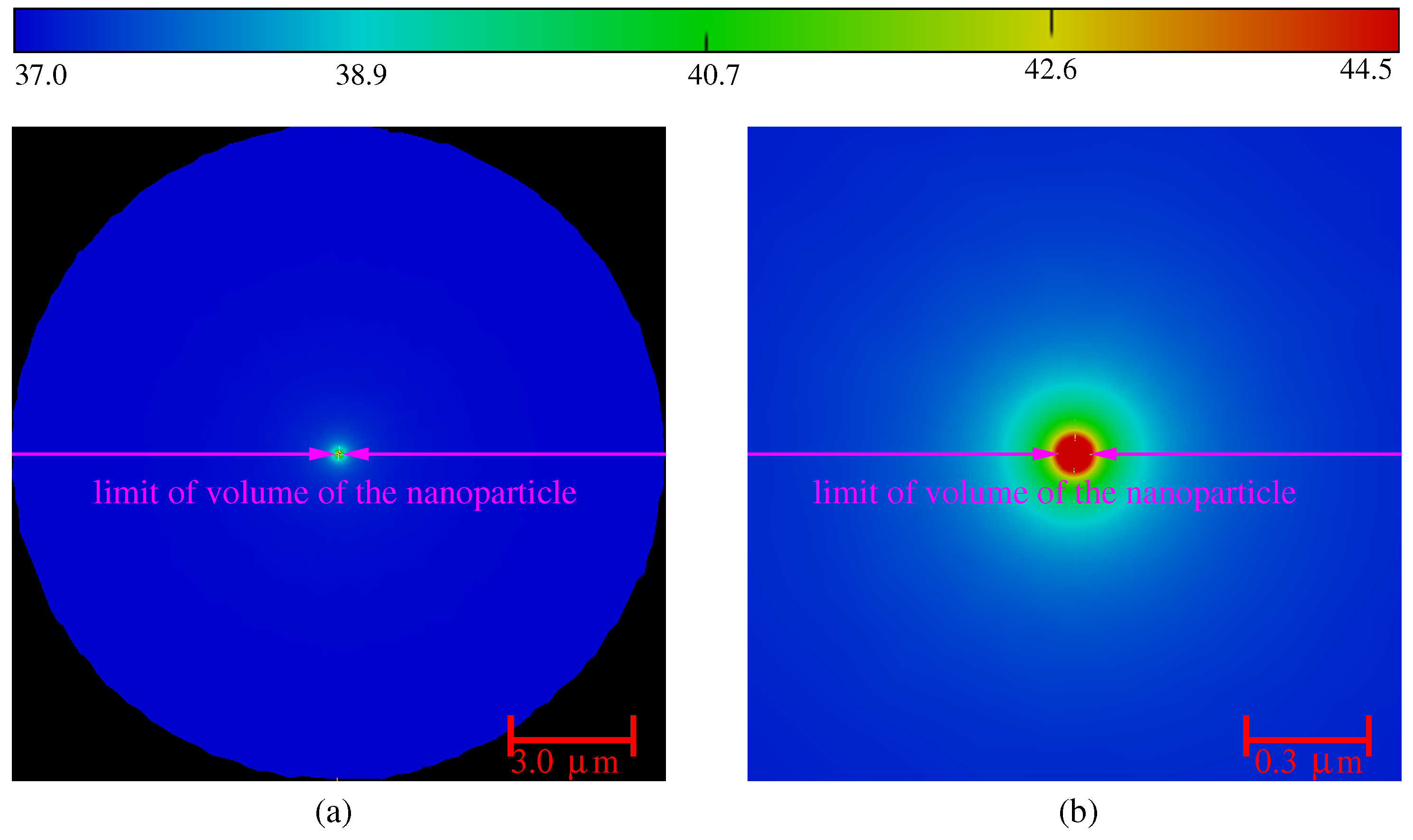
3. Numerical Results and Discussion
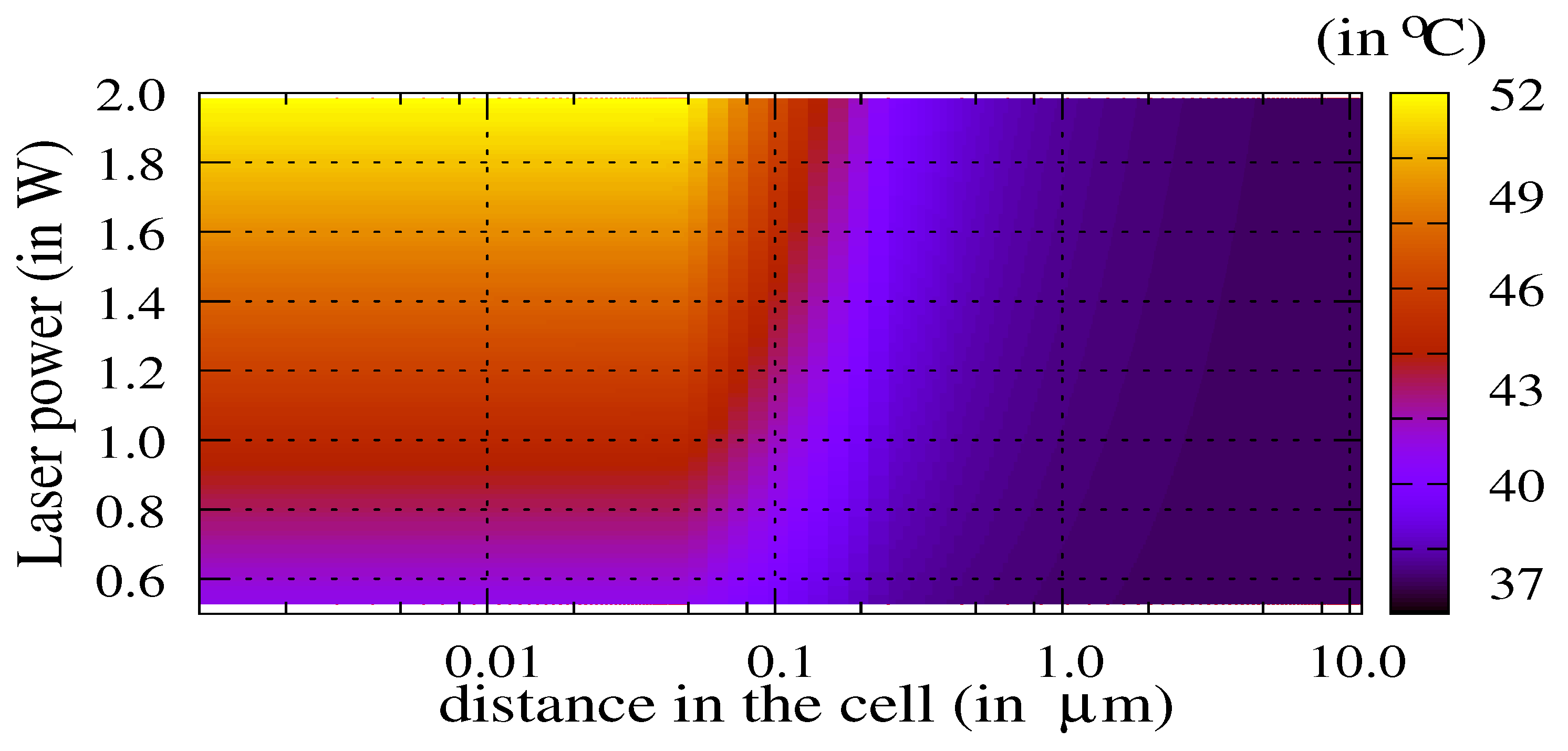
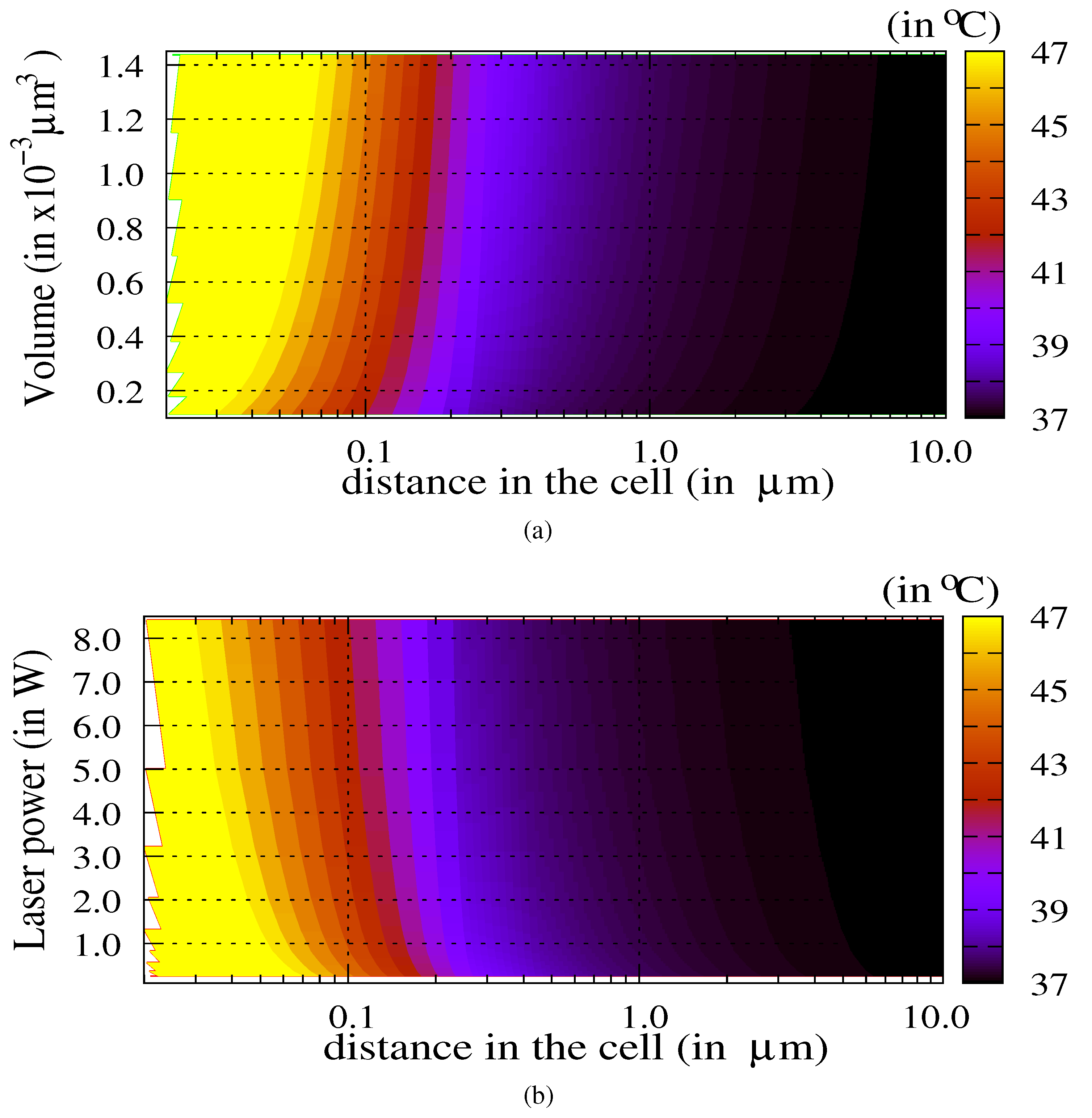
3.1. Influence of the Laser Power and of the Volume of Nanoparticles
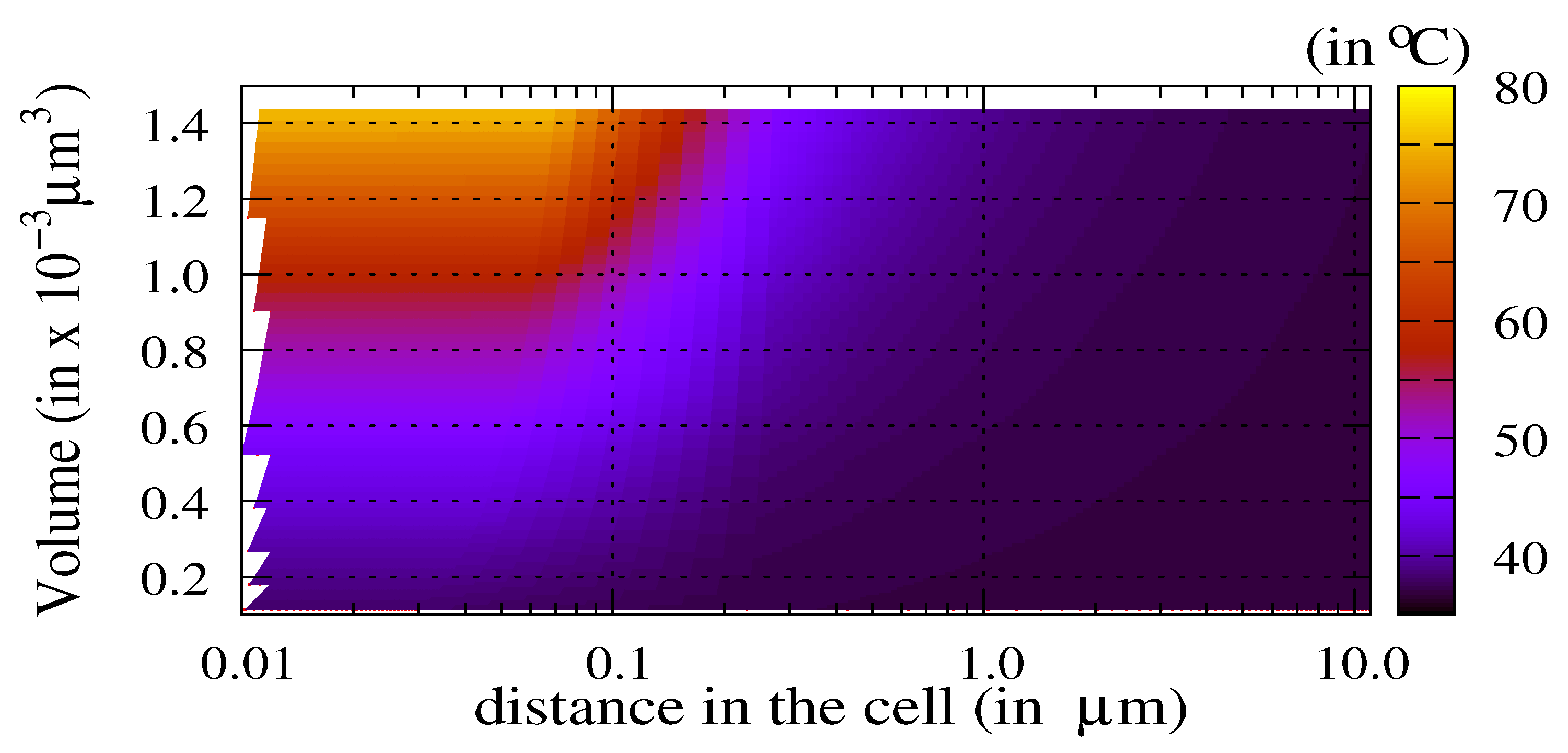
3.2. The Thermal Ablation Characteristic Length
3.3. Sensitivity Analysis
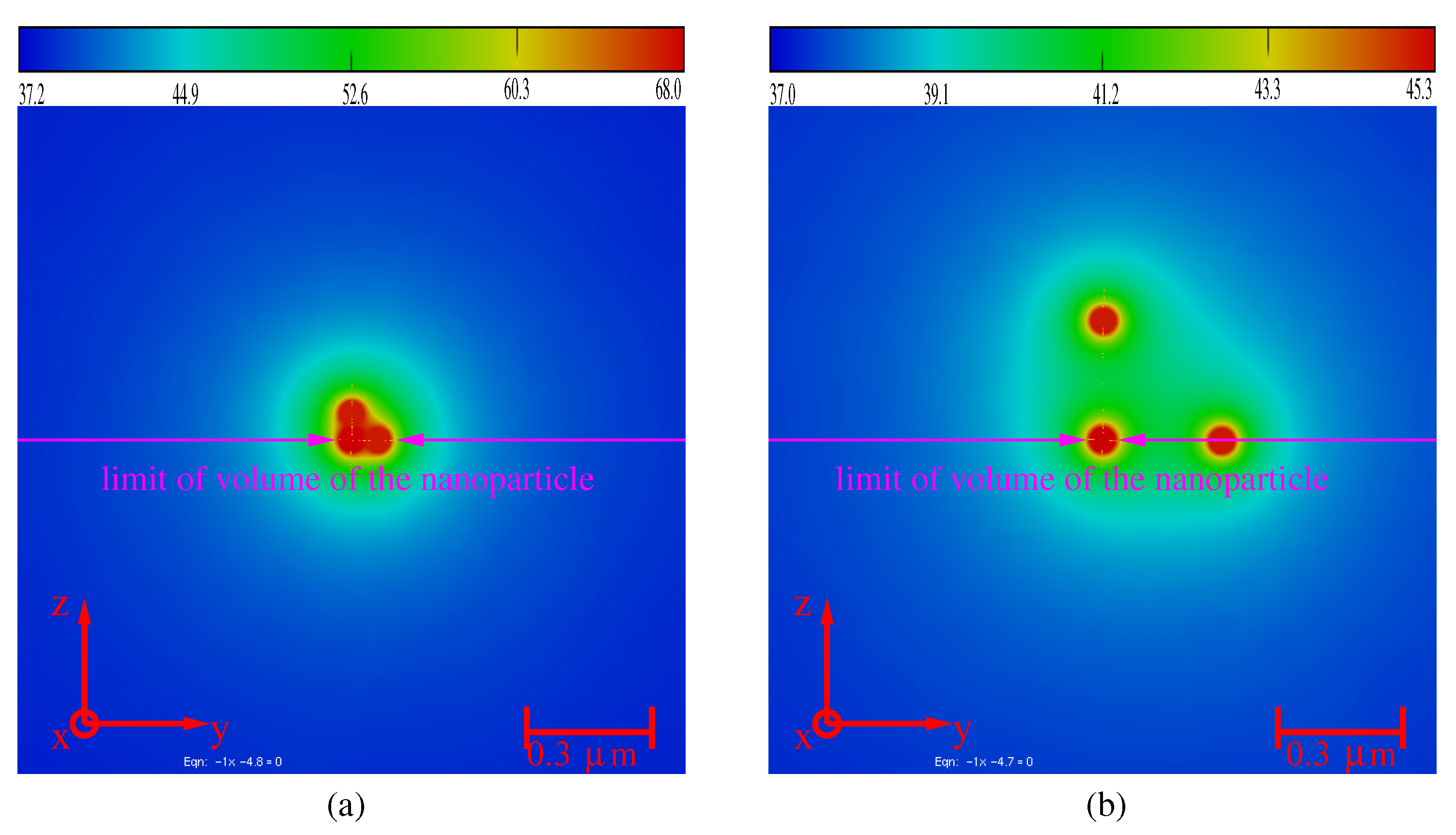
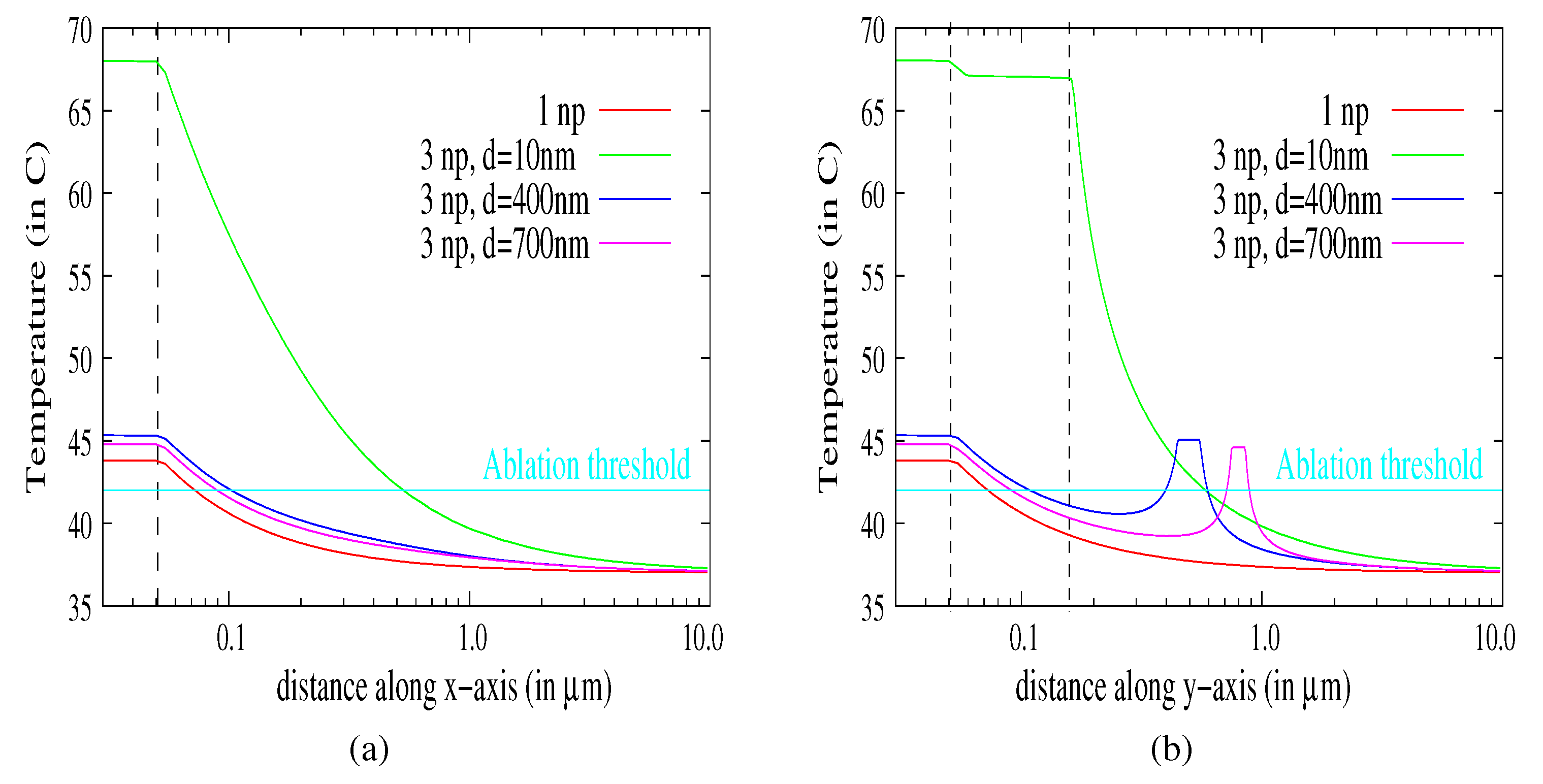
3.4. Aggregates of Nanoparticles
- : electromagnetic and thermal coupling,
- : thermal coupling,
- : no coupling.
3.5. Discussion of Material Parameters and Configuration
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Tam, A.C. Applications of photoacoustinc sensig techniques. Rev. Mod. Phys. 1986, 58, 381–431. [Google Scholar] [CrossRef]
- Shah, J.; Park, S.; Aglyamov, S.; Larson, T.; Ma, L.; Sokolov, K.; Johnston, K.; Milner, T.; Emelianov, S.Y. Photoacoustic imaging and temperature measurement for photothermal cancer therapy. J. Biomed. Opt. 2008, 13, 034024. [Google Scholar] [CrossRef] [PubMed]
- Shanmugam, V.; Selvakumar, S.; Yeh, C.S. Near-infrared light-responsive nanomaterials in cancer therapeutics. Chem. Soc. Rev. 2014, 43, 6254–6287. [Google Scholar] [CrossRef] [PubMed]
- Alkilany, A.M.; Thompson, L.B.; Boulos, S.P.; Sisco, P.N.; Murphy, C.J. Gold nanorods: Their potential for photothermal therapeutics and drug delivery, tempered by the complexity of their biological interactions. Adv. Drug Deliv. Rev. 2012, 64, 190–199. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wang, J.; Chen, C. Near-infrared light-mediated nanoplatforms for cancer thermo-chemotherapy and optical imaging. Adv. Mater. 2013, 25, 3869–3880. [Google Scholar] [CrossRef] [PubMed]
- Hirsch, L.R.; Stafford, R.J.; Bankson, J.A.; Sershen, S.R.; Rivera, B.; Price, R.E.; Hazle, J.D.; Halas, N.J.; West, J.L. Nanoshell-mediated near-infrared thermal therapy of tumors under magnetic resonance guidance. Proc. Natl. Acad. Sci. USA 2003, 100, 13549–13554. [Google Scholar] [CrossRef] [PubMed]
- Loo, C.; Lin, A.; Hirsch, L.; Lee, M.H.; Barton, J.; Halas, N.; West, J.; Drezek, R. Nanoshell-enabled photonics-based imaging and therapy of cancer. Technol. Cancer Res. Treat. 2004, 3, 33–40. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; El-Sayed, I.H.; Qian, W.; El-Sayed, M.A. Cancer cell imaging and photothermal therapy in the near-infrared region by using gold nanorods. J. Am. Chem. Soc. 2006, 128, 2115–2120. [Google Scholar] [CrossRef] [PubMed]
- Jelveh, S.; Chithrani, D.B. Gold Nanostructures as a Platform for Combinational Therapy in Future Cancer Therapeutics. Cancers 2011, 3, 1081–1110. [Google Scholar] [CrossRef] [PubMed]
- Manivasagan, P.; Bharathiraja, S.; Moorthy, M.S.; Mondal, S.; Nguyen, T.P.; Kim, H.; Phan, T.T.V.; Lee, K.D.; Oh, J. Biocompatible Chitosan Oligosaccharide Modified Gold Nanorods as Highly Effective Photothermal Agents for Ablation of Breast Cancer Cells. Polymers 2018, 10, 232. [Google Scholar] [CrossRef]
- Borouchaki, H.; Grosges, T.; Barchiesi, D. Improved 3D adaptive remeshing scheme applied in high electromagnetic field gradient computation. Finite Elem. Anal. Des. 2010, 46, 84–95. [Google Scholar] [CrossRef]
- Grosges, T.; Borouchaki, H.; Barchiesi, D. Three dimensional adaptive meshing scheme applied to the control of the spatial representation of complex field pattern in electromagnetics. Appl. Phys. B-Lasers Opt. 2010, 101, 883–889. [Google Scholar] [CrossRef]
- Grosges, T.; Barchiesi, D. Numerical Study of Photoacoustic Pressure For Cancer Therapy. Appl. Sci. 2016, 6, 357–359. [Google Scholar] [CrossRef]
- Jin, J. The Finite Element Method in Electromagnetics; John Wiley and Sons: New York, NY, USA, 1993. [Google Scholar]
- Mezghani, F.; Barchiesi, D.; Cherouat, A.; Grosges, T.; Borouchaki, H. Comparison of 3D Adaptive Remeshing Strategies for Finite Element Simulations of Electromagnetic Heating of Gold Nanoparticles. Adv. Math. Phys. 2015, 2015, 469310. [Google Scholar] [CrossRef]
- Courant, R. Variational methods for the solution of problems of equilibrium and vibrations. Bull. Am. Math. Soc. 1943, 49, 1–23. [Google Scholar] [CrossRef]
- Silvester, P.; Pelosi, G. Finite Elements for Wave Electromagnetics: Methods and Techniques; IEEE Press: New York, NY, USA, 1994. [Google Scholar]
- Ciarlet, P.G. Basic Error Estimates for Elliptic Problems; North Holland: New York, NY, USA, 1991. [Google Scholar]
- Xue, D.; Demkowicz, L. Modeling of electromagnetic absorption/scattering problems on curvilinear geometries using hp finite/infinite element method. Finite Elem. Anal. Des. 2006, 42, 570–579. [Google Scholar] [CrossRef]
- Bourouchaki, H.; Grosges, T.; Barchiesi, D. Enhancement of the accuracy of numerical field computation using adaptive three dimensional remeshing scheme. Comptes Rendus Mécanique 2010, 338, 127–131. [Google Scholar] [CrossRef]
- Radovitzky, R.; Ortiz, M. Error estimation and adaptive meshing in strongly non-linear dynamic problems. Comput. Method Appl. Mech. Eng. 1999, 172, 203–240. [Google Scholar] [CrossRef]
- Ainsworth, M.; Oden, J.T. A posteriori error estimation in finite element analysis. Comput. Method Appl. Mech. Eng. 1997, 142, 1–88. [Google Scholar] [CrossRef]
- Zou, L.; Wang, H.; Bin, H.; Zeng, L.; Tan, T.; Cao, H.; He, X.; Zhang, Z.; Guo, S.; Li, Y. Current Approaches of Photothermal Therapy in Treating Cancer Metastasis with Nanotherapeutics. Theranostics 2016, 6, 762–772. [Google Scholar] [CrossRef] [PubMed]
- Shiraga, K.; Ogawa, Y.; Suzuki, T.; Kondo, N.; Irisawa, A.; Imamura, M. Characterization of Dielectric Responses of Human Cancer Cells in the Terahertz Region. J. Infrared Millim. Terahertz Waves 2014, 35, 493–502. [Google Scholar] [CrossRef]
- Barchiesi, D.; Grosges, T. Propagation of uncertainties and applications in numerical modeling: Tutorial. J. Opt. Soc. Am. A 2017, 34, 1602–1619. [Google Scholar] [CrossRef] [PubMed]
- Fan, L.L.; Zhu, M.; Lee, X.; Zhang, R.J.; Wang, K.L.; Wei, J.Q.; Zhong, M.L.; Wu, D.H.; Zhu, H.W. Direct Synthesis of Graphene Quantum Dots by Chemical Vapor Deposit. Part. Part. Syst. Charact. 2013, 30, 764–769. [Google Scholar] [CrossRef]
- Bergamini, L.; Voliani, V.; Cappello, V.; Nifosi, R.; Corni, S. Non-linear optical response by functionalized gold nanospheres: Identifying design principles to maximize the molecular photo-release. Nanoscale 2015, 7, 13345–13357. [Google Scholar] [CrossRef] [PubMed]
- Grosges, T.; Barchiesi, D.; Kessentini, S.; Gréhan, G.; Lamy de la Chapelle, M. Nanoshells for photothermal therapy: A Monte-Carlo based numerical study of their design tolerance. Biomed. Opt. Express 2011, 2, 1584–1596. [Google Scholar] [CrossRef] [PubMed]
- Campbell, N.A.; Williamson, B.; Heyden, R.J. Biology: Exploring Life; Pearson Prentice Hall: Boston, MA, USA, 2006. [Google Scholar]

| (kg·m) | (msK) | (kg·m·sK) | (at 830 nm) | |
|---|---|---|---|---|
| cell | 1090 | 2185 | 1.20 | 2.04 |
| Au | 19,300 | 129 | 310 | −26.61 + j1.67 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grosges, T.; Barchiesi, D. Gold Nanoparticles as a Photothermal Agent in Cancer Therapy: The Thermal Ablation Characteristic Length. Molecules 2018, 23, 1316. https://doi.org/10.3390/molecules23061316
Grosges T, Barchiesi D. Gold Nanoparticles as a Photothermal Agent in Cancer Therapy: The Thermal Ablation Characteristic Length. Molecules. 2018; 23(6):1316. https://doi.org/10.3390/molecules23061316
Chicago/Turabian StyleGrosges, Thomas, and Dominique Barchiesi. 2018. "Gold Nanoparticles as a Photothermal Agent in Cancer Therapy: The Thermal Ablation Characteristic Length" Molecules 23, no. 6: 1316. https://doi.org/10.3390/molecules23061316
APA StyleGrosges, T., & Barchiesi, D. (2018). Gold Nanoparticles as a Photothermal Agent in Cancer Therapy: The Thermal Ablation Characteristic Length. Molecules, 23(6), 1316. https://doi.org/10.3390/molecules23061316






