Variety Identification of Raisins Using Near-Infrared Hyperspectral Imaging
Abstract
1. Introduction
2. Results and Discussion
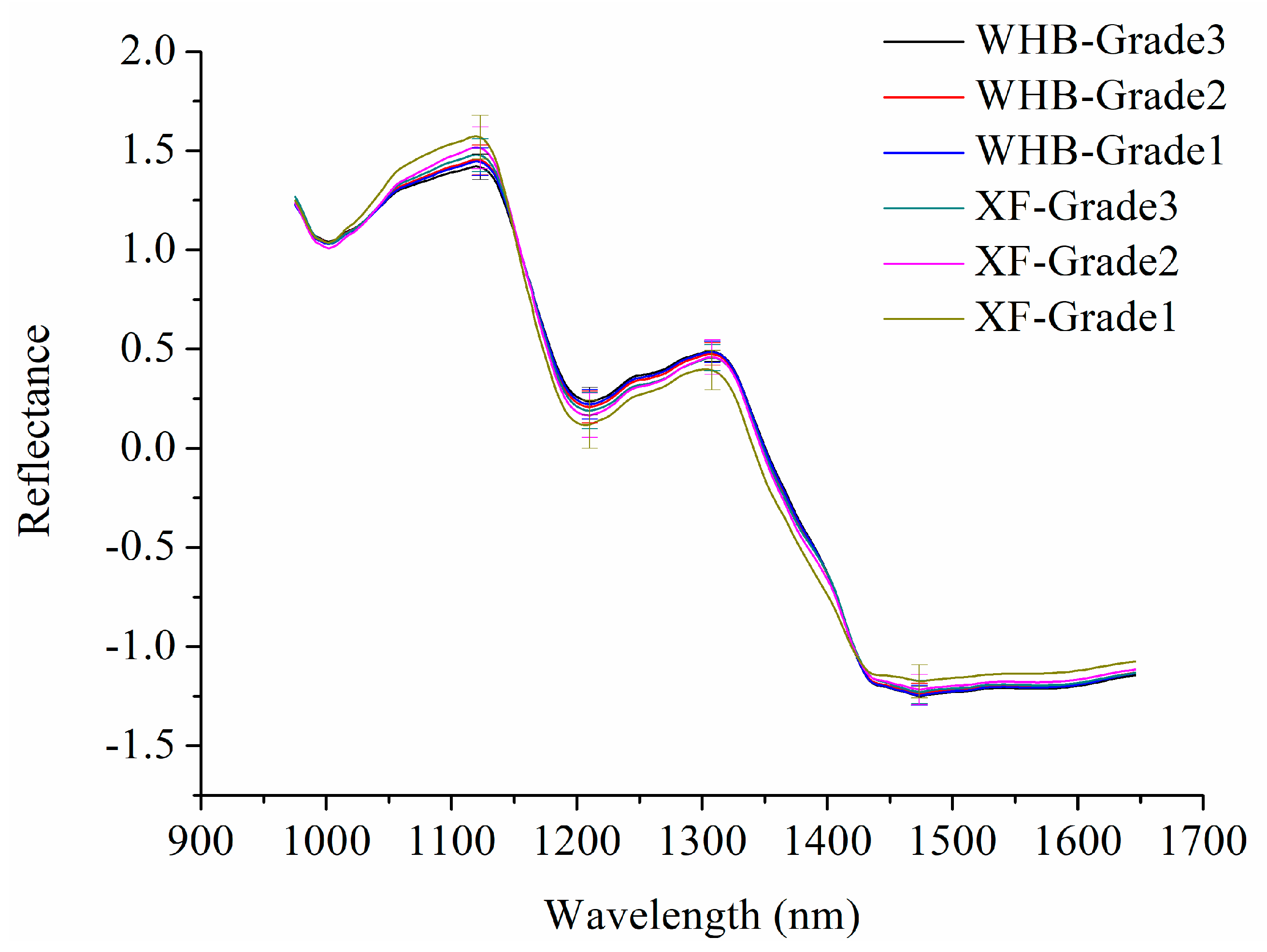
2.1. Spectral Profiles
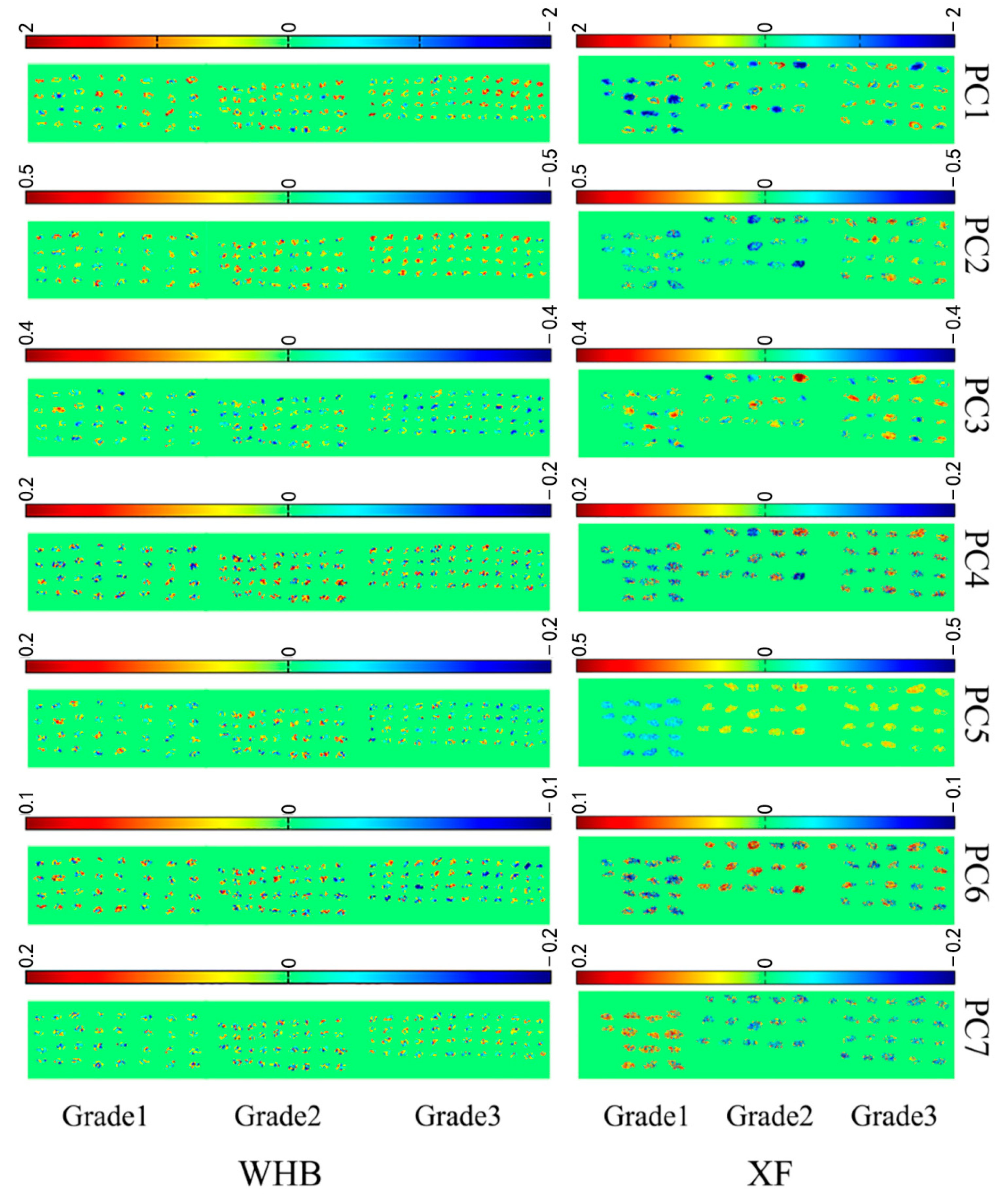
2.2. PCA Scores Image Visualization
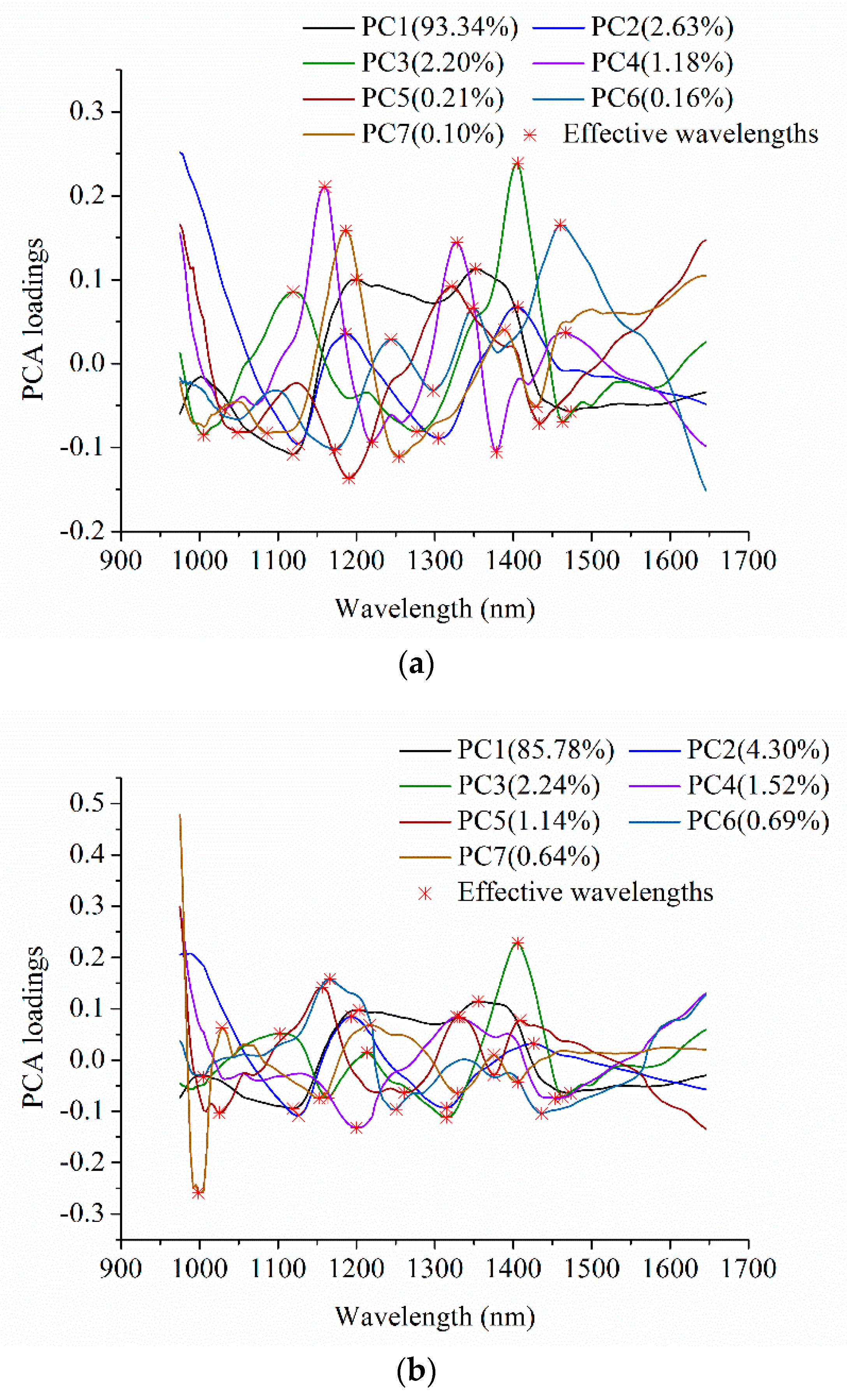
2.3. Effective Wavelength Selection
2.4. Raisin Variety Classification Models Based on Different Grades
2.5. Classification Results of Pixel-Wise and Object-Wise Spectra
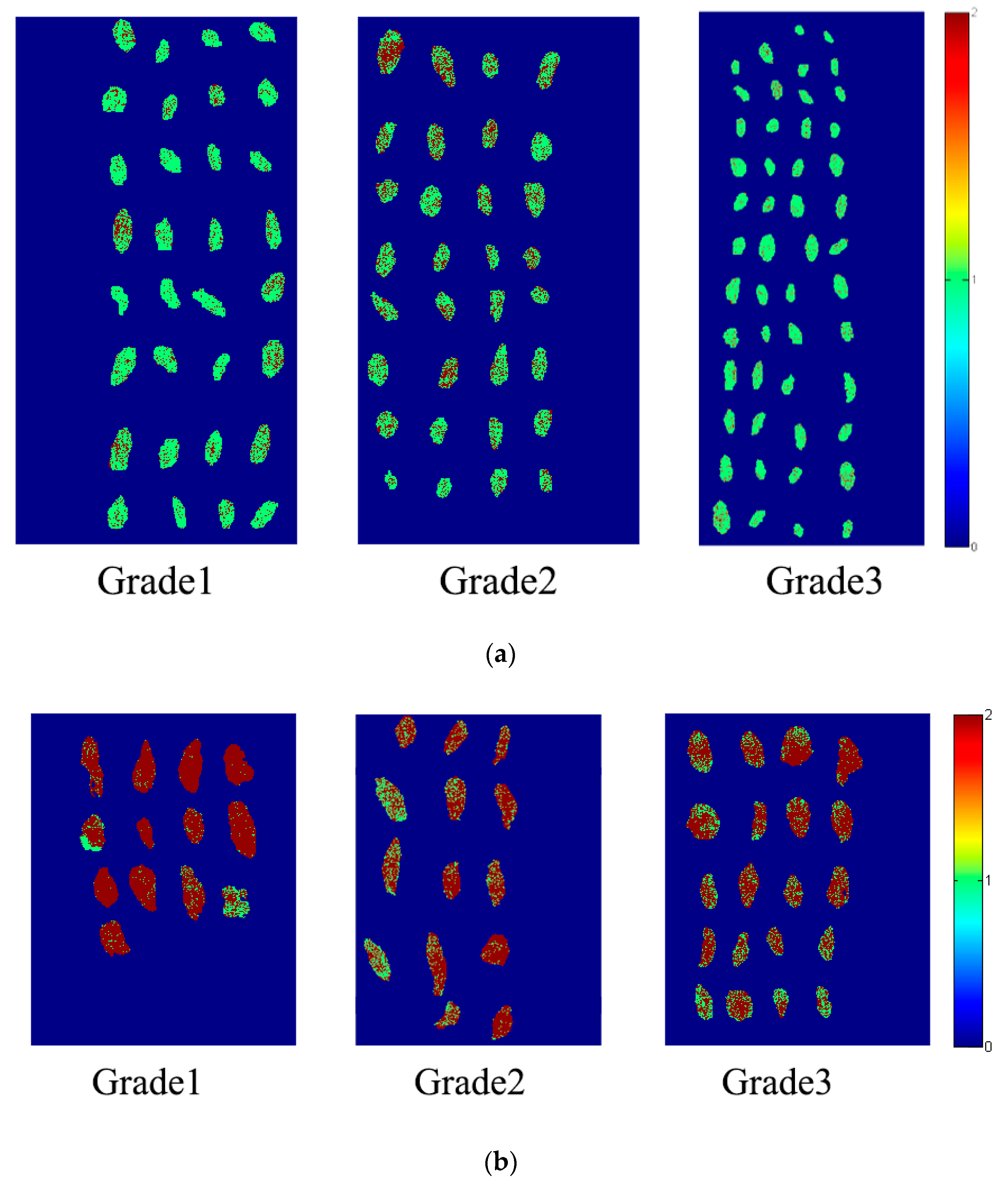
2.6. Prediction Maps of Raisin Variety Detection
3. Materials and Methods
3.1. Sample Preparation
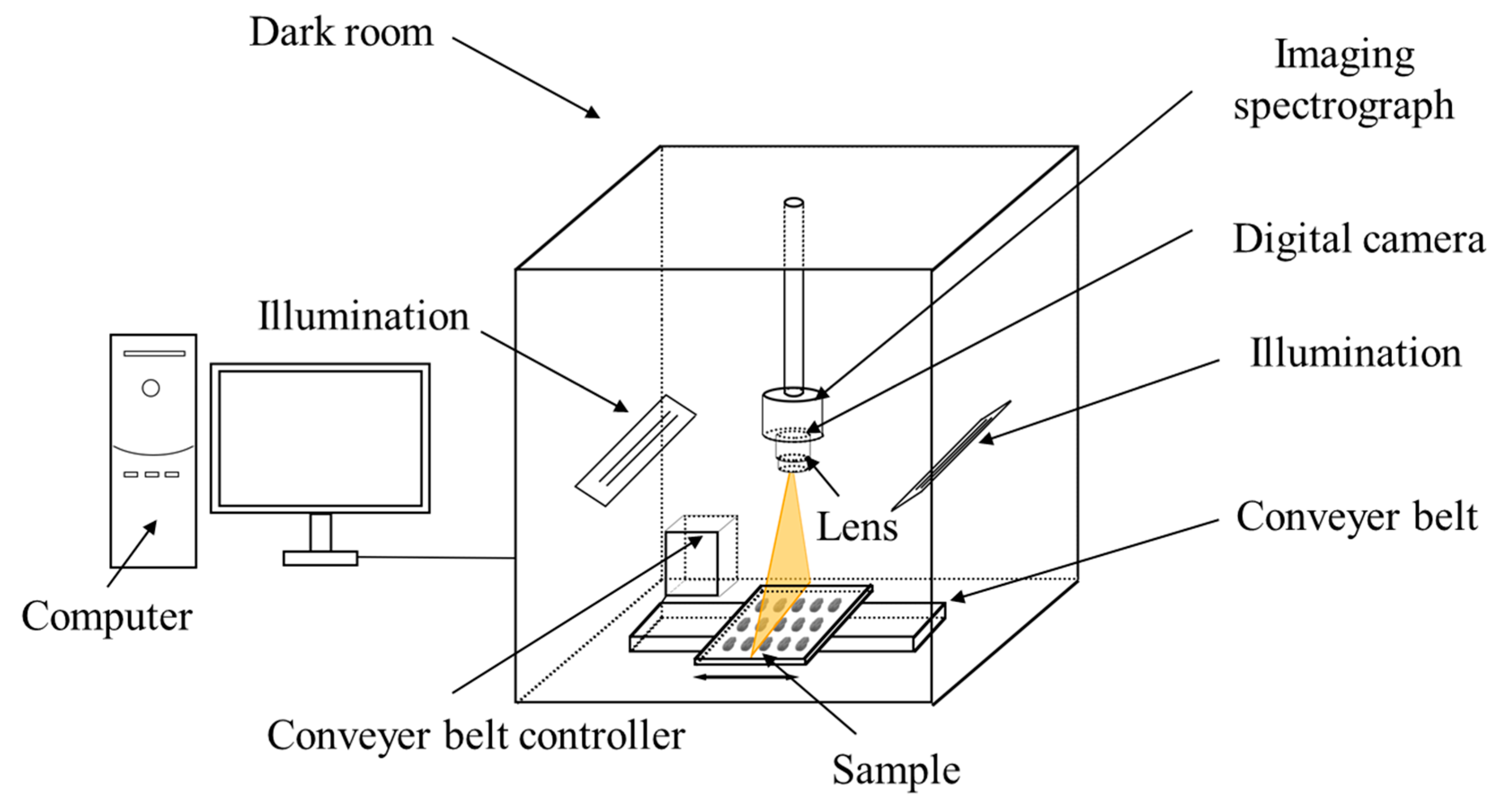
3.2. Hyperspectral Imaging System
3.3. Hyperspectral Image Acquisition and Correction
3.4. Spectral Data Preprocessing and Extraction
3.5. Sample Set Division
3.6. Data Analysis Methods
3.6.1. Principal Component Analysis
3.6.2. Independent Component Analysis
3.6.3. Discriminant Models
3.6.4. Software and Model Evaluation
3.6.5. Visualization of Prediction Maps
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Williamson, G.; Carughi, A. Polyphenol content and health benefits of raisins. Nutr. Res. 2010, 30, 511–519. [Google Scholar] [CrossRef] [PubMed]
- Margaret, J.S.; Xinyue, W.; Tiffany, H.; James, E.P. A Comprehensive review of raisins and raisin components and their relationship to human health. J. Nutr. Health 2017, 50, 203. [Google Scholar] [CrossRef]
- Kanellos, P.T.; Kaliora, A.C.; Gioxari, A.; Christopoulou, G.O.; Kalogeropoulos, N.; Karathanos, V.T. Absorption and bioavailability of antioxidant phytochemicals and increase of serum oxidation resistance in healthy subjects following supplementation with raisins. Plant Food Hum. Nutr. 2013, 68, 411–415. [Google Scholar] [CrossRef] [PubMed]
- Bays, H.E.; Schmitz, K.; Christian, A.; Ritchey, M.; Anderson, J. Raisins and Blood Pressure: A Randomized, Controlled Trial. J. Am. Coll. Cardiol. 2012, 59, E1721. [Google Scholar] [CrossRef]
- Huiling, M.; Wang, R.; Cheng, C.; Dong, W. Rapid Identification of Apple Varieties Based on Hyperspectral Imaging. Trans. CSAE 2017, 48, 305–312. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, C.; Liu, F.; He, Y. Mid-Infrared Spectroscopy for Coffee Variety Identification: Comparison of Pattern Recognition Methods. J. Spectrosc. 2016, 2016, 1–7. [Google Scholar] [CrossRef]
- Yang, S.; Zhu, Q.B.; Huang, M.; Qin, J.W. Hyperspectral Image-Based Variety Discrimination of Maize Seeds by Using a Multi-Model Strategy Coupled with Unsupervised Joint Skewness-Based Wavelength Selection Algorithm. Food Anal. Method 2017, 10, 1–10. [Google Scholar] [CrossRef]
- Bao, Y.; Liu, F.; Kong, W.; Sun, D.W.; He, Y.; Qiu, Z. Measurement of Soluble Solid Contents and pH of White Vinegars Using VIS/NIR Spectroscopy and Least Squares Support Vector Machine. Food Bioprocess Technol. 2014, 7, 54–61. [Google Scholar] [CrossRef]
- Wang, H.; Peng, J.; Xie, C.; Bao, Y.; He, Y. Fruit Quality Evaluation Using Spectroscopy Technology: A Review. Sensors 2015, 15, 11889. [Google Scholar] [CrossRef] [PubMed]
- Fernandes, A.M.; Oliveira, P.; Moura, J.P.; Oliveira, A.A.; Falco, V.; Correia, M.J.; Melopinto, P. Determination of anthocyanin concentration in whole grape skins using hyperspectral imaging and adaptive boosting neural networks. J. Food Eng. 2011, 105, 216–226. [Google Scholar] [CrossRef]
- Rodríguez-Pulido, F.J.; Barbin, D.F.; Sun, D.W.; Gordillo, B.; González-Miret, M.L.; Heredia, F.J. Grape seed characterization by NIR hyperspectral imaging. Postharvest Biol. Technol. 2013, 76, 74–82. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, C.; Zhu, S.; Gao, P.; Feng, L.; He, Y. Non-Destructive and Rapid Variety Discrimination and Visualization of Single Grape Seed Using Near-Infrared Hyperspectral Imaging Technique and Multivariate Analysis. Molecules 2018, 23, 1352. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Wang, Q.; Liu, F.; He, Y.; Xiao, Y. Rapid and non-destructive measurement of spinach pigments content during storage using hyperspectral imaging with chemometrics. Measurement 2016, 97, 149–155. [Google Scholar] [CrossRef]
- Kong, W.; Zhang, C.; Cao, F.; Liu, F.; Luo, S.; Tang, Y.; He, Y. Detection of Sclerotinia Stem Rot on Oilseed Rape (Brassica napus L.) Leaves Using Hyperspectral Imaging. Sensors 2018, 18, 1764. [Google Scholar] [CrossRef]
- Xing, J.; Symons, S.; Shahin, M.; Hatcher, D. Detection of sprout damage in Canada Western Red Spring wheat with multiple wavebands using visible/near-infrared hyperspectral imaging. Biosyst. Eng. 2010, 106, 188–194. [Google Scholar] [CrossRef]
- Williams, P.J.; Kucheryavskiy, S. Classification of maize kernels using NIR hyperspectral imaging. Food Chem. 2016, 209, 131–138. [Google Scholar] [CrossRef]
- Arngren, M.; Hansen, P.W.; Eriksen, B.; Larsen, J.; Larsen, R. Analysis of Pregerminated Barley Using Hyperspectral Image Analysis. J. Agric. Food Chem. 2011, 59, 11385–11394. [Google Scholar] [CrossRef] [PubMed]
- Yao, H.; Hruska, Z.; Kincaid, R.; Brown, R.L.; Bhatnagar, D.; Cleveland, T.E. Hyperspectral image classification and development of fluorescence index for single corn kernels infected with Aspergillus flavus. Trans. ASABE 2013, 56, 1977–1988. [Google Scholar] [CrossRef]
- Khodabux, K.; L’Omelette, M.S.S.; Jhaumeer-Laulloo, S.; Ramasami, P.; Rondeau, P. Chemical and near-infrared determination of moisture, fat and protein in tuna fishes. Food Chem. 2007, 102, 669–675. [Google Scholar] [CrossRef]
- Kinoshita, K.; Miyazaki, M.; Morita, H.; Vassileva, M.; Tang, C.; Li, D.; Ishikawa, O.; Kusunoki, H.; Tsenkova, R. Spectral pattern of urinary water as a biomarker of estrus in the giant panda. Sci. Rep. 2012, 2, 856. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Liu, F.; He, Y. Identification of coffee bean varieties using hyperspectral imaging: Influence of preprocessing methods and pixel-wise spectra analysis. Sci. Rep. 2018, 8, 2166. [Google Scholar] [CrossRef] [PubMed]
- Diezma, B.; Lleó, L.; Roger, J.M.; Herrero-Langreo, A.; Lunadei, L.; Ruiz-Altisent, M. Examination of the quality of spinach leaves using hyperspectral imaging. Postharvest Biol. Technol. 2013, 85, 8–17. [Google Scholar] [CrossRef]
- Lara, M.A.; Lleó, L.; Diezma-Iglesias, B.; Roger, J.M.; Ruiz-Altisent, M. Monitoring spinach shelf-life with hyperspectral image through packaging films. J. Food Eng. 2013, 119, 353–361. [Google Scholar] [CrossRef]
- Kang, J.; Ryu, K.R.; Kwon, H.C. Using Cluster-Based Sampling to Select Initial Training Set for Active Learning in Text Classification. In Pacific-Asia Conference on Knowledge Discovery and Data Mining; Springer: Berlin/Heidelberg, Germany, 2004; pp. 384–388. [Google Scholar]
- Rinnan, Å.; Berg, F.V.D.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. Trac-Trend Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
- Choudhary, R.; Mahesh, S.; Paliwal, J.; Jayas, D.S. Identification of wheat classes using wavelet features from near infrared hyperspectral images of bulk samples. Biosyst. Eng. 2009, 102, 115–127. [Google Scholar] [CrossRef]
- Sun, J.; Jiang, S.; Mao, H.; Wu, X.; Li, Q. Classification of Black Beans Using Visible and Near Infrared Hyperspectral Imaging. Int. J. Food Sci. Technol. 2016, 19, 1687–1695. [Google Scholar] [CrossRef]
- Huang, M.; He, C.; Zhu, Q.; Qin, J. Maize Seed Variety Classification Using the Integration of Spectral and Image Features Combined with Feature Transformation Based on Hyperspectral Imaging. Appl. Sci. 2016, 6, 183. [Google Scholar] [CrossRef]
- Du, H.; Qi, H.; Wang, X.; Ramanath, R. Band selection using independent component analysis for hyperspectral image processing. In Proceedings of the Applied Imagery Pattern Recognition Workshop, Washington, DC, USA, 15–17 October 2003; IEEE: New York, NY, USA, 2003; pp. 93–98. [Google Scholar]
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Feng, X.; Zhao, Y.; Zhang, C.; Cheng, P.; He, Y. Discrimination of Transgenic Maize Kernel Using NIR Hyperspectral Imaging and Multivariate Data Analysis. Sensors 2017, 17, 1894. [Google Scholar] [CrossRef] [PubMed]
- Dumont, J.; Hirvonen, T.; Heikkinen, V.; Mistretta, M.; Granlund, L.; Himanen, K.; Fauch, L.; Porali, I.; Hiltunen, J.; Keski-Saari, S. Thermal and hyperspectral imaging for Norway spruce (Picea abies) seeds screening. Comput. Electron. Agric. 2015, 116, 118–124. [Google Scholar] [CrossRef]
- Lee, H.; Kim, M.S.; Song, Y.R.; Oh, C.S.; Lim, H.S.; Lee, W.H.; Kang, J.S.; Cho, B.K. Non-destructive evaluation of bacteria-infected watermelon seeds using visible/near-infrared hyperspectral imaging. J. Sci. Food Agric. 2016, 97, 1084. [Google Scholar] [CrossRef] [PubMed]
- Guo, G.; Wang, H.; Bell, D.; Bi, Y.; Greer, K. KNN Model-Based Approach in Classification. In Proceedings of the Otm Confederated International Conferences on the Move to Meaningful Internet Systems, Catania, Sicily, Italy, 3–7 November 2003; Springer: Berlin, Germany, 2003; pp. 986–996. [Google Scholar]
- Hall, P.; Park, B.U.; Samworth, R.J. Choice of Neighbor Order in Nearest-Neighbor Classification. Ann. Stat. 2008, 36, 2135–2152. [Google Scholar] [CrossRef]
- Shcherbakov, V.; Larsson, E. Radial basis function partition of unity methods for pricing vanilla basket options. Comput. Math. Appl. 2016, 71, 185–200. [Google Scholar] [CrossRef]
- Fornberg, B.; Flyer, N.; Hovde, S.; Piret, C. Locality properties of radial basis function expansion coefficients for equispaced interpolation. IMA J. Numer. Anal. 2018, 28, 121–142. [Google Scholar] [CrossRef]
- Baratloo, A.; Hosseini, M.; Negida, A.; El Ashal, G. Part 1: Simple Definition and Calculation of Accuracy, Sensitivity and Specificity. Emergency 2015, 3, 48–49. [Google Scholar] [PubMed]
- He, J.; Zhang, C.; He, Y. Application of Near-Infrared Hyperspectral Imaging to Detect Sulfur Dioxide Residual in the Fritillaria thunbergii Bulbus Treated by Sulfur Fumigation. Appl. Sci. 2017, 7, 77. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are available from the authors. |

| Type of Analysis | No. | Optimal Wavelengths (nm) |
|---|---|---|
| Object-wise | 20 | 1005, 1032, 1049, 1086, 1119, 1160, 1173, 1187, 1200, 1220, 1244, 1254, 1278, 1305, 1328, 1352, 1379, 1406, 1433, 1473 |
| Pixel-wise | 17 | 1005, 1029, 1103, 1119, 1164, 1200, 1214, 1251, 1261, 1315, 1328, 1355, 1375, 1406, 1426, 1436, 1473 |
| Type of Analysis | No. | Optimal Wavelengths (nm) |
|---|---|---|
| Object-wise | 20 | 982, 985, 995, 999, 1002, 1009, 1012, 1015, 1019, 1022, 1025, 1029, 1032, 1035, 1039, 1042, 1046, 1049, 1052, 1056 |
| Pixel-wise | 17 | 1139, 1143, 1146, 1150, 1153, 1156, 1207, 1210, 1230, 1521, 1527, 1531, 1548, 1554, 1561, 1575, 1582 |
| WHB | XF | C 4 | γ 4 | Cal. Result | Pre. Results | |||
|---|---|---|---|---|---|---|---|---|
| WHB | XF | Pre. set | WHB | XF | ||||
| Grade1 1 | Grade1 | 1 | 3.0 | 665/665 | 245/246 | Grade3 | 1382/1382 | 0/602 |
| Grade2 | 930/931 | 22/453 | ||||||
| Grade1 | 380/380 | 99/116 | ||||||
| Grade2 2 | Grade2 | 256 | 16 | 622/622 | 304/305 | Grade3 | 1371/1382 | 559/602 |
| Grade2 | 305/309 | 146/148 | ||||||
| Grade1 | 1040/1045 | 323/362 | ||||||
| Grade3 3 | Grade3 | 48.5 | 9.1 | 950/950 | 405/405 | Grade3 | 419/432 | 197/197 |
| Grade2 | 658/931 | 434/453 | ||||||
| Grade1 | 1033/1045 | 51/362 | ||||||
| WHB | XF | C | γ | Cal. Result | Pre. Results | |||
|---|---|---|---|---|---|---|---|---|
| WHB | XF | Pre. set | WHB | XF | ||||
| Grade1 | Grade1 | 147.0 | 0.3 | 664/665 | 242/246 | Grade3 | 1380/1382 | 0/602 |
| Grade2 | 931/931 | 17/453 | ||||||
| Grade1 | 379/380 | 100/116 | ||||||
| Grade2 | Grade2 | 147.0 | 48.5 | 606/622 | 255/305 | Grade3 | 1360/1382 | 267/602 |
| Grade2 | 296/309 | 119/148 | ||||||
| Grade1 | 1014/1045 | 306/362 | ||||||
| Grade3 | Grade3 | 84.4 | 3.0 | 944/950 | 385/405 | Grade3 | 409/432 | 197/197 |
| Grade2 | 487/931 | 393/453 | ||||||
| Grade1 | 899/1045 | 15/362 | ||||||
| Model | Parameter 5 | Calibration Set | Prediction Set | |||||
|---|---|---|---|---|---|---|---|---|
| Acc. 6 (%) | Sen. 7 | Spe. 8 | Acc. (%) | Sen. | Spe. | |||
| Pixel to pixel 1 | SVM | (256, 5.28) | 91.83 | 0.898 | 0.939 | 80.10 | 0.800 | 0.802 |
| k-NN | 3 | 78.48 | 0.700 | 0.870 | 78.18 | 0.642 | 0.895 | |
| RBFNN | 7 | 88.40 | 0.842 | 0.926 | 80.89 | 0.797 | 0.819 | |
| Pixel to object 2 | SVM | (256, 5.28) | 91.83 | 0.898 | 0.939 | 93.62 | 0.785 | 0.998 |
| k-NN | 3 | 78.48 | 0.700 | 0.870 | 83.82 | 0.464 | 0.992 | |
| RBFNN | 7 | 88.40 | 0.842 | 0.926 | 91.40 | 0.711 | 0.997 | |
| Object to pixel 3 | SVM | (147, 9.12) | 99.72 | 0.994 | 0.998 | 71.10 | 0.817 | 0.626 |
| k-NN | 5 | 95.46 | 0.870 | 0.991 | 76.86 | 0.727 | 0.803 | |
| RBFNN | 3 | 99.78 | 0.994 | 0.999 | 54.14 | 0.819 | 0.317 | |
| Object to object 4 | SVM | (147, 9.12) | 99.72 | 0.994 | 0.998 | 99.12 | 0.987 | 0.993 |
| k-NN | 5 | 95.46 | 0.870 | 0.991 | 94.06 | 0.839 | 0.982 | |
| RBFNN | 3 | 99.78 | 0.994 | 0.999 | 99.30 | 0.983 | 0.997 | |
| Model | Parameter 5 | Calibration Set | Prediction Set | |||||
|---|---|---|---|---|---|---|---|---|
| Acc. 6 (%) | Sen. 7 | Spe. 8 | Acc. (%) | Sen. | Spe. | |||
| Pixel to pixel 1 | SVM | (256, 16) | 82.15 | 0.739 | 0.903 | 74.9 | 0.708 | 0.784 |
| k-NN | 3 | 85.60 | 0.791 | 0.896 | 71.13 | 0.618 | 0.789 | |
| RBFNN | 6 | 78.92 | 0.695 | 0.884 | 76.74 | 0.797 | 0.819 | |
| Pixel to object 2 | SVM | (256, 9.19) | 82.15 | 0.739 | 0.903 | 78.63 | 0.271 | 0.998 |
| k-NN | 3 | 85.60 | 0.791 | 0.896 | 79.58 | 0.393 | 0.962 | |
| RBFNN | 6 | 78.92 | 0.695 | 0.884 | 80.47 | 0.341 | 0.996 | |
| Object to pixel 3 | SVM | (147, 84.45) | 94.68 | 0.879 | 0.976 | 54.63 | 0.870 | 0.285 |
| k-NN | 5 | 93.64 | 0.849 | 0.974 | 62.17 | 0.709 | 0.551 | |
| RBFNN | 3 | 93.96 | 0.851 | 0.977 | 48.34 | 0.565 | 0.417 | |
| Object to object 4 | SVM | (147, 84.45) | 94.68 | 0.879 | 0.976 | 93.81 | 0.863 | 0.969 |
| k-NN | 5 | 93.64 | 0.849 | 0.974 | 90.58 | 0.805 | 0.947 | |
| RBFNN | 3 | 93.96 | 0.851 | 0.977 | 93.30 | 0.844 | 0.970 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, L.; Zhu, S.; Zhang, C.; Bao, Y.; Gao, P.; He, Y. Variety Identification of Raisins Using Near-Infrared Hyperspectral Imaging. Molecules 2018, 23, 2907. https://doi.org/10.3390/molecules23112907
Feng L, Zhu S, Zhang C, Bao Y, Gao P, He Y. Variety Identification of Raisins Using Near-Infrared Hyperspectral Imaging. Molecules. 2018; 23(11):2907. https://doi.org/10.3390/molecules23112907
Chicago/Turabian StyleFeng, Lei, Susu Zhu, Chu Zhang, Yidan Bao, Pan Gao, and Yong He. 2018. "Variety Identification of Raisins Using Near-Infrared Hyperspectral Imaging" Molecules 23, no. 11: 2907. https://doi.org/10.3390/molecules23112907
APA StyleFeng, L., Zhu, S., Zhang, C., Bao, Y., Gao, P., & He, Y. (2018). Variety Identification of Raisins Using Near-Infrared Hyperspectral Imaging. Molecules, 23(11), 2907. https://doi.org/10.3390/molecules23112907










