Dual QM and MM Approach for Computing Equilibrium Isotope Fractionation Factor of Organic Species in Solution
Abstract
1. Introduction
2. Methods
2.1. Potential Energy Surface
2.2. Path Integral-Free Energy Perturbation
2.3. Double Averaging
2.4. Equilibrium Isotope Effects
3. Computational Details
4. Results and Discussion
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barbour, M.M. Stable oxygen isotope composition of plant tissue: A review. Funct. Plant Biol. 2007, 34, 83–94. [Google Scholar] [CrossRef]
- Lehmann, M.M.; Gamarra, B.; Kahmen, A.; Siegwolf, R.T.W.; Saurer, M. Oxygen isotope fractionations across individual leaf carbohydrates in grass and tree species. Plant Cell Environ. 2017, 40, 1658–1670. [Google Scholar] [CrossRef] [PubMed]
- Sternberg, L.; Ellsworth, P.F.V. Divergent Biochemical Fractionation, Not Convergent Temperature, Explains Cellulose Oxygen Isotope Enrichment across Latitudes. PLoS ONE 2011, 6, e28040. [Google Scholar] [CrossRef] [PubMed]
- Saurer, M.; Kirdyanov, A.V.; Prokushkin, A.S.; Rinne, K.T.; Siegwolf, R.T.W. The impact of an inverse climate-isotope relationship in soil water on the oxygen-isotope composition of Larix gmelinii in Siberia. New Phytol. 2016, 209, 955–964. [Google Scholar] [CrossRef] [PubMed]
- Gonfiantini, R.; Stichler, W.; Rozanski, K. Standards and Intercomparison Materials Distributed by the International Atomic Energy Agency for Stable Isotope Measurements; Reference and Intercomparison Materials for Stable Isotopes of Light Elements; IAEA: Vienna, Austria, 1995. [Google Scholar]
- Sternberg, L.D.L.O.; Deniro, M.J.D. Biogeochemical Implications of the Isotopic Equilibrium Fractionation Factor between the Oxygen-Atoms of Acetone and Water. Geochim. Cosmochim. Acta 1983, 47, 2271–2274. [Google Scholar] [CrossRef]
- Sternberg, L.D.L.O. Oxygen stable isotope ratios of tree-ring cellulose: The next phase of understanding. New Phytol. 2009, 181, 553–562. [Google Scholar] [CrossRef] [PubMed]
- Cernusak, L.A.; Barbour, M.M.; Arndt, S.K.; Cheesman, A.W.; English, N.B.; Feild, T.S.; Helliker, B.R.; Holloway-Phillips, M.M.; Holtum, J.A.M.; Kahmen, A.; et al. Stable isotopes in leaf water of terrestrial plants. Plant Cell Environ. 2016, 39, 1087–1102. [Google Scholar] [CrossRef] [PubMed]
- Buchanan, B.B.; Gruissem, W.; Jones, R.I. Biochemistry and Molecular Biology of Plants; Wiley: New York, NY, USA, 2015. [Google Scholar]
- Schmidt, H.L.; Werner, R.A.; Rossmann, A. O-18 pattern and biosynthesis of natural plant products. Phytochemistry 2001, 58, 9–32. [Google Scholar] [CrossRef]
- Pu, J.; Gao, J.; Truhlar, D.G. Multidimensional tunneling, recrossing, and the transmission coefficient for enzymatic reactions. Chem. Rev. 2006, 106, 3140–3169. [Google Scholar] [CrossRef] [PubMed]
- MacKerell, A.D., Jr.; Bashford, D.; Bellott, M.; Dunbrack, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef] [PubMed]
- Bowman, J.M.; Wang, D.Y.; Huang, X.C.; Huarte-Larranaga, F.; Manthe, U. The importance of an accurate CH4 vibrational partition function in full dimensionality calculations of the H + CH4 -> H2 + CH3 reaction. J. Chem. Phys. 2001, 114, 9683–9684. [Google Scholar] [CrossRef]
- Gao, J. Methods and applications of combined quantum mechanical and molecular mechanical potentials. In Reviews in Computational Chemistry; Lipkowitz, K.B., Boyd, D.B., Eds.; VCH: New York, NY, USA, 1995; pp. 119–185. [Google Scholar]
- Liu, M.Y.; Wang, Y.J.; Chen, Y.K.; Field, M.J.; Gao, J.L. QM/MM through the 1990s: The First Twenty Years of Method Development and Applications. Israel J. Chem. 2014, 54, 1250–1263. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Viloca, M.; Nam, K.; Alhambra, C.; Gao, J. Solvent and Protein Effects on the Vibrational Frequency Shift and Energy Relaxation of the Azide Ligand in Carbonic Anhydrase. J. Phys. Chem. B 2004, 108, 13501–13512. [Google Scholar] [CrossRef]
- Major, D.T.; Gao, J. An Integrated Path Integral and Free-Energy Perturbation-Umbrella Sampling Method for Computing Kinetic Isotope Effects of Chemical Reactions in Solution and in Enzymes. J. Chem. Theory Comput. 2007, 3, 949–960. [Google Scholar] [CrossRef] [PubMed]
- Zwanzig, R. High-temperature equation of state by a perturbation method. I. Nonpolar gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
- Feynman, R.P.; Hibbs, A.R. Quantum Mechanics and Path Integrals; McGraw-Hill: New York, NY, USA, 1965. [Google Scholar]
- Wong, K.-Y.; Gao, J. Systematic Approach for Computing Zero-Point Energy, Quantum Partition Function, and Tunneling Effect Based on Kleinert’s Variational Perturbation Theory. J. Chem. Theory Comput. 2008, 4, 1409–1422. [Google Scholar] [CrossRef] [PubMed]
- Gao, J. Enzymatic Kinetic Isotope Effects from Path-Integral Free Energy Perturbation Theory. Methods Enzymol. 2016, 577, 359–388. [Google Scholar] [PubMed]
- Major, D.T.; Gao, J. Implementation of the bisection sampling method in path integral simulations. J. Mol. Graph. Model. 2005, 24, 121–127. [Google Scholar] [CrossRef] [PubMed]
- Wong, K.-Y.; Gao, J. An automated integration-free path-integral method based on Kleinert’s variational perturbation theory. J. Chem. Phys. 2007, 127, 211103. [Google Scholar] [CrossRef] [PubMed]
- Cao, J.; Voth, G.A. A unified framework for quantum activated rate processes. I. General theory. J. Chem. Phys. 1996, 105, 6856–6870. [Google Scholar]
- Hernandez, R.; Cao, J.; Voth, G.A. On the Feynman path centroid density as a phase space distribution in quantum statistical mechanics. J. Chem. Phys. 1995, 103, 5018–5026. [Google Scholar] [CrossRef]
- Hwang, J.K.; Warshel, A. A quantized classical path approach for calculations of quantum mechanical rate constants. J. Phys. Chem. 1993, 97, 10053–10058. [Google Scholar] [CrossRef]
- Sprik, M.; Klein, M.L.; Chandler, D. Staging: A sampling technique for the Monte Carlo evaluation of path integrals. Phys. Rev. B 1985, 31, 4234–4244. [Google Scholar] [CrossRef]
- Gao, J.; Ma, S.; Major, D.T.; Nam, K.; Pu, J.; Truhlar, D.G. Mechanisms and free energies of enzymatic reactions. Chem. Rev. 2006, 106, 3188–3209. [Google Scholar] [CrossRef] [PubMed]
- Warshel, A.; Levitt, M. Theoretical studies of enzymic reactions: Dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J. Mol. Biol. 1976, 103, 227–249. [Google Scholar] [CrossRef]
- Field, M.J.; Bash, P.; Karplus, M. A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations. J. Comput. Chem. 1990, 11, 700–733. [Google Scholar] [CrossRef]
- Gao, J. Absolute free energy of solvation from Monte Carlo simulations using combined quantum and molecular mechanical potentials. J. Phys. Chem. 1992, 96, 537–540. [Google Scholar] [CrossRef]
- Gao, J.; Xia, X. A prior evaluation of aqueous polarization effects through Monte Carlo QM-MM simulations. Science 1992, 258, 631–635. [Google Scholar] [CrossRef] [PubMed]
- Car, R.; Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 1985, 55, 2471–2474. [Google Scholar] [CrossRef] [PubMed]
- Titmuss, S.J.; Cummins, P.L.; Rendell, A.P.; Bliznyuk, A.A.; Gready, J.E. Comparison of linear-scaling semiempirical methods and combined quantum mechanical/molecular mechanical methods for enzymic reactions. II. An energy decomposition analysis. J. Comput. Chem. 2002, 23, 1314–1322. [Google Scholar] [PubMed]
- Rohrig, U.F.; Guidoni, L.; Rothlisberger, U. Solvent and protein effects on the structure and dynamics of the rhodopsin chromophore. ChemPhysChem 2005, 6, 1836–1847. [Google Scholar] [CrossRef] [PubMed]
- Stewart, J.J.P. Application of localized molecular orbitals to the solution of semiempirical self-consistent field equations. Int. J. Quantum Chem. 1996, 58, 133–146. [Google Scholar] [CrossRef]
- Gao, J.; Zhang, J.Z.H.; Houk, K.N. Beyond QM/MM: Fragment Quantum Mechanical Methods. Acc. Chem. Res. 2014, 47, 2711. [Google Scholar] [CrossRef] [PubMed]
- Byun, K.; Mo, Y.; Gao, J. New Insight on the Origin of the Unusual Acidity of Meldrum’s Acid from ab Initio and Combined QM/MM Simulation Study. J. Am. Chem. Soc. 2001, 123, 3974–3979. [Google Scholar] [CrossRef] [PubMed]
- Hudson, P.S.; Woodcock, H.L.; Boresch, S. Use of Nonequilibrium Work Methods to Compute Free Energy Differences Between Molecular Mechanical and Quantum Mechanical Representations of Molecular Systems. J. Phys. Chem. Lett. 2015, 6, 4850–4856. [Google Scholar] [CrossRef] [PubMed]
- Kearns, F.L.; Hudson, P.S.; Woodcock, H.L.; Boresch, S. Computing converged free energy differences between levels of theory via nonequilibrium work methods: Challenges and opportunities. J. Comput. Chem. 2017, 38, 1376–1388. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.Y.; Wang, M.T.; Shao, Y.H.; Konig, G.; Brooks, B.R.; Zhang, J.Z.H.; Mei, Y. Calculations of Solvation Free Energy through Energy Reweighting from Molecular Mechanics to Quantum Mechanics. J. Chem. Theory Comput. 2016, 12, 499–511. [Google Scholar] [CrossRef] [PubMed]
- Konig, G.; Mei, Y.; Pickard, F.C.; Simmonett, A.C.; Miller, B.T.; Herbert, J.M.; Woodcock, H.L.; Brooks, B.R.; Shao, Y.H. Computation of Hydration Free Energies Using the Multiple Environment Single System Quantum Mechanical/Molecular Mechanical Method. J. Chem. Theory Comput. 2016, 12, 332–344. [Google Scholar] [CrossRef] [PubMed]
- Olsson, M.A.; Ryde, U. Comparison of QM/MM Methods To Obtain Ligand-Binding Free Energies. J. Chem. Theory Comput. 2017, 13, 2245–2253. [Google Scholar] [CrossRef] [PubMed]
- Steinmann, C.; Olsson, M.A.; Ryde, U. Relative Ligand-Binding Free Energies Calculated from Multiple Short QM/MM MD Simulations. J. Chem. Theory Comput. 2018, 14, 3228–3237. [Google Scholar] [CrossRef] [PubMed]
- Gao, J. An Automated Procedure for Simulating Chemical Reactions in Solution. Application to the Decarboxylation of 3-Carboxybenzisoxazole in Water. J. Am. Chem. Soc. 1995, 117, 8600–8607. [Google Scholar]
- Gao, J. Computation of intermolecular interactions with a combined quantum mechanical and classical approach. ACS Symp. Ser. 1994, 569, 8–21. [Google Scholar]
- Freindorf, M.; Gao, J. Optimization of the Lennard-Jones parameters for a combined ab initio quantum mechanical and molecular mechanical potential using the 3–21 G basis set. J. Comput. Chem. 1996, 17, 386–395. [Google Scholar] [CrossRef]
- Orozco, M.; Luque, F.J.; Habibollahzadeh, D.; Gao, J. The polarization contribution to the free energy of hydration. J. Chem. Phys. 1995, 103, 9112. [Google Scholar] [CrossRef]
- Gao, J. Hybrid Quantum Mechanical/Molecular Mechanical Simulations: An Alternative Avenue to Solvent Effects in Organic Chemistry. Acc. Chem. Res. 1996, 29, 298–305. [Google Scholar] [CrossRef]
- Major, D.T.; York, D.M.; Gao, J. Solvent Polarization and Kinetic Isotope Effects in Nitroethane Deprotonation and Implications to the Nitroalkane Oxidase Reaction. J. Am. Chem. Soc. 2005, 127, 16374–16375. [Google Scholar] [CrossRef] [PubMed]
- Gao, J. Monte Carlo Quantum Mechanical-Configuration Interaction and Molecular Mechanics Simulation of Solvent Effects on the n. fwdarw.. pi.* Blue Shift of Acetone. J. Am. Chem. Soc. 1994, 116, 9324–9328. [Google Scholar] [CrossRef]
- Gao, J.; Byun, K. Solvent effects on the n -> pi* transition of pyrimidine in aqueous solution. Theor. Chem. Acc. 1997, 96, 151–156. [Google Scholar] [CrossRef]
- Lin, Y.-L.; Gao, J. Solvatochromic Shifts of the n -> pi* Transition of Acetone from Steam Vapor to Ambient Aqueous Solution: A Combined Configuration Interaction QM/MM Simulation Study Incorporating Solvent Polarization. J. Chem. Theory Comput. 2007, 3, 1484–1493. [Google Scholar] [CrossRef] [PubMed]
- Dewar, M.J.S.; Zoebisch, E.G.; Healy, E.F.; Stewart, J.J.P. Development and use of quantum mechanical molecular models. 76. AM1: A new general purpose quantum mechanical molecular model. J. Am. Chem. Soc. 1985, 107, 3902–3909. [Google Scholar]
- Stewart, J.J.P. Optimization of Parameters for Semiempirical Methods I. Method. J. Comp. Chem. 1989, 10, 209–220. [Google Scholar] [CrossRef]
- Cui, Q.; Elstner, M.; Kaxiras, E.; Frauenheim, T.; Karplus, M. A QM/MM Implementation of the Self-Consistent Charge Density Functional Tight Binding (SCC-DFTB) Method. J. Phys. Chem. B 2001, 105, 569–585. [Google Scholar] [CrossRef]
- Gaus, M.; Cui, Q.A.; Elstner, M. DFTB3: Extension of the Self-Consistent-Charge Density-Functional Tight-Binding Method (SCC-DFTB). J. Chem. Theory Comput. 2011, 7, 931–948. [Google Scholar] [CrossRef] [PubMed]
- Chandler, D.; Wolynes, P.G. Exploiting the isomorphism between quantum theory and classical statistical mechanics of polyatomic fluids. J. Chem. Phys. 1981, 74, 4078–4095. [Google Scholar] [CrossRef]
- Ceperley, D.M. Path integrals in the theory of condensed helium. Rev. Mod. Phys. 1995, 67, 279–355. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Ravimohan, C. Monte Carlo simulation of differences in free energies of hydration. J. Chem. Phys. 1985, 83, 3050–3054. [Google Scholar] [CrossRef]
- McCammon, J.A.; Roux, B.; Voth, G.; Yang, W. Special Issue on Free Energy. J. Chem. Theory Comput. 2014, 10, 2631. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Wong, K.-Y.; Major, D.T. Combined QM/MM and path integral simulations of kinetic isotope effects in the proton transfer reaction between nitroethane and acetate ion in water. J. Comput. Chem. 2008, 29, 514–522. [Google Scholar] [CrossRef] [PubMed]
- Feynman, R.P.; Kleinert, H. Effective classical partition functions. Phys. Rev. A 1986, 34, 5080. [Google Scholar] [CrossRef]
- Gillan, M.J. The quantum simulation of hydrogen in metals. Philos. Mag. A 1988, 58, 257–283. [Google Scholar] [CrossRef]
- Voth, G.A.; Chandler, D.; Miller, W.H. Rigorous formulation of quantum transition state theory and its dynamical corrections. J. Chem. Phys. 1989, 91, 7749–7760. [Google Scholar] [CrossRef]
- Messina, M.; Schenter, G.K.; Garrett, B.C. Centroid-density, quantum rate theory: Variational optimization of the dividing surface. J. Chem. Phys. 1993, 98, 8525–8536. [Google Scholar] [CrossRef]
- Cao, J.; Voth, G.A. The formulation of quantum statistical mechanics based on the Feynman path centroid density. V. Quantum instantaneous normal mode theory of liquids. J. Chem. Phys. 1994, 101, 6184–6192. [Google Scholar]
- Hwang, J.-K.; Warshel, A. How Important Are Quantum Mechanical Nuclear Motions in Enzyme Catalysis? J. Am. Chem. Soc. 1996, 118, 11745–11751. [Google Scholar] [CrossRef]
- Major, D.T.; Garcia-Viloca, M.; Gao, J. Path Integral Simulations of Proton Transfer Reactions in Aqueous Solution Using Combined QM/MM Potentials. J. Chem. Theory Comput. 2006, 2, 236–245. [Google Scholar] [CrossRef] [PubMed]
- Valleau, J.P.; Torrie, G.M. A guide to Monte Carlo for stastistical mechanics: 2. Byways. In Modern Theoretical Chemistry; Berne, B.J., Ed.; Plenum: New York, NY, USA, 1977; pp. 169–194. [Google Scholar]
- Makarov, D.E.; Topaler, M. Quantum transition-state theory below the crossover temperature. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1995, 52, 178–188. [Google Scholar] [CrossRef]
- Messina, M.; Schenter, G.K.; Garrett, B.C. A variational centroid density procedure for the calculation of transmission coefficients for asymmetric barriers at low temperature. J. Chem. Phys. 1995, 103, 3430–3435. [Google Scholar] [CrossRef]
- Mills, G.; Schenter, G.K.; Makarov, D.E.; Jonsson, H. Generalized path integral based quantum transition state theory. Chem. Phys. Lett. 1997, 278, 91–96. [Google Scholar] [CrossRef]
- Jang, S.; Voth, G.A. A relationship between centroid dynamics and path integral quantum transition state theory. J. Chem. Phys. 2000, 112, 8747–8757. [Google Scholar] [CrossRef]
- Habershon, S.; Manolopoulos, D.E.; Markland, T.E.; Miller, T.F. Ring-Polymer Molecular Dynamics: Quantum Effects in Chemical Dynamics from Classical Trajectories in an Extended Phase Space. Ann. Rev. Phys. Chem. 2013, 64, 387–413. [Google Scholar] [CrossRef] [PubMed]
- Villa, J.; Warshel, A. Energetics and Dynamics of Enzymatic Reactions. J. Phys. Chem. B 2001, 105, 7887–7907. [Google Scholar] [CrossRef]
- Major, D.T.; Heroux, A.; Orville, A.M.; Valley, M.P.; Fitzpatrick, P.F.; Gao, J. Differential quantum tunneling contributions in nitroalkane oxidase catalyzed and the uncatalyzed proton transfer reaction. Proc. Natl. Acad. Sci. USA 2009, 106, 20736–20739. [Google Scholar] [CrossRef] [PubMed]
- Marsalek, O.; Chen, P.Y.; Dupuis, R.; Benoit, M.; Meheut, M.; Bacic, Z.; Tuckerman, M.E. Efficient Calculation of Free Energy Differences Associated with Isotopic Substitution Using Path-Integral Molecular Dynamics. J. Chem. Theory Comput. 2014, 10, 1440–1453. [Google Scholar] [CrossRef] [PubMed]
- Cheng, B.Q.; Ceriotti, M. Direct path integral estimators for isotope fractionation ratios. J. Chem. Phys. 2014, 141, 244112. [Google Scholar] [CrossRef] [PubMed]
- Poltavsky, I.; DiStasio, R.A.; Tkatchenko, A. Perturbed path integrals in imaginary time: Efficiently modeling nuclear quantum effects in molecules and materials. J. Chem. Phys. 2018, 148, 102325. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Fried, S.D.; Boxer, S.G.; Markland, T.E. Quantum delocalization of protons in the hydrogen-bond network of an enzyme active site. Proc. Natl. Acad. Sci. USA 2014, 111, 18454–18459. [Google Scholar] [CrossRef] [PubMed]
- Ceriotti, M.; Markland, T.E. Efficient methods and practical guidelines for simulating isotope effects. J. Chem. Phys. 2013, 138, 014112. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Pollock, E.L.; Ceperley, D.M. Simulation of quantum many-body systems by path-integral methods. Phys. Rev. B 1984, 30, 2555–2568. [Google Scholar] [CrossRef]
- Lin, Y.-L.; Gao, J.; Rubinstein, A.; Major, D.T. Molecular dynamics simulations of the intramolecular proton transfer and carbanion stabilization in the pyridoxal 5′-phosphate dependent enzymesl-dopa decarboxylase and alanine racemase. Biochim. Biophys. Acta Prot. Proteom. 2011, 1814, 1438–1446. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Cembran, A.; Ma, S.; Gao, J. Connecting Protein Conformational Dynamics with Catalytic Function As Illustrated in Dihydrofolate Reductase. Biochemistry 2013, 52, 2036–2049. [Google Scholar] [CrossRef] [PubMed]
- Brooks, B.R.; Brooks, C.L.; Mackerell, A.D.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The Biomolecular Simulation Program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-L.; Gao, J. Kinetic Isotope Effects of L-Dopa Decarboxylase. J. Am. Chem. Soc. 2011, 133, 4398–4403. [Google Scholar] [CrossRef] [PubMed]

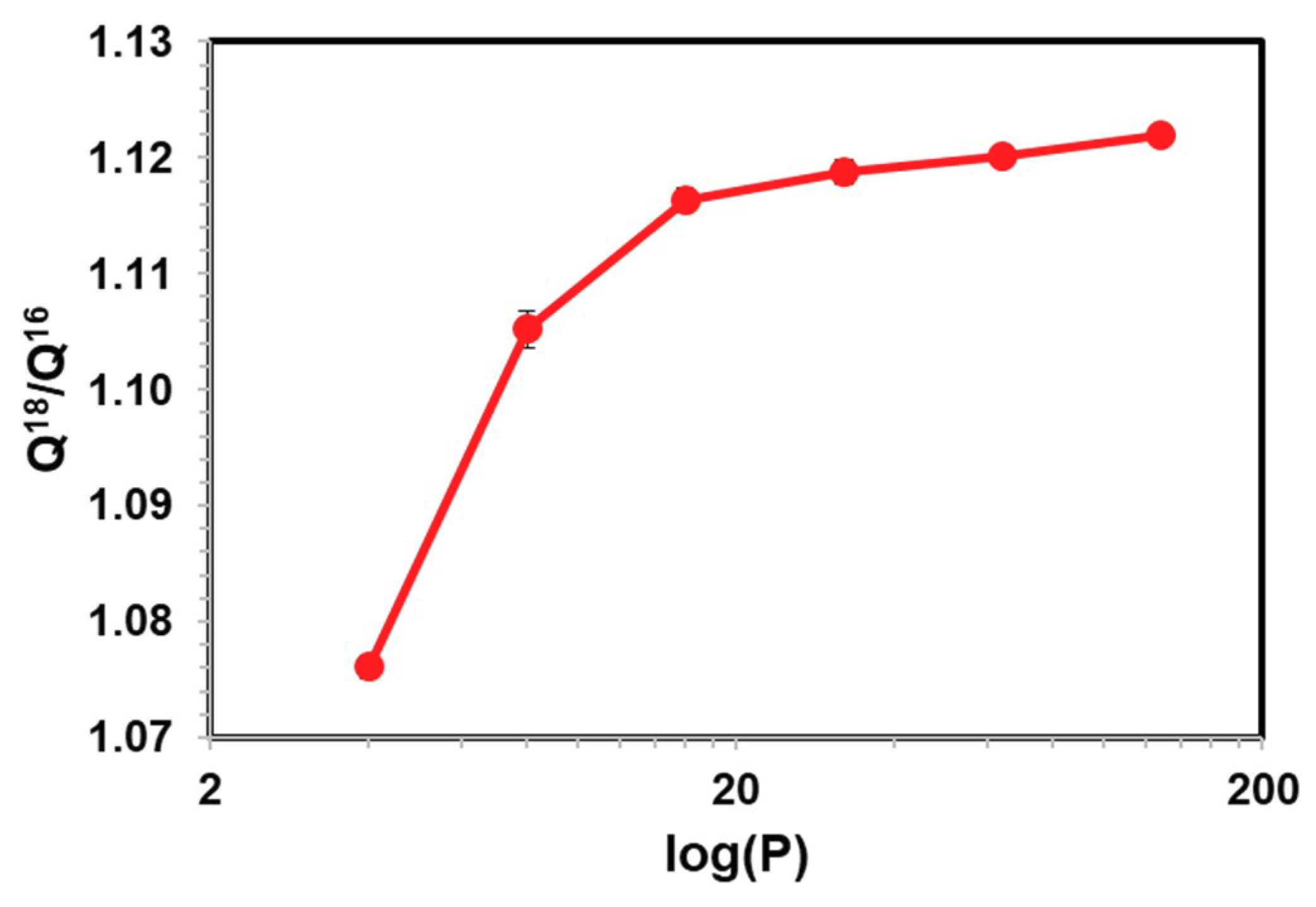
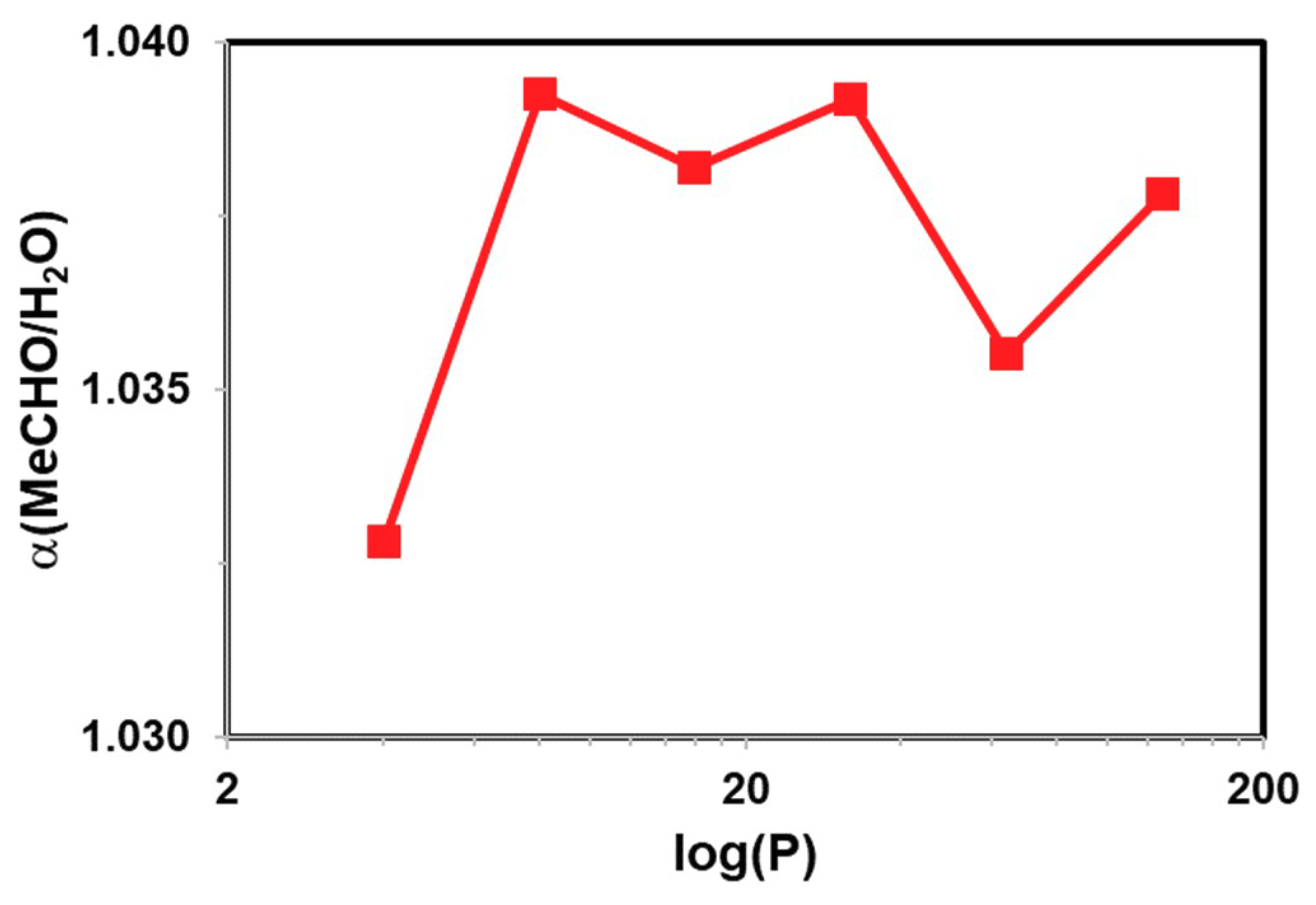
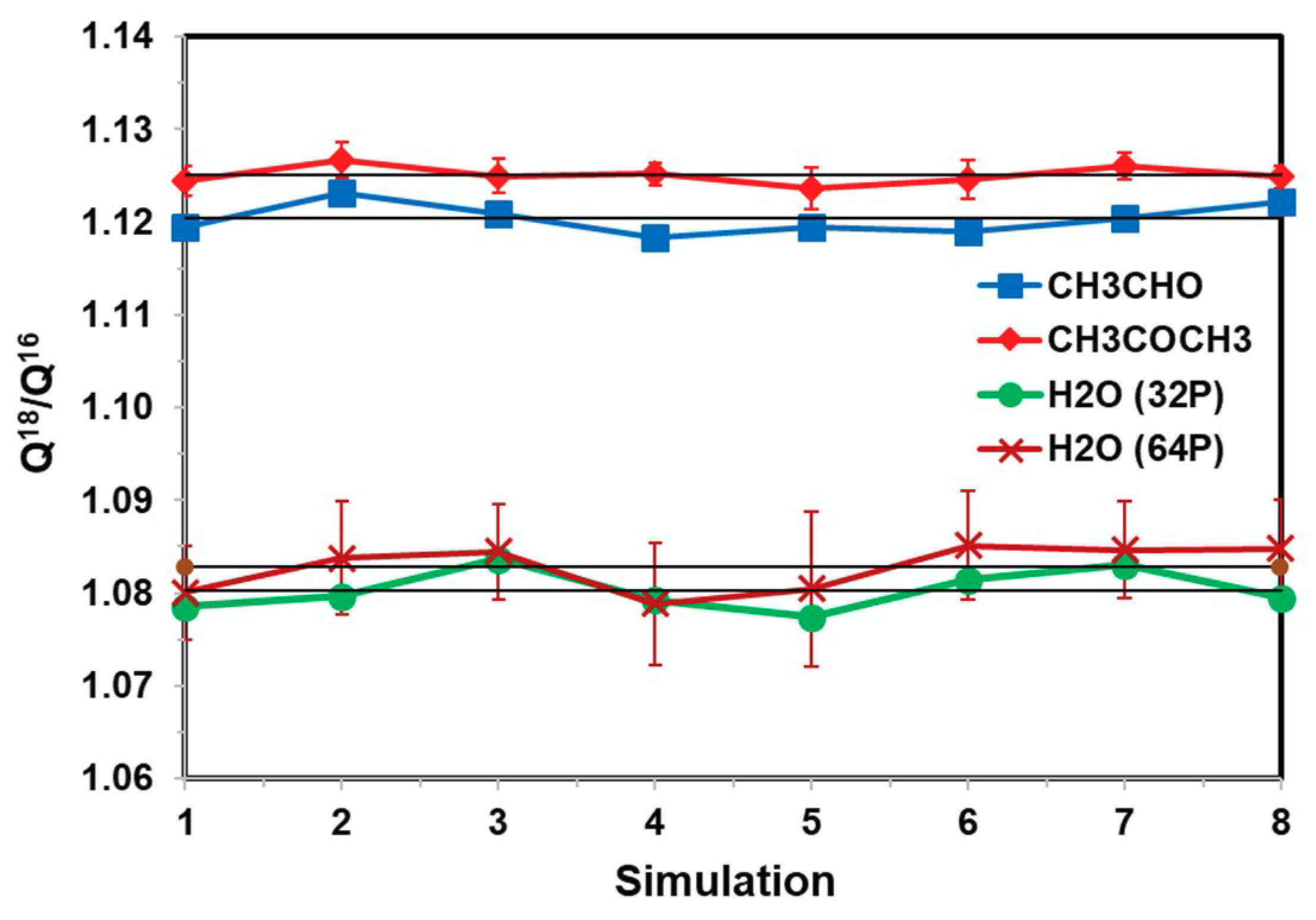
| H2O | CH3CHO | CH3COCH3 | |
|---|---|---|---|
| Q18/Q16 | 1.0828 ± 0.0024 | 1.1204 ± 0.0014 | 1.1251 ± 0.0007 |
| 1 | 0.035 | 0.039 |
| CH3C[D/H]O | [D/H]CH2CHO | |||
|---|---|---|---|---|
| Gas | Aqueous | Gas | Aqueous | |
| Q2/Q1 | 19.20 ± 0.36 | 19.63 ± 0.98 | 23.72 ± 0.86 | 24.01 ± 1.12 |
| 1 | 1 | 1.24 | 1.22 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Youmans, K.N.; Gao, J. Dual QM and MM Approach for Computing Equilibrium Isotope Fractionation Factor of Organic Species in Solution. Molecules 2018, 23, 2644. https://doi.org/10.3390/molecules23102644
Liu M, Youmans KN, Gao J. Dual QM and MM Approach for Computing Equilibrium Isotope Fractionation Factor of Organic Species in Solution. Molecules. 2018; 23(10):2644. https://doi.org/10.3390/molecules23102644
Chicago/Turabian StyleLiu, Meiyi, Katelyn N. Youmans, and Jiali Gao. 2018. "Dual QM and MM Approach for Computing Equilibrium Isotope Fractionation Factor of Organic Species in Solution" Molecules 23, no. 10: 2644. https://doi.org/10.3390/molecules23102644
APA StyleLiu, M., Youmans, K. N., & Gao, J. (2018). Dual QM and MM Approach for Computing Equilibrium Isotope Fractionation Factor of Organic Species in Solution. Molecules, 23(10), 2644. https://doi.org/10.3390/molecules23102644





