Application of a General Computer Algorithm Based on the Group-Additivity Method for the Calculation of Two Molecular Descriptors at Both Ends of Dilution: Liquid Viscosity and Activity Coefficient in Water at Infinite Dilution
Abstract
:1. Introduction
2. General Procedure
3. Results
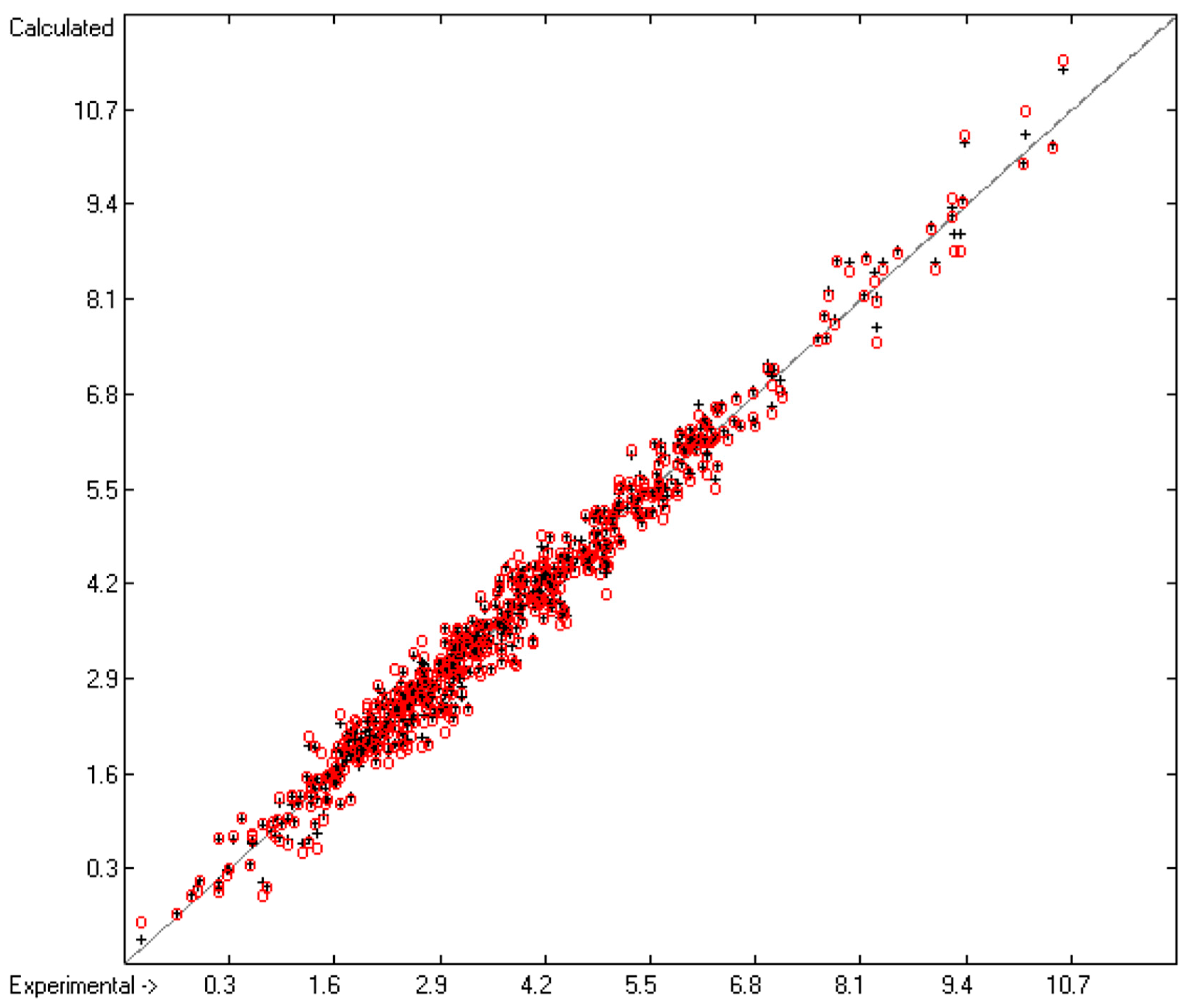
3.1. General Remarks
- (1)
- Cross-validation data in the following figures are superpositioned in red.
- (2)
- Generally, compounds, the experimental values of which exceeded by more than three times the cross-validated standard error, have been excluded from group-parameters calculations and have been collected in a list of outliers.
- (3)
- Lists of molecules used in these studies are available as standard SDF files, stored in the Supplementary Materials, which also encompasses the lists of results with molecule names, experimental, training and cross-validation values and, additionally, lists of experimental outliers.
3.2. Liquid Viscosity Coefficient
3.3. Activity Coefficient at Infinite Solution in Water
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Naef, R. A generally applicable computer algorithm based on the group additivity method for the calculation of seven molecular descriptors: Heat of combustion, LogPO/W, LogS, refractivity, polarizability, toxicity and LogBB of organic compounds; scope and limits of applicability. Molecules 2015, 20, 18279–18351. [Google Scholar] [CrossRef] [PubMed]
- Naef, R.; Acree, W.E. Calculation of five thermodynamic molecular descriptors by means of a general computer algorithm based on the group-additivity method: Standard enthalpies of vaporization, sublimation and solvation, and entropy of fusion of ordinaryorganic molecules and total phase-change entropy of liquid crystals. Molecules 2017, 22, 1059. [Google Scholar] [CrossRef]
- Monnery, W.D.; Mehrotra, A.K.; Svrcek, W.Y. Viscosity prediction of nonpolar, polar, and associating fluids over a wide PρT range from a modified square well intermolecular potential model. Ind. Eng. Res. 1998, 37, 652–659. [Google Scholar] [CrossRef]
- Suzuki, T.; Ebert, R.-U.; Schüürmann, G. Development of both Linear and nonlinear methods to predict the liquid viscosity at 20 °C of organic compounds. J. Chem. Inf. Comput. Sci. 1997, 37, 1122–1128. [Google Scholar] [CrossRef]
- Suzuki, T.; Ebert, R.-U.; Schüürmann, G. Application of neural networks to modeling and estimating temperature-dependent liquid viscosity of organic compounds. J. Chem. Inf. Comput. Sci. 2001, 41, 776–779. [Google Scholar] [CrossRef] [PubMed]
- Katritzky, A.R.; Chen, K.; Wang, Y.; Karelson, M.; Lucic, B.; Trinajstic, N.; Suzuki, T.; Schüürmann, G. Prediction of liquid viscosity for organic compounds by a quantitative structure-property relationship. J. Phys. Org. Chem. 2000, 13, 80–86. [Google Scholar] [CrossRef]
- Suzuki, T.; Ohtaguchi, K.; Koide, K. Computer-assisted approach to develop a new prediction method of liquid viscosity of organic compounds. Comput. Chem. Eng. 1996, 20, 161–173. [Google Scholar] [CrossRef]
- Abraham, M.H.; Acree, W.E., Jr.; Zissimos, A.M. The correlation and prediction of infinite dilution activity coefficients of compounds in water at 298.15 K. Fluid Phase Equilib. 2017, 449, 117–129. [Google Scholar] [CrossRef]
- Atabati, M.; Zarei, K.; Borhani, A. Predicting infinite dilution activity coefficients of hydrocarbons in water using ant colony optimization. Fluid Phase Equilib. 2010, 293, 219–224. [Google Scholar] [CrossRef]
- Hoffmann, R. An extended Hückel theory. I. Hydrocarbons. J. Chem. Phys. 1963, 39, 1397–1412. [Google Scholar] [CrossRef]
- Jiang, X.; He, G.; Guo, Y.; Fang, W.; Xu, L. Density, viscosity, refractive index, and freezing point for binary mixtures of 1,1′-bicyclohexyl with alkylcyclohexane. J. Chem. Eng. Data 2014, 59, 2499–2504. [Google Scholar] [CrossRef]
- Qin, X.; Cao, X.; Guo, Y.; Xu, L.; Hu, S.; Fang, W. Density, viscosity, surface tension, and refractive index for binary mixtures of 1,3-Dimethyladamantane with four C10 alkanes. J. Chem. Eng. Data 2014, 59, 775–783. [Google Scholar] [CrossRef]
- Luning, P.D.J.; Alexandre, S.M.; Cowart, J.S.; Trulove, P.C. Density, viscosity, speed of sound, bulk modulus, surface tension, and flash point of binary mixtures of n-Dodecane with 2,2,4,6,6-pentamethylheptane or 2,2,4,4,6,8,8-heptamethylnonane. J. Chem. Eng. Data 2014, 59, 1334–1346. [Google Scholar] [CrossRef]
- Li, G.; Chi, H.; Guo, Y.; Fang, W.; Hu, S. Excess molar volume along with viscosity and refractive index for binary systems of tricyclo[5.2.1.02.6]decane with five cycloalkanes. J. Chem. Eng. Data 2013, 58, 3078–3086. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, Z.-Q.; Lu, J.; Zhao, J.; Mao, W.; Lu, J. Measurements of density, viscosity, and vapor pressure for 1,1,1-trifluoro-2,3-dichloropropane. J. Chem. Eng. Data 2015, 60, 1688–1692. [Google Scholar] [CrossRef]
- Li, H.; Zhou, J.; Chen, X.-S. Density and Viscosity of 1,7-dibromoheptane–ethanol solutions in a temperature range 288–323 K. Russ. J. Phys. Chem. A 2012, 86, 1522–1525. [Google Scholar] [CrossRef]
- Parsa, J.B.; Haghro, M.F. Excess molar volume and viscosity deviation for binary mixtures of polyethylene glycol dimethyl ether 250 with 1,2-alkanediols (C3–C6) at T = (293.15 to 323.15) K. J. Chem. Thermodyn. 2008, 40, 782–788. [Google Scholar] [CrossRef]
- Nain, A.K. Ultrasonic and viscometric study of molecular interactions in binary mixtures of aniline with 1-propanol, 2-propanol, 2-methyl-1-propanol, and 2-methyl-2-propanol at different temperatures. Fluid Phase Equilib. 2007, 259, 218–227. [Google Scholar] [CrossRef]
- Ranjbar, S.; Soltanabadi, A.; Fakhri, Z. Experimental and computational studies of binary mixtures of cis and trans 2-methylcyclohexanol + cyclohexylamine. J. Mol. Liq. 2017, 234, 342–352. [Google Scholar] [CrossRef]
- Cwiklinska, A.; Dzikowski, T.; Szychowski, D.; Kinart, W.J.; Kinart, C.M. Viscosities of binary mixtures of some n-ethoxyethanols with ethyl tert-butyl ether at T = (293.15, 298.15, and 303.15) K. J. Chem. Thermodyn. 2007, 39, 1325–1330. [Google Scholar] [CrossRef]
- Yoshimura, M.; Boned, C.; Galliéro, G.; Bazile, J.-P.; Baylaucq, A.; Ushiki, H. Influence of the chain length on the dynamic viscosity at high pressure of some 2-alkylamines: Measurements and comparative study of some models. Chem. Phys. 2010, 369, 126–137. [Google Scholar] [CrossRef]
- Weng, W.-L.; Chen, J.-T. Density and viscosity measurement of n-butylamine with hexyl alcohol isomer binary systems. J. Chem. Eng. Data 2004, 49, 1748–1751. [Google Scholar] [CrossRef]
- Fang, S.; Zuo, X.-B.; Xu, X.-J.; Ren, D.-H. Density, viscosity and excess molar volume of binary mixtures of tri-n-octylamine + diluents (n-heptane, n-octane, n-nonane, and n-decane) at various temperatures. J. Chem. Thermodyn. 2014, 68, 281–287. [Google Scholar] [CrossRef]
- Panda, S.; Singh, D.; Sharma, G.; Basaiahgari, A.; Gardas, R.L. Measurement and correlation for acoustic, transport, refractive, and high-temperature volumetric data of substituted benzylamines. J. Chem. Eng. Data 2017, 62, 1189–1197. [Google Scholar] [CrossRef]
- Haghtalab, A.; Shojaeian, A. Volumetric and viscometric behaviour of the binary systems of N-methyldiethanolamine and diethanolamine with 1-butyl-3-methylimidazolium acetate at various temperatures. J. Chem. Thermodyn. 2014, 68, 128–137. [Google Scholar] [CrossRef]
- Blanco, A.; Garcia-Abuin, A.; Gomez-Diaz, D.; Navaza, J.M. Density, speed of sound, viscosity and surface tension of 3-dimethylamino-1-propylamine + water, 3-amino-1-propanol + 3-dimethylamino-1-propanol, and (3-amino-1-propanol + 3-dimethylamino-1-propanol) + water from T = (293.15 to 323.15) K. J. Chem. Eng. Data 2017, 62, 2272–2279. [Google Scholar] [CrossRef]
- Abu-Daabes, M.A.; Awwad, A.M. Volumetric and viscometric properties of aqueous solutions of N-(2-hydroxyethyl)morpholine at T = (293.15, 303.15, 313.15, 323.15, 333.15) K. J. Chem. Thermodyn. 2008, 40, 874–878. [Google Scholar] [CrossRef]
- Comelli, F.; Francesconi, R.; Bigi, A.; Rubini, K. Molar heat capacities, densities, viscosities, and refractive indices of dimethyl sulfoxide + tetrahydropyran and + 2-methyltetrahydrofuran at (293.15, 303.15, and 313.15) K. J. Chem. Eng. Data 2007, 52, 639–644. [Google Scholar] [CrossRef]
- Li, D.; Qin, X.; Fang, W.; Guo, M.; Wang, H.; Feng, Y. Densities, viscosities and refractive indices of binary liquid mixtures of methyl tert-butyl ether or ethyl tert-butyl ether with a hydrocarbon fuel. Exp. Therm. Fluid Sci. 2013, 48, 163–168. [Google Scholar] [CrossRef]
- Awwad, A.M.; Jbara, K.A. Densities and viscosities of aqueous solutions of n-methylmorpholine from (293.15 to 343.15) K. J. Chem. Eng. Data 2008, 53, 1635–1638. [Google Scholar] [CrossRef]
- Wankhede, D.S.; Lande, M.K.; Arbad, B.R. Densities and viscosities of binary mixtures of paraldehyde + propylene carbonate at (288.15, 293.15, 298.15, 303.15, and 308.15) K. J. Chem. Eng. Data 2005, 50, 261–263. [Google Scholar] [CrossRef]
- Lee, K.-H.; Park, S.-L.; Choi, Y.-Y. Density, refractive index and kinematic viscosity of MIPK, MEK and phosphonium-based ionic liquids and the excess and deviation properties of their binary systems. Korean J. Chem. Eng. 2017, 34, 214–224. [Google Scholar] [CrossRef]
- Djojoputro, H.; Ismadji, S. Density and viscosity for a binary mixture of cis-3-hexenyl formate, butyl acetate, trans-2-hexenyl acetate, and cis-3-hexenyl acetate with ethanol at several temperatures. J. Chem. Eng. Data 2005, 50, 1009–1013. [Google Scholar] [CrossRef]
- Djojoputro, H.; Ismadji, S. Density and viscosity of binary mixtures of ethyl-2-methylbutyrate and ethyl hexanoate with methanol, ethanol, and 1-Propanol at (293.15, 303.15, and 313.15) K. J. Chem. Eng. Data 2005, 50, 1343–1347. [Google Scholar] [CrossRef]
- Chen, J.-T.; Weng, W.-L.; Chu, H.-P. Densities and viscosities of binary mixtures of 1-butanol with methacrylic acid, benzyl methacrylate, and 2-hydroxyethyl methacrylate between 288.15 k and 318.15 k. J. Chem. Eng. Data 2006, 51, 1441–1445. [Google Scholar] [CrossRef]
- Droliya, P.; Nain, A.K. Experimental and theoretical studies of acoustic and viscometric properties of binary mixtures of tetrahydrofuran with some alkyl acrylates at temperatures from 293.15 to 318.15 K. J. Mol. Liq. 2017, 241, 549–562. [Google Scholar] [CrossRef]
- Shen, Y.-W.; Tu, C.-H. Densities and viscosities of binary mixtures of ethyl acetoacetate, ethyl isovalerate, methyl benzoate, benzyl acetate, ethyl salicylate, and benzyl propionate with ethanol at T = (288.15, 298.15, 308.15, and 318.15) K. J. Chem. Eng. Data 2006, 51, 545–553. [Google Scholar]
- Rathnam, M.V.; Ambavadekar, D.R.; Nandini, M. Densities, viscosities, and sound speed of binary mixtures of hexyl acetate with tetrahydrofuran, 1,4-dioxane, anisole, and butyl vinyl ether. J. Chem. Eng. Data 2013, 58, 3370–3377. [Google Scholar] [CrossRef]
- Indraswati, N.; Wicaksana, F.; Hindarso, H. Density and viscosity for a binary mixture of ethyl valerate and hexyl acetate with 1-pentanol and 1-hexanol at 293.15 K, 303.15 K, and 313.15 K. J. Chem. Eng. Data 2001, 46, 134–137. [Google Scholar] [CrossRef]
- Aissa, M.A.; Ivanis, G.R.; Radovic, I.R.; Kijevcanin, M.L. Experimental investigation and modeling of thermophysical properties of pure methyl and ethyl esters at high pressures. Energy Fuels 2017, 31, 7110–7122. [Google Scholar] [CrossRef]
- Orozco, M.; Camacho, A.; Canzonieri, S.; Mariano, A. Volumetric and viscosity properties of {propylpropanoate (1) + heptane (or octane) (2)} mixtures at several temperatures and correlation with the Jouyban–Acree model. Phys. Chem. Liq. 2017, 1–10. [Google Scholar] [CrossRef]
- Mylona, S.K.; Assael, M.J.; Antoniadis, K.D.; Polymatidou, S.K.; Karagiannidis, L. Measurements of the viscosity of bis(2-ethylhexyl) sebacate, squalane, and bis(2-ethylhexyl) phthalate between (283 and 363) K at 0.1 Mpa. J. Chem. Eng. Data 2013, 58, 2805–2808. [Google Scholar] [CrossRef]
- Harris, K.R. Temperature and pressure dependence of the viscosities of 2-ethylhexyl benzoate, bis(2-ethylhexyl) phthalate, 2,6,10,15,19,23-hexamethyltetracosane (squalane), and diisodecyl phthalate. J. Chem. Eng. Data 2009, 54, 2729–2738. [Google Scholar] [CrossRef]
- Bajic, D.M.; Zivkovic, E.M.; Serbanovic, S.P.; Kijevcanin, M.L. Experimental measurements and modelling of volumetric properties, refractive index and viscosity of selected binary systems with butyl lactate at 288.15–323.15 K and atmospheric pressure. New UNIFAC-VISCO interaction parameters. Thermochim. Acta 2013, 562, 42–55. [Google Scholar] [CrossRef]
- Bajic, D.M.; Zivkovic, E.M.; Jovanovic, J.; Serbanovic, S.P.; Kijevcanin, M.L. Experimental measurements and modelling of volumetric properties, refractive index and viscosity of binary systems of ethyl lactate with methyl ethyl ketone, toluene and n-methyl-2-pirrolidone at 288.15–323.15 K and atmospheric pressure. New UNIFAC–VISCO and ASOG–VISCO interaction parameter. Fluid Phase Equilib. 2015, 399, 50–65. [Google Scholar]
- Comelli, F.; Bigi, A.; Vitalini, D.; Rubini, K. Densities, viscosities, refractive indices, and heat capacities of poly(ethyleneglycol-ran-propylene glycol) + esters of carbonic acid at (293.15 and 313.15) K and at atmospheric pressure. J. Chem. Eng. Data 2010, 55, 205–210. [Google Scholar] [CrossRef]
- Hemmat, M.; Moosavi, M.; Dehghan, M.; Mousavi, E.; Rostami, A.A. Thermodynamic, transport and optical properties of formamide + 1,2-ethanediol, 1,3-propanediol and poly (ethylene glycol) 200 binary liquid mixtures. J. Mol. Liq. 2017, 233, 222–235. [Google Scholar] [CrossRef]
- Nain, A.K. Densities, ultrasonic speeds, viscosities and excess properties of binary mixtures of methyl methacrylate with N,N-dimethylformamide and N,N-dimethylacetamide at different temperatures. J. Chem. Thermodyn. 2013, 60, 105–116. [Google Scholar] [CrossRef]
- Zarei, H.; Golroudbari, S.A.; Behroozi, M. Experimental studies on volumetric and viscometric properties of binary and ternary mixtures of N,N-dimethylacetamide, N-methylformamide and propane-1,2-diol at different temperatures. J. Mol. Liq. 2013, 187, 260–265. [Google Scholar] [CrossRef]
- Awwad, A.M.; Alsyouri, H.A.; Jbara, K.A. Viscosities and densities of binary mixtures of (n-acetylmorpholine + alkanols) from (293.15 to 323.15) K. J. Chem. Eng. Data 2008, 53, 1655–1659. [Google Scholar] [CrossRef]
- Blanco, A.; Garcia-Abuin, A.; Gomez-Diaz, D.; Navaza, J.M.; Villaverde, O.L. Density, speed of sound, viscosity, surface tension, and excess volume of N-ethyl-2-pyrrolidone + ethanolamine (or diethanolamine or triethanolamine) from T = (293.15 to 323.15) K. J. Chem. Eng. Data 2013, 58, 653–659. [Google Scholar] [CrossRef]
- Lopez, A.B.; Garcia-Abuin, A.; Gomez-Diaz, D.; La Rubia, M.D.; Navaza, J.M. Density, speed of sound, viscosity, refractive index and surface tension of N-methyl-2-pyrrolidone + diethanolamine (or triethanolamine) from T = (293.15 to 323.15) K. J. Chem. Thermodyn. 2013, 61, 1–6. [Google Scholar] [CrossRef]
- Kannan, S.; Kishore, K. Absolute viscosity and density of trisubstituted phosphoric esters. J. Chem. Eng. Data 1999, 44, 649–655. [Google Scholar] [CrossRef]
- Fang, S.; Zhao, C.-X.; He, C.-H. Densities and viscosities of binary mixtures of tri-n-butyl phosphate + cyclohexane, + n-heptane at T = (288.15, 293.15, 298.15, 303.15, and 308.15) K. J. Chem. Eng. Data 2008, 53, 2244–2246. [Google Scholar] [CrossRef]
- Fang, S.; Zhao, C.-X.; He, C.-H.; Liu, J.-Q.; Sun, J.-H. Densities and Viscosities of binary mixtures of tris(2-ethylhexyl) phosphate + cyclohexane or n-hexane at T = (293.15, 298.15, and 303.15) K and p = 0.1 Mpa. J. Chem. Eng. Data 2008, 53, 2718–2720. [Google Scholar] [CrossRef]
- Taniewska-Osinska, S.; Jozwiak, M. Densimetric and viscosimetric investigations of NaI in hexamethylphosphoramide-water mixtures at 293.15, 298.15 and 303.15 K. J. Chem. Soc. Faraday Trans. I 1989, 85, 2141–2147. [Google Scholar] [CrossRef]
- Palczewska-Tulinska, M.; Oracz, P. Selected physicochemical properties of hexamethylcyclotrisiloxane, octamethylcyclotetrasiloxane, and decamethylcyclopentasiloxane. J. Chem. Eng. Data 2005, 50, 1711–1719. [Google Scholar] [CrossRef]
- Er, H.; Wang, H. Properties of protic ionic liquids composed of N-alkyl (= hexyl, octyl and 2-ethylhexyl) ethylenediaminum cations with trifluoromethanesulfonate and trifluoroacetate anion. J. Mol. Liq. 2016, 220, 649–656. [Google Scholar] [CrossRef]
- Ziyada, A.K.; Wilfred, C.D. Physical Properties of Ionic Liquids Consisting of 1-Butyl-3-propanenitrile- and 1-Decyl-3-propanenitrile Imidazolium-Based Cations: Temperature Dependence and Influence of the Anion. J. Chem. Eng. Data 2014, 59, 1232–1239. [Google Scholar] [CrossRef]
- Domanska, U.; Skiba, K.; Zawadski, M.; Paduszynski, K.; Krolikowski, M. Synthesis, physical, and thermodynamic properties of 1-alkyl-cyanopyridinium bis{(trifluoromethyl)sulfonyl}imide ionic liquids. J. Chem. Thermodyn, 2013, 56, 153–161. [Google Scholar] [CrossRef]
- Garcia-Mardones, M.; Gascon, I.; Carmen Lopez, M.; Royo, F.M.; Lafuente, C. Viscosimetric study of binary mixtures containing pyridinium-based ionic liquids and alkanols. J. Chem. Eng. Data 2012, 57, 3549–3556. [Google Scholar] [CrossRef]
- Tomida, D.; Kumagai, A.; Kenmochi, S.; Qiao, K.; Yokoyama, C. Viscosity of 1-Hexyl-3-methylimidazolium Hexafluorophosphate and 1-Octyl-3-methylimidazolium Hexafluoro-phosphate at High Pressure. J. Chem. Eng. Data 2007, 52, 577–579. [Google Scholar] [CrossRef]
- Ferreira, C.E.; Talavera-Prieto, N.M.C.; Fonseca, I.M.A.; Portugal, A.T.G.; Ferreira, A.G.M. Measurements of pVT, viscosity, and surface tension of trihexyltetradecylphosphonium tris(pentafluoroethyl)trifluorophosphate ionic liquid and modelling with equations of state. J. Chem. Thermodyn. 2012, 47, 183–196. [Google Scholar] [CrossRef]
- Anton, V.; Artigas, H.; Munoz-Embid, J.; Artal, M.; Lafuente, C. Thermophysical properties of two binary aqueous mixtures containing a pyridinium-based ionic liquid. J. Chem. Thermodyn. 2016, 99, 116–123. [Google Scholar] [CrossRef]
- Arumugam, V.; Redhi, G.G.; Gengan, R.M. Synthesis, characterization and thermophysical properties of novel 2′,3′-N-epoxypropyl-N-methyl-2-oxopyrrolidinium acetate ionic liquid and their binary mixture with water or methanol. J. Mol. Liq. 2017, 242, 1215–1227. [Google Scholar] [CrossRef]
- Larriba, M.; Garcia, S.; Garcia, J.; Torrecilla, J.S.; Rodriguez, F. Thermophysical properties of 1-ethyl-3-methylimidazolium 1,1,2,2-tetrafluoroethanesulfonate and 1-ethyl-3-methylimidazolium ethylsulfate ionic liquids as a function of temperature. J. Chem. Eng. Data 2011, 56, 3589–3597. [Google Scholar] [CrossRef]
- Widegren, J.A.; Magee, J.W. Density, Viscosity, speed of sound, and electrolytic conductivity for the ionic liquid 1-hexyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide and its mixtures with water. J. Chem. Eng. Data 2007, 52, 2331–2338. [Google Scholar] [CrossRef]
- Li, J.-G.; Hu, Y.-F.; Ling, S.; Zhang, J.-Z. Physicochemical properties of [C6mim][PF6] and [C6mim][(C2F5)3PF3] ionic liquids. J. Chem. Eng. Data 2011, 56, 3068–3072. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, B.; Qian, W.; Li, H. Properties of pure n-butylammonium nitrate ionic liquid and its binary mixtures of with alcohols at T = (293.15 to 313.15) K. J. Chem. Thermodyn. 2013, 58, 449–459. [Google Scholar] [CrossRef]
- Comunas, M.J.P.; Bazile, J.-P.; Lugo, L.; Baylauq, A.; Fernandez, J.; Boned, C. Influence of the molecular structure on the volumetric properties and viscosities of dialkyl adipates (dimethyl, diethyl, and diisobutyl adipates). J. Chem. Eng. Data 2010, 55, 3697–3703. [Google Scholar] [CrossRef]
- Krolikowska, M.; Paduszynski, K.; Zawadzki, M. Measurements, Correlations, and predictions of thermodynamic properties of N-octylisoquinolinium thiocyanate ionic liquid and its aqueous solutions. J. Chem. Eng. Data 2013, 58, 285–293. [Google Scholar] [CrossRef]
- Papovic, S.; Vranes, M.; Kordic, B.; Filipovic, S.; Bester-Rogac, M.; Gadzuric, S. Interactions of 1,2,3-trialkylimidazolium-based ionic liquids with γ-butyrolactone. J. Chem. Thermodyn. 2016, 101, 260–269. [Google Scholar] [CrossRef]
- Santos, A.F.S.; Costa e Silva, J.F.C.; Moita, M.-L.C.J.; Lampreia, I.M.S. Water activity in 1-propoxypropan-2-ol aqueous mixtures at T = 298 K. J. Chem. Thermodyn. 2014, 77, 87–90. [Google Scholar] [CrossRef]
- Wakita, K.; Yoshimoto, M.; Miyamoto, S.; Watanabe, H. A method for calculation of the aqueous solubility of organic compounds by using new fragment solubility constants. Chem. Pharm. Bull. 1986, 34, 4663–4681. [Google Scholar] [CrossRef]
- Qureshi, M.S.; Uusi-Kyyny, P.; Richon, D.; Nikiforow, K.; Alopaeus, V. Measurement of activity coefficient at infinite dilution for some bio-oil components in water and mass transfer study of bubbles in the dilutor. Fluid Phase Equilib. 2015, 392, 1–11. [Google Scholar] [CrossRef]
- Chantooni, M.K.; Kolthoff, I.M. Transfer activity coefficients of ortho-substituted and non-ortho-substituted benzoates between water, methanol, and polar aprotic solvents. J. Phys. Chem. 1974, 78, 839–846. [Google Scholar] [CrossRef]
- Niti, S.; Sira, S.; Natchanun, L.; Milan, H.; Ura, P. Determination and modeling of aqueous solubility of 4-position substituted benzoic acid compounds in a high-temperature solution. Fluid Phase Equilib. 2013, 338, 217–223. [Google Scholar]
- Perez-Camino, M.C.; Sanchez, E.; Balon, M.; Maestre, A. Thermodynamic functions for the transfer of 1-naphthoic acid from water to mixed aqueous solvents at 298 K. Phys. Chem. Condens. Phases 1985, 81, 1555–1561. [Google Scholar] [CrossRef]
- Zhou, B.; Cai, W.; Zou, L. Thermodynamics of transfer of naphthalene and 2-naphthoic acid from water to (water + ethanol) mixtures at T = 298.15 K. J. Chem. Thermodyn. 2003, 35, 1413–1424. [Google Scholar] [CrossRef]
- Shakeel, F.; Haq, N.; Iqbal, M.; Alanazi, F.K.; Alsarra, I.A. Measurement, correlation, and thermodynamics of solubility of isatin in nine different green solvents at (298.15 to 338.15) K. J. Chem. Eng. Data 2015, 60, 801–805. [Google Scholar] [CrossRef]
- Ren, Y.; Duan, X. Equilibrium solubilities of 2-cyanoguanidine in water + (ethane-1,2-diol or N,N-dimethylformamide) mixtures at different temperatures: An experimental and correlational study. J. Chem. Eng. Data 2013, 58, 3282–3288. [Google Scholar] [CrossRef]
- Zhou, J.; Fu, H.; Peng, G.; Cao, H.; Zhang, Y.; Liu, M.; Wu, W.; Qing, X.; Zhou, J. Solubility and solution thermodynamics of flofenicol in binary PEG 400 + water systems. Fluid Phase Equilib. 2014, 376, 159–164. [Google Scholar] [CrossRef]
- Li, X.; Wu, M.; Cong, Y.; Du, C.; Zhao, H. Solubility modeling and mixing thermodynamics of thiamphenicol in water and twelve neat organic solvents from T = (278.15 to 318.15) K. J. Chem. Eng. Data 2017, 62, 3534–3541. [Google Scholar] [CrossRef]
- Perlovich, G.L.; Kazachenko, V.P.; Strakhova, N.N.; Raevsky, O.A. Impact of sulfonamide structure on solubility and transfer processes in biologically relevant solvents. J. Chem. Eng. Data 2014, 59, 4217–4226. [Google Scholar] [CrossRef]
- Munoz, M.; del Mar Delgado, D.R.; Pena, M.A.; Jouyban, A.; Martinez, F. Solubility and preferential solvation of sulfadiazine, sulfamerazine and sulfamethazine in propylene glycol + water mixtures at 298.15 K. J. Mol. Liq. 2015, 204, 132–136. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are not available from the authors. |




| No. | Atom Type | Neighbours | Meaning | Example |
|---|---|---|---|---|
| 1 | B(−) | F4 | BF4− | tetrafluoroborate |
| 2 | C aromatic | H:C:N(+) | C:CH:N+ | C2 in pyridinium |
| 3 | C(+) aromatic | C:N2 | N:C+(C):N | C2 in 2-methylimidazolium |
| 4 | N aromatic | C2:C(+) | C-N(C):C+ | N1 in 1-methylimidazolium |
| 5 | N(+) aromatic | C:C2 | C:N+(C):C | N in 1-methylpyridinium |
| 6 | N(−) | S2 | S-N−-S | bis(trifluoromethanesulfonyl)amide |
| 7 | P(+) | C4 | PC4+ | tetramethylphosphonium |
| 8 | P(−) | F6 | PF6− | hexafluorophosphate |
| 9 | S4 | CO=O2(−) | C-SO3− | methylsulfonate |
| Entry | Atom Type | Neighbours | Contribution | Occurrences | Molecules |
|---|---|---|---|---|---|
| 1 | Const | −0.70 | 501 | 501 | |
| 2 | B(−) | F4 | 1.50 | 4 | 4 |
| 3 | C sp3 | H3C | −0.06 | 694 | 389 |
| 4 | C sp3 | H3C(+) | 2.07 | 3 | 3 |
| 5 | C sp3 | H3N | 0.54 | 31 | 21 |
| 6 | C sp3 | H3N(+) | 0.69 | 2 | 2 |
| 7 | C sp3 | H3O | 0.43 | 31 | 25 |
| 8 | C sp3 | H3S | 0.19 | 7 | 5 |
| 9 | C sp3 | H3Si | 0.13 | 18 | 2 |
| 10 | C sp3 | H2C2 | 0.09 | 1634 | 313 |
| 11 | C sp3 | H2CN | 0.63 | 87 | 51 |
| 12 | C sp3 | H2CN(+) | 1.75 | 13 | 12 |
| 13 | C sp3 | H2CO | 0.51 | 182 | 118 |
| 14 | C sp3 | H2CP(+) | 0.43 | 12 | 3 |
| 15 | C sp3 | H2CS | 0.36 | 20 | 15 |
| 16 | C sp3 | H2CCl | 0.33 | 23 | 20 |
| 17 | C sp3 | H2CBr | 0.44 | 14 | 12 |
| 18 | C sp3 | H2CJ | 0.59 | 3 | 3 |
| 19 | C sp3 | H2O2 | 0.93 | 1 | 1 |
| 20 | C sp3 | HC3 | 0.21 | 118 | 92 |
| 21 | C sp3 | HC2N | 0.65 | 8 | 7 |
| 22 | C sp3 | HC2N(+) | 0.89 | 1 | 1 |
| 23 | C sp3 | HC2O | 0.69 | 17 | 16 |
| 24 | C sp3 | H2CP | 0.08 | 2 | 1 |
| 25 | C sp3 | HC2S | 0.50 | 4 | 4 |
| 26 | C sp3 | HC2Cl | 0.41 | 5 | 5 |
| 27 | C sp3 | HC2Br | 0.58 | 1 | 1 |
| 28 | C sp3 | HC2J | 0.67 | 1 | 1 |
| 29 | C sp3 | HCO2 | 1.11 | 3 | 1 |
| 30 | C sp3 | HCF2 | 1.49 | 1 | 1 |
| 31 | C sp3 | HCCl2 | 0.37 | 3 | 3 |
| 32 | C sp3 | HCBr2 | 0.85 | 2 | 1 |
| 33 | C sp3 | C4 | 0.44 | 14 | 10 |
| 34 | C sp3 | C3O | 0.89 | 6 | 6 |
| 35 | C sp3 | C3S | 0.72 | 3 | 3 |
| 36 | C sp3 | C3Cl | 0.60 | 1 | 1 |
| 37 | C sp3 | C3J | 0.83 | 1 | 1 |
| 38 | C sp3 | C2O2 | 1.14 | 1 | 1 |
| 39 | C sp3 | CSF2 | 0.00 | 1 | 1 |
| 40 | C sp3 | CPF2(−) | 0.19 | 6 | 2 |
| 41 | C sp3 | CF3 | −0.15 | 10 | 6 |
| 42 | C sp3 | CF2Cl | 0.55 | 1 | 1 |
| 43 | C sp3 | CFCl2 | 0.00 | 1 | 1 |
| 44 | C sp3 | CCl3 | 0.72 | 1 | 1 |
| 45 | C sp3 | SF3 | 0.43 | 14 | 7 |
| 46 | C sp2 | H2=C | −0.06 | 42 | 40 |
| 47 | C sp2 | HC=C | 0.05 | 74 | 52 |
| 48 | C sp2 | HC=O | 0.26 | 7 | 7 |
| 49 | C sp2 | H=CN | 0.48 | 28 | 14 |
| 50 | C sp2 | H=CO | −0.01 | 6 | 5 |
| 51 | C sp2 | H=CS | 0.26 | 5 | 3 |
| 52 | C sp2 | H=CCl | 0.17 | 5 | 3 |
| 53 | C sp2 | HN=O | 0.51 | 3 | 3 |
| 54 | C sp2 | HO=O | 0.12 | 9 | 9 |
| 55 | C sp2 | C2=C | 0.13 | 11 | 11 |
| 56 | C sp2 | C2=O | 0.37 | 15 | 14 |
| 57 | C sp2 | C=CS | 0.35 | 1 | 1 |
| 58 | C sp2 | CN=O | 0.66 | 4 | 4 |
| 59 | C sp2 | CN=O(+) | −3.99 | 1 | 1 |
| 60 | C sp2 | CO=O | 0.26 | 100 | 83 |
| 61 | C sp2 | CO=O(−) | 0.95 | 3 | 3 |
| 62 | C sp2 | C=OBr | 0.44 | 1 | 1 |
| 63 | C sp2 | =CCl2 | 0.32 | 4 | 3 |
| 64 | C sp2 | O2=O | 0.29 | 3 | 3 |
| 65 | C aromatic | H:C2 | 0.07 | 441 | 97 |
| 66 | C aromatic | H:C:N | 0.24 | 7 | 4 |
| 67 | C aromatic | H:C:N(+) | 0.00 | 18 | 9 |
| 68 | C aromatic | :C3 | 0.31 | 4 | 2 |
| 69 | C aromatic | C:C2 | 0.20 | 90 | 73 |
| 70 | C aromatic | C:C:N | 0.40 | 3 | 2 |
| 71 | C aromatic | :C2N | 0.28 | 9 | 9 |
| 72 | C aromatic | :C2N(+) | 0.83 | 3 | 3 |
| 73 | C aromatic | :C2O | 0.22 | 9 | 6 |
| 74 | C aromatic | :C2S | 1.42 | 3 | 3 |
| 75 | C aromatic | :C2F | 0.09 | 4 | 4 |
| 76 | C aromatic | :C2Cl | 0.25 | 6 | 4 |
| 77 | C aromatic | :C2Br | 0.36 | 2 | 2 |
| 78 | C aromatic | :C2J | 0.57 | 1 | 1 |
| 79 | C(+) aromatic | H:N2 | 0.40 | 10 | 10 |
| 80 | C(+) aromatic | C:N2 | −3.06 | 3 | 3 |
| 81 | C sp | H#C | −0.17 | 1 | 1 |
| 82 | C sp | C#C | 0.00 | 1 | 1 |
| 83 | C sp | C#N | 0.35 | 19 | 19 |
| 84 | C sp | N#N(−) | −0.02 | 2 | 1 |
| 85 | C sp | #NS(−) | 1.59 | 1 | 1 |
| 86 | N sp3 | H2C | −0.21 | 19 | 18 |
| 87 | N sp3 | H2C(pi) | 0.66 | 7 | 7 |
| 88 | N sp3 | HC2 | −0.74 | 12 | 12 |
| 89 | N sp3 | HC2(pi) | 0.02 | 3 | 3 |
| 90 | N sp3 | HC2(2pi) | −0.23 | 1 | 1 |
| 91 | N sp3 | C3 | −1.38 | 12 | 12 |
| 92 | N sp3 | C3(pi) | −0.92 | 6 | 6 |
| 93 | N sp3 | C2P | −0.66 | 3 | 1 |
| 94 | N(+) sp3 | H3C | 0.14 | 2 | 2 |
| 95 | N(+) sp3 | C4 | −0.95 | 1 | 1 |
| 96 | N aromatic | :C2 | −0.12 | 5 | 5 |
| 97 | N aromatic | C2:C(+) | −0.05 | 26 | 13 |
| 98 | N(+) aromatic | C:C2 | −0.54 | 9 | 9 |
| 99 | N(+) sp2 | CO=O(−) | −0.18 | 5 | 5 |
| 100 | N(+) sp2 | O2=O(−) | 0.74 | 1 | 1 |
| 101 | N(−) | C2 | 0.00 | 1 | 1 |
| 102 | N(−) | S2 | 0.86 | 7 | 7 |
| 103 | O | HC | 0.58 | 58 | 45 |
| 104 | O | HC(pi) | 0.63 | 18 | 18 |
| 105 | O | C2 | −0.79 | 40 | 31 |
| 106 | O | C2(pi) | −0.25 | 97 | 80 |
| 107 | O | C2(2pi) | 0.20 | 6 | 6 |
| 108 | O | CP | −0.13 | 9 | 3 |
| 109 | O | CP(pi) | 0.29 | 3 | 1 |
| 110 | O | CS | −0.06 | 2 | 2 |
| 111 | O | Si2 | 0.00 | 9 | 2 |
| 112 | P4 | C2O=O(−) | −0.88 | 1 | 1 |
| 113 | P4 | N3=O | 0.00 | 1 | 1 |
| 114 | P4 | O3=O | 0.00 | 4 | 4 |
| 115 | P(+) | C4 | −0.22 | 3 | 3 |
| 116 | P(−) | F6 | 0.84 | 2 | 2 |
| 117 | P(−) | C3F3 | −0.07 | 2 | 2 |
| 118 | S2 | HC | −0.09 | 13 | 13 |
| 119 | S2 | HC(pi) | −0.98 | 1 | 1 |
| 120 | S2 | C2 | −0.21 | 9 | 9 |
| 121 | S2 | C2(2pi) | −0.10 | 3 | 3 |
| 122 | S4 | C2=O | 0.67 | 1 | 1 |
| 123 | S4 | CN=O2(−) | 0.00 | 14 | 7 |
| 124 | S4 | CO=O2(−) | −1.08 | 4 | 4 |
| 125 | S4 | O2=O2(−) | 0.00 | 2 | 2 |
| 126 | Si | C2O2 | 0.00 | 9 | 2 |
| A | Based on | Valid groups | 76 | 501 | |
| B | Goodness of fit | R2 | 0.9831 | 460 | |
| C | Deviation | Average | 0.07 | 460 | |
| D | Deviation | Standard | 0.10 | 460 | |
| E | K-fold cv | K | 10 | 413 | |
| F | Goodness of fit | Q2 | 0.975 | 413 | |
| G | Deviation | Average (cv) | 0.08 | 413 | |
| H | Deviation | Standard (cv) | 0.11 | 413 |
| Entry | Atom Type | Neighbours | Contribution | Occurrences | Molecules |
|---|---|---|---|---|---|
| 1 | C sp3 | H3C | 0.99 | 776 | 422 |
| 2 | C sp3 | H3N | 0.91 | 27 | 20 |
| 3 | C sp3 | H3N(+) | 0.38 | 1 | 1 |
| 4 | C sp3 | H3O | 0.86 | 50 | 45 |
| 5 | C sp3 | H3S | 1.2 | 9 | 6 |
| 6 | C sp3 | H2C2 | 0.6 | 972 | 284 |
| 7 | C sp3 | H2CN | 0.27 | 52 | 29 |
| 8 | C sp3 | H2CN(+) | 0.8 | 3 | 3 |
| 9 | C sp3 | H2CO | 0.21 | 131 | 101 |
| 10 | C sp3 | H2CS | 0.19 | 9 | 6 |
| 11 | C sp3 | H2CF | 0.7 | 1 | 1 |
| 12 | C sp3 | H2CCl | 1.41 | 23 | 19 |
| 13 | C sp3 | H2CBr | 1.81 | 15 | 13 |
| 14 | C sp3 | H2CJ | 2.45 | 5 | 5 |
| 15 | C sp3 | HC3 | 0.14 | 96 | 71 |
| 16 | C sp3 | HC2N | 0.28 | 6 | 6 |
| 17 | C sp3 | HC2N(+) | 0.37 | 1 | 1 |
| 18 | C sp3 | HC2O | −0.39 | 52 | 49 |
| 19 | C sp3 | HC2S | −0.14 | 3 | 2 |
| 20 | C sp3 | HC2Cl | 1.02 | 4 | 4 |
| 21 | C sp3 | HC2Br | 1.25 | 3 | 3 |
| 22 | C sp3 | HC2J | 1.85 | 1 | 1 |
| 23 | C sp3 | HCCl2 | 1.79 | 7 | 6 |
| 24 | C sp3 | HCBr2 | 2.23 | 2 | 1 |
| 25 | C sp3 | C4 | −0.46 | 37 | 33 |
| 26 | C sp3 | C3O | −1.14 | 21 | 20 |
| 27 | C sp3 | C3F | 1.29 | 1 | 1 |
| 28 | C sp3 | C2F2 | 1.12 | 18 | 4 |
| 29 | C sp3 | CF3 | 1.82 | 10 | 6 |
| 30 | C sp3 | CF2Cl | 2.43 | 4 | 3 |
| 31 | C sp3 | CFCl2 | 2.19 | 1 | 1 |
| 32 | C sp3 | CCl3 | 2.76 | 5 | 4 |
| 33 | C sp2 | H2=C | 0.98 | 54 | 45 |
| 34 | C sp2 | HC=C | 0.6 | 109 | 69 |
| 35 | C sp2 | HC=O | −0.3 | 17 | 17 |
| 36 | C sp2 | H=CN | 0.9 | 6 | 4 |
| 37 | C sp2 | H=CO | 0.88 | 8 | 6 |
| 38 | C sp2 | H=CS | −0.99 | 3 | 3 |
| 39 | C sp2 | H=CCl | 1.54 | 7 | 5 |
| 40 | C sp2 | HN=O | −0.7 | 2 | 2 |
| 41 | C sp2 | HO=O | 0.84 | 8 | 8 |
| 42 | C sp2 | C2=C | 0.24 | 15 | 15 |
| 43 | C sp2 | C2=N | 1.59 | 2 | 2 |
| 44 | C sp2 | C=CN | −2.47 | 1 | 1 |
| 45 | C sp2 | C2=O | −1.17 | 38 | 35 |
| 46 | C sp2 | C=CO | 0.54 | 7 | 5 |
| 47 | C sp2 | C=CS | 0.09 | 1 | 1 |
| 48 | C sp2 | CN=O | −0.23 | 34 | 25 |
| 49 | C sp2 | CO=O | 0.06 | 91 | 83 |
| 50 | C sp2 | =CF2 | 1.51 | 2 | 1 |
| 51 | C sp2 | =CCl2 | 2.3 | 3 | 2 |
| 52 | C sp2 | N2=N | 0.4 | 1 | 1 |
| 53 | C sp2 | N2=O | 0.41 | 15 | 15 |
| 54 | C sp2 | N=NS | −0.04 | 2 | 2 |
| 55 | C sp2 | O2=O | 0.88 | 2 | 2 |
| 56 | C aromatic | H:C2 | 0.56 | 1318 | 270 |
| 57 | C aromatic | H:C:N | −0.39 | 25 | 17 |
| 58 | C aromatic | :C3 | 0.16 | 92 | 27 |
| 59 | C aromatic | C:C2 | 0.06 | 209 | 138 |
| 60 | C aromatic | C:C:N | −1.04 | 10 | 8 |
| 61 | C aromatic | :C2N | −0.65 | 90 | 65 |
| 62 | C aromatic | :C2N(+) | 0.56 | 43 | 33 |
| 63 | C aromatic | :C2O | 0.13 | 67 | 58 |
| 64 | C aromatic | :C2S | 0.34 | 42 | 40 |
| 65 | C aromatic | :C2F | 0.72 | 22 | 8 |
| 66 | C aromatic | :C2Cl | 1.26 | 108 | 59 |
| 67 | C aromatic | :C2Br | 1.5 | 30 | 16 |
| 68 | C aromatic | :C2J | 1.88 | 6 | 5 |
| 69 | C aromatic | :CN:N | −0.66 | 3 | 3 |
| 70 | C aromatic | :C:NCl | 1.22 | 2 | 2 |
| 71 | C aromatic | N:N2 | 0.14 | 4 | 3 |
| 72 | C aromatic | :N2Cl | −0.74 | 1 | 1 |
| 73 | C sp | H#C | 0.69 | 13 | 10 |
| 74 | C sp | C#C | 0.22 | 11 | 9 |
| 75 | C sp | C#N | −0.07 | 10 | 10 |
| 76 | C sp | N#N | 0 | 1 | 1 |
| 77 | C sp | =N=S | 3.15 | 1 | 1 |
| 78 | N sp3 | H2C | −1.57 | 10 | 10 |
| 79 | N sp3 | H2C(pi) | 0.16 | 38 | 37 |
| 80 | N sp3 | HC2 | −1.62 | 6 | 6 |
| 81 | N sp3 | HC2(pi) | −0.11 | 6 | 5 |
| 82 | N sp3 | HC2(2pi) | −0.95 | 37 | 28 |
| 83 | N sp3 | HCS | −0.59 | 1 | 1 |
| 84 | N sp3 | HCS(pi) | −1.13 | 32 | 32 |
| 85 | N sp3 | C3 | −1.62 | 10 | 9 |
| 86 | N sp3 | C3(pi) | −1.48 | 6 | 6 |
| 87 | N sp3 | C3(2pi) | −1.59 | 4 | 4 |
| 88 | N sp3 | C2N(pi) | −1.91 | 1 | 1 |
| 89 | N sp3 | C2N(2pi) | 0 | 1 | 1 |
| 90 | N sp3 | C2O(pi) | −0.33 | 2 | 2 |
| 91 | N sp3 | C2S | −0.97 | 2 | 2 |
| 92 | N sp3 | C2S(2pi) | −2.06 | 1 | 1 |
| 93 | N sp2 | H=C | 0.79 | 1 | 1 |
| 94 | N sp2 | C=C | −1.63 | 5 | 5 |
| 95 | N sp2 | C=N | 0.21 | 2 | 1 |
| 96 | N aromatic | :C2 | 0.31 | 24 | 20 |
| 97 | N aromatic | :C:N | −0.16 | 2 | 1 |
| 98 | N(+) sp2 | CO=O(−) | 0.12 | 48 | 38 |
| 99 | O | HC | −0.84 | 81 | 77 |
| 100 | O | HC(pi) | −0.9 | 67 | 63 |
| 101 | O | HO | −0.39 | 3 | 2 |
| 102 | O | C2 | −0.37 | 36 | 34 |
| 103 | O | C2(pi) | −0.41 | 96 | 84 |
| 104 | O | C2(2pi) | −0.61 | 11 | 11 |
| 105 | O | CN | 0 | 2 | 2 |
| 106 | O | CO | −0.15 | 3 | 2 |
| 107 | S2 | HC | 1.12 | 7 | 6 |
| 108 | S2 | C2 | 0.29 | 3 | 3 |
| 109 | S2 | C2(2pi) | 2.31 | 5 | 5 |
| 110 | S2 | CS | 0.42 | 2 | 1 |
| 111 | S4 | C2=O | −4.04 | 2 | 2 |
| 112 | S4 | C2=O2 | −1.81 | 2 | 2 |
| 113 | S4 | CN=O2 | −0.07 | 36 | 36 |
| 114 | H | H Acceptor | 0.14 | 6 | 6 |
| 115 | Alkane | No of C atoms | 0.19 | 272 | 39 |
| 116 | Unsaturated HC | No of C atoms | 0.03 | 844 | 92 |
| A | Based on | Valid groups | 75 | 675 | |
| B | Goodness of fit | R2 | 0.9789 | 634 | |
| C | Deviation | Average | 0.21 | 634 | |
| D | Deviation | Standard | 0.27 | 634 | |
| E | K-fold cv | K | 10 | 616 | |
| F | Goodness of fit | Q2 | 0.9737 | 616 | |
| G | Deviation | Average (cv) | 0.23 | 616 | |
| H | Deviation | Standard (cv) | 0.31 | 616 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naef, R.; Acree, W.E. Application of a General Computer Algorithm Based on the Group-Additivity Method for the Calculation of Two Molecular Descriptors at Both Ends of Dilution: Liquid Viscosity and Activity Coefficient in Water at Infinite Dilution. Molecules 2018, 23, 5. https://doi.org/10.3390/molecules23010005
Naef R, Acree WE. Application of a General Computer Algorithm Based on the Group-Additivity Method for the Calculation of Two Molecular Descriptors at Both Ends of Dilution: Liquid Viscosity and Activity Coefficient in Water at Infinite Dilution. Molecules. 2018; 23(1):5. https://doi.org/10.3390/molecules23010005
Chicago/Turabian StyleNaef, Rudolf, and William E. Acree. 2018. "Application of a General Computer Algorithm Based on the Group-Additivity Method for the Calculation of Two Molecular Descriptors at Both Ends of Dilution: Liquid Viscosity and Activity Coefficient in Water at Infinite Dilution" Molecules 23, no. 1: 5. https://doi.org/10.3390/molecules23010005
APA StyleNaef, R., & Acree, W. E. (2018). Application of a General Computer Algorithm Based on the Group-Additivity Method for the Calculation of Two Molecular Descriptors at Both Ends of Dilution: Liquid Viscosity and Activity Coefficient in Water at Infinite Dilution. Molecules, 23(1), 5. https://doi.org/10.3390/molecules23010005






