A Robust Manifold Graph Regularized Nonnegative Matrix Factorization Algorithm for Cancer Gene Clustering
Abstract
:1. Introduction
2. The NMF-Based and GNMF-Based Method
3. The RM-GNMF-Based Method for Gene Clustering
3.1. The -Norm
3.2. Spectral-Based Manifold Learning to Constrained GNMF
3.3. Computation of Z
3.4. Computation of W and H
3.5. Updating of and
| Algorithm 1: The RM-GNMF-based Algorithm |
| Input: The dataset , a predefined number of clusters k, parameters , , the nearest neighbor graph parameter p, maximum iteration number . Initialization: , , . Repeat Fix other parameters, and then update Z by formula (17); Fix other parameters, and then update W by: ; Update H by , where U and V are the left and right singular values of the SVD decomposition; Fix other parameters, and then update and by formulas (26)(27); t = t + 1; Until . Output: matrix , matrix . |
4. Results and Discussion
4.1. Datasets
4.2. Evaluation Metrics
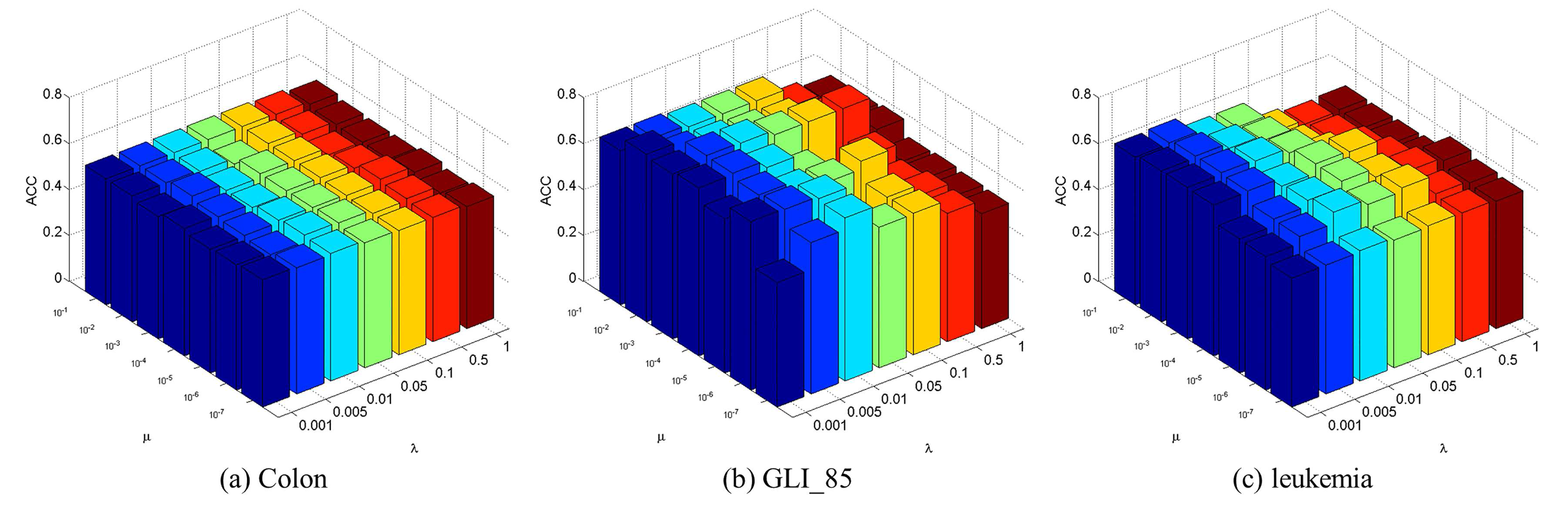
4.3. Parameter Selection
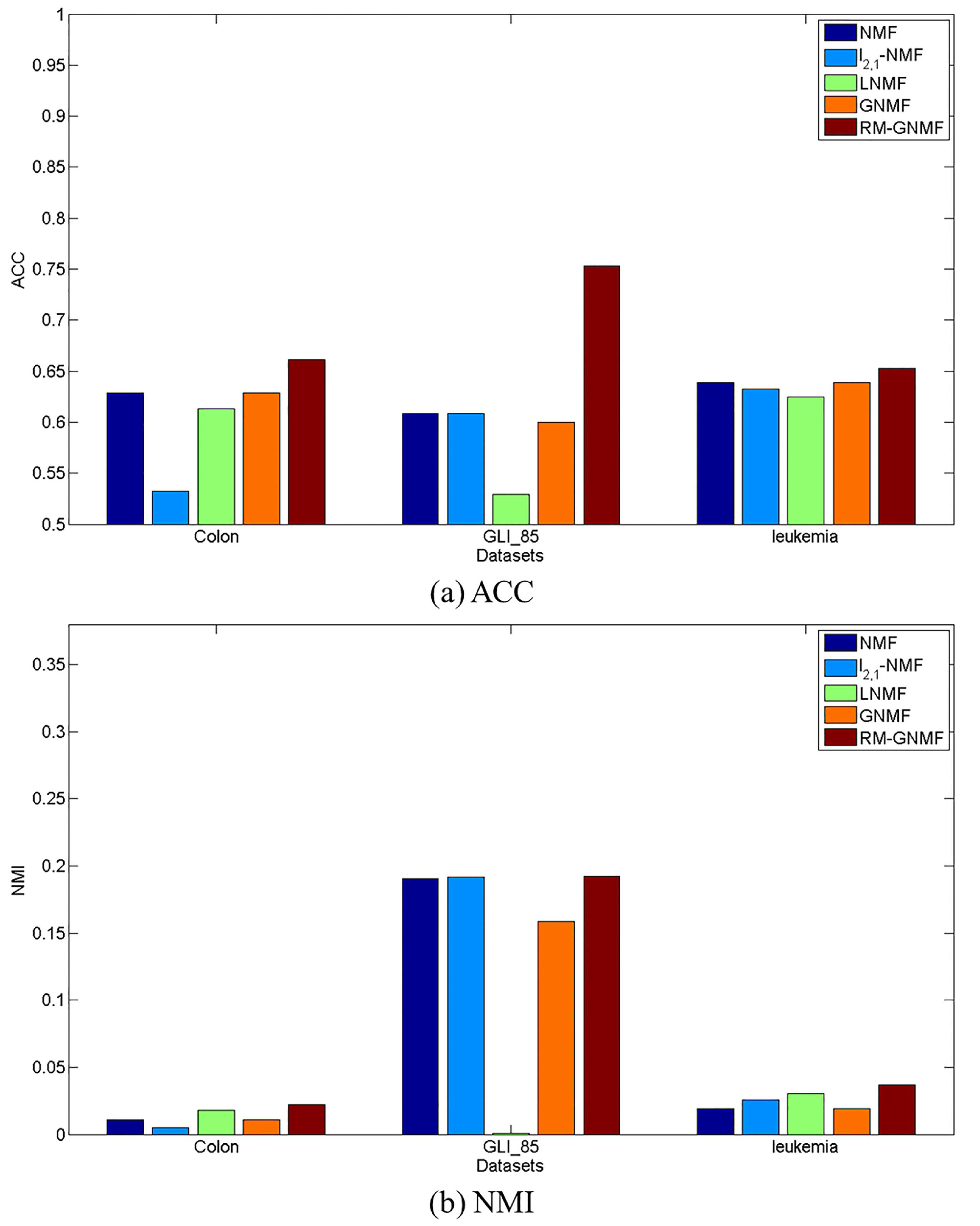
4.4. Clustering Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Golub, T.R.; Slonim, D.K.; Tamayo, P.; Huard, C.; Gaasenbeek, M.; Mesirov, J.P.; Coller, H.; Loh, M.L.; Downing, J.R.; Caligiuri, M.A.; et al. Molecular classification of cancer: Class discovery and class prediction by gene expression monitoring. Science 1999, 286, 531–537. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.; Tang, C.; Zhang, A. Cluster analysis for gene expression data: Survey. IEEE Trans. Knowl. Data Eng. 2004, 16, 1370–1386. [Google Scholar] [CrossRef]
- Devarajan, K. Nonnegative matrix factorization: an analytical and interpretive tool in computational biology. PLoS Comput. Biol. 2008, 4, e1000029. [Google Scholar] [CrossRef] [PubMed]
- Luo, F.; Khan, L.; Bastani, F.; Yen, I.L.; Zhou, J. A dynamically growing self-organizing tree (DGSOT) for hierarchical clustering gene expression profiles. Bioinformatics 2004, 20, 2605–2617. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788. [Google Scholar] [PubMed]
- Lee, D.D.; Seung, H.S. Algorithms for non-negative matrix factorization. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2001; pp. 556–562. [Google Scholar]
- Brunet, J.P.; Tamayo, P.; Golub, T.R.; Mesirov, J.P. Metagenes and molecular pattern discovery using matrix factorization. Proc. Natl. Acad. Sci. USA 2004, 101, 4164–4169. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Ding, C.H. Nonnegative Matrix Factorizations for Clustering: A Survey. In Data Clustering: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Ding, C.; He, X.; Simon, H.D. On the equivalence of nonnegative matrix factorization and spectral clustering. In Proceedings of the 2005 SIAM International Conference on Data Mining; SIAM: Philadelphia, PA, USA, 2005; pp. 606–610. [Google Scholar]
- Kuang, D.; Ding, C.; Park, H. Symmetric nonnegative matrix factorization for graph clustering. In Proceedings of the 2012 SIAM International Conference on Data Mining; SIAM: Philadelphia, PA, USA, 2012; pp. 106–117. [Google Scholar]
- Akata, Z.; Thurau, C.; Bauckhage, C. Non-negative matrix factorization in multimodality data for segmentation and label prediction. In Proceedings of the 16th Computer vision winter workshop, Mitterberg, Austria, 2–4 February 2011. [Google Scholar]
- Liu, J.; Wang, C.; Gao, J.; Han, J. Multi-view clustering via joint nonnegative matrix factorization. In Proceedings of the 2013 SIAM International Conference on Data Mining; SIAM: Philadelphia, PA, USA, 2013; pp. 252–260. [Google Scholar]
- Singh, A.P.; Gordon, G.J. Relational learning via collective matrix factorization. In Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and Data Mining, Las Vegas, Nevada, USA, 24–27 August 2008; pp. 650–658. [Google Scholar]
- Huang, Z.; Zhou, A.; Zhang, G. Non-negative matrix factorization: A short survey on methods and applications. In Computational Intelligence and Intelligent Systems; Springer: Berlin, Germany, 2012; pp. 331–340. [Google Scholar]
- Wang, Y.X.; Zhang, Y.J. Nonnegative matrix factorization: A comprehensive review. IEEE Trans. Knowl. Data Eng. 2013, 25, 1336–1353. [Google Scholar] [CrossRef]
- Kim, J.; He, Y.; Park, H. Algorithms for nonnegative matrix and tensor factorizations: A unified view based on block coordinate descent framework. J. Glob. Optim. 2014, 58, 285–319. [Google Scholar] [CrossRef]
- Cai, D.; He, X.; Han, J.; Huang, T.S. Graph regularized nonnegative matrix factorization for data representation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1548–1560. [Google Scholar] [PubMed]
- Kim, H.; Park, H. Sparse non-negative matrix factorizations via alternating non-negativity-constrained least squares for microarray data analysis. Bioinformatics 2007, 23, 1495–1502. [Google Scholar] [CrossRef] [PubMed]
- Pascual-Montano, A.; Carazo, J.M.; Kochi, K.; Lehmann, D.; Pascual-Marqui, R.D. Nonsmooth nonnegative matrix factorization (nsNMF). IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 403–415. [Google Scholar] [CrossRef] [PubMed]
- Li, S.Z.; Hou, X.W.; Zhang, H.J.; Cheng, Q.S. Learning spatially localized, parts-based representation. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Kauai, HI, USA, 8–14 December 2001. [Google Scholar]
- Paatero, P.; Tapper, U. Positive matrix factorization: A non-negative factor model with optimal utilization of error estimates of data values. Environmetrics 1994, 5, 111–126. [Google Scholar] [CrossRef]
- Chung, F.R. Spectral Graph Theory; Number 92; American Mathematical Soc.: Providence, RI, USA, 1997. [Google Scholar]
- Nie, F.; Huang, H.; Cai, X.; Ding, C.H. Efficient and robust feature selection via joint l2, 1-norms minimization. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2010; pp. 1813–1821. [Google Scholar]
- Argyriou, A.; Evgeniou, T.; Pontil, M. Multi-task feature learning. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2007; pp. 41–48. [Google Scholar]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Huang, H.; Ding, C. Robust tensor factorization using r1 norm. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Tao, H.; Hou, C.; Nie, F.; Zhu, J.; Yi, D. Scalable Multi-View Semi-Supervised Classification via Adaptive Regression. IEEE Trans. Image Process. 2017, 26, 4283–4296. [Google Scholar] [CrossRef] [PubMed]
- Shawe-Taylor, J.; Cristianini, N.; Kandola, J.S. On the concentration of spectral properties. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2002; pp. 511–517. [Google Scholar]
- Yin, M.; Gao, J.; Lin, Z. Laplacian regularized low-rank representation and its applications. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 504–517. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Robert, T.; Tang, J.; Liu, H. Feature Selection: A Data Perspective. arxiv, 2017; arXiv:1601.07996. [Google Scholar]
- Lovász, L.; Plummer, M.D. Matching Theory; American Mathematical Soc.: Providence, RI, USA, 2009; Volume 367. [Google Scholar]

| Data Sets | Instances | Features | Classes |
|---|---|---|---|
| Colon | 62 | 2000 | 2 |
| GLI_85 | 85 | 22,283 | 2 |
| Leukemia | 72 | 7070 | 2 |
| Methods | Colon | GLI_85 | Leukemia | |||
|---|---|---|---|---|---|---|
| ACC | NMI | ACC | NMI | ACC | NMI | |
| NMF | 0.6290 | 0.0110 | 0.6088 | 0.1906 | 0.6389 | 0.0193 |
| -NMF | 0.5323 | 0.0048 | 0.6088 | 0.1916 | 0.6328 | 0.0258 |
| LNMF | 0.6129 | 0.0181 | 0.5294 | 0.0011 | 0.6250 | 0.0306 |
| GNMF | 0.6290 | 0.0110 | 0.6000 | 0.1584 | 0.6389 | 0.0193 |
| RM-GNMF | 0.6613 | 0.0220 | 0.7529 | 0.1925 | 0.6528 | 0.0369 |
| Statistic | p-Value | Result |
|---|---|---|
| 7.00000 | 0.01003 | is rejected |
| Rank | Algorithm |
|---|---|
| 1.33333 | LNMF |
| 2.33333 | NMF |
| 2.66667 | -NMF |
| 3.66667 | GNMF |
| 5.00000 | RM-GNMF |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, R.; Liu, J.-X.; Zhang, Y.-K.; Guo, Y. A Robust Manifold Graph Regularized Nonnegative Matrix Factorization Algorithm for Cancer Gene Clustering. Molecules 2017, 22, 2131. https://doi.org/10.3390/molecules22122131
Zhu R, Liu J-X, Zhang Y-K, Guo Y. A Robust Manifold Graph Regularized Nonnegative Matrix Factorization Algorithm for Cancer Gene Clustering. Molecules. 2017; 22(12):2131. https://doi.org/10.3390/molecules22122131
Chicago/Turabian StyleZhu, Rong, Jin-Xing Liu, Yuan-Ke Zhang, and Ying Guo. 2017. "A Robust Manifold Graph Regularized Nonnegative Matrix Factorization Algorithm for Cancer Gene Clustering" Molecules 22, no. 12: 2131. https://doi.org/10.3390/molecules22122131
APA StyleZhu, R., Liu, J.-X., Zhang, Y.-K., & Guo, Y. (2017). A Robust Manifold Graph Regularized Nonnegative Matrix Factorization Algorithm for Cancer Gene Clustering. Molecules, 22(12), 2131. https://doi.org/10.3390/molecules22122131





