Drug-Target Interaction Prediction through Label Propagation with Linear Neighborhood Information
Abstract
:1. Introduction
2. Results and Discussion
2.1. Evaluation Metrics
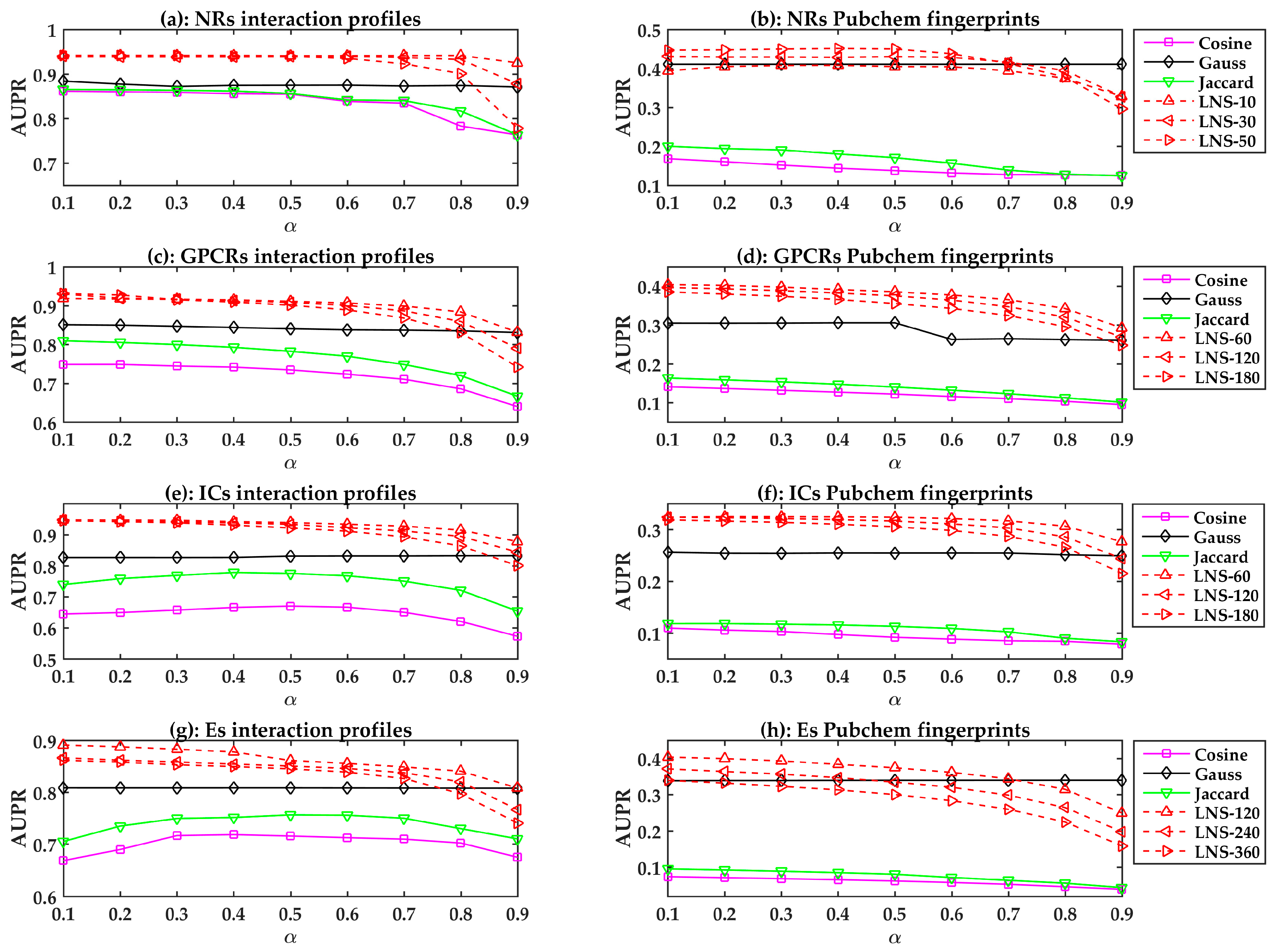
2.2. The Performances of the LPLNI Models
2.3. The Performances of LPLNI Models with Integrated Information
2.4. Comparison with State-of-the-Art Methods
2.5. Case Study
3. Materials and Methods
3.1. Datasets
3.2. Features
3.3. The Label Propagation Method with Linear Neighborhood Information
3.3.1. Linear Neighborhood Similarity
3.3.2. Label Propagation
3.4. LPLNI with Integrated Information
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ding, H.; Takigawa, I.; Mamitsuka, H.; Zhu, S. Similarity-based machine learning methods for predicting drug-target interactions: A brief review. Brief. Bioinform. 2013, 15, 734–747. [Google Scholar] [CrossRef] [PubMed]
- Whitebread, S.; Hamon, J.; Bojanic, D.; Urban, L.; Hamon, J. In vitro safety pharmacology profiling: An essential tool for successful drug development. Drug Discov. Today 2005, 10, 1421–1433. [Google Scholar] [CrossRef]
- Ballesteros, J.; Palczewski, K. G protein-coupled receptor drug discovery: Implications from the crystal structure of rhodopsin. Curr. Opin. Drug Discov. Dev. 2001, 4, 561–574. [Google Scholar]
- Hansch, C.; Maloney, P.P.; Fujita, T.; Muir, R.M. Correlation of biological activity of phenoxyacetic acids with hammett substituent constants and partition coefficients. Nature 1962, 194, 178–180. [Google Scholar] [CrossRef]
- Kuhn, M.; Campillos, M.; Gonzalez, P.; Jensen, L.J.; Bork, P. Large-scale prediction of drug-target relationships. FEBS Lett. 2008, 582, 1283–1290. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Sosa, A.T.; Oja, M.; Hetenyi, C.; Maran, U. Druglogit: Logistic discrimination between drugs and nondrugs including disease-specificity by assigning probabilities based on molecular properties. J. Chem. Inf. Model. 2012, 52, 2165–2180. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Sosa, A.T.; Maran, U. Drugs, non-drugs, and disease category specificity: Organ effects by ligand pharmacology. SAR QSAR Environ. Res. 2013, 24, 585–597. [Google Scholar] [CrossRef] [PubMed]
- Cao, R.Z.; Cheng, J.L. Deciphering the association between gene function and spatial gene-gene interactions in 3D human genome conformation. BMC Genom. 2015, 16, 880. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Xiong, Y.; Dai, H.; Kumari, K.M.; Xu, Q.; Ou, H.Y.; Wei, D.Q. PDC-SGB: Prediction of effective drug combinations using a stochastic gradient boosting algorithm. J. Theor. Biol. 2017, 417, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Zeng, J.C.; Li, D.P.; Wu, Y.F.; Zou, Q.; Liu, X.R. An empirical study of features fusion techniques for protein–protein interaction prediction. Curr. Bioinform. 2016, 11, 4–12. [Google Scholar] [CrossRef]
- Wei, L.Y.; Zou, Q.; Liao, M.H.; Lu, H.J.; Zhao, Y.M. A novel machine learning method for cytokine-receptor interaction prediction. Comb. Chem. High Throughput Screen. 2016, 19, 144–152. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Xing, P.; Zeng, J.; Chen, J.; Su, R.; Guo, F. Improved prediction of protein–protein interactions using novel negative samples, features, and an ensemble classifier. Artif. Intell. Med. 2017, 83, 67–74. [Google Scholar] [CrossRef] [PubMed]
- Nagamine, N.; Sakakibara, Y. Statistical prediction of protein chemical interactions based on chemical structure and mass spectrometry data. Bioinformatics 2007, 23, 2004–2012. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.C.; Yang, Z.X.; Wang, Y.; Deng, N.Y. Computationally probing drug-protein interactions via support vector machine. Lett. Drug Des. Discov. 2010, 7, 370–378. [Google Scholar] [CrossRef]
- Tabei, Y.; Pauwels, E.; Stoven, V.; Takemoto, K.; Yamanishi, Y. Identification of chemogenomic features from drug-target interaction networks using interpretable classifiers. Bioinformatics 2012, 28, I487–I494. [Google Scholar] [CrossRef] [PubMed]
- Gonen, M. Predicting drug-target interactions from chemical and genomic kernels using bayesian matrix factorization. Bioinformatics 2012, 28, 2304–2310. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Ding, H.; Mamitsuka, H.; Zhu, S. Collaborative matrix factorization with multiple similarities for predicting drug-target interactions. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Chicago, IL, USA, 11–14 August 2013; ACM: New York, NY, USA, 2013; pp. 1025–1033. [Google Scholar]
- Ezzat, A.; Zhao, P.L.; Wu, M.; Li, X.L.; Kwoh, C.K. Drug-target interaction prediction with graph regularized matrix factorization. IEEE ACM Trans. Comput. Bioinform. 2017, 14, 646–656. [Google Scholar] [CrossRef] [PubMed]
- Jacob, L.; Vert, J.P. Protein-ligand interaction prediction: An improved chemogenomics approach. Bioinformatics 2008, 24, 2149–2156. [Google Scholar] [CrossRef] [PubMed]
- Xia, Z.; Wu, L.Y.; Zhou, X.; Wong, S.T. Semi-supervised drug-protein interaction prediction from heterogeneous biological spaces. BMC Syst. Biol. 2010, 4 (Suppl. 2), S6. [Google Scholar] [CrossRef] [PubMed]
- Van Laarhoven, T.; Nabuurs, S.B.; Marchiori, E. Gaussian interaction profile kernels for predicting drug-target interaction. Bioinformatics 2011, 27, 3036–3043. [Google Scholar] [CrossRef] [PubMed]
- Bleakley, K.; Yamanishi, Y. Supervised prediction of drug-target interactions using bipartite local models. Bioinformatics 2009, 25, 2397–2403. [Google Scholar] [CrossRef] [PubMed]
- Mei, J.P.; Kwoh, C.K.; Yang, P.; Li, X.L.; Zheng, J. Drug-target interaction prediction by learning from local information and neighbors. Bioinformatics 2013, 29, 238–245. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Liu, M.X.; Yan, G.Y. Drug-target interaction prediction by random walk on the heterogeneous network. Mol. Biosyst. 2012, 8, 1970–1978. [Google Scholar] [CrossRef] [PubMed]
- Cheng, F.; Liu, C.; Jiang, J.; Lu, W.; Li, W.; Liu, G.; Zhou, W.; Huang, J.; Tang, Y. Prediction of drug-target interactions and drug repositioning via network-based inference. PLoS Comput. Biol. 2012, 8, e1002503. [Google Scholar] [CrossRef] [PubMed]
- Ezzat, A.; Wu, M.; Li, X.L.; Kwoh, C.K. Drug-target interaction prediction using ensemble learning and dimensionality reduction. Methods 2017, 129, 81–88. [Google Scholar] [CrossRef] [PubMed]
- Kuang, Q.F.; Li, Y.Z.; Wu, Y.M.; Li, R.; Dong, Y.C.; Li, Y.; Xiong, Q.; Huang, Z.Y.; Li, M.L. A kernel matrix dimension reduction method for predicting drug-target interaction. Chemom. Intell. Lab. 2017, 162, 104–110. [Google Scholar] [CrossRef]
- Buza, K.; Peska, L. Drug-target interaction prediction with bipartite local models and hubness-aware regression. Neurocomputing 2017, 260, 284–293. [Google Scholar] [CrossRef]
- Ding, Y.J.; Tang, J.J.; Guo, F. Identification of drug-target interactions via multiple information integration. Inf. Sci. 2017, 418, 546–560. [Google Scholar] [CrossRef]
- Peska, L.; Buza, K.; Koller, J. Drug-target interaction prediction: A bayesian ranking approach. Comput. Methods Programs Biomed. 2017, 152, 15–21. [Google Scholar] [CrossRef] [PubMed]
- Davis, J.; Goadrich, M. The relationship between precision-recall and roc curves. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; ACM: New York, NY, USA, 2006; pp. 233–240. [Google Scholar]
- Zhang, W.; Chen, Y.L.; Tu, S.K.; Liu, F.; Qu, Q.L. Drug side effect prediction through linear neighborhoods and multiple data source integration. In Proceedings of the 2016 IEEE International Conference on Bioinformatics and Biomedicine, Shenzhen, China, 15–18 December 2016; pp. 427–434. [Google Scholar]
- Zhang, W.; Chen, Y.L.; Liu, F.; Luo, F.; Tian, G.; Li, X.H. Predicting potential drug-drug interactions by integrating chemical, biological, phenotypic and network data. BMC Bioinform. 2017, 18, 18. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhu, X.P.; Fu, Y.; Tsuji, J.; Weng, Z.P. The prediction of human splicing branchpoints by multi-label learning. In Proceedings of the 2016 IEEE International Conference on Bioinformatics and Biomedicine, Shenzhen, China, 15–18 December 2016; pp. 254–259. [Google Scholar]
- Li, D.F.; Luo, L.Q.; Zhang, W.; Liu, F.; Luo, F. A genetic algorithm-based weighted ensemble method for predicting transposon-derived pirnas. BMC Bioinform. 2016, 17. [Google Scholar] [CrossRef] [PubMed]
- Luo, L.Q.; Li, D.F.; Zhang, W.; Tu, S.K.; Zhu, X.P.; Tian, G. Accurate prediction of transposon-derived pirnas by integrating various sequential and physicochemical features. PLoS ONE 2016, 11. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Liu, F.; Luo, L.Q.; Zhang, J.X. Predicting drug side effects by multi-label learning and ensemble learning. BMC Bioinform. 2015, 16. [Google Scholar] [CrossRef] [PubMed]
- Gunther, S.; Kuhn, M.; Dunkel, M.; Campillos, M.; Senger, C.; Petsalaki, E.; Ahmed, J.; Urdiales, E.G.; Gewiess, A.; Jensen, L.J.; et al. Supertarget and matador: Resources for exploring drug-target relationships. Nucleic Acids Res. 2008, 36, D919–D922. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Xiao, J.; Suzek, T.O.; Zhang, J.; Wang, J.; Bryant, S.H. Pubchem: A public information system for analyzing bioactivities of small molecules. Nucleic Acids Res. 2009, 37, W623–W633. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.L.; Chen, T.J.; Wang, Y.L.; Bryant, S.H. Pubchem as a public resource for drug discovery. Drug Discov. Today 2010, 15, 1052–1057. [Google Scholar] [CrossRef] [PubMed]
- Wishart, D.S.; Knox, C.; Guo, A.C.; Shrivastava, S.; Hassanali, M.; Stothard, P.; Chang, Z.; Woolsey, J. Drugbank: A comprehensive resource for in silico drug discovery and exploration. Nucleic Acids Res. 2006, 34, D668–D672. [Google Scholar] [CrossRef] [PubMed]
- Wishart, D.S.; Knox, C.; Guo, A.C.; Cheng, D.; Shrivastava, S.; Tzur, D.; Gautam, B.; Hassanali, M. Drugbank: A knowledgebase for drugs, drug actions and drug targets. Nucleic Acids Res. 2008, 36, D901–D906. [Google Scholar] [CrossRef] [PubMed]
- Knox, C.; Law, V.; Jewison, T.; Liu, P.; Ly, S.; Frolkis, A.; Pon, A.; Banco, K.; Mak, C.; Neveu, V.; et al. Drugbank 3.0: A comprehensive resource for ‘omics’ research on drugs. Nucleic Acids Res. 2011, 39, D1035–D1041. [Google Scholar] [CrossRef] [PubMed]
- Law, V.; Knox, C.; Djoumbou, Y.; Jewison, T.; Guo, A.C.; Liu, Y.F.; Maciejewski, A.; Arndt, D.; Wilson, M.; Neveu, V.; et al. Drugbank 4.0: Shedding new light on drug metabolism. Nucleic Acids Res. 2014, 42, D1091–D1097. [Google Scholar] [CrossRef] [PubMed]
- Kanehisa, M.; Goto, S.; Hattori, M.; Aoki-Kinoshita, K.F.; Itoh, M.; Kawashima, S.; Katayama, T.; Araki, M.; Hirakawa, M. From genomics to chemical genomics: New developments in kegg. Nucleic Acids Res. 2006, 34, D354–D357. [Google Scholar] [CrossRef] [PubMed]
- Kanehisa, M.; Goto, S.; Furumichi, M.; Tanabe, M.; Hirakawa, M. Kegg for representation and analysis of molecular networks involving diseases and drugs. Nucleic Acids Res. 2010, 38, D355–D360. [Google Scholar] [CrossRef] [PubMed]
- Schomburg, I.; Chang, A.; Ebeling, C.; Gremse, M.; Heldt, C.; Huhn, G.; Schomburg, D. Brenda, the enzyme database: Updates and major new developments. Nucleic Acids Res. 2004, 32, D431–D433. [Google Scholar] [CrossRef] [PubMed]
- Yamanishi, Y.; Araki, M.; Gutteridge, A.; Honda, W.; Kanehisa, M. Prediction of drug-target interaction networks from the integration of chemical and genomic spaces. Bioinformatics 2008, 24, I232–I240. [Google Scholar] [CrossRef] [PubMed]
- Steinbeck, C.; Hoppe, C.; Kuhn, S.; Floris, M.; Guha, R.; Willighagen, E.L. Recent developments of the (cdk)—An open-source java library for chemo- and bioinformatics. Curr. Pharm. Des. 2006, 12, 2111–2120. [Google Scholar] [CrossRef] [PubMed]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Zhang, C.S. Label propagation through linear neighborhoods. IEEE Trans. Knowl. Data Eng. 2008, 20, 55–67. [Google Scholar] [CrossRef]
- Zhang, W.; Qu, Q.; Zhang, Y.; Wang, W. The linear neighborhood propagation method for predicting long non-coding RNA–protein interactions. Neurocomputing 2018, 273, 526–534. [Google Scholar] [CrossRef]
- Zhang, W.; Zou, H.; Luo, L.Q.; Liu, Q.C.; Wu, W.J.; Xiao, W.Y. Predicting potential side effects of drugs by recommender methods and ensemble learning. Neurocomputing 2016, 173, 979–987. [Google Scholar] [CrossRef]
- Zhang, W.; Niu, Y.Q.; Zou, H.; Luo, L.Q.; Liu, Q.C.; Wu, W.J. Accurate prediction of immunogenic T-cell epitopes from epitope sequences using the genetic algorithm-based ensemble learning. PLoS ONE 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Niu, Y.Q.; Xiong, Y.; Zhao, M.; Yu, R.W.; Liu, J. Computational prediction of conformational B-cell epitopes from antigen primary structures by ensemble learning. PLoS ONE 2012, 7. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Liu, J.; Zhao, M.; Li, Q.J. Predicting linear B-cell epitopes by using sequence-derived structural and physicochemical features. Int. J. Data Min. Bioinform. 2012, 6, 557–569. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Not available. |


| Features | Methods | NRs | ICs | GPCRs | Es |
|---|---|---|---|---|---|
| Daylight | LPLNI | 0.4519 | 0.3326 | 0.4254 | 0.4094 |
| 0.7868 | 0.7605 | 0.8771 | 0.8307 | ||
| EState | LPLNI | 0.2958 | 0.2437 | 0.3096 | 0.2770 |
| 0.6903 | 0.7098 | 0.8480 | 0.8055 | ||
| Extended | LPLNI | 0.4452 | 0.3382 | 0.4317 | 0.4153 |
| 0.7820 | 0.7741 | 0.8783 | 0.8261 | ||
| GraphOnly | LPLNI | 0.3177 | 0.3226 | 0.3525 | 0.3507 |
| 0.7478 | 0.7606 | 0.8483 | 0.7939 | ||
| Hybridization | LPLNI | 0.4226 | 0.3462 | 0.4047 | 0.4050 |
| 0.8001 | 0.7962 | 0.8747 | 0.8224 | ||
| Klekota-Roth | LPLNI | 0.4665 | 0.3030 | 0.3819 | 0.3360 |
| 0.8103 | 0.7355 | 0.8580 | 0.8179 | ||
| MACCS | LPLNI | 0.3764 | 0.3400 | 0.3881 | 0.3804 |
| 0.7712 | 0.7543 | 0.8621 | 0.8360 | ||
| Pubchem | LPLNI | 0.4470 | 0.3234 | 0.4038 | 0.4039 |
| 0.7561 | 0.7522 | 0.8822 | 0.8405 | ||
| Substructure | LPLNI | 0.3202 | 0.3092 | 0.2942 | 0.2875 |
| 0.7539 | 0.7662 | 0.8465 | 0.8068 | ||
| Interaction profile | LPLNI | 0.9464 | 0.9658 | 0.9461 | 0.9051 |
| 0.9532 | 0.9890 | 0.9683 | 0.9465 | ||
| Day&Ext&Hyb&Int | LPLNI-II | 0.9492 | 0.9684 | 0.9469 | 0.9069 |
| 0.9919 | 0.9947 | 0.9769 | 0.9700 |
| Datasets | Features | Methods | AUC | AUPR |
|---|---|---|---|---|
| Es | Interaction profile | RLS-Kron | 0.9830 | 0.8850 |
| LPLNI | 0.9465 | 0.9051 | ||
| GPCRs | Interaction profile | RLS-Kron | 0.9470 | 0.7130 |
| LPLNI | 0.9683 | 0.9461 | ||
| ICs | Interaction profile | RLS-Kron | 0.9860 | 0.9270 |
| LPLNI | 0.9890 | 0.9658 | ||
| NRs | Interaction profile | RLS-Kron | 0.9060 | 0.6100 |
| LPLNI | 0.9532 | 0.9464 |
| Datasets | Features | Methods | AUC | AUPR |
|---|---|---|---|---|
| Es | chem&gen&int | RLS-Kron | 0.9780 | 0.9150 |
| chem&gen&int | NetLapRLS | 0.9830 | N.A. | |
| chem&int | LPLNI-II | 0.9700 | 0.9069 | |
| GPCRs | chem&gen&int | RLS-Kron | 0.9540 | 0.7130 |
| chem&gen&int | NetLapRLS | 0.9710 | N.A. | |
| chem&int | LPLNI-II | 0.9769 | 0.9469 | |
| ICs | chem&gen&int | RLS-Kron | 0.9840 | 0.9430 |
| chem&gen&int | NetLapRLS | 0.9860 | 0.N.A. | |
| chem&int | LPLNI-II | 0.9947 | 0.9684 | |
| NRs | chem&gen&int | RLS-Kron | 0.9220 | 0.6840 |
| chem&gen&int | NetLapRLS | 0.8880 | 0.N.A. | |
| chem&int | LPLNI-II | 0.9919 | 0.9492 |
| Rank | Pair | Description | Confirmed? |
|---|---|---|---|
| 1 | D00574 | Aminoglutethimide (USP/INN) | |
| hsa1589 | cytochrome P450, family 21, subfamily A, polypeptide 2 | ||
| 2 | D00437 | Nifedipine (JP15/USP/INN) | Yes |
| hsa1559 | cytochrome P450, family 2, subfamily C, polypeptide 9 | ||
| 3 | D00542 | Halothane (JP15/USP/INN) | Yes |
| hsa1571 | cytochrome P450, family 2, subfamily E, polypeptide 1 | ||
| 4 | D00410 | Metyrapone (JP15/USP/INN) | |
| hsa1583 | cytochrome P450, family 11, subfamily A, polypeptide 1 | ||
| 5 | D00139 | Methoxsalen (JP15/USP) | Yes |
| hsa1543 | cytochrome P450, family 1, subfamily A, polypeptide 1 | ||
| 6 | D00437 | Nifedipine (JP15/USP/INN) | |
| hsa1585 | cytochrome P450, family 11, subfamily B, polypeptide 2 | ||
| 7 | D00691 | Diprophylline (JAN/INN) | |
| hsa8654 | phosphodiesterase 5A, cGMP-specific | ||
| 8 | D00691 | Diprophylline (JAN/INN) | |
| hsa5152 | phosphodiesterase 9A | ||
| 9 | D00691 | Diprophylline (JAN/INN) | Yes |
| hsa5150 | phosphodiesterase 7A | ||
| 10 | D00691 | Diprophylline (JAN/INN) | |
| hsa50940 | Peptidyl-prolyl cis-trans isomerase A |
| Datasets | Sparsity | |||||
|---|---|---|---|---|---|---|
| Es | 445 | 664 | 2926 | 6.5753 | 4.4066 | 0.0099 |
| GPCRs | 223 | 95 | 635 | 2.8475 | 6.6842 | 0.0299 |
| ICs | 210 | 204 | 1476 | 7.0286 | 7.2353 | 0.0345 |
| NRs | 54 | 26 | 90 | 1.6667 | 3.4615 | 0.0641 |
| Fingerprints | Descriptions |
|---|---|
| Daylight | Daylight fingerprints based on hashing molecular subgraphs |
| EState | This fingerprinter generates 79 bit fingerprints using the E-State fragments |
| Extended | These fingerprints extends the CDK with additional bits describing ring features |
| Graph Only | Specialized version of the CDK Fingerprinter that does not take bond orders into account |
| Hybridization | This fingerprinter takes into account SP2 hybridization states |
| Klekota-Roth | This fingerprinter presence of 4860 substructures |
| MACCS | This fingerprinter generates 166 bit MACCS keys. |
| Pubchem | These fingerprints are of the structural key type, of length 881 |
| Substructure | The fingerprint currently supports 307 substructures |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Chen, Y.; Li, D. Drug-Target Interaction Prediction through Label Propagation with Linear Neighborhood Information. Molecules 2017, 22, 2056. https://doi.org/10.3390/molecules22122056
Zhang W, Chen Y, Li D. Drug-Target Interaction Prediction through Label Propagation with Linear Neighborhood Information. Molecules. 2017; 22(12):2056. https://doi.org/10.3390/molecules22122056
Chicago/Turabian StyleZhang, Wen, Yanlin Chen, and Dingfang Li. 2017. "Drug-Target Interaction Prediction through Label Propagation with Linear Neighborhood Information" Molecules 22, no. 12: 2056. https://doi.org/10.3390/molecules22122056
APA StyleZhang, W., Chen, Y., & Li, D. (2017). Drug-Target Interaction Prediction through Label Propagation with Linear Neighborhood Information. Molecules, 22(12), 2056. https://doi.org/10.3390/molecules22122056




