Molecular Electron Density Theory: A Modern View of Reactivity in Organic Chemistry
Abstract
:1. Structure and Reactivity in Organic Chemistry Based on Quantum Chemical Models
2. Quantum Chemical Topological Analysis of the Electron Density and Molecular Mechanisms
3. Global Electron Density Transfer (GEDT) and Activation Energy of Polar Organic Reactions
4. GEDT Favours the Electron Density Changes Required to Reach the TS Structure
5. Molecular Electron Density Theory (MEDT)
6. Conclusions
7. Computational Methods
Acknowledgments
Conflicts of Interest
References
- Trautz, M. Das gesetz der reaktionsgeschwindigkeit und der gleichgewichte in gasen. Bestätigung der additivität von Cv-3/2R. Neue bestimmung der integrationskonstanten und der moleküldurchmesser. Z. Anorg. Allg. Chem. 1916, 96, 1–28. (In German) [Google Scholar] [CrossRef]
- Arrhenius, S.A. Über die dissociationswärme und den einflusß der temperatur auf den dissociationsgrad der elektrolyte. Z. Phys. Chem. 1889, 4, 96–116. (In German) [Google Scholar]
- Lewis, G.N. The atom and the molecule. J. Am. Chem. Soc. 1916, 38, 762–785. [Google Scholar] [CrossRef]
- Slater, J.C. Directed valence in polyatomic molecules. Phys. Rev. B 1931, 37, 481–489. [Google Scholar] [CrossRef]
- Slater, J.C. Molecular energy levels and valence bonds. Phys. Rev. B 1931, 38, 1109–1144. [Google Scholar] [CrossRef]
- Pauling, L. The metallic state. Nature 1948, 161, 1019–1020. [Google Scholar] [CrossRef] [PubMed]
- Mulliken, R.S. Spectroscopy, molecular orbitals and chemical bonding. Science 1967, 157, 13–24. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Su, P.; Shaik, S.; Hiberty, P.C. Classical Valence Bond Approach by Modern Methods. Chem. Rev. 2011, 111, 7557–7593. [Google Scholar] [CrossRef] [PubMed]
- Schrödinger, E. An ondulatory theory of the mechanics of atoms and molecules. Phys. Rev. B 1926, 28, 1049–1070. [Google Scholar] [CrossRef]
- Matta, C.F.; Gillespie, R.J. Understanding and interpreting molecular electron density distributions. J. Chem. Educ. 2002, 79, 1141–1152. [Google Scholar] [CrossRef]
- Lennard-Jones, J.E. The electronic structure and the interaction of some simple radicals. Trans. Faraday Soc. 1934, 30, 70–85. [Google Scholar] [CrossRef]
- Hehre, W.J.; Radom, L.; von R. Schleyer, P.; Pople, J.A. AB INITIO Molecular Orbital Theory; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Hückel, E. Quantum-theoretical contributions to the benzene problem. I. The electron configuration of benzene and related compounds. Z. Phys. 1931, 70, 204–286. [Google Scholar] [CrossRef]
- Hückel, E. Quantum contributions to the benzene problem. II. Z. Phys. 1931, 72, 310–337. [Google Scholar] [CrossRef]
- Hückel, E. Quantum contributions to the problem of aromatic and unsaturated compounds. III. Z. Phys. 1932, 76, 628–648. (In German) [Google Scholar] [CrossRef]
- Coulson, C.A.; O’Leary, B.; Mallion, R.B. Hückel Theory for Organic Chemists; Academic Press: Londen, UK, 1978. [Google Scholar]
- Fukui, K. Molecular Orbitals in Chemistry Physics and Biology; Academic Press: New York, NY, USA, 1964. [Google Scholar]
- Fleming, I. Molecular Orbitals and Organic Chemical Teactions; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. B 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Scerri, E.R. Have Orbitals Really Been Observed? J. Chem. Educ. 2000, 77, 1492–1494. [Google Scholar] [CrossRef]
- Coppens, P. X-ray Charge Densities and Chemical Bonding; Oxford University Press: New York, UK, USA, 1997. [Google Scholar]
- Koritsanszky, T.S.; Coppens, P. Chemical applications of X-ray charge-density analysis. Chem. Rev. 2001, 101, 1583–1628. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, G.D. Hybrid meta density functional theory methods for thermochemistry, thermochemical kinetics, and noncovalent Interactions: The MPW1B95 and MPWB1K models and comparative assessments for hydrogen bonding and van der Waals interactions. J. Phys. Chem. A 2004, 108, 6908–6918. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinectics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Diels, O.; Alder, K. Synthesen in der hydroaromatischen Reihe. Justus Liebigs Ann. Chem. 1928, 460, 98–122. (In German) [Google Scholar] [CrossRef]
- Sutcliffe, B.T. The development of the idea of a chemical bond. Int. J. Quantum Chem. 1996, 58, 645–655. [Google Scholar] [CrossRef]
- Abraham, R.H.; Shaw, C.D. Dynamics: The Geometry of Behavior; Addison-Wesley: Redwood City, CA, USA, 1992. [Google Scholar]
- Bader, R.F.W. Molecular Fragments or Chemical Bonds. Acc. Chem. Res. 1975, 8, 34–40. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules. A Quantum Theory; Claredon Press: Oxford, UK, 1990. [Google Scholar]
- Bader, R.F.W.; Anderson, S.G.; Duke, A.J. Quantum topology of molecular charge distributions. 1. J. Am. Chem. Soc. 1979, 101, 1389–1395. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Nguyendang, T.T.; Tal, Y. Quantum topology of molecular charge distributions. II. Molecular structure and its change. J. Chem. Phys. 1979, 70, 4316. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization n atomic and molecular-systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Savin, A.; Becke, A.D.; Flad, J.; Nesper, R.; Preuss, H.; von Schnering, H.G. A new look at electron localization. Angew. Chem. Int. Ed. 1991, 30, 409–412. [Google Scholar] [CrossRef]
- Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
- Savin, A.; Silvi, B.; Colonna, F. Topological analysis of the electron localization function applied to delocalized bonds. Can. J. Chem. 1996, 74, 1088–1096. [Google Scholar] [CrossRef]
- Savin, A.; Nesper, R.; Wengert, S.; Fassler, T.F. ELF: The Electron Localization Function. Angew. Chem. Int. Ed. 1997, 36, 1808–1832. [Google Scholar] [CrossRef]
- Silvi, B. The synaptic order: A key concept to understand multicenter bonding. J. Mol. Struct. 2002, 614, 3–10. [Google Scholar] [CrossRef]
- Berski, S.; Andrés, J.; Silvi, B.; Domingo, L.R. The joint use of catastrophe theory and electron localization function to characterize molecular mechanisms. A density functional study of the Diels-Alder reaction between ethylene and 1,3-butadiene. J. Phys. Chem. A 2003, 107, 6014–6024. [Google Scholar] [CrossRef]
- Polo, V.; Andrés, J.; Berskit, S.; Domingo, L.R.; Silvi, B. Understanding reaction mechanisms in organic chemistry from catastrophe theory applied to the electron localization function topology. J. Phys. Chem. A 2008, 112, 7128–7136. [Google Scholar] [CrossRef] [PubMed]
- Andrés, J.; Gonzáez-Navarrete, P.; Safont, V. Unravelling reaction mechanisms by means of quantum chemical topology analysis. Int. J. Quantum Chem. 2014, 114, 1239–1252. [Google Scholar] [CrossRef]
- Thom, R. Structural Stability and Morphogenesis: An Outline of a General Theory of Models; Westview Press: Boulder, CO, USA, 1976. [Google Scholar]
- Woodcock, A.E.R.; Poston, T. A Geometrical Study of Elementary Catastrophes; Spinger: Berlin, Germany, 1974. [Google Scholar]
- Gilmore, R. Catastrophe Theory for Scientists and Engineers; Courier Corporation: North Chelmsford, MA, USA, 1981. [Google Scholar]
- Krokidis, X.; Noury, S.; Silvi, B. Characterization of elementary chemical processes by catastrophe theory. J. Phys. Chem. A 1997, 101, 7277–7282. [Google Scholar] [CrossRef]
- Krokidis, X.; Goncalves, V.; Savin, A.; Silvi, B. How malonaldehyde bonds change during proton transfer. J. Phys. Chem. A 1998, 102, 5065–5073. [Google Scholar] [CrossRef]
- Fourre, I.; Silvi, B.; Chaquin, P.; Sevin, A. Electron localization function comparative study of ground state, triplet state, radical anion, and cation in model carbonyl and imine compounds. J. Comput. Chem. 1999, 20, 897–910. [Google Scholar] [CrossRef]
- Chesnut, D.B.; Bartolotti, L.J. The pair density description of aromaticity in some substituted cyclopentadienyl systems: A comparison of AIM and ELF bonding descriptors. Chem. Phys. 2000, 257, 175–181. [Google Scholar] [CrossRef]
- Fuster, F.; Sevin, A.; Silvi, B. Topological Analysis of the Electron Localization Function (ELF) Applied to the Electrophilic Aromatic Substitution. J. Phys. Chem. A 2000, 104, 852–858. [Google Scholar] [CrossRef]
- Chamorro, E.; Santos, J.C.; Gómez, B.; Contreras, R.; Fuentealba, P. The bonding nature of some simple sigmatropic transition states from the topological analysis of the electron localization function. J. Phys. Chem. A 2002, 106, 11533–11539. [Google Scholar] [CrossRef]
- Chaquin, P.; Scemama, A. Theoretical study of the electrocyclization product of butadiyne: Structure, stability and possible formations. Chem. Phys. Lett. 2004, 394, 244–249. [Google Scholar] [CrossRef]
- Polo, V.; González-Navarrete, P.; Silvi, B.; Andrés, J. An electron localization function and catastrophe theory analysis on the molecular mechanism of gas-phase identity SN2 reactions. Theor. Chem. Acc. 2008, 120, 341–349. [Google Scholar] [CrossRef]
- Salinas-Olvera, J.P.; Gomez, R.M.; Cortes-Guzman, F. Structural evolution: Mechanism of olefin insertion in hydroformylation reaction. J. Phys. Chem. A 2008, 112, 2906–2912. [Google Scholar] [CrossRef] [PubMed]
- Ndassa, I.M.; Silvi, B.; Volatron, F. Understanding reaction mechanisms in organic chemistry from catastrophe theory: Ozone addition on benzene. J. Phys. Chem. A 2010, 114, 12900–12906. [Google Scholar] [CrossRef] [PubMed]
- Gillet, N.; Chaudret, R.; Contreras-Garcia, J.; Yang, W.T.; Silvi, B.; Piquemal, J.P. Coupling Quantum Interpretative Techniques: Another Look at Chemical Mechanisms in Organic Reactions. J. Chem. Theory Comput. 2012, 8, 3993–3997. [Google Scholar] [CrossRef] [PubMed]
- Domingo, L.R. State of the art of the bonding changes along the Diels-Alder reaction between butadiene and ethylene: Refuting the pericyclic mechanism. Org. Chem. Curr. Res. 2013, 2, 120. [Google Scholar]
- Woodward, R.B.; Hoffmann, R. The conservation of orbital symmetry. Angew. Chem. Int. Ed. Engl. 1969, 8, 781–853. [Google Scholar] [CrossRef]
- Houk, K.N.; González, J.; Li, Y. Pericyclic reaction transition states: Passions and punctilios, 1935–1995. Acc. Chem. Res. 1995, 28, 81–90. [Google Scholar] [CrossRef]
- Domingo, L.R. A new C–C bond formation model based on the quantum chemical topology of electron density. RSC Adv. 2014, 4, 32415–32428. [Google Scholar] [CrossRef]
- Domingo, L.R.; Arnó, M.; Andrés, J. Influence of reactant polarity on the course of the inverse-electron-demand Diels-Alder reaction. A DFT study of regio- and stereoselectivity, presence of Lewis acid catalyst, and inclusion of solvent effects in the reaction between nitroethene and substituted ethenes. J. Org. Chem. 1999, 64, 5867–5875. [Google Scholar]
- Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural population analysis. J. Chem. Phys. 1985, 83, 735. [Google Scholar] [CrossRef]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Domingo, L.R.; Sáez, J.A. Understanding the mechanism of polar Diels-Alder reactions. Org. Biomol. Chem. 2009, 7, 3576–3583. [Google Scholar] [CrossRef] [PubMed]
- Domingo, L.R.; Pérez, P.; Sáez, J.A. Understanding the regioselectivity in hetero Diels-Alder reactions. An ELF analysis of the reaction between nitrosoethylene and 1-vinylpyrrolidine. Tetrahedron 2013, 69, 107–114. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P.; Chamorro, E. Understanding the [2n+2n] reaction mechanism between a carbenoid intermediate and CO2. Mol. Phys. 2016, 114, 1374–1391. [Google Scholar] [CrossRef]
- Parr, R.G.; von Szentpaly, L.; Liu, S. Electrophilicity index. J. Am. Chem. Soc. 1999, 121, 1922–1924. [Google Scholar] [CrossRef]
- Domingo, L.R.; Aurell, M.J.; Pérez, P.; Contreras, R. Quantitative characterization of the global electrophilicity power of common diene/dienophile pairs in Diels-Alder reactions. Tetrahedron 2002, 58, 4417–4423. [Google Scholar] [CrossRef]
- Domingo, L.R.; Chamorro, E.; Pérez, P. Understanding the reactivity of captodative ethylenes in polar cycloaddition reactions. A theoretical study. J. Org. Chem. 2008, 73, 4615–4624. [Google Scholar] [CrossRef] [PubMed]
- Domingo, L.R.; Pérez, P. The nucleophilicity N index in organic chemistry. Org. Biomol. Chem. 2011, 9, 7168–7175. [Google Scholar] [CrossRef] [PubMed]
- Domingo, L.R.; Aurell, M.J.; Pérez, P.; Contreras, R. Origin of the synchronicity on the transition structures of polar Diels-Alder reactions. Are these reactions [4+2] processes? J. Org. Chem. 2003, 68, 3884–3890. [Google Scholar] [CrossRef] [PubMed]
- Sauer, J.; Wiest, H.; Mielert, A. Eine studie der Diels-Alder-reaktion, I. Die reaktivität von dienophilen gegenüber cyclopentadien und 9.10-dimethyl-anthracen. Chem. Ber. 1964, 97, 3183–3207. [Google Scholar] [CrossRef]
- Carruthers, W. Some Modern Methods of Organic Synthesis; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Geerlings, P.; de Proft, F.; Langenaeker, W. Conceptual density functional theory. Chem. Rev. 2003, 103, 1793–1873. [Google Scholar] [CrossRef] [PubMed]
- Domingo, L.R.; Ríos-Gutérrez, M.; Pérez, P. Applications of the conceptual density functional theory indices to organic chemistry reactivity. Molecules 2016, 21, 748. [Google Scholar] [CrossRef] [PubMed]
- Sanderson, R.T. Partial charges on atoms in organic compounds. Science 1955, 121, 207–208. [Google Scholar] [CrossRef] [PubMed]
- Parr, R.G.; Donnelly, R.A.; Levy, M.; Palke, W.E. Electronegativity: The density functional viewpoint. J. Chem. Phys. 1978, 68, 3801. [Google Scholar] [CrossRef]
- Errede, L.A.; Hoyt, J.M.; Gregorian, R.S. The Chemistry of Xylylenes. VII. Some reactions of p-Xylylene that occur via cationic intermediates. J. Am. Chem. Soc. 1960, 53, 5224–5227. [Google Scholar] [CrossRef]
- Domingo, L.R.; Chamorro, E.; Pérez, P. Understanding the high reactivity of the azomethine ylides in [3+2] cycloaddition reactions. Lett. Org. Chem. 2010, 432–439. [Google Scholar] [CrossRef]
- Domingo, L.R.; Pérez, P.; Sáez, J.A. Understanding the local reactivity in polar organic reactions through electrophilic and nucleophilic Parr functions. RSC Adv. 2013, 3, 1486–1494. [Google Scholar] [CrossRef]
- Chamorro, E.; Pérez, P.; Domingo, L.R. On the nature of Parr functions to predict the most reactive sites along organic polar reactions. Chem. Phys. Lett. 2013, 582, 141–143. [Google Scholar] [CrossRef]
- Domingo, L.R.; Chamorro, E.; Pérez, P. Understanding the mechanism of non-polar Diels–Alder reactions. A comparative ELF analysis of concerted and stepwise diradical mechanisms. Org. Biomol. Chem. 2010, 8, 5495–5504. [Google Scholar] [CrossRef] [PubMed]
- Johnson, E.R.; Keinan, S.; Mori-Sanchez, P.; Contreras-Garcia, J.; Cohen, J.; Yang, A.W. Revealing noncovalent interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed]
- Ríos-Gutiérrez, M.; Domingo, L.R.; Pérez, P. Understanding the high reactivity of carbonyl compounds towards nucleophilic carbenoid intermediates generated from carbene isocyanides. RSC Adv. 2015, 5, 84797–84809. [Google Scholar] [CrossRef]
- Domingo, L.R.; Emamian, S.R. Understanding the mechanisms of [3+2] cycloaddition reactions. The pseudoradical versus the zwitterionic mechanism. Tetrahedron 2014, 70, 1267–1273. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. A new model for C-C bond formation processes derived from the Molecular Electron-Density Theory in the study of the mechanism of [3+2] cycloaddition reactions of carbenoid nitrile ylides with electron-deficient ethylenes. Tetrahedron 2016, 72, 1524–1532. [Google Scholar] [CrossRef]
- Huisgen, R. 1,3-Dipolar Cycloadditions. Past and Future. Angew. Chem. Int. Ed. 1963, 2, 565–598. [Google Scholar] [CrossRef]
- Domingo, L.R.; Aurell, M.J.; Pérez, P. A Mechanistic Study of the Participation of Azomethine Ylides and Carbonyl Ylides in [3+2] Cycloaddition Reactions. Tetrahedron 2015, 71, 1050–1057. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Duque-Noreña, M.; Chamorro, E.; Pérez, P. Understanding the carbenoid-type reactivity of nitrile ylides in [3+2] cycloaddition reactions towards electron-deficient ethylenes. A molecular electron density theory study. Theor. Chem. Acc. 2016, 135, 160. [Google Scholar] [CrossRef]
- Domingo, L.R.; Aurell, M.J.; Pérez, P. A DFT analysis of the participation of TACs in zw-type [3+2] Cycloaddition Reactions. Tetrahedron 2014, 70, 4519–4525. [Google Scholar] [CrossRef]
- Houk, K.N.; Sims, J.; Duke, R.E.; Strozier, R.W.; George, J.K. Frontier molecular orbitals of 1,3-dipoles and dipolarophiles. J. Am. Chem. Soc. 1973, 95, 7287–7301. [Google Scholar] [CrossRef]
- Noury, S.; Krokidis, X.; Fuster, F.; Silvi, B. Computational tools for the electron localization function topological analysis. Comput. Chem. 1999, 23, 597–604. [Google Scholar] [CrossRef]
- Gaussian, version 09; Gaussian: Wallingford, CT, USA, 2009.
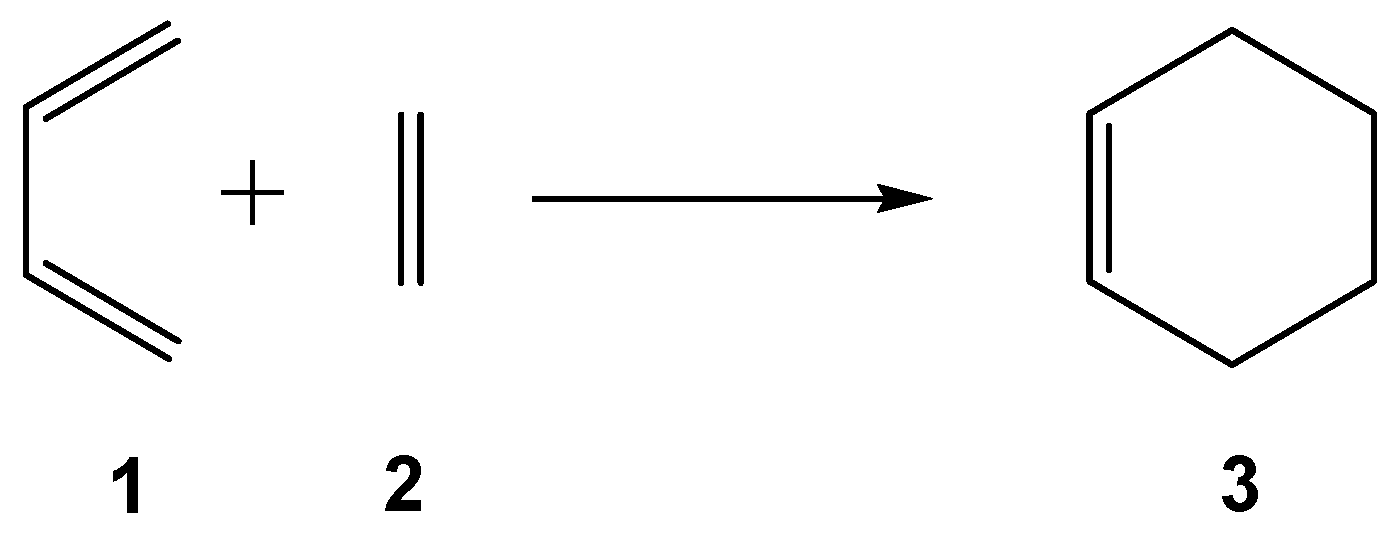

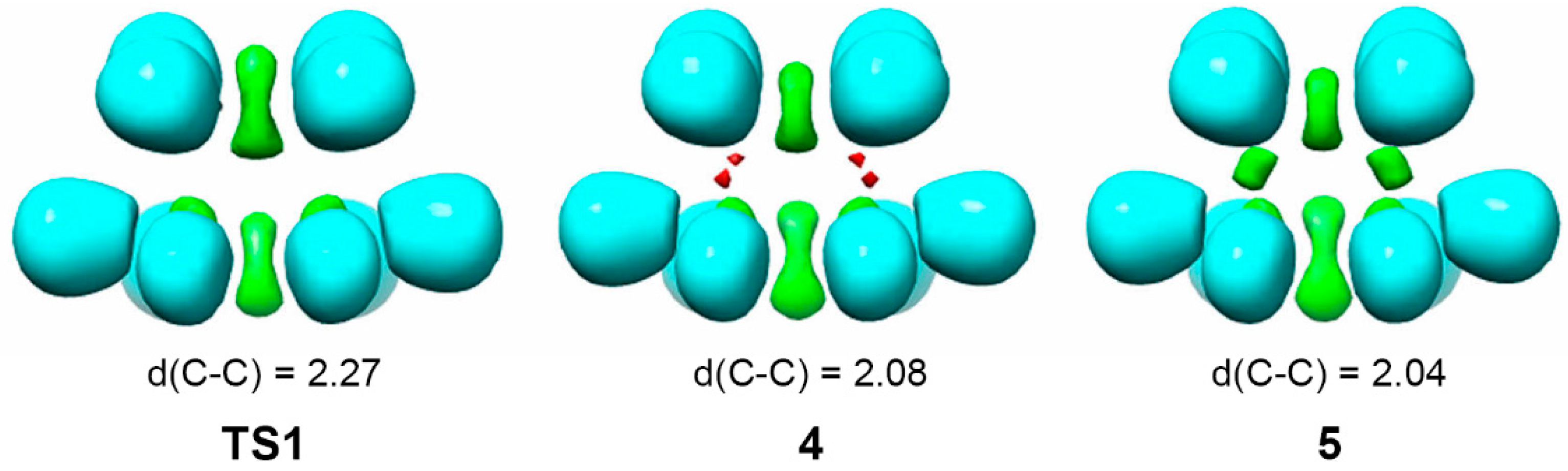
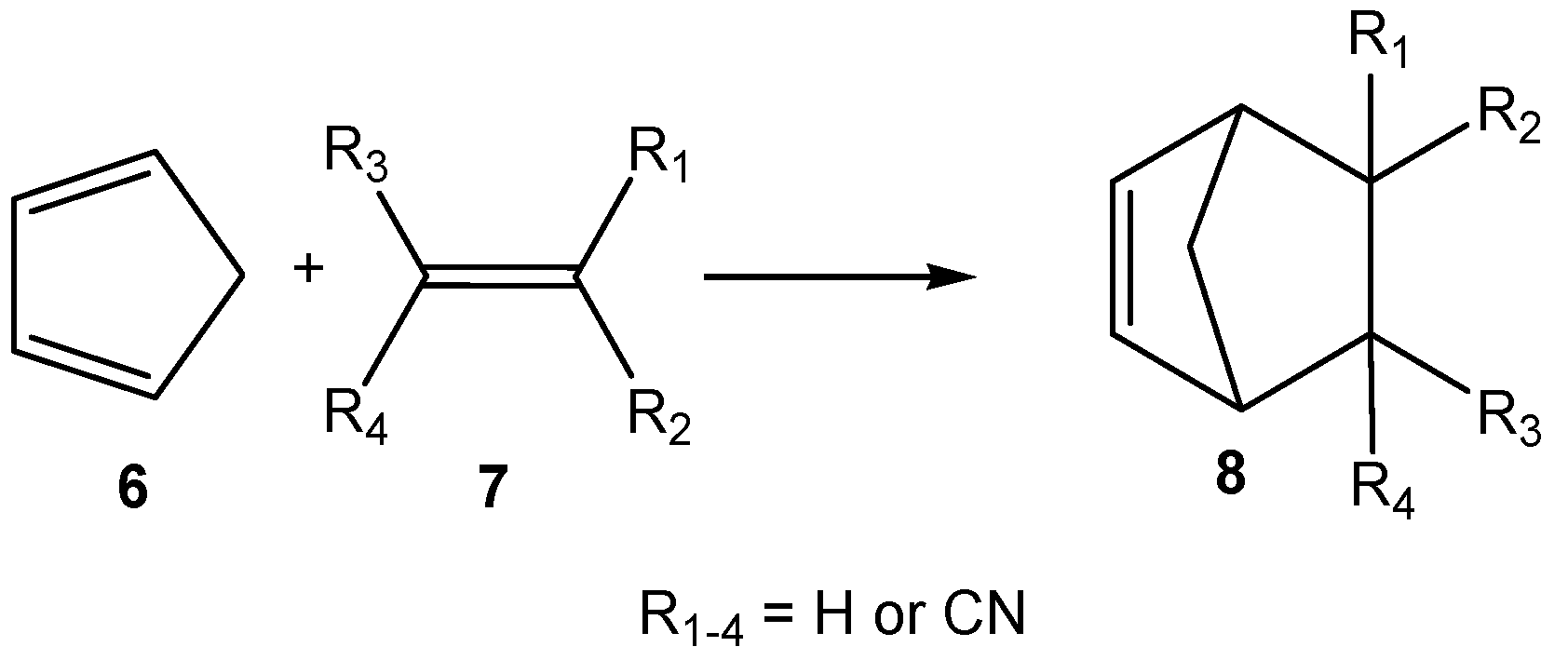
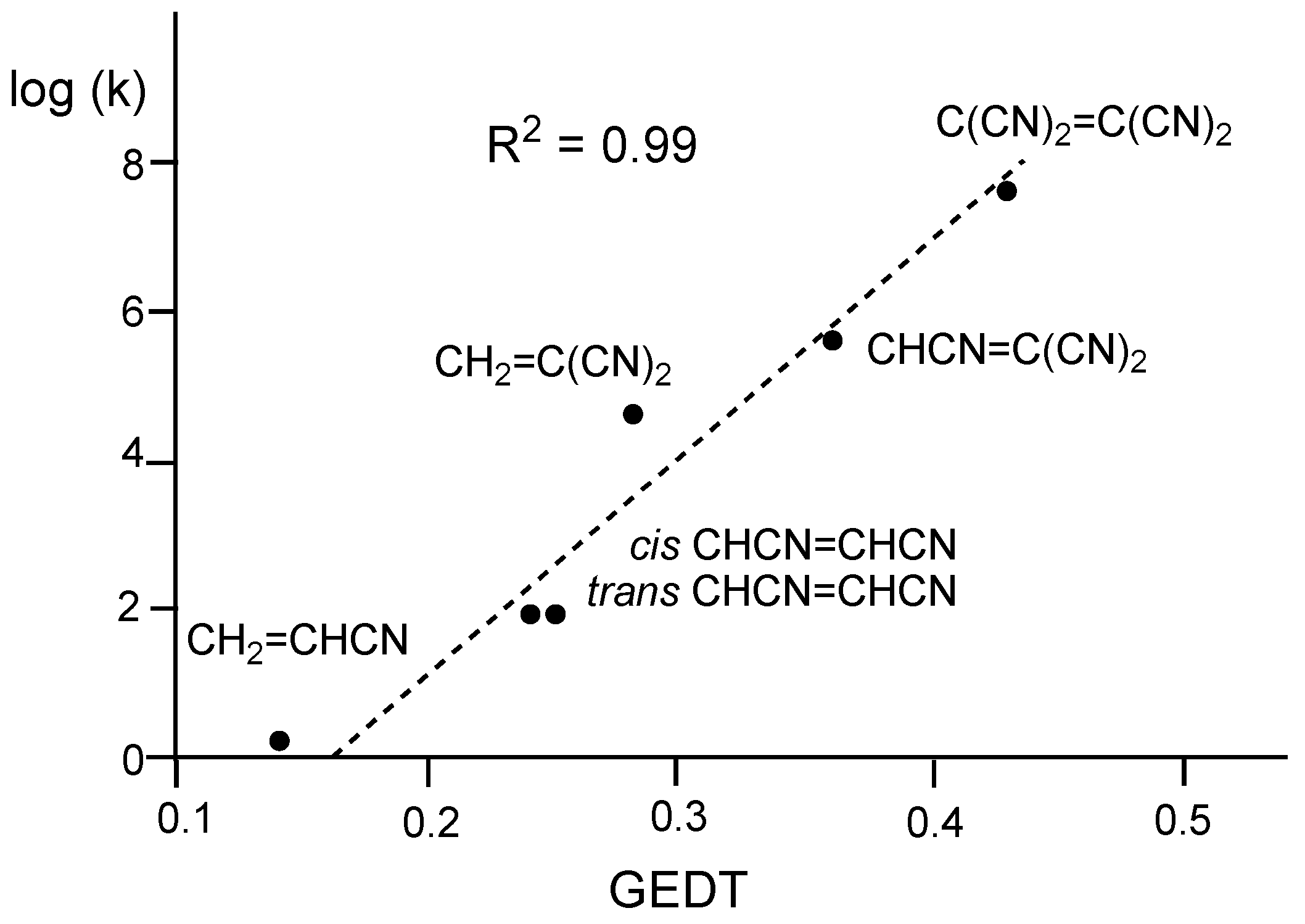

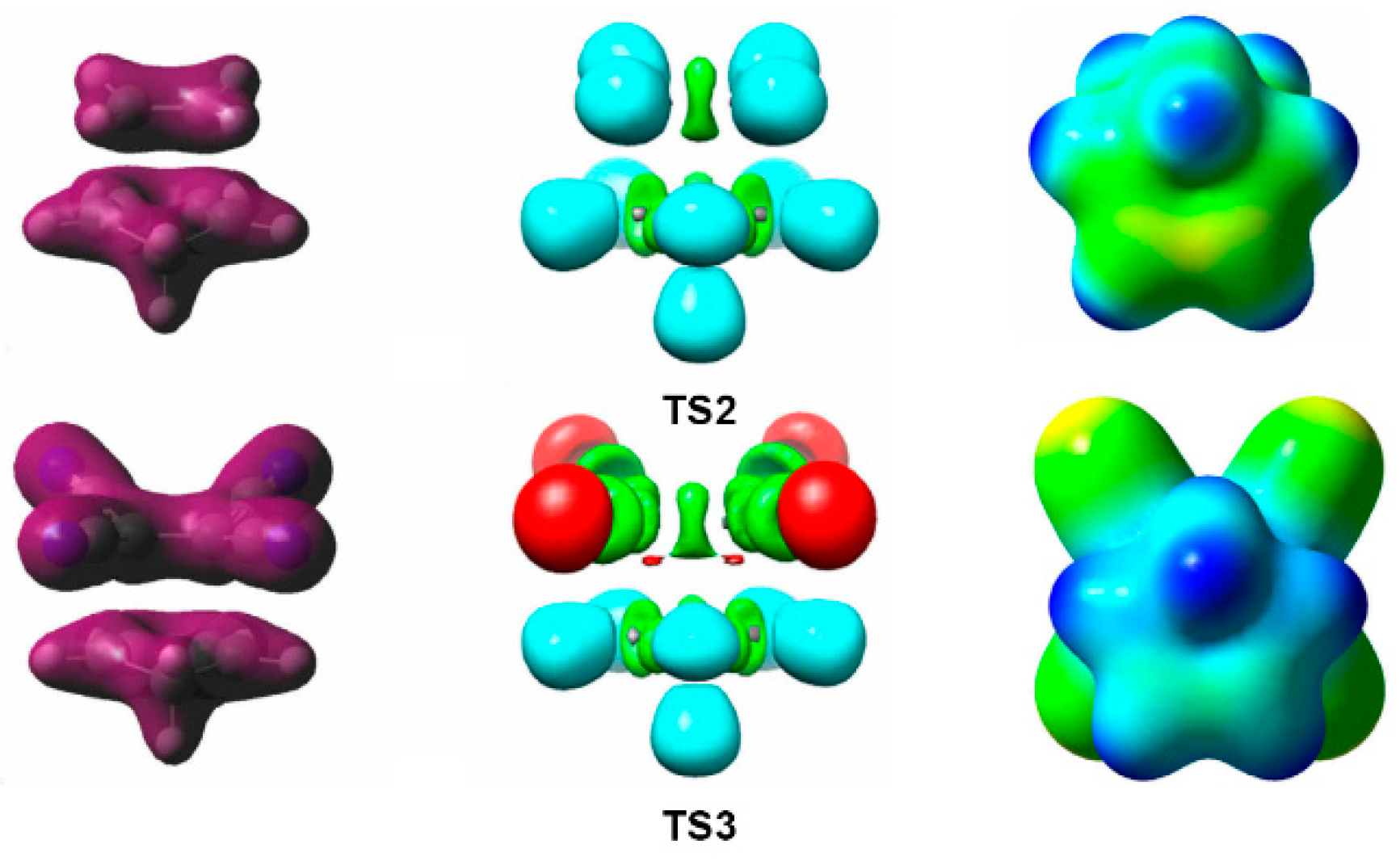
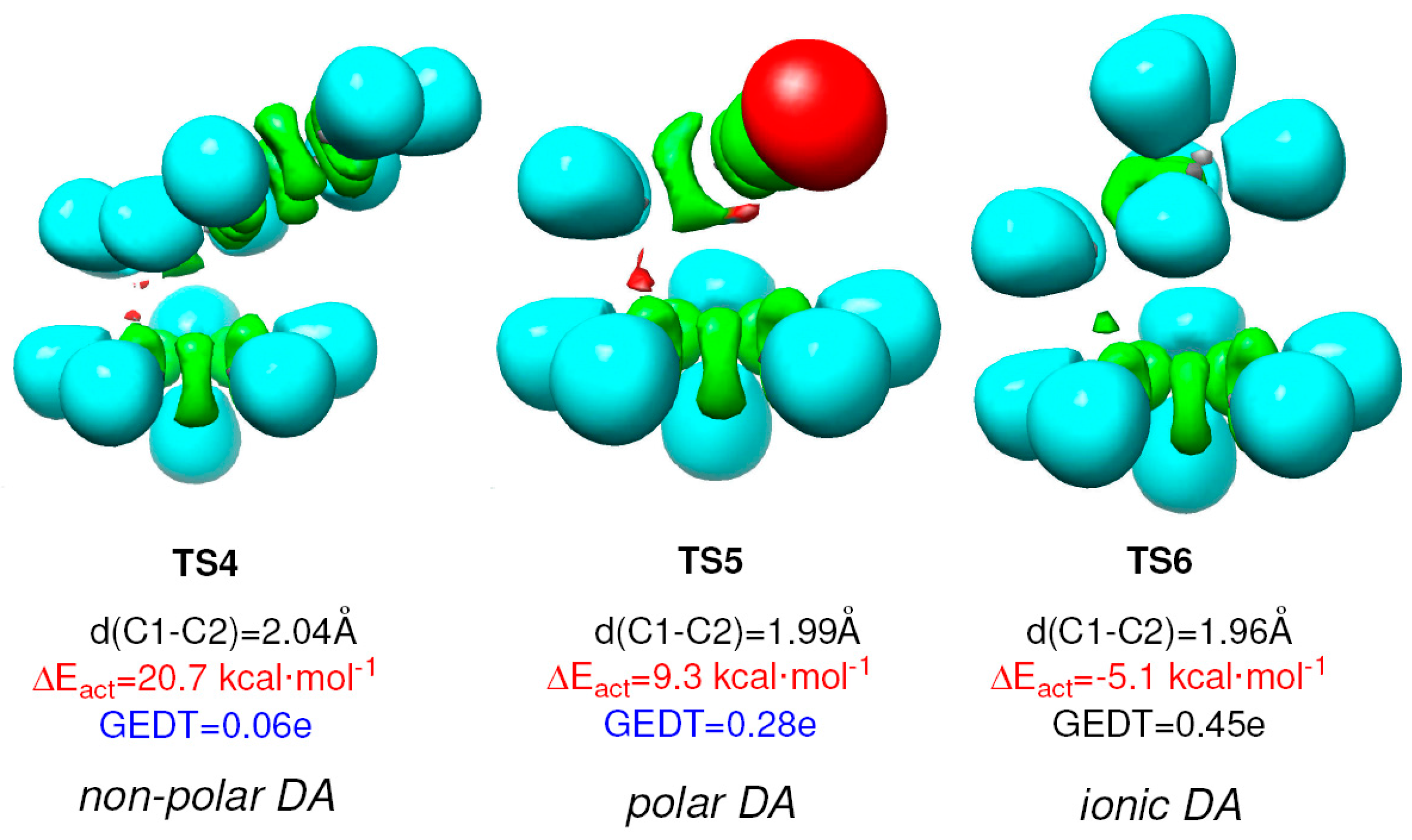
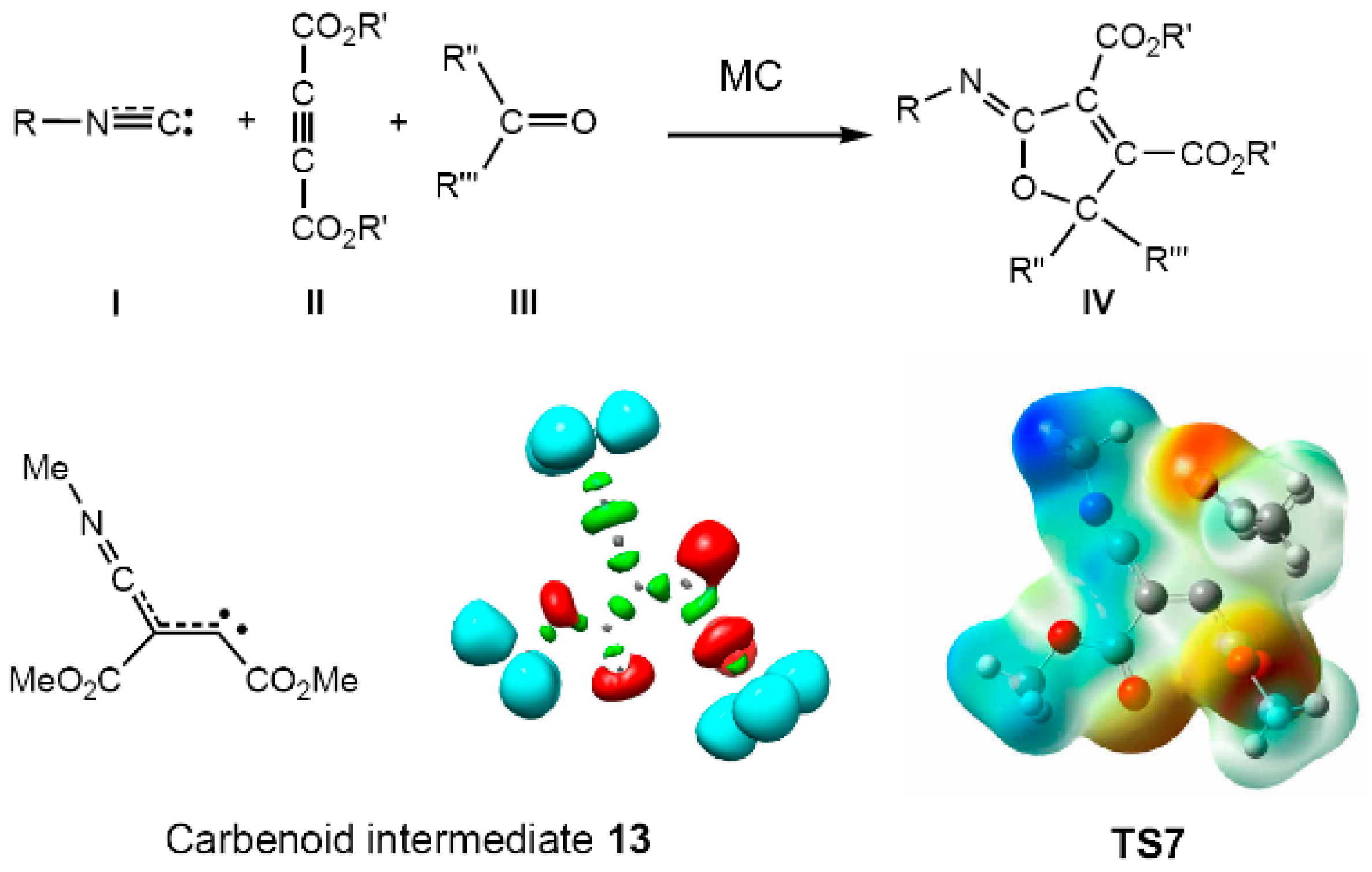
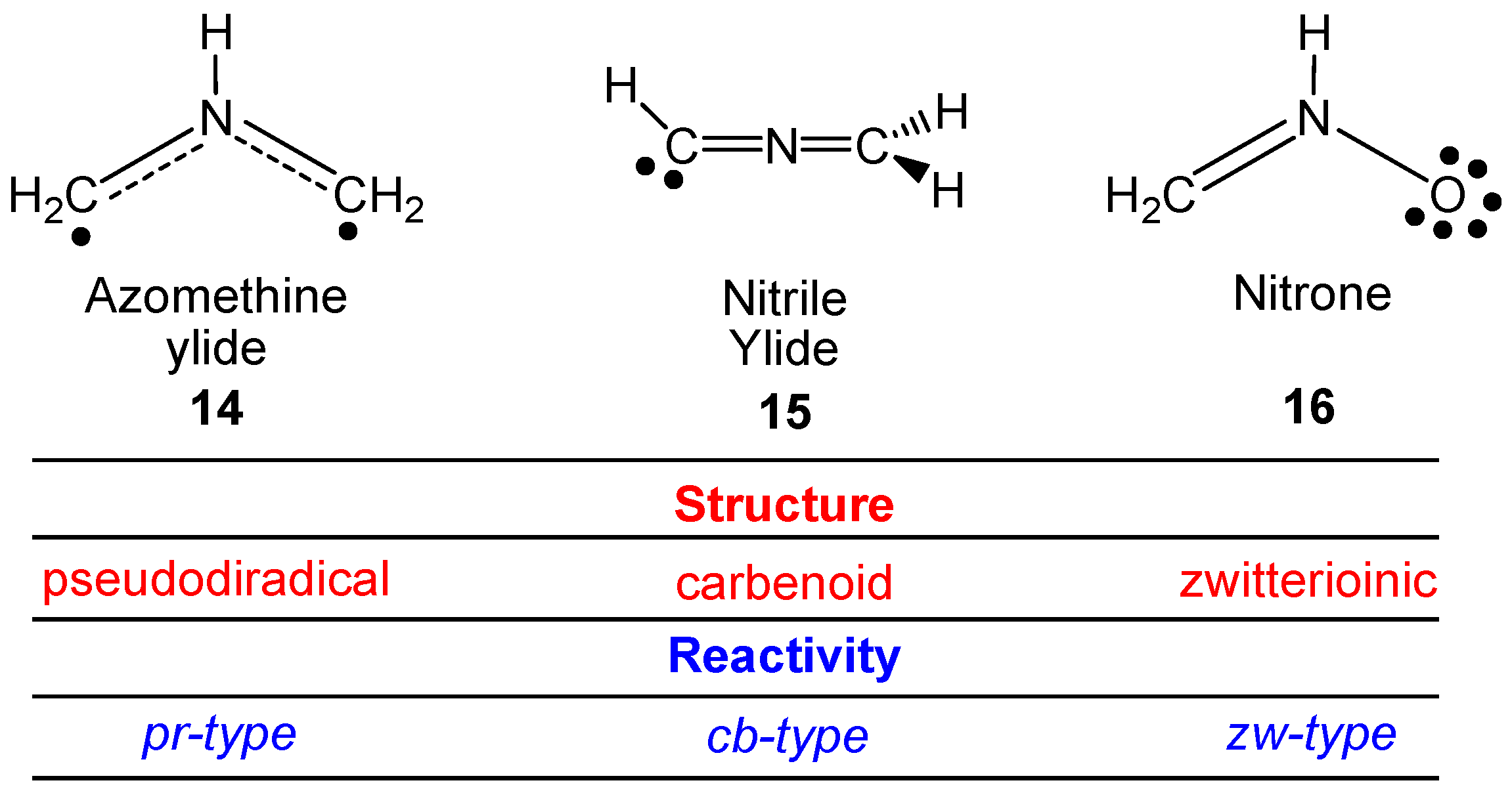
| Method | ΔEact | ΔEreac | d(C–C) |
|---|---|---|---|
| Experimental | 27.5 | −38.4 | |
| HF/6-31G(d) | 47.4 | −36.0 | 2.201 |
| MP2/6-31G(d) | 20.0 | −45.9 | 2.286 |
| B3LYP/6-31G(d) | 24.8 | −32.9 | 2.273 |
| MPWB1K/6-31G(d) | 22.1 | −57.7 | 2.252 |
| M06-2X/6-31G(d) | 19.4 | −43.5 | 2.269 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Domingo, L.R. Molecular Electron Density Theory: A Modern View of Reactivity in Organic Chemistry. Molecules 2016, 21, 1319. https://doi.org/10.3390/molecules21101319
Domingo LR. Molecular Electron Density Theory: A Modern View of Reactivity in Organic Chemistry. Molecules. 2016; 21(10):1319. https://doi.org/10.3390/molecules21101319
Chicago/Turabian StyleDomingo, Luis R. 2016. "Molecular Electron Density Theory: A Modern View of Reactivity in Organic Chemistry" Molecules 21, no. 10: 1319. https://doi.org/10.3390/molecules21101319
APA StyleDomingo, L. R. (2016). Molecular Electron Density Theory: A Modern View of Reactivity in Organic Chemistry. Molecules, 21(10), 1319. https://doi.org/10.3390/molecules21101319







