Modeling the Photocatalytic Mineralization in Water of Commercial Formulation of Estrogens 17-β Estradiol (E2) and Nomegestrol Acetate in Contraceptive Pills in a Solar Powered Compound Parabolic Collector
Abstract
:1. Introduction
2. Results and Discussion
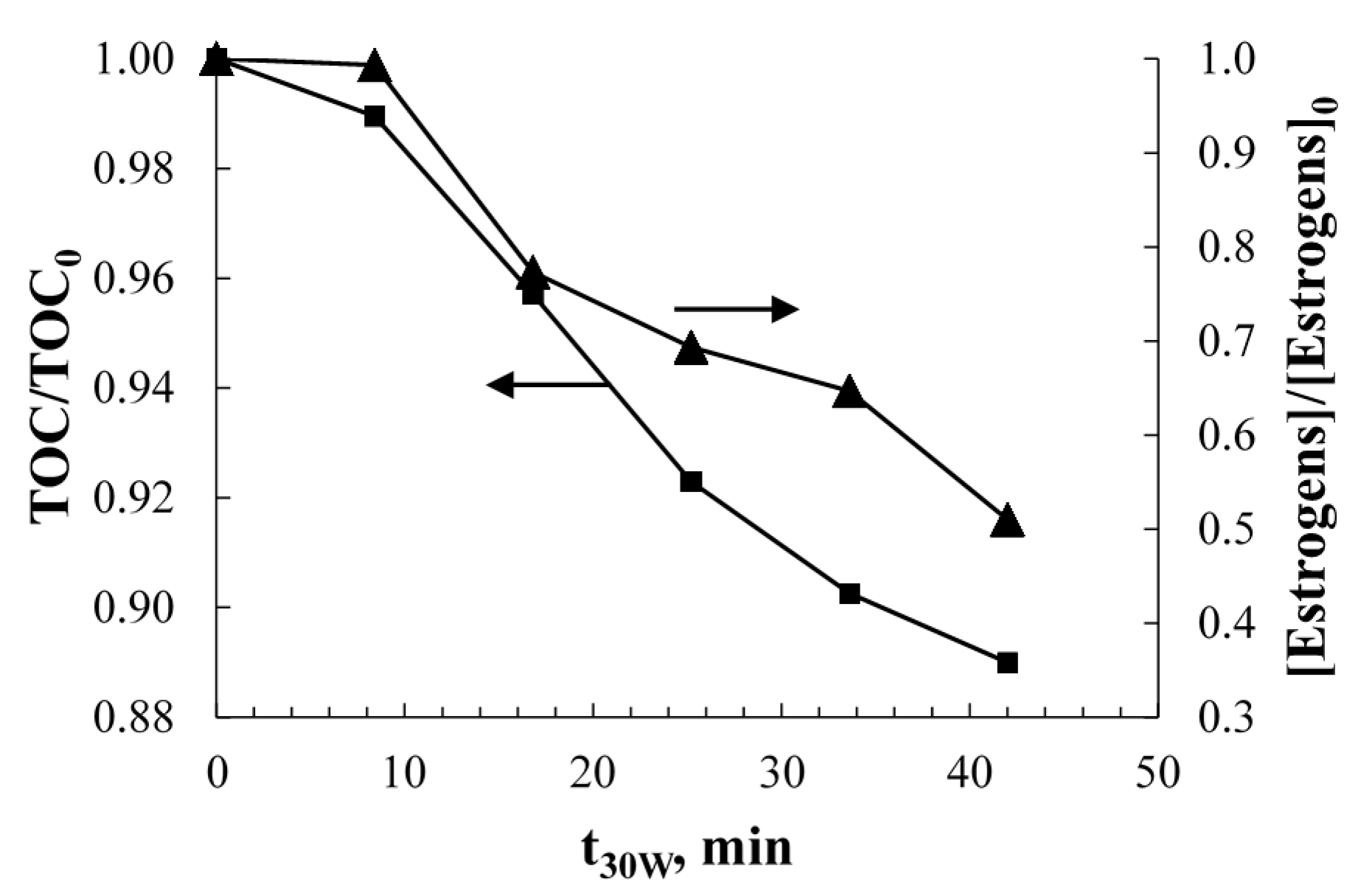
2.1. Solar Photolysis
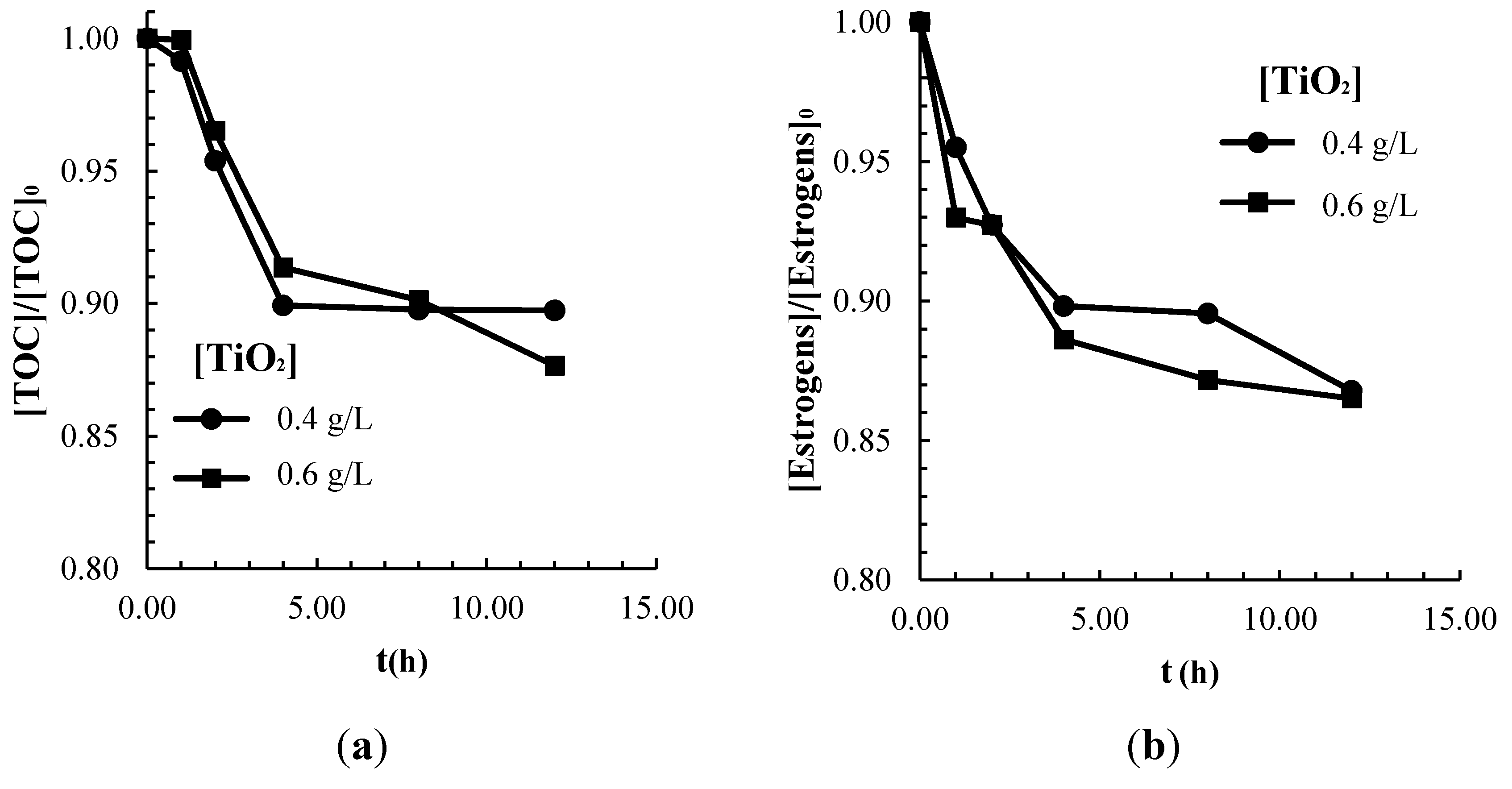
2.2. Adsorption of Contaminants on the TiO2 Catalyst Surface
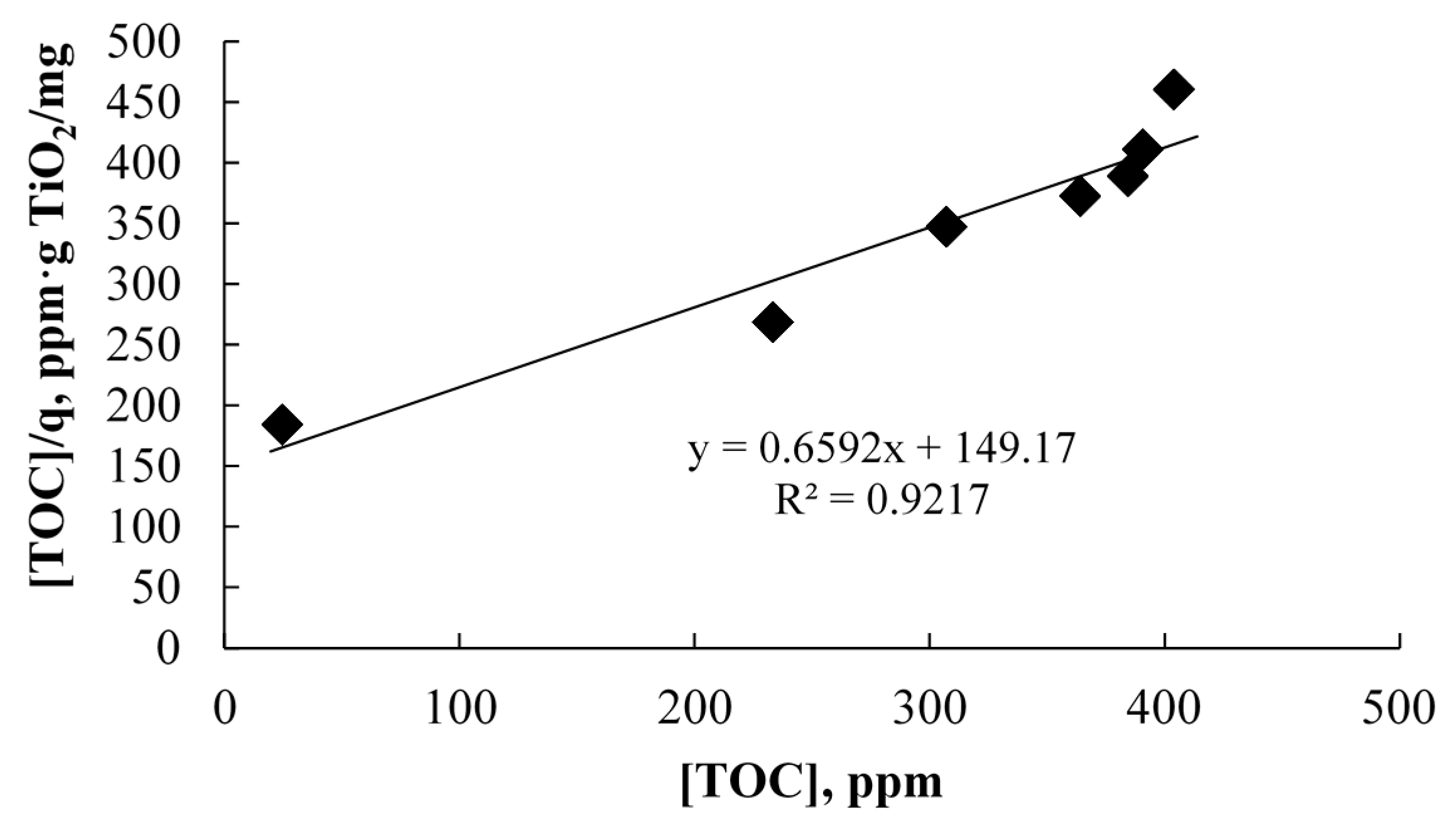
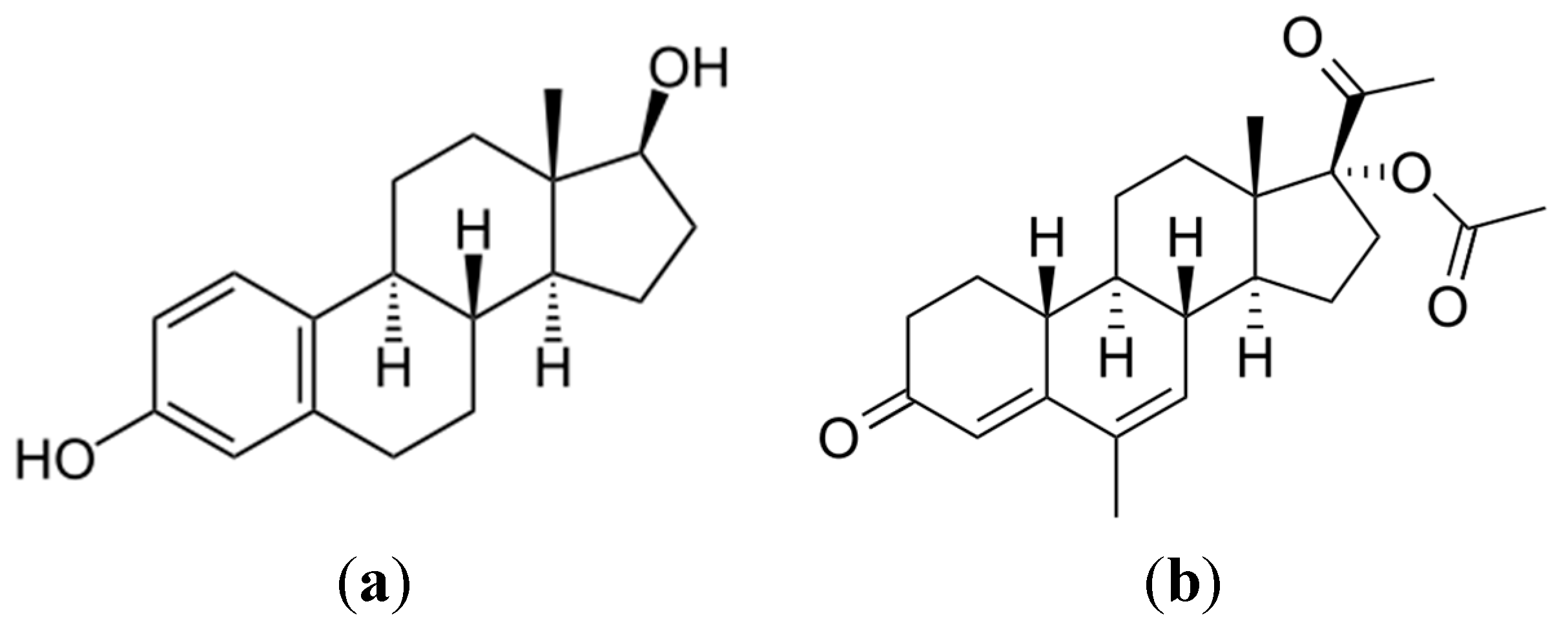
2.2.1. Photocatalytic Oxidation of a Commercial Formulation of Estrogens
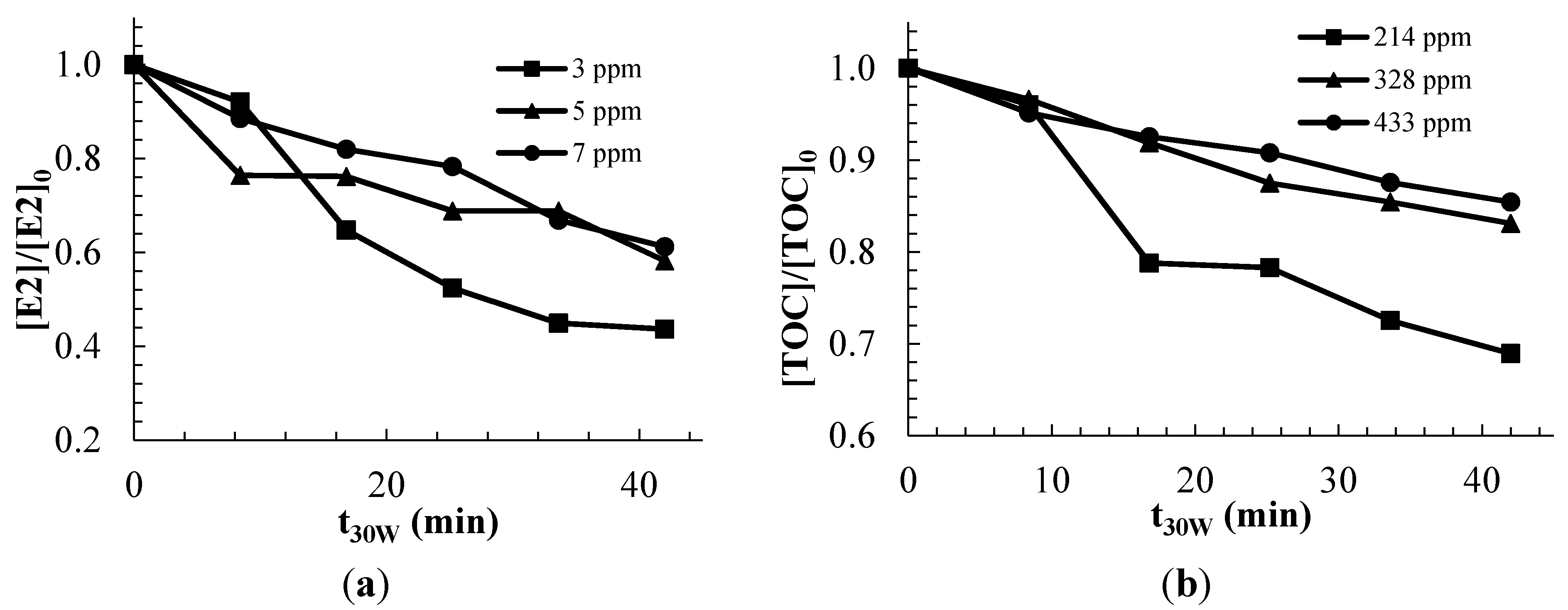
2.2.2. Modeling and Experimental Validation of the Solar Photocatalytic Degradation of Contraceptive Pills Formulations
- (1)
- Reactor mass balance (expressed as differential equation in polar coordinates):
- (2)
- Contaminant rate law:
- (3)
- Mass balance in the batch recirculation system:
- (4)
- Hydrodynamic model for turbulent flow in the CPC, which was operated in the turbulent flow regime:
- (5)
- Optical properties of the catalyst and SFM parameters:
- (6)
- The local volumetric rate of photon absorption (LVRPA) calculated from the SFM:
| Parameter | Value |
|---|---|
| Absorption coefficient (κ) | 174.7 m2/kg |
| Extinction coefficient (β) | 1470.5 m2/kg |
| Scattering coefficient (σ) | 1295.8 m2/kg |
| Forward scattering probability (pf) | 0.110 |
| Backward scattering probability (pb) | 0.710 |
| Side scattering probability (ps) | 0.045 |
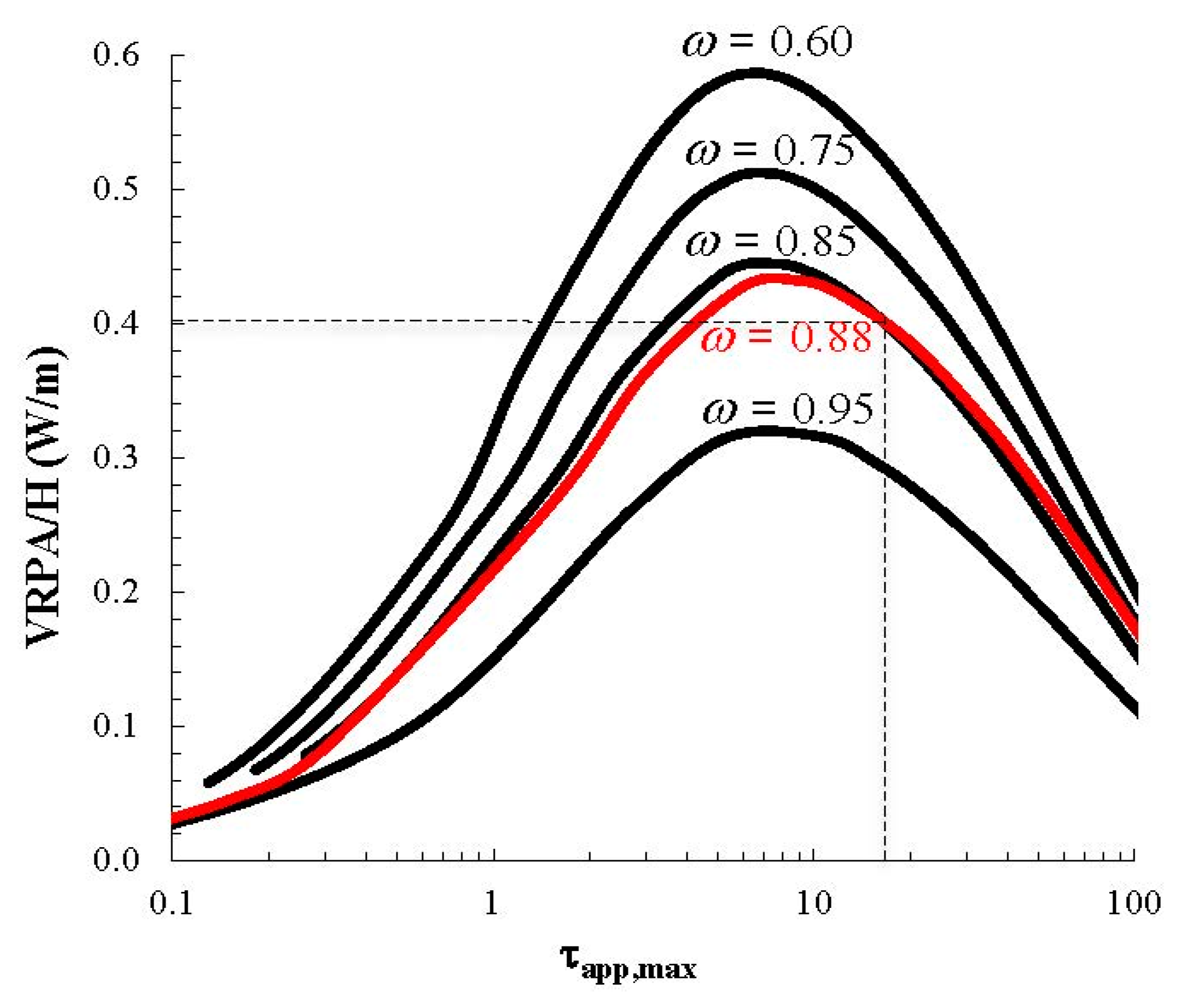
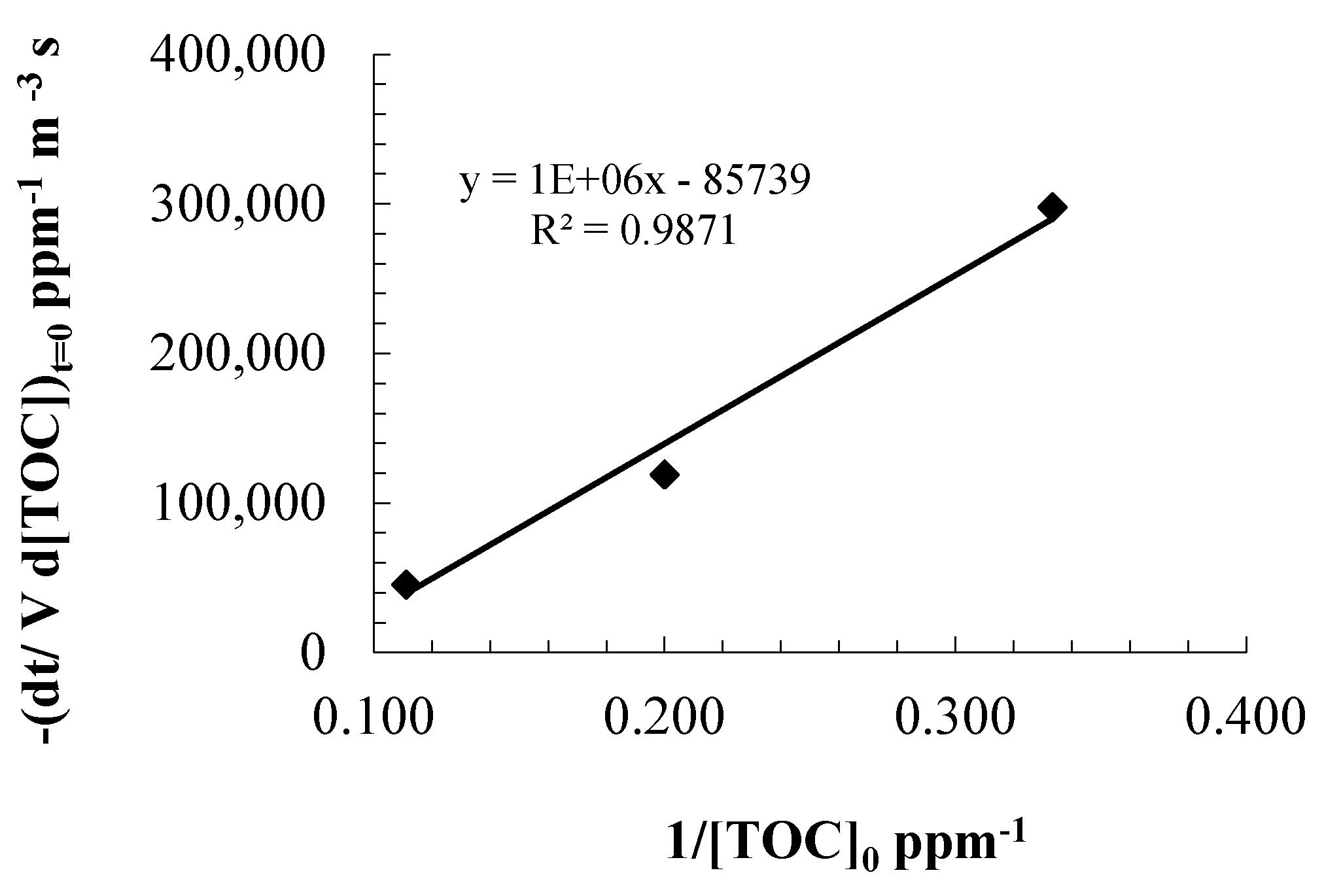
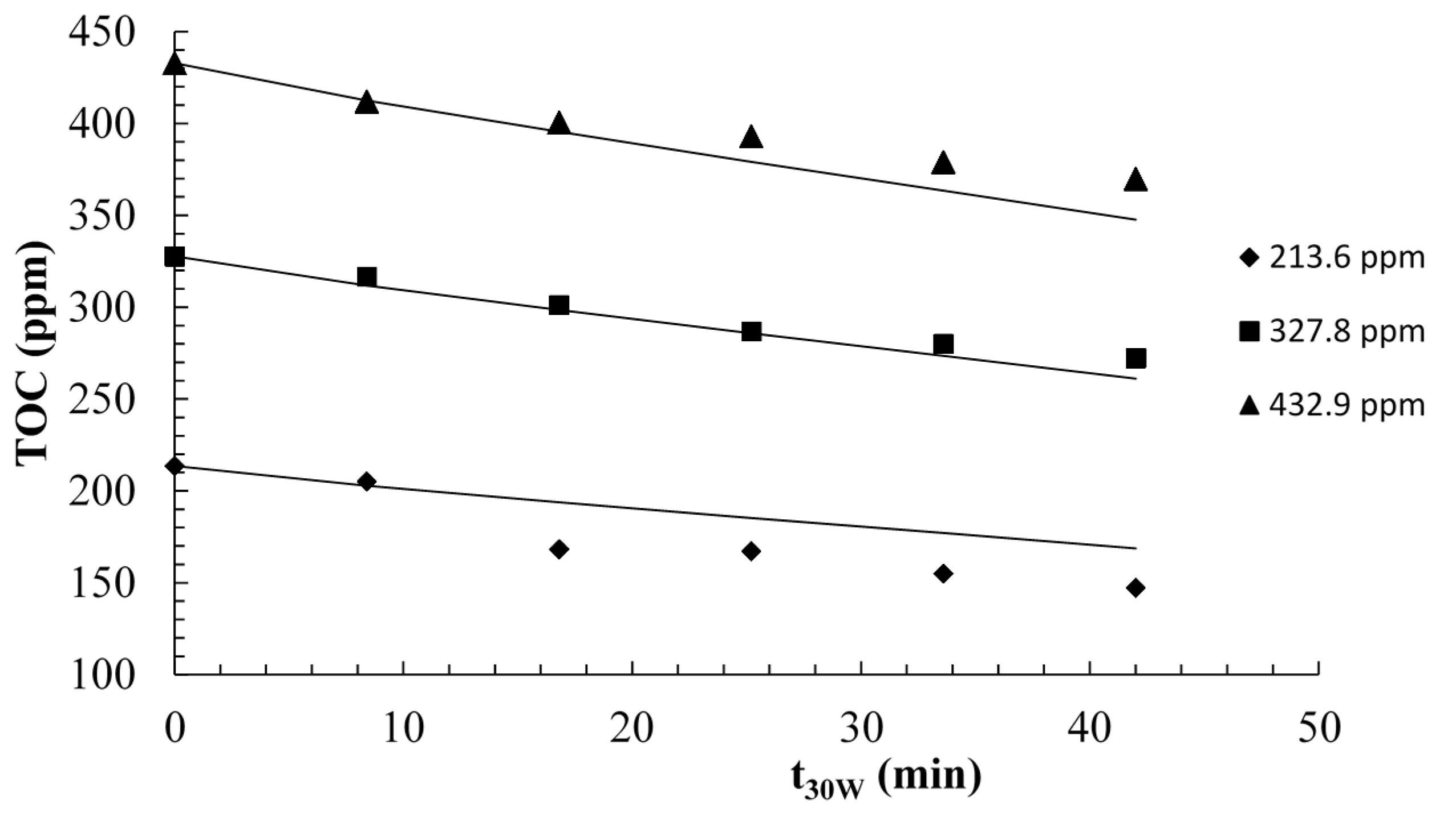
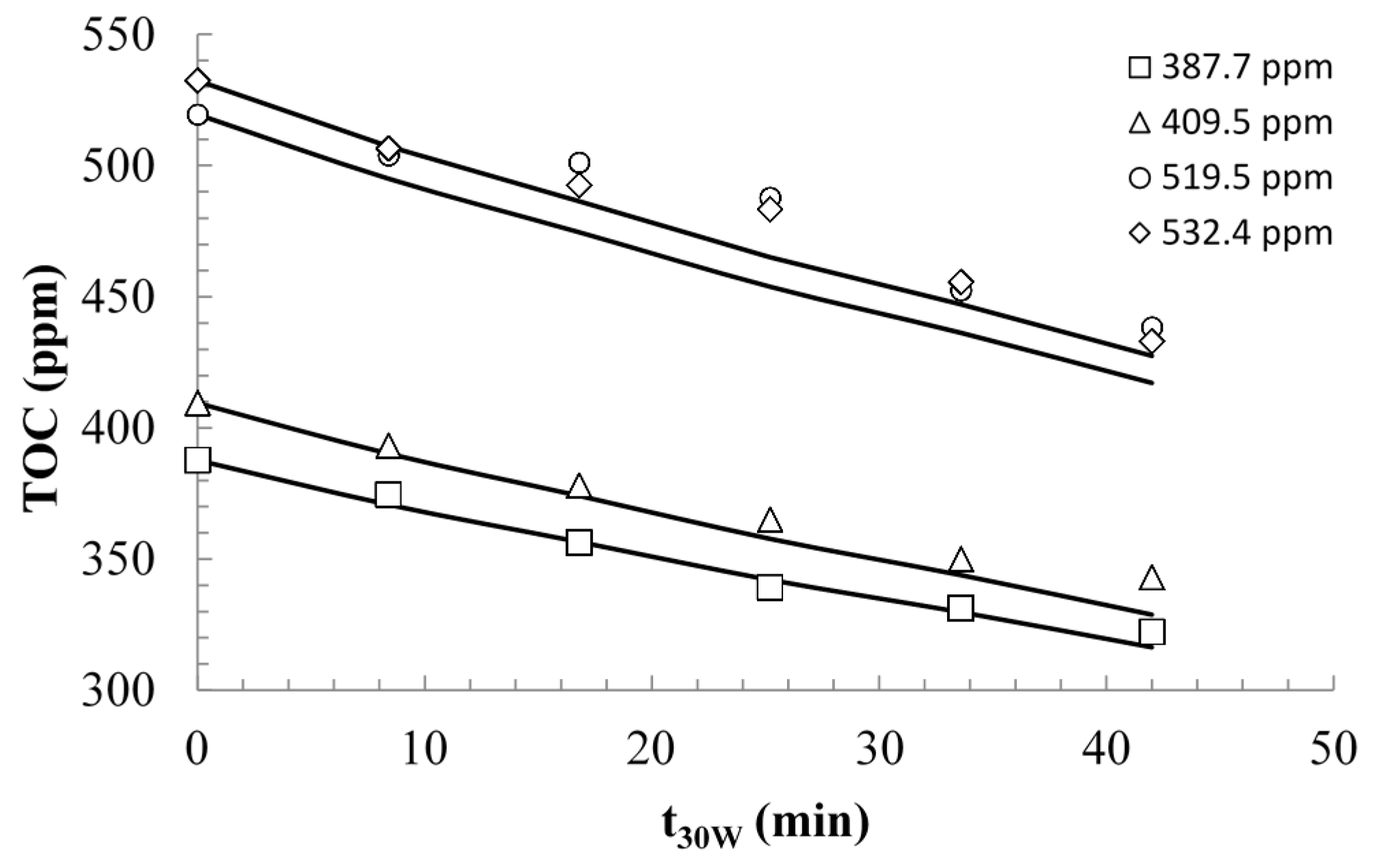
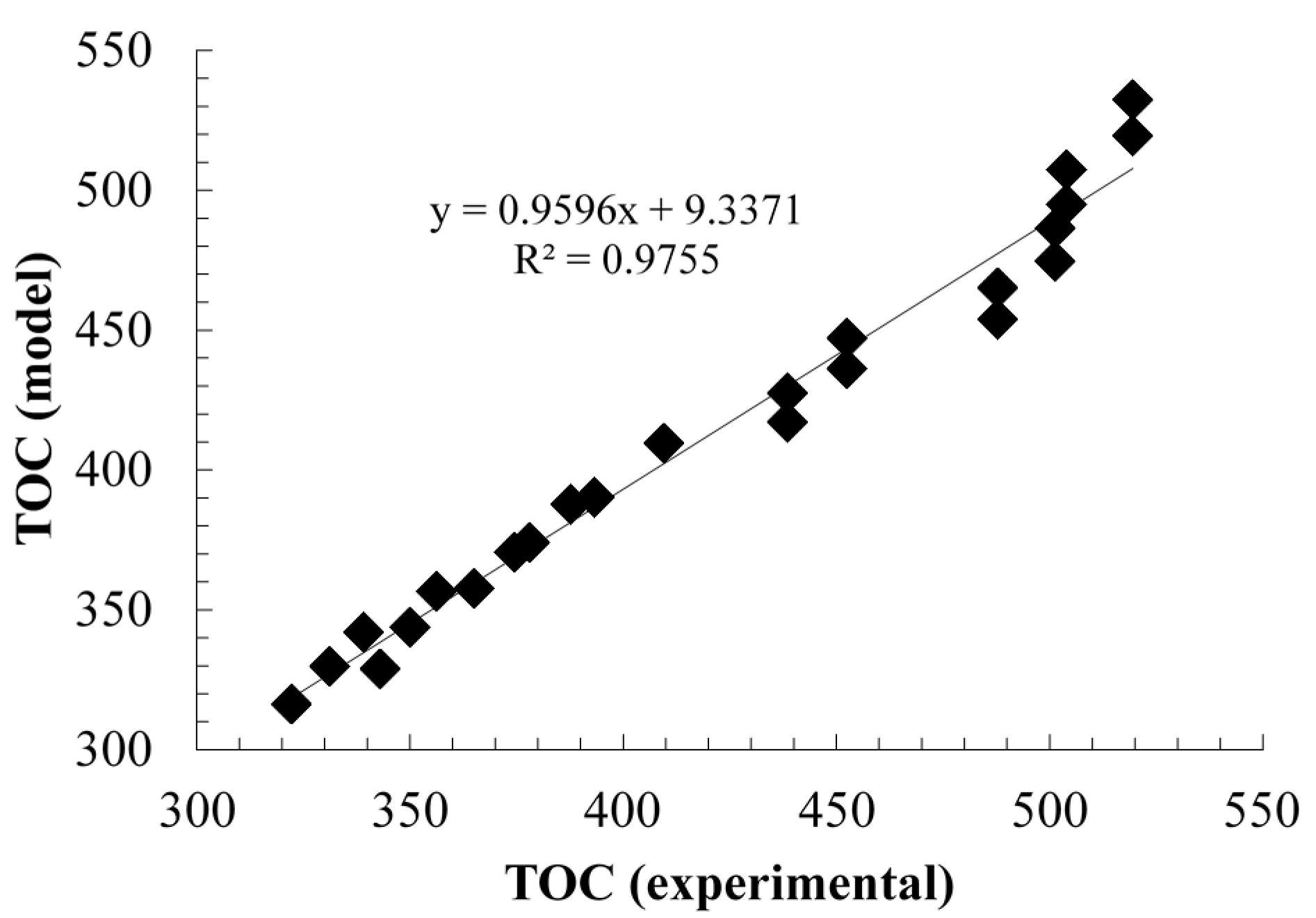
3. Experimental Section
3.1. Materials and Methods
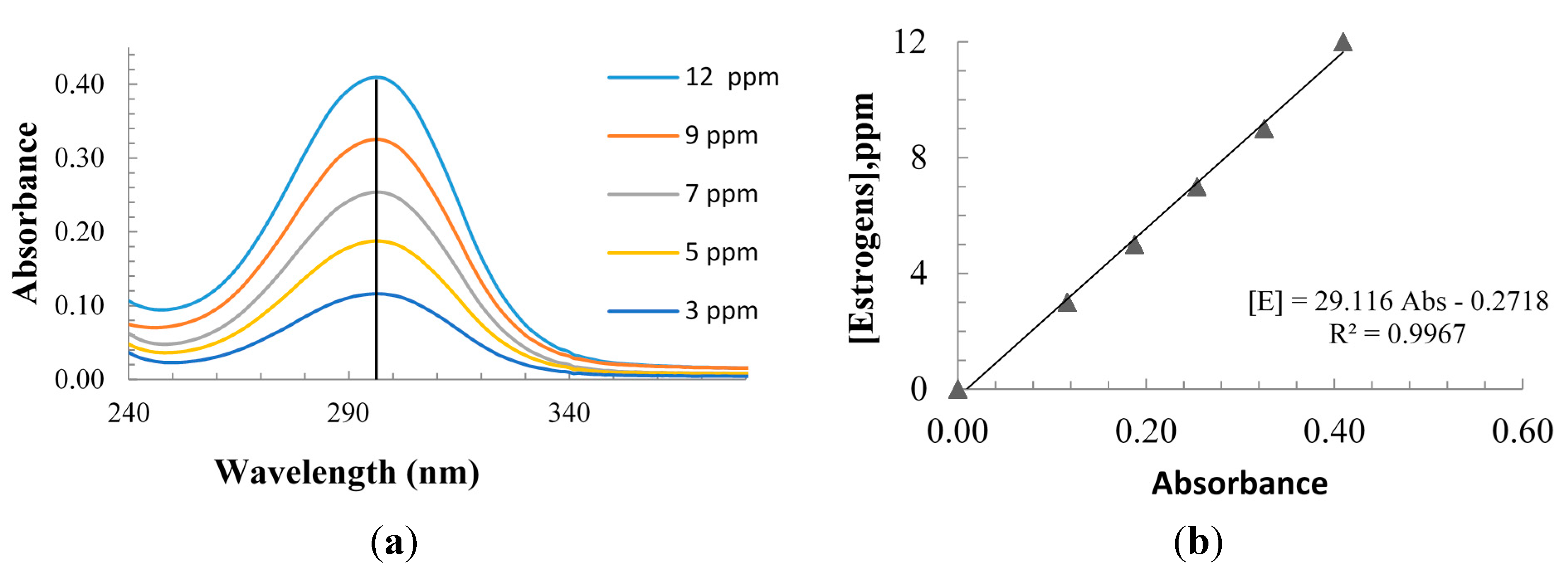
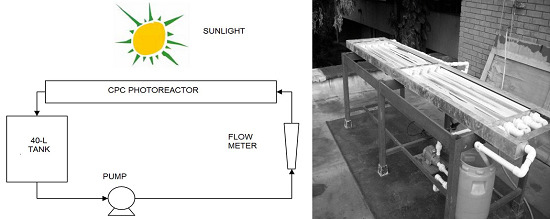
3.2. Photocatalytic Reactor
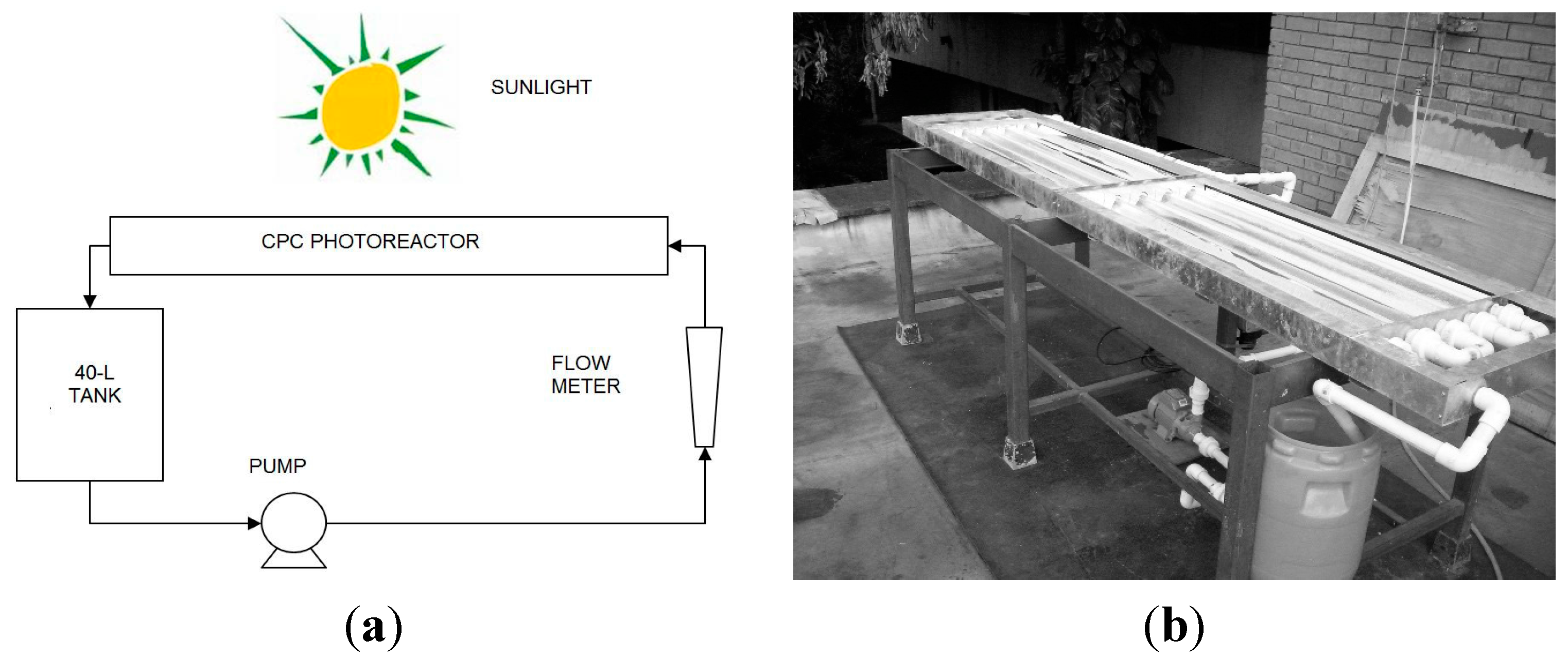
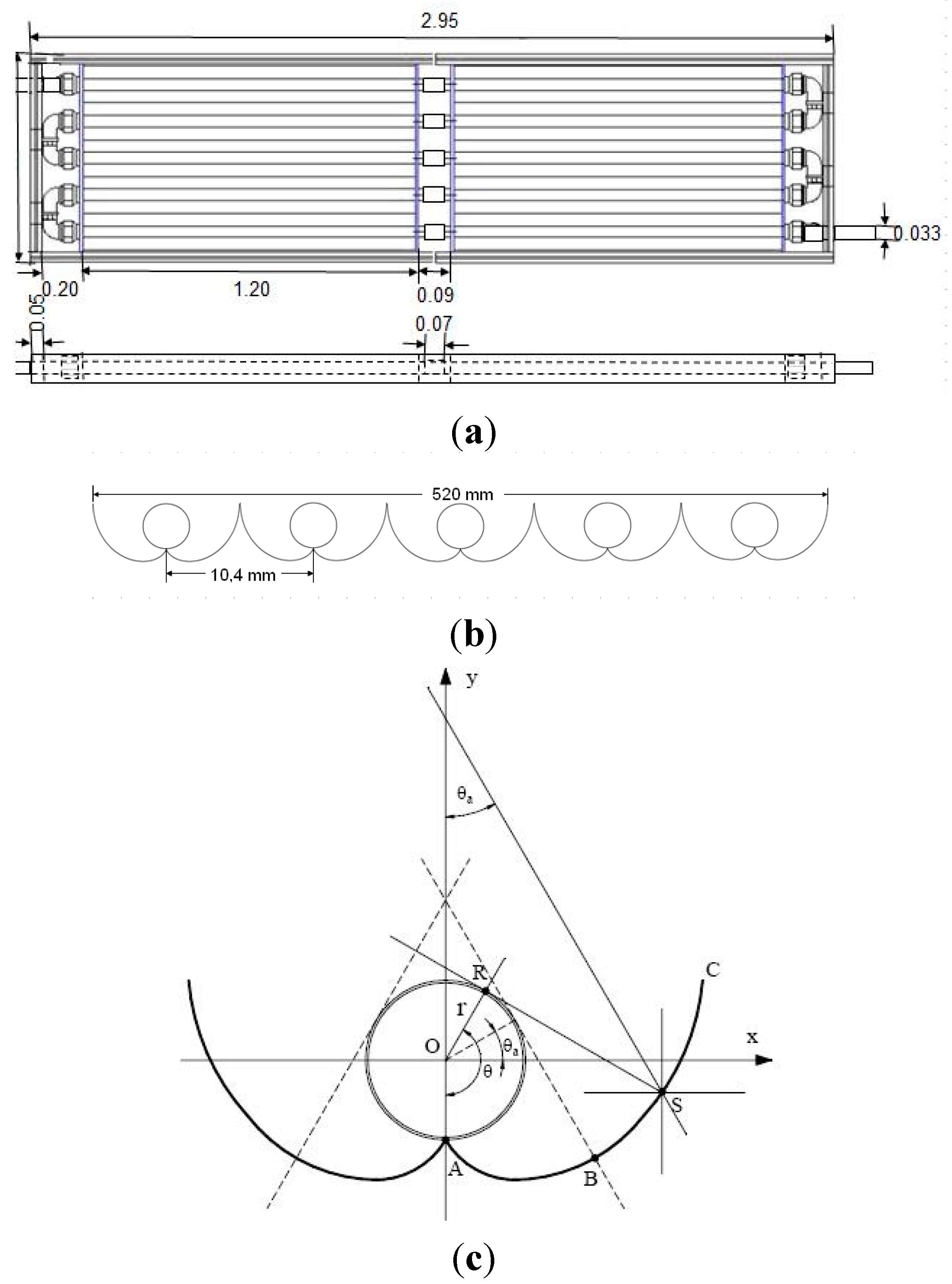
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| a | SFM parameter, dimensionless |
| b | SFM parameter, dimensionless |
| f | friction factor, dimensionless |
| I | UV radiation intensity, W·m−2 |
| kT | kinetic constant, mol·L−1·s−1·W−0.5·m1.5 |
| Kads | adsorption equilibrium constant, L·mol−1 |
| KR | reaction binding constant, L·mol−1 |
| L | reactor length, m |
| LVRPA | local volumetric rate of photon absorption, W·m−3 |
| m | reaction order respect to the LVRPA, dimensionless |
| n | parameter of velocity profile for turbulent regime, dimensionless |
| npass | number of pass of the fluid through the reactor space, dimensionless |
| pb | probability of backward scattering, dimensionless |
| pf | probability of forward scattering, dimensionless |
| ps | probability of side scattering, dimensionless |
| Q | flow rate, m3·s−1 |
| r | radial coordinate, m |
| rp | auxiliary coordinate in the photon flux direction, m |
| R | reactor radius, m |
| t | time, s |
| t30W | standardized 30 W time, s |
| TOC | TOC concentration, mol·L−1 |
| v | fluid velocity, m·s−1 |
| V | volume, m3 |
| VRPA | overall volumetric rate of photon absorption, W·m−3 |
| Greek Letters | |
| δ | reactor thickness, m |
| γ | SFM parameter, dimensionless |
| κ | specific mass absorption coefficient, m2·kg−1 |
| λ | radiation wavelength, nm |
| θ | polar coordinate, radians |
| σ | specific mass scattering coefficient, m2·kg−1 |
| τ | optical thickness, dimensionless |
| ϖ | declination angle, radians |
| ω | scattering albedo, dimensionless |
| Subscripts | |
| app | apparent |
| average | average |
| corr | corrected |
| max | maximum |
| min | minimum |
| r | radial coordinate |
| R | reactor |
| total | total radiation |
| T | total |
| z | axial coordinate |
| 0 | relative to incident radiation, or initial condition |
| λ | radiation wavelength |
| θ | angular coordinate |
| ωcorr | corrected albedo |
| Superscripts | |
| in | reactor inlet |
| out | reactor outlet |
References
- Thomaidi, V.S.; Stasinakis, A.S.; Borova, V.L.; Thomaidis, N.S. Is there a risk for the aquatic environment due to the existence of emerging organic contaminants in treated domestic wastewater? Greece as a case-study. J. Hazard. Mater. 2015, 283, 740–747. [Google Scholar] [CrossRef] [PubMed]
- Ramirez, A.J.; Brain, R.A.; Usenko, M.A.; Mottaleb, M.A.; O’Donnell, J.G.; Stahl, L.L.; Wathen, J.B.; Snyder, B.D.; Pitt, J.L.; Perez-Hurtado, P.; et al. Occurrence of pharmaceuticals and personal care products in fish: Results of a national pilot study in the United States. Environ. Toxicol. Chem. 2009, 28, 2587–2597. [Google Scholar] [CrossRef] [PubMed]
- Loos, R.; Gawlik, B.M.; Locoro, G.; Rimaviciute, E.; Contini, S.; Bidoglio, G. EU-wide survey of polar organic persistent pollutants in European river waters. Environ. Pollut. 2009, 157, 561–568. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Fu, J.; Peng, H.; Hou, L.; Liu, M.; Zhou, J.L. Occurrence and phase distribution of selected pharmaceuticals in the Yangtze Estuary and its coastal zone. J. Hazard. Mater. 2011, 190, 588–596. [Google Scholar] [CrossRef] [PubMed]
- Lindberg, R.H.; Östman, M.; Olofsson, U.; Grabic, R.; Fick, J. Occurrence and behaviour of 105 active pharmaceutical ingredients in sewage waters of a municipal sewer collection system. Water Res. 2014, 58, 221–229. [Google Scholar] [CrossRef] [PubMed]
- Bu, Q.; Wang, B.; Huang, J.; Deng, S.; Yu, G. Pharmaceuticals and personal care products in the aquatic environment in China: A review. J. Hazard. Mater. 2013, 262, 189–211. [Google Scholar] [CrossRef]
- Liu, Z.H.; Ogejo, J.A.; Pruden, A.; Knowlton, K.F. Occurrence, fate and removal of synthetic oral contraceptives (SOCs) in the natural environment: A review. Sci. Total. Environ. 2011, 409, 5149–5161. [Google Scholar] [CrossRef]
- Landrigan, P.; Garg, A.; Droller, D.B.J. Assessing the effects of endocrine disruptors in the National Children’s Study. Environ. Health Perspect. 2003, 111, 1678–1682. [Google Scholar] [CrossRef] [PubMed]
- Colborn, T.; Vom Saal, F.S.; Soto, A.M. Developmental effects of endocrine-disrupting chemicals in wildlife and humans. Environ. Health Perspect. 1993, 101, 378–384. [Google Scholar] [CrossRef] [PubMed]
- Corcoran, J.; Winter, M.J.; Tyler, C.R. Pharmaceuticals in the aquatic environment: A critical review of the evidence for health effects in fish. Environ. Health Perspect. 2010, 40, 287–304. [Google Scholar] [CrossRef] [PubMed]
- Kidd, K.A.; Blanchfield, P.J.; Mills, K.H.; Palace, V.P.; Evans, R.E.; Lazorchak, J.M.; Flick, R.W. Collapse of a fish population after exposure to a synthetic estrogen. PNAS 2007, 104, 8897–8901. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.P.H.; Plosker, G.L. Nomegestrol acetate/estradiol: In oral contraception. Drugs 2012, 72, 1917–1928. [Google Scholar] [CrossRef] [PubMed]
- Fernández, M.; Fernández, M.; Laca, A.; Laca, A.; Díaz, M. Seasonal occurrence and removal of pharmaceutical products in municipal wastewaters. J. Environ. Chem. Eng. 2014, 2, 495–502. [Google Scholar] [CrossRef]
- Collado, N.; Rodriguez-Mozaz, S.; Gros, M.; Rubirola, A.; Barceló, D.; Comas, J.; Rodriguez-Roda, I.; Buttiglieri, G. Pharmaceuticals occurrence in a WWTP with significant industrial contribution and its input into the river system. Environ. Pollut. 2014, 185, 202–212. [Google Scholar] [CrossRef] [PubMed]
- Prieto-Rodriguez, L.; Miralles-Cuevas, S.; Oller, I.; Agüera, A.; Puma, G.L.; Malato, S. Treatment of emerging contaminants in wastewater treatment plants (WWTP) effluents by solar photocatalysis using low TiO2 concentrations. J. Hazard. Mater. 2012, 211–212, 131–137. [Google Scholar] [CrossRef] [PubMed]
- Kanakaraju, D.; Glass, B.D.; Oelgemöller, M. Titanium dioxide photocatalysis for pharmaceutical wastewater treatment. Environ. Chem. Lett. 2014, 12, 27–47. [Google Scholar] [CrossRef]
- Choi, J.; Lee, H.; Choi, Y.; Kim, S.; Lee, S.; Lee, S.; Choi, W.; Lee, J. Heterogeneous photocatalytic treatment of pharmaceutical micropollutants: Effects of wastewater effluent matrix and catalyst modifications. Appl. Catal. B Environ. 2014, 147, 8–16. [Google Scholar] [CrossRef]
- Yang, H.; An, T.; Li, G.; Song, W.; Cooper, W.J.; Luo, H.; Guo, X. Photocatalytic degradation kinetics and mechanism of environmental pharmaceuticals in aqueous suspension of TiO2: A case of β-blockers. J. Hazard. Mater. 2010, 179, 834–839. [Google Scholar] [CrossRef]
- Mboula, V.M.; Héquet, V.; Andrès, Y.; Gru, Y.; Colin, R.; Doña-Rodríguez, J.M.; Silva, A.M.T.; Pastrana-Martínez, L.M.; Leleu, M.; Tindall, A.J.; et al. Photocatalytic degradation of estradiol under simulated solar light and assessment of estrogenic activity. J. Hazard. Mater. 2010, 179, 834–839. [Google Scholar] [CrossRef]
- Koutantou, V.; Kostadima, M.; Chatzisymeon, E.; Frontistis, Z.; Binas, V.; Venieri, D.; Mantzavinos, D. Solar photocatalytic decomposition of estrogens over immobilized zinc oxide. Catal. Today 2013, 209, 66–73. [Google Scholar] [CrossRef]
- Frontistis, Z.; Fatta-Kassinos, D.; Mantzavinos, D.; Xekoukoulotakis, N.P. Photocatalytic degradation of 17α-ethynylestradiol in environmental samples by ZnO under simulated solar radiation. J. Chem. Technol. Biotechnol. 2012, 87, 1051–1058. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Y.; Su, Y.; Mao, K.; Wang, Q. Effect of water composition on TiO2 photocatalytic removal of endocrine disrupting compounds (EDCs) and estrogenic activity from secondary effluent. J. Hazard. Mater. 2012, 215–216, 252–258. [Google Scholar] [CrossRef] [PubMed]
- Li Puma, G.; Puddu, V.; Tsang, H.K.; Gora, A.; Toepfer, B. Photocatalytic oxidation of multicomponent mixtures of estrogens (estrone (E1), 17β-estradiol (E2), 17α-ethynylestradiol (EE2) and estriol (E3)) under UVA and UVC radiation: Photon absorption, quantum yields and rate constants independent of photon absorption. Appl. Catal. B Environ. 2010, 99, 388–397. [Google Scholar]
- Benotti, M.J.; Stanford, B.D.; Wert, E.C.; Snyder, S.A. Evaluation of a photocatalytic reactor membrane pilot system for the removal of pharmaceuticals and endocrine disrupting compounds from water. Water Res. 2009, 43, 1513–1522. [Google Scholar] [CrossRef]
- Li Puma, G.; Brucato, A. Dimensionless analysis of slurry photocatalytic reactors using two-flux and six-flux radiation absorption-scattering models. Catal. Today 2007, 122, 78–90. [Google Scholar] [CrossRef]
- Brucato, A.; Cassano, A.E.; Grisafi, F.; Montante, G.; Rizzuti, L.; Vella, G. Estimating radiant fields in flat heterogeneous photoreactors by the six-flux model. AICHE J. 2006, 52, 3882–3890. [Google Scholar] [CrossRef]
- Li Puma, G.; Gora, A.; Toepfer, B. Photocatalytic oxidation of multicomponent solutions of herbicides: Reaction kinetics analysis with explicit photon absorption effects. Appl. Catal. B Environ. 2006, 68, 171–180. [Google Scholar]
- Chowdhury, R.R.; Charpentier, P.A.; Ray, M.B. Photodegradation of 17β-estradiol in aquatic solution under solar irradiation: Kinetics and influencing water parameters. J. Photochem. Photobiol. A 2011, 219, 67–75. [Google Scholar] [CrossRef]
- Leech, D.M.; Snyder, M.T.; Wetzel, R.G. Natural organic matter and sunlight accelerate the degradation of 17β-estradiol in water. Sci. Total Environ. 2009, 407, 2087–2092. [Google Scholar] [CrossRef] [PubMed]
- Dillert, R.; Cassano, A.; Goslich, R.; Bahnemann, D. Large scale studies in solar catalytic wastewater treatment. Catal. Today 1999, 54, 267–282. [Google Scholar] [CrossRef]
- Alfano, O.M.; Bahnemann, D.; Cassano, A.E.; Dillert, R.; Goslich, R. Photocatalysis in water environments using artificial and solar light. Catal. Today 2000, 58, 199–230. [Google Scholar] [CrossRef]
- Konstantinou, K.; Albanis, T. Degradation pathways and intermediates of photocatalytic transformation of major pesticide groups in aqeous TiO2 suspensions using artificial and solar light: A review. Appl. Catal. B Environ. 2003, 42, 319–335. [Google Scholar] [CrossRef]
- Méndez-Arriaga, F.; Maldonado, M.; Giménez, J.; Esplugas, S.; Malato, S. Abatement of ibuprofen by solar photocatalysis process: Enhancement and scale up. Catal. Today 2009, 144, 112–116. [Google Scholar] [CrossRef]
- Minero, C.; Pelizzetti, E.; Malato, S.; Blanco, J. Large solar plant photocatalytic water decontamination: Effect of operational parameters. Sol. Energy 1996, 56, 421–428. [Google Scholar] [CrossRef]
- Ohko, Y.; Iuchi, K.I.; Niwa, C.; Tatsuma, T.; Nakashima, T.; Iguchi, T.; Kubota, Y.; Fujishima, A. 17β-estradiol degradation by TiO2 photocatalysis as a means of reducing estrogenic activity. Environ. Sci. Technol. 2002, 36, 4175–4181. [Google Scholar] [CrossRef]
- Colina-Márquez, J.; Machuca-Martínez, F.; Li Puma, G. Photocatalytic mineralization of commercial herbicides in a pilot-scale solar CPC reactor: Photoreactor modeling and reaction kinetics constants independent of radiation field. Environ. Sci. Technol. 2009, 43, 8953–8960. [Google Scholar] [CrossRef] [PubMed]
- Colina-Márquez, J.; Machuca, F.; Li Puma, G. Radiation Absorption and Optimization of Solar Photocatalytic Reactors for Environmental Applications. Environ. Sci. Technol. 2010, 44, 5112–5120. [Google Scholar] [CrossRef] [PubMed]
- Turchi, C.S.; Ollis, D.F. Photocatalytic degradation of organic water contaminants: Mechanisms involving hydroxyl radical attack. J. Catal. 1990, 122, 178–192. [Google Scholar]
- Valente, J.P.S.; Padilha, P.M.; Florentino, A.O. Studies on the adsorption and kinetics of photodegradation of a model compound for heterogeneous photocatalysis onto TiO2. Chemosphere 2006, 64, 1128–1133. [Google Scholar]
- Sample Availability: Samples of the compounds are not available from the authors.
© 2015 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colina-Márquez, J.; Machuca-Martínez, F.; Li Puma, G. Modeling the Photocatalytic Mineralization in Water of Commercial Formulation of Estrogens 17-β Estradiol (E2) and Nomegestrol Acetate in Contraceptive Pills in a Solar Powered Compound Parabolic Collector. Molecules 2015, 20, 13354-13373. https://doi.org/10.3390/molecules200713354
Colina-Márquez J, Machuca-Martínez F, Li Puma G. Modeling the Photocatalytic Mineralization in Water of Commercial Formulation of Estrogens 17-β Estradiol (E2) and Nomegestrol Acetate in Contraceptive Pills in a Solar Powered Compound Parabolic Collector. Molecules. 2015; 20(7):13354-13373. https://doi.org/10.3390/molecules200713354
Chicago/Turabian StyleColina-Márquez, José, Fiderman Machuca-Martínez, and Gianluca Li Puma. 2015. "Modeling the Photocatalytic Mineralization in Water of Commercial Formulation of Estrogens 17-β Estradiol (E2) and Nomegestrol Acetate in Contraceptive Pills in a Solar Powered Compound Parabolic Collector" Molecules 20, no. 7: 13354-13373. https://doi.org/10.3390/molecules200713354
APA StyleColina-Márquez, J., Machuca-Martínez, F., & Li Puma, G. (2015). Modeling the Photocatalytic Mineralization in Water of Commercial Formulation of Estrogens 17-β Estradiol (E2) and Nomegestrol Acetate in Contraceptive Pills in a Solar Powered Compound Parabolic Collector. Molecules, 20(7), 13354-13373. https://doi.org/10.3390/molecules200713354