Determination of Solubility Parameters of Ibuprofen and Ibuprofen Lysinate
Abstract
:1. Introduction
1.1. Calculation Methods
1.2. Experimental Approach
1.2.1. Extended Hansen’s Approach (EHA)
1.2.2. Inverse Gas Chromatography (IGC)
2. Results
2.1. Calculation Methods
2.1.1. Ibuprofen
| Method | ||||||
|---|---|---|---|---|---|---|
| Hansen and Beerbower | Fedors | Hoftyzer and Van Krevelen | Hoy | Stefanis and Panayiotou | Just and Breitkreutz | Median δt (MPa0.5) |
| δt = 19.89 | δt = 20.91 | δt = 19.36 | δt = 19.71 | δt = 19.7 | δt = 19.20 | δt = 19.71 |
| δd = 17.85 | δd = 17.56 | δd = 16.59 | ||||
| δp = 2.22 | δp = 3.22 | δp = 4.27 | ||||
| δh = 7.15 | δh = 8.31 | δh = 8.67 | ||||
2.1.2. Polymers and Excipients
| Excipient | Method | ||||||
|---|---|---|---|---|---|---|---|
| Hansen and Beerbower | Fedors | Hoftyzer and Van Krevelen | Hoy | Stefanis and Panayiotou | Just and Breitkreutz | Median δt (MPa0.5) | |
| Copovidone | δt = 19.01 | δt = 22.89 | δt = 24.37 | δt = 20.25 | δt = 22.39 | δt = 21.24 | δt = 21.82 |
| δd = 19.23 | δd = 18.18 | δd = 15.45 | |||||
| δp = 11.15 | δp = 10.15 | δp = 8.61 | |||||
| δh = 9.67 | δh = 7.82 | δh = 11.42 | |||||
| Povidone K30 | δt = 18.96 | δt = 23.75 | δt = 26.28 | δt = 20.05 | δt = 23.60 | δt = 21.75 | δt = 22.68 |
| δd = 20.44 | δd = 19.05 | δd = 16.67 | |||||
| δp = 13.67 | δp = 12.09 | δp = 9.85 | |||||
| δh = 9.28 | δh = 6.86 | δh = 9.9 | |||||
| PEG 6000 | δt = 18.38 | δt = 19.17 | δt = 22.86 | δt = 21.44 | δt = 20.45 | δt = 17.76 | δt = 19.81 |
| δd = 17.78 | δd = 17.33 | δd = 13.6 | |||||
| δp = 11.1 | δp = 7.93 | δp = 11.09 | |||||
| δh = 9.13 | δh = 7.42 | δh = 2.75 | |||||
| Eudragit® E PO | δt = 17.34 | δt = 19.59 | δt = 19.70 | δt = 18.28 | δt = 23.51 | δt = 16.04 | δt = 19.00 |
| δd = 17.35 | δd = 16.90 | δd = 12.19 | |||||
| δp = 3.06 | δp = 15.45 | δp = 1.89 | |||||
| δh = 8.81 | δh = 5.31 | δh = 10.26 | |||||
| Eudragit® S100 | δt = 20.02 | δt = 21.86 | δt = 21.1 | δt = 19.29 | δt = 22.37 | δt = 18.63 | δt = 20.56 |
| δd = 18.01 | δd = 16.31 | δd = 12.18 | |||||
| δp = 3.64 | δp = 12.3 | δp = 4.54 | |||||
| δh = 10.38 | δh = 9.11 | δh = 13.34 | |||||
| Poloxamer 188 | δt = 18.30 | δt = 18.81 | δt = 22.10 | δt = 20.9 | δt = 20.33 | δt = 17.31 | δt = 19.57 |
| δd = 17.49 | δd = 17.30 | δd = 13.66 | |||||
| δp = 10.23 | δp = 7.72 | δp = 10.24 | |||||
| δh = 8.74 | δh = 7.37 | δh = 2.64 | |||||
| Poloxamer 407 | δt = 18.26 | δt = 18.64 | δt = 21.75 | δt = 20.66 | δt = 20.28 | δt = 17.12 | δt = 19.46 |
| δd = 17.36 | δd = 17.29 | δd = 13.68 | |||||
| δp = 9.85 | δp = 7.63 | δp = 9.89 | |||||
| δh = 8.57 | δh = 7.35 | δh = 2.58 | |||||
| Methylcellulose (DS = 1) | δt = 27.05 | δt = 29.78 | δt = 32.29 | δt = 27.23 | δt = 24.82 | δt = 27.45 | δt = 27.34 |
| δd = 20.73 | δd = 18.38 | δd = 17.91 | |||||
| δp = 10.26 | δp = 7.15 | δp = 17.74 | |||||
| δh = 22.54 | δh = 14.82 | δh = 10.66 | |||||
| Ethylcellulose (DS = 3) | δt = 15.86 | δt = 18.79 | δt = 20.18 | δt = 20.1 | δt = 19.58 | δt = 21.42 | δt = 19.84 |
| δd = 17.59 | δd = 17.79 | δd = 16.09 | |||||
| δp = 4.59 | δp = 6.44 | δp = 14.05 | |||||
| δh = 8.77 | δh = 5.05 | δh = 1.61 | |||||
| Xylitol | δt = 36.86 | δt = 40.60 | δt = 41.53 | δt = 36.60 | δt = 30.56 | δt = 31.3 | δt = 36.73 |
| δd = 20.75 | δd = 18.62 | δd = 16.07 | |||||
| δp = 12.68 | δp = 11.87 | δp = 21.15 | |||||
| δh = 33.67 | δh = 21.13 | δh = 16.54 | |||||
| Sucrose | δt = 35.81 | δt = 39.95 | δt = 40.38 | δt = 33.53 | δt = 40.83 | δt = 31.15 | δt = 37.88 |
| δd = 21.76 | δd = 21.35 | δd = 18.55 | |||||
| δp = 9.87 | δp = 18.44 | δp = 19.63 | |||||
| δh = 32.55 | δh = 29.51 | δh = 15.53 | |||||
| Lactose | δt = 34.07 | δt = 38.86 | δt = 40.46 | δt = 31.48 | δt = 37.45 | δt = 38.94 | δt = 38.16 |
| δd = 22.62 | δd = 21.78 | δd = 20.07 | |||||
| δp = 9.63 | δp = 19.71 | δp = 27.90 | |||||
| δh = 32.14 | δh = 23.14 | δh = 18.30 | |||||
2.2. Experimental Approach
2.2.1. Extended Hansen’s Approach (EHA)
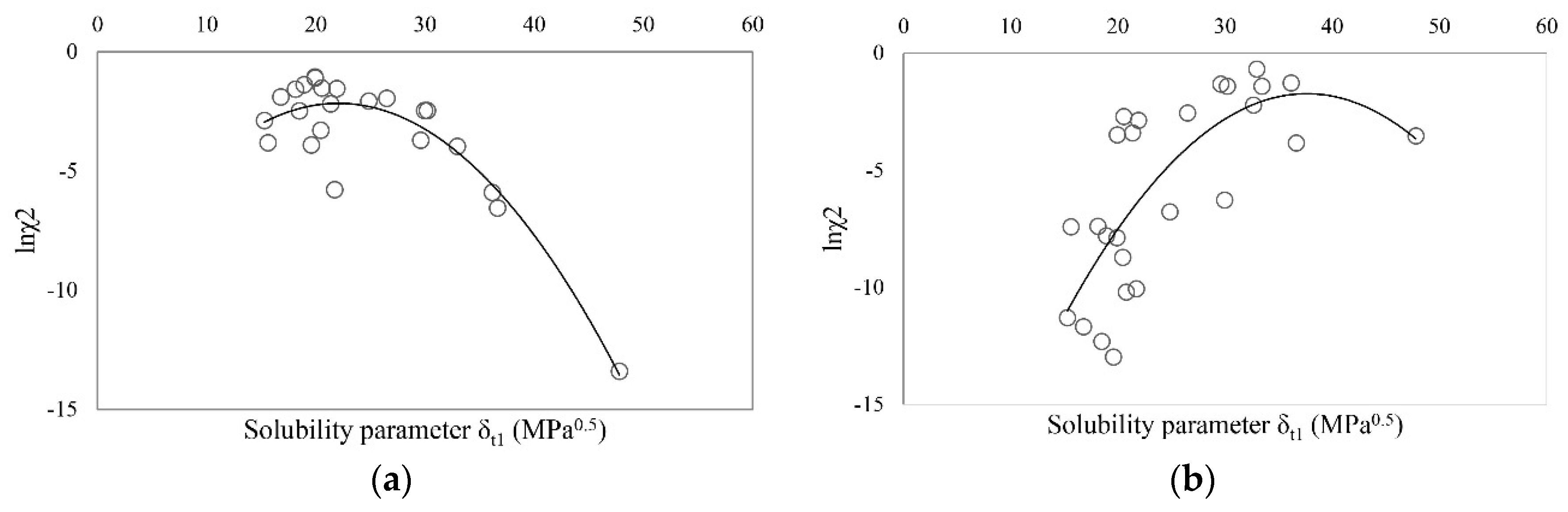
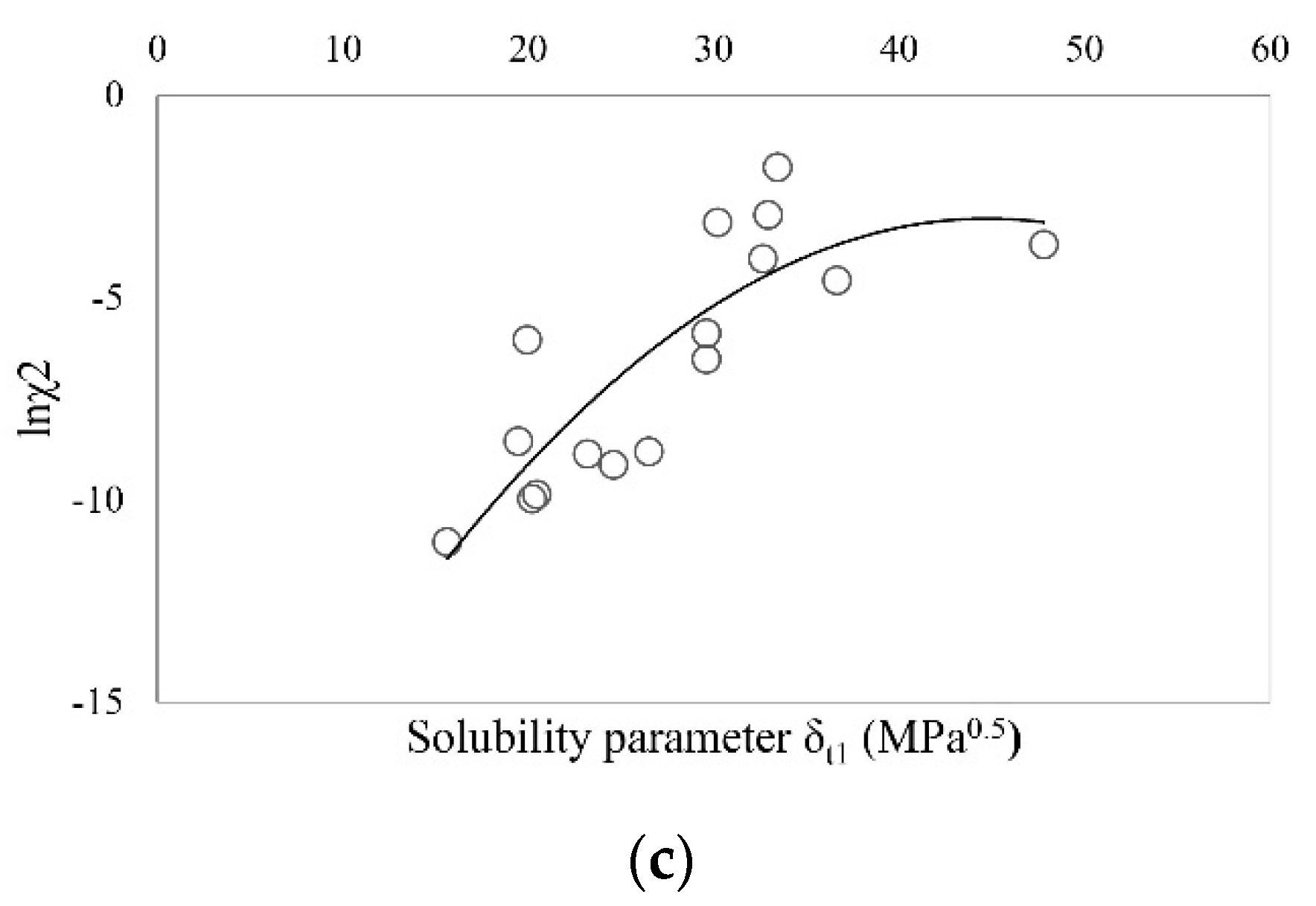
| Solvent | δt (MPa0.5) | Ibuprofen | Sodium Ibuprofen | Ibuprofen Lysinate |
|---|---|---|---|---|
| lnχ2 | ||||
| Ethanol | 26.52 | −1.9503 | −2.5573 | −8.8013 |
| Chloroform | 18.95 | −1.3712 | −7.7910 | / |
| Methanol | 29.61 | −3.7017 | −1.3116 | −5.8776 |
| Benzene | 18.51 | −2.4684 | −12.3017 | / |
| Dioxane | 20.47 | −3.2918 | −8.7174 | −9.8535 |
| Acetic acid | 21.37 | −2.1746 | −3.3999 | −3.0117 |
| 1-Pentanol | 21.93 | −1.5436 | −2.8702 | / |
| 1-Butanol | 23.20 | / | / | −8.8584 |
| 1-Propanol | 24.60 | / | / | −9.1191 |
| Cyclohexane | 16.80 | −1.8834 | −11.6705 | / |
| 1,2-Propanediol | 30.22 | −2.4547 | −1.4146 | −3.1307 |
| Formamide | 36.65 | −6.5485 | −3.8359 | −4.5675 |
| Ethylene glycol | 32.95 | −3.9612 | −0.6762 | −2.9535 |
| Glycerol | 36.16 | −5.8932 | −1.2651 | / |
| Ethyl acetate | 18.15 | −1.0942 | −7.3852 | −9.6817 |
| Propionic acid | 19.95 | −1.5611 | −3.4886 | / |
| 1-Octanol | 20.56 | −1.5134 | −2.7018 | / |
| Heptane | 15.30 | −2.8827 | −11.2964 | −9.1165 |
| Chlorobenzene | 19.58 | −3.9057 | −12.9644 | / |
| Diethyl ether | 15.64 | −3.8065 | −7.4103 | −11.039 |
| Acetone | 19.94 | −1.0474 | −7.8829 | −6.0326 |
| Acetophenone | 21.72 | −5.7807 | −10.0583 | / |
| N,N-Dimethylformamide | 24.86 | −2.058 | −6.7721 | / |
| Dichloromethane | 20.20 | / | / | −9.9672 |
| Water | 47.81 | −13.398 | −3.5326 | −3.6882 |
| N-Methylformamide | 29.98 | / | −6.2656 | / |
| 1,4-Butanediol | 33.44 | / | −1.4053 | / |
| 1,3-Propanediol | 32.65 | / | −2.2121 | / |
| Ethylene dichloride | 20.80 | −2.4549 | −10.1933 | / |
| Tetrahydrofuran | 23.20 | / | / | 8.5397 |
| Drug | Solubility Parameter (MPa0.5) | Analysis Parameters | ||||||
|---|---|---|---|---|---|---|---|---|
| δt | δd | δp | δh | No. of Solvents | No. of Combinations | No. of Errors | R2 | |
| Ibuprofen | 20.56 | 16.60 | 6.91 | 9.97 | 23 | 490,314 | 109,416 | 0.9964 |
| Sodium ibuprofenate | 34.12 | 16.38 | 12.52 | 27.19 | 26 | 1,562,275 | 220,884 | 0.9964 |
| Ibuprofen lysinate | 31.15 | 16.97 | 22.75 | 12.83 | 16 | 12,870 | 1573 | 0.7594 |
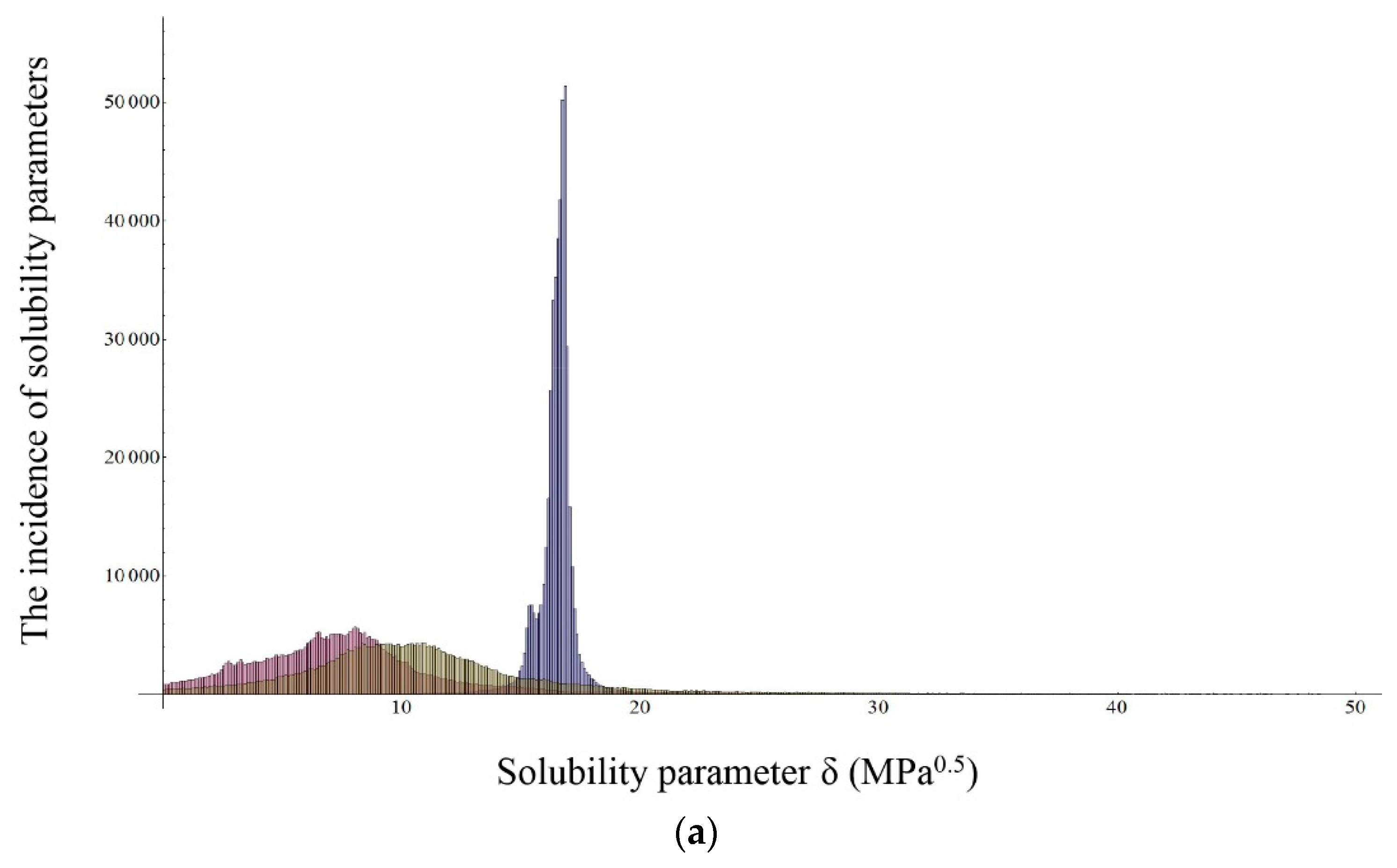
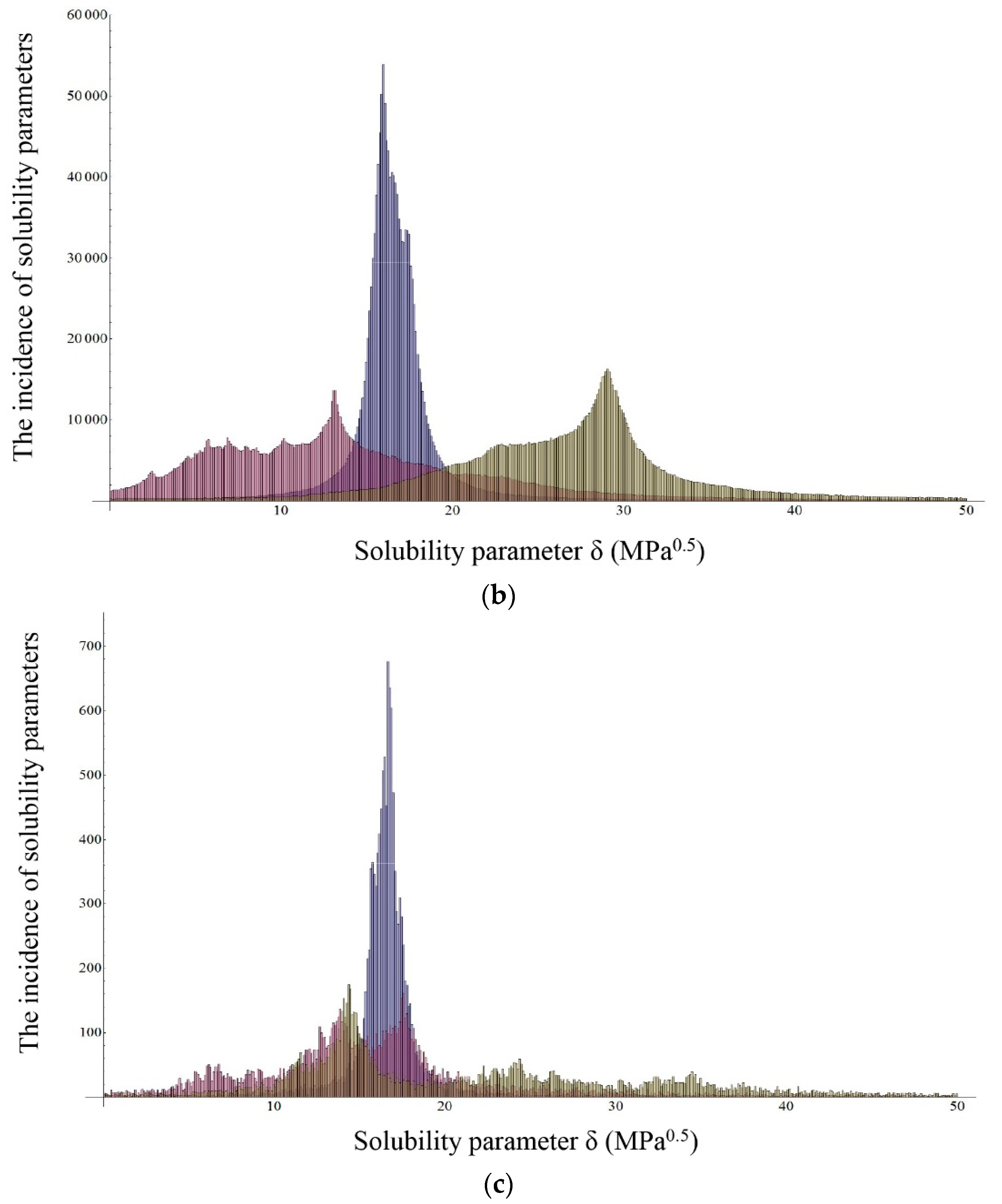
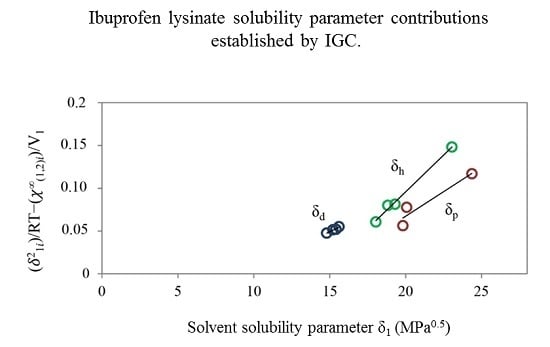
2.2.2. Inverse Gas Chromatography (IGC)
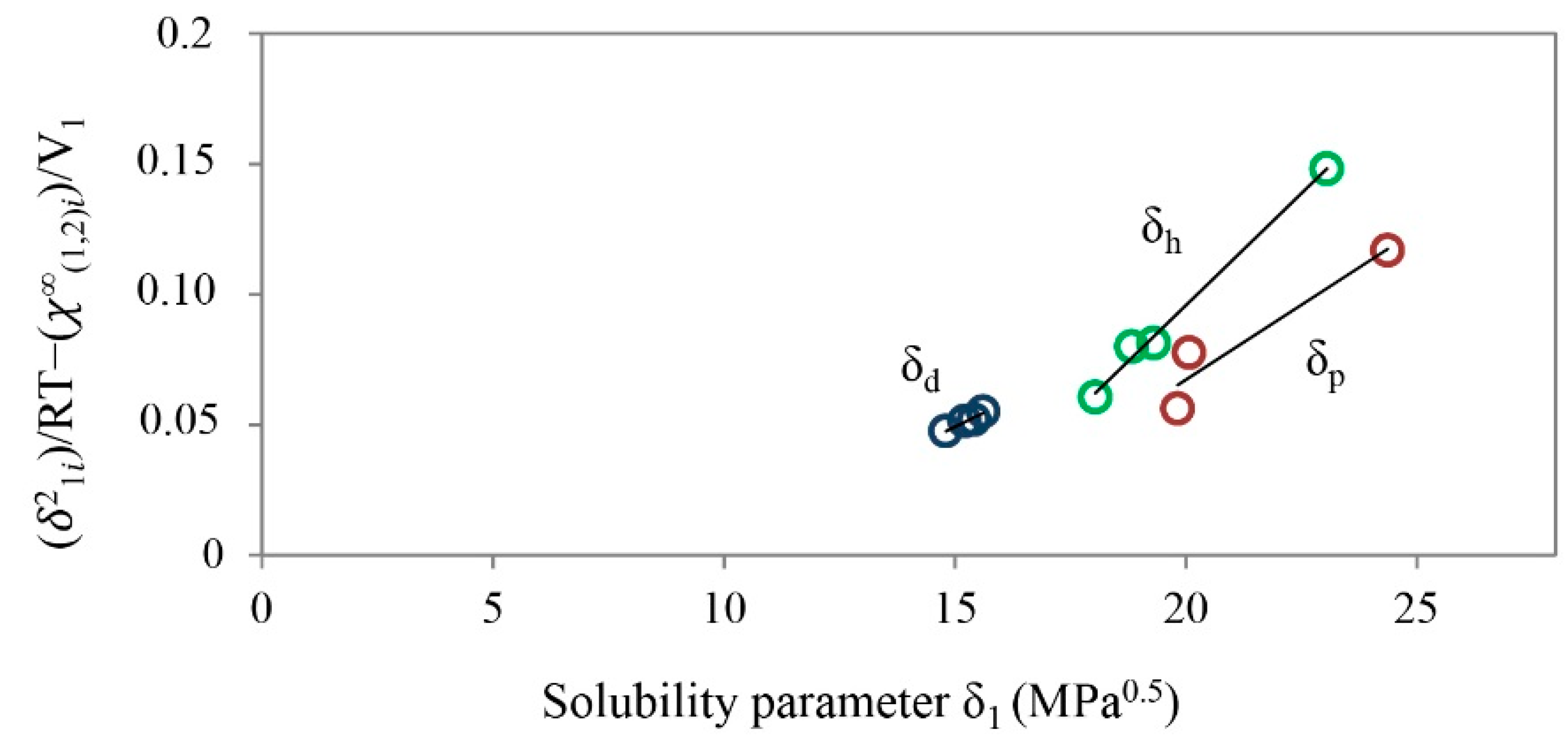
| Drug | Solubility Parameters | |||
|---|---|---|---|---|
| δd | δp | δh | δt | |
| Ibuprofen | 12.90 | 6.30 | 12.30 | 18.90 |
| Ibuprofen lysinate | 15.74 | 19.18 | 24.92 | 35.17 |
3. Discussion of Results
| Drug | Method | Solubility Parameters (MPa0.5) | ||||
|---|---|---|---|---|---|---|
| δd | δp | δh | δt | |||
| Ibuprofen | Group contribution method | |||||
| 17.56 | 3.22 | 8.31 | 19.71 | ||
| Experimental | ||||||
| 16.60 | 6.91 | 9.97 | 20.56 | ||
| 12.90 | 6.30 | 12.30 | 18.90 | ||
| Ibuprofen lysinate | Experimental | |||||
| 16.97 | 22.75 | 12.83 | 31.15 | ||
| 15.74 | 19.18 | 24.92 | 35.17 | ||
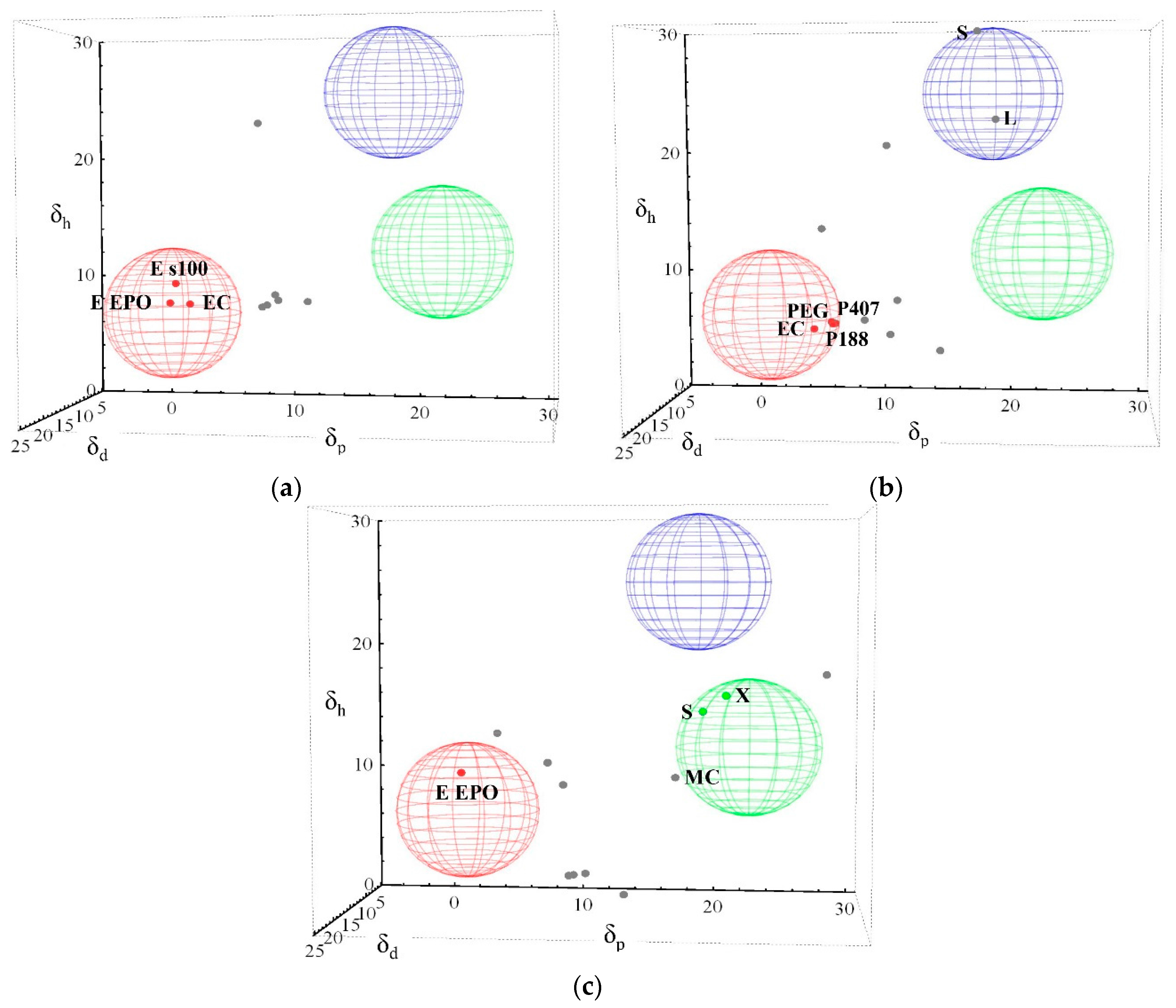
3.1. Three-Dimensional Evaluation
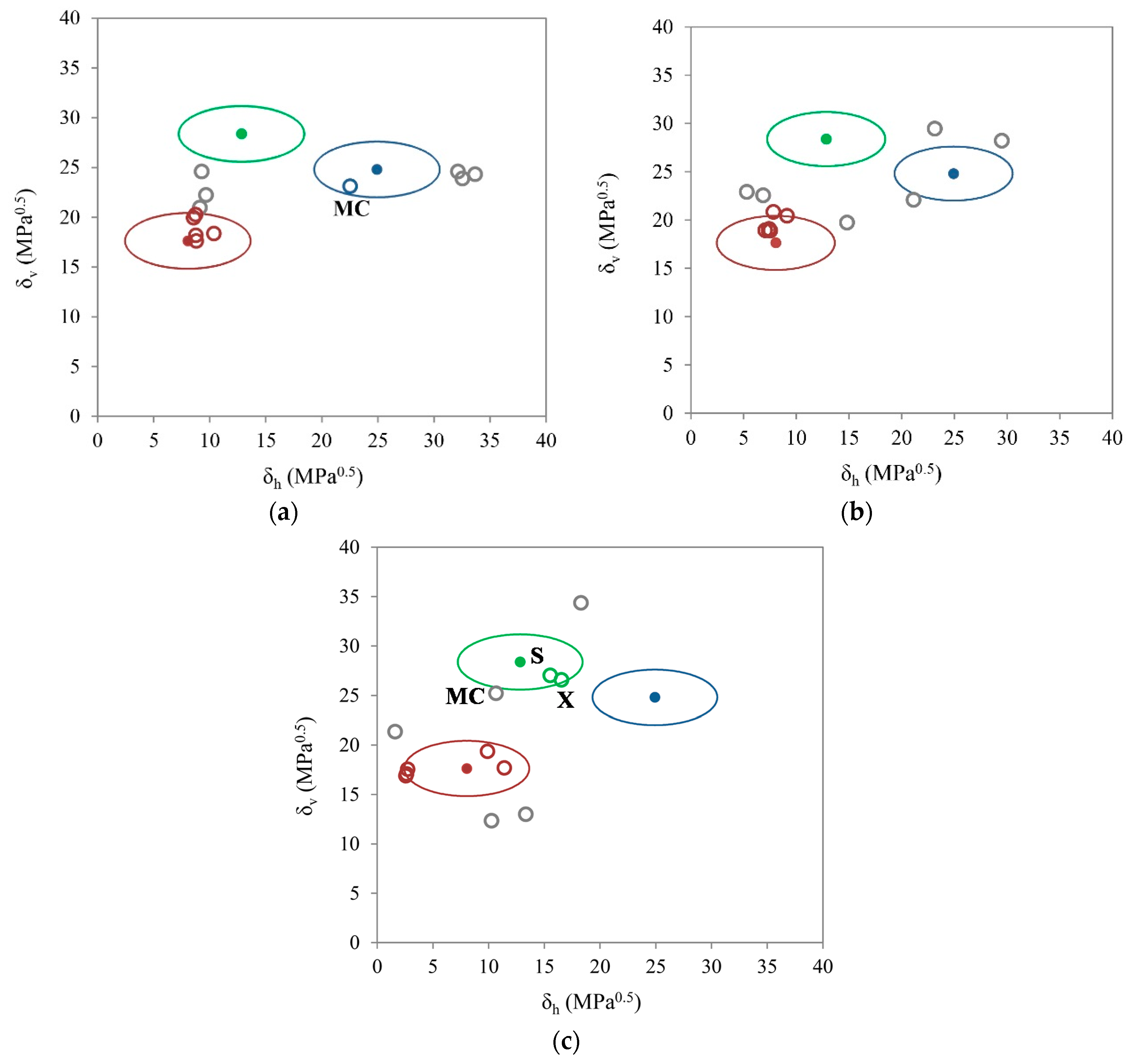
3.2. Two-Dimensional Evaluation
3.3. One-Dimensional Evaluation
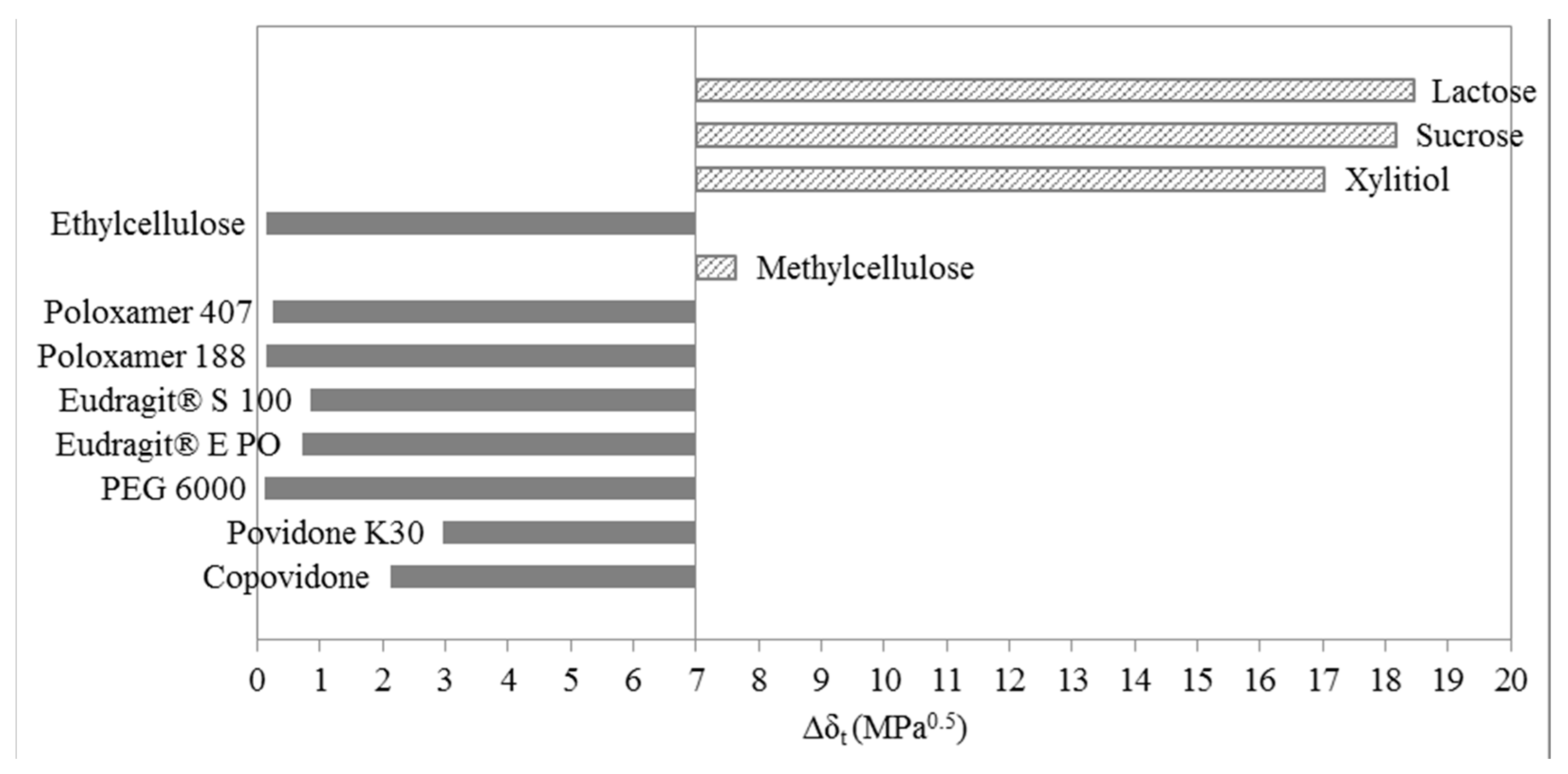
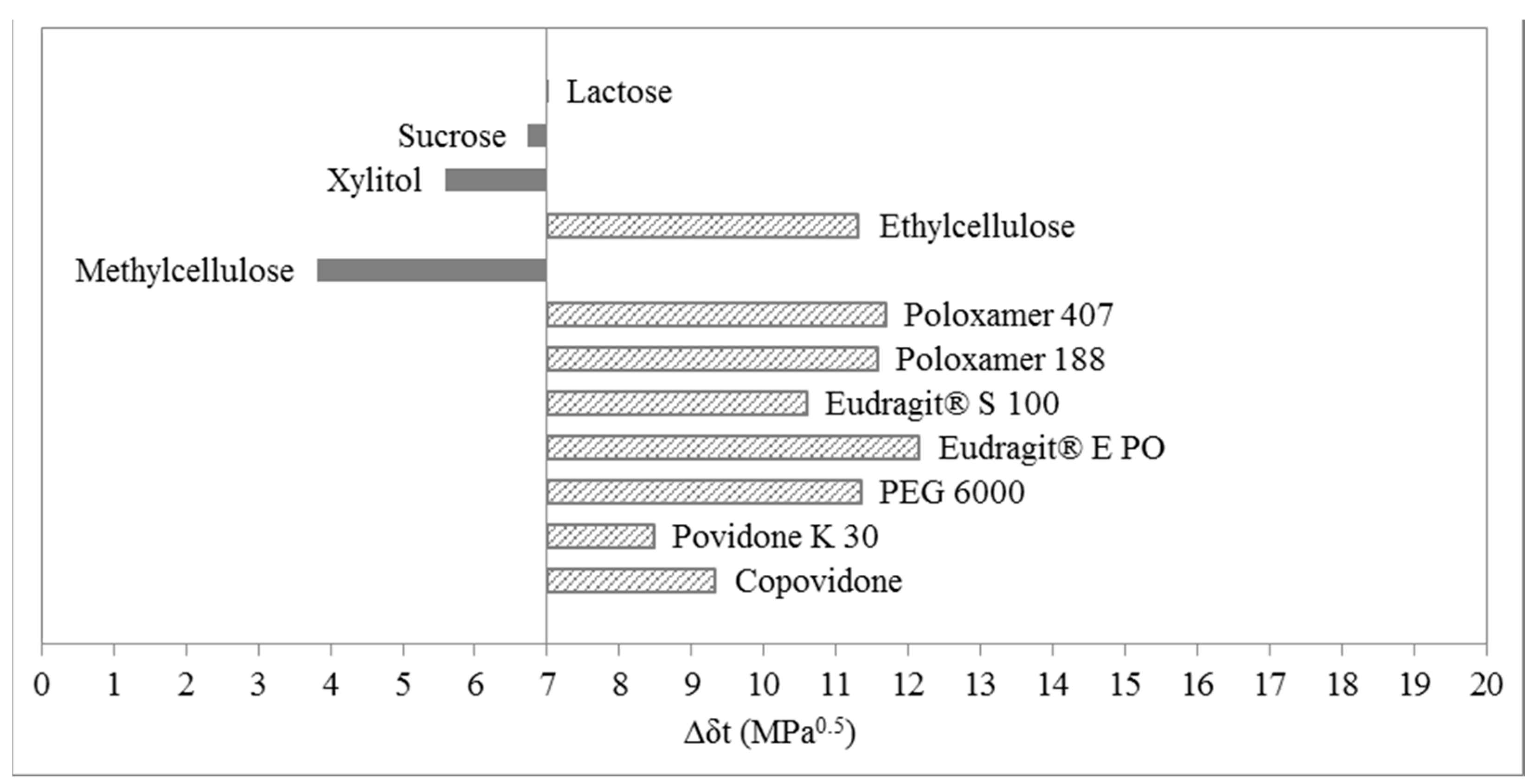
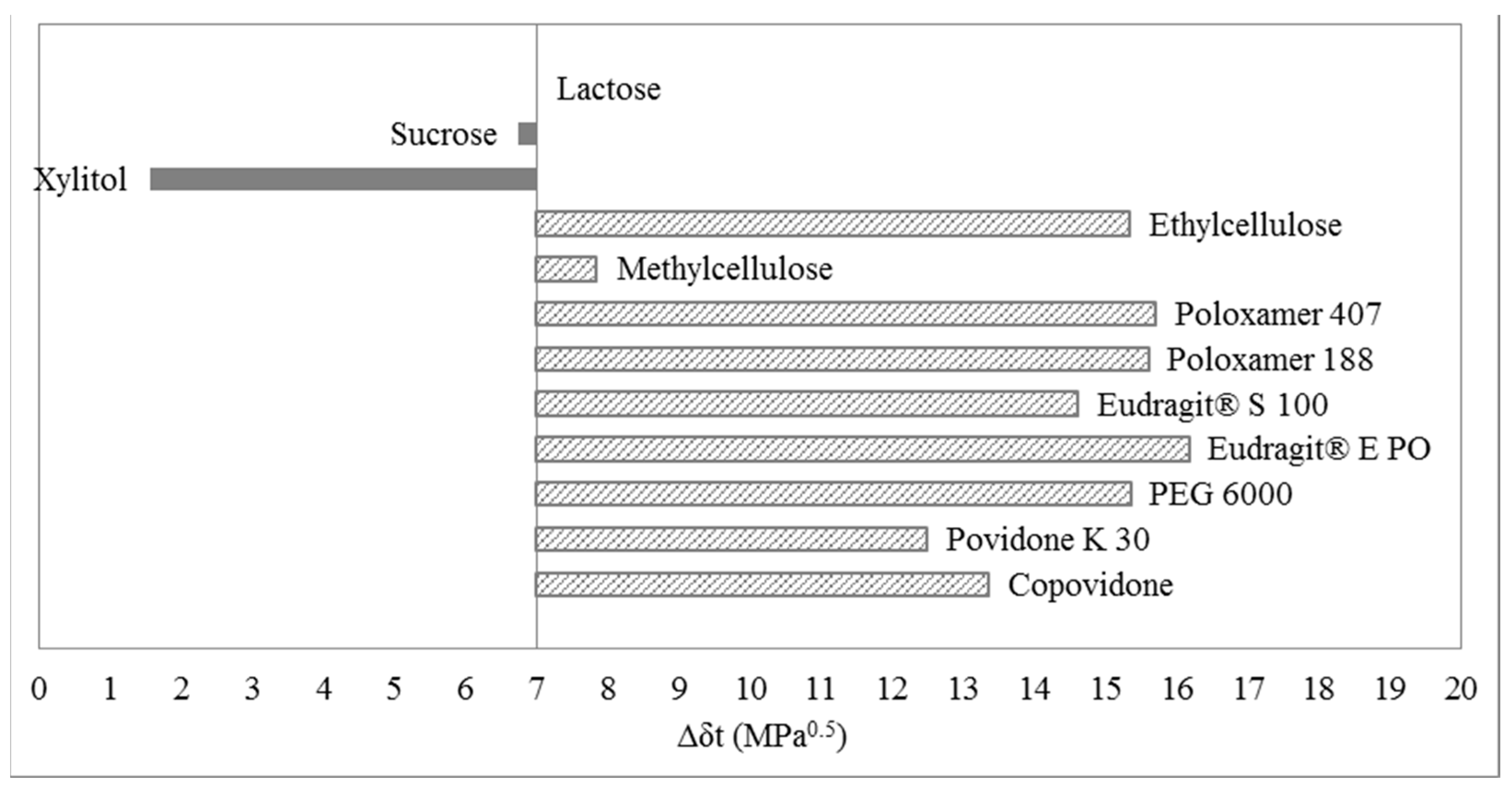
4. Materials and Methods
4.1. Materials
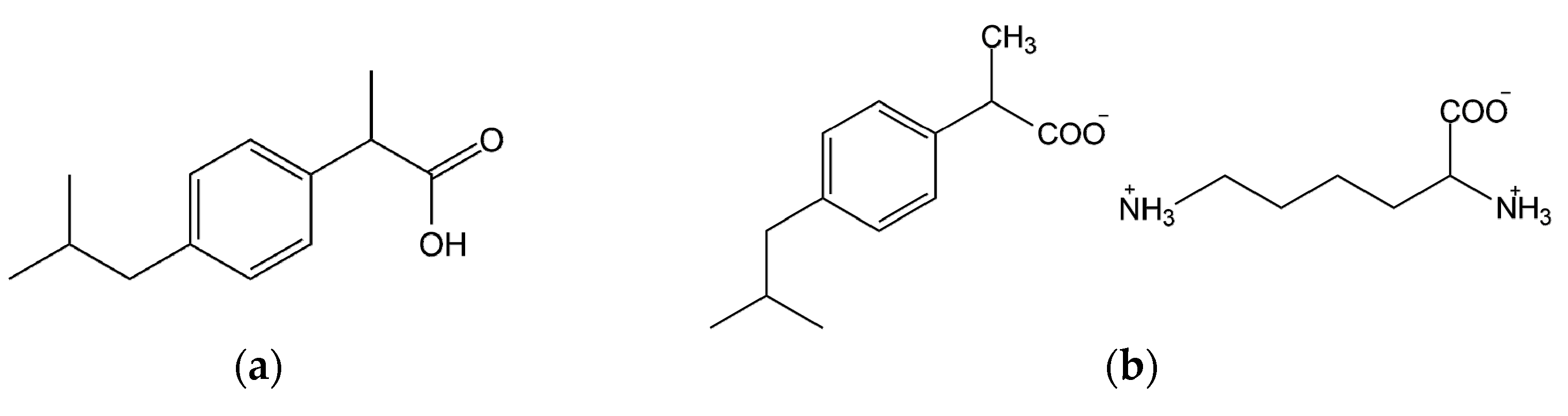
4.2. Methods
4.2.1. Calculation Methods
Group Contribution Methods (GCM)
| Individual Functional Group | Frequency | Fdi (MJ/m3)0.5·mol−1 | Fpi2 (MJ/m3)0.5·mol−1 | Ehi (J/mol) | Vm (cm3/mol) | |
|---|---|---|---|---|---|---|
| –CH3 | 3 | 420 × 3 | 0 | 0 | 33.5 × 3 | |
| >CH– | 2 | 80 × 2 | 0 | 0 | −1.0 × 2 | |
| –CH2– | 1 | 270 | 0 | 0 | 16.1 | |
| phenylene (p) | 1 | 1270 | 1102 | 0 | 52.4 | |
| –COOH | 1 | 530 | 4202 | 10,000 | 28.5 | |
| Sum | - | 3490 | 188,500 | 10,000 | 195.5 | |
| Calculations and results | δd = 17.85 | |||||
| δp = 2.22 | ||||||
| δh = 7.15 | ||||||
| δt = 19.36 | ||||||
| Individual Functional Group | Frequency | Fdi (MJ/m3)0.5·mol−1 | Fpi2 (MJ/m3)0.5·mol−1 | Ehi (J/mol) | Vm (cm3/mol) | |
|---|---|---|---|---|---|---|
| –CH2– | 4 | 270 × 4 | 0 | 0 | 16.1 × 4 | |
| >CH– | 1 | 80 | 0 | 0 | −1.0 | |
| –N< | 1 | 20 | 8002 | 5000 | −9.0 | |
| >C=O | 1 | 290 | 7702 | 2000 | 10.8 | |
| ring (5) | 1 | 190 | - | - | 16.0 | |
| Sum | - | 1660 | 1,232,900 | 7000 | 81.2 | |
| Calculations and results | δd = 20.44 | |||||
| δp = 13.67 | ||||||
| δh = 9.28 | ||||||
| δt = 26.28 | ||||||
4.2.2. Experimental Approach
Extended Hansen Approach (EHA)
Inverse Gas Chromatography (IGC)
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hildebrand, J.H.; Scott, R.L. The Solubility of Nonelectrolytes; Reinhold Pub. Corp.: New York, NY, USA, 1950; p. 514. [Google Scholar]
- Hildebrand, J.H.; Scott, R.L. Regular Solutions; Prentice-Hall: Saddle River, NJ, USA, 1962; p. 202. [Google Scholar]
- Van Krevelen, D.W.; te Nijenhuis, K. Properties of Polymers: Their Correlation with Chemical Structure; Their Numerical Estimation and Prediction from Additive Group Contributions; Elsevier: Amsterdam, The Netherland; Tokyo, Japan, 2009; p. 189. [Google Scholar]
- Hancock, B.C.; York, P.; Rowe, R.C. The use of solubility parameters in pharmaceutical dosage form design. Int. J. Pharm. 1997, 148, 1–21. [Google Scholar] [CrossRef]
- Hansen, C.M. The Three Dimensional Solubility Parameter—Key to Paint Component Affinities I.—Solvents, Plasticizers, Polymers, and Resins. J. Paint Technol. 1967, 39, 104–117. [Google Scholar]
- Hansen, C.M. The Three Dimensional Solubility Parameter—Key to Paint Component Affinities II.—Dyes, Emulsifiers, Mutual Solubility and Compatibility, and Pigments. J. Paint Technol. 1967, 39, 511–514. [Google Scholar]
- Hansen, C.M. The Universality of the Solubility Parameter. Ind. Eng. Chem. Prod. Res. Dev. 1969, 8, 2–11. [Google Scholar] [CrossRef]
- Hansen, C.M. Hansen Solubility Parameters: A User’s Handbook, 2nd ed.; CRC Press, Taylor Francis Group: Boca Raton, FL, USA, 2007; p. 544. [Google Scholar]
- Güner, A. The algorithmic calculations of solubility parameter for the determination of interactions in dextran/certain polar solvent systems. Eur. Polym. J. 2004, 40, 1587–1594. [Google Scholar] [CrossRef]
- Swarbrick, J. Encyclopedia of Pharmaceutical Technology: Stat-Zeta; Informa Healthcare: New York, NY, USA; London, UK, 2007; p. 888. [Google Scholar]
- Mohammad, M.A.; Alhalaweh, A.; Velaga, S.P. Hansen solubility parameter as a tool to predict cocrystal formation. Int. J. Pharm. 2011, 407, 63–71. [Google Scholar] [CrossRef] [PubMed]
- Bagley, E.B.; Nelson, T.P.; Scigliano, J.M. Three-dimensional solubility parameters and their relationship to internal pressure measurements in polar and hydrogen bonding solvents. J. Paint Technol. 1971, 43, 35–42. [Google Scholar]
- Albers, J. Hot-Melt Extrusion with Poorly Soluble Drugs; Cuvillier Verlag: Goettingen, Germany, 2008; p. 145. [Google Scholar]
- Greenhalgh, D.J.; Williams, A.C.; Timmins, P.; York, P. Solubility parameters as predictors of miscibility in solid dispersions. J. Pharm. Sci. 1999, 88, 1182–1190. [Google Scholar] [CrossRef] [PubMed]
- Ghebremeskel, A.N.; Vemavarapu, C.; Lodaya, M. Use of surfactants as plasticizers in preparing solid dispersions of poorly soluble API: Selection of polymer-surfactant combinations using solubility parameters and testing the processability. Int. J. Pharm. 2007, 328, 119–129. [Google Scholar] [CrossRef] [PubMed]
- He, H.; Yang, R.; Tang, X. In vitro and in vivo evaluation of fenofibrate solid dispersion prepared by hot-melt extrusion. Drug Dev. Ind. Pharm. 2010, 36, 681–687. [Google Scholar] [CrossRef] [PubMed]
- Chokshi, R.J.; Sandhu, H.K.; Iyer, R.M.; Shah, N.H.; Malick, A.W.; Zia, H. Characterization of physico-mechanical properties of indomethacin and polymers to assess their suitability for hot-melt extrusion processs as a means to manufacture solid dispersion/solution. J. Pharm. Sci. 2005, 94, 2463–2474. [Google Scholar] [CrossRef] [PubMed]
- Nair, R.; Nyamweya, N.; Gönen, S.; Martínez-Miranda, L.J.; Hoag, S.W. Influence of various drugs on the glass transition temperature of poly(vinylpyrrolidone): A thermodynamic and spectroscopic investigation. Int. J. Pharm. 2001, 225, 83–96. [Google Scholar] [CrossRef]
- Zheng, X.; Yang, R.; Tang, X.; Zheng, L. Part I: Characterization of solid dispersions of nimodipine prepared by hot-melt extrusion. Drug Dev. Ind. Pharm. 2007, 33, 791–802. [Google Scholar] [CrossRef] [PubMed]
- Babu, P.R.S.; Subrahmanyam, C.V.S.; Thimmasetty, J.; Manavalan, R.; Valliappan, K. Extended Hansen’s solubility approach: Meloxicam in individual solvents. Pak. J. Pharm. Sci. 2007, 20, 311–316. [Google Scholar] [PubMed]
- Liu, J.; Xiao, Y.; Allen, C. Polymer-drug compatibility: A guide to the development of delivery systems for the anticancer agent, ellipticine. J. Pharm. Sci. 2004, 93, 132–143. [Google Scholar] [CrossRef] [PubMed]
- Forster, A.; Hempenstall, J.; Tucker, I.; Rades, T. Selection of excipients for melt extrusion with two poorly water-soluble drugs by solubility parameter calculation and thermal analysis. Int. J. Pharm. 2001, 226, 147–161. [Google Scholar] [CrossRef]
- Barra, J.; Peña, M.A.; Bustamante, P. Proposition of group molar constants for sodium to calculate the partial solubility parameters of sodium salts using the van Krevelen group contribution method. Eur. J. Pharm. Sci. Off. J. Eur. Fed. Pharm. Sci. 2000, 10, 153–161. [Google Scholar] [CrossRef]
- Beerbower, A.; Wu, P.L.; Martin, A. Expanded solubility parameter approach. I: Naphthalene and benzoic acid in individual solvents. J. Pharm. Sci. 1984, 73, 179–188. [Google Scholar] [CrossRef] [PubMed]
- Kiselev, A.V.; I︠A︡shin, I.I. Gas-Adsorption Chromatography; Plenum Press: New York, NY, USA, 1969; p. 272. [Google Scholar]
- Voelkel, A.; Milczewska, K.; Jȩczalik, J. Characterization of the interactions in polymer/silica systems by inverse gas chromatography. Macromol. Symp. 2001, 169, 45–55. [Google Scholar] [CrossRef]
- Voelkel, A.; Janas, J. Solubility parameters of broad and narrow distributed oxyethylates of fatty alcohols. J. Chromatogr. A 1993, 645, 141–151. [Google Scholar] [CrossRef]
- Price, G.J.; Lloyd, D.R.; Ward, T.C.; Schreiber, H.P. Calculation of Solubility Parameters by Inverse Gas Chromatography. In ACS Symposium Series; Oxford University Press: Oxford, UK, 1989; Volume 391, pp. 48–58. [Google Scholar]
- Voelkel, A.; Kopczyński, T. Inverse gas chromatography in the examination of organic compounds: Polarity and solubility parameters of isoquinoline derivatives. J. Chromatogr. A 1998, 795, 349–357. [Google Scholar] [CrossRef]
- Adamska, K.; Voelkel, A.; Héberger, K. Selection of solubility parameters for characterization of pharmaceutical excipients. J. Chromatogr. A 2007, 1171, 90–97. [Google Scholar] [CrossRef] [PubMed]
- Adamska, K.; Bellinghausen, R.; Voelkel, A. New procedure for the determination of Hansen solubility parameters by means of inverse gas chromatography. J. Chromatogr. A 2008, 1195, 146–149. [Google Scholar] [CrossRef] [PubMed]
- Adamska, K.; Voelkel, A. Inverse gas chromatographic determination of solubility parameters of excipients. Int. J. Pharm. 2005, 304, 11–17. [Google Scholar] [CrossRef] [PubMed]
- Fowkes, F.M. Dispersion force contribution to surface and interfacial tension, contact angles and heats of immersions. Adv. Chem. Ser. 1964, 43, 99–111. [Google Scholar]
- Van Oss, C.J.; Chaudhury, M.K.; Good, R.J. Monopolar surfaces. Adv. Colloid Interface Sci. 1987, 28, 35–64. [Google Scholar] [CrossRef]
- Bustamante, P.; Pena, M.A.; Barra, J. The modified extended Hansen method to determine partial solubility parameters of drugs containing a single hydrogen bondi ng group and their sodium derivatives: Benzoic acid/Na and ibuprofen/Na. Int. J. Pharm. 2000, 194, 117–124. [Google Scholar] [CrossRef]
- Voelkel, A.; Adamska, K.; Strzemiecka, B.; Batko, K. Determination of Hansen solubility parameters of solid materials by inverse gas-solid chromatography. Acta Chromatogr. 2008, 20, 1–14. [Google Scholar] [CrossRef]
- Standen, A.; Kirk, R.E.; Othmer, D.F.; Hansen, C.M.; Beerbower, A. “Solubility Parameters” v Kirk-Othmer Encyclopedia of Chemical Technology, 2nd Completely Rev., Ed ed; Adamantane to Units. Interscience: New York, NY, USA, 1971; pp. 889–910. [Google Scholar]
- Fedors, R.F. A method for estimating both the solubility parameters and molar volumes of liquids. Polym. Eng. Sci. 1974, 14, 147–154. [Google Scholar] [CrossRef]
- Hoy, K.L. The Hoy: Tables of Solubility Parameters; Union Carbide Corp., Solvents & Coatings Materials, Research & Development Dept.: South Charleston, WV, USA, 1985. [Google Scholar]
- Stefanis, E.; Panayiotou, C. Prediction of Hansen Solubility Parameters with a New Group-Contribution Method. Int. J. Thermophys. 2008, 29, 568–585. [Google Scholar] [CrossRef]
- Just, S.; Sievert, F.; Thommes, M.; Breitkreutz, J. Improved group contribution parameter set for the application of solubility parameters to melt extrusion. Eur. J. Pharm. Biopharm. 2013, 85 (3, Part B), 1191–1199. [Google Scholar] [CrossRef] [PubMed]
- Sample Availability: Samples of the compounds are not available from the authors.
© 2015 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kitak, T.; Dumičić, A.; Planinšek, O.; Šibanc, R.; Srčič, S. Determination of Solubility Parameters of Ibuprofen and Ibuprofen Lysinate. Molecules 2015, 20, 21549-21568. https://doi.org/10.3390/molecules201219777
Kitak T, Dumičić A, Planinšek O, Šibanc R, Srčič S. Determination of Solubility Parameters of Ibuprofen and Ibuprofen Lysinate. Molecules. 2015; 20(12):21549-21568. https://doi.org/10.3390/molecules201219777
Chicago/Turabian StyleKitak, Teja, Aleksandra Dumičić, Odon Planinšek, Rok Šibanc, and Stanko Srčič. 2015. "Determination of Solubility Parameters of Ibuprofen and Ibuprofen Lysinate" Molecules 20, no. 12: 21549-21568. https://doi.org/10.3390/molecules201219777
APA StyleKitak, T., Dumičić, A., Planinšek, O., Šibanc, R., & Srčič, S. (2015). Determination of Solubility Parameters of Ibuprofen and Ibuprofen Lysinate. Molecules, 20(12), 21549-21568. https://doi.org/10.3390/molecules201219777