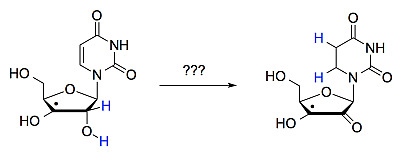
Transfer Hydrogenation in Open-Shell Nucleotides — A Theoretical Survey
Abstract
:1. Introduction
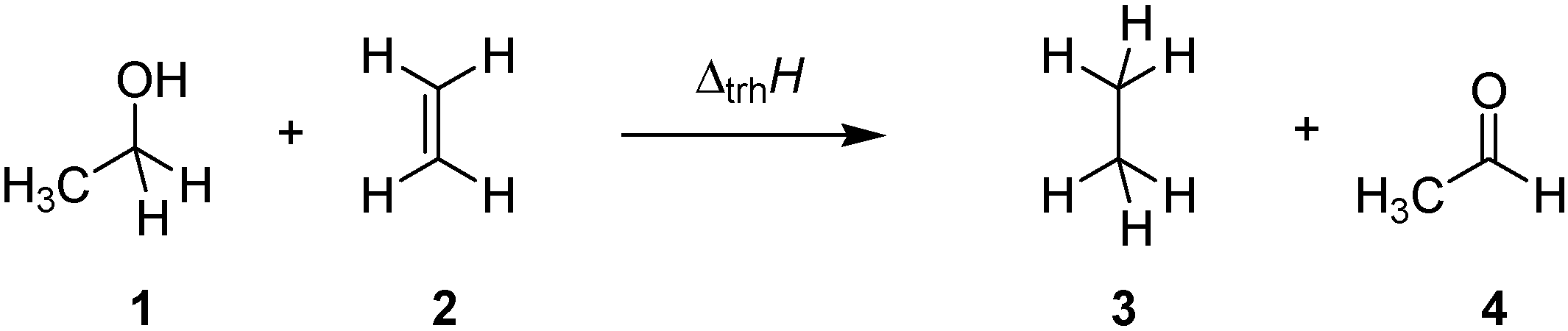
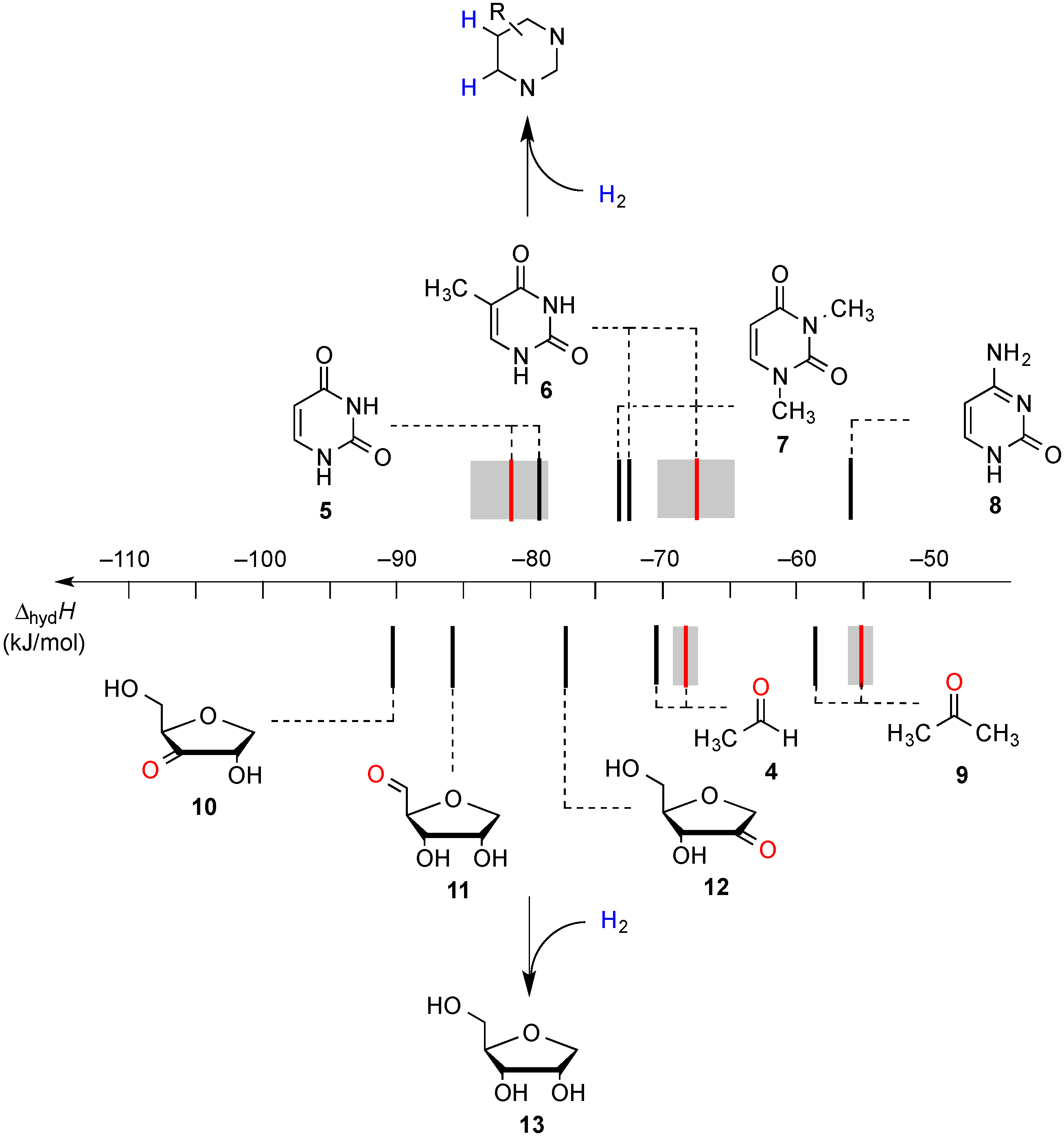
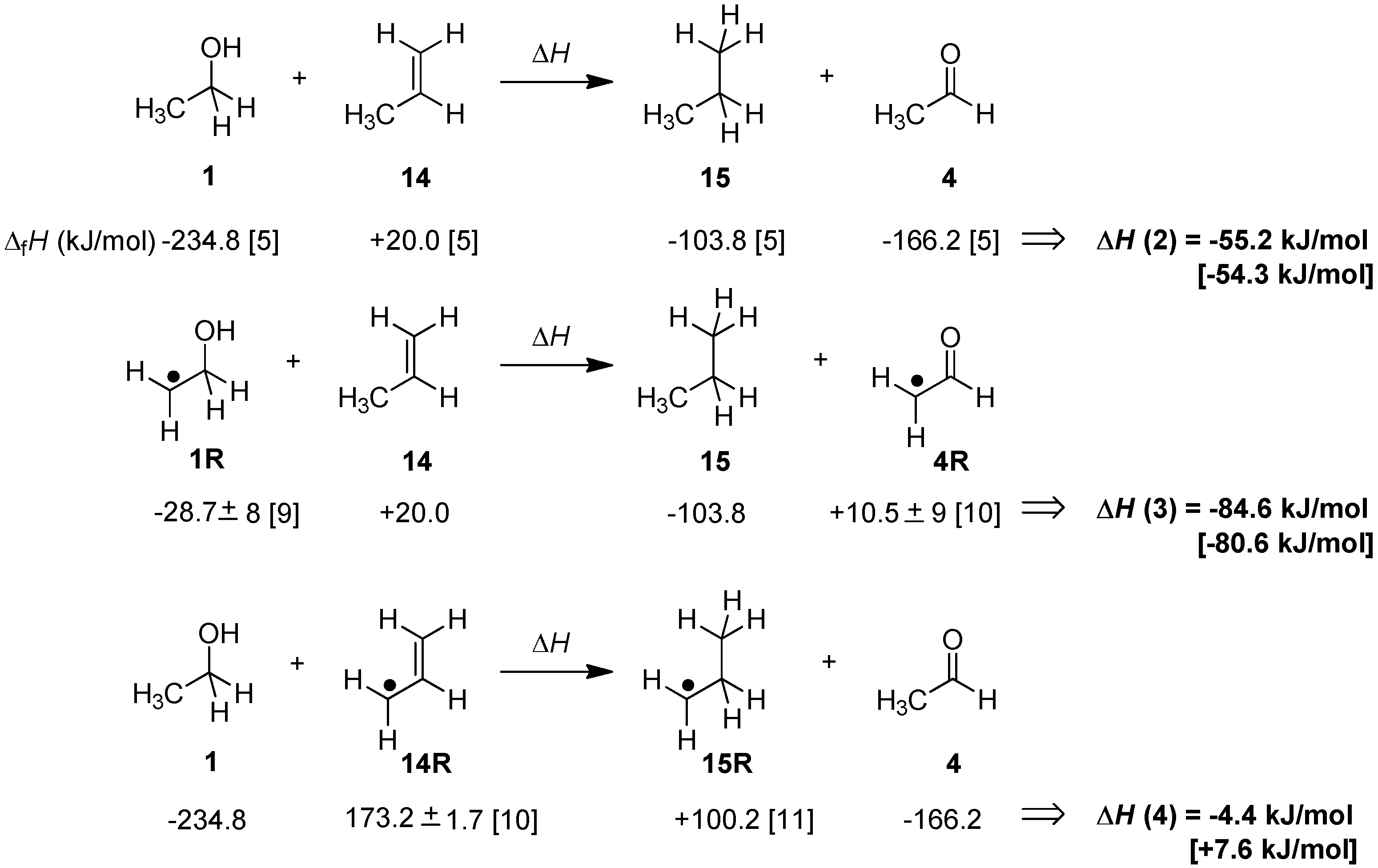
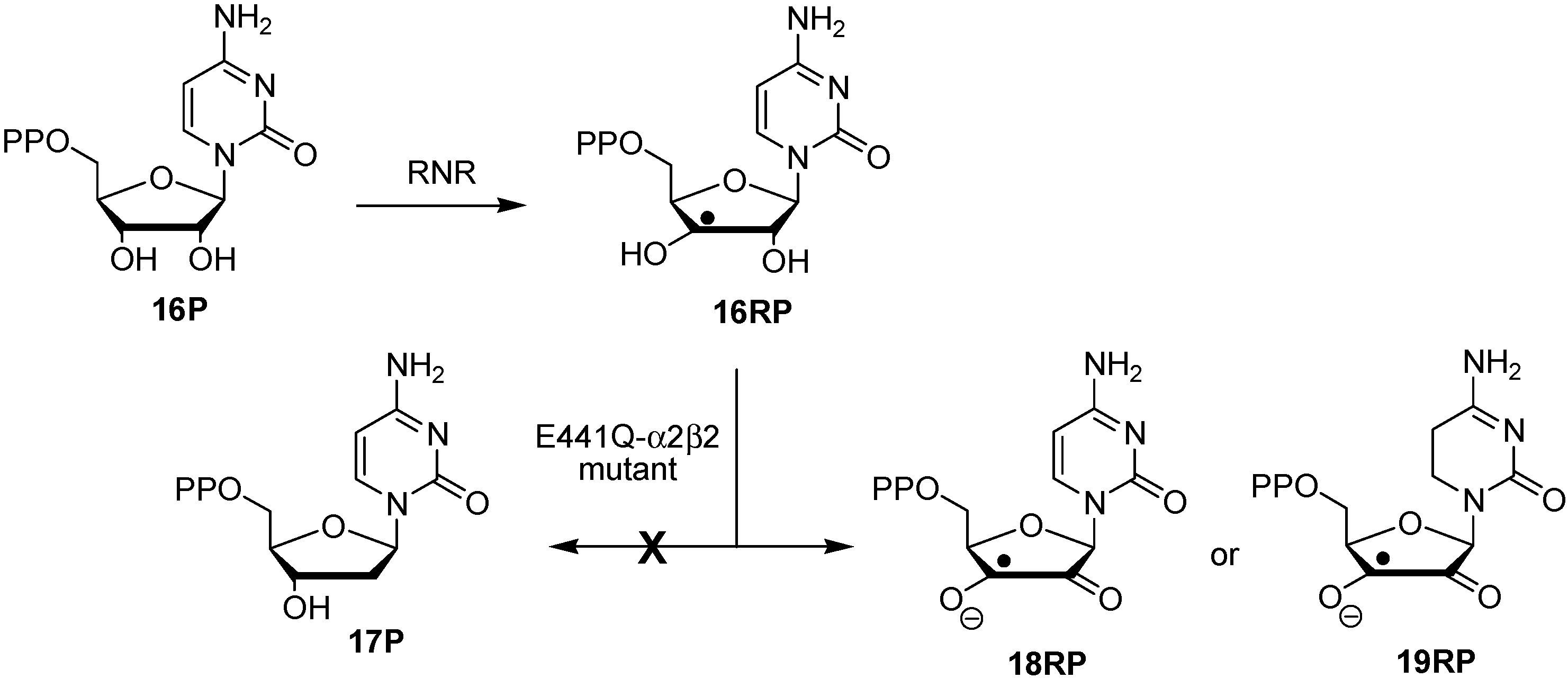
2. Results and Discussion
2.1. Closed-Shell Systems
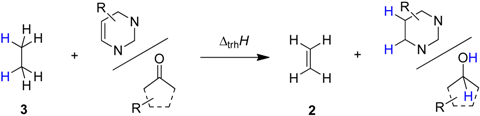 | ||||||
|---|---|---|---|---|---|---|
| Reactants | MP2(FC)/ 6-311 + G(3df,2p) | G3(MP2)-RAD | Exp. | |||
| ∆trhH a | ∆hydH b | ∆trhH a | ∆hydH b | ∆trhH a | ∆hydH b | |
| Ethylene (2) | 0.0 | −136.3 | 0.0 | −136.3 | 0.0 c | −136.3 ± 0.2 [23] |
| Propene (14) | +12.4 | −123.9 | +10.8 | −125.5 | +12.6 c | −125.0 ± 0.2 [24] |
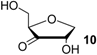 | +44.5 | −91.8 | +44.9 | −91.4 | n/a | n/a |
 | +50.3 | −86.0 | +50.2 | −86.1 | n/a | n/a |
| Uracil (5) | +56.1 | −80.2 | +57.0 | −79.3 | +53.6 ± 2.1 [7] | −82.7 ± 2.1 [7] |
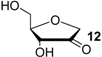 | +58.3 | −78.0 | +58.8 | −77.5 | n/a | n/a |
| 1,3-Dimethyluracil (7) | +62.4 | −73.9 | +62.7 | −73.6 | +68.5 ± 2.1 [7] | −67.8 ± 2.1 [7] |
| Thymine (6) | +64.2 | −72.1 | +63.8 | −72.5 | +68.8 ± 4.2 [7] | −67.5 ± 2.3 [7] |
| Acetaldehyde (4) | +65.8 | −70.5 | +65.1 | −71.2 | +67.8 c | −69.1 ± 0.4 [25] |
| Acetone (9) | +77.8 | −58.5 | +76.5 | −59.8 | +80.9 c | −55.6 ± 0.4 [26] |
| Cytosine (8) | +82.4 | −53.9 | +80.2 | −56.1 | n/a | n/a |
| Adenine (25) | +152.6 | +16.3 | +139.0 | +2.7 | n/a | n/a |
| Guanine (26) | +155.2 | +18.9 | +141.2 | +4.9 | n/a | n/a |
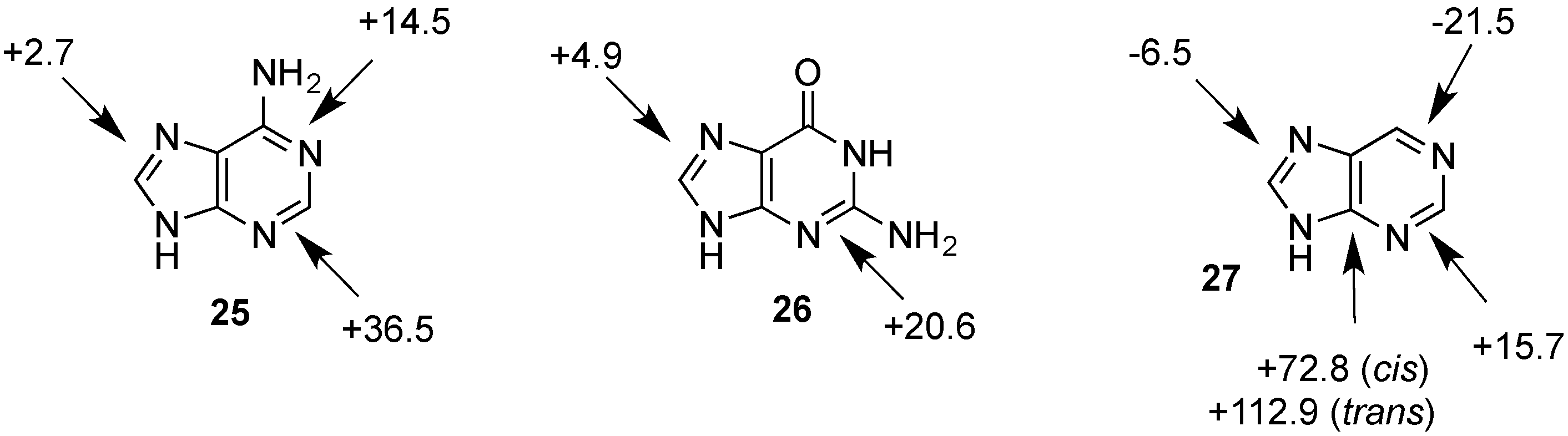
2.2. Open-Shell Systems
 | |||||||
|---|---|---|---|---|---|---|---|
| Initial radicals | UB3LYP/ 6-31G(d) | ROMP2(FC)/ 6-311+G(3df,2p) | G3(MP2)-RAD | Exp. c | |||
| ∆trhH a | ∆hydH b | ∆trhH a | ∆hydH b | ∆trhH a | ∆hydH b | ∆trhH a | |
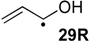 | +79.5 | −56.8 | +62.5 | −73.8 | +64.9 | −71.4 | +55.4 ± 17.3 |
 | +82.8 | −53.5 | +71.5 | −64.8 | +72.7 | −63.7 | +65.4 ± 5.9 |
 | +88.4 | −47.9 | +72.9 | −63.4 | +72.8 | −63.5 | +64.6 ± 2.2 |
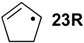 | +88.3 | −48.0 | +79.9 | −56.5 | +75.9 | −60.4 | +82.7 ± 7.6 |
 | +96.3 | −40.0 | +85.8 | −50.5 | +81.6 | −54.7 | +74.9 ± 4.9 |
 | +137.3 | +1.0 | +90.1 | −46.2 | +91.4 | −44.9 | +94.9 ± 17.1 |
 | +149.0 | +12.7 | +98.3 | −38.0 | +99.3 | −37.0 | +74.1 ± 8.1 |
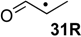 | +154.6 | +18.3 | +104.8 | −31.5 | +104.6 | −31.7 | +91.9 ± 9.3 |
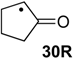 | +161.6 | +25.3 | +105.7 | −30.6 | +106.6 | −29.7 | +106.6 ± 13.5 |
 | |||||||
|---|---|---|---|---|---|---|---|
| RSE a | Exp. b | RSE a | Exp. b | ∆RSE c | ∆∆trhH d | ||
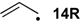 | −72.0 | −70.7 | 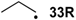 | −12.2 | −17.1 | −59.8 | −61.8 |
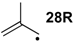 | −66.1 | −66.5 | 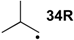 | −10.6 | −20.1 | −55.5 | −55.4 |
 | −85.4 | −96.6 | 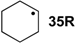 | −20.7 | −23.0 | −64.7 | −64.6 |
 | −84.7 | −94.6 | 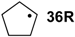 | −33.4 | −39.3 | −51.3 | −51.3 |
 | −36.7 | −44.7 | 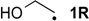 | −10.3 | −15.5 | −26.4 | −26.3 |
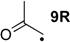 | −32.4 | −38.1 | 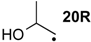 | −8.4 | −44.9 | −24.0 | −22.8 |
 | ||||
|---|---|---|---|---|
| ROMP2(FC)/ 6-311+G(3df,2p) | G3(MP2)-RAD | |||
| <∆trhH> a | <∆hydH> b | <∆trhH> a | <∆hydH> b | |
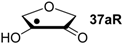 | +192.0 | −7.28 | +124.7 | −11.6 |
 | +128.2 | −8.09 | +121.9 | −14.4 |
 | +125.4 | −11.0 | +121.3 | −15.0 |
 | +118.8 | −17.5 | +114.8 | −21.5 |
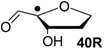 | +115.7 | −20.7 | +109.6 | −26.7 |
 | +115.5 | −20.8 | +108.8 | −27.5 |
 | +105.3 | −31.0 | +103.2 | −33.1 |
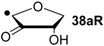 | +104.6 | −31.7 | +101.4 | −34.9 |
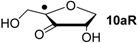 | +104.0 | −32.3 | +100.1 | −36.2 |
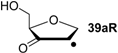 | +93.3 | −43.0 | +94.1 | −42.3 |
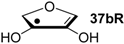 | +76.5 | −59.8 | +73.8 | −62.5 |
 | +65.9 | −70.4 | +65.2 | −71.1 |
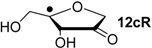 | +39.5 | −96.8 | +41.8 | −94.5 |
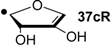 | +13.8 | −122.5 | +18.1 | −118.2 |


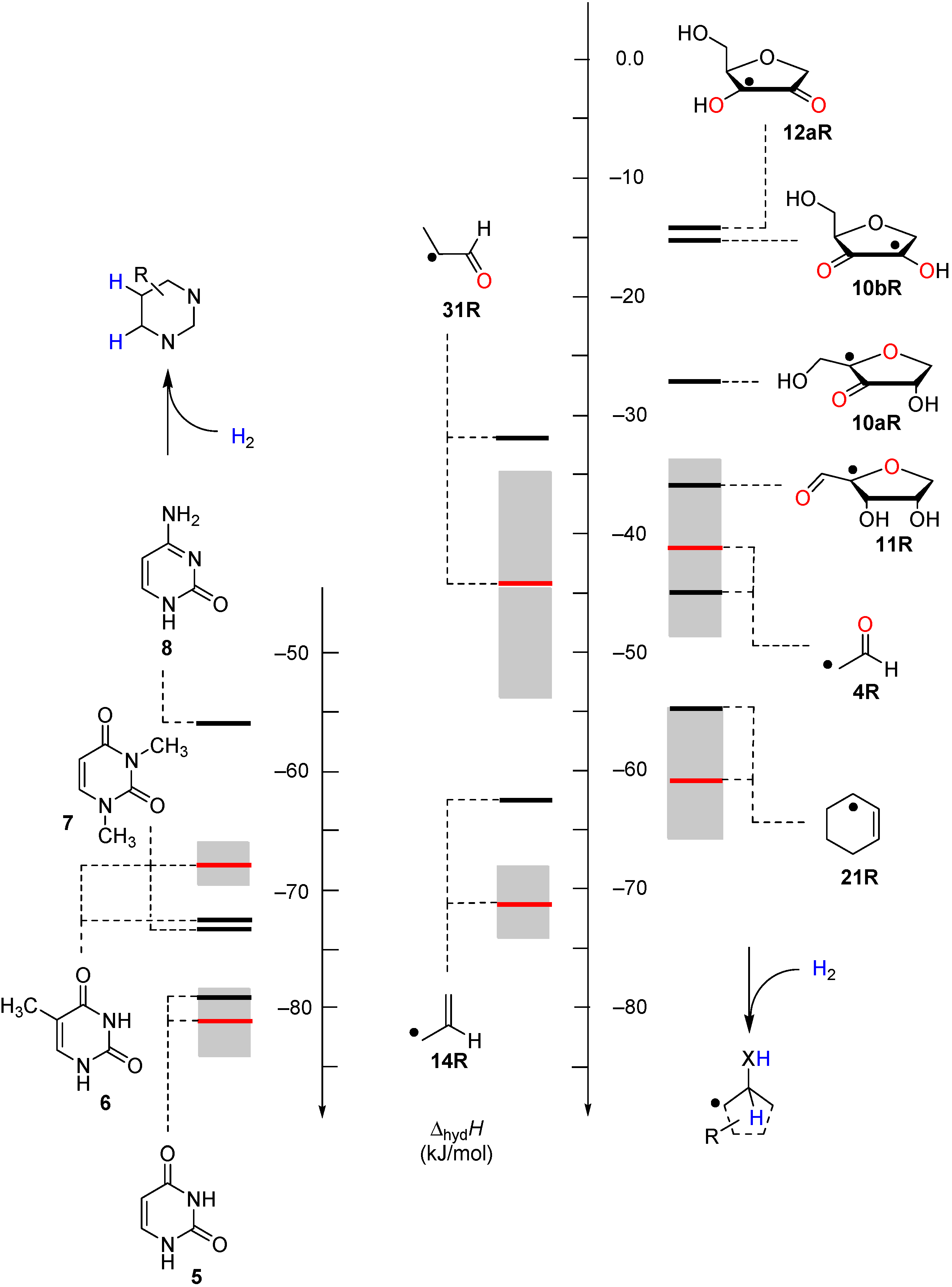
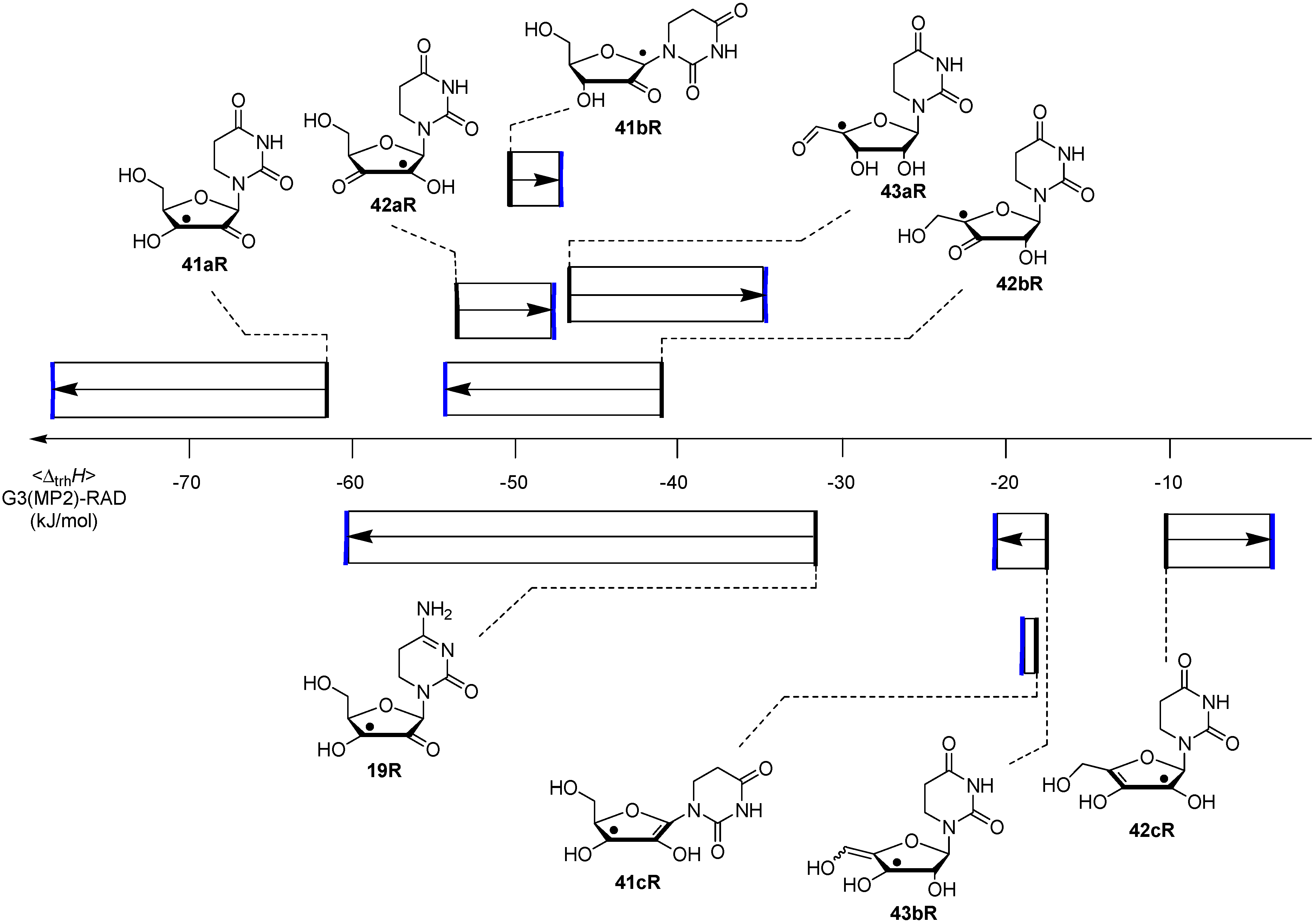
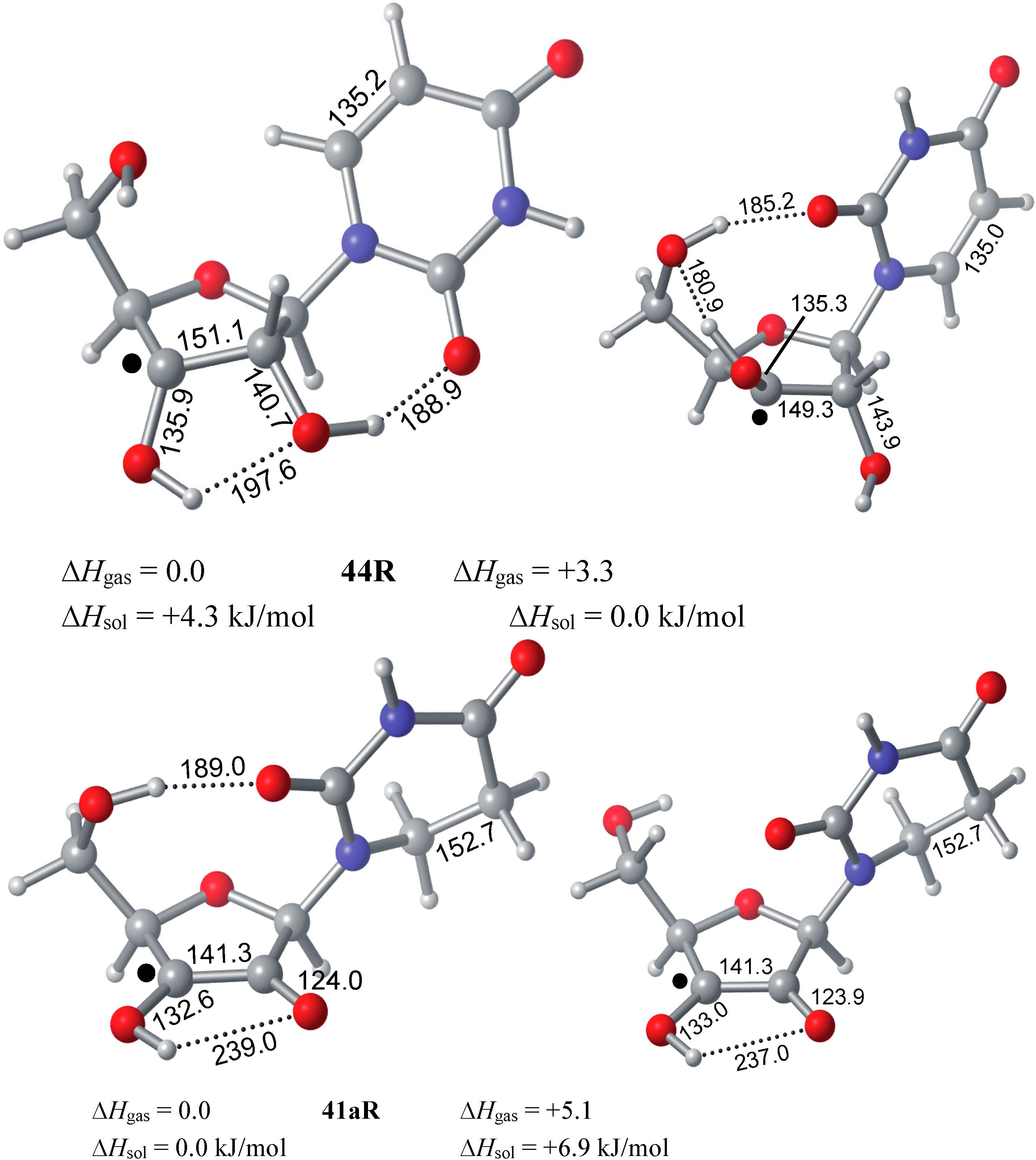
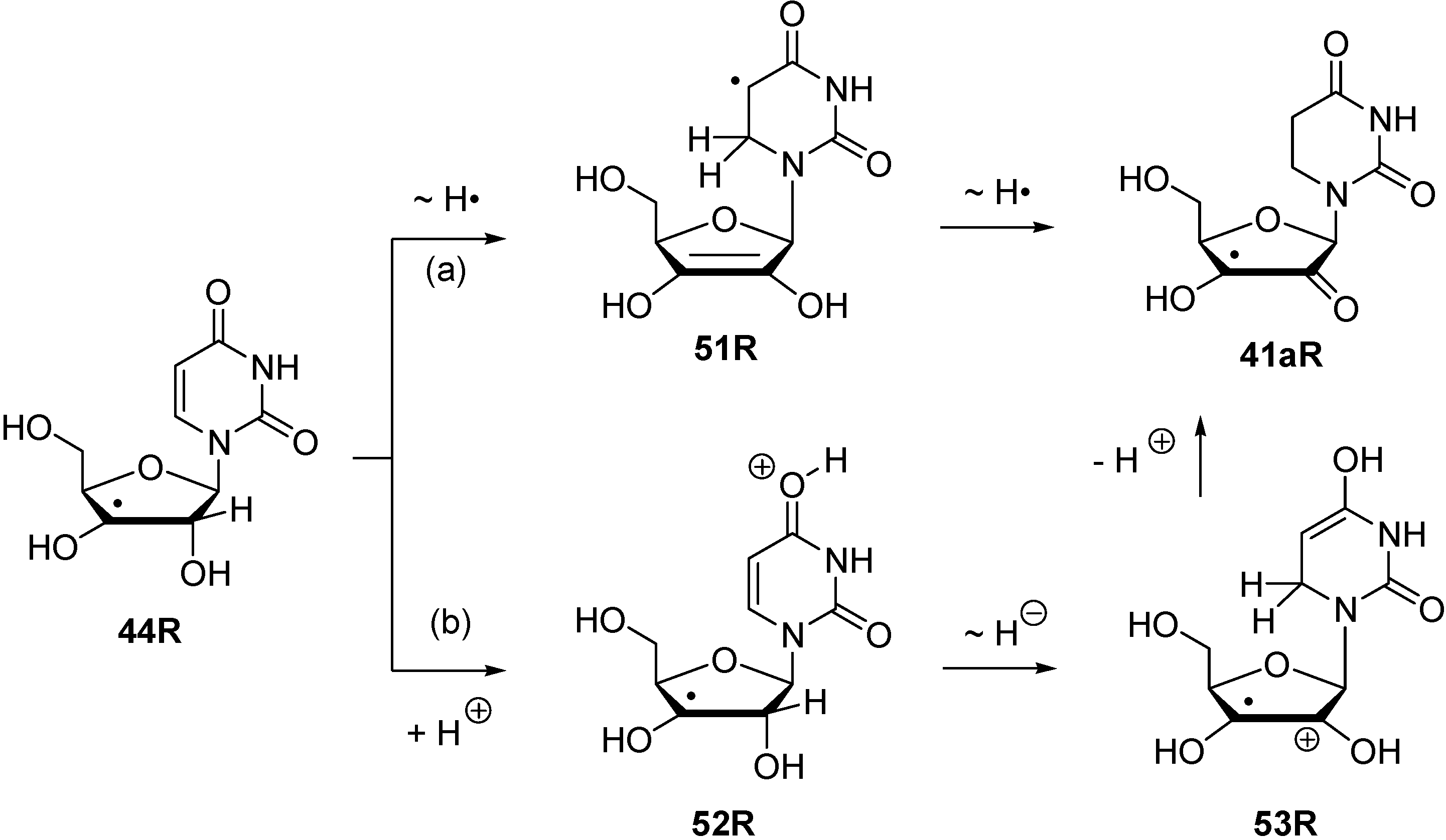
3. Experimental Section
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Johnstone, R.A.W.; Wilby, A.H.; Entwistle, I.D. Heterogenous catalytic transfer hydrogenation and its relations to other methods for reduction of organic compounds. Chem. Rev. 1985, 85, 129–170. [Google Scholar] [CrossRef]
- Gladiali, S.; Alberico, E. Asymmetric transfer hydrogenation: Chiral ligands and applications. Chem. Soc. Rev. 2006, 35, 226–236. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.W.; Hechavarria Fonseca, M.T.; List, B. A Metal-Free Transfer Hydrogenation: Organocatalytic Conjugate Reduction of α,β-Unsaturated Aldehydes. Angew. Chem. Int. Ed. 2004, 43, 6660–6662. [Google Scholar] [CrossRef]
- Ouellet, S.G.; Walji, A.M.; Macmillan, D.W.C. Enantioselective Organocatalytic Transfer Hydrogenation Reactions using Hantzsch Ester. Acc. Chem. Res. 2007, 40, 1327–1339. [Google Scholar] [CrossRef] [PubMed]
- Lide, D.R. CRC Handbook of Chemistry and Physics, 89th ed.; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Henry, D.J.; Sullivan, M.B.; Radom, L. G3-RAD and G3X-RAD: Modified Gaussian-3 (G3) and Gaussian-3X (G3X) procedures for radical thermochemistry. J. Chem. Phys. 2003, 118, 4849–4860. [Google Scholar] [CrossRef]
- Achrainer, F.; Emel’yanenko, V.N.; Tantawy, W.; Verevkin, S.P.; Zipse, H. Transfer Hydrogenation as a Redox Process in Nucleotides. J. Phys. Chem. B 2014, 118, 10426–10429. [Google Scholar] [CrossRef] [PubMed]
- Hioe, J.; Zipse, H. Radical Stability—Thermochemical Aspects. In Encyclopedia of Radicals in Chemistry, Biology and Materials; Chatgilialoglu, C., Studer, A., Eds.; John Wiley & Sons Ltd.: Chichester, UK, 2012; Volume 1, pp. 449–475. [Google Scholar]
- Barnerdes, C.E.S.; Minas da Piedade, M.E.; Amaral, L.M.P.F.; Ferreira, A.I.M.C.L.; Ribeiro da Silva, M.A.V.; Diogo, H.P.; Cabral, B.J.C. Energetics of C-F, C-Cl, C-Br, and C-I Bonds in 2-Haloethanols. Enthalpies of Formation of XCH2CH2OH (X = F, Cl, Br, I) Compounds and of the 2-Hydroxyethyl Radical. J. Phys. Chem. A 2007, 111, 1713–1720. [Google Scholar] [CrossRef] [PubMed]
- Blanksby, S.J.; Ellison, G.B. Bond Dissociation Energies of Organic Molecules. Acc. Chem. Res. 2003, 36, 255–263. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.-R. Comprehensive Handbook of Chemical Bond Energies; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Van der Donk, W.A.; Yu, G.; Silva, D.J.; Stubbe, J.; McCarthy, J.R.; Jarvi, E.T.; Matthews, D.P.; Resvick, R.J.; Wagner, E. Inactivation of Ribonucleotide Reductase by (E)-2′-Fluoromethylene-2'-deoxycytidine 5'-Diphosphate: A Paradigm for Nucleotide Mechanism-Based Inhibitors. Biochemistry 1996, 35, 8381–8391. [Google Scholar] [CrossRef] [PubMed]
- Persson, A.L.; Eriksson, M.; Katterle, B.; Potsch, S.; Sahlin, M.; Sjoberg, B.-M. A New Mechanism-based Radical Intermediate in a Mutant R1 Protein Affecting the Catalytically Essential Glu441 in Escherichia coli Ribonucleotide Reductase. J. Biol. Chem. 1997, 272, 31533–31541. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, C.C.; Bennati, M.; Obias, H.V.; Bar, G.; Griffin, R.G.; Stubbe, J. High-field EPR detection of a disulfide radical anion in the reduction of cytidine 5'-diphosphate by the E441QW R1 mutant. Proc. Natl. Acad. Sci. USA 1999, 96, 8979–8984. [Google Scholar] [CrossRef] [PubMed]
- Zipse, H.; Artin, E.; Wnuk, S.; Lohman, G.J.S.; Martino, D.; Griffin, R.G.; Kacprzak, S.; Kaupp, M.; Hoffman, B.; Bennati, M.; et al. Structure of the Nucleotide Radical Formed during Reaction of CDP/TTP with the E441Q-α2β2 of E. coli Ribonucleotide Reductase. J. Am. Chem. Soc. 2009, 131, 200–211. [Google Scholar] [CrossRef] [PubMed]
- Stubbe, J.; van der Donk, W.A. Protein Radicals in Enzyme Catalysis. Chem. Rev. 1998, 98, 705–762. [Google Scholar] [CrossRef] [PubMed]
- Bennati, M.; Lendzian, F.; Schmittel, M.; Zipse, H. Spectroscopic and Theoretical Approaches for Studying Radical Reactions in Ribonucleotide Reductase. Biol. Chem. 2005, 386, 1007–1022. [Google Scholar] [CrossRef] [PubMed]
- Nordlund, P.; Reichard, P. Ribonucleotide Reductases. Annu. Rev. Biochem. 2006, 75, 681–706. [Google Scholar] [CrossRef] [PubMed]
- Ruszczycky, M.W.; Choi, S.-H.; Mansoorabadi, S.O.; Liu, H.-W. Mechanistic Studies of the Radical S-Adenosyl-l-methionine Enzyme DesII: EPR Characterization of a Radical Intermediate Generated During Its Catalyzed Dehydrogenation of TDP-d-Quinovose. J. Am. Chem. Soc. 2011, 133, 7292–7295. [Google Scholar] [CrossRef] [PubMed]
- Zipse, H. Radical Stability—A Theoretical Perspective. Top. Curr. Chem. 2006, 263, 163–189. [Google Scholar]
- Coote, M.L. Reliable Theoretical Procedures for the Calculation of Electronic-Structure Information in Hydrogen Abstraction Reactions. J. Phys. Chem. A 2004, 108, 3865–3872. [Google Scholar] [CrossRef]
- Scott, A.P.; Radom, L. Harmonic Vibrational Frequencies: An Evaluation of Hartree-Fock, Møller-Plesset, Quadratic Configuration Interaction, Density Functional Theory, and Semiempirical Scale Factors. J. Phys. Chem. 1996, 100, 16502–16513. [Google Scholar] [CrossRef]
- Cox, J.D.; Pilcher, G. Thermochemistry of Organic and Organometallic Compounds; Academic Press: London, UK; New York, NY, USA, 1970. [Google Scholar]
- Kistiakowsky, G.B.; Nickle, A.G. Ethane-ethylene and propane-propylene equilibria. Discuss. Faraday Soc. 1951, 10, 175–187. [Google Scholar] [CrossRef]
- Wiberg, K.B.; Crocker, L.S.; Morgan, K.M. Thermochemical studies of carbonyl compounds 5 Enthalpies of reductions of carbonyl groups. J. Am. Chem. Soc. 1991, 113, 3447–3450. [Google Scholar] [CrossRef]
- Dolliver, M.A.; Gresham, T.L.; Kistiakowsky, G.B.; Smith, E.A.; Vaughan, W.E. Heats of Organic Reactions. VI. Heats of Hydrogenation of Some Oxygen-containing Compounds. J. Am. Chem. Soc. 1938, 60, 440–450. [Google Scholar] [CrossRef]
- Roth, W.R.; Lennartz, H.-W.; Hydrierwärmen, I. Bestimmung von Hydrierwärmen mit einem isothermen Titrationskalorimeter. Chem. Ber. 1980, 113, 1806–1817. [Google Scholar] [CrossRef]
- Rogers, D.W.; Crooks, E.; Dejroongruang, K.J. Enthalpies of hydrogenation of the hexanes. J. Chem. Thermodyn. 1987, 19, 1209–1215. [Google Scholar] [CrossRef]
- Peerboom, R.A.L.; Ingemann, S.; Nibbering, N.M.M.; Liebman, J.F. Proton Affinities and Heats of Formation of the Imines CH2=NH, CH2=NMe and PHCH=NH. J. Chem. Soc. Perkin Trans. 2 1990, 11, 1825–1828. [Google Scholar] [CrossRef]
- Viehe, H.G.; Janousek, Z.; Merenyi, R.; Stella, L. The Captodative Effect. Acc. Chem. Res. 1985, 18, 148–154. [Google Scholar] [CrossRef]
- Lenz, R.; Giese, B. Studies on the Mechanism of Ribonucleotide Reductases. J. Am. Chem. Soc. 1997, 119, 2784–2794. [Google Scholar] [CrossRef]
- Zipse, H. The Influence of Hydrogen Bonding Interactions on the C-H Bond Activation Step in Class 1 Ribonucleotide Reductases. Org. Biomol. Chem. 2003, 1, 692–699. [Google Scholar] [CrossRef] [PubMed]
- Mohr, M.; Zipse, H. C-H Bond Activation In Ribonucleotide Reductases—Do Short Strong Hydrogen Bonds Play a Role? Chem. Eur. J. 1999, 5, 3046–3054. [Google Scholar] [CrossRef]
- Schiemann, O.; Feresin, E.; Carl, T.; Giese, B. 4'-Pivaloyl Substituted Thymidine as a Precursor for the Thymyl Radical: An EPR Spectroscopic Study. ChemPhysChem 2004, 5, 270–274. [Google Scholar] [CrossRef] [PubMed]
- MacroModel 9.7; Schrödinger, LLC: New York, NY, USA, 2009.
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
- Barone, V.; Cossi, M.; Tomasi, J. A new definition of cavities for the computation of solvation free energies by the polarizable continuum model. J. Chem. Phys. 1997, 107, 3210–3221. [Google Scholar] [CrossRef]
- MOLPRO, version 2010.1; A Package of ab initio Programs; University College Cardiff Consultants Limited: Cardiff, UK, 2010.
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 03; Revision D.01; Gaussian, Inc.: Wallingford, CT, USA, 2004. [Google Scholar]
- Sample Availability: Not available.
© 2014 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Achrainer, F.; Zipse, H. Transfer Hydrogenation in Open-Shell Nucleotides — A Theoretical Survey. Molecules 2014, 19, 21489-21505. https://doi.org/10.3390/molecules191221489
Achrainer F, Zipse H. Transfer Hydrogenation in Open-Shell Nucleotides — A Theoretical Survey. Molecules. 2014; 19(12):21489-21505. https://doi.org/10.3390/molecules191221489
Chicago/Turabian StyleAchrainer, Florian, and Hendrik Zipse. 2014. "Transfer Hydrogenation in Open-Shell Nucleotides — A Theoretical Survey" Molecules 19, no. 12: 21489-21505. https://doi.org/10.3390/molecules191221489
APA StyleAchrainer, F., & Zipse, H. (2014). Transfer Hydrogenation in Open-Shell Nucleotides — A Theoretical Survey. Molecules, 19(12), 21489-21505. https://doi.org/10.3390/molecules191221489