Computational Prediction of Blood-Brain Barrier Permeability Using Decision Tree Induction
Abstract
:1. Introduction
2. Results and Discussion
2.1. Data Set
2.2. Chemical Space and Compound Classification
| Parameter | Range of values |
|---|---|
| Molecular weight | 46–1201 Da |
| Partition coefficient (aLogP) | −4.3–2.4 |
| Polar surface area (tPSA) | 3.2–279 Å2 |
| Rotatable bonds count | 0–18 |
| Hydrogen bond acceptor count | 1–23 |
2.3. Descriptors and Modeling
| Paradigm | Splitting criteria | Comment |
|---|---|---|
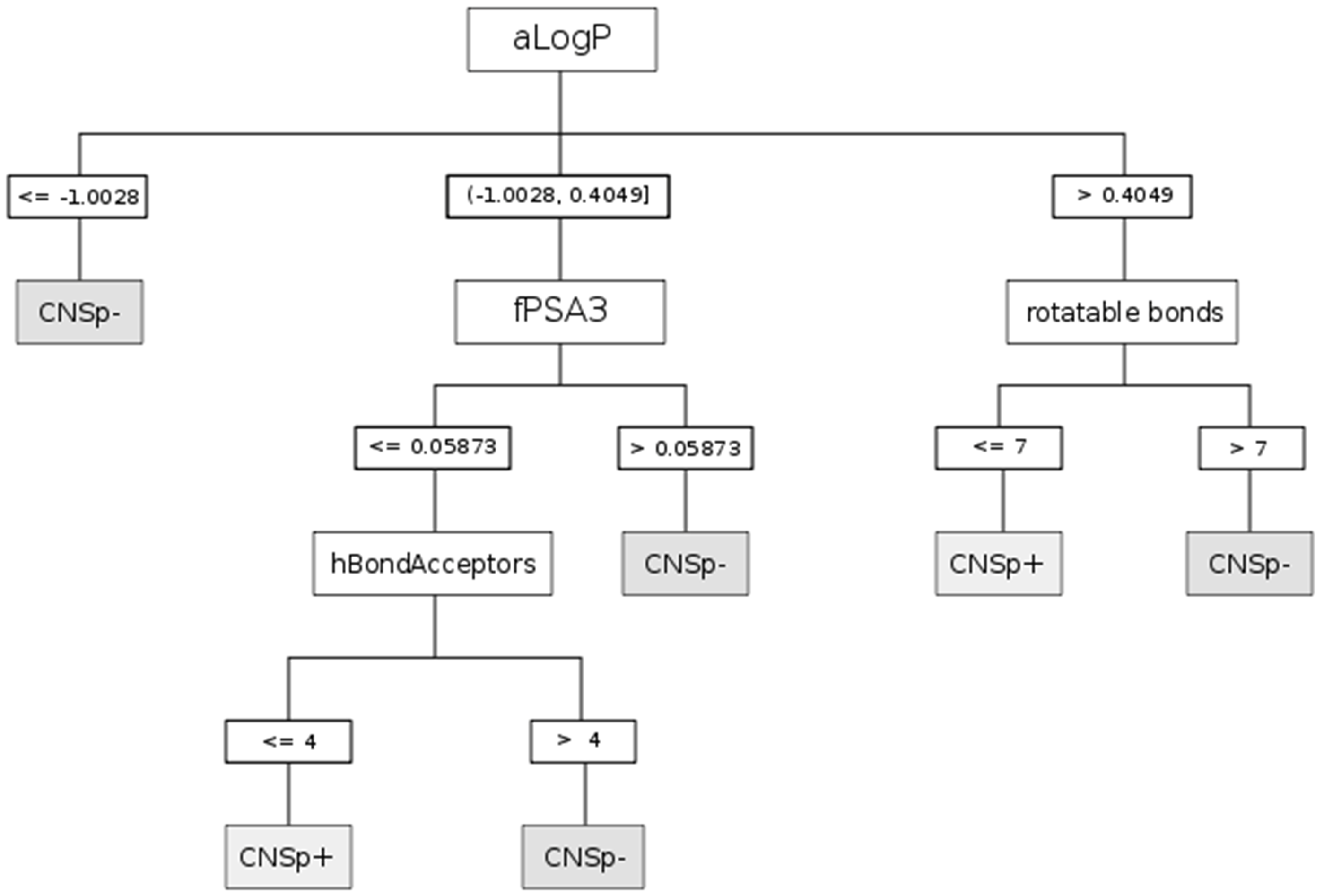
| CHAID | aLogP | Partition coefficient according to Ghoose-Crippen |
| fPSA3 | Charge weighted partial positive surface area/total molecular surface area | |
| hBondAcceptors | Hydrogen bond acceptor count | |
| rotatable bonds | Rotatable bonds count | |
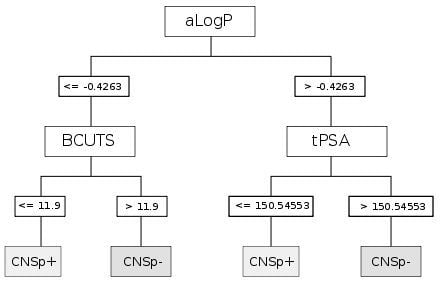
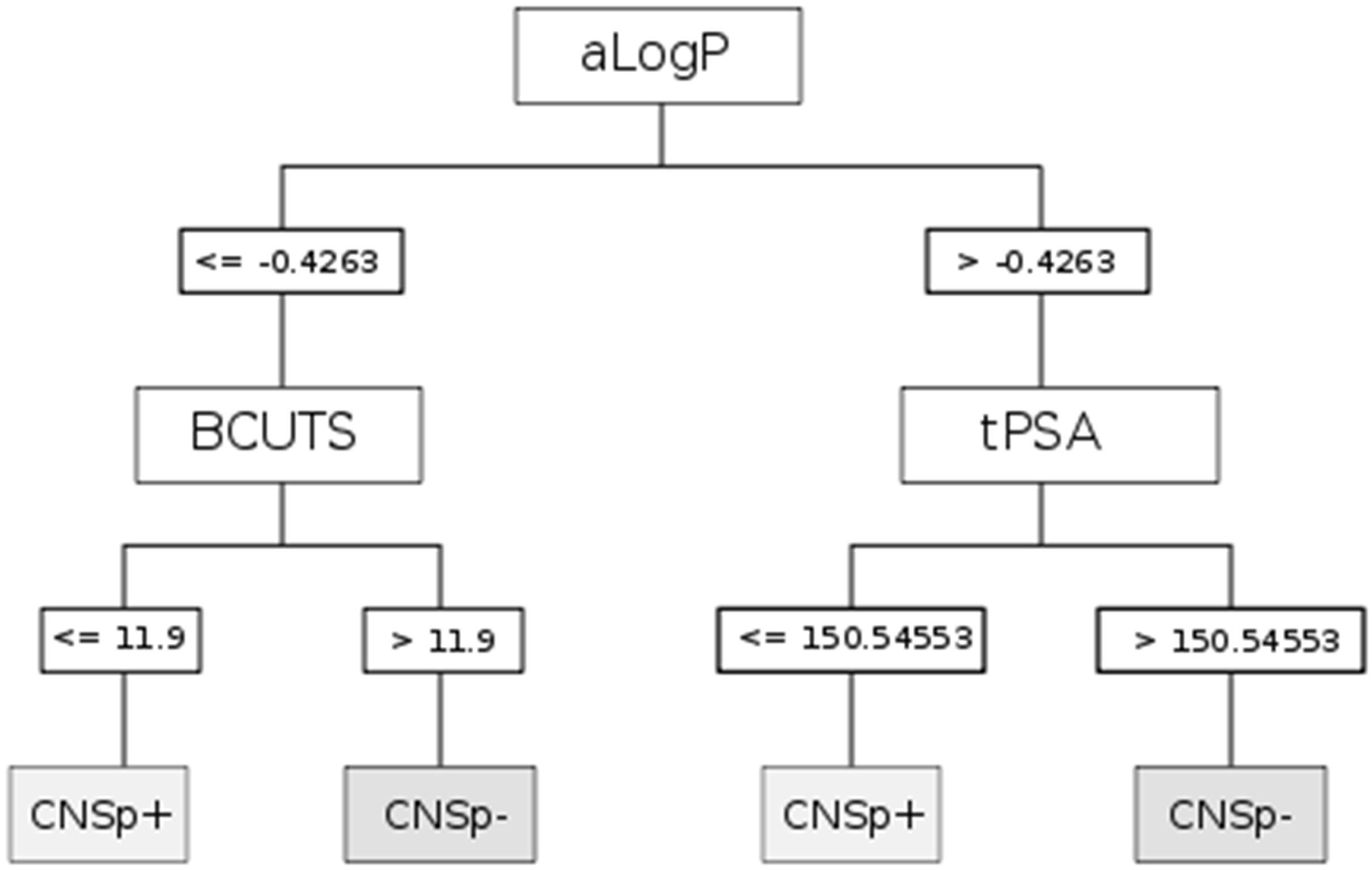
| CART | aLogP | Partition coefficient according to Ghoose-Crippen |
| BCUTS | The number of highest eigenvalue, weighted for the lowest atom | |
| tPSA | Topological polar surface area |
| Chemical structure |  | 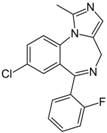 |
|---|---|---|
| Substance | Sucrose | Midazolam |
| Molecular weight | 342.12 Da | 325.08 Da |
| aLogP | −4.3105 | 0.4073 |
| tPSA | 189.53 Å2 | 27.96 Å2 |
| fPSA3 | 0.072136 | 0.033577 |
| Rotatable bonds | 5 | 1 |
| BCUTS | 11.9962 | 11.9974 |
| Prediction (CHAID/CART) | CNSp− | CNSp+ |
2.4. Fragment Based Predictors
| No | Sample Structure | SMARTS | Description |
|---|---|---|---|
| 23 | 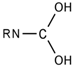 | [#7]~[#6](~[#8])~[#8] | Nitrogen connected to carbon atom, which is connected to two oxygen atoms. |
| 36 | 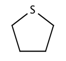 | [#16R] | Any heterocycle containing a sulfur atom. |
| 60 | 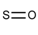 | [#16]=[#8] | Oxygen and sulfur connected by a double bond. |
| 82 | 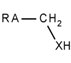 | *~[CH2]~[!#6;!#1;!H0] | Any atom connected to CH2, which is itself connected to a heteroatom with at least one hydrogen atom. |
| 122 | 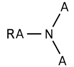 | *~[#7](~*)~* | Any atom connected to nitrogen. Nitrogen has to be connected with any two additional atoms. |
| 130 | 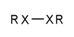 | [!#6;!#1]~[!#6;!#1] | Two heteroatoms connected to each other. |
| 145 | 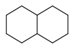 | *1~*~*~*~*~*~1 | Six ring structure, occurring twice in molecule. (They do not have to be directly connected) |
| 150 | 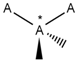 | *!@*@*!@* | One intramolecular chirality center. |
| 156 | 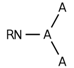 | [#7]~*(~*)~* | Nitrogen connected to any three atoms. |
3. Experimental
3.1. Data Set
3.2. Physicochemical Descriptors
3.3. Chemical Fingerprints
3.4. Decision Tree Induction (DTI)
3.5. Ant Colony Optimization Classification (ACO)
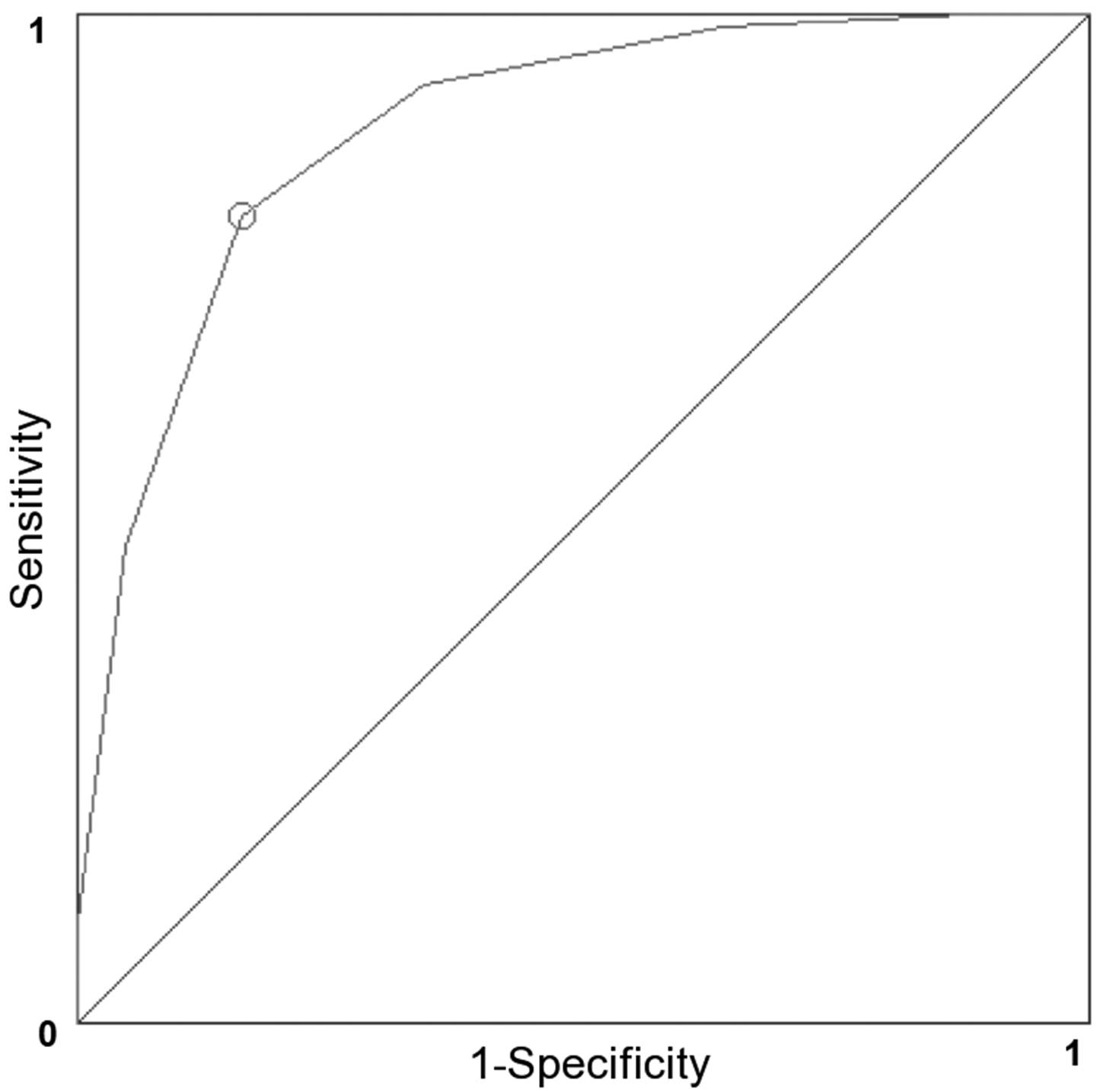
3.6. Validation
3.7. Chemical Similarity
3.8. Quality Measures
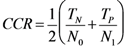
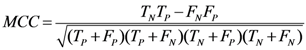
4. Conclusions
Supplementary Materials
Acknowledgements
References
- Takasato, Y.; Rapoport, S.I.; Smith, Q.R. An in situ brain perfusion technique to study cerebrovascular transport in the rat. Am. J. Physiol. 1984, 247, H484–H493. [Google Scholar]
- Triguero, D.; Buciak, J.; Pardridge, W.M. Capillary depletion method for quantification of blood-brain barrier transport of circulating peptides and plasma proteins. J. Neurochem. 1990, 54, 1882–1888. [Google Scholar] [CrossRef]
- Cerletti, A.; Drewe, J.; Fricker, G.; Eberle, A.N.; Huwyler, J. Endocytosis and transcytosis of an immunoliposome-based brain drug delivery system. J. Drug Target. 2000, 8, 435–446. [Google Scholar] [CrossRef]
- Pardridge, W.M. Log(BB), PS products and in silico models of drug brain penetration. Drug Discov. Today 2004, 9, 392–393. [Google Scholar] [CrossRef]
- Abbott, N.J.; Ronnback, L.; Hansson, E. Astrocyte-endothelial interactions at the blood-brain barrier. Nat. Rev. Neurosci. 2006, 7, 41–53. [Google Scholar] [CrossRef]
- Clark, D.E. In silico prediction of blood-brain barrier permeation. Drug Discov. Today 2003, 8, 927–933. [Google Scholar] [CrossRef]
- Platts, J.A.; Abraham, M.H.; Zhao, Y.H.; Hersey, A.; Ijaz, L.; Butina, D. Correlation and prediction of a large blood-brain distribution data set—An LFER study. Eur. J. Med. Chem. 2001, 36, 719–730. [Google Scholar] [CrossRef]
- Lanevskij, K.; Japertas, P.; Didziapetris, R.; Petrauskas, A. Ionization-specific QSAR models of blood-brain penetration of drugs. Chem. Biodivers. 2009, 6, 2050–2054. [Google Scholar] [CrossRef]
- Bendels, S.; Kansy, M.; Wagner, B.; Huwyler, J. In silico prediction of brain and CSF permeation of small molecules using PLS regression models. Eur. J. Med. Chem. 2008, 43, 1581–1592. [Google Scholar] [CrossRef]
- Seddon, A.M.; Casey, D.; Law, R.V.; Gee, A.; Templer, R.H.; Ces, O. Drug interactions with lipid membranes. Chem. Soc. Rev. 2009, 38, 2509–2519. [Google Scholar]
- Pardridge, W.M. CNS drug design based on principles of blood-brain barrier transport. J. Neurochem. 1998, 70, 1781–1792. [Google Scholar] [CrossRef]
- Goodwin, J.T.; Clark, D.E. In silico predictions of blood-brain barrier penetration: Considerations to “keep in mind”. J. Pharmacol. Exp. Ther. 2005, 315, 477–483. [Google Scholar] [CrossRef]
- van Asperen, J.; Schinkel, A.H.; Beijnen, J.H.; Nooijen, W.J.; Borst, P.; van Tellingen, O. Altered pharmacokinetics of vinblastine in Mdr1a P-glycoprotein-deficient Mice. J. Natl. Cancer Inst. 1996, 88, 994–999. [Google Scholar] [CrossRef]
- Schinkel, A.H.; Wagenaar, E.; van Deemter, L.; Mol, C.A.; Borst, P. Absence of the mdr1a P-Glycoprotein in mice affects tissue distribution and pharmacokinetics of dexamethasone, digoxin, and cyclosporin A. J. Clin. Invest. 1995, 96, 1698–1705. [Google Scholar] [CrossRef]
- Cordon-Cardo, C.; O’Brien, J.P.; Casals, D.; Rittman-Grauer, L.; Biedler, J.L.; Melamed, M.R.; Bertino, J.R. Multidrug-resistance gene (P-glycoprotein) is expressed by endothelial cells at blood-brain barrier sites. Proc. Natl. Acad. Sci. USA 1989, 86, 695–698. [Google Scholar]
- Schinkel, A.H.; Jonker, J.W. Mammalian drug efflux transporters of the ATP binding cassette (ABC) family: An overview. Adv. Drug Deliv. Rev. 2003, 55, 3–29. [Google Scholar] [CrossRef]
- Poller, B.; Drewe, J.; Krahenbuhl, S.; Huwyler, J.; Gutmann, H. Regulation of BCRP (ABCG2) and P-glycoprotein (ABCB1) by cytokines in a model of the human blood-brain barrier. Cell. Mol. Neurobiol. 2010, 30, 63–70. [Google Scholar] [CrossRef]
- Cooray, H.C.; Blackmore, C.G.; Maskell, L.; Barrand, M.A. Localisation of breast cancer resistance protein in microvessel endothelium of human brain. Neuroreport 2002, 13, 2059–2063. [Google Scholar] [CrossRef]
- Schwab, D.; Fischer, H.; Tabatabaei, A.; Poli, S.; Huwyler, J. Comparison of in vitro P-glycoprotein screening assays: Recommendations for their use in drug discovery. J. Med. Chem. 2003, 46, 1716–1725. [Google Scholar] [CrossRef]
- Dauchy, S.; Dutheil, F.; Weaver, R.J.; Chassoux, F.; Daumas-Duport, C.; Couraud, P.O.; Scherrmann, J.M.; de Waziers, I.; Decleves, X. ABC transporters, cytochromes P450 and their main transcription factors: Expression at the human blood-brain barrier. J. Neurochem. 2008, 107, 1518–1528. [Google Scholar] [CrossRef]
- Lin, J.H.; Yamazaki, M. Clinical relevance of P-glycoprotein in drug therapy. Drug Metab. Rev. 2003, 35, 417–454. [Google Scholar] [CrossRef]
- Kelder, J.; Grootenhuis, P.D.; Bayada, D.M.; Delbressine, L.P.; Ploemen, J.P. Polar molecular surface as a dominating determinant for oral absorption and brain penetration of drugs. Pharm. Res. 1999, 16, 1514–1519. [Google Scholar] [CrossRef]
- Mahar Doan, K.M.; Humphreys, J.E.; Webster, L.O.; Wring, S.A.; Shampine, L.J.; Serabjit-Singh, C.J.; Adkison, K.K.; Polli, J.W. Passive permeability and P-glycoprotein-mediated efflux differentiate central nervous system (CNS) and non-CNS marketed drugs. J. Pharmacol. Exp. Ther. 2002, 303, 1029–1037. [Google Scholar] [CrossRef]
- Norinder, U.; Haeberlein, M. Computational approaches to the prediction of the blood-brain distribution. Adv. Drug Deliv. Rev. 2002, 54, 291–313. [Google Scholar] [CrossRef]
- Katritzky, A.R.; Kuanar, M.; Slavov, S.; Dobchev, D.A.; Fara, D.C.; Karelson, M.; Acree, W.E., Jr.; Solov’ev, V.P.; Varnek, A. Correlation of blood-brain penetration using structural descriptors. Bioorg. Med. Chem. 2006, 14, 4888–4917. [Google Scholar]
- Hammann, F.; Drewe, J. Decision tree models for data mining in hit discovery. Expert Opin. Drug Discov. 2012, 7, 341–352. [Google Scholar] [CrossRef]
- Pardridge, W.M. Transport of small molecules through the blood-brain barrier: Biology and methodology. Adv. Drug Deliv. Rev. 1995, 15, 5–36. [Google Scholar] [CrossRef]
- Dagenais, C.; Avdeef, A.; Tsinman, O.; Dudley, A.; Beliveau, R. P-glycoprotein deficient mouse in situ blood-brain barrier permeability and its prediction using an in combo PAMPA model. Eur. J. Pharm. Sci. 2009, 38, 121–137. [Google Scholar] [CrossRef]
- Dagenais, C.; Rousselle, C.; Pollack, G.M.; Scherrmann, J.M. Development of an in situ mouse brain perfusion model and its application to mdr1a P-glycoprotein-deficient mice. J. Cereb. Blood Flow Metab. 2000, 20, 381–386. [Google Scholar]
- Hammann, F.; Gutmann, H.; Jecklin, U.; Maunz, A.; Helma, C.; Drewe, J. Development of decision tree models for substrates, inhibitors, and inducers of P-glycoprotein. Curr. Drug Metab. 2009, 10, 339–346. [Google Scholar] [CrossRef]
- Clark, D.E. Rapid calculation of polar molecular surface area and its application to the prediction of transport phenomena. 2. Prediction of blood-brain barrier penetration. J. Pharm. Sci. 1999, 88, 815–821. [Google Scholar]
- Pardridge, W.M.; Triguero, D.; Yang, J.; Cancilla, P.A. Comparison of in vitro and in vivo models of drug transcytosis through the blood-brain barrier. J. Pharmacol. Exp. Ther. 1990, 253, 884–891. [Google Scholar]
- Smith, Q.R.; Takasato, Y. Kinetics of amino acid transport at the blood-brain barrier studied using an in situ brain perfusion technique. Ann. NY Acad. Sci. 1986, 481, 186–201. [Google Scholar] [CrossRef]
- Greig, N.H.; Momma, S.; Sweeney, D.J.; Smith, Q.R.; Rapoport, S.I. Facilitated transport of melphalan at the rat blood-brain barrier by the large neutral amino acid carrier system. Cancer Res. 1987, 47, 1571–1576. [Google Scholar]
- Momma, S.; Aoyagi, M.; Rapoport, S.I.; Smith, Q.R. Phenylalanine transport across the blood-brain barrier as studied with the in situ brain perfusion technique. J. Neurochem. 1987, 48, 1291–1300. [Google Scholar] [CrossRef]
- Levin, V.A. Relationship of octanol/water partition coefficient and molecular weight to rat brain capillary permeability. J. Med. Chem. 1980, 23, 682–684. [Google Scholar] [CrossRef]
- Gratton, J.A.; Abraham, M.H.; Bradbury, M.W.; Chadha, H.S. Molecular factors influencing drug transfer across the blood-brain barrier. J. Pharm. Pharmacol. 1997, 49, 1211–1216. [Google Scholar]
- Tamai, I.; Yamashita, J.; Kido, Y.; Ohnari, A.; Sai, Y.; Shima, Y.; Naruhashi, K.; Koizumi, S.; Tsuji, A. Limited distribution of new quinolone antibacterial agents into brain caused by multiple efflux transporters at the blood-brain barrier. J. Pharmacol. Exp. Ther. 2000, 295, 146–152. [Google Scholar]
- Murakami, H.; Takanaga, H.; Matsuo, H.; Ohtani, H.; Sawada, Y. Comparison of blood-brain barrier permeability in mice and rats using in situ brain perfusion technique. Am. J. Physiol. Heart Circ. Physiol. 2000, 279, H1022–H1028. [Google Scholar]
- Liu, X.; Tu, M.; Kelly, R.S.; Chen, C.; Smith, B.J. Development of a computational approach to predict blood-brain barrier permeability. Drug Metab. Dispos. 2004, 32, 132–139. [Google Scholar] [CrossRef]
- Youdim, K.A.; Qaiser, M.Z.; Begley, D.J.; Rice-Evans, C.A.; Abbott, N.J. Flavonoid permeability across an in situ model of the blood-brain barrier. Free Radic. Biol. Med. 2004, 36, 592–604. [Google Scholar] [CrossRef]
- Parepally, J.M.; Mandula, H.; Smith, Q.R. Brain uptake of nonsteroidal anti-inflammatory drugs: Ibuprofen, flurbiprofen, and indomethacin. Pharm. Res. 2006, 23, 873–881. [Google Scholar] [CrossRef]
- Summerfield, S.G.; Read, K.; Begley, D.J.; Obradovic, T.; Hidalgo, I.J.; Coggon, S.; Lewis, A.V.; Porter, R.A.; Jeffrey, P. Central nervous system drug disposition: The relationship between in situ brain permeability and brain free fraction. J. Pharmacol. Exp. Ther. 2007, 322, 205–213. [Google Scholar] [CrossRef]
- Lanevskij, K.; Japertas, P.; Didziapetris, R.; Petrauskas, A. Ionization-specific prediction of blood-brain permeability. J. Pharm. Sci. 2009, 98, 122–134. [Google Scholar] [CrossRef]
- Schinkel, A.H.; Wagenaar, E.; Mol, C.A.; van Deemter, L. P-glycoprotein in the blood-brain barrier of mice influences the brain penetration and pharmacological activity of many drugs. J. Clin. Invest. 1996, 97, 2517–2524. [Google Scholar] [CrossRef]
- Fischer, H.; Gottschlich, R.; Seelig, A. Blood-brain barrier permeation: Molecular parameters governing passive diffusion. J. Membr. Biol. 1998, 165, 201–211. [Google Scholar] [CrossRef]
- Wang, X.; Ratnaraj, N.; Patsalos, P.N. The pharmacokinetic inter-relationship of tiagabine in blood, cerebrospinal fluid and brain extracellular fluid (frontal cortex and hippocampus). Seizure 2004, 13, 574–581. [Google Scholar] [CrossRef]
- Sonquist, J.A.; Morgan, J.N. The Detection of Interaction Effects : A Report on a Computer Program for the Selection of Optimal combiNations of Explanatory Variables; Survey research center, University of Michigan: Ann Arbor, MI, USA, 1964. [Google Scholar]
- Breiman, L. Classification and Regression Trees; Chapman & Hall/CRC: Boca Raton, FL, USA, 1984. [Google Scholar]
- van de Waterbeemd, H.; Camenisch, G.; Folkers, G.; Chretien, J.R.; Raevsky, O.A. Estimation of blood-brain barrier crossing of drugs using molecular size and shape, and H-bonding descriptors. J. Drug Target. 1998, 6, 151–165. [Google Scholar] [CrossRef]
- Waterhouse, R.N. Determination of lipophilicity and its use as a predictor of blood-brain barrier penetration of molecular imaging agents. Mol. Imaging Biol. 2003, 5, 376–389. [Google Scholar] [CrossRef]
- Pardridge, W.M. The blood-brain barrier: Bottleneck in brain drug development. NeuroRx 2005, 2, 3–14. [Google Scholar] [CrossRef]
- Wang, R.B.; Kuo, C.L.; Lien, L.L.; Lien, E.J. Structure-activity relationship: Analyses of P-glycoprotein substrates and inhibitors. J. Clin. Pharm. Ther. 2003, 28, 203–228. [Google Scholar] [CrossRef]
- Iyer, M.; Tseng, Y.J.; Senese, C.L.; Liu, J.; Hopfinger, A.J. Prediction and mechanistic interpretation of human oral drug absorption using MI-QSAR analysis. Mol. Pharm. 2007, 4, 218–231. [Google Scholar] [CrossRef]
- Huang, J.; Ma, G.; Muhammad, I.; Cheng, Y. Identifying P-glycoprotein substrates using a support vector machine optimized by a particle swarm. J. Chem. Inf. Model. 2007, 47, 1638–1647. [Google Scholar] [CrossRef]
- Hammann, F.; Gutmann, H.; Vogt, N.; Helma, C.; Drewe, J. Prediction of adverse drug reactions using decision tree modeling. Clin. Pharmacol. Ther. 2010, 88, 52–59. [Google Scholar] [CrossRef]
- Suenderhauf, C.; Hammann, F.; Maunz, A.; Helma, C.; Huwyler, J. Combinatorial QSAR modeling of human intestinal absorption. Mol. Pharm. 2011, 8, 213–224. [Google Scholar] [CrossRef]
- Didziapetris, R.; Japertas, P.; Avdeef, A.; Petrauskas, A. Classification analysis of P-glycoprotein substrate specificity. J. Drug Target. 2003, 11, 391–406. [Google Scholar] [CrossRef]
- Abraham, M.H. The factors that influence permeation across the blood-brain barrier. Eur. J. Med. Chem. 2004, 39, 235–240. [Google Scholar] [CrossRef]
- Muehlbacher, M.; Spitzer, G.M.; Liedl, K.R.; Kornhuber, J. Qualitative prediction of blood-brain barrier permeability on a large and refined dataset. J. Comput. Aided Mol. Des. 2011, 25, 1095–1106. [Google Scholar]
- Hammann, F.; Suenderhauf, C.; Huwyler, J. A binary ant colony optimization classifier for molecular activities. J. Chem. Inf. Model. 2011, 51, 2690–2696. [Google Scholar] [CrossRef]
- Bonabeau, E.; Dorigo, M.; Theraulaz, G. Inspiration for optimization from social insect behaviour. Nature 2000, 406, 39–42. [Google Scholar]
- Pham, Y.T.; Nosten, F.; Farinotti, R.; White, N.J.; Gimenez, F. Cerebral uptake of mefloquine enantiomers in fatal cerebral malaria. Int. J. Clin. Pharmacol. Ther. 1999, 37, 58–61. [Google Scholar]
- Strolin Benedetti, M.; Frigerio, E.; Tocchetti, P.; Brianceschi, G.; Castelli, M.G.; Pellizzoni, C.; Dostert, P. Stereoselective and species-dependent kinetics of reboxetine in mouse and rat. Chirality 1995, 7, 285–289. [Google Scholar] [CrossRef]
- Hassinen, T.; Peräkylä, M. New Energy Terms for Reduced Protein Models Implemented in an Off-Lattice Force Field. J. Comput. Chem. 2001, 22, 1229–1242. [Google Scholar] [CrossRef]
- Steinbeck, C.; Han, Y.; Kuhn, S.; Horlacher, O.; Luttmann, E.; Willighagen, E. The Chemistry Development Kit (CDK): An open-source Java library for Chemo- and Bioinformatics. J. Chem. Inf. Comput. Sci. 2003, 43, 493–500. [Google Scholar] [CrossRef]
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An open chemical toolbox. J. Cheminform. 2011, 3, 33. [Google Scholar]
- Gini, C. Memorie di metodologica statistica (Reprint of: Variabilità e mutabilità); Libreria Eredi Virgilio Veschi: Rome, Italy, 1955; p. 156. [Google Scholar]
- Youden, W.J. Index for Rating Diagnostic Tests. Cancer 1950, 3, 32–35. [Google Scholar] [CrossRef]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach, 2nd ed; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Tropsha, A. Best Practices for QSAR Model Development, Validation, and Exploitation. Mol. Inf. 2010, 29, 476–488. [Google Scholar] [CrossRef]
- Willett, P. Similarity-based virtual screening using 2D fingerprints. Drug Discov. Today 2006, 11, 1046–1053. [Google Scholar] [CrossRef]
- Sample Availability: Not available.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Suenderhauf, C.; Hammann, F.; Huwyler, J. Computational Prediction of Blood-Brain Barrier Permeability Using Decision Tree Induction. Molecules 2012, 17, 10429-10445. https://doi.org/10.3390/molecules170910429
Suenderhauf C, Hammann F, Huwyler J. Computational Prediction of Blood-Brain Barrier Permeability Using Decision Tree Induction. Molecules. 2012; 17(9):10429-10445. https://doi.org/10.3390/molecules170910429
Chicago/Turabian StyleSuenderhauf, Claudia, Felix Hammann, and Jörg Huwyler. 2012. "Computational Prediction of Blood-Brain Barrier Permeability Using Decision Tree Induction" Molecules 17, no. 9: 10429-10445. https://doi.org/10.3390/molecules170910429
APA StyleSuenderhauf, C., Hammann, F., & Huwyler, J. (2012). Computational Prediction of Blood-Brain Barrier Permeability Using Decision Tree Induction. Molecules, 17(9), 10429-10445. https://doi.org/10.3390/molecules170910429