QSPR Models for Predicting Log Pliver Values for Volatile Organic Compounds Combining Statistical Methods and Domain Knowledge
Abstract
:1. Introduction
2. Results and Discussion
2.1. Dataset and Calculation of the Molecular Descriptors
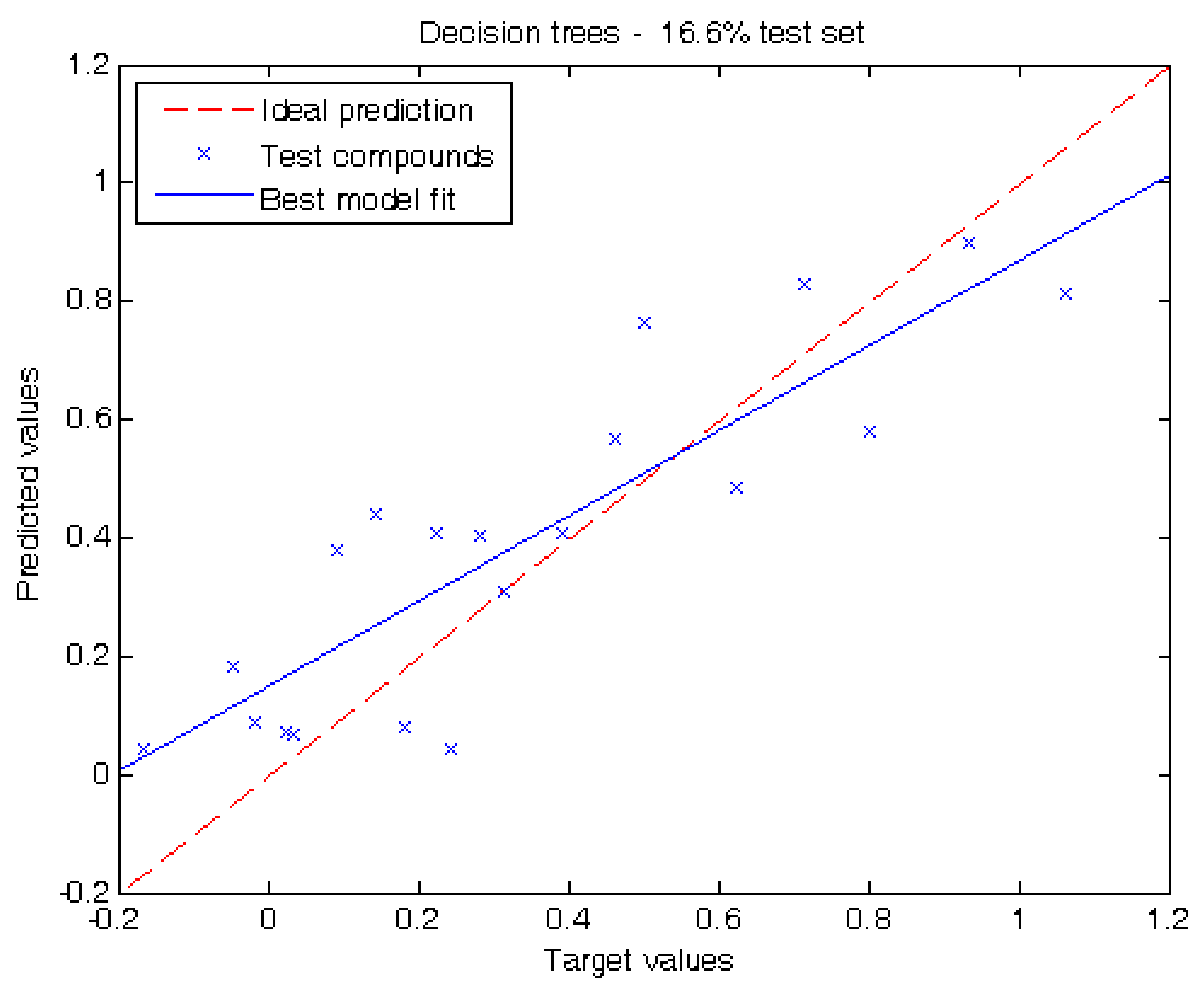
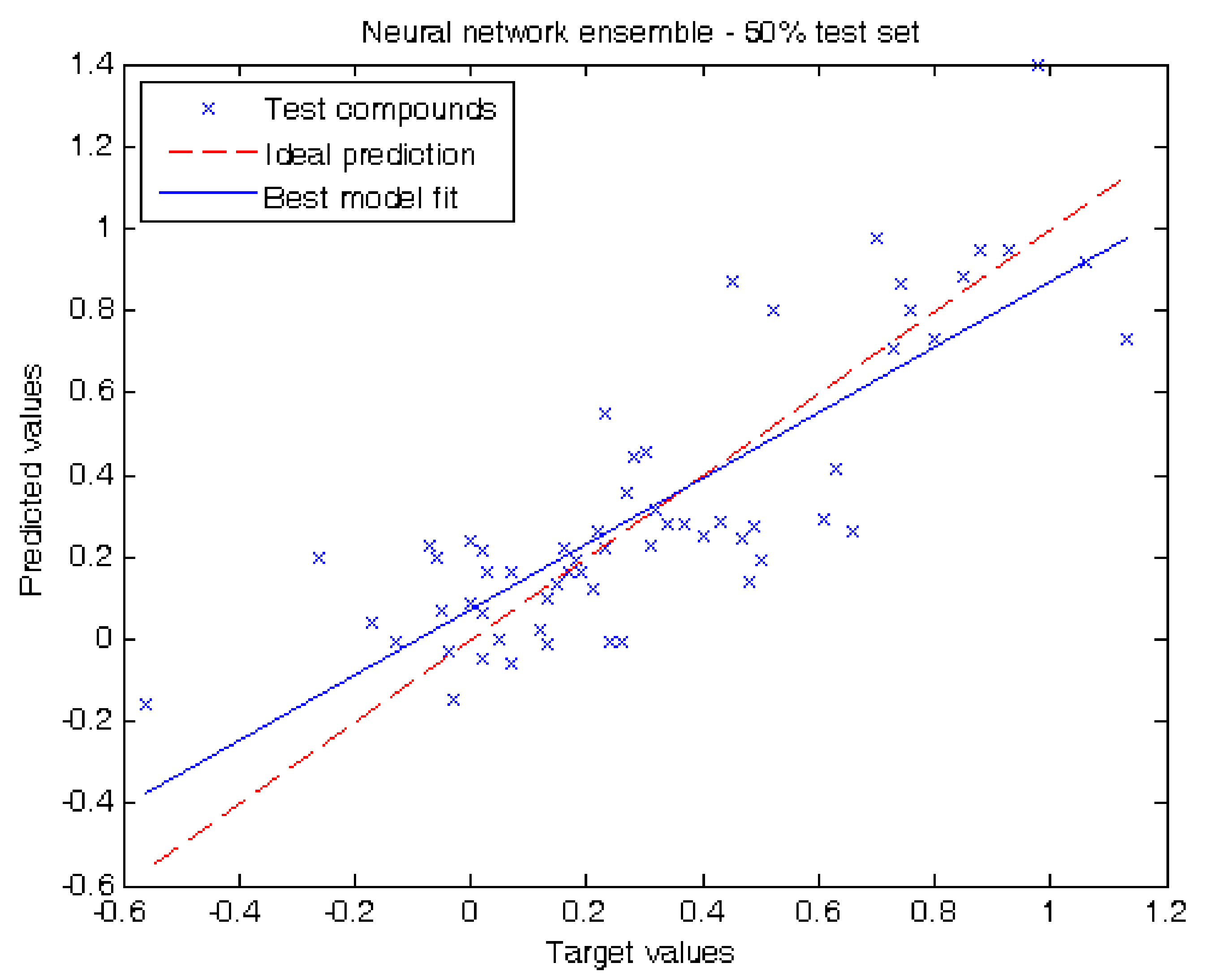
2.2. Performance of Our Model
3. Computational Methods and Experiments
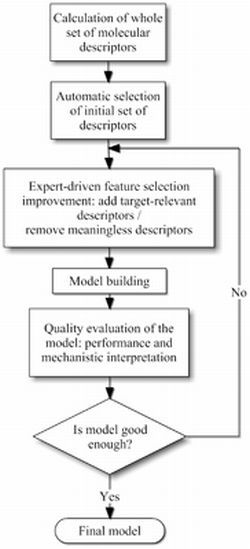
3.1. Molecular Descriptor Selection
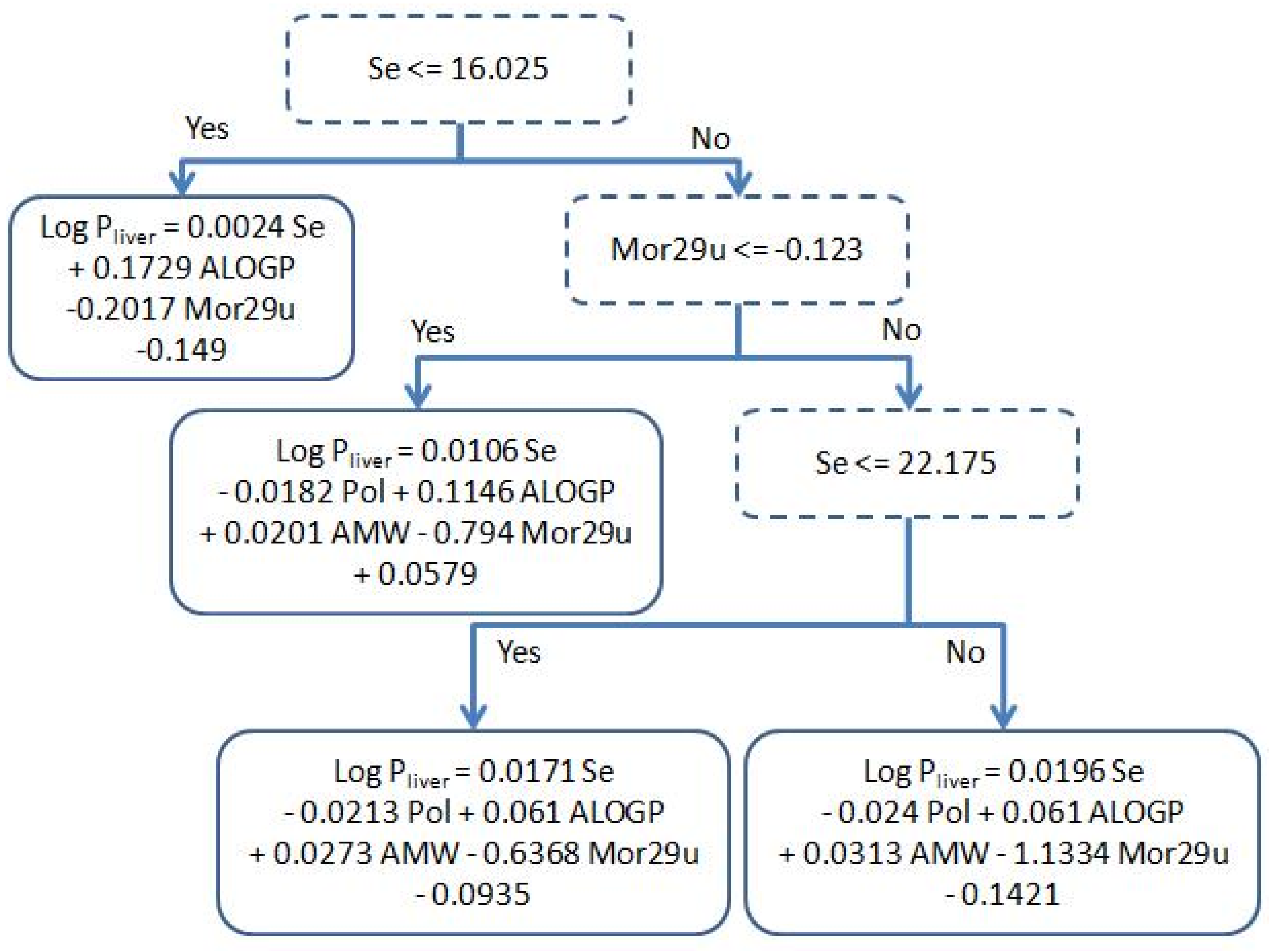
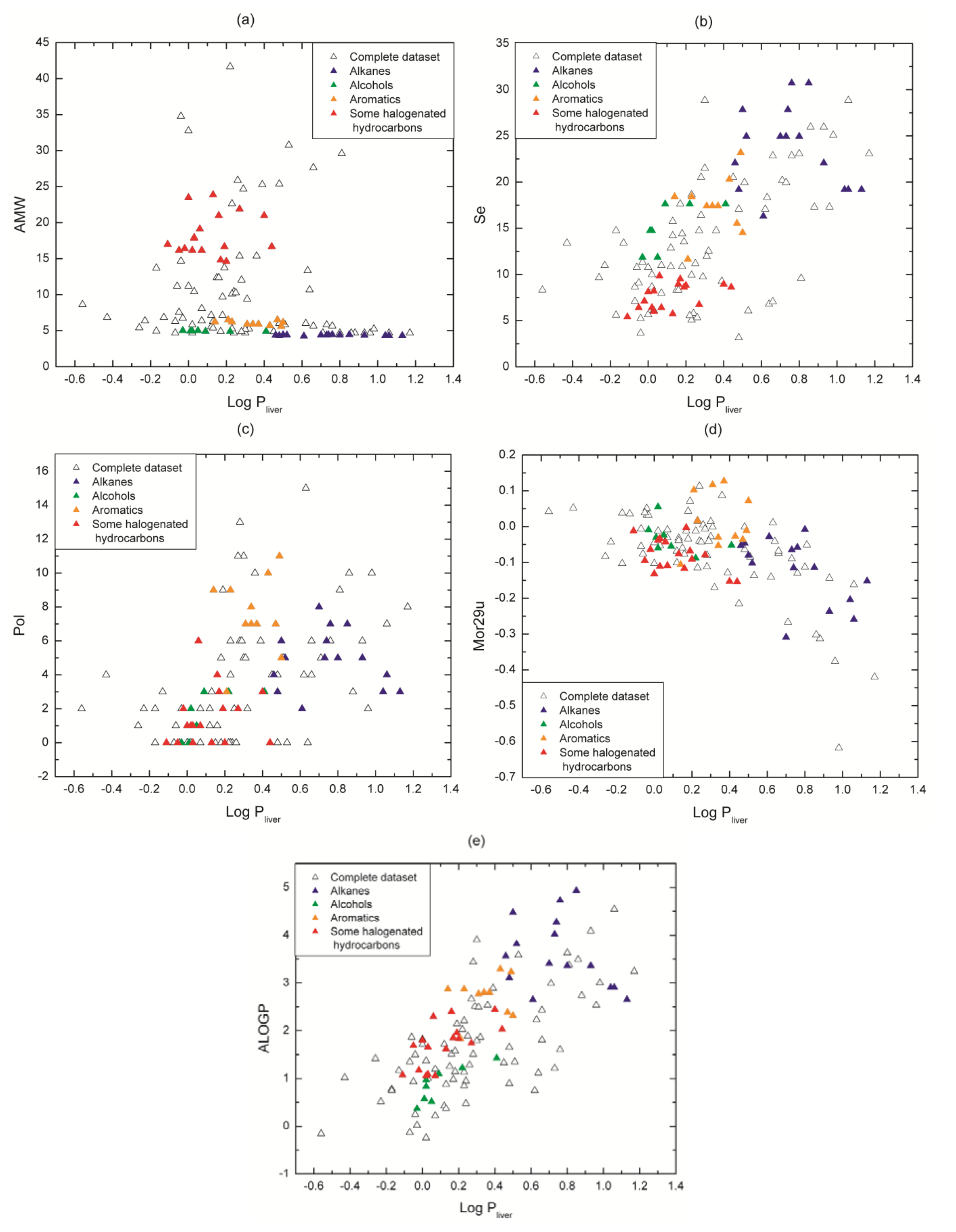
3.2. Physicochemical Relevance of Molecular Descriptors
3.3. Regression Algorithms
4. Conclusions
Supplementary Materials
Acknowledgments
References
- Vallero, D. Fundamentals of Air Pollution, 4th ed.; Academic Press: San Diego, CA, USA, 2008. [Google Scholar]
- Williams, J.; Koppmann, R. Volatile Organic Compounds in the Atmosphere: An Overview. In Volatile Organic Compounds in the Atmosphere; Koppmann, R., Ed.; Blackwell Publishing Ltd.: Oxford, UK, 2007. [Google Scholar]
- Woodruff, T.J.; Burke, T.A.; Zeise, L. The Need for Better Public Health Decisions on Chemicals Released Into Our Environment. Health Aff. 2011, 30, 957–967. [Google Scholar] [CrossRef] [PubMed]
- Tronde, A. Pulmonary Drug Absorption. In Vitro and In Vivo Investigations of Drug Absorption Across the Lung Barrier and Its Relation to Drug Physicochemical Properties. Ph.D. Thesis, Uppsala University, Uppsala, Sweden, 2002. [Google Scholar]
- Katritzky, A.R.; Kuanar, M.; Fara, D.C.; Karelson, M.; Acree, W.E., Jr.; Solov’ev, V.P.; Varnek, A. QSAR modeling of blood:air and tissue:air partition coefficients using theoretical descriptors. Bioorg. Med. Chem. 2005, 13, 6450–6463. [Google Scholar] [CrossRef] [PubMed]
- Dashtbozorgi, Z.; Golmohammadi, H. Prediction of air to liver partition coefficient for volatile organic compounds using QSAR approaches. Eur. J. Med. Chem. 2010, 45, 2182–2190. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.H.; Ibrahim, A.; Acree, W.E., Jr. Air to liver partition coefficients for volatile organic compounds and blood to liver partition coefficients for volatile organic compounds and drugs. Eur. J. Med. Chem. 2007, 42, 743–751. [Google Scholar] [CrossRef] [PubMed]
- Abraham, M.H.; Weathersby, P.K. Hydrogen bonding. 30. Solubility of gases and vapors in biological liquids and tissues. J. Pharm. Sci. 1994, 83, 1450–1456. [Google Scholar] [CrossRef] [PubMed]
- Balaz, S.; Luckacova, V. A Model-based Dependence of the Human Tissue/Blood Partition Coefficients of Chemicals on Lipophilicity and Tissue Composition. Quant. Struct.-Act. Rel. 1999, 18, 361–368. [Google Scholar] [CrossRef]
- Poulin, P.; Theil, F.P. Prediction of pharmacokinetics prior to In Vivo studies. II. Generic physiologically based pharmacokinetic models of drug disposition. J. Pharm. Sci. 2002, 91, 1358–1370. [Google Scholar] [CrossRef] [PubMed]
- Poulin, P.; Theil, F.P. A priori prediction of tissue:plasma partition coefficients of drugs to facilitate the use of physiologically-based pharmacokinetic models in drug discovery. J. Pharm. Sci. 2000, 89, 16–35. [Google Scholar] [CrossRef]
- Zhang, H. A new nonlinear equation for the tissue/blood partition coefficients of neutral compounds. J. Pharm. Sci. 2004, 93, 1595–1604. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.X.; Yao, X.J.; Zhang, R.S.; Liu, M.C.; Hu, Z.D.; Fan, B.T. Prediction of the tissue/blood partition coefficients of organic compounds based on the molecular structure using least-squares support vector machines. J. Comput. Aid. Mol. Des. 2005, 19, 499–508. [Google Scholar] [CrossRef] [PubMed]
- Rodgers, T.; Leahy, D.; Rowland, M. Physiologically based pharmacokinetic modeling 1: Predicting the tissue distribution of moderate-to-strong bases. J. Pharm. Sci. 2005, 94, 1259–1276. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Zhang, Y. Convenient Nonlinear Model for Predicting the Tissue/Blood Partition Coefficients of Seven Human Tissues of Neutral, Acidic, and Basic Structurally Diverse Compounds. J. Med. Chem. 2006, 49, 5815–5829. [Google Scholar] [CrossRef] [PubMed]
- Martín-Biosca, Y.; Torres-Cartas, S.; Villanueva-Camañas, R.M.; Sagrado, S.; Medina-Hernández, M.J. Biopartitioning micellar chromatography to predict blood to lung, blood to liver, blood to fat and blood to skin partition coefficients of drugs. Anal. Chim. Acta 2009, 632, 296–303. [Google Scholar] [CrossRef] [PubMed]
- HyperChemTM, Molecular Modeling System, Release 8.0.7 for Windows; Hypercube, Inc.: Gainesville, FL, USA, 2009.
- DRAGON for Windows (Software for Molecular Descriptor Calculations), Version 5.5; Talete srl: Milan, Italy, 2007.
- Todeschini, R.; Consonni, V.; Mauri, A.; Pavan, M. E-Dragon for VCCLAB. Available online: http://michem.disat.unimib.it/chm/Help/edragon/index.html (accessed on 14 November 2012).
- Picard, R.; Cook, D. Cross-Validation of Regression Models. J. Am. Stat. Assoc. 1994, 79, 575–583. [Google Scholar] [CrossRef]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA Data Mining Software: An Update. ACM SIGKDD Explor. Newsl. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Wang, Y.; Witten, I.H. Induction of model trees for predicting continuous classes. Working paper. University of Waikato: Hamilton, New Zealand, 1996. Available online: http://researchcommons.waikato.ac.nz/bitstream/handle/10289/1183/uow-cs-wp-1996-23.pdf?sequence=1 (accessed on 14 November 2012).
- Guidance Document on the Validation of (Quantitative) Structure-Activity Relationships [(Q)SAR] Models. In OECD Environment Health and Safety Publications. Series on Testing and Assessment. No 69; Chapter 6: Guidance on the Principle of Mechanistic Interpretation; Organisation for Economic Co-operation and Development: Paris, France, 2007; Available online: http://www.oecd.org (accessed on 14 November 2012).
- Gramatica, P. Chemometric Methods and Theoretical Molecular Descriptors in Predictive QSAR Modeling of the Environmental Behavior of Organic Pollutants. In Recent Advances in QSAR Studies: Methods and Applications; Puzin, T., Leszczynski, J., Cronin, M.T.D., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 327–366. [Google Scholar]
- Platt, J. Influence of Neighbor Bonds on Additive Bond Properties in Paraffins. J. Chem. Phys. 1947, 22, 1448–1455. [Google Scholar] [CrossRef]
- Schuur, J.; Selzer, P.; Gasteiger, J. The Coding of the Three-Dimensional Structure of Molecules by Molecular Transforms and Its Application to Structure-Spectra Correlations and Studies of Biological Activity. J. Chem. Inf. Comput. Sci. 1996, 36, 334–344. [Google Scholar] [CrossRef]
- Saíz-Urra, L.; Pérez González, M.; Teijeira, M. QSAR studies about cytotoxicity of benzophenazines with dual inhibition toward both topoisomerases I and II: 3D-MoRSE descriptors and statistical considerations about variable selection. Bioorg. Med. Chem. 2006, 14, 7347–7358. [Google Scholar] [CrossRef] [PubMed]
- Viswanadhan, V.; Ghose, A.; Revankar, G.; Robins, R. Atomic physicochemical parameters for three dimensional structure directed quantitative structure-activity relationships. 4. Additional parameters for hydrophobic and dispersive interactions and their application for an automated superposition of certain naturally occurring nucleoside antibiotics. J. Chem. Inf. Comput. Sci. 1989, 29, 163–172. [Google Scholar]
- Viswanadhan, V.; Reddy, M.; Bacquet, R.; Erion, M. Assessment of Methods Used for Predicting Lipophilicity: Application to Nucleosides and Nucleoside Bases. J. Comput. Chem. 1993, 14, 1019–1026. [Google Scholar] [CrossRef]
- Ghose, A.; Viswanadhan, V.; Wendoloski, J. Prediction of Hydrophobic (Lipophilic) Properties of Small Organic Molecules Using Fragmental Methods: An Analysis of ALOGP and CLOGP Methods. J. Phys. Chem. A 1998, 102, 3762–3772. [Google Scholar] [CrossRef]
- Niculescu, S.P. Artificial Neural Networks and Genetic Algorithms in QSAR. J. Mol. Struc.: Theochem 2003, 622, 71–83. [Google Scholar] [CrossRef]
- Soto, A.J.; Vazquez, G.E.; Strickert, M.; Ponzoni, I. Target-Driven Subspace Mapping Methods and Their Applicability Domain Estimation. Mol. Inf. 2011, 30, 779–789. [Google Scholar] [CrossRef] [PubMed]
- Dragos, H.; Marcou, G.; Varnek, A. Predicting the predictability: A unified approach to the applicability domain problem of QSAR models. J. Chem. Inf. Model. 2009, 49, 1762–1776. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Samples in .mol file format are available upon request from the authors. |

| Compound | Log Pliver | Experiment 1 | Experiment 2 | |||||
|---|---|---|---|---|---|---|---|---|
| Set | DT | NNE | Set | DT | NNE | |||
| 1w | Nitrous oxide | −0.04 | Trn | −0.101 | −0.031 | Tst | −0.210 | −0.028 |
| 2 b | Pentane | 0.61 | Trn | 0.438 | 0.465 | Tst | 0.356 | 0.293 |
| 3 b | Hexane | 0.48 | Trn | 0.507 | 0.567 | Trn | 0.475 | 0.460 |
| 4 b | Heptane | 0.46 | Tst | 0.568 | 0.621 | Trn | 0.577 | 0.595 |
| 5 b | Octane | 0.73 | Trn | 0.684 | 0.680 | Tst | 0.687 | 0.706 |
| 6 b | Nonane | 0.50 | Tst | 0.762 | 0.746 | Trn | 0.801 | 0.786 |
| 7 b | Decane | 0.85 | Trn | 0.862 | 0.843 | Tst | 0.946 | 0.883 |
| 8 b | 2-Methylpentane | 1.04 | Trn | 0.789 | 0.857 | Trn | 0.702 | 0.859 |
| 9 b | 3-Methylpentane | 1.06 | Tst | 0.814 | 0.898 | Trn | 0.789 | 0.916 |
| 10 b | 3-Methylhexane | 0.93 | Trn | 0.863 | 0.910 | Tst | 0.845 | 0.947 |
| 11 b | 2-Methylheptane | 0.52 | Trn | 0.713 | 0.751 | Tst | 0.724 | 0.800 |
| 12 b | 2-Methyloctane | 0.74 | Trn | 0.789 | 0.807 | Tst | 0.835 | 0.864 |
| 13 b | 2-Methylnonane | 0.76 | Trn | 0.786 | 0.733 | Tst | 0.836 | 0.799 |
| 14 b | 2,2-Dimethylbutane | 1.13 | Trn | 0.719 | 0.741 | Tst | 0.594 | 0.731 |
| 15 b | 2,2,4-Trimethylpentane | 0.80 | Tst | 0.579 | 0.556 | Trn | 0.528 | 0.602 |
| 16 b | 2,3,4-Trimethylpentane | 0.70 | Trn | 0.902 | 0.886 | Tst | 1.007 | 0.976 |
| 17 w | Cyclopropane | 0.02 | Trn | 0.118 | 0.075 | Tst | 0.082 | 0.213 |
| 18 w | Methylcyclopentane | 0.96 | Trn | 0.888 | 0.905 | Trn | 0.906 | 1.013 |
| 19 w | Cyclohexane | 0.88 | Trn | 0.843 | 0.918 | Tst | 0.828 | 0.944 |
| 20 w | Methylcyclohexane | 0.71 | Tst | 0.830 | 0.892 | Trn | 0.826 | 0.922 |
| 21 w | 1,2-Dimethylcyclohexane | 1.17 | Trn | 0.957 | 0.949 | Trn | 1.136 | 1.099 |
| 22 w | 1,2,4-Trimethylcyclohexane | 0.86 | Trn | 0.886 | 0.820 | Trn | 1.020 | 0.932 |
| 23 w | tert-Butylcyclohexane | 0.30 | Trn | 0.529 | 0.447 | Trn | 0.608 | 0.407 |
| 24 w | JP-10 | 0.98 | Trn | 1.083 | 0.972 | Tst | 1.452 | 1.400 |
| 25 w | Ethene | 0.24 | Tst | 0.044 | 0.084 | Trn | 0.039 | 0.226 |
| 26 w | Propene | −0.07 | Trn | 0.123 | 0.092 | Tst | 0.148 | 0.228 |
| 27 w | 1-Octene | 0.80 | Trn | 0.687 | 0.719 | Tst | 0.693 | 0.732 |
| 28 w | 1-Nonene | 0.93 | Tst | 0.901 | 0.815 | Trn | 0.833 | 0.854 |
| 29 w | 1-Decene | 1.06 | Trn | 0.981 | 0.871 | Tst | 0.952 | 0.915 |
| 30 w | 1,3-Butadiene | −0.26 | Trn | 0.143 | 0.083 | Tst | 0.213 | 0.199 |
| 31 w | 2-Methyl-1,3-butadiene | 0.32 | Trn | 0.244 | 0.321 | Tst | 0.440 | 0.318 |
| 32 w | Difluoromethane | 0.24 | Trn | −0.068 | −0.053 | Tst | −0.251 | −0.004 |
| 33 w | Chloromethane | 0.23 | Trn | 0.013 | 0.058 | Trn | −0.072 | 0.140 |
| 34 r | Dichloromethane | −0.11 | Trn | 0.059 | 0.057 | Trn | 0.002 | 0.073 |
| 35 r | Chloroform | 0.13 | Trn | 0.167 | 0.141 | Tst | 0.165 | 0.099 |
| 36 w | Carbon tetrachloride | 0.53 | Trn | 0.520 | 0.607 | Trn | 0.472 | 0.517 |
| 37 w | Chloroethane | 0.07 | Trn | 0.085 | 0.035 | Tst | 0.049 | 0.162 |
| 38 w | 1,1-Dichloroethane | 0.15 | Trn | 0.106 | 0.031 | Tst | 0.140 | 0.133 |
| 39 w | 1,2-Dichloroethane | 0.16 | Trn | 0.155 | 0.078 | Trn | 0.194 | 0.164 |
| 40 r | 1,1,1-Trichloroethane | 0.44 | Trn | 0.261 | 0.238 | Trn | 0.374 | 0.287 |
| 41 r | 1,1,2-Trichloroethane | 0.19 | Trn | 0.230 | 0.145 | Tst | 0.231 | 0.165 |
| 42 r | 1,1,1,2-Tetrachloroethane | 0.40 | Trn | 0.333 | 0.288 | Tst | 0.421 | 0.252 |
| 43 r | 1,1,2,2-Tetrachloroethane | 0.16 | Trn | 0.318 | 0.262 | Tst | 0.360 | 0.221 |
| 44 w | Pentachloroethane | 0.39 | Tst | 0.406 | 0.447 | Trn | 0.435 | 0.415 |
| 45 w | Hexachloroethane | 0.81 | Trn | 0.475 | 0.714 | Trn | 0.368 | 0.835 |
| 46 w | 1-Chloropropane | 0.12 | Trn | 0.201 | 0.148 | Trn | 0.292 | 0.227 |
| 47 w | 2-Chloropropane | 0.18 | Trn | 0.163 | 0.083 | Tst | 0.171 | 0.191 |
| 48 w | 1,2-Dichloropropane | 0.25 | Trn | 0.220 | 0.112 | Trn | 0.223 | 0.165 |
| 49 w | Dibromomethane | −0.04 | Trn | 0.123 | 0.069 | Trn | −0.025 | 0.039 |
| 50 r | 1,2-Dibromoethane | 0.00 | Trn | 0.215 | 0.107 | Trn | 0.308 | 0.160 |
| 51 w | 1-Bromopropane | −0.06 | Trn | 0.221 | 0.129 | Tst | 0.266 | 0.198 |
| 52 w | 2-Bromopropane | 0.00 | Trn | 0.201 | 0.138 | Tst | 0.293 | 0.238 |
| 53 w | Fluorochloromethane | −0.17 | Trn | −0.002 | −0.002 | Tst | −0.105 | 0.040 |
| 54 w | Bromochloromethane | 0.26 | Trn | 0.092 | 0.055 | Tst | −0.004 | −0.007 |
| 55 w | Bromodichloromethane | 0.00 | Trn | 0.195 | 0.144 | Tst | 0.136 | 0.085 |
| 56 w | Chlorodibromomethane | 0.22 | Trn | 0.224 | 0.180 | Tst | 0.104 | 0.264 |
| 57 r | 1,1-Dichloro-1-fluoroethane | 0.20 | Trn | 0.214 | 0.154 | Trn | 0.257 | 0.211 |
| 58 r | 1-Bromo-2-chloroethane | 0.03 | Trn | 0.186 | 0.095 | Trn | 0.261 | 0.150 |
| 59 r | 2-Chloro-1,1,1-trifluoroethane | 0.17 | Trn | 0.202 | 0.089 | Trn | 0.131 | 0.126 |
| 60 r | 2;2-Dichloro-1,1,1-trifluoroethane | 0.06 | Trn | 0.288 | 0.223 | Trn | 0.246 | 0.225 |
| 61 w | 1,1-Difluoroethene | 0.64 | Trn | 0.075 | 0.051 | Trn | 0.073 | 0.155 |
| 62 w | Chloroethene | 0.03 | Trn | 0.057 | 0.058 | Tst | 0.070 | 0.162 |
| 63 r | 1,1-Dichloroethene | −0.05 | Tst | 0.184 | 0.189 | Trn | 0.212 | 0.207 |
| 64 r | cis-1,2-Dichloroethene | 0.02 | Trn | 0.064 | 0.009 | Tst | 0.057 | 0.064 |
| 65 r | trans-1,2-Dichloroethene | 0.07 | Trn | 0.078 | 0.030 | Trn | 0.168 | 0.102 |
| 66 r | Trichloroethene | 0.27 | Trn | 0.191 | 0.133 | Trn | 0.198 | 0.123 |
| 67 w | Tetrachloroethene | 0.66 | Trn | 0.310 | 0.320 | Tst | 0.268 | 0.264 |
| 68 r | Bromoethene | 0.03 | Tst | 0.067 | 0.029 | Trn | 0.046 | 0.056 |
| 69 r | 1-Chloro-2,2-difluoroethene | −0.02 | Tst | 0.090 | 0.001 | Trn | 0.120 | 0.070 |
| 70 w | 1,2-Epoxy-3-butene | −0.23 | Trn | −0.018 | −0.078 | Trn | 0.076 | −0.008 |
| 71 g | 1-Propanol | 0.05 | Trn | −0.020 | −0.047 | Tst | 0.059 | 0.001 |
| 72 g | 2-Propanol | −0.03 | Trn | −0.048 | −0.042 | Trn | 0.020 | −0.007 |
| 73 g | 1-Butanol | 0.02 | Tst | 0.073 | 0.115 | Trn | 0.207 | 0.114 |
| 74 g | 2-Methyl-1-propanol | 0.02 | Trn | 0.026 | −0.053 | Tst | 0.011 | −0.050 |
| 75 g | tert-Butanol | 0.01 | Trn | −0.002 | 0.100 | Trn | 0.118 | 0.098 |
| 76 g | 1-Pentanol | 0.41 | Trn | 0.398 | 0.330 | Trn | 0.285 | 0.291 |
| 77 g | 3-Methyl-1-butanol | 0.22 | Tst | 0.408 | 0.362 | Trn | 0.320 | 0.388 |
| 78 g | tert-Amyl alcohol | 0.09 | Tst | 0.379 | 0.290 | Trn | 0.255 | 0.280 |
| 79 w | Acetone | 0.02 | Trn | −0.148 | −0.018 | Trn | 0.008 | −0.029 |
| 80 w | Butanone | 0.12 | Trn | −0.024 | 0.024 | Tst | 0.134 | 0.023 |
| 81 w | 2-Pentanone | 0.13 | Trn | 0.054 | 0.093 | Trn | 0.168 | 0.081 |
| 82 w | 4-Methyl-2-pentanone | 0.23 | Trn | 0.426 | 0.433 | Tst | 0.368 | 0.551 |
| 83 w | 2-Heptanone | 0.30 | Trn | 0.436 | 0.483 | Tst | 0.343 | 0.455 |
| 84 w | Methyl acetate | −0.03 | Trn | −0.118 | −0.166 | Tst | −0.089 | −0.147 |
| 85 w | Ethyl acetate | 0.13 | Trn | −0.036 | −0.002 | Tst | 0.102 | −0.012 |
| 86 w | Propyl acetate | 0.48 | Trn | 0.372 | 0.215 | Trn | 0.240 | 0.248 |
| 87 w | Isopropyl acetate | 0.62 | Tst | 0.485 | 0.318 | Trn | 0.345 | 0.499 |
| 88 w | Butyl acetate | 0.51 | Trn | 0.436 | 0.478 | Trn | 0.364 | 0.524 |
| 89 w | Isobutyl acetate | 0.73 | Trn | 0.431 | 0.470 | Trn | 0.357 | 0.540 |
| 90 w | Pentyl acetate | 0.66 | Trn | 0.527 | 0.572 | Trn | 0.428 | 0.617 |
| 91 w | Isopentyl acetate | 0.76 | Trn | 0.592 | 0.642 | Trn | 0.504 | 0.762 |
| 92 w | Diethyl ether | −0.17 | Tst | 0.043 | 0.183 | Trn | 0.251 | 0.195 |
| 93 w | tert-Butyl methyl ether | 0.17 | Trn | 0.345 | 0.201 | Tst | 0.175 | 0.161 |
| 94 w | tert-Butyl ethyl ether | 0.45 | Trn | 0.624 | 0.634 | Tst | 0.575 | 0.869 |
| 95 w | tert-Amyl methyl ether | 0.28 | Tst | 0.405 | 0.492 | Trn | 0.380 | 0.470 |
| 96 w | Divinyl ether | 0.07 | Trn | −0.072 | −0.100 | Tst | 0.026 | −0.059 |
| 97 w | Ethylene oxide | −0.07 | Trn | −0.146 | −0.128 | Trn | −0.108 | −0.042 |
| 98 w | Cyanoethylene oxide | −0.56 | Trn | −0.158 | −0.205 | Tst | −0.168 | −0.157 |
| 99 w | Halothane | 0.29 | Trn | 0.323 | 0.290 | Trn | 0.262 | 0.298 |
| 100 w | Teflurane | 0.23 | Trn | 0.261 | 0.194 | Tst | 0.147 | 0.220 |
| 101 w | Fluroxene | 0.18 | Tst | 0.081 | −0.042 | Trn | 0.057 | 0.019 |
| 102 w | Enflurane | 0.27 | Trn | 0.356 | 0.327 | Tst | 0.300 | 0.357 |
| 103 w | Isoflurane | 0.36 | Trn | 0.314 | 0.317 | Trn | 0.139 | 0.320 |
| 104 w | Sevoflurane | 0.63 | Trn | 0.393 | 0.354 | Tst | 0.281 | 0.413 |
| 105 w | Methoxyflurane | 0.19 | Trn | 0.247 | 0.234 | Trn | 0.105 | 0.241 |
| 106 w | 1-nitropropane | −0.13 | Trn | 0.084 | −0.052 | Tst | 0.056 | −0.005 |
| 107 w | 2-nitropropane | −0.43 | Trn | 0.056 | −0.088 | Trn | 0.015 | −0.033 |
| 108 w | Carbon disulfide | 0.48 | Trn | 0.151 | 0.298 | Tst | 0.012 | 0.142 |
| 109 o | Benzene | 0.21 | Trn | 0.182 | 0.108 | Tst | −0.005 | 0.121 |
| 110 o | Toluene | 0.50 | Trn | 0.279 | 0.275 | Tst | 0.137 | 0.194 |
| 111 o | Ethylbenzene | 0.31 | Tst | 0.310 | 0.329 | Trn | 0.157 | 0.276 |
| 112 o | o-Xylene | 0.34 | Trn | 0.399 | 0.364 | Tst | 0.428 | 0.281 |
| 113 o | m-Xylene | 0.37 | Trn | 0.306 | 0.334 | Tst | 0.144 | 0.281 |
| 114 o | p-Xylene | 0.34 | Trn | 0.406 | 0.367 | Trn | 0.391 | 0.285 |
| 115 o | 1,2,4-Trimethylbenzene | 0.43 | Trn | 0.414 | 0.370 | Tst | 0.481 | 0.288 |
| 116 o | tert-Butylbenzene | 0.49 | Trn | 0.434 | 0.368 | Tst | 0.492 | 0.276 |
| 117 o | Styrene | 0.47 | Trn | 0.314 | 0.298 | Tst | 0.329 | 0.246 |
| 118 o | m-Methylstyrene | 0.23 | Trn | 0.364 | 0.326 | Trn | 0.341 | 0.272 |
| 119 o | p-Methylstyrene | 0.14 | Tst | 0.441 | 0.409 | Trn | 0.533 | 0.298 |
| 120 w | Chlorobenzene | 0.31 | Trn | 0.318 | 0.316 | Tst | 0.232 | 0.225 |
| 121 w | 4-Chlorobenzotrifluoride | 0.28 | Trn | 0.519 | 0.418 | Tst | 0.572 | 0.443 |
| 122 w | Furan | −0.05 | Trn | 0.033 | −0.053 | Tst | −0.038 | 0.067 |
| Descriptor | r (correlation coefficient of Se vs. descriptor) | |
|---|---|---|
| Se ≤ 16.025 | Se > 16.025 | |
| AMW | −0.55 | −0.33 |
| Pol | 0.57 | 0.32 |
| ALOGP | 0.12 | 0.75 |
| Mor29u | 0.09 | −0.15 |
| Descriptor | Meaning | Family |
|---|---|---|
| AMW | average molecular weight | Constitutional |
| Mor29u | 3D-MoRSE - signal 29/unweighted | 3D-MoRSE |
| ALOGP | Ghose-Crippen octanol-water partition coeff. (logP) | Molecular properties |
| Pol | polarity number | Topological |
| Se | sum of atomic Sanderson electronegativities | Constitutional |
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Palomba, D.; Martínez, M.J.; Ponzoni, I.; Díaz, M.F.; Vazquez, G.E.; Soto, A.J. QSPR Models for Predicting Log Pliver Values for Volatile Organic Compounds Combining Statistical Methods and Domain Knowledge. Molecules 2012, 17, 14937-14953. https://doi.org/10.3390/molecules171214937
Palomba D, Martínez MJ, Ponzoni I, Díaz MF, Vazquez GE, Soto AJ. QSPR Models for Predicting Log Pliver Values for Volatile Organic Compounds Combining Statistical Methods and Domain Knowledge. Molecules. 2012; 17(12):14937-14953. https://doi.org/10.3390/molecules171214937
Chicago/Turabian StylePalomba, Damián, María J. Martínez, Ignacio Ponzoni, Mónica F. Díaz, Gustavo E. Vazquez, and Axel J. Soto. 2012. "QSPR Models for Predicting Log Pliver Values for Volatile Organic Compounds Combining Statistical Methods and Domain Knowledge" Molecules 17, no. 12: 14937-14953. https://doi.org/10.3390/molecules171214937
APA StylePalomba, D., Martínez, M. J., Ponzoni, I., Díaz, M. F., Vazquez, G. E., & Soto, A. J. (2012). QSPR Models for Predicting Log Pliver Values for Volatile Organic Compounds Combining Statistical Methods and Domain Knowledge. Molecules, 17(12), 14937-14953. https://doi.org/10.3390/molecules171214937