Influence of the Dielectric Medium on the Carbonyl Infrared Absorption Peak of Acetylferrocene
Abstract
:Introduction
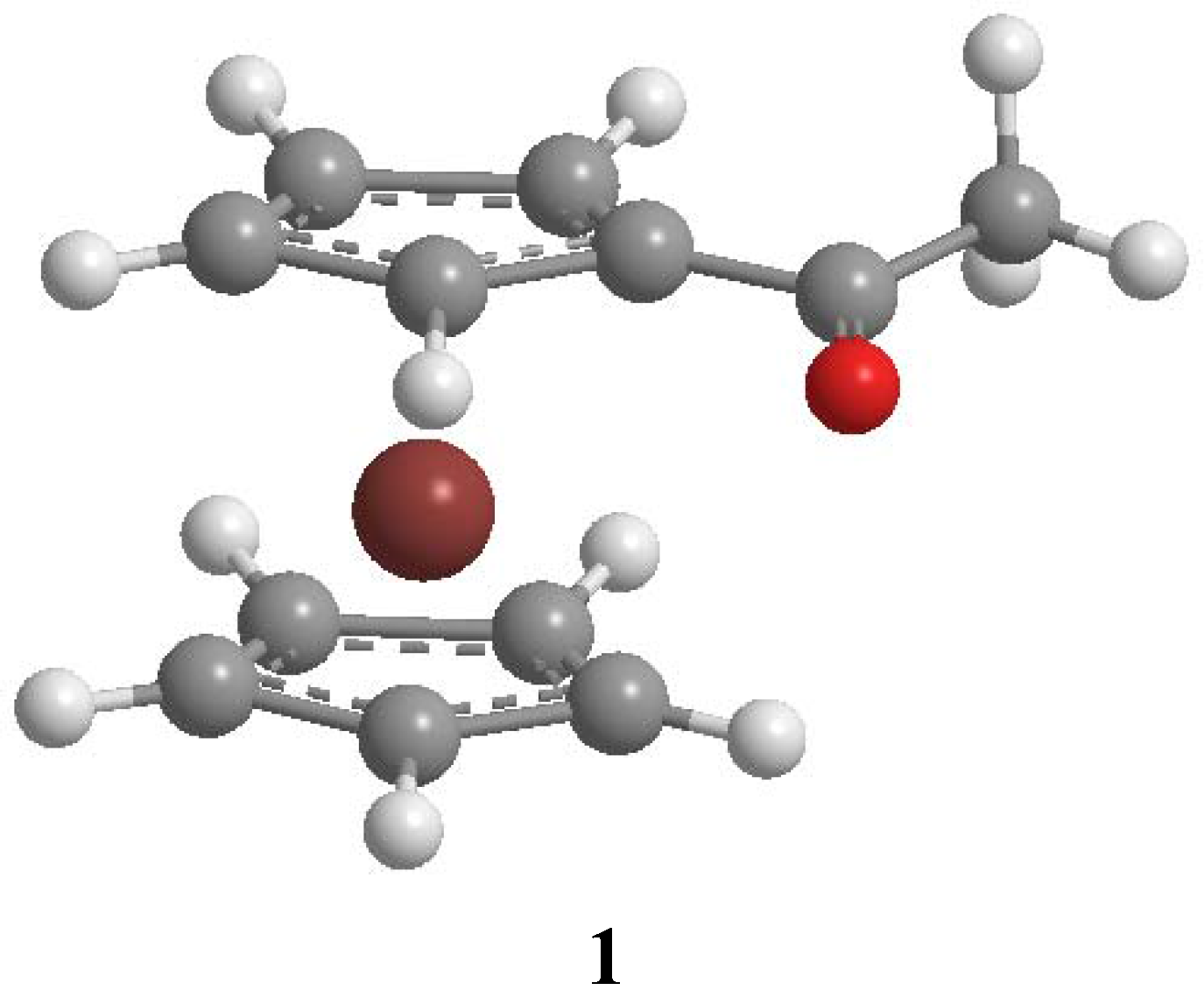
Theory
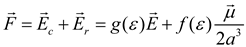
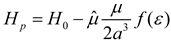

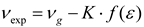
| Year | Universities | Colleges |
|---|---|---|
| Born | 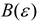 | 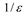 |
| Kirkwood-Bauer | 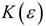 | 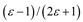 |
| Block-Walker | 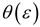 | 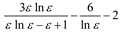 |
| Brady-Carr | 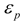 | 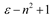 |
| Marcus | 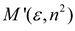 | 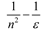 |
| McRae | 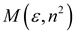 | 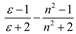 |
| London–Onsager | 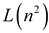 |  |
| Bekarek–Kolling | 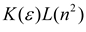 | 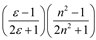 |
| Brady–Carr–Kolling | 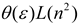 |  |
Results and Discussion
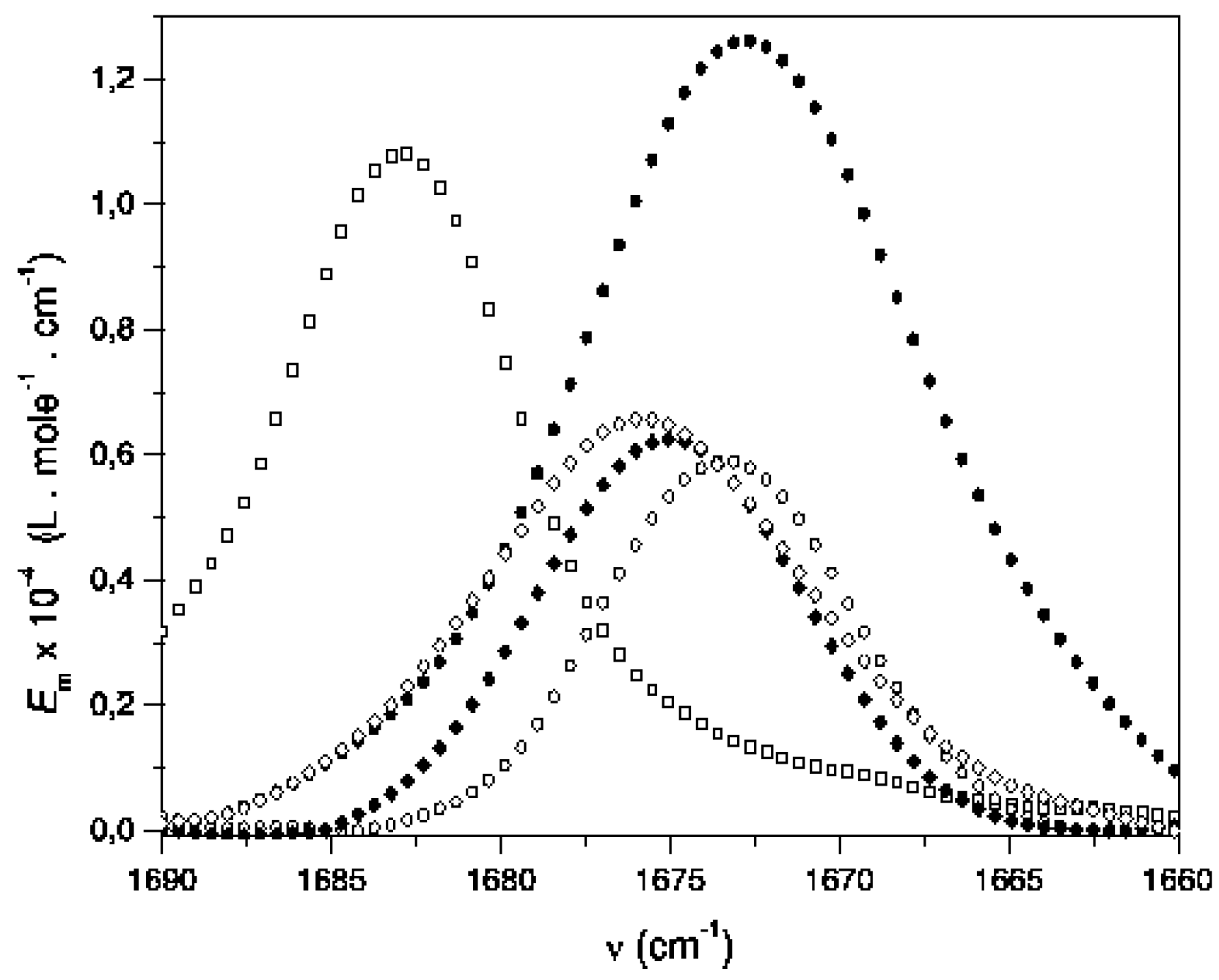
| Solvent a, b | Ethyl acetate c | 2-Butanone d | Acetylferrocene e |
|---|---|---|---|
| Acetonitrile (●) | 1736.5 | 1714.1 | 1668.3 |
| Bromobenzene (●) | - | - | 1671.2 |
| Butyl methyl ether (●) | - | - | 1679.4 |
| Butyronitrile (●) | 1736.7 | 1714.4 | 1670.2 |
| Carbon disulfide (●) | 1741.2 | 1719.8 | 1674.1 |
| Chlorobenzene (●) | - | - | 1671.7 |
| Chlorobutane (●) | - | - | 1662.0 |
| Cyclohexane (●) | 1749.6 | 1726.1 | 1682.8 |
| Cyclohexene (●) | - | - | 1681.3 |
| Diethyl ether (●) | 1743.5 | 1721.2 | 1679.9 |
| Diisopropyl ether (●) | 1744.6 | 1721.6 | 1679.7 |
| Dimethyl sulfoxide (●) | 1731.3 | 1710.6 | 1663.5 |
| 1,4-Dioxane (●) | - | - | 1673.6 |
| Isooctane (●) | 1750.1 | 1726.8 | 1683.7 |
| Tetrahydrofuran (●) | 1739.0 | 1716.2 | 1675.1 |
| Benzene (□) | 1740.2 | 1719.0 | 1672.7 |
| Ethylbenzene (□) | - | - | 1676.5 |
| Nitrobenzene (□) | 1736.3 | 1714.4 | 1669.9 |
| Toluene (□) | 1739.5 | 1717.7 | 1676.0 |
| Carbon tetrachloride (►) | 1742.4 | 1721.0 | 1675.5 |
| Chloroform (►) | 1731.7 | 1710.3 | 1662.5 |
| Dichlorometane (►) | 1733.4 | 1712.7 | 1665.4 |
| Tetrachloroethylene (►) | 1744.1 | 1721.2 | 1667.8 |
| Pyridine (◊) | 1736.2 | 1714.0 | 1662.9 |
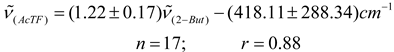
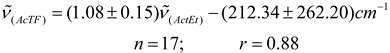
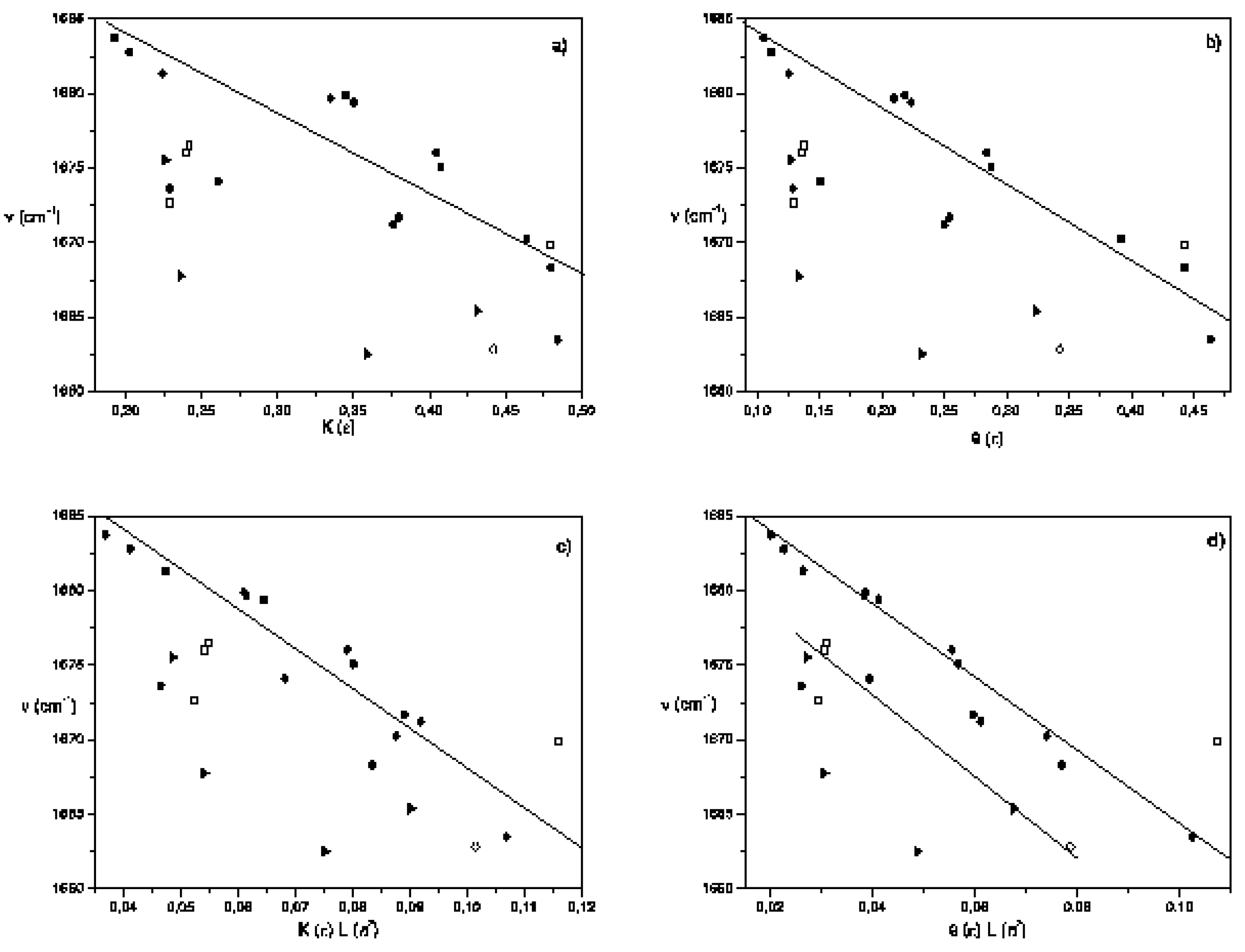
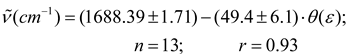
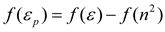
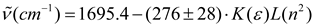
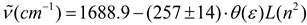
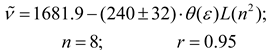
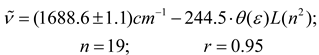
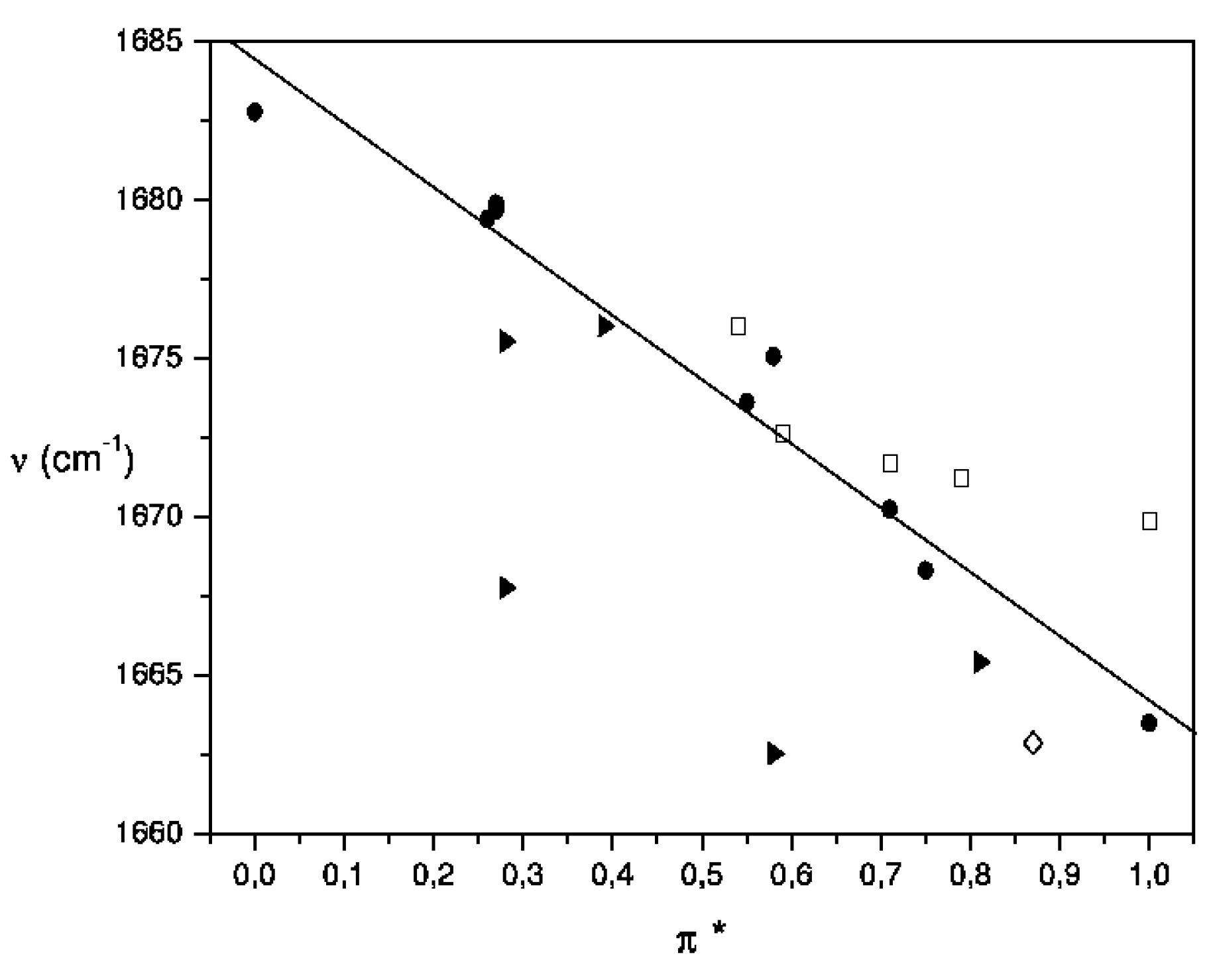

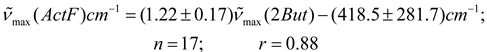
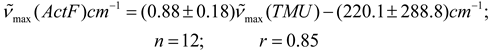
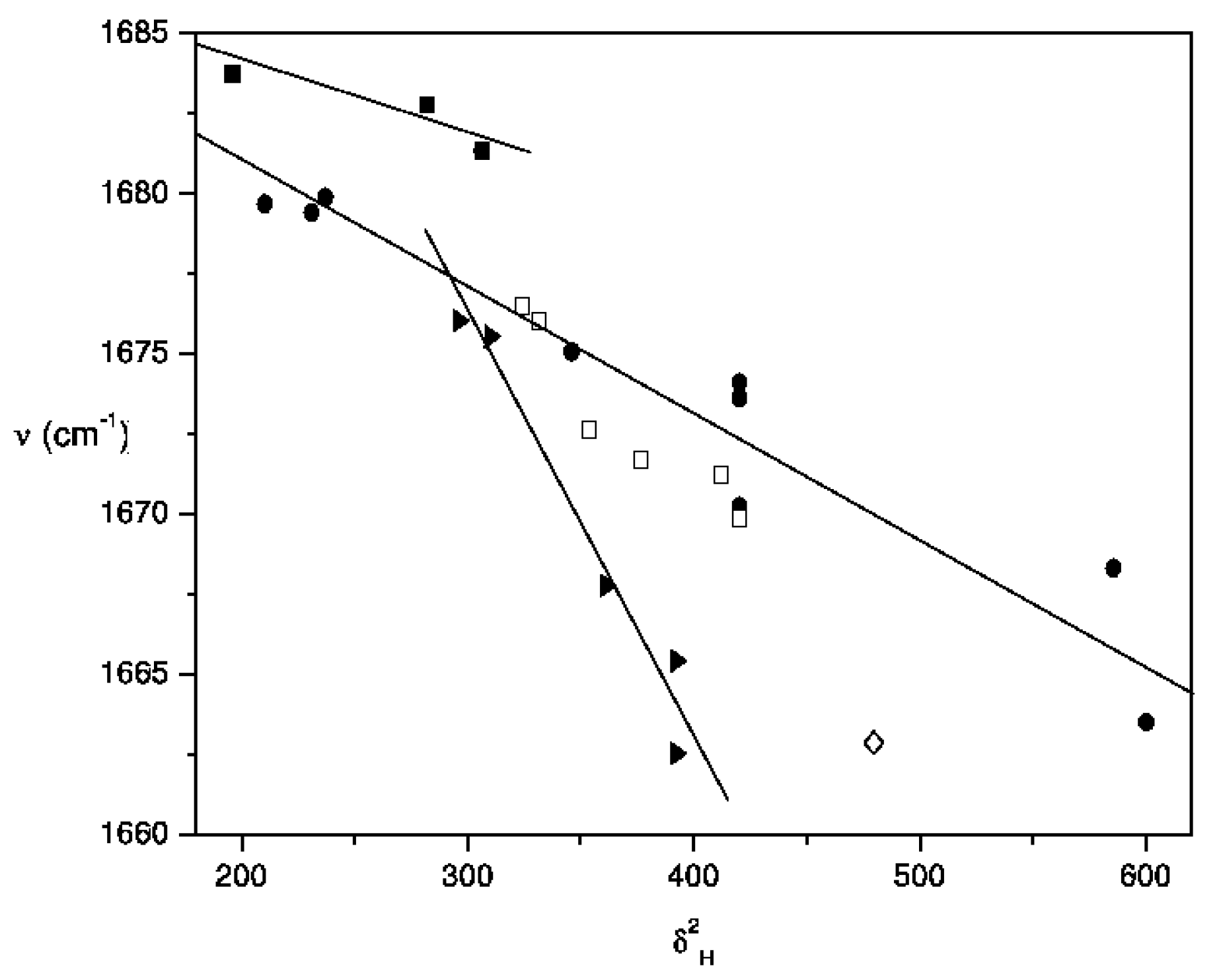

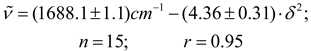
Conclusions
Experimental
References and Notes
- Kolling, O.W. Aprotic solvent effects upon the fundamental vibrational peak of the nitrile group in benzonitrile. Appl. Spectrosc. 2000, 54, 890–893. [Google Scholar] [CrossRef]
- Abboud, J.; Thaft, R. An interpretation of a general scale of solvent polarities. A simplified reaction field theory modification. J. Phys. Chem. 1979, 83, 412–419. [Google Scholar] [CrossRef]
- Kolling, O.W. FTIR study of the solvent influence on the carbonyl absorption peak of ethyl acetate. J. Phys. Chem. 1992, 96, 6217–6220. [Google Scholar] [CrossRef]
- Kolling, O.W. Reaction field model for the solvent influence upon the fundamental carbonyl vibrational peak of 2-butanone in aprotic media. J. Phys. Chem. 1996, 100, 16087–16091. [Google Scholar] [CrossRef]
- Ben-Amotz, D.; Lee, M.; Cho, S.; List, D. Solvent and pressure-induced perturbations of the vibrational potential surface of acetonitrile. J. Chem. Phys. 1992, 96, 8781–8792. [Google Scholar] [CrossRef]
- Meredith, G.R.; Buchalter, B. Solvent dependence of apparent third-order hyperpolarizability in paranitroaniline. J. Chem. Phys. 1983, 78, 1938–1945. [Google Scholar] [CrossRef]
- Lawrentz, U.; Grahn, W.; Lukaszuk, K.; Klein, C.; Wortmann, R.; Feldner, A.; Scherer, D. Donor-acceptor oligoenes with a locked all-trans conformation: Synthesis and linear and nonlinear optical properties. Chem. Eur. J. 2002, 8, 1573–1590. [Google Scholar] [CrossRef]
- Burnham, A.K.; Alms, G.R.; Flygare, W.H. The local electric field. I. The effect on isotropic and anisotropic Rayleigh scattering. J. Chem. Phys. 1975, 62, 3289–3297. [Google Scholar] [CrossRef]
- Brady, J.E.; Carr, P.W. An analysis of dielectric models of solvatochromism. J. Phys. Chem. 1985, 89, 5759–5766. [Google Scholar] [CrossRef]
- Cha, D.; Kloss, A.; Tikanen, A.; Fawcett, W. Solvent-induced frequency shifts in the infrared spectrum of acetone in organic solvents. Phys. Chem. Chem. Phys. 1999, 1, 4785–4790. [Google Scholar]
- Fawcett, W.R.; Liu, G.; Kessler, T.E. Solvent-induced frequency shifts in the infrared spectrum of acetonitrile in organic solvents. J. Phys. Chem. 1993, 97, 9293–9298. [Google Scholar] [CrossRef]
- Capelli, C.; Silva, C.; Tomasi, J. Solvent effects on vibrational modes: ab initio calculations, scaling and solvent functions with applications to the carbonyl stretch of dialkyl ketones. J. Mol. Struct. (THEOCHEM) 2001, 544, 2027–2094. [Google Scholar] [CrossRef]
- Reichardt, C. Solvatochromic dyes as solvent polarity indicators. Chem. Rev. 1994, 94, 2319–2358. [Google Scholar] [CrossRef]
- Reimers, J.; Hall, L. The solvation of acetonitrile. J. Am. Chem. Soc. 1999, 121, 3730–3744. [Google Scholar] [CrossRef]
- Picquart, M.; Lefévre, T.; Lacrampe, G. Solvation of lauric acid studied by vibrational spectroscopies. Appl. Spectrosc. 1995, 49, 1268–1274. [Google Scholar] [CrossRef]
- Luo, Y.; Norman, P.; Agren, H. Onsager reaction field description of optical properties of octupolar molecules in solution. J. Am. Chem. Soc. 1998, 120, 11188–11189. [Google Scholar] [CrossRef]
- Munn, R.W.; Luo, Y.; Macák, P.; Ågren, H. Role of the cavity field in nonlinear optical response in the condensed phase. J. Chem. Phys. 2000, 114, 3105–3108. [Google Scholar] [CrossRef]
- Bruni, S.; Cariati, E.; Cariati, F.; Porta, F.A.; Quici, S.; Roberto, D. Determination of the quadratic hyperpolarizability of trans-4-[4-(dimethylamino)styryl]pyridine and 5-dimethylamino-1,10-phenanthroline from solvatochromism of absorption and fluorescence spectra: a comparison with the electric-field-induced second-harmonic generation technique. Spectrochim. Acta A 2001, 57, 1417–1426. [Google Scholar]
- Paley, M.S.; Harris, J.M.; Looser, H.; Baumert, J.C.; Bjorklund, G.C.; Jundt, D.; Twieg, R.J. A solvatochromic method for determining second-order polarizabilities of organic molecules. J. Org. Chem. 1989, 54, 3774–3778. [Google Scholar] [CrossRef]
- Bosshard, C.; Knöpfle, G.; Prêtre, P.; Günter, P. Second-order polarizabilities of nitropyridine derivatives determined with electric-field-induced second-harmonic generation and a solvatochromic method: A comparative study. J. Appl. Phys. 1992, 71, 1594–1605. [Google Scholar] [CrossRef]
- Alvarado, Y.; Cubillán, N.; Labarca, P.H.; Karam, A.; Arrieta, F.; Castellano, O.; Soscún, H. Static and dynamic dipole polarizabilities of 2-and 3-methylthiophenes in solution: Experimental and theoretical determination. J. Phys. Org. Chem. 2002, 15, 154–164. [Google Scholar] [CrossRef]
- Alvarado, Y.J.; H. Labarca, P.; Cubillán, N.; Osorio, E.; Karam, A. Solvent effect on the electronic polarizability of benzonitrile. Z. Naturforsch 2003, 58a, 68–74. [Google Scholar] [CrossRef]
- Suppan, P.; Ghoneim, N. Solvatochromism; The Royal Society of Chemistry: Cambridge, U.K., 1997. [Google Scholar]
- Tomasi, J.; Persico, M. Molecular interactions in solution: An overview of methods based on continuous distributions of the solvent. Chem. Rev. 1994, 94, 2027–2094. [Google Scholar] [CrossRef]
- Milischuk, A.; Matsyushov, D. On the validity of dielectric continuum models in application to solvation in molecular solvents. J. Chem. Phys. 2003, 118, 1859–1862. [Google Scholar] [CrossRef]
- Wortmann, R.; Bishop, D. Effective polarizabilities and local field corrections for nonlinear optical experiments in condensed media. J. Chem. Phys. 1998, 108, 1001–1007. [Google Scholar] [CrossRef]
- Kolling, O.W. Polarizability-hyperpolarizability influences upon solvatochromism in polychloroalkane and polychloroalkene media. J. Phys. Chem. 1996, 100, 519–522. [Google Scholar] [CrossRef]
- Abboud, J.-L.; Notario, R. Critical compilation of scales of solvent parameters. Part I. Pure, non-hydrogen bond donor solvents. Pure Appl. Chem. 1999, 71, 645–718. [Google Scholar] [CrossRef]
- Kolling, O.W. Re-examination of the effect of aprotic solvents upon the fundamental vibrational peak of the carbonyl group in 1,1,3,3-tetramethylurea. Appl. Spectrosc. 1999, 53, 29–34. [Google Scholar] [CrossRef]
- Liu, T.Y.; Chen, Y.J.; Tai, C.C.; Kwan, K.S. Solvent-dependent studies of intervalence transfer of mixed-valence complexes containing ferrocenylpyridine and rutheniumammines. Inorg. Chem. 1999, 38, 674–679. [Google Scholar] [CrossRef]
- Abraham, M.; Benjelloun-Dakhama, N.; Gola, J.M.R.; Acree, W.E.; Cain, W.S.; Cometto-Muñiz, J.E. Solvation descriptors for ferrocene, and the estimation of some physicochemical and biochemical properties. New J. Chem. 2000, 24, 825–829. [Google Scholar] [CrossRef]
- Fabinskii, P.V.; Tverdokhlebov, V.P.; Dmitrenko, G.A.; Fedorov, V.A. Solvation of ferrocene and dimethylferrocenylcarbinol in mixtures of water. Russ. J. Phys. Chem. 1999, 73, 1413–1416. [Google Scholar]
- Kassab, A.; Marzouk, M.I.; El-hashash, M. Substituted ferrocenes: Synthesis and correlation of their electronic spectra with structure (LFER). J. Serb. Chem. Soc. 2002, 67, 593–603. [Google Scholar] [CrossRef]
- Szpakowska, M.; Naggy, O. Application of the competitive preferential solvation theory to coordinative solute-solvent interactions. J. Chem. Soc., Faraday Trans. 1, 1989, 85, 2891–2899. [Google Scholar] [CrossRef]
- Hudson, R.D.A.; Asselberghs, I.; Clays, K.; Cuffe, L.P.; Gallagher, J.F.; Manning, A.R.; Persoons, A.; Wostyn, K. The linear and nonlinear optical properties of organometallic chromophores derived from ferrocene, [Fe2(η5-C5H5)(CO)2(μ-CO)(μ-C---CH3)]+[BF4]- and terthienyl spacers. Crystal structure of 2-[(e)-2-ferrocenylethenyl]-5-(2-thienyl)thiophene. J. Organomet. Chem. 2002, 637–639, 435–444. [Google Scholar] [CrossRef]
- Streiff, J.H.; Daniel Edwards, W.; McHale, J.L. Investigation of the solvatochromic electronic transitions of [ru(nh3)4bipyridine]2+. Chem. Phys. Lett. 1999, 312, 369–375. [Google Scholar] [CrossRef]
- Nair, R.B.; Yeung, L.K.; Murphy, C.J. Synthesis and solvent-dependent properties of ru(acac)2dppz. Inorg. Chem. 1999, 38, 2536–2538. [Google Scholar] [CrossRef]
- Birge, R. Molecular and biomolecular electronics; American Chemical Society: Washington, D.C., USA, 1994. [Google Scholar]
- Wang, Z.; Zhu, J.; Chen, K.; Tian, H. Synthesis of novel ferrocene-naphtilimide dyads. J. Chem. Res. (S) 1999, 438–439. [Google Scholar] [CrossRef]
- Alain, V.; Fort, A.; Barzoukas, M.; Chin-Ti, C.; Blanchard-Desce, M.; Marder, S.; Perry, J. The linear and non-linear optical properties of some conjugated ferrocene compounds with potent heterocyclic acceptors. Inorg. Chim. Acta 1996, 242, 43–49. [Google Scholar] [CrossRef]
- Long, N.J. Organometallic compounds for nonlinear optics-the search for en-light-enment! Angew. Chem. Int. Edit. Eng. 1995, 34, 21–38. [Google Scholar] [CrossRef]
- Baghlaf, A.O.; Banaser, K.; Hashem, H.Y.; Albrishry, A.; Ishaq, M. Synthesis and spectroscopic studies of complexes containing the schiff base 1-acetylferrocene(thio)semicarbazone. Transit. Met. Chem. 1996, 21, 16–18. [Google Scholar] [CrossRef]
- Wong, M.W.; Frisch, M.J.; Wiberg, K.B. Solvent effects. 1. The mediation of electrostatic effects by solvents. J. Am. Chem. Soc. 1991, 113, 4776–4782. [Google Scholar] [CrossRef]
- Onsager, L. Electric moments of molecules in liquids. J. Am. Chem. Soc. 1936, 58, 1486–1493. [Google Scholar] [CrossRef]
- Tapia, O.; Goscinski, O. Self-consistent reaction field theory of solvent effects. Mol. Phys. 1975, 29, 1653–1661. [Google Scholar] [CrossRef]
- Di Bella, S.; Marks, T.J.; Ratner, M.A. Environmental effects on nonlinear optical chromophore performance. calculation of molecular quadratic hyperpolarizabilities in solvating media. J. Am. Chem. Soc. 1994, 116, 4440–4445. [Google Scholar] [CrossRef]
- Kirkwood, J. On the theory of strong electrolyte solutions. J. Chem. Phys. 1934, 2, 767–781. [Google Scholar] [CrossRef]
- Block, H.; Walker, S.M. A modification of the Onsager theory for a dielectric. Chem. Phys. Lett. 1973, 19, 363–364. [Google Scholar] [CrossRef]
- Brady, J.; Carr, P. Development of a generalized model for the scale of solvent polarity. J. Chem. Phys. 1982, 86, 3053–3058. [Google Scholar] [CrossRef]
- McRae, E.G. Theory of solvent effects on molecular electronic spectra. Frequency shifts. J. Phys. Chem. 1957, 61, 562–572. [Google Scholar] [CrossRef]
- Marcus, R.A. On the theory of oxidation-reduction reactions involving electron transfer. V. Comparison and properties of electrochemical and chemical rate constants. J. Phys. Chem. 1963, 67, 853–857. [Google Scholar] [CrossRef]
- Conway, B.E. Electrolyte solutions: Solvation and structural aspects. Annu. Rev. Phys. Chem. 1966, 17, 481–490. [Google Scholar] [CrossRef]
- Bekarek, V. Contribution to the interpretation of a general scale of solvent polarities. J. Phys. Chem. 1981, 85, 722–723. [Google Scholar] [CrossRef]
- Kono, H.; Ohtsuki, Y.; Abe, T. Electrostatic free energy of solvation of an arbitrary charge distribution in the block-walker inhomogeneus dielectric. J. Phys. Chem. 1996, 100, 9935–9942. [Google Scholar] [CrossRef]
- Laurence, E.; Nicolet, P.; Tawfik Dalati, M.; Abboud, J.-L.; Notario, R. The empirical treatment of solvent-solute interactions: 15 years of π *. J. Chem. Phys. 1994, 98, 5807–5816. [Google Scholar] [CrossRef]
- Rablen, P.R.; Pearlman, S.A.; Miller, D.A. Solvent effects on the barrier to C-N bond rotation in N,N-dimethylaminoacrylonitrile: Modeling by reaction field theory and by Monte Carlo simulations. J. Am. Chem. Soc. 1999, 121, 227–237. [Google Scholar] [CrossRef]
- Le Fèvre, R.; Radford, D.; Ritchie, G.; Stiles, P. The configurations of some weak complexes of benzene. J. Chem. Soc. B 1968, 148–156. [Google Scholar] [CrossRef]
- Le Fèvre, R.; Murthy, D.; Stiles, P. The stereospecific solvation of non-polar organic solutes in liquid benzene. Aust. J. Chem. 1969, 22, 1421–1426. [Google Scholar]
- Khajehpour, M.; Kauffman, J. Emission peak shifts of a dipolar solute dissolved in nondipolar solvents: A quantitative measure of quadrupole-dipole interactions in supercritical CO2. J. Phys. Chem. A 2000, 104, 9512–9517. [Google Scholar] [CrossRef]
- Reichardt, C. Solvent and solvent effects in organic chemistry; VCH: Weinheim, Federal Republic of Germany, 1990. [Google Scholar]
- Ehrenson, S. Continuum radial dielectric functions for ion and dipole solution systems. J. Comput. Chem. 1988, 10, 77–93. [Google Scholar] [CrossRef]
- Reynolds, L.; Gardecki, J.A.; Frankland, S.J.V.; Horng, M.L.; Maroncelli, M. Dipole solvation in nondipolar solvents: Experimental studies of reorganization energies and solvation dynamics. J. Phys. Chem. 1996, 100, 10337–10354. [Google Scholar] [CrossRef]
- Kamlet, M.J.; Abboud, J.L.M.; Abraham, M.H.; Taft, R.W. Linear solvation energy relationships. 23. A comprehensive collection of the solvatochromic parameters, π*, α , and β and some methods for simplifying the generalized solvatochromic equation. J. Org. Chem. 1983, 48, 2877–2887. [Google Scholar]
- Bekárek, V.; Mikulecká, A. A note on evaluation of solvent shifts in IR spectroscopy. Collect. Czech. Chem. Commun. 1978, 43, 2879–2884. [Google Scholar] [CrossRef]
- Horák, M.; Plíva, J. Studies of solute-solvent interactions I. General considerations. Spectrochim. Acta 1965, 21, 911–917. [Google Scholar] [CrossRef]
- Rao, C.; Singh, S.; Senthilnathan, V. Spectroscopic studies of solute-solvent interactions. Chem. Soc. Rev. 1976, 5, 297–316. [Google Scholar] [CrossRef]
- Buckingham, A. Solvent effects in vibrational spectroscopy. Trans. Faraday Soc. 1960, 56, 753–760. [Google Scholar] [CrossRef]
- Schweizer, K.; Chandler, D. Vibrational dephasing and frequency shifts of polyatomic molecules in solution. J. Chem. Phys. 1982, 76, 2296–2314. [Google Scholar] [CrossRef]
- Fukuda, T.; Ikawa, S.; Kimura, M. Vibrational relaxation and frequencies of liquid molecules. II. Comparison of theoretical and experimental results. Chem. Phys. 1989, 133, 151–163. [Google Scholar] [CrossRef]
- Fowkes, F.M.; Tischler, D.O.; Wolfe, J.A.; Lannigan, L.A.; Ademu-John, C.M.; Halliwell, M.J. Acid-base complexes of polymers. J. Polym. Sci. Polym. Chem. Ed. 1984, 22, 547–566. [Google Scholar] [CrossRef]
- Riddle, F.L.; Fowkes, F.M. Spectral shifts in acid-base chemistry. 1. van der Waals contributions to acceptor numbers. J. Am. Chem. Soc. 1990, 112, 3259–3264. [Google Scholar] [CrossRef]
- Barton, A.F.M. Solubility parameters. Chem. Rev. 1975, 75, 731–753. [Google Scholar] [CrossRef]
- Ritchie, G.; Cooper, M.; Calvert, R.; Dennis, G.; Phillips, L.; Urbancich, J. Molecular quadrupole moments, magnetic anisotropies, and charge distributions of ferrocene and ruthenocene. J. Am. Chem. Soc. 1983, 105, 5215–5219. [Google Scholar] [CrossRef]
- Rivail, J.L.; Rivaldi, D.; Dillet, V. Solvent effects an infrared spectroscopy: A computational approach. Mol. Phys. 1996, 89, 1521–1529. [Google Scholar] [CrossRef]
- Rivail, J.L.; Rivaldi, D.; Dillet, V. Modèlisation des systèmes complexes. Effets de solvant sur les modes de vibration d´un soluté au sein d´une solution. J. Chem. Phys. 1998, 95, 1818–1830. [Google Scholar]
- Proutiere, A.; Megnassan, E.; Hucteau, H. Refractive index and density variations in pure liquids. A new theoretical relation. J. Phys. Chem. 1992, 96, 3485–3489. [Google Scholar] [CrossRef]
- Riddick, J.; Bunger, W.; Sakano, T. Organic Solvents: Physical Properties and Methods of Purification; Wiley-Interscience: New York, USA, 1986. [Google Scholar]
- Laurence, C.; Nicolet, P.; Lucon, M.; Dalati, T. Electrolyte solutions: Solvation and structural aspects. J. Chem. Soc., Perkin Trans. 2 1989, 873–880. [Google Scholar] [CrossRef]
- Hernanz, A. Solvent influence on the (C = O) band shape of ethyl acetate. J. Mol. Liq. 1989, 39, 111–114. [Google Scholar] [CrossRef]
- Abboud, J.L.M.; Guiheneuf, G.; Essfar, M.; Taft, R.W.; Kamlet, M.J. Linear solvation energy relationships. 21. Gas-phase data as tools for the study of medium effects. J. Phys. Chem. 1984, 88, 4414–4420. [Google Scholar] [CrossRef]
- Chastrette, M.; Rajzmann, M.; Chanon, M. Approach to a general classification of solvents using a multivariate statistical treatment of quantitative solvent parameters. J. Phys. Chem. 1985, 107, 1–11. [Google Scholar] [CrossRef]
© 2005 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Alvarado, Y.; Peña-Suárez, J.; Cubillán, N.; Labarca, P.; Caldera-Luzardo, J.; López-Linares, F. Influence of the Dielectric Medium on the Carbonyl Infrared Absorption Peak of Acetylferrocene. Molecules 2005, 10, 457-474. https://doi.org/10.3390/10020457
Alvarado Y, Peña-Suárez J, Cubillán N, Labarca P, Caldera-Luzardo J, López-Linares F. Influence of the Dielectric Medium on the Carbonyl Infrared Absorption Peak of Acetylferrocene. Molecules. 2005; 10(2):457-474. https://doi.org/10.3390/10020457
Chicago/Turabian StyleAlvarado, Y., J. Peña-Suárez, N. Cubillán, P. Labarca, J. Caldera-Luzardo, and F. López-Linares. 2005. "Influence of the Dielectric Medium on the Carbonyl Infrared Absorption Peak of Acetylferrocene" Molecules 10, no. 2: 457-474. https://doi.org/10.3390/10020457
APA StyleAlvarado, Y., Peña-Suárez, J., Cubillán, N., Labarca, P., Caldera-Luzardo, J., & López-Linares, F. (2005). Influence of the Dielectric Medium on the Carbonyl Infrared Absorption Peak of Acetylferrocene. Molecules, 10(2), 457-474. https://doi.org/10.3390/10020457




