Introduction
Homo and heterocycles were studied as models of fluorescers, organic conducting polymers or nonlinear optical (NLO) materials. New fluorescers contain heteroaromatic components. Some heterocycles recur often in industrial fluorescers. They do not fluoresce themselves, but have a fluorescence enhancing effect when coupled to conjugated systems. Reiser
et al. measured the absorption and emission spectra, and fluorescence yields of aromatic benzoxazole derivatives [
1]. Lippert
et al. reviewed the photophysics of internal twisting [
2]. Dey and Dogra measured and calculated the solvatochromism and prototropism in 2-(aminophenyl)benzothiazoles [
3]. Catalán
et al. studied the role of the torsion of the phenyl moiety in the mechanism of stimulated ultraviolet light generation in 2-phenylbenzazoles [
4]. Levitus
et al. performed photophysical measurements and semiempirical calculations with 1,4-bis(phenylethynyl)benzene [
5]. Organic conducting polymers have a highly anisotropic quasi-one-dimensional (quasi-1D) structure similar to that of charge-transfer (CT) salts [
6]. In the conducting state, both materials are ionic. In CT complexes conductivity is greater along the stacking direction, while in conducting polymers conductivity is higher along the chain direction. In these polymers, the chainlike structure leads to strong coupling of the electronic states to conformational excitations peculiar to 1D systems. The relatively weak interchain binding allows diffusion of dopant molecules into the structure, while the strong intrachain C–C bonds maintain the integrity of the polymer. The modulation of the electronic properties of conjugated polymers was studied through design of polymer backbone [
7].
The search for NLO organic materials with large values of the second hyperpolarizability (
γ) attracted interest from the experimental and theoretical points of view [
8,
9]. Morley
et al. calculated the first hyperpolaizability (
β) of S-heteromolecules [
10]. Zhao
et al. computed
γ for modified benzothiazoles, benzoxazoles and benzimidazoles [
11]. Meyers
et al. calculated the geometries and electronic and NLO properties of CT molecules based on the 2-methylene-2
H-pyrrole repeating unit [
12]. Li
et al. computed structure–performance characteristics for
β and
γ of
π-conjugated organic chromophores with the Pariser–Parr–Pople model [
13]. Yeates
et al. analyzed (X-ray) and calculated 2-(2-benzothiazolyl)-1-(2-thienyl)ethene as a model for high
γ [
14]. Gao
et al. studied the effect of conjugated length on the computed
β of organic molecules [
15]. Tomonari
et al. calculated the simplified sum-over-states and missing-orbital analysis on
β and
γ of benzene derivatives [
16]. Glaser and Chen computed asymmetrization effects on structures of dipolar donor–acceptor-substituted molecular organic NLO materials [
17]. Raptis
et al. calculated the polarizability (
α),
β and
γ of polysulfanes [
18]. Rao and Bhanuprakash computed donor and acceptor organic molecules separated by a saturated C–C
σ bond, which show large
β [
19]. Nakano
et al. calculated
γ of tetrathiapentalene and tetrathiafulvalene [
20]. Cheng
et al. computed
α and
β of H-silsesquioxanes [
21]. Levitus
et al. analyzed and calculated the photophysics of 1,4-bis(phenylethynyl)benzene [
22] and 1,4-diethynyl- 2-fluorobenzene [
23] to demarcate the effects of chromophore aggregation and planarization in poly(phenyleneethynylene)s. Öberg
et al. computed
β and
γ of organic compounds [
24].
Organic electronic materials are conjugated solids where both optical absorption and charge transport are dominated by partly delocalized
π and
π* orbitals [
25]. Organic photovoltaic materials differ from inorganic semiconductors in the following important respects. (1) Photogenerated excitations (
excitons) are strongly bound and do not spontaneously dissociate into charge pairs. This means that carrier generation does not necessarily result for the absorption of light. (2) Charge transport proceeds by
hopping between localized states, rather than transport within a band, and mobilities are low. (3) The spectral range of optical absorption is relatively narrow compared to the solar spectrum. (4) Absorption coefficients are high so that high optical densities can be achieved, at peak wavelength, with films less than 100nm thick. (5) Many materials are susceptible to degradation in the presence of oxygen or water. (6) As 1D semiconductors, their electronic and optical properties can be highly anisotropic. These properties impose some constraints on organic photovoltaic devices. (1) A strong driving force such as an electric field should be present to break up the photogenerated excitons. (2) Low charge carrier mobilities limit the useful thickness of devices. (3) Limited light absorption across the solar spectrum limits the photocurrent. (4) Very thin devices mean interference effects can be important. (5) Photocurrent is sensitive to temperature through hopping transport.
In earlier publications,
α of benzothiazole (A)–benzobisthiazole (B) A–B
n–A (
n≤13) oligomers was calculated and extrapolated to
n→∞ [
26]. Torsional effects were analyzed [
27,
28]. CT indices were brought to the calculation of the dipole moment
μ of hydrocarbons [
29]. The model was extended to heteroatoms [
30]. An index inspired by plastic evolution improved the results [
31,
32]. The method was applied to the valence-isoelectronic series of benzene and styrene (2–4 molecules) [
33,
34]. This study presents a reparametrization of the method for
sp3-heteromolecules. The next section introduces CT indices. Following that, the correction for
sp3-heteromolecules is presented. Next, the results are discussed. The last section summarizes the conclusions.
Topological Charge-Transfer Indices
The most important matrices that delineate the labelled chemical graph are the
adjacency (
A) [
35] and the
distance (
D)
matrices, wherein
Dij=
lij if
i=
j, “0” otherwise;
lij is the shortest edge count between vertices
i and
j [
36]. In
A,
Aij=1 if vertices
i and
j are adjacent, “0” otherwise. The
D[-2] matrix is the matrix whose elements are the squares of the reciprocal distances
Dij-2. The intermediate matrix
M is defined as the matrix product of
A by
D[-2]:
The
charge-transfer matrix C is defined as
C =
M –
MT, where
MT is the transpose of
M [
37]. By agreement,
Cii=
Mii. For
i≠
j, the
Cij terms represent a measure of the intramolecular
net charge transferred from atom
j to
i. The
topological CT
indices Gk are described as the sum, in absolute value, of the
Cij terms defined for the vertices
i,j placed at a topological distance
Dij equal to
k
where
N is the number of vertices in the graph,
Dij are the entries of the
D matrix, and
δ is the Kronecker
δ function, being
δ=1 for
i=
j and
δ=0 for
i≠
j.
Gk represents the sum of all the
Cij terms, for every pair of vertices
i and
j at topological distance
k. Other topological CT index,
Jk, I defined as:
This index represents the mean value of the CT for each edge, since the number of edges for acyclic compounds is N–1.
The
algebraic semisum CT
index μalg is defined as
where
Ce is the
Cij index for vertices
i and
j connected by edge
e [
29]. The sum extends for all pairs of adjacent vertices in the molecular graph and
μalg is a graph invariant. An edge-to-edge analysis of
μ suggests that each edge dipole moment
μe connecting vertices
i and
j can be evaluated from the corresponding edge
Ce index as
Each edge dipole can be associated with a vector
μe in space. This vector has magnitude |
μe|, lies in the edge
e connecting vertices
i and
j, and its direction is from
j to
i. The molecular dipole moment vector
μ results the vector sum of the edge dipole moments as
summed for all the
m edges in the molecular graph. The
vector semisum CT
indexμvec is defined as the module of
μ:
and
μvec is a graph invariant.
When heteroatoms are present, some way of discriminating atoms of different kinds needs to be considered [
38]. In valence CT indices terms, the presence of each heteroatom is taken into account by introducing its electronegativity value in the corresponding entry of the main diagonal of the adjacency matrix
A. For each heteroatom
X, its entry
Aii is redefined as
to give the
valence adjacency AV matrix where
χX and
χC are the electronegativities of heteroatom
X and carbon, respectively, in Pauling units. Notice that the subtractive term keeps
AiiV=0 for the C atom (Equation 5). Moreover, the multiplicative factor reproduces
AiiV=2.2 for O, which was taken as standard. From the valence
AV,
MV and
CV matrices,
μalgV,
μvecV and topological CT indices
GkV and
JkV can be calculated by following the former procedure with the
AV matrix. The
CiiV,
GkV,
JkV,
μalgV and
μvecV descriptors are graph invariants. The main difference between
μvec and
μvecV is that
μvec is sensitive only to the
steric effect of the heteroatoms, while
μvecV is sensitive to both electronic and steric effects.
Correction for sp3-Heteroatom-Containing Compounds
Kubinyi showed that the poor hydrogen-bond-formation capacity of the
sp3-oxygen atoms that are directly linked to an
sp2-carbon atom (like in esters, aromatic ethers and furans) is also reflected by a significant decrease of their polarity (MedChem database 1-octanol–water partition coefficient,
P) in going from aliphatic to araliphatic and to aromatic ethers R–O–R’ (
Table 1) [
39]. Therefore, in this study it is suggested to halve the factor in Equation (5) as
for
sp3-
X (–
X–),
X = O.
Table 1 gives the molecular dipole moments
μ for hydrocarbons and ethers calculated with different charge-transfer indices. The polarity decrease is also reflected by a significant decrease of the differential dipole moment (
μether –
μhydrocarbon) denoted as Δ(O – CH
2). The Δ(O – CH
2)
μexperiment decreases with minus Δ(O – CH
2) log
P. The Δ(O – CH
2)
μvec does not show this diminution, while Δ(O – CH
2)
μvecV gives very great values. However, Δ(O – CH
2)
μvecV,corrected is of the same order of magnitude as both
μexperiment and
μMOPAC-AM1 references. As similar effects were shown for
sp3-Si, P, Ge, As, Sn, Sb, Pb and Bi heteromolecules [
34], Equation (6) is used for all
sp3-
X (–
X–),
X = O, Si, P, S, Ge, As, Se, Sn, Sb, Te, Pb, Bi, Po.
Table 1.
Molecular dipole moment (in D) for hydrocarbons and ethers with charge indices.
Table 1.
Molecular dipole moment (in D) for hydrocarbons and ethers with charge indices.
| Method | Compound | X = –CH2– | X = –O– | Δ(O – CH2) | Δ(O–CH2) log Pa |
|---|
| Vector semisum | Et–X–Et | 0.407 | 0.436 | 0.029 | – |
| | Phe–X–Et | 0.739 | 0.659 | -0.080 | – |
| | Phe–X–Phe | 0.427 | 0.333 | -0.094 | – |
| Valence vector semisum | Et–X–Et | 0.407 | 2.854 | 2.447 | – |
| | Phe–X–Et | 0.739 | 2.621 | 1.882 | – |
| | Phe–X–Phe | 0.427 | 2.742 | 2.315 | – |
| Corrected valence vectorsemisum | Et–X–Et | 0.407 | 1.209 | 0.802 | – |
| | Phe–X–Et | 0.739 | 1.211 | 0.472 | – |
| | Phe–X–Phe | 0.427 | 1.204 | 0.777 | – |
| Experimentb | Et–X–Et | 0.087c | 1.170 | 1.083 | -2.50 |
| | Phe–X–Et | 0.350 | 1.410 | 1.060 | -1.21 |
| | Phe–X–Phe | 0.260 | 1.150 | 0.890 | 0.07 |
| AM1 | Et–X–Et | 0.006 | 1.246 | 1.240 | – |
| | Phe–X–Et | 0.257 | 1.264 | 1.007 | – |
| | Phe–X–Phe | 0.080 | 1.252 | 1.172 | – |
Calculation Results and Discussion
The molecular CT indices
Gk,
Jk,
GkV and
JkV (with
k<6) are listed in
Table 2 for the valence-isoelectronic series of benzene (C
6H
6). As one might have expected, all the molecules show the same set of
Gk (and, consequently,
Jk) values. For instance,
G1 is related to the degree of branching and
G2 is related to the number of unsaturations in the molecule, which are constant throughout the series. On the other hand,
GkV, which also depends on the electronegativity of the heteroatom through Equations (5–6), is influenced, in general, by the substitution.
In particular, G1V is related to the absolute differential electronegativity of the heteroatom |χX–χC| in the molecule. However, an exception occurs: G2V (and, as a result, J2V) is equal throughout the series. C5H6Si, C5H6Ge, C5H6Sn and C5H6Pb show the same results for all GkV and JkV. This is due to the fact that Si, Ge, Sn and Pb have the same electonegativity (χSi=χGe=χSn=χPb=1.8). The same happens for C5H5Sb and C5H5Bi (χSb=χBi=1.9). Although in pyridine and C5H5As, the N and As atoms have the same absolute differential electronegativity |χN–χC|=|χAs–χC|=0.5, pyridine is calculated by Equation (5) while C5H5As, by Equation (6), and so G2V(pyridine) = 2G2V(C5H5As).
Table 2.
Charge indices up to the fifth order for the valence-isoelectronic series of benzene.a
| Molecules | N | G1 | G2 | J1 | J2 |
|---|
| all molecules | 6 | 0.0000 | 5.3333 | 0.0000 | 1.0667 |
| Molecules | G1V | G3V | J1V | J3V |
|---|
| benzene | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| pyridine | 2.2000 | 0.1222 | 0.4400 | 0.0244 |
| C5SiH6 | 1.5400 | 0.0856 | 0.3080 | 0.0171 |
| C5PH5 | 0.8800 | 0.0489 | 0.1760 | 0.0098 |
| C5GeH6 | 1.5400 | 0.0856 | 0.3080 | 0.0171 |
| C5AsH5 | 1.1000 | 0.0611 | 0.2200 | 0.0122 |
| C5SnH6 | 1.5400 | 0.0856 | 0.3080 | 0.0171 |
| C5SbH5 | 1.3200 | 0.0733 | 0.2640 | 0.0147 |
| C5PbH6 | 1.5400 | 0.0856 | 0.3080 | 0.0171 |
| C5BiH5 | 1.3200 | 0.0733 | 0.2640 | 0.0147 |
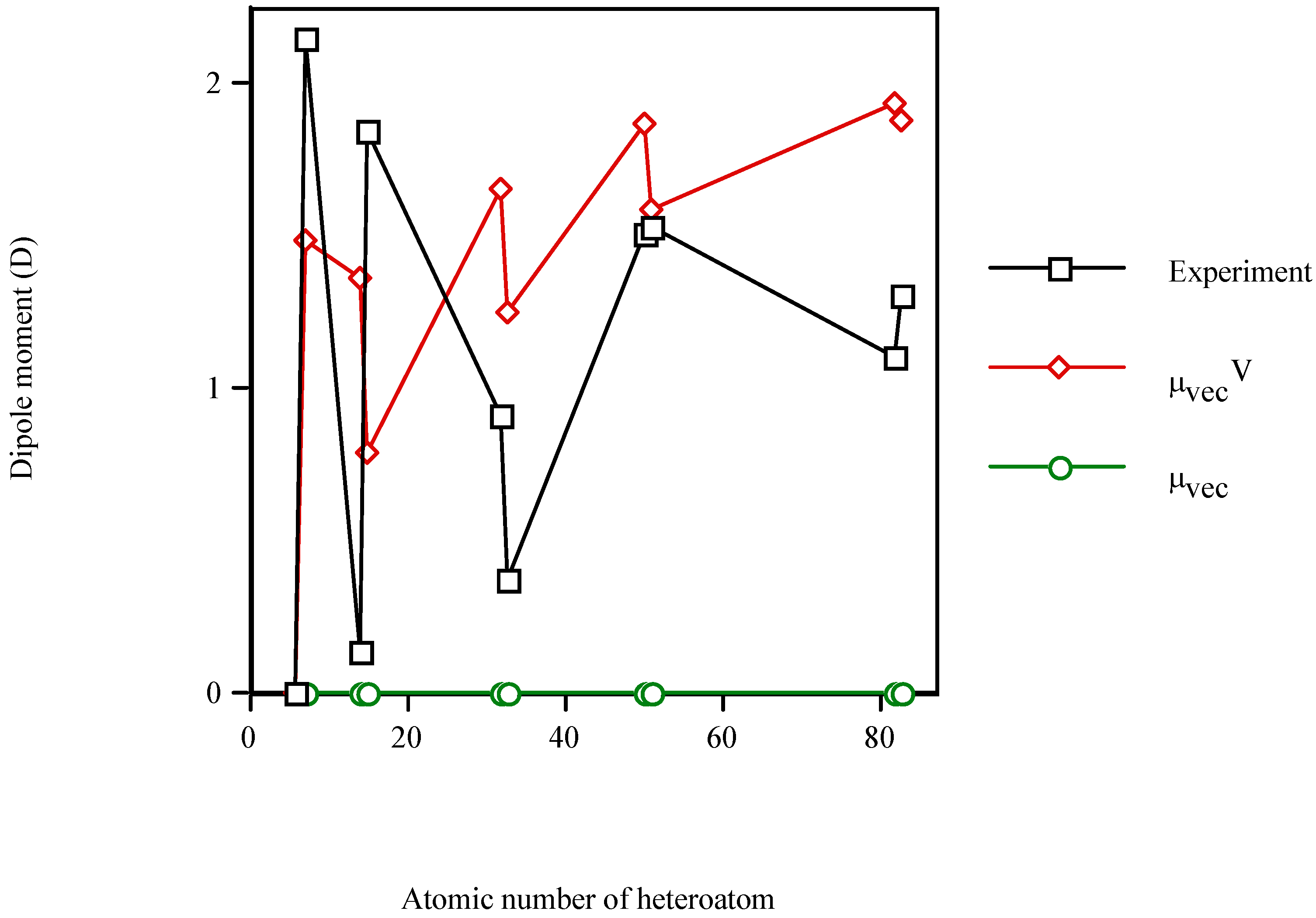
Figure 1 illustrates the increment in the dipole moment of benzene in the presence of the heteroatom. The calculated
μvecV is of the same order of magnitude as
μexperiment, while the calculated
μvec=0 remains constant. Since
μvec is sensitive to the steric effect but not to the electronic effect of the heteroatom, it is clear that the electronic effect (
μvecV) dominates over the steric one (
μvec). In particular, the best results are obtained for the fourth long-period (Sn–Sb) and for the group-V heteromolecules.
Figure 1.
Dipole moment of the valence-isolectronic series of benzene vs. the atomic number of the heteroatom. Experimental data from Reference 40. Points with Z = 14, 15, 32, 33, 50, 51, 82 and 83 are AM1 calculations.
Figure 1.
Dipole moment of the valence-isolectronic series of benzene vs. the atomic number of the heteroatom. Experimental data from Reference 40. Points with Z = 14, 15, 32, 33, 50, 51, 82 and 83 are AM1 calculations.
Table 3.
Charge indices up to the fifth order for the valence-isoelectronic series of styrene.
| Molecule | N | G1 | G2 | G3 | G4 | G5 |
|---|
| all molecules | 8 | 1.0000 | 6.8889 | 0.4375 | 0.2133 | 0.0625 |
| Molecules | J1 | J2 | J3 | J4 | J5 |
|---|
| all molecules | 0.1429 | 0.9841 | 0.0625 | 0.0305 | 0.0089 |
| Molecules | G1V | G2V | G3V | G4V | G5V |
|---|
| styrene | 1.0000 | 6.8889 | 0.4375 | 0.2133 | 0.0625 |
| benzaldimine | 1.6000 | 7.1639 | 0.5569 | 0.2708 | 0.0185 |
| benzaldehyde | 2.7000 | 7.4389 | 0.8014 | 0.4083 | 0.0255 |
| C6H5–CH=SiH2 | 2.5400 | 6.5039 | 0.5297 | 0.3436 | 0.1241 |
| C6H5–CH=PH | 1.8800 | 6.6689 | 0.4375 | 0.2611 | 0.0977 |
| thiobenzaldehyde | 1.0000 | 6.8889 | 0.4375 | 0.2133 | 0.0625 |
| C6H5–CH=GeH2 | 2.5400 | 6.5039 | 0.5297 | 0.3436 | 0.1241 |
| C6H5–CH=AsH | 2.1000 | 6.6139 | 0.4375 | 0.2886 | 0.1065 |
| C6H5–CH=Se | 1.2200 | 6.8339 | 0.4375 | 0.2133 | 0.0713 |
| C6H5–CH=SnH2 | 2.5400 | 6.5039 | 0.5297 | 0.3436 | 0.1241 |
| C6H5–CH=SbH | 2.3200 | 6.5589 | 0.4808 | 0.3161 | 0.1153 |
| C6H5–CH=Te | 1.8800 | 6.6689 | 0.4375 | 0.2611 | 0.0977 |
| C6H5–CH=PbH2 | 2.5400 | 6.5039 | 0.5297 | 0.3436 | 0.1241 |
| C6H5–CH=BiH | 2.3200 | 6.5589 | 0.4808 | 0.3161 | 0.1153 |
| C6H5–CH=Po | 2.1000 | 6.6139 | 0.4375 | 0.2886 | 0.1065 |
| Molecules | J1V | J2V | J3V | J4V | J5V |
|---|
| styrene | 0.1429 | 0.9841 | 0.0625 | 0.0305 | 0.0089 |
| benzaldimine | 0.2286 | 1.0234 | 0.0796 | 0.0387 | 0.0026 |
| benzaldehyde | 0.3857 | 1.0627 | 0.1145 | 0.0583 | 0.0036 |
| C6H5–CH=SiH2 | 0.3629 | 0.9291 | 0.0757 | 0.0491 | 0.0177 |
| C6H5–CH=PH | 0.2686 | 0.9527 | 0.0625 | 0.0373 | 0.0140 |
| thiobenzaldehyde | 0.1429 | 0.9841 | 0.0625 | 0.0305 | 0.0089 |
| C6H5–CH=GeH2 | 0.3629 | 0.9291 | 0.0757 | 0.0491 | 0.0177 |
| C6H5–CH=AsH | 0.3000 | 0.9448 | 0.0625 | 0.0412 | 0.0152 |
| C6H5–CH=Se | 0.1743 | 0.9763 | 0.0625 | 0.0305 | 0.0102 |
| C6H5–CH=SnH2 | 0.3629 | 0.9291 | 0.0757 | 0.0491 | 0.0177 |
| C6H5–CH=SbH | 0.3314 | 0.9370 | 0.0687 | 0.0452 | 0.0165 |
| C6H5–CH=Te | 0.2686 | 0.9527 | 0.0625 | 0.0373 | 0.0140 |
| C6H5–CH=PbH2 | 0.3629 | 0.9291 | 0.0757 | 0.0491 | 0.0177 |
| C6H5–CH=BiH | 0.3314 | 0.9370 | 0.0687 | 0.0452 | 0.0165 |
| C6H5–CH=Po | 0.3000 | 0.9448 | 0.0625 | 0.0412 | 0.0152 |
The molecular CT indices
Gk,
Jk,
GkV and
GkV for the valence-isoelectronic series of styrene (C
6H
5–CH=CH
2) are collected in
Table 3. As expected, all the molecules show the same set of
Gk and
Jk values. However,
GkV are influenced by the atomic number of the heteroatom. In particular, the results for thiobenzaldehyde are equal to those for styrene. This is because the electronegativity for the S atom has been taken equal to that of C (
χS=
χC=2.5). The same happens for the Si/Ge/Sn/Pb (
χSi=
χGe=
χSn=
χPb=1.8), P/Te (
χP=
χTe=2.1), As/Po (
χAs=
χPo=2.0) and Sb/Bi compounds (
χSb=
χBi=1.9).
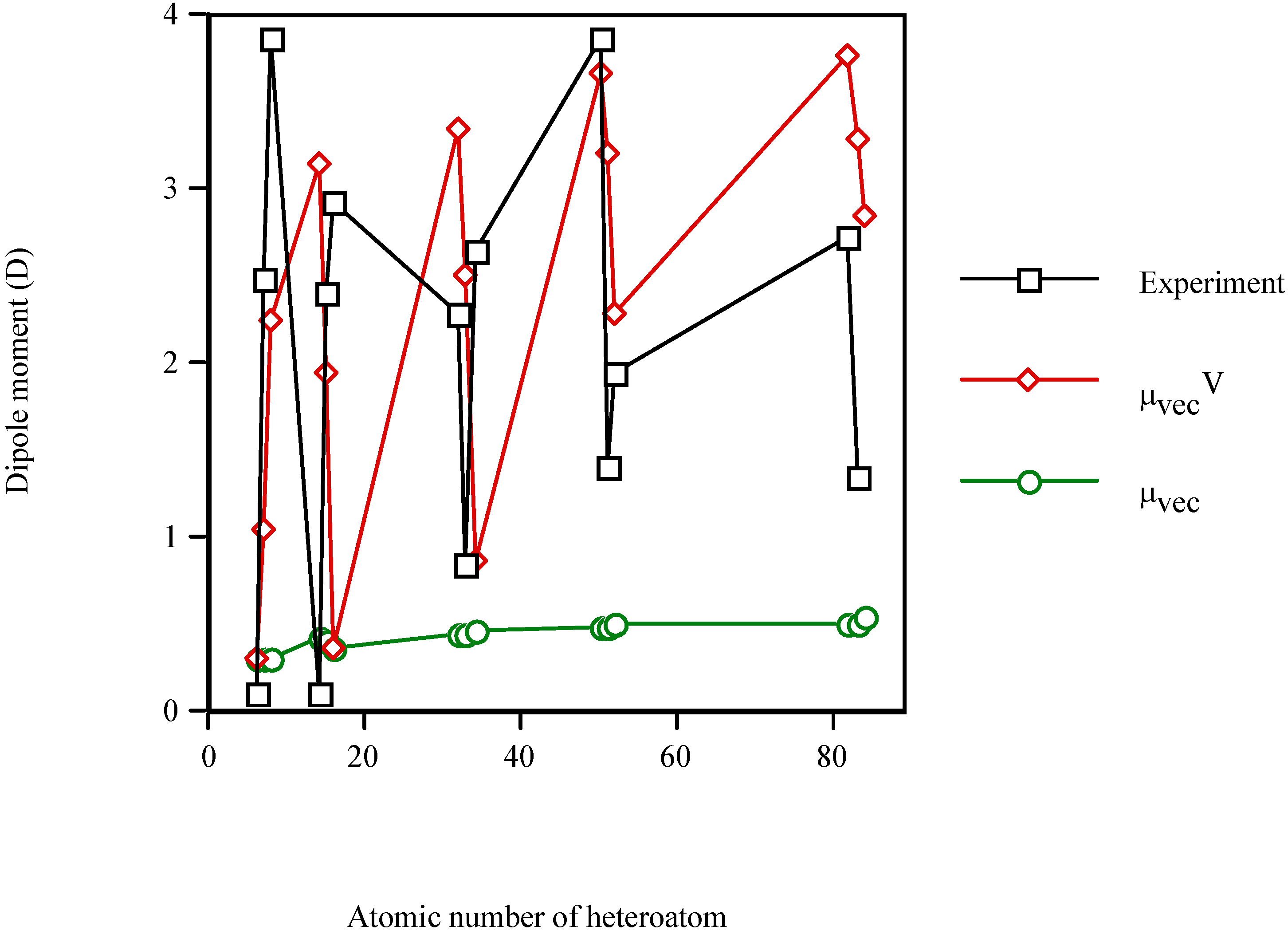
Figure 2 shows the increase in the dipole moment of the valence-isoelectronic series of styrene when the heteroatom is present. Again,
μexperiment and
μvecV vary in a similar fashion, while
μvec remains almost constant (
μvec~0.43D for the three groups IV–VI). The electronic effect of the heteroatom (
μvecV) dominates, in general, over the steric one (
μvec). In particular, for thiobenzaldehyde (
Z=16) the result of
μvecV =
μvec (because
χS=
χC) should be taken with care. It is an artefact of the model for S-heteromolecules. Furthermore, the best results are obtained, in general, for the fourth long-period (Sn–Te) and for the group-VI heteromolecules.
Figure 2.
Dipole moment of the valence-isolectronic series of styrene vs. the atomic number of the heteroatom. Point with Z = 6 from Reference 42; Z = 7, 14–16, 32–34, 51 and 52 are computed with AM1; Z = 8 from Reference 43; Z = 50, 82 and 83 are PM3 calculations.
Figure 2.
Dipole moment of the valence-isolectronic series of styrene vs. the atomic number of the heteroatom. Point with Z = 6 from Reference 42; Z = 7, 14–16, 32–34, 51 and 52 are computed with AM1; Z = 8 from Reference 43; Z = 50, 82 and 83 are PM3 calculations.
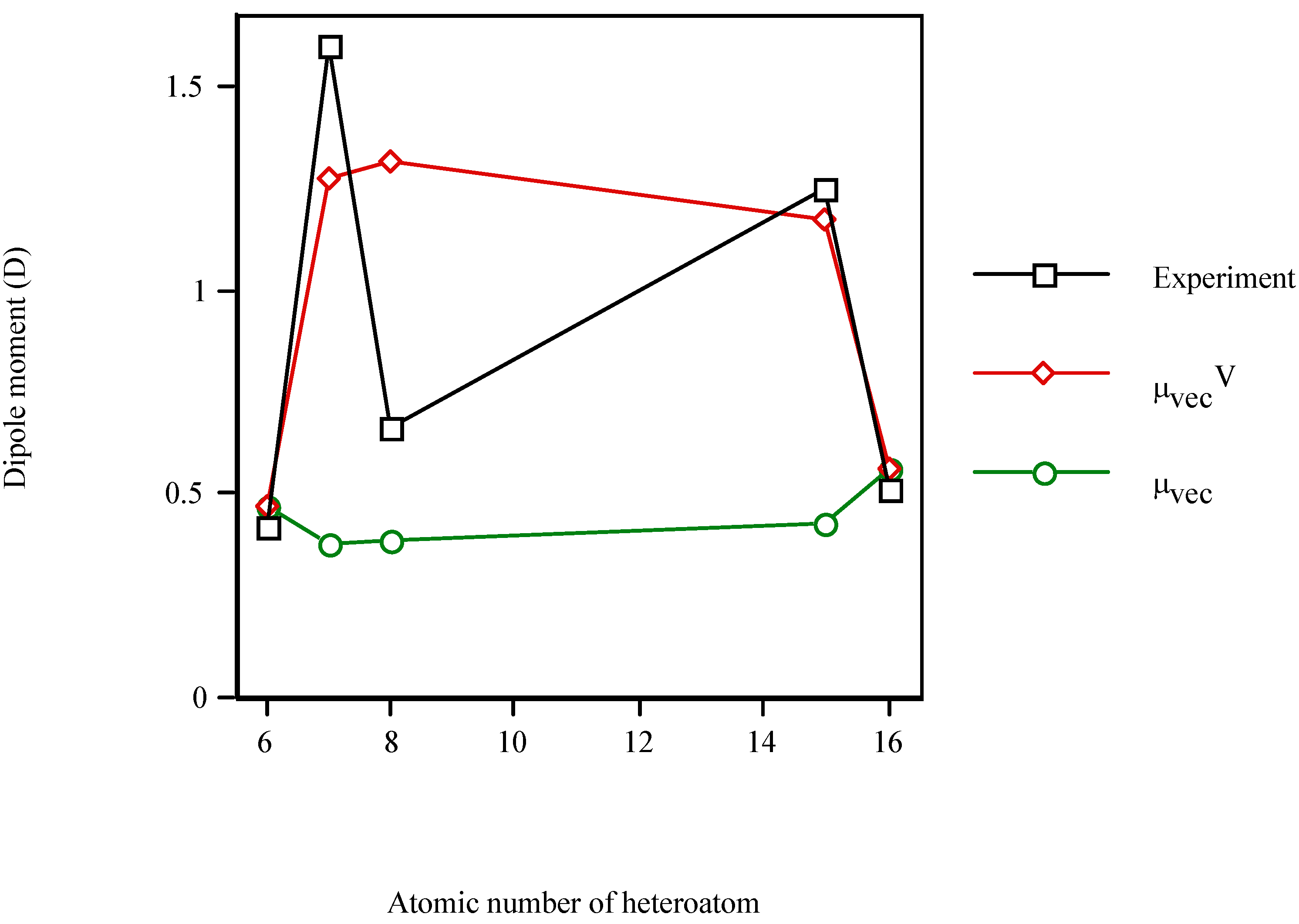
In order to test the model for other S-containing heterocycle,
Figure 3 displays the increase in the dipole moment of the valence-isoelectronic series of cyclopentadiene when the heteroatom is present. Once more,
μexperiment and
μvecV vary in a similar fashion while
μvec remains almost constant (
μvec~0.45D). The electronic effect of the heteroatom (
μvecV) dominates over the steric one (
μvec). In particular, for thiophene (
Z=16)
μvecV =
μvec (because
χS=
χC). However, the
μvecV relative error for thiophene (10%) is even smaller than for cyclopentadiene (12%).
Figure 3.
Dipole moment of the valence-isolectronic series of cyclopentadiene vs. the atomic number of the heteroatom. Point with Z = 15 is AM1 calculation.
Figure 3.
Dipole moment of the valence-isolectronic series of cyclopentadiene vs. the atomic number of the heteroatom. Point with Z = 15 is AM1 calculation.